Revision Notes on Work, Energy and Power for NEET 2024

Work

When an object is compelled to move from one spot to another, work is accomplished. Work is equal to force multiplied by displacement. Determining how far a body travels is termed displacement. 

• If the force F and the displacement d are both in the same direction, the work W can be calculated using the formula, $W{\text{ }} = F \times d$

• Work is equal to the product of displacement and force. In SI (international system) units, unit of the force is Newton (N), and the distance & displacement unit is the metre (m)

• A Newton-metre can thus be used to express the work unit. It's also known as a Joule, or J. Because the Newton is a composite unit, a Joule is also comparable to it. $1{\text{J}} = 1{\text{N}} \cdot {\text{m}} = 1{\text{kg}} \cdot \dfrac{{{{\text{m}}^2}}}{{{{\text{s}}^2}}}$

• The equation $W{\text{ }} = F \times d$ depends on the same direction as force and displacement.

• There are a variety of situations where, for example, someone pushing on a box near the floor is moving in a specific direction.

• Although the box's resulting direction is forward, a portion of the force is directed down. In a case like this, only the force along the route of the displacement contributes to the job being done. If we treat force and displacement as vectors, then we can find the work by using the dot product (also known as the scalar product).

$W = \vec F \cdot \vec d$

$W = Fd\cos \theta $

• In the above formula, θ is the angle between the force and displacement vectors, and F and d  are the magnitudes of the vectors.

• When work is performed against gravity, the amount of work performed equals the body's weight product plus the vertical distance lifted.

• Work done in lifting body = Weight of Body $ \times $ Vertical Distance

$W = mgh$ 

Where, W = Work Done 

M = Mass of body, g = acceleration due to gravity, 

h = Height through which the body is lifted

• The quantity of work is a scalar quantity. Joule is the SI unit of work, and erg is the CGS unit of work.

$\therefore 1$ Joule $ = {10^7}{\text{erg}}$

• Its dimensional formula is $\left[ {{\text{M}}{{\text{L}}^2}{{\text{T}}^{ - 2}}} \right]$.

• Work done by a force is zero, if

• Body is not displaced actually, i.e., $s = 0$.

• The body is shifted perpendicular to the force direction. i.e., $\theta  = {90^\circ }$.

• When the angle between F and s is acute, the work done by a force is positive.

• If the angle between F and s is obtuse, then the force's work is negative.

• The work done by a constant force is dependent only on the initial and final places, not on the actual path taken between them.

Work Done in Different Conditions:

Work done by a variable force is given by,

$W = \int {{F^{}}} ds$

It corresponds to the area underneath the force-displacement graph with the proper sign.

Energy

Energy is the ability of a body to perform work. Energy is a scalar quantity, meaning it has magnitude and no direction. The joule is the S.I unit, while the erg is the CGS unit. Its dimensional formula is as follows: 

$\left[ {M{L^3}{T^{ - 3}}} \right].$

Mechanical energy (kinetic and potential energy), chemical energy, light energy, heat energy, sound energy, nuclear energy, electric energy, and other types of energy exist.

Potential Energy

The ability to do work in a body because of its situation or setup or we can say a body's energy because of its position or shape change is called potential energy. For example, compressed string energy, gathered water energy at a height, spring energy in a watch, etc.

• A body's energy is called gravitational potential energy because of its position above the floor.

• A body's energy is called elastic potential energy due to changing its shape and size.

Kinetic Energy

An object's kinetic energy (K) is equal to the amount of work needed to accelerate the object from rest to speed (v) can be expressed as,

$W=\dfrac{1}{2}mv^2-0$

This relationship between kinetic energy and work is called the theorem of work-energy. An object's kinetic energy is a scalar value, which means it is not dependent on the direction in which the object moves.

• The kinetic energy value is always positive or zero.

• The kinetic energy unit is the same as the Joule (J) unit of work.

An object's kinetic energy can be associated with its mass and velocity with the formula,

$K = \dfrac{1}{2}m{v^2}$

If the force is in the same direction as the displacement of the object, this formula for kinetic energy can be discovered from the equation for work. This formula relies on the formula of kinematic.

$v_2^2 = v_1^2 + 2{a_x}\left( {x - {x_0}} \right)$

The position change $\left( {x - {x_0}} \right)$ is equivalent to the magnitude of the displacement, d. 

The formula can be rearranged for acceleration, a;

$a = \dfrac{{v_2^2 - v_1^2}}{{2d}}$

Force is equal to the mass of an object multiplied by its acceleration, so the force is, F = ma. 

• This force formula can be replaced by the work formula, $W{\text{ }} = F\times d$

$\therefore W = m\left( {\dfrac{{v_2^2 - v_1^2}}{{2d}}} \right)d$  

$\therefore W = \dfrac{1}{2}m\left( {v_2^2 - v_1^2} \right)$  

$\therefore W = \dfrac{1}{2}mv_2^2 - \dfrac{1}{2}mv_1^2$

• The work performed by force on an object is therefore equivalent to the shift in the kinetic energy of the object, 

$W = {K_2} - {K_1}$,$W{\text{ }} = \Delta K$.

The Greek uppercase letter ("delta") is used in this formula to mean "change in."  

• Work can be used to comprehend the energy of many objects experiencing forces. The work needed to extend a spring is one instance. If the object's displacement magnitude is marked x, and this represents the displacement away from a position of equilibrium $x = 0$, the force required to pull the object on the spring to a position x is,

            $F{\text{ }} = {\text{ }}kx$

• The expression of work done in extending the spring from position $x_1$ to $x_2$ is given as $W = \dfrac{1}{2}k{x_2}^2 - \dfrac{1}{2}k{x_1}^2$.

• The constant k in this equation is the spring constant, which is different for every spring. The spring constant has units Newton per metre, N/m. 

Power

Power is a measure of work rate. It is a measurement of how fast work is performed. For a quantity of work W performed in time t, the power performed is $P = \dfrac{W}{t}$.

• The Power unit is the Watt (W), which equals one Joule per second. 1 W = 1 J/s

• Power P can also be expressed as force F times velocity v. Since work is provided by force times displacement, $W{\text{ }} = {\text{ }}F \times d$, then we know that, $P = \dfrac{W}{t}$

              $\therefore P = \dfrac{{(Fd)}}{t}$

             $\therefore P = F\left( {\dfrac{d}{t}} \right)$

             $\therefore P = Fv$

• Power is a scalar quantity. Its SI unit is watt and its dimensional formula is $\left[ {{\text{M}}{{\text{L}}^2}{{\text{T}}^{ - 3}}} \right]$.

• Its other units are kilowatt and horsepower,

1 kilowatt $ = 1000$ watt

            1 horsepower $ = 746$ watt.

Spring Potential Energy

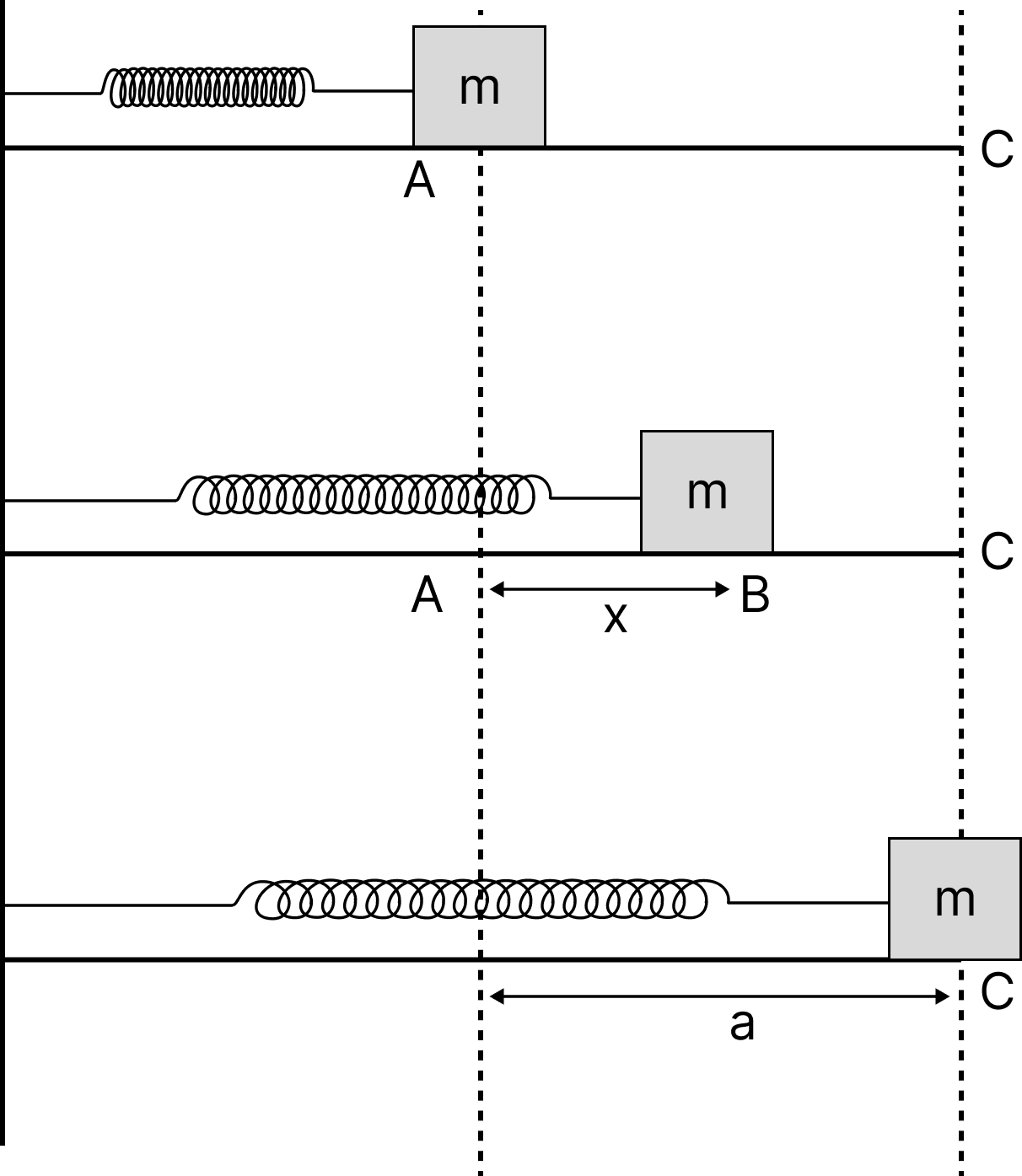
Consider a massless spring with a mass of $m$ attached to one end and linked to a stiff wall at the other. When we draw the mass in the direction of $\mathrm{C}$, the restoring force pointed at $\mathrm{A}$ is prepared in spring. We must exert effort to move the mass in opposition to this restoring force, and this effort is then stored as potential energy in the spring.

Let at any instant, mass $m$ be at $\mathrm{B}$ at a distance $x$ from $\mathrm{A}$. The restoring force at this instance is,

$\vec{F}_{r}=-k \vec{x}$

Therefore to keep the mass in equilibrium, we have to apply the force $\vec{F}_{a}$ equal and opposite to $-\vec{F}_{r}$. If we further displace the mass $m$ by

$\overrightarrow{d x}$, the amount of work done $d W$ for this displacement by applied force will be

$d W =\vec{F}_{\mathrm{a}} \cdot \vec{d} x=F_{\mathrm{a}} d x $

$=k x d x$

Spring Potential Energy

The total amount of work done to displace the mass $m$ from mean position $A$ to $C$ by applied force $\overrightarrow{F_{a}}$ is,

$W=\int_{A}^{\mathrm{c}} d W=\int_{0}^{a} k x d x=\left.\dfrac{1}{2} k x^{2}\right|_{0} ^{a}=\dfrac{1}{2} k a^{2}$

Potential energy is used to store the work done by applied force against restoring force.

$\therefore \quad W=P=\dfrac{1}{2} k a^{2}$

Collision

The collision of two objects occurs if they collide physically or if the path of one object is affected by force exerted by the other object.

There are mainly two types of collision:

1. Elastic Collision:  Collisions in which there is no loss of kinetic energy are called elastic collisions.

The following are the characteristics of elastic collisions:

• There is conservation of kinetic energy.

• The total amount of energy is conserved.

• Collisions involve conservative forces.

2. Inelastic Collision: We know that, inelastic collision is a collision in which there is a loss of kinetic energy. While momentum of the system is conserved in an inelastic collision, kinetic energy is not

Inelastic collisions have the following characteristics:

• There is no conservation of kinetic energy.

• Momentum is conserved.

• Total Energy is conserved.

• It is non-conservative or non-conservative at least in part.

Law of Conservation of Momentum in Collision

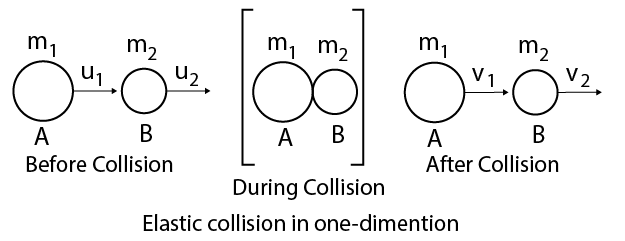
1. Particles of masses ${m_1}$ and ${m_2}$, proceed  with velocities ${u_1}$ and ${u_2}$ before collision and after collision with velocities ${v_1}$ and ${v_2}$, then from law of conservation of momentum.

${m_1}{u_1} + {m_2}{u_2} = {m_1}{v_1} + {m_2}{v_2}$

2. If an object of mass $m$ strikes horizontally a wall with velocity $v$ and bounces back with the same velocity, then the change in momentum$ = 2{\text{mv}}$.

Elastic Collision in One-Dimension:

• We know that, Consider two perfectly elastic objects $A$ and $B$ of masses ${m_1}$ and ${m_2}$ moving along the same straight line with velocities ${u_1}$, and ${u_2}$, respectively.

• If ${u_1} > {u_2}$ after some time, the two objects collide head-on and continue moving in the same direction with velocities ${v_1}$ and ${v_2}$, respectively. The two objects will separate after the collision, if ${v_2} > {v_1}$.

• The linear momentum is conserved in elastic collision, so

${m_1}{u_1} + {m_2}{u_2} = {m_1}{v_1} + {m_2}{v_2}$

Elastic Collision

• If, kinetic energy is also conserved in an elastic collision, so

$\dfrac{1}{2}{m_1}u_1^2 + \dfrac{1}{2}{m_2}u_2^2 = \dfrac{1}{2}{m_1}v_1^2 + \dfrac{1}{2}{m_2}v_2^2$

• Solving the above two equations, we get

${v_1} = \left( {\dfrac{{{m_1} - {m_2}}}{{{m_1} + {m_2}}}} \right){u_1} + \left( {\dfrac{{2{m_2}}}{{{m_1} + {m_2}}}} \right){u_2}$

${v_2} = \left( {\dfrac{{{m_2} - {m_1}}}{{{m_1} + {m_2}}}} \right){u_2} + \left( {\dfrac{{2{m_1}}}{{{m_1} + {m_2}}}} \right){u_1}$

Inelastic Collision in One-Dimension

If we consider an object of mass ${m_1}$ moving with velocity ${u_1}$ collides head-on with another object of mass ${m_2}$ at rest. After the collision, the two objects move together with a common velocity$v$.

• If the linear momentum is conserved, so

${m_1}{u_1} + {m_2} \times 0{\text{ }} = \left( {{m_1} + {m_2}} \right)v$

$v = \dfrac{{{m_1}}}{{\left( {{m_1} + {m_2}} \right)}}{u_1}$

• The loss in kinetic energy on collision is

• $\Delta K{\text{ }} = {K_i} - {K_f}= \dfrac{1}{2}{m_1}u_1^2 - \dfrac{1}{2}\left( {{m_1} + {m_2}} \right){v^2}$

• After putting the value of $v$ in the above equation, we get

$\Delta K = \dfrac{1}{2}\dfrac{{{m_1}{m_2}}}{{\left( {{m_1} + {m_2}} \right)}}u_1^2$

Elastic Collision in Two-Dimensions

• If a particle of mass ${m_1}$ moving along $X$-axis with velocity ${u_1}$ collides with another particle of mass ${m_2}$ at rest.

• Then the collision, let the two particles move with velocities ${v_1}$ and ${v_2}$, making angles ${\theta _1}$ and ${\theta _2}$ with $X$-axis.

Elastic Collision in 2d

• If the collision, the rectangular components of the momentum of ${m_1}$ are as below

• ${m_1}{v_1}\cos {\theta _1}$, along +ve $X$-axis

• ${m_1}{v_1}\sin {\theta _1}$, along + ve $Y$-axis

• Then  the collision, the rectangular components of the momentum of ${m_2}$ are as below

• ${m_2}{v_2}\cos {\theta _2}$, along + ve $X$-axis

• ${m_2}{v_2}\sin {\theta _2}$, along + ve $Y$-axis

• Here applying the principle of conservation of momentum along $X$-axis,

${m_1}{u_1} = {m_1}{v_1}\cos {\theta _1} + {m_2}{v_2}\cos {\theta _2} \ldots {\text{ (i) }}$

The initial momentum of ${m_1}$ or ${m_2}$ along $Y$-axis is zero.

• Applying the principle of conservation of momentum along $Y$-axis,

$0 = {m_1}{v_1}\sin {\theta _1} - {m_2}{v_2}\sin {\theta _2} \ldots {\text{ (ii) }}$

• Then the ${\text{KE}}$ is conserved in an elastic collision. So, 

$\quad \dfrac{1}{2}{m_1}u_1^2 = \dfrac{1}{2}{m_1}v_1^2 + \dfrac{1}{2}{m_2}v_2^2$

• The four unknown quantities ${v_1},{v_2},{\theta _1}$ and ${\theta _2}$ can be calculated using the three Eqs. (i), (ii) and (iii). By measuring one of the four unknowns, say ${\theta _1}$ experimentally the values of the other three unknowns can be solved.

Coefficient of Restitution (e)

The ratio of relative velocity of particles after and before collision is known as coefficient of restitution.

$e = \dfrac{{{\text{ Relative velocity of separation (after collision) }}}}{{{\text{ Relative velocity of approach (before collision) }}}}$ $ = \dfrac{{{v_2} - {v_1}}}{{{u_1} - {u_2}}}$

• For a perfectly elastic collision, $e = 1$.

• For an inelastic collision, $e = 0$.

Important Formula Chart:

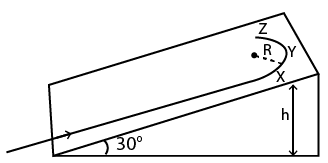
Example 1: A student skates up a ramp that makes an angle 30 degree with the horizontal. He/she starts (as shown in the figure) at the bottom of the ramp with speed v0 and wants to turn around over a semicircular path xyz of radius R during which he/she reaches a maximum height h (at point y) from the ground as shown in the figure. Assume that the energy loss is negligible and the force required for this turn at the highest point is provided by his/her weight only. Then (g is the acceleration due to gravity)

Ramp

(A) $v_{0}^{2}-2 g h=\dfrac{1}{2} g R$

(B) $v_{0}^{2}-2 g h=\dfrac{\sqrt{3}}{2} g R$

(C) the centripetal force required at points $x$ and $z$ is zero

(D) the centripetal force required is maximum at points $x$ and $z$

Answer: B, D

Hint: Centripetal force refers to any force that induces a shift in velocity direction toward the centre of a circular motion. The centripetal force is produced by the component of the force that is perpendicular to the velocity.

Complete Solution: Apply energy conservation,

$\dfrac{1}{2} m v_{0}^{2}=m g h+\dfrac{1}{2} m v^{2} $

$\dfrac{1}{2} m v^{2}=\dfrac{1}{2} m v_{0}^{2}-m g h \ldots . \text { (i) }$

At top point $y$, the centripetal force provided by the component of mg,

mg $\sin \theta=$ centripetal force $=\dfrac{m v^{2}}{R}$

$\dfrac{m v^{2}}{R}=m g \sin \theta$

Putting this value in Eq. (i), we get

$\dfrac{m g R \sin \theta}{2}=\dfrac{1}{2} m v_{0}^{2}-m g h $

$\dfrac{m g R}{2} \dfrac{1}{2}=\dfrac{1}{2} m v_{0}^{2}-m g h$

$\dfrac{g R}{2}=v_{0}^{2}-2 g h$

At point $x$ and a circular path, the points are at the same height but less than $h$. So the velocity is more than point $y$

So the required centripetal force $=\dfrac{m v^{2}}{r}$ is more.

Example 2: A body of mass 'm' dropped from a height 'h' reaches the ground with a speed of $0.8 \sqrt{g h}$. The value of work done by the air-friction is :

(A) $-0.68 \mathrm{mgh}$

(B) mgh

(C) $1.64 \mathrm{mgh}$

(D) $0.64 \mathrm{mgh}$

Answer: A

Hint: Work is done when a force works on an object, causing it to move. To compute the amount of labour, three quantities must be known. Force, displacement, and the angle between the force and displacement are the three quantities.

Complete Solution: Given, the mass of the body $=m$

The height from which the body dropped $=\mathrm{h}$

The speed of the body when reached the ground, $v_{f}=0.8 \sqrt{g h}$

Initial velocity of the body, $v=0 \mathrm{~m} / \mathrm{s}$

Using the work-energy theorem,

Work done by gravity + Work done by air-friction = Final kinetic energy - Initial kinetic energy.

$W_{m g}+W_{a i r-\text { friction }}=\dfrac{1}{2} m v_{f}^{2}-\dfrac{1}{2} m v_{i}^{2}$

Here, work done by gravity = mgh

$\Rightarrow m g h+W_{a i r-\text { friction }}=\dfrac{1}{2} m(0.8 \sqrt{g h})^{2}-\dfrac{1}{2} m(0)^{2} $

$\Rightarrow W_{a i r-\text { friction }}=\dfrac{0.64 m g h}{2}-m g h $

$\Rightarrow 0.32 m g h-m g h=-0.68 m g h$

The value of the work done by the air friction is $-0.68 \mathrm{mgh}$.

Common Errors or Mistakes that Should be Avoided by the Students Keeping the Exam Point of View:

• Students forget to write the working formula.

• Students also write improper units without checking their compatibility.

• Calculation errors when doing problems

•  Students forget to put in the correct data they used in the working formula, which is used by teachers to check how effective the students' learning is.

• A  law stated by someone cannot be restructured, it should be reiterated like how it was stated.

• While drawing a graph, students forget to state the variables of the graph and just plot the graph.

• mechanics students don't understand how to use the formula of kinetic energy, work-energy theorem 

Importance of Class 11 Physics NEET Work Energy and Power

The chapter of Work, Energy and Power explains how forces acting on a body can change its state of rest or motion. Students will learn how to calculate the changes in the body’s state by using the laws of motion and the scientific principles of kinematics. They will learn to use determining vector components to find out the resultant force acting on a body.

On proceeding further, they will also learn how to find the dimensions and units of work, force, power, and energy. The determination of these units and dimensions will help students to develop a deeper foundation of concepts related to kinematics and mechanics.

Students will also learn how to find the gravitational units by using the laws of gravitation to find the formula of gravitational forces. They will also find the correlation of the formulae of work, power and energy in this topic also. The reference to the Work Power and Energy Class 11 notes for NEET will enable students to grab these concepts faster and better.

This chapter is of utmost importance as it creates a fundamental concept of physical quantities and their derivations. They will learn how to calculate the units and the outcomes of given problems using the laws.

Benefits of Vedantu’s Work Energy and Power Notes for NEET

• These notes have been designed and developed by the top subject matter experts to offer exemplary guidance for the preparation of this chapter. There is no need to worry about making concise notes on your own while covering all important areas when you can download and access these notes for easy reference.

• These notes can be used to prepare and revise the chapter faster. The concepts, scientific derivations, formulae, explanations of the laws, dimensions, units, etc. are described in a concise version. This methodical presentation of the content of this chapter will help you remember everything in the exam hall.

• You can conveniently solve the problems related to this chapter without any difficulty. Use Work Energy and Power notes PDF to build a foundation of these concepts and principles of work, power and energy and score more in the main exam. Check your preparation level by solving sample questions and evaluating your answers from the solutions provided.

Download Work Energy and Power NEET Notes in PDF

Get the free version of these notes and add them to your study material. Make your preparation and revision sessions shorter by referring to these notes. Prepare this crucial chapter in the Class 11 Physics NEET syllabus perfectly and learn how to answer questions accurately. Refer to the YouTube lectures on this chapter to get more insights.

Other Important Links

NEET Physics Revision Notes - Chapter Pages