NEET 2024 Revision Notes for Physics Mathematical Tools

Basic Mathematics for Physics

Physical Constants:

• Mass of an electron $\left(\mathrm{M}_{\mathrm{e}}\right)=9.1 \times 10^{-31} \mathrm{~kg}$.

• Mass of a proton $\left(M_{p}\right)=1.6725 \times 10^{-27} \mathrm{~kg}$.

• Mass of a neutron $\left(\mathrm{M}_{n}\right)=1.6746 \times 10^{-27} \mathrm{~kg}$.

• Charge of an electron $(\mathrm{e})=-1.6 \times 10^{-19} \mathrm{C}$.

• Speed of light in vacuum (c) $=3 \times 10^{8} \mathrm{~m} / \mathrm{sec}$.

• Planck Constant $(\mathrm{h})=6.6256 \times 10^{-34} \mathrm{~J} \times \mathrm{sec}$.

• Universal Gravitation constant $(\mathrm{G})=6.67 \times 10^{-11} \mathrm{Nm}^{2} / \mathrm{kg}^{2}$.

• Avogadro Number (NA) $=6.023 \times 10^{23} \mathrm{~mol}^{-1}$.

• Boltzmann constant $(\mathrm{K})=1.38 \times 10^{-23} \mathrm{~J} / \mathrm{K}$

• Stefan Constant \[(\sigma)=5.67 \times 10-8\mathrm{~W} \mathrm{~m}-2 \mathrm{~K}-4\].

• Wien Displacement Constant (b) $=2.898 \times 10^{-3} \mathrm{~m} \mathrm{~K}$.

• Solar Constant $(S)=1.388 \times 103 \mathrm{~W} \mathrm{~m}^{-2}$.

• Mass of the sun $(\mathrm{MS})=2 \times 10^{30} \mathrm{~kg}$.

• Mass of the earth $(\mathrm{ME})=5.98 \times 10^{24} \mathrm{~kg}$.

• Radius of the earth $(\mathrm{Re})=6400 \mathrm{Km}$. $=6.4 \times 10^{6} \mathrm{~m}$.

• Density of earth $5.522 \times 10^{3} \mathrm{~kg} / \mathrm{m}^{3}$.

• Average angular velocity of the earth $=7.29 \times 10^{-5} \mathrm{rad} . / \mathrm{sec}$.

• Average distance between the sun and earth $=1.5 \times 10^{11} \mathrm{~m}$.

• Average distance between moon and the earth $=3.84 \times 10^{8} \mathrm{~m}$.

• Magnetic Moment of the earth $=6.4 \times 10^{21} \mathrm{Amp} . \mathrm{X} \mathrm{} \mathrm{m}^{2}$.

• 1 Light year $=9.46 \times 10^{15} \mathrm{~m}$.

• $1 \mathrm{~A} . \mathrm{U} .=1.496 \times 10^{11} \mathrm{~m}$.

• $1 \hat{\mathrm{A}}=10^{-10} \mathrm{~m}$.

• 1 Pound $=0.4536 \mathrm{~kg}=453.6 \mathrm{gm}$

• 1 Fermi $=10^{-15} \mathrm{~m}$.

• 1 C.S.L. $=1.4 \times$ Mass of the sun.

• 1 Shake $=10^{-8} \mathrm{sec}$.

• $1 \mathrm{ev}=1.6 \times 10^{-19}$ Joule.

• 1 Horse Power $=746$ Watt.

Indices

While a number is written in the form $2^{4}$, here 2 is known as base and 4 is known as power, index or exponent.

Rules of Exponent

Consider we want to multiply 4 and 8 which is equal to 32

$4 \times 8=32$

Now $4=2^{2}$ and $8=2^{3}$.

As $4 \times 8=32 $

$2^{2} \times 2^{3}=32 $

$(2 \times 2) \times(2 \times 2 \times 2)=32 $

$2^{5}=32$

From above we can conclude that if two number in exponential form, if their base is same then power or index or exponent gets added or

$a^{m} \times a^{n}=a^{(m+n)}$

Similarly it can be proved that

$a^{m} \div a^{n}=a^{(m-n)}$

Logarithm

• Consider the expression $16=2^{4}$. Remember that 2 is the base, and 4 is the power. An alternative, yet equivalent, way of writing this expression is $\log _{2} 16=4$

• This is stated as 'log of 16 to base 2 equals $4^{\prime}$.

• We see that the logarithm is the same as the power or index in the original expression. In general we can write,

$x=a^{m}$ then $\log _{a} x=m$ From above $10=10^{1}$ thus $\log _{10} 10=1$ Or $2=2^{1}$ thus $\log _{2} 2=1$ In general $\log _{a} a=1$

Laws of Logarithms

1) The first law of logarithms

Suppose $x=a^{n} \text { and } y=a^{m}$

Then the equivalent logarithmic forms are

$\log _{a} x=n$ and $\log _{a} y=m$ ……(i)

Using the first rule of indices $x y=a^{(n+m)}$ $\log _{a} x y=n+m$ and from $(1)$ and so putting these results together we have $\log _{a} x y=\log _{a} x+\log _{a} y$ 2) The second law of logarithms Suppose $x=a^{n}$, or equivalently $\log _{a} x=$ n. suppose we raise both sides of $x=a^{n}$ to the power m:

$x^{\mathrm{m}}=\left(\mathrm{a}^{\mathrm{n}}\right)^{\mathrm{m}}$

Using the rules of indices we can write this as

$x^{m}=a^{n m}$

Thinking of the quantity $x^{m}$ as a single term, the logarithmic form is

$\log _{a} x^{m}=n m=\operatorname{mlog}_{a} x$

This is the second law. It states that when finding the logarithm of a power of a number, this can be evaluated by multiplying the logarithm of the number by that power.

3) The third law of logarithms

As before, suppose

$x=a^{n} \text { and } y=a^{m}$

with equivalent logarithmic forms

$\log _{a} x=n$ and $\log _{a} y=m$

Consider $x \div y$

$\dfrac{x}{y}=\dfrac{a^{n}}{a^{m}}=a^{(n-m)}$

Using the rules of indices.

In logarithmic form

$\log _{a}\left(\dfrac{x}{y}\right)=\log _{a} a^{(n-m)} $

$\log _{a}\left(\dfrac{x}{y}\right)=n-m$

which from (2) can be written

$\log _{a}\left(\dfrac{x}{y}\right)=\log _{a} x-\log _{a} x$

This is the third law.

The logarithm of 1

Recall that any number raised to the power zero is $1: a^{0}=1$. The logarithmic form of this is $\log _{a} 1=0$

In general

$\log _{a} b=\dfrac{1}{\log _{b} a}$

$\dfrac{\log _{e} b}{\log _{e} a}=\dfrac{\log _{c} b}{\log _{c} a}=\log _{a} b$

Common Bases:

$\log$ means $\log _{10}$

In means loge where e is the exponential constant. We can convert In to log as follows

$\ln a=2.303 \log a$

Using log Table

Four figure logarithms can be used to calculate lengthy multiplication and division numerical We can use log tables , for four figure logarithms. Logarithm of number consists of two parts Characteristic : Integral part of log Mantissa : Fractional or decimal part of the log Characteristic If number is >1, then count number of digits before decimal, then reduce one from the number of digits.

Trigonometry:

$\operatorname{Cosec} \theta=\dfrac{1}{\operatorname{Sin} \theta}$

$\operatorname{Sec} \theta=\dfrac{1}{\operatorname{Cos} \theta}$

$\operatorname{Cot} \theta=\dfrac{\operatorname{Cos} \theta}{\operatorname{Sin} \theta}=\dfrac{1}{\operatorname{Tan} \theta}$

$\operatorname{Tan} \theta=\dfrac{\operatorname{Sin} \theta}{\operatorname{Cos} \theta}$

$\operatorname{Sin}^{2} \theta+\operatorname{Cos}^{2} \theta=1$

$1+\tan ^{2} \theta=\operatorname{Sec}^{2} \theta$

$1+\operatorname{Cot}^{2} \theta=\operatorname{cosec}^{2} \theta$

$\operatorname{Cot} \theta=\dfrac{\operatorname{Cos} \theta}{\operatorname{Sin} \theta}=\dfrac{1}{\operatorname{Tan} \theta}$

$\operatorname{Tan} \theta=\dfrac{\operatorname{Sin} \theta}{\operatorname{Cos} \theta}$

$\operatorname{Sin}^{2} \theta+\operatorname{Cos}^{2} \theta=1$

$1+\tan ^{2} \theta=\operatorname{Sec}^{2} \theta$

$1+\operatorname{Cot}^{2} \theta=\operatorname{Cosec}^{2} \theta$

Definition of a Radian

Consider a circle of radius $r$ as shown, In Figure we have highlighted part of the circumference of the circle chosen to have the same length as the radius. The angle at the centre, so formed, is 1 radian. Length of arc $s=$ $r \theta$. Here $\theta$ is in radians.

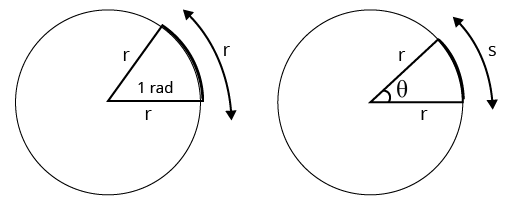
Radian

Equivalent Angles in Degrees and in Radians

We know that the arc length for a full circle is the same as its circumference, $2 \pi r$.

We also know that the arc length $=r \theta$.

So for a full circle

$2 \pi r=r \theta $

$\theta=2 \pi$

In other words, when we are working in radians, the angle in a full circle is $2 \pi$ radians, in other words

$360^{\circ}=2 \pi$ radians

This enables us to have a set of equivalences between degrees and radians.

Trigonometric Ratios for Angles in a Right-angled Triangle

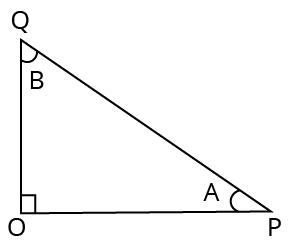
Right-angled Triangle

The side opposite the right-angle is called the hypotenuse

Recall the following important definitions:

$\sin A=\dfrac{O Q}{Q P}$ but $\cos B=\dfrac{O Q}{Q P}$

$\therefore \sin \mathrm{A}=\cos \mathrm{B} $

$\text { We know that } \angle \mathrm{A}+\angle \mathrm{B}=90 \therefore \angle \mathrm{B}=90-\angle \mathrm{A} $

$\therefore \sin \mathrm{A}=\cos (90-\mathrm{A})$

$\cos A=\dfrac{O P}{Q P} \text { but } \sin B=\dfrac{O P}{Q P} $

$\therefore \cos \mathrm{A}=\sin \mathrm{B} $

$\mathrm{OR} \cos \mathrm{A}=\sin (90-\mathrm{A})$

$\tan A=\dfrac{O Q}{O P} \text { but } \cot B=\dfrac{O Q}{O P} $

$\therefore \tan \mathrm{A}=\cot \mathrm{B} \quad \text { OR } \tan \mathrm{A}=\cot (90-\mathrm{A})$

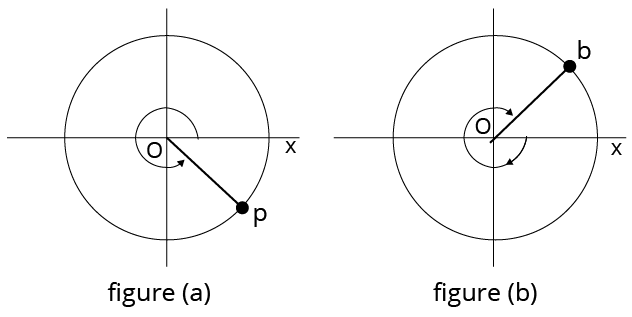
Angle Measurement

If angle is measured in anticlockwise direction from positive x-axis as shown in figure a. is positive and if angle is measured in clockwise direction from positive x axis as shown in figure b is negative.

The Sign of an Angle in Any Quadrant

Sin of an Angle in the First Quadrant

Consider Figure which shows a circle of radius 1 unit. The side opposite θ has the same length as the projection of OP onto the y axis OY. The arm OP is in the first quadrant and we have dropped a perpendicular line drawn from P to the x axis in order to form the right-angled triangle shown. Consider angle 𝜃. The side opposite this angle has the same length as the projection of OP onto the y axis. So we define.

First Quadrant

$\sin \theta=\dfrac{\text { Projection of } O P \text { on } y-\text { axis }}{O P}$

$\operatorname{Sin} \theta=$ Projection of OP on $y$ axis

Sin of an Angle in Second Quadrant

Second Quadrant

Consider adjacent figure here OP makes angle is $90+\theta$ with positive $x$-axis

Now as stated earlier $\sin (90+\theta)=\cos \theta$

Projection of OP on $y$-axis $=$ ON

From the geometry of figure we can find that $\cos \theta=\dfrac{P M}{O P}$

Thus $\sin (90+\theta)=\cos \theta$

By using above we can obtain various relations, which can be quickly remembered by following way:

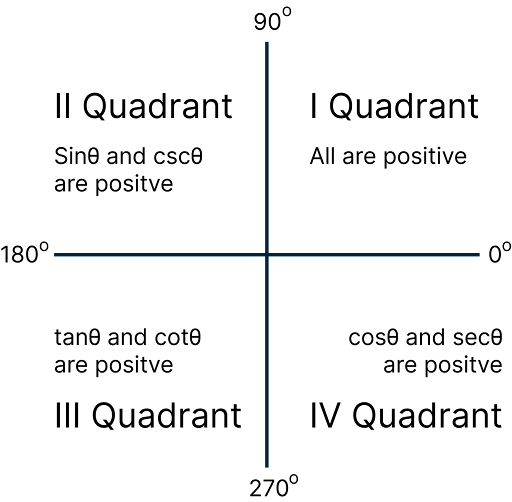
Trigonometric Quadrant

Quadrant I: All ratios sin, cos, tan, cosec, sec, cot have POSITIVE value 

Quadrant II: Only sine or cosec have POSITIVE value Remaining have negative value 

Quadrant III: Only tan and cot have POSITIVE value. 

Remaining have negative value. 

Quadrant IV: Only cos and sec have POSITIVE value

Remaining have negative values

Angles $\pi+\theta$ function do not change

For example $\sin (\pi+\theta)=-\sin \theta$

Here $\pi+\theta$ is in Third quadrant where sin is NEGATIVE thus negative sign appears.

Trigonometric Identities

$\sin ^{2} \theta+\cos ^{2} \theta=1$

$1+\tan ^{2} \theta=\sec ^{2} \theta$

$1+\cot ^{2} \theta=\operatorname{cosec}^{2} \theta$

$\sec ^{2} \theta-\tan ^{2} \theta=1$

$\operatorname{cosec}^{2} \theta-\cot ^{2} \theta=1$

$\sin 2 \theta=2 \sin \theta \cos \theta=\dfrac{2 \tan \theta}{1+\tan ^{2} \theta}$

$\cos 2 \theta=\cos ^{2} \theta-\sin ^{2} \theta=2 \cos ^{2} \theta-1=1-2 \sin ^{2} \theta=\dfrac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}$

$\sin (\alpha \pm \beta)=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta$

$\cos (\alpha \pm \beta)=\cos \alpha \cos \beta \mp \sin \alpha \sin \beta($ note sign changed $)$

$\sin \alpha+\sin \beta=2 \sin \left(\dfrac{\alpha+\beta}{2}\right) \cos \left(\dfrac{\alpha-\beta}{2}\right)$

$\sin \alpha-\sin \beta=2 \cos \left(\dfrac{\alpha+\beta}{2}\right) \sin \left(\dfrac{\alpha-\beta}{2}\right)$

$\cos \alpha+\cos \beta=2 \cos \left(\dfrac{\alpha+\beta}{2}\right) \cos \left(\dfrac{\alpha-\beta}{2}\right)$

$\cos \alpha-\cos \beta=-2 \sin \left(\dfrac{\alpha+\beta}{2}\right) \sin \left(\dfrac{\alpha-\beta}{2}\right)$

$2 \sin \alpha \cos \beta=\sin (\alpha+\beta)+\sin (\alpha-\beta)$

$2 \cos \alpha \sin \beta=\sin (\alpha+\beta)-\sin (\alpha-\beta)$

$2 \cos \alpha \cos \beta=\cos (\alpha+\beta)+\cos (\alpha-\beta)$

$-2 \sin \alpha \sin \beta=\cos (\alpha+\beta)-\cos (\alpha-\beta)$

$\sin 3 \theta=3 \sin \theta-4 \sin ^{3} \theta$

$\cos 3 \theta=4 \cos ^{3} \theta-3 \cos \theta$

$\tan (\alpha \pm \beta)=\dfrac{\tan \alpha \pm \tan \beta}{1 \mp \tan \alpha \tan \beta}$

$\tan 2\theta =\frac{2\tan \theta }{1-{{\tan }^{2}}\theta }$

Vector Algebra

A vector has direction and magnitude both but scalar has only magnitude.

Magnitude of a vector a is denoted by $|\mathrm{a}|$ or $\mathrm{a}$. It is non-negative scalar.

Equality of Vectors

Two vectors $a$ and $b$ are said to be equally written as $a=b$, if they have (i) same length (ii) the same or parallel support and (iii) the same sense.

Types of Vectors

(i) Zero or Null Vector: A vector whose initial and terminal points are coincident is called zero or null vector. It is denoted by 0 .

(ii) Unit Vector: A vector whose magnitude is unity is called a unit vector which is denoted by $\mathrm{n}$

(iii) Free Vectors: If the initial point of a vector is not specified, then it is said to be a free vector.

(iv) Negative of a Vector: A vector having the same magnitude as that of a given vector a and the direction opposite to that of $a$ is called the negative of $a$ and it is denoted by $-\mathrm{a}$.

(v) Like and Unlike Vectors: Vectors are said to be like when they have the same direction and unlike when they have opposite direction.

(vi) Collinear or Parallel Vectors: Vectors having the same or parallel supports are called collinear vectors.

(vii) Coinitial Vectors: Vectors having the same initial point are called coinitial vectors.

(viii) Coterminous Vectors: Vectors having the same terminal point are called coterminous vectors.

(ix) Localized Vectors: A vector which is drawn parallel to a given vector through a specified point in space is called a localized vector.

(x) Coplanar Vectors: A system of vectors is said to be coplanar, if their supports are parallel to the same plane. Otherwise they are called non-coplanar vectors.

(xi) Reciprocal of a Vector: A vector having the same direction as that of a given vector but magnitude equal to the reciprocal of the given vector is known as the reciprocal of a.

i.e., if $|a|=a$, then $\left|a^{-1}\right|=1 / a$.

Addition of Vectors

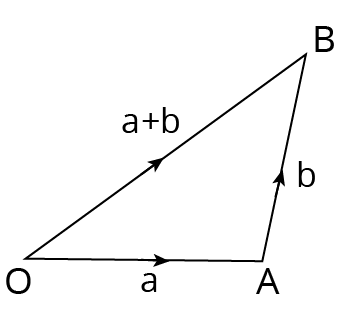
Addition of Vectors

Parallelogram Law

Let a and b be any two vectors. From the initial point of a, vector b is drawn and parallelogram OACB is completed with OA and OB as adjacent sides. The vector OC is defined as the sum of a and b. This is called the parallelogram law of addition of vectors. The sum of two vectors is also called their resultant and the process of addition as composition.

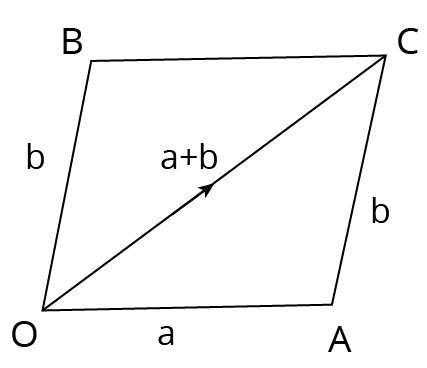
Parallelogram Law

Properties of Vector Addition

(i) $\mathrm{a}+\mathrm{b}=\mathrm{b}+\mathrm{a}$ (commutativity)

(ii) $\mathrm{a}+(\mathrm{b}+\mathrm{c})=(\mathrm{a}+\mathrm{b})+\mathrm{c}$ (associativity)

(iii) $\mathrm{a}+\mathrm{O}=\mathrm{a}$ (additive identity)

(iv) $\mathrm{a}+(-\mathrm{a})=0$ (additive inverse)

(v) $\left(\mathrm{k}_{1}+\mathrm{k}_{2}\right) \mathrm{a}=\mathrm{k}_{1} \mathrm{a}+\mathrm{k}_{2} \mathrm{a}$ (multiplication by scalars)

(vi) $\mathrm{k}(\mathrm{a}+\mathrm{b})=\mathrm{k} a+\mathrm{kb}$ (multiplication by scalars)

(vii) $|a+b| \leq|a|+|b|$ and $|a-b| \geq|a|-|b|$

Difference (Subtraction) of Vectors

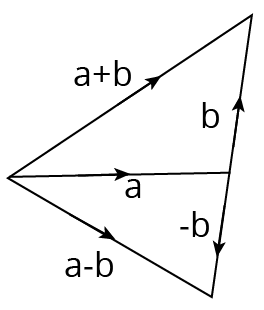
Difference (Subtraction) of Vectors

Multiplication of a Vector by a Scalar

Let a be a given vector and $\lambda$ be a scalar. Then, the product of the vector a by the scalar $\lambda$ is $\lambda$ and is called the multiplication of a vector by the scalar.

Important Properties

(i) $|\lambda \mathrm{a}|=|\lambda||\mathrm{a}|$

(ii) $\lambda \mathrm{O}=\mathrm{O}$

(iii) $\mathrm{m}(-\mathrm{a})=-\mathrm{ma}=-(\mathrm{m} a)$

(iv) $(-\mathrm{m})(-\mathrm{a})=\mathrm{ma}$

(v) $m(n a)=m n a=n(m a)$

(vi) $(\mathrm{m}+\mathrm{n}) \mathrm{a}=\mathrm{m} \mathrm{a}+\mathrm{n} \mathrm{a}$

(vii) $\mathrm{m}(\mathrm{a}+\mathrm{b})=\mathrm{m} \mathrm{a}+\mathrm{mb}$

Vector Equation of Joining by Two Points

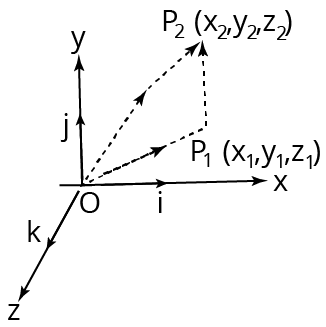
Vector Equation of Joining by Two Points

The component vectors of $\mathrm{P}$ and $\mathrm{Q}$ are

$O P=x_{1} i+y_{1} j+z_{1} k$

$\text { and } O Q=x_{2} i+y_{2} j+z_{2} k $

$\text { i.e., } P_{1} P_{2}=\left(x_{2} i+y_{2} j+z_{2} k\right)-\left(x_{1} i+y_{1} j+z_{1} k\right) $

$=\left(x_{2}-x_{1}\right) i+\left(y_{2}-y_{1}\right) j+\left(z_{2}-z_{1}\right) k$

Its magnitude is

$\mathrm{P}_{1} \mathrm{P}_{2}=\sqrt{\left(\mathrm{x}_{2}-\mathrm{x}_{1}\right)^{2}+\left(\mathrm{y}_{2}-\mathrm{y}_{1}\right)^{2}+\left(\mathrm{z}_{2}-\mathrm{z}_{1}\right)^{2}}$

Scalar Product of Two Vectors

If $\mathrm{a}$ and $\mathrm{b}$ are two non-zero vectors, then the scalar or dot product of $\mathrm{a}$ and $\mathrm{b}$ is denoted by $\mathrm{a} * \mathrm{~b}$ and is defined as $\mathrm{a} * \mathrm{~b}=|\mathrm{a}||\mathrm{b}| \cos \theta$, where $\theta$ is the angle between the two vectors and $0<\theta<\pi$

(i) The angle between two vectors $a$ and $b$ is defined as the smaller angle $\theta$ between them, when they are drawn with the same initial point.

Usually, we take $0<\theta<\pi$.Angle between two like vectors is $\mathrm{O}$ and angle between two unlike vectors is $\pi$.

(ii) If either $a$ or $b$ is the null vector, then the scalar product of the vector is zero.

(iii) If $\mathrm{a}$ and $\mathrm{b}$ are two unit vectors, then $\mathrm{a} * \mathrm{~b}=\cos \theta$.

(iv) The scalar product is commutative

i.e., $a * b=b * a$

(v) If $\mathrm{i}, \mathrm{j}$ and $\mathrm{k}$ are mutually perpendicular unit vectors $\mathrm{i}, \mathrm{j}$ and $\mathrm{k}$, then

$\mathrm{i} * \mathrm{i}=\mathrm{j} * \mathrm{j}=\mathrm{k} * \mathrm{k}=1$

and $\mathrm{i} * \mathrm{j}=\mathrm{j} * \mathrm{k}=\mathrm{k} * \mathrm{i}=0$

(vi) The scalar product of vectors is distributive over vector addition.

(a) $a *(b+c)=a * b+a * c$ (left distributive)

(b) $(b+c) * a=b * a+c * a$ (right distributive)

Note Length of a vector as a scalar product

If a be any vector, then the scalar product

$a * a=|a||a| \cos \theta \Rightarrow|a|^{2}=a^{2} \Rightarrow a=|a|$

Condition of perpendicularity $\mathrm{a} * \mathrm{~b}=0<=>\mathrm{a} \perp \mathrm{b}$, $\mathrm{a}$ and $\mathrm{b}$ being non-zero vectors.

Important Points to be Remembered

(i) $(\mathrm{a}+\mathrm{b}) *(\mathrm{a}-\mathrm{b})=|\mathrm{a}|^{2} 2-|\mathrm{b}|^{2}$

(ii) $|\mathrm{a}+\mathrm{b}|^{2}=|\mathrm{a}|^{2} 2+|\mathrm{b}|^{2}+2(\mathrm{a} * \mathrm{~b})$

(iii) $|\mathrm{a}-\mathrm{b}|^{2}=|\mathrm{a}|^{2} 2+|\mathrm{b}|^{2}-2(\mathrm{a} * \mathrm{~b})$

(iv) $|\mathrm{a}+\mathrm{b}|^{2}+|\mathrm{a}-\mathrm{b}|^{2}=\left(|\mathrm{a}|^{2} 2+|\mathrm{b}|^{2}\right)$ and $|\mathrm{a}+\mathrm{b}|^{2}-|\mathrm{a}-\mathrm{b}|^{2}=4(\mathrm{a} * \mathrm{~b})$ or $a * b=1 / 4\left[|a+b|^{2}-|a-b|^{2}\right]$

(v) If $|a+b|=|a|+|b|$, then a is parallel to $b$.

(vi) If $|a+b|=|a|-|b|$, then $a$ is parallel to $b$.

(vii) $(\mathrm{a} * \mathrm{~b})^{2} \leq|\mathrm{a}|^{2} 2|\mathrm{~b}|^{2}$

Projection and Component of a Vector

Projection of $a$ on $b=a * b /|a|$

Projection of $\mathrm{b}$ on $\mathrm{a}=\mathrm{a} * \mathrm{~b} /|\mathrm{a}|$

Vector component of a vector $a$ on $b$

$=\dfrac{a \cdot b}{|b|} \cdot \hat{b}=\dfrac{a \cdot b}{|b|} \cdot \dfrac{b}{|b|}=\dfrac{(a \cdot b)}{\left|b^{2}\right|} \mathbf{b}$

Similarly, the vector component of $\mathrm{b}$ on $\mathrm{a}=\left((\mathrm{a} * \mathrm{~b}) /\left|\mathrm{a}^{2}\right|\right) * \mathrm{a}$

Vector or Cross Product of Two Vectors

The vector product of the vectors $\mathrm{a}$ and $\mathrm{b}$ is denoted by $\mathrm{a} * \mathrm{~b}$ and it is defined as $\text{a}*~\text{b}=(|\text{a}||\text{b}|\sin \theta )\overset{\wedge }{\mathop{\text{n}}}\,=\text{ab}\sin \theta \overset{\wedge }{\mathop{\text{n}}}\,\ldots $ (i)

where, $\mathrm{a}=|\mathrm{a}|, \mathrm{b}=|\mathrm{b}|, \theta$ is the angle between the vectors $\mathrm{a}$ and $\mathrm{b}$ and $\mathrm{n}$ is a unit vector which is perpendicular to both $a$ and $b$, such that $a, b$ and $n$ form a right-handed triad of vectors.

Quadratic Equation

An equation of second degree is called a quadratic equation. It is of the form

$-a x^{2}+b x+c=0$

The roots of a quadratic equation are

$x=-b \pm\left(b^{2}+4 a c\right)^{1 / 2} / 2 a$

Binomial Theorem

If $n$ is any integer, positive or negative or a fraction and $x$ is any real number, then

$(1+x)^{n}=1+n x+n(n-1) x^{2}+\ldots / ! 2$

If $|x|<<1$, then $(1+x)^{n}=1+n x$.

Mensuration :

1. Area of a circle $=\pi r^{2}=\pi D^{2} / 4$

2. Surface area of a sphere $=4 \pi r^{2}=\pi D^{2}$

3. Volume of a sphere $=4 / 3 \pi r^{3}$

4. Surface area of a cylinder $=2 \pi r(r+l)$

5. Volume of a cylinder $=\pi r^{2}$ ।

6. Curved surface area of a cone $=\pi r l$

7. Volume of a cone $=1 / 3 \pi r^{2} h$

8. Surface area of a cube $=6 x(\text { side })^{2}$

9. Volume of a cube $=(\text { side })^{3}$

Differentiation

Another name for differentiation is derivative. Suppose $y$ is a function of $x$ or $y=f(x)$ Differentiation of $y$ with respect to $x$ is denoted by symbol $f^{\prime}(x)$

where $f^{\prime}(x)=\dfrac{d y}{d x}$

$\mathrm{dx}$ is very small change in $\mathrm{x}$ and dy is corresponding very small change in $\mathrm{y}$.

The Derivative of a Fuction

We know that, average rate of change of $y$ w.r.t. $x$ is $\dfrac{\Delta y}{\Delta x}=\dfrac{f(x+\Delta x)-f(x)}{\Delta x}$.

If the limit of this ratio exists as $\Delta x \rightarrow 0$, then it is called the derivative of given function $f(x)$ and is denoter as

$f^{\prime}(x)=\dfrac{d y}{d x}=\lim _{\Delta x \rightarrow 0} \dfrac{f(x+\Delta x)-f(x)}{\Delta x}$

If $u$ and $v$ are differentiable at $x$, then so is their product $u v$, and $\dfrac{d}{d x}(u v)=u \dfrac{d v}{d x}+v \dfrac{d u}{d x}$.

The derivative of the product $u v$ is $u$ times the derivative of $v$ plus $v$ times the derivative of $u$. In prime notation $(u v)^{\prime}=u v^{\prime}+v u^{\prime}$.

If $u$ and $v$ are differentiable at $x$, and $v(x) \neq 0$, then the quotient $u / v$ is differentiable at $x$,

and $\quad \dfrac{d}{d x}\left(\dfrac{u}{v}\right)=\dfrac{v \dfrac{d u}{d x}-u \dfrac{d v}{d x}}{v^{2}}$

Double Differentiation

If $f$ is differentiable function, then its derivative $f^{\prime}$ ' is also a function, so $f^{\prime}$ may have a derivative of its own, denoted by $\left(f^{\prime}\right)^{\prime}=f^{\prime \prime}$. This new function $f^{\prime \prime}$ is called the second derivative of $f$ because it is the derivative of the derivative of $f$. Using Leibniz notation, we write the second derivative of $y=f(x)$ as

$\dfrac{d}{d x}\left(\dfrac{d y}{d x}\right)=\dfrac{d^{2} y}{d x^{2}}$

Another notation is $f^{\prime \prime}(x)=D_{2} f(x)=D^{2} f(x)$

1. Differentiation of a constant c is zero

$\dfrac{d c}{d x}=0$

2. \[\dfrac{\mathrm{d}(\mathrm{cy})}{\mathrm{dx}}=\mathrm{c} \dfrac{\mathrm{dy}}{\mathrm{dx}}\]

3. $\dfrac{d\left(x^{n}\right)}{d x}=n x^{n-1}$

4. $\dfrac{d[f(x) \pm g(x)]}{d x}=\dfrac{d f(x)}{d x} \pm \dfrac{d g(x)}{d x}$

5. $\dfrac{d\{f(x) g(x)\}}{d x}=\dfrac{f(x) d g(x)}{d x}+\dfrac{g(x) d f(x)}{d x}$

6. $\dfrac{d}{d x}\left\{\dfrac{f(x)}{g(x)}\right\}=\dfrac{g(x) \dfrac{d f(x)}{d x}-f(x) \dfrac{d g(x)}{d x}}{\{g(x)\}^{2}}$

7. $\dfrac{d y}{d x}=\dfrac{d y}{d u} \dfrac{d u}{d x}$

8. $\quad \dfrac{d e^{x}}{d x}=e^{x}$

9. $\dfrac{d u^{n}}{d x}=n u^{n-1} \dfrac{d u}{d x}$

10. $\dfrac{d \log _{e^{x}}}{d x}=\dfrac{1}{x}$

11. $\dfrac{d\left(a^{x}\right)}{d x}=a^{x} \log _{e^{a}}$

12. $\dfrac{d \log _{a} x}{d x}=\dfrac{1}{x} \log _{e} a$

13. $\dfrac{d(\sin x)}{d x}=\cos x$

14. $\dfrac{d(\cos x)}{d x}=-\sin x$

15. $\dfrac{d(\tan x)}{d x}=\sec ^{2} x$

16. $\dfrac{d(\cot x)}{d x}=-\operatorname{cosec}^{2} x$

17. $\dfrac{d(\operatorname{cosec} x)}{d x}=-\operatorname{cosec} x \cot x$

18. $\dfrac{d(\sec x)}{d x}=\sec x \tan x$

Integration:

In mathematics, for each mathematical operation, there has been defined an inverse operation. For example- Inverse operation of addition is subtruction, inverse operation of multiplication is division and inverse operation of square is square root. Similarly there is a inverse operation for differentiation which is known as integration.

A function is an antiderivative of a constant multiple $k f$ of a function $f$ if and only if it is $k$ times an antiderivative of $f$.

$\int x^{n} d x=\dfrac{x^{n+1}}{n+1}+C, n \neq-1$. Particularly, $\int d x=x+c$

1. $\int \mathrm{dx}=\mathrm{x}+\mathrm{c} \quad$ Where $\mathrm{c}=$ constant

2. $\int \mathrm{x}^{n+1} \mathrm{dx}=\dfrac{x^{n+1}}{n+1}+C$

3. $\int d x / x=\log _{e} x+c$

4. $\int \operatorname{Sin} x d x=-\operatorname{Cos} x+c$

5. $\int{\operatorname{Sin}}axdx=-\operatorname{Cos}\frac{ax}{a}$

6. $\int \cos x d x=\operatorname{Sin} x+c$

7. $\int \operatorname{Sec}^{2} x d x=\tan x+c$

8. $\int \operatorname{cosec}^{2} x d x=-\operatorname{Cot} x+c$

9. $\int \operatorname{Sec} x \tan x d x=\operatorname{Sec} x+c$

10. $\int \operatorname{cosec} x \cot x d x=-\operatorname{cosec} x+c$

11. $\int e^{x} d x=e^{x}+c$

12. $\int x^{n} d x=\dfrac{x^{n+1}}{n+1}+C, n \neq-1, n$ rational $\int \mathrm{dx}=\int 1 \mathrm{dx}=\mathrm{x}+\mathrm{C}($ special case)

13. $\int \sin (A x+B) d x=\dfrac{-\cos (A x+B)}{A}+C$

14. $\int \cos k x d x=\dfrac{\sin k x}{k}+C$

15. $\int \cos x d x=\sin x+C$

16. $\int \sin x d x=-\cos x+C$

17. $\int \sec ^{2} x d x=\tan x+c$

18. $\int \operatorname{cosec}^{2} x d x=-\cot x+c$

19. $\int \sec x \tan x d x=\sec x+c$

20. $\int \operatorname{cosec} x \cot x d x=-\operatorname{cosec} x+c$

21. $\int \dfrac{d x}{\sqrt{1-x^{2}}}=\sin ^{-1} x+c$

22. $\int \dfrac{d x}{\sqrt{1-x^{2}}}=-\cos ^{-1} x+c$

Formula Logarithmic 

Formula Differentiation

1. $\dfrac{d}{d x}(\sin x)=\cos x$

2. $\dfrac{d}{d x}(\cos x)=-\sin x$

3. $\dfrac{d}{d x}(\tan x)=\sec ^{2} x$

4. $\dfrac{d}{d x}\left(\cot x)=-\csc ^{2} x\right.$

5. $\dfrac{d}{d x}(\sec x)=\sec x \tan x$

6. $\dfrac{d}{d x}(\csc x)=-\csc x \cot x$

7. $\dfrac{d}{d x}(\sinh x)=\cosh x$

8. $\dfrac{d}{d x}(\cosh x)=\sinh x$

9. $\dfrac{d}{d x}(\tanh x)=\operatorname{sech}^{2} x$

10. $\dfrac{d}{d x}(\operatorname{coth} x)=-\operatorname{csch}^{2} x$

11. $\dfrac{d}{d x}(\operatorname{sech} x)=-\operatorname{sech} x \tanh x$

12. $\dfrac{d}{d x}(\operatorname{csch} x)=-\operatorname{csch} x \cdot \operatorname{coth} x$

Some other Formulas are:

1. $\dfrac{d}{d x}\left(\sin ^{-1} x\right)=\dfrac{1}{\sqrt{1-x^{2}}}$

2. $\dfrac{d}{d x}\left(\cos ^{-1} x\right)=-\dfrac{1}{\sqrt{1-x^{2}}}$

3. $\dfrac{d}{d x}\left(\tan ^{-1} x\right)=\dfrac{1}{1+x^{2}}$

4. $\dfrac{d}{d x}\left(\cot ^{-1} x\right)=-\dfrac{1}{1+x^{2}}$

5. $\dfrac{d}{d x}\left(\sec ^{-1} x\right)=\dfrac{1}{|x| \sqrt{x^{2}-1}}$

6. $\dfrac{d}{d x}\left(\csc ^{-1} x\right)=-\dfrac{1}{|x| \sqrt{x^{2}-1}}$

7. $\dfrac{d}{d x}\left(a^{x}\right)=a^{x} \ln a$

8. $\dfrac{d}{d x}\left(e^{x}\right)=e^{x}$

9. $\dfrac{d}{d x}\left(\log _{a} x\right)=\dfrac{1}{(\ln a) x}$

10. $\dfrac{d}{d x}(\ln x)=1 / x$

11. Chain Rule: $\dfrac{d y}{d x}=\dfrac{d y}{d u} \times \dfrac{d u}{d x}=\dfrac{d y}{d v} \times \dfrac{d v}{d u} \times \dfrac{d u}{d x}$

Formula Integration

• $\int 1 d x=x+C $

• $\int a d x=a x+C $

• $\int x^{n} d x=\left(\left(x^{n+1}\right) /(n+1)\right)+C ; n \neq 1$

• $\int \sin x d x=-\cos x+C $

• $\int \cos x d x=\sin x+C $

• $\int \sec ^{2} x d x=\tan x+C $

• $\int \csc ^{2} x d x=-\cot x+C $

• $\int \sec _{x}(\tan x) d x=\sec x+C $

• $\int \csc x(\cot x) d x=-\csc x+C $

• $\int(1 / x) d x=\ln |x|+C$

• $\int e^{x} d x=e^{x}+C $

• $\int a^{x} d x=\left(a^{x} / \ln a\right)+C ; a>0, a \neq 1$

• $\int x^{n} d x=\dfrac{x^{n+1}}{n+1}+\mathrm{C}, n \neq-1$

• $\int d x=x+C$

• $\int \cos x d x=\sin x+C$

• $\int \sin x d x=-\cos x+C$

• $\int \sec ^{2} x d x=\tan x+C$

• $\int \operatorname{cosec}^{2} x d x=-\cot x+C$

• $\int \sec x \tan x d x=\sec x+C$

• $\int \operatorname{cosec} x \cot x d x=-\operatorname{cosec} x+\mathrm{C}$

• $\int \dfrac{d x}{\sqrt{1-x^{2}}}=\sin ^{-1} x+C$

• $\int \dfrac{d x}{\sqrt{1-x^{2}}}=-\cos ^{-1} x+C$

• $\int \dfrac{d x}{1+x^{2}}=\tan ^{-1} x+\mathrm{C}$

• $\int \dfrac{d x}{1+x^{2}}=-\cot ^{-1} x+C$

Example 1: If $\mathrm{n}$ is the number of solutions of the equation

$2 \cos x\left(4 \sin \left(\dfrac{\pi}{4}+x\right) \sin \left(\dfrac{\pi}{4}-x\right)-1\right)=1, x \in[0, \pi]$ and $\mathrm{S}$ is the sum of all these solutions, then the ordered pair $(n, S)$ is :

(A) $(3,13 \pi / 9)$

(B) $(2,2 \pi / 3)$

(C) $(2,8 \pi / 9)$

(D) $(3,5 \pi / 3)$

Ans: A

$2 \cos x\left(4 \sin \left(\dfrac{\pi}{4}+x\right) \sin \left(\dfrac{\pi}{4}-x\right)-1\right)=1$

$2 \cos x\left(4\left(\sin ^{2} \dfrac{\pi}{4}-\sin ^{2} x\right)-1\right)=1$

$2 \cos x\left(4\left(\dfrac{1}{2}-\sin ^{2} x\right)-1\right)=1$

$2 \cos x\left(2-4 \sin ^{2} x-1\right)=1$

$2 \cos x\left(1-4 \sin ^{2} x\right)=1$

$2 \cos x\left(4 \cos ^{2} x-3\right)=1$

$4 \cos ^{3} x-3 \cos x=\dfrac{1}{2}$

$\cos 3 x=\dfrac{1}{2}$

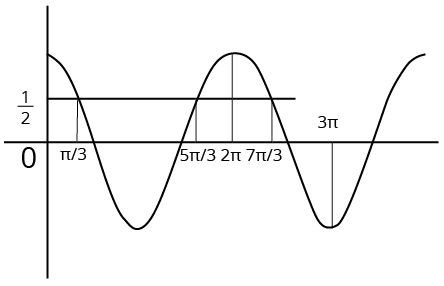
Example 1

The way that investors and money managers invest has altered as a result of derivatives, which also allow them a way to protect their capital. The advantages of derivative products should also be taken into account notwithstanding their complexity and the challenges associated in understanding them for the casual investor.

Example 2: The derivative of $\tan ^{-1}\left(\dfrac{\sqrt{1+x^{2}}-1}{x}\right)$ with respect to $\tan ^{-1}\left(\dfrac{2 x \sqrt{1-x^{2}}}{1-2 x^{2}}\right)$ at $\mathrm{x}=\dfrac{1}{2}$ is:

(A) $\dfrac{2 \sqrt{3}}{3}$

(B) $\dfrac{2 \sqrt{3}}{5}$

(C) $\dfrac{\sqrt{3}}{10}$

(D) $\dfrac{\sqrt{3}}{12}$

Ans: C

Let $\mathrm{f}=\tan ^{-1}\left(\dfrac{\sqrt{1+x^{2}}-1}{x}\right)$

Put $\mathrm{x}=\tan \theta \Rightarrow \theta=\tan ^{-1} \mathrm{x}$

$f=\tan ^{-1}\left(\dfrac{\sec \theta-1}{\tan \theta}\right)$

$\Rightarrow \mathrm{f}=\tan ^{-1}\left(\dfrac{1-\cos \theta}{\sin \theta}\right)=\dfrac{\theta}{2}$

$\Rightarrow \mathrm{f}=\dfrac{\tan ^{-1} x}{2}$

$\therefore \dfrac{d f}{d x}=\dfrac{1}{2\left(1+x^{2}\right)} \ldots(1)$

Let $\mathrm{g}=\tan ^{-1}\left(\dfrac{2 x \sqrt{1-x^{2}}}{1-2 x^{2}}\right)$

Put $x=\sin \theta \Rightarrow \theta=\sin ^{-1} x$

$\Rightarrow g=\tan ^{-1}\left(\dfrac{2 \sin \theta \cos \theta}{1-2 \sin ^{2} \theta}\right) $

$\Rightarrow g=\tan ^{-1}(\tan 2 \theta)=2 \theta$

$\Rightarrow g=2 \sin ^{-1} x $

$\Rightarrow \dfrac{d g}{d x}=\dfrac{2}{\sqrt{1-x^{2}}} \ldots(2)$

Using (i) and (ii),

$\therefore \dfrac{d f}{d g}=\dfrac{1}{2\left(1+x^{2}\right)} \dfrac{\sqrt{1-x^{2}}}{2}$

At $\mathrm{x}=\dfrac{1}{2},\left(\dfrac{d f}{d g}\right)_{x=\dfrac{1}{2}}=\dfrac{\sqrt{3}}{10}$

Hence,the derivative of $\tan ^{-1}\left(\dfrac{\sqrt{1+x^{2}}-1}{x}\right)$ with respect to $\tan ^{-1}\left(\dfrac{2 x \sqrt{1-x^{2}}}{1-2 x^{2}}\right)$ at $\mathrm{x}=\dfrac{1}{2}$ is $\dfrac{\sqrt{3}}{10}$

Example 3: The integral $\int \dfrac{1}{\sqrt[4]{(x-1)^{3}(x+2)^{5}}} d x$ is equal to : (where $\mathrm{C}$ is a constant of integration)

(A) $\dfrac{3}{4}\left(\dfrac{x+2}{x-1}\right)^{\dfrac{1}{4}}+C$

(B) $\dfrac{3}{4}\left(\dfrac{x+2}{x-1}\right)^{\dfrac{5}{4}}+C$

(C) $\dfrac{4}{3}\left(\dfrac{x-1}{x+2}\right)^{\dfrac{1}{4}}+C$

(D) $\dfrac{4}{3}\left(\dfrac{x-1}{x+2}\right)^{\dfrac{5}{4}}+C$

Ans: C

$\int \dfrac{d x}{(x-1)^{3 / 4}(x+2)^{5 / 4}}$

$=\int \dfrac{d x}{\left(\dfrac{x+2}{x-1}\right)^{5 / 4} \cdot(x-1)^{2}}$

put $\dfrac{x+2}{x-1}=t$

$=-\dfrac{1}{3} \int \dfrac{d t}{t^{5 / 4}}$

$=\dfrac{4}{3} \cdot \dfrac{1}{t^{1 / 4}}+C$

The integral $\int\dfrac{1}{\sqrt[4]{(x-1)^{3}(x+2)^{5}}} d x$ is equal to $\dfrac{4}{3}\left(\dfrac{x-1}{x+2}\right)^{\dfrac{1}{4}}+C$

Common Errors or Mistakes That Should Be Avoided By the Students Keeping the Exam Point of View:

1. Inadequate Steps While Solving

2. Getting confused With the Units

3. Using Vector Addition Technique When Adding Vectors

4.Don't forget to learn definitions

5. Students forget to put in the correct data they used in the working formula, which is used by teachers to check how effective the students' learning is.

6. For questions which require the reason for a certain condition, firstly students are required to state the cause of the condition and then the consequence of the condition.

7. Don't forget to show full working of your solution

8. Give right amount of time to each topic

Importance of Physics Mathematical Tools

As mentioned earlier, scientific principles related to physics need a proper explanation to check their validity. When there is a notion or a thought, it has to be researched and experimented with to find a solid platform. Once a platform is reached, mathematical tools are used to explain the facts and prove the validity of the thought. This is why it is important for students to learn the implication of mathematical tools.

Learning these tools will help you understand the laws and theories explained in the different chapters of Physics at the higher secondary level. The complex equations proving the laws can be easily derived when you know where to use the mathematical tools appropriately.

Solving Physics problems logically will also need the clarified presentation of a scientific principle using a mathematical tool. By studying the Mathematical Tools for Physics notes, you can easily find out where the tools can be used to prove a point and to determine the right answers to a fundamental question.

Hence, this chapter is of utmost importance when it comes to learning laws, principles, and theories of physics and answering questions coming in the NEET exam.

Benefits of Vedantu’s Mathematical Tools for Physics Notes

• These revision notes have been composed with the prime objective of delivering a simpler explanation of the mathematical terms, equations, formulae, etc. used in representing the fundamental concepts of physics. You will also learn how to use a formula to find the right answer to a question when you know the meaning and use of these mathematical tools.

• These notes will enable you to revise this chapter faster due to its concise and simple format. Moreover, you will also be able to remember the terms used in every tool and identify its need while solving a problem. Make it easier to prepare this chapter by checking the simple definition and description of mathematical tools compiled by the experts.

• Recall what you have studied in this chapter using these notes before an exam. Resolve doubts on your own using these notes and remember what you have studied in the exam hall without facing any difficulty. These notes will help you remember the format of these tools conveniently.

Download Mathematical Tools for Physics NEET PDF

Why wait then? Get the free PDF version of these revision notes and prepare this fundamental chapter for easier to comprehend. This chapter is the foundation of all the chapters you will study in the NEET Physics syllabus. Complete your study material for this chapter and make your study sessions more productive. Find out your preparation level by using these notes and enjoy strengthening your concepts.

NEET Physics Revision Notes - Chapter Pages

Other Important Links