Revision Notes on Nuclei for NEET 2024

All positive charges and almost all masses of an atom are concentrated in a very small space called the nucleus. The nucleus is composed of protons and neutrons. They are called nucleons.

Atomic Mass Unit

The term used to describe the term atomic mass associated with the Nucleus Atomic Mass Unit (AMU)  is called the atomic mass unit. The atomic mass unit is defined as \[{\dfrac{1}{{12}}^{th}}\]of the mass of a carbon atom $_6{C^{12}}$.

$1a.m.u = \dfrac{1}{{12}} \times \dfrac{{12}}{{6.023 \times {{10}^{23}}}} = 1.66 \times {10^{ - 27}}kg$

Composition of Nucleus

Atomic Number:  The number of protons in the nucleus of an elemental atom  is called the elemental atomic number (Z). 

${\text{Atomic number  =  Number of protons  +  Number of neutrons }} $

${\text{Atomic number =  Number of electrons  +  Number of neutron}}$

Isotopes:

The atoms of the same elements having the same atomic number but different mass numbers are called isotopes.

Isobars:

The atoms with a different element have the same mass number, but the different atomic number shows similar physical properties but different chemical properties.

Ex: $C_{6}^{14},N_{7}^{14}$

Isotones:

The nuclides with the different elements with different atomic number and mass number but having the same number of neutrons.

(A-Z): Shows different physical and chemical properties

Iso Diaphers:

Iso diaphers are nuclides with the same isotopic number (A-2Z). They differ in the same way that neutrons and protons do (n-p).

Isosteres:

Isosteres' are molecules that have the same atomicity and number of electrons.

Atomicity = total number of atoms in molecules

Iso-Electronic Species: 

The molecules or ions with same number of electrons are called isoelectronic species.

Mass Number: The total number of protons and neutrons present in the nucleus of an  element is called the mass number (A) of the element.

${\text{A  =  Z  +  N}}$

Size of Nucleus:  Size of the nucleus ${{R \alpha  }}{{\text{A}}^{{\text{1/3}}}}$

$R = {R_0}{A^{1/3}}$

Where, empirical constant ${R_0} = 1.1 \times {10^{ - 15}}\,m$

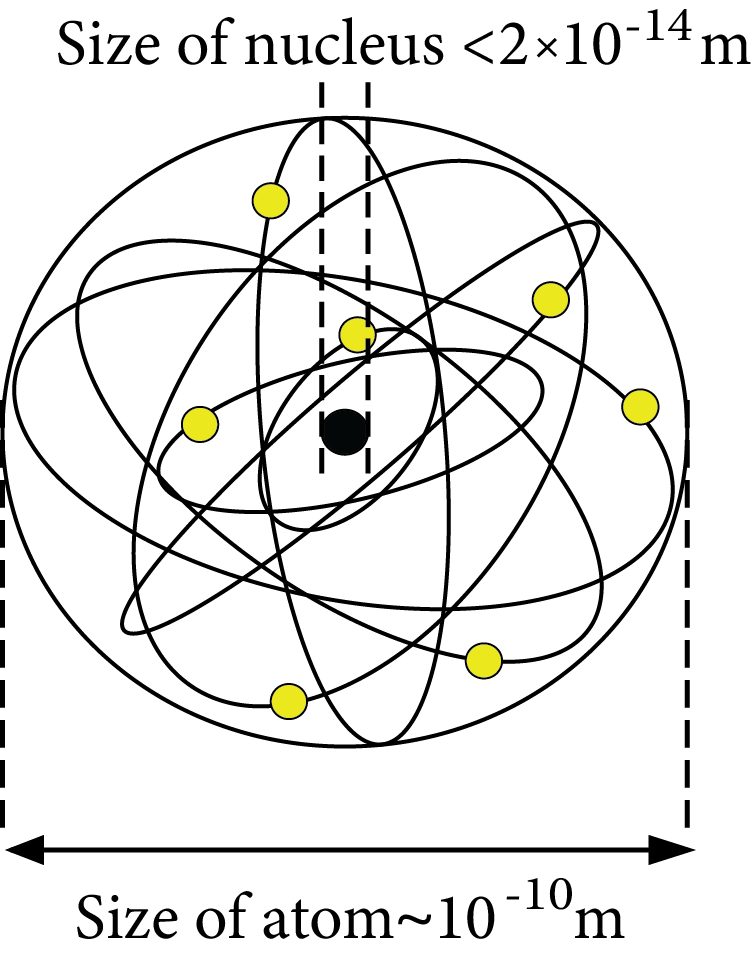
Size of the Nucleus

Density Of Nucleus: The density of nuclei does not depend on the mass number, so it is the same for all nuclei.

$\rho  = \dfrac{{3m}}{{4\pi R_0^3}}$; m is the average mass of a nucleus.

Nuclear density is the density of the nucleus of an atom, averaging about $2.3 \times 10^{17} \mathrm{~kg} / \mathrm{m}^{3}$.

${{\rho   =  }}\dfrac{{{\text{Mass of nucleus}}}}{{{\text{Volume of nucleus}}}}$

Radioactivity: This is a phenomenon in which nuclei spontaneously decay and emit one or more radiations such as alpha particles, beta particles, and gamma rays. 

Radioactivity Decay: This is a transmutation process in which  radioactive rays are emitted from the nucleus. This process cannot be accelerated or decelerated by  physical or chemical processes. 

Radioactivity Law: According to this law, the decay rate  of radioactive atoms at a given time is proportional to the number of atoms present at that time.

Nuclear Force: The force that acts within the nucleus or  between nucleons is called nuclear force. Nuclear force is the strongest force in nature. 

• It's a very short-distance force of attraction

• It's not central. Non-conservative force. 

• It is neither gravitational or electrostatic force. It's free. 

• 100 times the electrostatic force and 1038 times the gravity.

Mass Defect 

The difference between the total mass (M) of all nucleons and the mass (m) of the nucleus  is called a mass defect.

$\Delta m = M - m $

$\Delta m = \left[ {Z{m_p} + (A - Z){m_n} - {m_n}} \right]$

Nuclear Binding Energy

The minimum energy required to separate a nucleon from a nucleus to an infinite distance  is called the nuclear binding energy.

${\text{Nuclear binding energy per nucleon  =  }}\dfrac{{{\text{Nuclear binding energy}}}}{{{\text{Total number of nucleons binding energy}}}}$

Binding Energy Per Nucleon:

Nuclear binding energy is the minimum amount of energy required to disassemble or break down an atom's nucleus into its constituent subatomic particles (protons and neutrons).

The term nucleon refers to the group of subatomic particles known as protons and neutrons that reside in the nucleus.

The difference between nuclear attraction and electric force disruptive energy is equal to the net binding energy associated with a given nucleus.

It is important to note that the net binding energy per nucleon increases as the number of nucleons increases.

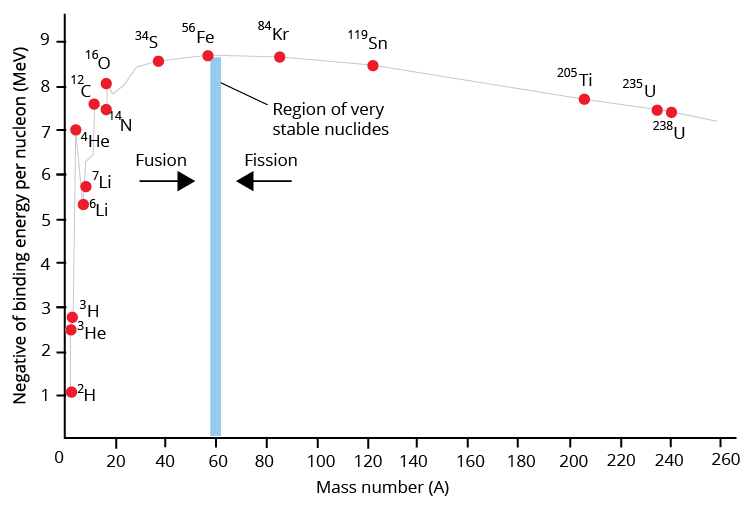
Binding Energy Per Nucleon Versus Mass Number.

As a result, the atomic number determines the net binding energy per nucleon.

Iron, with a mass of 56, is one of the most stable elements. Iron is said to have a high binding energy per nucleon.

Elements with lower and higher mass numbers per nucleon have lower and higher stability.

A nucleus' total mass is less than the total mass of the nucleons that make up the nucleus. This difference is referred to as the mass defect. It is equivalent to the nucleus's binding energy when using $E=m c^{2}$.

Fission is when an unstable nucleus is converted into more stable nuclei with a lower total mass. The binding energy is released due to the mass difference, or mass defect.

The mass of the nucleus formed during fusion is slightly less than the total mass of the original nuclei. Because the nucleus formed is more stable, the mass defect is the released binding energy.

Radioactivity: 

When a particular nucleus emits the radiation spontaneously, such certain nuclei are known to be radioactive and this phenomenon of disintegration of nuclei spontaneously is called radioactivity.

Types of Radioactive Radiation

• Alpha rays: The rays which bends towards the negative plate by carrying the positive charge.

• Beta rays: The rays which bends towards the positive plate by carrying the negative charge.

• Gamma rays are uncharged rays that pass straight through the electric field.

Different Types of Radiations:

Alpha Radiation: 

The α- particle which is similar to the helium nucleus includes protons and  two neutrons. It is the emission part of an alpha particle from an atom’s nucleus. When an α-particle is emitted by an atom the mass of an atom decreases by 4 units.

$U_{92}^{238} \to He_2^4 + Th_{90}^{234}$.

Beta Radiation:

When an atom emits β- particles, it transmutes the neutron into a neutron and an electron. During this emission. The mass of the atom will not change. This resulted in the increase of atomic number by one.

$C_6^{14} \to e_{ - 1}^0 + N_7^{14}$

Gamma Radiation:

It involves the emigration of electromagnetic energy from a snippet’s nucleus. During gamma radiation, no patches are emitted; therefore, it doesn't beget the vacillation of atoms.

$Co_{27}^{60} \to Ni_{28}^{60} + e_{ - 1}^0 + 2\gamma _0^0$

Radioactive Disintegration:

Converting one radioactive nuclei into another by emitting the 𝛂, 𝛃 and 𝛄 rays. Methods of Radioactive disintegration:

• Alpha Decay: Emission of an alpha particle, decreases the atomic number by 2 units and mass number by 4 units.

$U_{92}^{238} \to He_2^4 + Th_{90}^{234}$

Number of $\alpha $-particle emitted=$\dfrac{{{\text{Change in mass number}}}}{{\text{4}}}$

• Beta Decay: Emission of $\beta  - $particle, increases the atomic number y 1 unit but does not affect the mass. 

This emission gives isotopes. 

$C_6^{14} \to e_{ - 1}^0 + N_7^{14}$

Number of $\beta  - $particles emitted = $2 \times \text{Number of} \alpha  - \text{particles  -  (change in atomic number)}$

• Gamma Decay: Emission of γ-rays does not affect the atomic and mass numbers.

• 
  

The Properties of Alpha, Beta & Gamma Decay:

Alpha Rays:

Positively charged particles are alpha rays. The alpha particle is a highly active and energetic helium atom with two neutrons and two protons. These particles have the least penetration power but the greatest ionisation power. Because of their high ionisation power, they can cause serious harm if they enter the body. They are capable of ionising a large number of atoms over a short distance. It is because radioactive substances emitting alpha particles must be handled with rubber gloves.

Beta Rays:

The inner nucleus releases extremely energetic electrons known as beta particles. They have a negligible mass and a negative charge. A neutron in the nucleus splits into a proton and an electron when a beta particle emits. As a result, the electron is rapidly emitted by the nucleus. Beta particles have a higher penetration power than alpha particles and can easily pass through the skin. Even though their ionisation power is low, beta particles can be dangerous and any contact with the body should be avoided.

Gamma Rays:

Gamma rays are waves that originate at the high-frequency end of the electromagnetic spectrum and have no mass. They have the greatest penetrating power. They are the most penetrating but least ionising, and keeping them out of the body is extremely difficult. Gamma rays have a high energy density and can travel through thick concrete and thin lead.

Rate of Disintegration:

The number of atoms of radioactive elements that disintegrate in a unit time.

Rate of decay = $\dfrac{{ - DN}}{{dt}}\alpha N$

(Or) $\dfrac{{ - dN}}{{dt}} = kN$

Where, k= decay constant

$k = \dfrac{{2.303}}{t}\log \dfrac{{{N_0}}}{{{N_t}}}$

Here, ${N_0}$=number of atoms initially

${N_t}$= number of atoms after time t.

All radioactive changes follow first order kinetics. Total life span of a radioactive element is infinite.

Half-Life Period $\left( {{t_{\dfrac{1}{2}}}} \right)$:

For a first-order reaction, the rate constant can be mathematically expressed as follows:

$k=\dfrac{2.303}{t} \log \dfrac{[R]_{0}}{[R]}$

From the definition of reaction half-life, at $t=t_{1 / 2},[R]=[R]_{0} / 2$. Substituting these values in the expression for the first-order rate constant, the following equation is obtained:

$k=\dfrac{2.303}{t_{1 / 2}} \log \dfrac{\left[R_{0}\right]}{[R]_{0} / 2}$

Rearranging the expression to find the value of $t_{1 / 2}$ :

$t_{1 / 2}=\dfrac{2.303}{k} \log (2)=\dfrac{0.693}{k}$

Thus, the half-life of a first-order reaction is given by $0.693 / \mathrm{k}$.

The amount of time required by a radioactive substance (or one half the atoms) to disintegrate or transform into a different substance.

${t_{\dfrac{1}{2}}} = 0.693/k$

Half life is related to the total time as, $T = n \times {t_{\dfrac{1}{2}}}$

Where, n is calculated from the relation ${N_t} = {N_0}{\left( {\dfrac{1}{2}} \right)^n}$

${N_0}$= initial amount.

${N_1}$= amount after time T.

n = number of half-lives.

Average Life $\left( \lambda  \right)$

Life expectancy or median lifetime (τ) of a radioactive element is the ratio of the total lifetime of all atoms to the  total number of atoms initially present  in the sample.

$N_{t}=N_{0} e^{-\lambda t}$

$N_{0}=$ initial quantity $\quad \lambda=$ decay constant

$N_{t}=$ quantity after time $t \quad t=$ time period

Hence,

$N_{t}=\dfrac{N_{0}}{2}$

$t=t_{1 / 2}$

$\dfrac{N_{0}}{2}=N_{0} e^{-\lambda t_{12}}$

$\dfrac{1}{2}=1: e^{-\lambda t_{1 / 2}} $

$\log _{e}{ }_{e}^{1 / 2}=-\lambda t_{1 / 2}$

$t_{1 / 2}=\dfrac{\log _{0}^{2}}{\lambda} $

$t_{1 / 2}=\dfrac{0.693}{\lambda}$

$\lambda  = \dfrac{1}{k}$

$\dfrac{1}{k} = \dfrac{1}{{0.693/{t_{1/2}}}} = 1.44 \times {t_{1/2}}$

Activity of Radioactive Substance:

Activity is defined as the number of disintegrations occurring in a radioactive substance per second. Higher is the activity of a substance, faster will be its disintegration.

$Activity = kN = \dfrac{k \times \text{ wt. of the element} \times N_A}{\text{ atomic wt. of the element}}$

(${N_A}$=Avogadro’s number =$6.023 \times {10^{23}}$).

Nuclear Reactions:

Nuclear Fission: Nucleus in the atoms splits into smaller parts releasing a huge amount of energy in the process.

$_{92}{U^{235}}{ + _0}{n^1} \to B{a_{56}}^{141} + Kr_{36}^{92}$

Nuclear Fusion: The reaction in which two or more elements fuse together to form a large element, by releasing a large amount of energy.

$H_1^2 + H_2^2 + H_3^2 \to He_2^4 + H_1^1 + n_0^1 + 21.6Mev$

Application of Radioactivity:

• Estimation of age (Dating Technique)

Carbon dating technique.

Uranium dating technique.

• Medical use

In therapeutic procedures.

Imaging procedure.

Carbon Dating:

Carbon dating is one of the most widely used methods in archaeology for dating organic objects up to 50,000 years old. This method is based on the idea of carbon-14 isotopes radiatively decaying over thousands of years. Scientists have discovered that radioactive molecules decay at a specific rate determined by the atomic number and mass of the decaying atoms.

The ratio of radioactive isotopes to the estimated initial concentration of these isotopes at the time of the organism's death can be used to calculate the approximate age of the decaying material. Scientists have concluded that the ratio of Carbon-12 to Carbon-14 isotopes in the atmosphere has changed very little, implying that the relationship between these two should be very similar to how it is today.

Radioactive Series:

Any of four independent sets of unstable heavy atomic nuclei that decay through a series of alpha and beta decays until a stable nucleus is obtained. These four chains of consecutive parent and daughter nuclei start and end among elements with atomic numbers greater than 81, the atomic number of thallium; the members of each set are genetically related through alpha and beta decay.

The thorium, uranium, and actinium series, known as natural or classical series, are led by naturally occurring species of unstable nuclei with half-lives comparable to the elements' ages. These three radioactive series had been fully defined by 1935. The neptunium series, the fourth set, is led by neptunium-237, which has a half-life of 2,144,000 years.

(1) If the isotope that results from radioactive decay is itself radioactive, then it will also decay and so on.

(2) The sequence of decays is known as the radioactive decay series. Most of the radionuclides found in nature are members of four radioactive series. 

These are as follows:

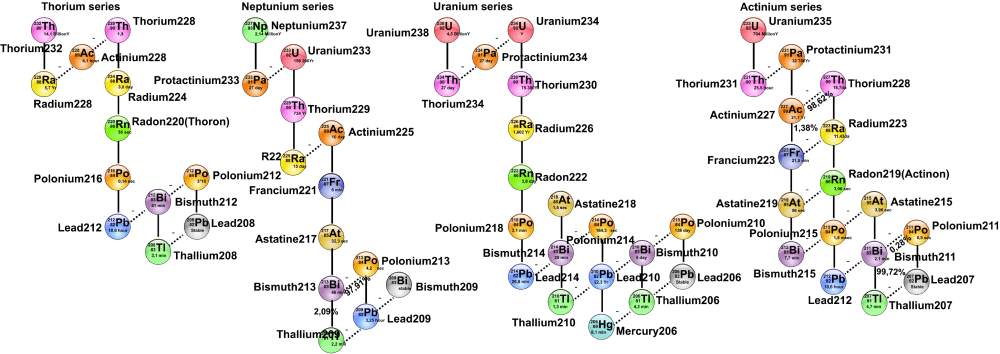
Decay Series

Important Formulas:

• Einstein’s Mass-Energy Equivalence: $E=m c^{2}$1 a.m.u $\equiv 931.5$ Me.V, where $1 \mathrm{eV}=1.6 \times 10^{-19} \mathrm{~J}$ and $1 \mathrm{MeV}=1.6 \times 10^{-13} \mathrm{~J}$

• Binding Energy Per Nucleon: $\bar{B}=\dfrac{\text { Total binding energy }}{\text { Total number of nucleons }}=\dfrac{B E}{A}=\dfrac{\Delta m c^{2}}{A}$

$=\dfrac{c^{2}}{A}\left[Z m_{p}+(A-Z) m_{n}-M\left({ }_{Z} X^{A}\right)\right]$ 

• Half Life of a Radioactive Substance: $T_{1 / 2}=\dfrac{0.693}{\lambda}=\dfrac{\log _{e} 2}{\lambda}$

• Mean life of a Radioactive Substance: $\tau=\dfrac{1}{\lambda}=\dfrac{\mathrm{T}_{1 / 2}}{0.693}$

• Bohr's Atomic Model

(a) $\mathrm{L}=\mathrm{mvr}=\dfrac{\mathrm{nh}}{2 \pi}$

(b) $\mathrm{hv}=\mathrm{E}_{i}=\mathrm{E}_{f}=\dfrac{\mathrm{hc}}{\lambda}$

(c) Radius of nth orbit :

$r_{n} \propto \dfrac{n^{2}}{Z}, \quad r_{n}=\dfrac{n^{2}}{Z}\left(\dfrac{h^{2}}{4 \pi^{2} m k^{2}}\right)$

(d) Velocity of electron in nth orbit :

$\mathrm{v}_{\mathrm{n}}=\dfrac{\mathrm{Z}}{\mathrm{n}}\left(\dfrac{\mathrm{c}}{137}\right)=\dfrac{\mathrm{Z}}{\mathrm{n}} \alpha \mathrm{c}$ (where $\alpha=\dfrac{2 \pi \mathrm{Ke}^{2}}{\mathrm{ch}}=\dfrac{1}{137}=$ fine structures constant)

• Distance of Closest Approach:

• $r_{0}=\dfrac{2 Z \mathrm{e}^{2}}{\left(4 \pi \varepsilon_{0}\right) \mathrm{E}},\left(\text { where } \mathrm{E}=\dfrac{1}{2} \mathrm{mu}^{2}=\mathrm{KE} \text { of the } \alpha-\text { particle }\right)$

• Number of Emission Lines from Excited State: $\mathrm{n}=\mathrm{n}(\mathrm{n}-1) / 2$

• Time period of revolution: $T_{n} \propto\left(n^{3} / Z^{2}\right)$

• Frequency of Revolution: $\mathrm{V}_{\mathrm{n}} \propto\left(\mathrm{Z}^{2} / \mathrm{n}^{3}\right)$

• Current due to Orbital Motion: $\mathrm{I}_{\mathrm{n}} \propto\left(\mathrm{Z}^{2} / \mathrm{n}^{3}\right)$

• Magnetic Moment:

(a) $\mathrm{M}_{\mathrm{n}}=(\mathrm{eL} / 2 \mathrm{~m})=(\mathrm{nhe} / 4 \pi \mathrm{m})$;

(b) $\mathrm{M}_{1}=(\mathrm{eh} / 4 \pi \mathrm{m})=\mu_{\mathrm{B}}=$ Bohr Magneton $=9.27 \times 10^{-24} \mathrm{Am}^{2}$

• Magnitude of Angular Momentum: $\mathrm{L}=\sqrt{[\ell(\ell+1)]}(\mathrm{h} / 2 \pi)$

• Angle of Angular Momentum Vector from $z$ - Axis

(a) $\cos \theta=\left[\mathrm{m}_{l} \sqrt{ }\{\ell(\ell+1)\}\right]$

(b) the least angle is for $\mathrm{m}_{\ell}=\ell$ i.e. $\cos \theta_{\min }=[\ell / \sqrt{ }\{\ell(\ell+1)\}]$

Common Errors or Mistakes that Should Be Avoided By the Students Keeping the Exam Point of View:

• Students should have the proper command over the following topics as they are considered to be the most important topics in this chapter: Nuclear size and nuclear density, Mass energy relation and nuclear binding energy, Radioactivity, Alpha, beta and Gamma decay and Nuclear fission and fusion

• Students also write improper units without checking their compatibility.

• The student should avoid calculation errors when doing problems as lots of calculation problems are asked in the exams.

• Before sitting for exams, students must remember important formulas like Mass energy relation and nuclear binding energy, the Law of Radioactive Decay, and Nuclear size and density.

• Students forget to put the correct data in the working formula, which teachers use to check how effectively the students are learning.

• For questions requiring the reason for a certain condition, first, students are required to state the cause and then the consequence of the condition.

Importance of the Chapter Nuclei

This chapter will explain the advanced fundamental principles based on the nucleus of an atom. The structure of a nucleus will be substantiated by the experiments conducted. Students will learn how the outcomes of these experiments consolidated the fact that a nucleus is made of protons and neutrons.

Students will learn what protons and neutrons are and how they differ from each other. This chapter will also teach how the aggregate mass of neutrons and protons constitutes the mass of an atom. It will also conclude that the aggregate mass of electrons outside the nucleus is negligible.

Students will learn how the entire mass of an atom is densely packed in the nucleus. They will find out that a major part of the volume of an atom is covered by the electrons and their shells. A small part of the volume of an atom is occupied by the nucleus compared to the mass packed in it.

This chapter will also explain how to measure the mass of an atom using an atomic mass unit. It will teach other scientific terms related to the nuclei of an atom such as atomic number, mass number and their relationship.

Advanced concepts related to nuclei will be imparted in the domains of radioactivity, radioactive decay, nuclear density, and half-life. The laws related to radioactive decay will also be explained elaborately in this chapter.

As you can see, this chapter is of utmost importance as it imparts the fundamental knowledge about a nucleus of an atom and the subatomic particles it contains.

Benefits of Vedantu’s Class 12 Physics Nuclei Notes

• These notes have been prepared to offer a simpler explanation of all the scientific terms, laws, and derivations of this chapter. Students will not have to prepare a concise note when the experts have already done it for them.

• The concise version of the concepts, principles, and definitions related to the nuclear structure of an atom will help you to revise this chapter without wasting time. You can make good use of these notes during your revision sessions.

• Recall what you have studied in this chapter by reading these notes before an exam. Its simpler structure will help you remember what you have studied very quickly.

Download Atoms and Nuclei NEET Notes PDF

Make your NEET preparation more efficient by performing Nuclei Class 12 notes PDF download for free. These notes will deliver the simplest explanation of the features of a nucleus and its structure. You will also learn about protons and neutrons in a better way when you refer to the revision notes. Get these notes today and prepare for the NEET exam in a better way.

NEET Physics Revision Notes - Chapter Pages

Other Important Links