Laws of Motion Class 11 Notes NEET 2024 Physics

Aristotle’s Fallacy:

The Aristotelian law says that external forces are necessary to keep a body in motion, but external forces are also necessary to overcome frictional forces in solids and viscous forces in fluids. These forces are always present in nature.

Newton studied the Ideas of Galileo regarding the motion of an object. He formulated three fundamental laws that govern the motion of objects. These three laws are known as Newton's laws of motion, which are as given below:

Newton's First Law of Motion

Any object remains in the state of rest or in a uniform Motion along a straight line until it is compelled to change the state by applying an external force. This law as also known as Law of Inertia.

Tips: How to find causes the motion of a body which is initially in the state of rest.

• First apply the first law of motion. 

• Now check the options by putting law.

• Now if only one option matches then that option is correct, if not then hop on to the other options.

Applications of Newton's First Law of Motion

The following applications are based on Newton's first law of motion:

1. The passengers in a bus fall backward when it starts suddenly.

2. This is because the sudden start of the bus brings motion to the bus as well as to our feet in contact with the floor of the bus but the rest of our body opposes this motion because of inertia, so they fall backwards.

3. When a carpet or a blanket is beaten with a stick, then the dust particles separate out from it.
   
   

Newton's Second Law of Motion

The second law of motion states that the rate of change of momentum of an object is proportional to the applied external force and takes place in the direction in which external force acts.

According to the second law of motion, force $F \propto \dfrac{\text { change in momentum }}{\text { time }}$

We know that, change in velocity with respect to time is called acceleration, $\left[ a=\dfrac{v-u}{t} \right]$

And also we know that momentum $(p)=m\times v$

Then, ${{p}_{2}} = mv$ and ${{p}_{1}} = mu$

$F = K\dfrac{{{p}_{2}}-{{p}_{1}}}{t}=K\dfrac{mv-mV}{t}=K\dfrac{m(v-u)}{t}=Kma\quad $

$K=\text { constant of proportionality. }$

Application of Newton's Second Law of Motion

The following applications are based on Newton’s second law of motion:

1. A cricket player (or fielder) moves his hands backward on catching a fast cricket ball.

2. During athletics meet, a high jumping athlete is provided either a cushion or a heap of send on the ground to fall upon.
   
   

Law of Conservation of Linear Momentum

When no external force acts on a system of several interacting particles, the total linear momentum of the system is conserved. The total linear momentum is the vector sum of the linear momentum of all the particles of the system.

Consider an isolated system (the system on which no external force acts) of particles. Suppose the m particles have masses ${{m}_{1}},{{m}_{2}},{{m}_{3}}$……${{m}_{n}}$ and are moving with velocities ${{v}_{1,}}{{v}_{2}},{{v}_{3,\ldots }}{{v}_{n}}$ respectively.

Then total linear momentum of the system is

$\text{p}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}+{{m}_{3}}{{v}_{3}}+\ldots +{{m}_{n}}{{v}_{n}}$

$\text{p}={{p}_{1}}+{{p}_{2}}+{{p}_{3}}+\ldots +{{p}_{n}}$

If $F$ is the external force acting on the system, then according to Newton’s second law $F=\dfrac{dp}{\text{ dt }}$

For an isolated system, $F=0$ or $\dfrac{dp}{dt}=0$

As the derivative of a constant is zero, so

${{\text{p}}_{1}}+{{\text{p}}_{2}}+{{\text{p}}_{3}}+\ldots {{\text{p}}_{n}}=\text{ constant }$

Thus in the ambiance of any external force, the total linear momentum of the system is constant. This is the law of conservatism of linear momentum.

Newton's Third Law of Motion

When two bodies interact, they apply forces to one another that are equal in magnitude and opposite in direction. The third law is also known as the law of action and reaction.

Applications of Newton's Third Law of Motion

Some application of Newton’s third law is as follows:

1. Walking of a person, a person can walk because of Newton's third law of motion. During walking a person pushes the ground in a backward direction and in the reaction the ground also pushes the person with an equal magnitude of force but in the opposite direction. This enables him to move in a forwarding direction against the push.

2. Recoil of the gun when the bullet is fired from a gun, the bullet also pushes the gun in the opposite direction with an equal magnitude of force. This results in the gunman feeling a backward push, i.e., recoil force from the butt of the gun.

Equilibrium of a Particle

A particle is in equilibrium if it does not move when acted upon by two or more forces. Thus, the force resultant is zero, and the particle remains stationary.

i.e., $\Sigma \vec{F}=0$

Then $\Sigma \mathrm{F}_{\mathrm{x}}=0, \Sigma \mathrm{F}_{\mathrm{y}}=0$ and $\Sigma \mathrm{F}_{\mathrm{z}}=0$

Stable Equilibrium

When a body is slightly displaced from equilibrium position, it tends to regain its original position, it is said to be in stable equilibrium. This means that P.E. is minimum  $\left(\dfrac{d^{2} u}{d r^{2}}=+v e\right)$

So the centre of gravity is at its lowest point.

Unstable Equilibrium

A body is considered to be in unstable equilibrium if it travels in the direction of the displacement after being displaced from the equilibrium position.

P.E. is the maximum in this instance.$\left(\dfrac{d^{2} u}{d r^{2}}=-v e\right)$

As a result, the centre of gravity is highest.

Impulse

A large force that acts on an object for a very short time and produces a large change in its momentum is called an impulsive force.

The impulse of a force acting on an object is equal to the product of the large force and small time interval for which it acts on the object.

Impulse $(I)=$ Force $\times $ Time

Its unit is Newton second.

Friction

Friction is a force which opposes the relative motion between the two objects when one object moves or tries to move over the surface of another object.

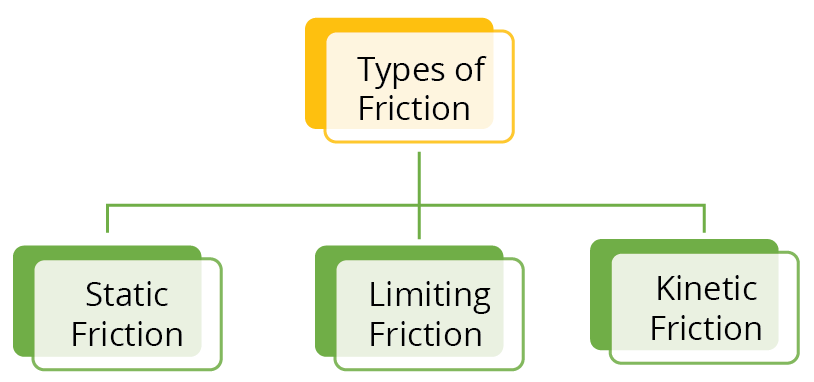
Types of Friction

There are three types of friction:

Types of Friction

Static Friction: It is an opposing force which comes into play when one object tends to move over the surface of another object.

Limiting Friction: The maximum static frictional force which comes into play when one object just begins to slide over the surface of another object.

Kinetic Friction: The opposing force that comes into play when one object moves over the Surface of another object.

Kinetic Friction is of Two Types: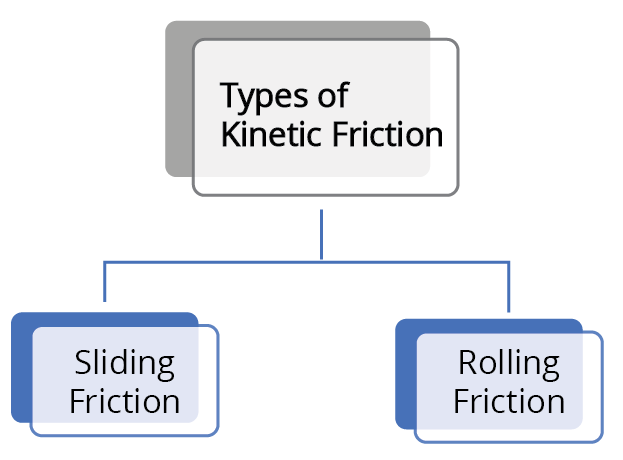

Types of Kinetic Friction

Sliding Friction: It comes into play when one object slides over the surface of another object.

Rolling Friction: It comes into play when one object rolls over the surface of another object.

Force and its Types

Force is the interaction that alters or seeks to alter the body's resting or moving condition after acting on a body. Six different types of forces rule nature.

Conservative Force

It is the term for a force whose actions are unaffected by the direction taken. The conservative force's work depends solely on the starting and ending points. Therefore, a conservative force in a closed loop does not work. Examples include the forces of gravity, static electricity, and elastic force.

Non-conservative Force

The term "nonconservative force" refers to a force whose work depends on the path a particle takes.

Example: Friction force, air drag force, etc.

Constant Force

Constant force is the term used to describe a force that is constant over time and space. It always stays the same.

Variable Force

Variable force is defined as a force that varies in time and distance. It depends on various factors, such as time, space, velocity, etc.

Contact Force

Requires physical contact between the body and the force's application.

The Non-Contact Force doesn't need the body and the force's agent to make eye contact. 

In mechanics, gravity is the sole non-contact force that we deal with. Other non-contact forces include magnetic force, electrostatic force, and others. They do not, however, fall under the mechanic's category. In the following articles, we will learn more about them. However, many exam questions focus primarily on the various Contact Forces. We will thus research them.

Types of Contact Forces

1. Tension force

2. Friction force

3. Spring force

4. Drag force

5. Pseudo force

1. Tension Force

The mass that is connected to the string is balanced by the tension in the string.

2. Friction Force

"The frictional force occurs between the two surfaces when two items are in touch and one of the objects moves or desires to move."

Alternatively stated, "the force preventing the relative motion of solid surfaces is known as friction."

For instance, the car's tyres experience friction as it travels along the road. When we push a big stone and it doesn't move, friction force stops the motion.

The friction force is usually denoted by "f".

Friction force $(f)=\mu \mathrm{N}$

Here $\mathrm{N}$ is the normal force and is $\mu$ the coefficient of friction.

Types of Friction

Friction is divided into the following categories according to its state of motion and its state of rest:

Static Friction:

• Static friction is the friction that exists between the surfaces of two bodies when they are not moving relative to one another but nevertheless have a tendency to move. When the body is at rest, there is friction.

• For example: when trying to move a block that is resting on a table while applying force, yet the block does not move. So, in this instance, static friction is acting. In this case, the static friction force balances the applied force.
  
  

Static Friction

• Friction is being adjusted via static friction. The amount of static friction grows along with an increase in the applied external force until it reaches a specified maximum value. The limiting value of static friction is referred to as this maximum value.

• When an external force is applied to the body, static friction only becomes a factor. Static friction won't exist if a body is held at rest and no force is used to move it.

• Static friction has a limit value that is independent of the contact area. The only factors are the surface's composition and the normal force.$\left(f_{s}\right)_{\max }=\mu_{s} N$

• Here $\mu_{s}$ is the coefficient of static friction and $\mathrm{N}$ is the normal force acting on the block.

• The force of static friction is typically expressed by:$\left(f_{s}\right)_{\max } \leq \mu_{s} N$.

• If the external force $(\mathrm{F})$ exceeds this limiting friction $\left(f_{s}\right)_{\max }$ then the block starts moving on the surface.

• Rolling friction is the friction that occurs between a body's surface and a surface when a body is rolling on it.

• When a body is rolling, the point of contact with the surface is not moving relative to the surface that the body is rolling on.

• A finite area (not a point) of the body comes into contact with the surface as a body rolls because the surfaces in contact temporarily flex a little. The overall result is that motion is opposed by the contact force component that is parallel to the surface.

• Rolling friction is denoted by $\left(f_{R}\right)$.

• For example: The friction caused by the road on the wheel of a moving vehicle is known as rolling friction. friction on the bicycle wheel.
  
  

Rolling Friction

Points to Remember

• There is a difference between the static and kinetic coefficients of friction. The type of surface and temperature have an impact on the coefficient of friction.

• Because any object must have enough force of friction between it and the surface in order to prevent sliding on it and conduct a pure rolling motion, rolling friction is always less than static friction. Because there is no relative motion at the point of contact, the rolling friction produces no effort.

Pseudo Forces:

There is a force exerted on the object we are witnessing whenever we observe it in relation to an accelerating body. A pseudo force is what we refer to as here.

Imaginary force is known as pseudo force.

Pseudo force $\left(F_{P}\right)=$ ma

Where $a$ is the acceleration of the body with respect to which we are watching the object, and $m$ is the mass of the object that we are observing.

A pseudo force will exert itself on a body outside the car, for instance, if we see it while we are seated inside a speeding vehicle.

Types of Non-Contact Forces

These forces act at a distance.

1. Gravitational Force: Gravitational force is the pull of gravity that one object experiences from another due to their respective masses. It is inversely proportional to the square and directly proportional to the product of the masses of those items. 

$\mathrm{F}\propto\dfrac{\left(\mathrm{m}_{1}\mathrm{~m}_{2}\right)}{\mathrm{r}^{2}}$

Where,

$F$ is the gravitational force between two bodies

$m_{1}$ is the mass of the first body

$m_{2}$ is the mass of the second body

$r$ is the distance between the centres of two bodies

The force exerted by two bodies with mass $\mathrm{m}_{1}$ and $\mathrm{m}_{2}$, whose centres is $\mathrm{r}$ units apart is given as:

$F=G \dfrac{\left(m_{1} m_{2}\right)}{r^{2}}$

2. Electrical Force: Electric force is the interaction of any two charged bodies that is either attractive or repulsive. 

The magnitude of the electrostatic interaction between two point charges is inversely proportional to the square of the distance between them and directly proportional to the scalar multiplication of the charges.

Electric force formula can be obtained from Coulomb’s law as follows:

$\vec{F}=K \dfrac{q_{0} q_{1}}{r^{2}} \hat{r}$

Where,

- $\vec{F}$ is the electric force directed between two charged bodies

- $\mathrm{K}$ is the constant of proportionality

- $q_{0}$ and $q_{1}$ are the amounts of charge on each body

- $r$ is the distance between the charged bodies

- $\hat{r}$ is the variable unit vector

3. Magnetic Force: The attraction or repulsion that develops between electrically charged particles as a result of their motion is known as magnetic force.

We know that the formula of magnetic force is $F=q v B \sin \theta$

$\boldsymbol{F}=$ magnetic force

$q$ = charge of moving particle

$v=$ particle velocity

$B=$ magnetic field

$\theta=$ angle between velocity and magnetic field vectors

The Expression for Velocity of Body Moving in a Vertical Circle:

Consider a little object with mass m that is strung up on one end and rotated in a vertical circle with radius r. In this instance, the body's acceleration rises while it moves up the vertical circle and falls when it moves down it. As a result, the body's speed is constantly changing. The vertical circle's bottom position is where it is highest, and its top position is where it is lowest. As a result, the body is not moving in a circular motion that is constant. The weight "mg," regardless of the particle's location on the circle, always works vertically downward.

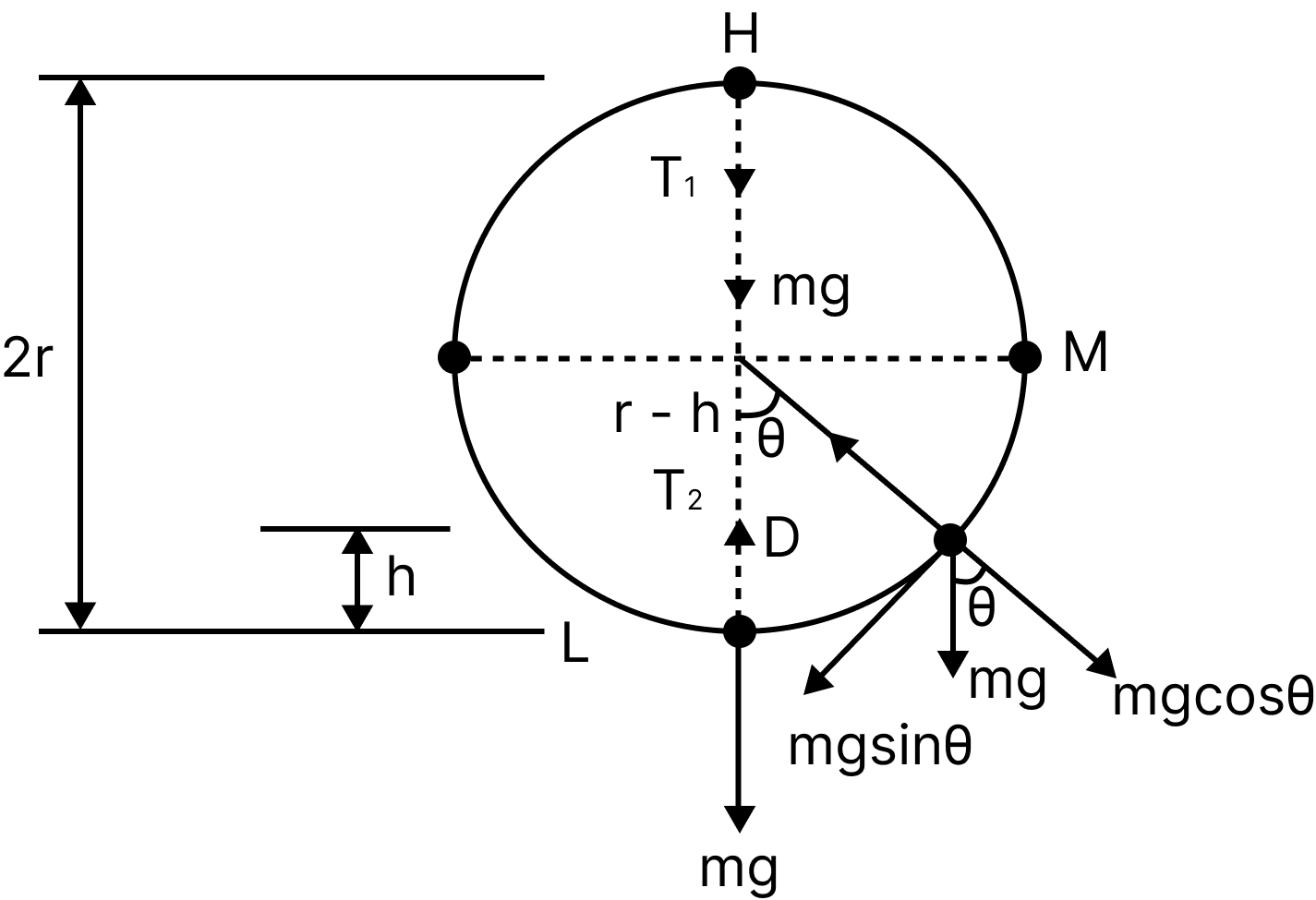
Velocity of Body Moving in a Vertical Circle

Energy at point $P=$ Energy at point $L$

$\dfrac{1}{2} m v^{2}+m g h=\dfrac{1}{2} m u^{2} $

$\therefore v^{2}+2 g h=u^{2} $

$\therefore v^{2}=u^{2}-2 g h $

$\therefore v=\sqrt{u^{2}-2 g h} \ldots \ldots \ldots . .(1)$

This is an expression for the velocity of a particle at any point performing a circular motion in a vertical circle.

Consider the centripetal force at point $P$

$T-\mathrm{mg} \cos \theta=\dfrac{m v^{2}}{r} \ldots \ldots \ldots.(2) $

$\therefore T=\mathrm{mg} \cos \theta+\dfrac{m v^{2}}{r}$

From figure, $\cos \theta=\dfrac{r-h}{r}$

Substituting in equation (2)

$T=\mathrm{mg}\left(\dfrac{r-h}{r}\right)+\dfrac{m v^{2}}{r} $

$\therefore T=\dfrac{\mathrm{m}}{r}\left(\mathrm{~g}(r-h)+v^{2}\right) $

$\text { But } v^{2}=u^{2}-2 g h $

$T=\dfrac{\mathrm{m}}{r}\left(g r-g h+u^{2}-2 g h\right) $

$T=\dfrac{\mathrm{m}}{r}\left(u^{2}-3 g h+g r\right)$

This is the expression for the tension in the string.

Case - I: When the body is at the lowermost position i.e. body is at L)

$(\mathrm{h}=0)$

$\text { We have, } T=\dfrac{\mathrm{m}}{r}\left(u^{2}-3 g h+g r\right) $

$T_{L}=\dfrac{\mathrm{m}}{r}\left(u^{2}-3g(0)+gr\right)=\dfrac{\mathrm{m}}{r}\left(u^{2}+g r\right)$

Case - II: When the body is at the uppermost position i.e. body is at $\mathrm{H}(\mathrm{h}=2 \mathrm{r})$

$\text { We have, } T=\dfrac{\mathrm{m}}{r}\left(u^{2}-3 g h+g r\right) $

$T_{H}=\dfrac{\mathrm{m}}{r}\left(u^{2}-3g(2r)+gr\right)=\dfrac{\mathrm{m}}{r}\left(u^{2}-5 g r\right)$

Case - III: When the string is horizontal i.e. body is at $M(h=r)$

$\text { We have, } T=\dfrac{\mathrm{m}}{r}\left(u^{2}-3 g h+g r\right) $

$T_{M}=\dfrac{\mathrm{m}}{r}\left(u^{2}-3g(r)+gr\right)=\dfrac{\mathrm{m}}{r}\left(u^{2}-2 g r\right)$

Relation Between Tension at the Highest point and at the Lowest Point:

$T_{L}-T_{H}=\dfrac{\mathrm{m}}{r}\left(u^{2}+g r\right)-\dfrac{\mathrm{m}}{r}\left(u^{2}-5 g r\right) $

$\therefore T_{L}-T_{H}=\dfrac{\mathrm{m}}{r} u^{2}+m g-\dfrac{\mathrm{m}}{r} u^{2}+5 m g $

$\therefore T_{L}-T_{H}=6 \mathrm{mg}$

Lowest Point $\mathrm{L}(\mathrm{h}=0)$ :

This is the least speed at which the body must move in order for it to loop, or complete one full round of the circle.

Hence at the highest point $T_{H} \geq 0$

$\therefore \dfrac{\mathrm{m}}{r}\left(u^{2}-5 g r\right) \geq 0 $

$\therefore u^{2}-5 g r \geq 0$

$\therefore u^{2} \geq 5 g r $

$\therefore u \geq \sqrt{5 g r}$

When String is Horizontal $(\mathrm{h}=\mathrm{r})$ :

We have,

$ v=\sqrt{u^{2}-2 g h} $

$\therefore v =\sqrt{(\sqrt{5 g r})^{2}-2 g(r)}$

$\therefore v =\sqrt{5 g r-2 g r}=\sqrt{3 g r}$

Tension in String and Acceleration of Particle:

At the Highest Point:

$T_{H}=\dfrac{m v^{2}}{r}+m g$

$a=v^{2} / r$

Banking of Roads:

Banking of roads is the practice of raising the outer borders of curving roads over the inner edge in order to provide cars the required centripetal force to make a turn safely. Let's review what centripetal force is now. It is the force that causes an item to move in an angular or circular fashion by pulling or pushing it in that direction as it moves. Let's talk about the angle of banking and the vocabulary used in road banking in the following parts.

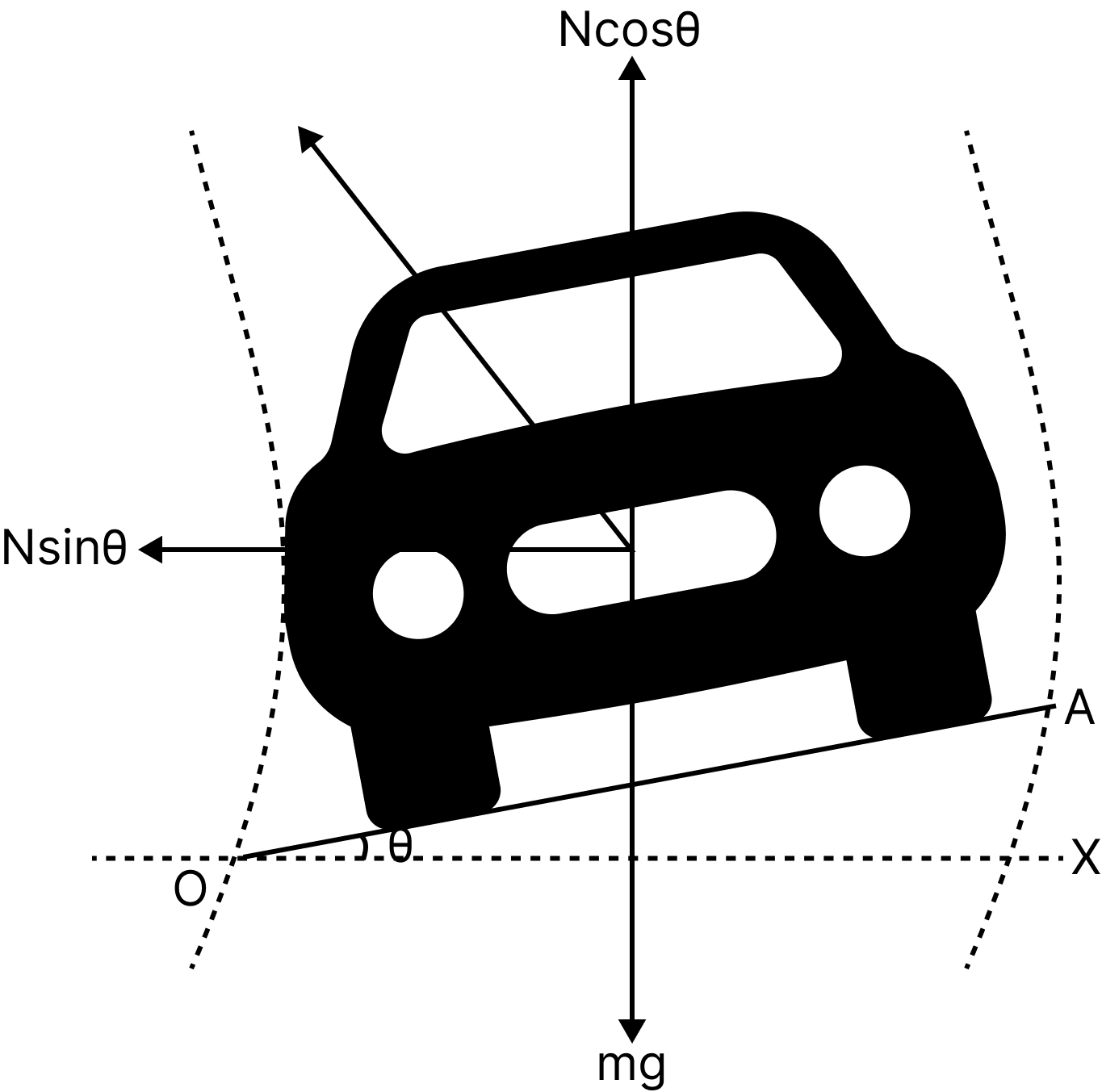
Banking of Roads

Consider a vehicle of mass "m" travelling at speed "v" on a radius "r" banked road. Let the banking angle be and the amount of friction between the vehicle's tyres and the road be f.

Total force upwards equals Total force downwards.

$N \cos \Theta=m g+f \sin \Theta$

Where,

$N \cos \Theta$

one of the components of normal reaction along the vertical axis

mg: weight of the vehicle acting vertically downward

$f \sin \Theta$

one of the components of frictional force along the vertical axis

therefore,

$m g=N \cos \Theta-f \sin \Theta$

(eq.1)

$\dfrac{m v^{2}}{r}=N \sin \Theta+f \cos \Theta$

Where,

$N \sin \Theta$ one of the components of normal reaction along the horizontal axis

$f \cos \Theta$

one of the components of frictional force along the horizontal axis

$\dfrac{\dfrac{m v^{2}}{r}}{m g}=\dfrac{N \sin \Theta+f \cos \Theta}{N \cos \Theta-f \sin \Theta}$

(after diving eq.1 and eq.2)

therefore,

$\dfrac{v^{2}}{r g}=\dfrac{N \sin \Theta+f \cos \Theta}{N \cos \Theta-f \sin \Theta}$

Frictional force

$f=\mu_{s} N$

$\dfrac{v^{2}}{r g}=\dfrac{N \sin \Theta_{+} \mu_{s} N \cos \Theta}{N \cos \Theta-\mu_{s} N \sin \Theta} $

$\dfrac{v^{2}}{r g}=\dfrac{N\left(\sin \Theta+\mu_{s} \cos \Theta\right)}{N\left(\cos \Theta-\mu_{s} \sin \Theta\right)}$

$\dfrac{v^{2}}{r g}=\dfrac{\left(\sin \Theta+\mu_{s} \cos \Theta\right)}{\left(\cos \Theta-\mu_{s} \sin \theta\right)}$

$\dfrac{v^{2}}{r g}=\dfrac{\left(\tan \Theta+\mu_{s}\right)}{\left(1-\mu_{s} \tan \Theta\right)}$

therefore,

$v=\sqrt{\dfrac{r g\left(\tan \Theta+\mu_{s}\right)}{\left(1-\mu_{s} \tan \Theta\right.}}$

$v_{\max }=\sqrt{r g \tan \Theta} $

$\tan \Theta=\dfrac{v^{2}}{r g} $

$\Theta=\tan ^{-1} \dfrac{v^{2}}{r g}$

Important Formula

Name of the Concept	Formula
Static friction	$\mathbf{f}_{\mathrm{s}} \leq \boldsymbol{\mu}_{\mathrm{s}} \mathbf{N}$
Kinetic friction	$\mathbf{f}_{\mathbf{k}}=\boldsymbol{\mu}_{\mathrm{k}} \mathbf{N}$
Rolling friction	$\mathbf{f}_{\mathbf{r}}=\boldsymbol{\mu}_{\mathbf{r}} \mathbf{N}$
Calculation of Necessary Force in Different Conditions:
Minimum pulling force $P$ at an angle $\alpha$ from the horizontal.	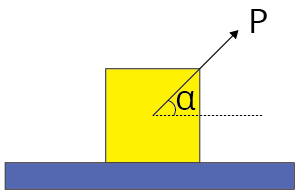$P=\dfrac{W \sin \theta}{\cos (\alpha-\theta)}$
Minimum pushing force $P$ at an angle $\alpha$ from the horizontal.	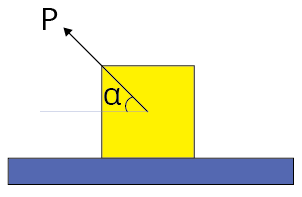$P=\dfrac{W \sin \theta}{\cos (\alpha+\theta)}$
Minimum pulling force $P$ to move the body up an inclined plane.	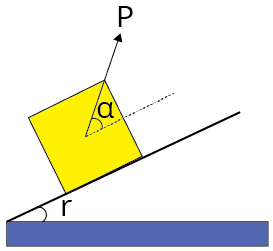$P=\dfrac{W \sin (\theta+\lambda)}{\cos (\alpha-\theta)}$
Minimum force on body in downward direction along the surface of inclined plane to start its motion.	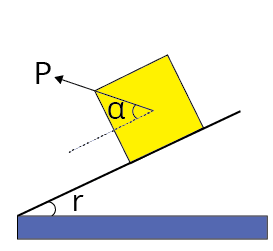$P=\dfrac{W \sin (\theta-\lambda)}{\cos (\alpha-\theta)}$
Minimum force to avoid sliding a body down an inclined plane.	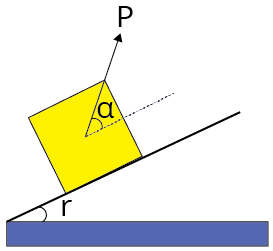$P=W\left[\dfrac{\sin (\lambda-\theta)}{\cos (\theta+\alpha)}\right]$
Minimum force for motion and its direction.	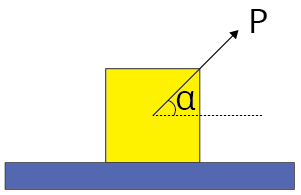$P_{\min }=\dfrac{\mu m g}{\sqrt{1+\mu^{2}}}$
Co-Efficient of Friction	$\boldsymbol{\mu}=\mathbf{F} / \mathbf{R}$

Example 1: A small block of mass $0.1 \mathrm{~kg}$ lies on a fixed inclined plane PQ which makes an angle $\theta$ with the horizontal. A horizontal force of $1 \mathrm{~N}$ acts on the block through its centre of mass as shown in the figure. The block remains stationary if (take $g=10 \mathrm{~m} / \mathrm{s}^{2}$ )

Block

(A) $\theta=45^{\circ}$

(B) $\theta>45^{\circ}$ and a frictional force acts on the block towards $P$.

(c) $\theta>45^{\circ}$ and a frictional force acts on the block towards $Q$.

(D) $\theta<45^{\circ}$ and a frictional force acts on the block towards Q.

Answer: A, C

Hint: The opposing force that is produced when two surfaces attempt to move in the same direction or in opposite directions is known as frictional force. A frictional force is primarily intended to produce resistance to the mobility of one surface across another surface.

Complete Solution:

The forces acting on the block are $F=1 \mathrm{~N}$ towards the left, weight $\mathrm{mg}=0.1 \times 10=1 \mathrm{~N}$ downwards, normal force N, and the frictional force f. Resolve F and mg along and perpendicular to the inclined plane.

Different Components of Forces Acting on a Block.

When $\theta=45^{\circ}$, the net force that brings the block down is

$F_{d}=m g \sin \theta-F \cos \theta=\dfrac{1}{\sqrt{2}}-\dfrac{1}{\sqrt{2}}=0$

Thus, the block is stationary if $\theta=45^{\circ}$. When $\theta>45^{\circ}$, the force $F_{d}>0$, and hence the block tends to move down. Thus, the frictional force f acts on the block upwards i.e., towards Q.

Example 2: Three objects A, B and C are kept in a straight line on a frictionless horizontal surface. The masses of A, B and C are m, 2m and 2m respectively. A moves towards B with a speed of 9 m/s and makes an elastic collision with it. Thereafter B makes a completely inelastic collision with C. All motions occur along the same straight line. The final speed of C is :

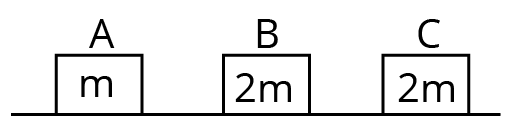
Objects

(A) $6 \mathrm{~m} / \mathrm{s}$

(B) $9 \mathrm{~m} / \mathrm{s}$

(C) $4 \mathrm{~m} / \mathrm{s}$

(D) $3 \mathrm{~m} / \mathrm{s}$

Answer: D

Hint:

Complete Solution:

Collision between A and B

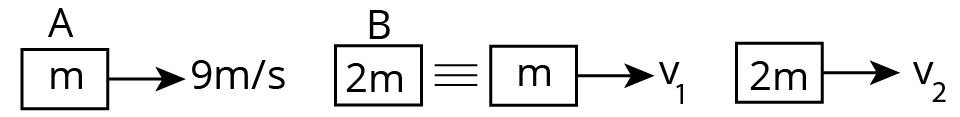
Collision between A and B

$m \times 9=m v_{1}+2 m v_{2}($ from momentum conservation $)$

$e=1=\dfrac{v_{2}-v_{1}}{9}$

$\Rightarrow v_{2}=6 \mathrm{~m} / \mathrm{sec} \cdot \mathrm{v}_{1}=-3 \mathrm{~m} / \mathrm{sec} \text {. }$

collision between $\mathrm{B}$ and $\mathrm{C}$

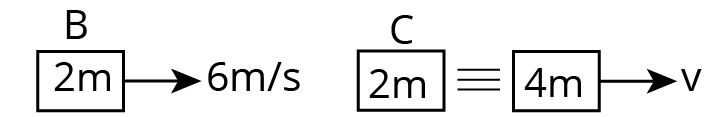
Collision between B and C

$2 \mathrm{~m} \times 6=4 \mathrm{mv}$ (from momentum conservation)

$\mathrm{v}=3 \mathrm{~m} / \mathrm{s}$

Hence, the final speed of C is 3m/s.

Importance of Class 11 Physics NEET Laws of Motion

This chapter is the advanced version of the laws of motion you have studied in the previous classes. In this chapter, you will be introduced to the three laws of motion framed and proved by Sir Isaac Newton. Get in-depth knowledge of how these laws are scientifically proved. Find out how the derivations of these laws result into the formulation of new terms related to kinematics and mechanics.

Refer to the Laws of Motion notes to find out how the mathematical tools of derivatives are used to explain all three laws. This chapter will also explain how the concepts of displacement, velocity, acceleration, force, work, and power can be derived from these derivations.

Find out the meaning of advanced terminologies such as impulse, mass, weight, and the above-mentioned terms and their correlations. You will also get a good idea of what inertia is and how it affects the motion of objects in different cases.

The chapter is very important as it describes the fundamental concepts of force, work, and power used in the conceptual chapters of advanced physics. Understand how the laws define such terms and how these physical quantities can be calculated using their formulae and units.

Benefits of Vedantu’s Revision Notes on Laws of Motion

• These revision notes are compiled to offer a simpler version of all the fundamental concepts related to the motion of objects. Study these terms and find the interrelation between them. Understand how these terms are determined from the explanation of laws of motion and how to calculate them easily.

• Get to know how the experts have framed the topics easily and enhance your understanding of this chapter. Gaing in-depth knowledge and understanding of these topics of this chapter using the revision notes on Laws of Motion and make your study sessions more productive.

• Revise these notes to complete preparing this chapter before a crucial exam. Remember all you have studied due to the simpler and concise representation of all definitions and derivations of the scientific principles of laws of motion.

• Proceed to answer the sample questions to evaluate your preparation level. Check where you need to work more in this fundamental Physics chapter to make your preparation better.

Download Laws of Motion Class 11 Notes PDF

Get the free PDF version of Laws of Motion NEET notes and complete your study material for this chapter. Make your study sessions more productive and take a step ahead. Utilise the easier description of all the concepts related to laws of motion and become better at solving questions asked in the NEET exam and perform excellently.

NEET Physics Revision Notes - Chapter Pages

Other Important Links