NEET Revision Notes for Physics Gravitation

The universe's constituents are galaxies, stars, planets, comets, asteroids, and meteoroids. The force which keeps them bound together is called gravitational force. Gravitation is a natural phenomenon by which material objects attract one another.

In 1687 A.D., English Physicist Sir Isaac Newton published Principia Mathematica, which explains the inverse-square law of gravitation.

Newton’s Law of Gravitation:

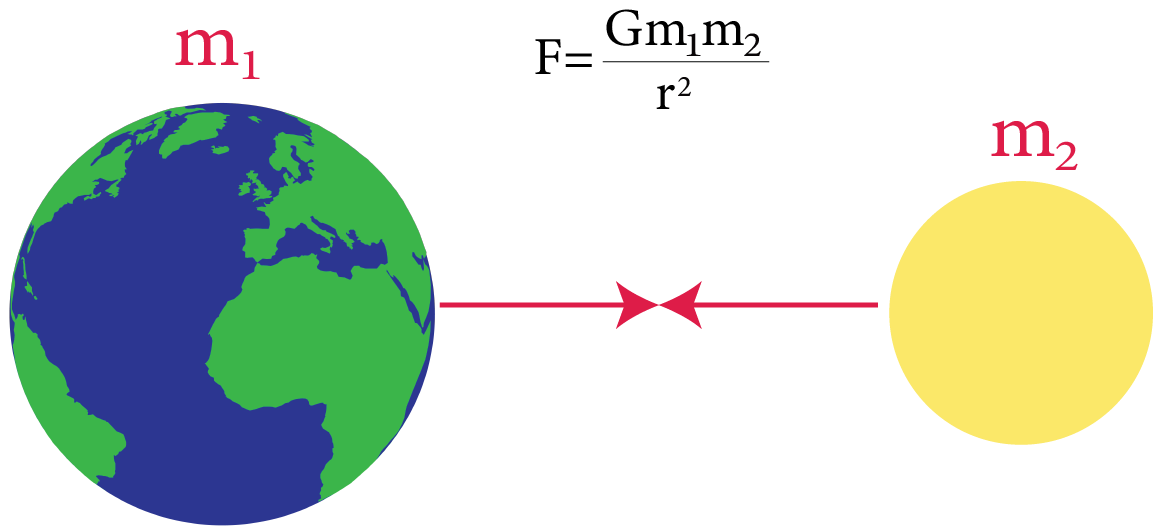
• According to Newton's law of gravitation, “Everybody in the universe attracts every other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them”. The directions of this force are along the line joining the two bodies.

• The magnitude of gravitational force acting between two bodies of masses ${m_1}$ and ${m_2}$ placed distance apart is

$\left| {{{\vec F}_{12}}} \right| = \left| {{{\vec F}_{21}}} \right| = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}$

Where ${\vec F_{12}} =  - {\vec F_{21}}$

• It is a universal law.

• Universal Gravitational constant G is a scalar quantity. Its value is the same throughout the universe and is independent of the nature and size of the bodies as well as the nature of the medium between the bodies.

• The value of G in SI system is $6.67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$ and in CGS system is $6.67 \times {10^{ - 8}}dynec{m^2}{g^{ - 2}}$.

• The dimensional formula for G is $\left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]$.

• The value of the universal gravitational constant G was determined experimentally by English scientist Henry Cavendish in 1798.
  
  

Newton’s Law of Gravitation

• Newton’s law of gravitation in vector form is,

$\vec F =  - \dfrac{{G{m_1}{m_2}}}{{{r^2}}}.\hat r$

-ve sign shows that gravitational force is always attractive.

Characteristics of Gravitational Force:

The characteristics of gravitational force are as follows:

1. It is always attractive in nature

2. It obeys the inverse square law.

3. It is independent of the nature of the intervening medium.

4. It is independent of the presence or absence of other bodies.

5. It is independent of nature and the size of the bodies, till their masses remain the same and the distance between their centres is fixed.

Principle of Superposition of Gravitation:

It states that the resultant gravitational force $\vec F$ acting on a particle due to the number of other particles is equal to the vector sum of the gravitational forces exerted by individual particles on the given particle.

i.e., $\vec F = {\vec F_{01}} + {\vec F_{02}} + {\vec F_{03}} + ...... + {\vec F_{0n}} = \sum\limits_{i = 1}^n {{{\vec F}_{0i}}} $ 

Where ${\vec F_{01}},{\vec F_{02}},{\vec F_{03}},...,{\vec F_{0n}}$ are the gravitational forces on a particle of mass ${m_0}$ due to particles of masses ${m_1},{m_2},....,{m_n}$ respectively.

Gravity:

• It is defined as the force of attraction exerted by the earth towards its centre on a body lying on or near the surface of the earth.

• It is merely a special case of gravitation and is also called earth's gravitational pull.

• It is the measure of weight of the body. 

• The weight of the body = mass(m) × acceleration due to gravity (g) = mg.

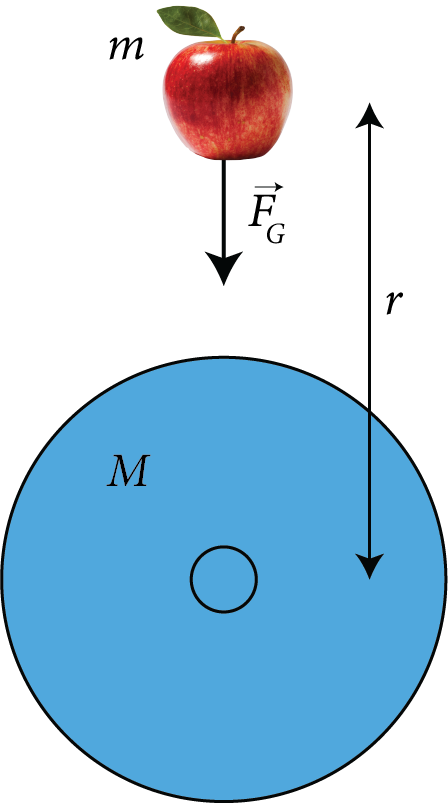
Acceleration Due to Gravity:

• Acceleration produced in a body due to the force of gravity is called acceleration due to gravity. It is denoted by symbol ‘g’ and mathematically it is given by

$g = \dfrac{{G{M_e}}}{{{r^2}}}$

Where ${M_e}$ the mass of the earth and r is is the distance of the body from the centre of the earth

• If the body is on the surface of the earth i.e. $r=R_{e}$ (radius of the earth), then

$g = \dfrac{{G{M_e}}}{{{R_e}^2}}$

• It is also defined as the acceleration produced in the body while falling freely under the effect of gravity alone.

• It is a vector quantity. Its SI unit is $m{s^{ - 2}}$ and its dimensional formula is $\left[ {{M^0}L{T^{ - 2}}} \right]$.

• The value of g on the surface of earth is taken to be $9.8m{s^{ - 2}}$.

• The value of g varies with altitude, depth, shape, and the rotation of earth.

• The acceleration due to gravity (g) is related with gravitational constant (G) by the relation

$g = \dfrac{{G{M_e}}}{{{R^2}_e}} = \dfrac{{G\dfrac{4}{3}\pi R_e^3\rho }}{{R_e^2}} = \dfrac{4}{3}\pi G{R_e}\rho $

Where ${M_e}$ is the mass of the earth,${R_e}$ is the radius of the earth and $\rho $ in the uniform density of the material of the earth.

• The acceleration value due to gravity is independent of the body's shape, size, mass etc. of the body but depends upon mass and radius of the earth or planet due to which there is a gravity pull.

$F=m a$

$\frac{G M m}{r^{2}}=m a$

Then, cancelling $\mathrm{m}$ on both sides

Acceleration Due To Gravity Formula

Variation of Acceleration Due to Gravity:

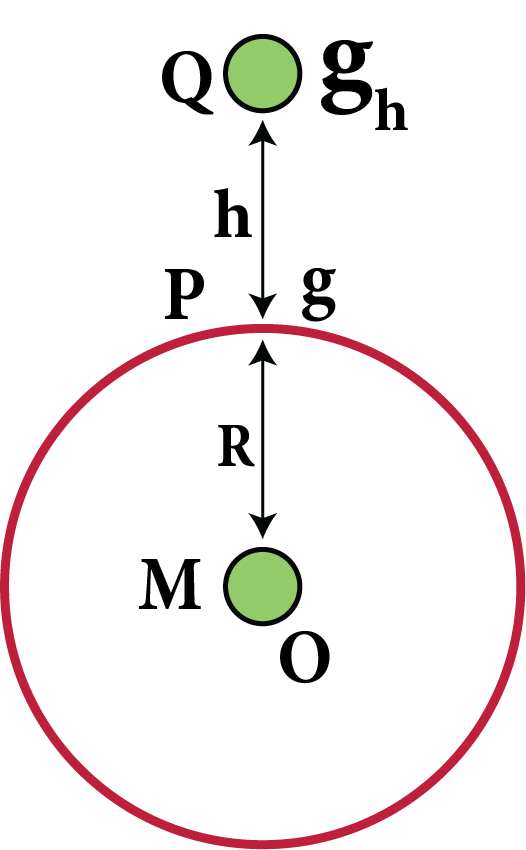
• Due to altitude (h): The acceleration due to gravity at height h above the earth’s surface is given by 

${g_h} = \dfrac{{G{M_e}}}{{{{\left( {{R_e} + h} \right)}^2}}} = g{\left( {1 + \dfrac{h}{{{R_e}}}} \right)^{ - 2}}$$\left( {\therefore g = \dfrac{{G{M_e}}}{{R_e^2}}} \right)$

For  $h <  < {R_e}$

$\therefore {g_h} = g\left( {1 - \dfrac{{2h}}{{R_e^{}}}} \right)$

When we move above the earth’s surface, the acceleration value due to gravity decreases.

Variation of Acceleration Due To Gravity at a Height h

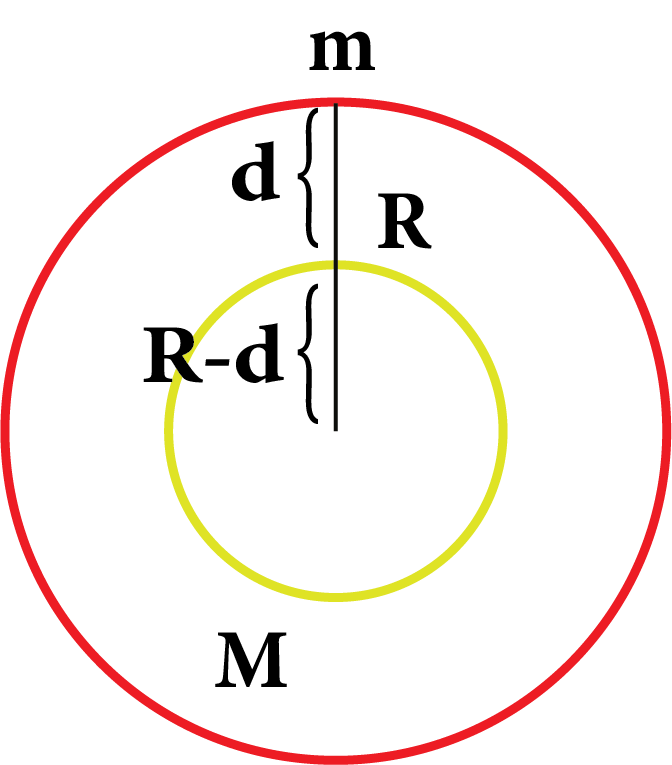
• Due to Depth(d): The acceleration due to gravity at a depth d below the earth’s surface is given by

${g_d} = \dfrac{{G{M_e}}}{{R_e^3}}\left( {{R_e} - d} \right)$

${g_d}= g\left( {\dfrac{{{R_e} - d}}{{{R_e}}}} \right) = g\left( {1 - \dfrac{d}{{{R_e}}}} \right)$

Variation of Acceleration Due To Gravity at a depth d

Gravitational Field:

The space around a material body in which its gravitational pull can be experienced is called its gravitational field.

Intensity of Gravitational Field:

• The intensity of the gravitational field of a body at a point in the field is defined as the force experienced by a body of unit mass placed at that point provided the presence of unit mass does not disturb the original gravitational field.It is denoted by symbol E.

• The intensity of gravitational field at a point due to a body of mass M, at a distance r from the centre of the body is

$E =  - \dfrac{{GM}}{{{R^2}}}$

Gravitational Potential:

• The gravitational potential at a point in the gravitational field of a body is defined as the amount of work done in bringing a unit mass from Infinity to that point.It is denoted by symbol V.

• The gravitational potential at a point in the gravitational field due to a body of mass M at a distance r from the centre of the body is given by

$V =  - \dfrac{{GM}}{r}$

• Gravitational potential is a scalar quantity.

• The gravitational potential in the SI unit is J kg and in the CGS system is $erg{g^{ - 1}}$.

• Gravitational potential (V) is related with gravitational field intensity(E) by a relation

$E =  - \dfrac{{dV}}{{dr}}$

Gravitational Field Intensity and Gravitational potential Fue to a Spherical Shell:

• The gravitational field intensity and gravitational potential due to a spiritual shell of radius R and mass M at a point distant r from the centre of the shell is given as follows:
  
  

Gravitational Field Intensity and Gravitational Potential Due To A Spherical Shell.

• At a point outside the shell i.e. r > a

${E_{outside}} =  - \dfrac{{GM}}{{{r^2}}}$,  ${V_{outside}} =  - \dfrac{{GM}}{r}$

• At a point on the surface of the shell i.e. r = a

${E_{surface}} =  - \dfrac{{GM}}{{{a^2}}}$,${V_{surface}} =  - \dfrac{{GM}}{a}$

• At a point inside the shell i.e.  r < a

${E_{inside}} = 0$,  ${V_{inside}} =  - \dfrac{{GM}}{a}$

Gravitational Field Intensity and Gravitational Potential Due To A Solid Sphere:

• The gravitational field intensity and gravitational potential duty a solid sphere of radius R and mass M at a distance r from the centre of the sphere is given as follows:

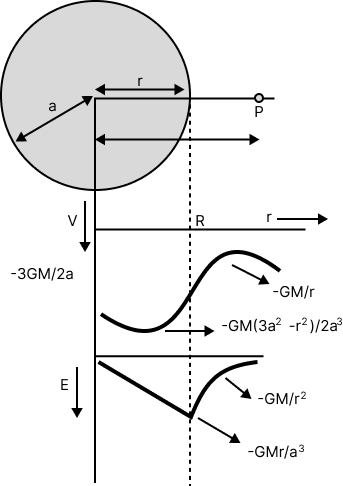
Gravitational Field Intensity and Gravitational Potential Due to a Solid Sphere

• At a point outside the sphere, i.e. r > a

${E_{outside}} =  - \dfrac{{GM}}{{{r^2}}}$ ${V_{outside}} =  - \dfrac{{GM}}{r}$

• At a point on the surface of the sphere, i e. r = a

${E_{surface}} =  - \dfrac{{GM}}{{{a^2}}}$ ${V_{surface}} =  - \dfrac{{GM}}{a}$

• At a point inside the sphere, i.e. r < a

${E_{inside}} =  - \dfrac{{GMr}}{{{a^3}}}$, ${V_{inside}} =  - \dfrac{{GM\left( {3{a^2} - {r^2}} \right)}}{{2{a^3}}}$

Gravitational Potential Energy:

• The gravitational potential energy of a body at a point in a gravitational field of another body is defined as the amount of work done in bringing the given body from Infinity to that point.

• Gravitational potential energy = Gravitational potential × mass of the body 

• The gravitational potential energy of mass m in the gravitational field of mass M at a distance r from it is

$U =  - \dfrac{{GMm}}{r}$

Where, r is the distance between M and m.

• The gravitational potential energy of a mass M at a distance r($\left( { > {R_e}} \right)$ from the centre of the earth is

$U = mV =  - \dfrac{{G{M_e}m}}{r}$

• Gravitational potential energy of a body of mass m at height h above the earth's surface is given by

${U_h} = \dfrac{{ - G{M_e}m}}{{\left( {{R_e} - h} \right)}}$

• Gravitational potential energy of a body of mass m on the earth surface is given by

${U_0} = \dfrac{{ - G{M_e}m}}{{{R_e}}}$

Gravitational Potential Energy

Satelite

• Satellite is a natural or artificial body describing an orbit around a planet under its gravitational attraction. Moon is a natural satellite while INSAT-1B is an artificial satellite of the earth.

• Orbital speed of a satellite is defined as the minimum speed required to put the satellite into a given orbit around earth.

• Orbital speed of the satellite when it is revolving around the earth at height is given by

${v_0} = \sqrt {\dfrac{{G{M_e}}}{r}}  = \sqrt {\dfrac{{G{M_e}}}{{{R_e} + h}}}  = {R_e}\sqrt {\dfrac{g}{{{R_e} + h}}} $$\left( {asg = \dfrac{{G{M_e}}}{{R_e^2}}} \right)$

When the satellite is orbiting close to the earth’s surface i.e.,  $h <  < {R_e}$, then  

${v_0} = {R_e}\sqrt {\dfrac{g}{{{R_e}}}}  \approx \sqrt {g{R_e}} $

${v_0} = \sqrt {9.8 \times 6.4 \times {{10}^6}}  = 7.92 \times {10^3}m{s^{ - 1}} \approx 8km{s^{ - 1}}$

• The orbital speed of the satellite is independent of the mass of the satellite. The orbital speed of the satellite depends upon the mass and radius of the earth around which the revolution of the satellite is taking place.

• Time period of a satellite: It is the time taken by satellite to complete one revolution around the earth and it is given by

$T = \dfrac{{2\pi r}}{{{v_0}}} = 2\pi \sqrt {\dfrac{{{r^3}}}{{G{M_e}}}}  = 2\pi \sqrt {\dfrac{{{{\left( {{R_e} + h} \right)}^3}}}{{G{M_e}}}}  = \dfrac{{2\pi }}{{{R_e}}}\sqrt {\dfrac{{{{\left( {{R_e} + h} \right)}^3}}}{g}} $

For a satellite orbiting close to the earth’s surface i.e. $h <  < {R_e}$

$T = 2\pi \sqrt {\dfrac{{{R_e}}}{g}}  = 84.6\min $.

• Kinetic energy of a satellite

$K = \dfrac{1}{2}mv_0^2 = \dfrac{1}{2}\dfrac{{G{M_e}m}}{r} = \dfrac{1}{2}\dfrac{{G{M_e}m}}{{\left( {{R_e} + h} \right)}}$

• Potential energy of a satellite

$U =  - \dfrac{{G{M_e}m}}{r} =  - \dfrac{{G{M_e}m}}{{{R_e} + h}}$

• Total energy (mechanical) of a satellite

$E = K + U =  - \dfrac{{G{M_e}m}}{{2r}} =  - \dfrac{{G{M_e}m}}{{2\left( {{R_e} + h} \right)}}$

For satellite orbiting very close to the surface i.e., $h <  < {R_e}$then $E =  - \dfrac{{G{M_e}m}}{{2{R_e}}}$ .

• Binding energy of a satellite

${E_B} =  - E = \dfrac{{G{M_e}m}}{{2r}} = \dfrac{{G{M_e}m}}{{2\left( {{R_e} + h} \right)}}$ 

• Escape speed of a satellite is defined as the minimum speed which is required for a body to project itself from the surface of earth such that it escapes the earth’s gravitational field. Escape speed ${v_e}$ is given by

${v_e} = \sqrt {\dfrac{{2GM}}{R}} $ 

Where M = Mass of the earth/planet

R = Radius of the earth/planet

${v_e} = \sqrt {\dfrac{{2G \times volume \times density}}{R}} $ 

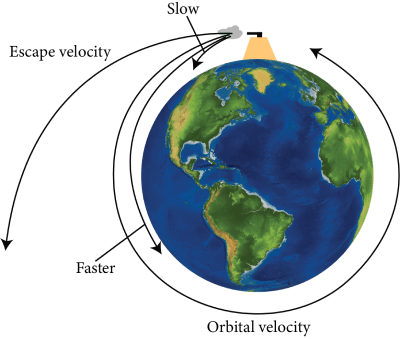
Orbital and Escape Velocity of Earth

• For earth, ${v_e} = 11.2\,km{s^{ - 1}}$ 

• For a point close to earth’s surface the escape speed and orbital speed are related as

${v_e} = \sqrt 2 {v_0}$ 

• Moon has no atmosphere because the R.M.S. the speed of gas molecules there is greater than the escape speed of the moon.

Kepler’s law of Planetary Motion:

Kepler’s first law (law of orbits): All planets move in elliptical orbits with the sun at one of the ellipse's foci.

Kepler’s second law (law of area): The radius vector drawn from the sun to the planet sweeps out equal areas in equal intervals of time i.e. the area velocity of the planet (or the area swept out by the planet per unit time) around the sun is constant. 

i.e. Areal velocity $= \dfrac{{d\vec A}}{{dt}} = K$ which is a constant.

Angular momentum ($\vec L$) of a planet is related with areal velocity $\left( {\dfrac{{d\vec A}}{{dt}}} \right)$ by the relation $\vec L = 2m\left( {\dfrac{{d\vec A}}{{dt}}} \right)$ 

Kepler’s second law follows from the law of conservation of angular momentum.

The area covered by the radius vector in dt seconds$= \dfrac{1}{2}{r^2}d\theta $. 

The areal velocity $= \dfrac{1}{2}{r^2}\dfrac{{d\theta }}{{dt}} = \dfrac{1}{2}{r^2}\omega  = \dfrac{1}{2}rv$ .

According to Kepler’s second law, the speed of the planet is maximum when it is closest to the sun and it is minimum when the planet is farthest from the sun.

Kepler’s Third Law (Law of Periods):   The Square of the time period of revolution of a planet around the sun is directly proportional to the cube of the semi major axis of the elliptical orbit i.e. $T^{2} \alpha a^{3}$ where a is the semi-major axis of the elliptical orbit of the planet around the sun.

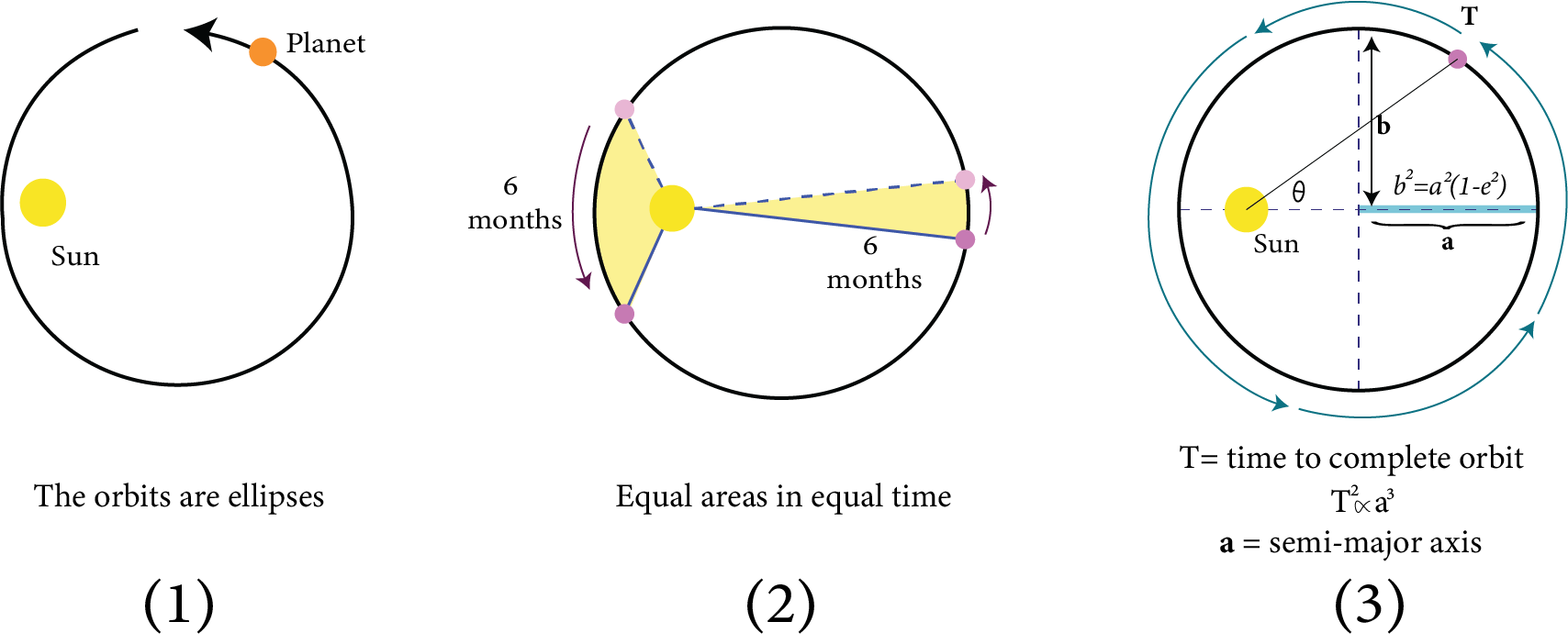
Kepler’s Laws of Planetary Motion

Geostationary Satellites:

Geostationary satellites are satellites that revolve around the earth and these are placed above the earth’s equator, it revolves around the earth in the same direction as that of earth and takes 24 hours to complete one rotation. They are called communication satellites as these satellites have same orbital period as that of earth and appears at a fix position with respect to earth so, the satellites antennas do not required to track their position and they can be pointed permanently towards a particular position in the sky where the geostationary satellite is located that is information can be sent or received easily.

Uses:-

• Satellites which are used for weather forecasting.

• Communication satellites such as Dish antennas of TV.

• Satellites for GPS or Global Positioning System.

Points to Remember:

• Kepler’s first law (law of orbits): All planets move in elliptical orbits with the sun at one of the ellipse's foci.

• Kepler’s second law (law of area): The radius vector drawn from the sun to the planet sweeps out equal areas in equal intervals of time i.e. the area velocity of the planet (or the area swept out by the planet per unit time) around the sun is constant. 

• Kepler’s third law (Law of periods):   The Square of the time period of revolution of a planet around the sun is directly proportional to the cube of the semi-major axis of the elliptical orbits. $T^{2}$ proportional to  $a^{3}$ where a is the semi-major axis of the planet's elliptical orbit around the sun. 

• According to Newton’s law of gravitation “Everybody in the universe attracts every other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them”. The directions of this force are along the line joining the two bodies.

• The magnitude of gravitational force acting between two bodies of masses $m_1$ and ${m_2}$ placed distance apart is

$\left| {{{\vec F}_{12}}} \right| = \left| {{{\vec F}_{21}}} \right| = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}$ where ${\vec F_{12}} =  - {\vec F_{21}}$.

It is a universal law.

• The value of G in

SI system is $6.67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$and in

CGS system is$6.67 \times {10^{ - 8}}dynec{m^2}{g^{ - 2}}$.

The dimensional formula for G is$\left[ {{M^{ - 1}}{L^3}{T^{ - 2}}} \right]$.

• Gravitational force is attractive in nature, independent of presence or absence of bodies etc…

• Principle of superposition of gravitational force: It states that the resultant gravitational force $\vec F$ acting on a particle due to the number of other particles is equal to the vector sum of the gravitational forces exerted by individual particles on the given particle.

• i.e.,   $\vec F = {\vec F_{01}} + {\vec F_{02}} + {\vec F_{03}} + ...... + {\vec F_{0n}} = \sum\limits_{i = 1}^n {{{\vec F}_{0i}}} $ Where ${\vec F_{01}},{\vec F_{02}},{\vec F_{03}},...,{\vec F_{0n}}$ are the gravitational forces on a particle of mass ${m_0}$ due to particles of masses ${m_1},{m_2},....,{m_n}$respectively.

• Gravity: It is defined as the force of attraction exerted by the earth towards its centre on a body lying on or near the surface of the earth.

• Acceleration produced in a body due to the force of gravity is called acceleration due to gravity. It is denoted by symbol ‘g’ and mathematically it is given by

$g = \dfrac{{G{M_e}}}{{{r^2}}}$

Where ${M_e}$ the mass of the earth and r is is the distance of the body from the centre of the earth

• The value of acceleration due to gravity is independent of the shape, size, mass etc. of the body but depends upon mass and radius of the earth or planet due to which there is a gravity pull.

• Acceleration due to gravity varies with height, depth in the earth.

• Gravitational field of a body is defined as the field produced by a body when it is experiencing a force on some other body.

• The amount of work done to bring a body from a point of space (invariant or infinite) point to another point is called gravitational potential.

• The work done bringing a body from space to a point is called gravitational potential energy.

• An object orbiting around the sun or earth or any celestial body is called a satellite.

• Orbital speed of a satellite: For a satellite to be placed or maintained the minimum velocity required is called orbital velocity.

• Orbital speed of the satellite : ${v_0} = \sqrt {\dfrac{{G{M_e}}}{r}}  = \sqrt {\dfrac{{G{M_e}}}{{{R_e} + h}}}  = {R_e}\sqrt {\dfrac{g}{{{R_e} + h}}} $$\left( {asg = \dfrac{{G{M_e}}}{{R_e^2}}} \right)$

• Time period of a satellite: It is the time taken by satellite to complete one revolution around the earth and it is given by

$T = \dfrac{{2\pi r}}{{{v_0}}} = 2\pi \sqrt {\dfrac{{{r^3}}}{{G{M_e}}}}  = 2\pi \sqrt {\dfrac{{{{\left( {{R_e} + h} \right)}^3}}}{{G{M_e}}}}  = \dfrac{{2\pi }}{{{R_e}}}\sqrt {\dfrac{{{{\left( {{R_e} + h} \right)}^3}}}{g}} $

• Kinetic energy of a satellite is equal to negative of total energy while potential energy is equal to twice the total energy i.e. K = -E, U = 2E

• The escape speed on earth (or any planet) is defined as the minimum speed with which a body has to be projected vertically upwards from the surface of earth (or any other planet) so that it just crosses the gravitational field of earth (or of that planet) and never returns on its own.

• Moon has no atmosphere because the R.M.S. the speed of gas molecules there is greater than the escape speed of the moon.

• For earth, ${v_e} = 11.2\,km{s^{ - 1}}$ 

• For a point close to earth’s surface the escape speed and orbital speed are related as

${v_e} = \sqrt 2 {v_0}$ 

• Geostationary satellites are satellites that revolve around the earth and these are placed above the earth’s equator, it revolves around the earth in the same direction as that of earth and takes 24 hours to complete one rotation.

Important Formulae:

• $\vec L = 2m\left( {\dfrac{{d\vec A}}{{dt}}} \right)$ 

• The magnitude of gravitational force acting between two bodies of masses $m_1$ and ${m_2}$ placed distance apart is

$\left| {{{\vec F}_{12}}} \right| = \left| {{{\vec F}_{21}}} \right| = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}$

Where ${\vec F_{12}} =  - {\vec F_{21}}$

• $g = \dfrac{{G{M_e}}}{{{r^2}}}$

• The acceleration due to gravity (g) is related to the gravitational constant (G) by the relation

$g = \dfrac{{G{M_e}}}{{{R^2}_e}} = \dfrac{{G\dfrac{4}{3}\pi R_e^3\rho }}{{R_e^2}} = \dfrac{4}{3}\pi G{R_e}\rho $

• Due to altitude (h): The acceleration due to gravity at height h above the earth’s surface is given by 

${g_h} = \dfrac{{G{M_e}}}{{{{\left( {{R_e} + h} \right)}^2}}} = g{\left( {1 + \dfrac{h}{{{R_e}}}} \right)^{ - 2}}$$\left( {\therefore g = \dfrac{{G{M_e}}}{{R_e^2}}} \right)$

For  $h <  < {R_e}$

$\therefore {g_h} = g\left( {1 - \dfrac{{2h}}{{R_e^{}}}} \right)$

When we move above the earth’s surface, the value of acceleration due to gravity goes on decreasing.

• Due to depth(d): The acceleration due to gravity at a depth d below the earth’s surface is given by

${g_d} = \dfrac{{G{M_e}}}{{R_e^3}}\left( {{R_e} - d} \right)$

$= g\left( {\dfrac{{{R_e} - d}}{{{R_e}}}} \right) = g\left( {1 + \dfrac{d}{{{R_e}}}} \right)$

At the centre of the earth, $d = {R_e}$. $\therefore {g_d} = 0$.

• The gravitational potential at a point in the gravitational field due to a body of mass M at a distance r from the centre of the body is given by

$V =  - \dfrac{{GM}}{r}$

• The gravitational potential energy of mass m in the gravitational field of mass M at a distance r from it is

$U =  - \dfrac{{GMm}}{r}$

• Gravitational potential energy of a body of mass m at height h above the earth's surface is given by

${U_h} = \dfrac{{ - G{M_e}m}}{{\left( {{R_e} - h} \right)}}$

• The orbital speed of the satellite when it is revolving around the earth at height is given by

${v_0} = \sqrt {\dfrac{{G{M_e}}}{r}}  = \sqrt {\dfrac{{G{M_e}}}{{{R_e} + h}}}  = {R_e}\sqrt {\dfrac{g}{{{R_e} + h}}} $$\left( {asg = \dfrac{{G{M_e}}}{{R_e^2}}} \right)$

When the satellite is orbiting close to the earth’s surface i.e.,  $h <  < {R_e}$, then  

${v_0} = {R_e}\sqrt {\dfrac{g}{{{R_e}}}}  \approx \sqrt {g{R_e}} $

${v_0} = \sqrt {9.8 \times 6.4 \times {{10}^6}}  = 7.92 \times {10^3}m{s^{ - 1}} \approx 8km{s^{ - 1}}$

• Time period of a satellite: It is the time taken by satellite to complete one revolution around the earth and it is given by

$T = \dfrac{{2\pi r}}{{{v_0}}} = 2\pi \sqrt {\dfrac{{{r^3}}}{{G{M_e}}}}  = 2\pi \sqrt {\dfrac{{{{\left( {{R_e} + h} \right)}^3}}}{{G{M_e}}}}  = \dfrac{{2\pi }}{{{R_e}}}\sqrt {\dfrac{{{{\left( {{R_e} + h} \right)}^3}}}{g}} $

For a satellite orbiting close to the earth’s surface i.e. $h <  < {R_e}$

$T = 2\pi \sqrt {\dfrac{{{R_e}}}{g}}  = 84.6\min$

• Kinetic energy of a satellite

$K = \dfrac{1}{2}mv_0^2 = \dfrac{1}{2}\dfrac{{G{M_e}m}}{r} = \dfrac{1}{2}\dfrac{{G{M_e}m}}{{\left( {{R_e} + h} \right)}}$

• Potential energy of a satellite

$U =  - \dfrac{{G{M_e}m}}{r} =  - \dfrac{{G{M_e}m}}{{{R_e} + h}}$

• Total energy (mechanical) of a satellite

$E = K + U =  - \dfrac{{G{M_e}m}}{{2r}} =  - \dfrac{{G{M_e}m}}{{2\left( {{R_e} + h} \right)}}$

For satellite orbiting very close to the surface i.e., $h <  < {R_e}$then $E =  - \dfrac{{G{M_e}m}}{{2{R_e}}}$ .

• Binding energy of a satellite

${E_B} =  - E = \dfrac{{G{M_e}m}}{{2r}} = \dfrac{{G{M_e}m}}{{2\left( {{R_e} + h} \right)}}$ 

• For a point close to the earth’s surface the escape speed and orbital speed are related as

${v_e} = \sqrt 2 {v_0}$ 

Questions:

1. At what height from the surface of earth the gravitational potential and the value of g are $- 5.4 \times {10^7}Jk{g^{ - 2}}$ and $6.0m{s^{ - 2}}$ respectively? Take the radius of earth as 6400 km.

(a) 1400 km

(b) 2000 km

(c) 2600 km

(d) 1600 km

Ans: (c) 2600 km

Gravitational potential at a height h from the surface of earth,${V_h} =  - 5.4 \times {10^7}Jk{g^{ - 2}}$ . At the same point acceleration due to gravity, ${g_h} = 6.0m{s^{ - 2}}$  

$R = 6400km = 6.4 \times {10^6}m$ 

We know,

${V_h} =  - \dfrac{{GM}}{{(R + h)}}$

${g_h} = \dfrac{{GM}}{{{{(R + h)}^2}}} =  - \dfrac{{{V_h}}}{{(R + h)}}$

$\Rightarrow R + h = \dfrac{{ - {V_h}}}{{{g_h}}}$

$h = \dfrac{{ - {V_h}}}{{{g_h}}} - R =  - \left( {\dfrac{{ - 5.4 \times {{10}^7}}}{6}} \right) - 6.4 \times {10^6}$

$= 9 \times {10^6} - 6.4 \times {10^6} = 2600km$

Therefore, the height is 2600km.

2. Two astronauts are floating in gravitational free space after having lost contact with their spaceship. The two will:

(a) Move towards each other

(b) Follow Newton’s law of gravitation 

(c) Will become stationary

(d) Keep floating at the same distance between them

Ans: option (a) and (b)

Since two astronauts are floating in gravitational free space. The only force acting on the two astronauts is the gravitational pull of their masses,

$F = \dfrac{{G{m_1}{m_2}}}{{{r^2}}}$ 

Where,

F is their gravitational pull, ${m_1}{m_2}$ are the masses of the astronauts, and r is the distance between them.

Since this pull is attractive, they move towards each other and follow Newton’s law of gravitation as above. 

The List of Common Mistakes To Avoid In Exams is as Follows: 

1. G is not to be confused with g, which stands for acceleration owing to gravity. Therefore, it follows the law that the gravitational force acting between two bodies will be less the farther apart.

2. The gravitational force between two bodies will increase proportion to their respective masses.

3. The earth's gravitational pull on a specific body is referred to as its weight. Anyone travelling to the moon will feel less gravitational pull because the earth's mass is significantly greater than that of the moon, making them lighter.

4. While solving numerical problems, take care of the units you are using. 

5. To solve the question easily, always make a free body diagram as it will reduce the complexity.

Importance of Physics Gravitation

This chapter explains how a gravitational force acts on two objects. The laws related to gravitational attraction have been explained using scientific terms. Formulas related to calculating the gravitational force between two objects are determined using these formulas.

Students will also find the relevance of Kepler’s law of planetary motion with Newton’s laws of gravitation. This chapter will explain how these laws are interrelated and support each other. The mathematical derivation of all these laws will also prove the same.

This chapter will explain how the gravitational constant is calculated and it is valid for all objects. Every object feels the gravitational force of attraction from other objects. This phenomenon is proved by the laws mentioned above.

The motion of planets in their respective orbits is also influenced by the gravitational forces of other planets and the sun. Based on the explanation of the laws, it becomes easier to comprehend why a planet follows an elliptical orbit in our solar system.

This chapter is very important for the students as it explains the trajectory path of a projectile thrown. It will explain how a projectile travels from one point to the other following a parabolic path. Its explanation can be given when the gravitational interpretation of Newton’s laws of motion is used.

To make this chapter easy to comprehend, students prefer using the Gravitation Class 11 notes for NEET prepared by the subject matter experts of Vedantu.

Benefits of Vedantu’s Gravitation Class 11 Notes for NEET

• These revision notes are designed solely to serve a concise format of all the definitions, derivations, laws, and scientific explanations given in this chapter. It will help you to find out the gist of an elaborate topic related to gravitation.

• You can also use these notes to find out the right answers to all your doubts. The easier explanation given in these notes will help you to understand the fundamental principles easily.

• Once you are done preparing this chapter, you can proceed to solve the Gravitation NEET questions given as samples in these notes and evaluate your preparation level. Find out where you need to concentrate more and prepare this chapter in a better way.
  
  

Download Gravitation Class 11 Revision Notes PDF

Students can download the free PDF version of Gravitation Class 11 notes and make their revision sessions more productive. It will take less time to comprehend and revise the concepts when a student uses these notes to prepare this chapter. These notes will help students to remember the laws, formulas, and principles faster and answer NEET questions accurately.

NEET Physics Revision Notes - Chapter Pages

Other Important Links