Revision Notes on Waves for NEET 2024

Wave

A wave is a vibratory disturbance in a medium which carries energy from one point to another point without any actual movement of the medium. There are mainly three types of waves.

Mechanical Waves: The waves which can be propagated or produced only in a material medium are called mechanical waves.

Electromagnetic Waves: The waves which require no medium for their propagation or production are called electromagnetic waves.

Matter Waves: The waves associated with moving particles like electrons, protons, etc, are called matter waves.

Types of Mechanical Waves:

Longitudinal Waves

• A wave in which the particles of the medium vibrate in the same direction of propagation of the wave is called a longitudinal wave.

• Longitudinal waves can be produced in all the three media such as solids, liquids and gases. 

• The waves which are produced in the air are always longitudinal. e.g., those waves which travel along a spring when it is pushed and pulled at one end, are longitudinal waves.

• When coils are closer to each other than normal, compressions are observed in the spring. 

• When coils are farther apart than normal, rarefactions are observed. 

• A long feasible spring which can be compressed or extended easily is called a slinky.

• When a longitudinal wave passes through the air, the density of air changes continuously and the pressure and energy are transferred.

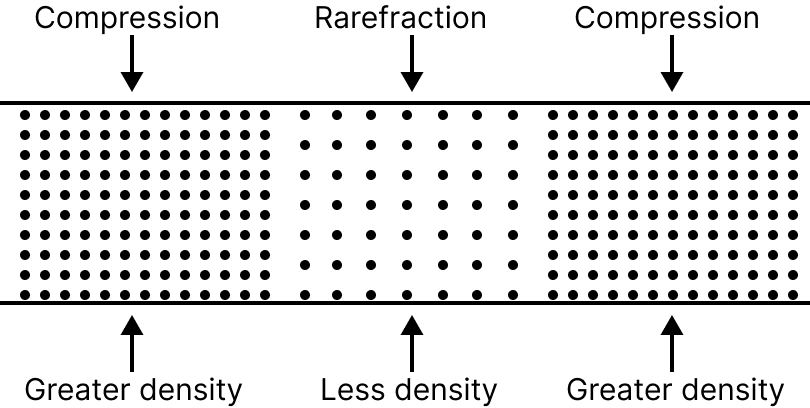
Longitudinal Wave

Transverse Waves

• A wave, in which the particles of the medium vibrate perpendicular to the direction of propagation of the wave, is called a transverse wave.

• Transverse waves can be produced only in solids and liquids.

• Light is a transverse wave but it is not a mechanical wave.

• The waves produced by moving one end of a long spring or rope up and down rapidly and whose other end is fixed, are transverse waves.

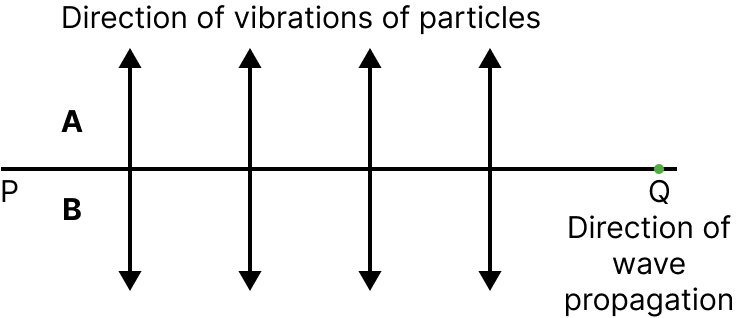
Transverse Wave

• The water waves (or ripples) formed on the surface of the water in a pond (when a stone is dropped in the pond of water), are transverse waves.

• A transverse wave travels horizontally in a medium and the particles of the medium vibrate up and down in the vertical direction. In transverse waves, crests and troughs are formed.

• A crest is that part of the transverse wave which is above the line of zero disturbance of the medium. A trough is that part of the transverse wave which is below the line of zero disturbances.

A transverse wave has been represented by a displacement-distance graph as shown below

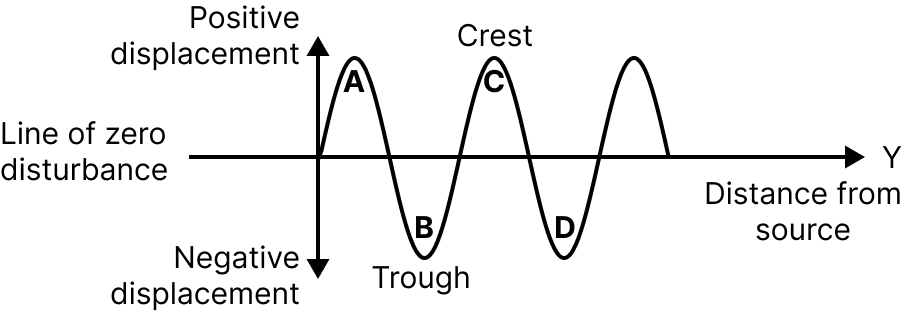
Transverse Wave Graph

Wave Motion

When a large number of particles vibrate simultaneously in a medium, then disturbance propagates in the medium.

The motion of disturbance is called wave motion. The energy of momentum is transferred to the neighbouring particles of the medium as the wave proceeds.

Some Definitions Related to Wave Motion

• Amplitude: It is the maximum displacement suffered by the particles of the medium about their mean positions. It is denoted by A.

• Time Period: The time period of a wave is the time in which a particle of medium completes one vibration to and forth about its mean position. It is denoted by T.

• Frequency: The frequency of a wave is the number of waves produced per unit time in the given medium. It is equal to the reciprocal of the time period T of the particle and is denoted by n. Thus $n=\dfrac{1}{T}$ . S.I unit of n is $\mathrm{S}^{-1}$ or hertz

• Angular Frequency: The rate of change of phase with time is called the angular frequency of the wave. It is denoted by $\omega$. Thus $\omega=\dfrac{2 \pi}{T}=2 \pi n$. SI unit of $\omega$ is rad $\mathrm{S}^{-1}$

• Wavelength: The distance between two nearest particles of the medium which are vibrating in the same phase. It is denoted by $\lambda$.

• Wave Number: The number of waves present in a unit distance of the medium is called wave number. It is equal to the reciprocal of wavelength $\lambda$. Thus, Wave number, $\bar{v}=\dfrac{1}{\lambda}$ .SI unit of wave number is $m^{-1}$.

• Angular wave number of propagation constant: The quantity $\dfrac{2 \pi}{\lambda}$ is called angular wave number or propagation constant of a wave. It represents phase change per unit path difference. It is denoted by K. Thus $K=\dfrac{2 \pi}{\lambda}$. The SI unit of K is radian per metre or rad $\mathrm{m}^{-1}$.

• Wave velocity or phase velocity: The distance covered by a wave per unit time in its directions of propagation is called its wave velocity or phase velocity. It is denoted by v.

Relation Between Wave Velocity, Frequency and Wavelength

Wave velocity $=\dfrac{\text { Distance }}{\text { Time }}$

$v=\dfrac{\lambda}{T}$ or $v=n \lambda \quad\left\{\because n=\dfrac{1}{\lambda}\right\}$ i.e, Wave velocity = Frequency $\times$ Wavelength

Equation of a Harmonic Wave:

As waves move, they can carry energy and information. The simplest wave is a harmonic wave. Harmonic waves have the following form:

$y =A \sin (\omega t-k x)$…..(i)

As we know, $\omega=\dfrac{2 \pi}{T}$ that is called angular frequency, $\mathrm{k}=\dfrac{2 \pi}{\lambda}$, angular wave number.

Putting all values in (i) equation we get

$y=A\sin \left\{ 2\pi \left( \dfrac{t}{T}-\dfrac{x}{\lambda } \right) \right\}$…….(ii)

We know that, $v=\dfrac{1}{T}$

Putting in eq. (ii) and simplifying we get, 

$y=A\sin \left\{ \dfrac{2\pi }{\lambda }(vt-x) \right\}$

We know here,

$y=$ Displacement of the particle of the medium,$\mathrm{A}=$ Amplitude of the wave,$\lambda=$ Wavelength, $\mathrm{T}=$ Time period, $\text{v}=\upsilon \lambda$, wave velocity in the medium

If the wave is travelling in the opposite direction of the x-axis, then 

$y=A\sin \left\{ 2\pi \left( \dfrac{t}{T}+\dfrac{x}{\lambda } \right) \right\}$

Differential Equation of Wave Motion:

The formula for the progressive wave equation is

$y=A \sin (\omega t-k x) \ldots \ldots \ldots \ldots (i)$

When we double-differentiate the aforementioned equation (i) w.r.t t, 

We obtain : $\dfrac{\partial {{\text{y}}^{2}}}{\partial {{\text{t}}^{2}}}=-\text{A}{{\omega }^{2}}\text{y}\ldots \ldots \ldots \ldots (ii)$

With equation (i) double-differentiated in relation to, we obtain:$\dfrac{\partial {{y}^{2}}}{\partial {{x}^{2}}}=-A{{k}^{2}}y \ldots \ldots \ldots \ldots (iii)$

If we compare eq. (ii) and (iii), we obtain:

$\dfrac{\partial \mathrm{y}^{2}}{\partial \mathrm{t}^{2}}=\left(\dfrac{\omega}{\mathrm{k}}\right)^{2} \dfrac{\partial \mathrm{y}}{\partial \mathrm{x}^{2}}$

As we know that, $v=\dfrac{\omega}{k}$

The differential equation of a wave should be written as follows:$\dfrac{\partial \mathrm{y}^{2}}{\partial \mathrm{t}^{2}}=\mathrm{v}^{2} \dfrac{\partial \mathrm{y}^{2}}{\partial \mathrm{x}^{2}}$

Relationship Between Particle and Wave Velocity:

Particle speed is the speed of a media particle travelling through the medium at any given moment as a progressive wave.

The speed at which a progressive wave moves through a medium is known as wave velocity.

Particle displacement at any time t is,

$y=A \sin (\omega t-k x)$........... (1)

Differentiating with respect to t we get

 $v=\dfrac{dy}{dt}=A\omega \cos (\omega t-kx)$........... (2)

Again differentiating with respect to x we get,

$\dfrac{d y}{d x}=-A k \cos (\omega t-k x)$........... (3)

Eq. (2) divided by (3) gives us

$\dfrac{\mathrm{dy} / \mathrm{dt}}{-\mathrm{dy} / \mathrm{dx}}=\dfrac{\omega}{\mathrm{k}}$

$\Rightarrow \dfrac{{v_p}}{-\text{dy}/\text{dx}}=\text{v}$

$\Rightarrow v_p =-{{v}_{\text{wave velocity}}}\cdot \dfrac{dy}{dx}$

Relation Between Phase Differences, Path Difference:

The phase difference is the difference between the two waves' phase angles. The difference in the two waves' paths is known as their "path difference." Phase difference and route difference have a direct relationship. They are related to one another in a direct proportion.

Phase Difference and Path Difference for any two waves with the same frequency are related as follows:

$\Delta x=\dfrac{\lambda}{2 \pi} \Delta \phi$ 

There are several methods to express the relationship between the difference in phase angle and the difference in path length:

Speed of Transverse Waves:

• Crests and troughs make transverse waves. The peak is the top of the wave, while the trough is the bottom of the wave.

• Vibrating strings are used by musical instruments like the piano and guitar to create sound. The square root of the tension in the string and the square root of the linear density of the string are both related to the speed of a wave on this type of string. The following formulation applies to this:

$v=\sqrt{\dfrac{T}{\mu}}$

Speed of Longitudinal Waves:

• Speed of longitudinal waves in an elastic material e and density $\rho$ is given by $v=\sqrt{\dfrac{e}{\rho }}$.

• In solids, E is replaced by Young's modulus (Y), $v=\sqrt{\dfrac{Y}{\rho }}$.

• In gases/liquid, E is replaced by bulk modulus of elasticity ($\beta $), ${{v}_{\text{ }}}=\sqrt{\dfrac{\beta }{\rho }}$.

• A solid's density is significantly greater than that of a gas, yet its flexibility is much greater $\mathrm{v}_{\text {solid }}>\mathrm{v}_{\text {liquid }}>\mathrm{v}_{\mathrm{gas}}$.

Laplace's Correction:

Laplace Correction modifies the speed of sound in the gas. Newton estimated the formula for the speed of sound in a gaseous medium, assuming that the propagation of sound waves in air or gas is isothermal.

$\mathrm{PV}^{\gamma}=$ Constant

Here,$\gamma$ is adiabatic index

And we know, $\gamma=\dfrac{C_{p}}{C_{v}}$

$C_{p}$ Specific heat for constant pressure

$C_{v}$ Specific heat for a constant volume.

When we differentiating both sides, we get

$V^{\gamma} d P+P_{\gamma} V^{\gamma-1} d V=0$

Dividing both the sides by $\mathrm{V}^{-1}$

$V d P+P \gamma V d V=0$ 

$P \gamma=-\dfrac{d P}{\left(\dfrac{d V}{V}\right)}=B$

The velocity of sound is given by

$v=\sqrt{\dfrac{B}{\rho}}$

Substituting $\mathrm{B}=\gamma \mathrm{P}$ in above equation we get:

$v=\sqrt{\dfrac{\gamma P}{\rho}}$

Power and Intensity of Wave Motion:

• Energy is transmitted along a stretched string as a wave travels across it.

• The wave's power is provided by $P=\dfrac{1}{2} \mu \omega^{2} A^{2} v$ ,Here $\mu$ is mass per unit length.

• Intensity is defined as the flow of energy per unit area of string cross-section per unit time. Intensity $I=\dfrac{1}{2} \rho \omega^{2} A^{2} v$

Principle of Superposition of Waves:

Superposition: At any point, the displacement is the vector sum of the displacements of all waves passing through that point at that instant.

Fourier's theorem states that any complex periodic wave may be expressed as the sum of sinusoidal waves with varying amplitudes, frequencies, and phases.

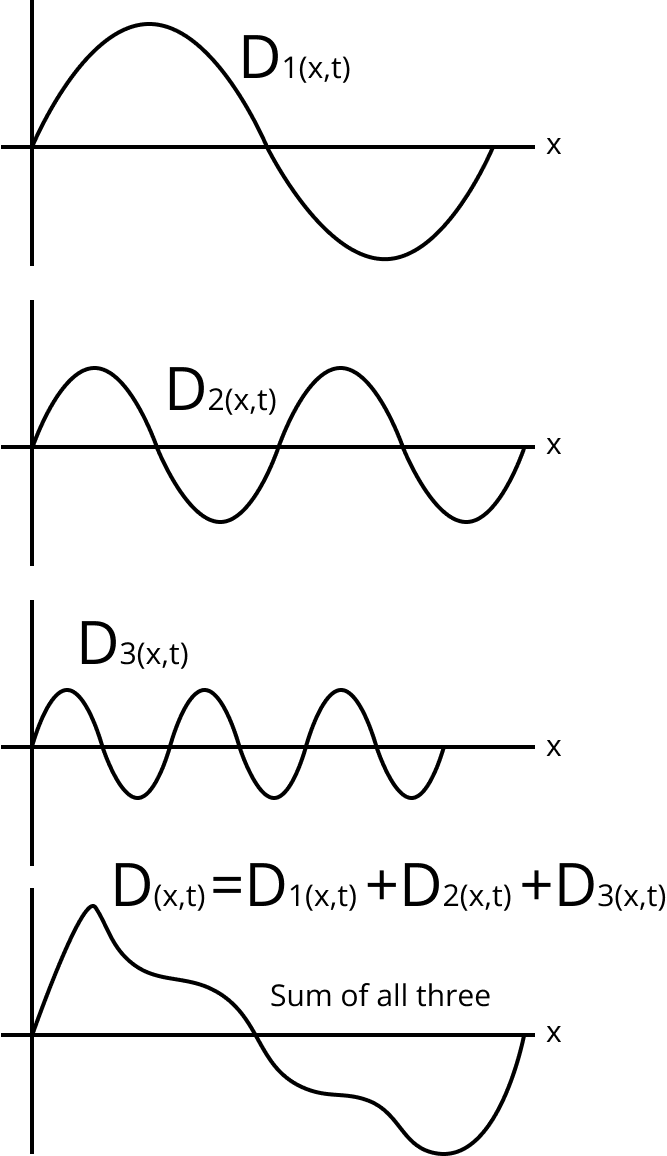
Superposition Waves

Interference of Waves

Wave interference happens when two waves collide while travelling through the same medium. Wave interference causes the medium to take on a shape determined by the net effect of the two distinct waves on the medium's particles. Consider two pulses of the same amplitude flowing in opposite directions along the same medium to begin our investigation of wave interference.

• If we consider two waves $\mathrm{y}_{1}=\mathrm{A}_{1} \sin (\omega \mathrm{t}-\mathrm{kx}) \,\text { and }\mathrm{y}_{2}=\mathrm{A}_{2} \sin (\omega \mathrm{t}-\mathrm{kx}+\phi)$.

• Using Superposition, $\mathrm{y}_{2}=\mathrm{A}_{2} \sin (\omega \mathrm{t}-\mathrm{kx}+\phi)$.

Here, $A^{2}=A_{1}^{2}+A_{2}^{2}+2 A_{1} A_{2} \cos \phi$, and $\tan \delta=\dfrac{A_{2} \sin \phi}{A_{1}+A_{2} \cos \phi}$.

As the intensity $\mathrm{I} \propto \mathrm{A}^{2}$.

As a result, resultant intensity $I=I_{l}+I_{2}+2 \sqrt{I_{1} I_{2}} \cos \phi$.

Reflection of Waves:

• According to the standard rules of reflection and refraction, a mechanical wave is reflected and refracted at a boundary separating two mediums. 

• If a sound wave is reflected from a stiff barrier or a denser medium, the wave undergoes a pi phase reversal but its nature remains unchanged, i.e., compression is reflected back as compression and rarefaction as rarefaction.

• There is no phase shift when a sound wave is reflected from an open boundary or rarer medium, but the character of the wave changes, i.e., compression is reflected back as rarefaction and rarefaction as compression.

Beats

• Beats are the increase and decrease in sound intensity caused by the superposition of two sound waves of slightly different frequencies travelling in the same direction.

• Beats are intriguing phenomena caused by wave interference. When two slightly different frequencies are experienced at the same moment, we hear a similar frequency but also something else: a periodic variation in volume whose rate is the difference between the two frequencies. 

• As the sounds alternately interfere constructively and destructively, the volume changes like a tremolo. As the two tones get closer to harmony, the beating slows down and may become unnoticeable. While tuning musical instruments, beats are easily discernible.

• When the two waves are about 180 degrees out of phase, the maxima of one wave cancels the minima of the other, and when they are nearly in phase, their maxima sum up, increasing the perceived volume.

• Beats are created as a result of wave superposition/interference.

$\mathrm{y}_{2}=\mathrm{A} \sin \omega_{1} \mathrm{t}$

$\mathrm{y}_{2}=\mathrm{A} \sin \omega_{2} \mathrm{t}$

$\mathrm{y}_{1}+\mathrm{y}_{2}=\mathrm{A}\left(\sin \omega_{1}+\sin \omega_{2} \mathrm{t}\right)$

$2 \mathrm{~A} \sin \dfrac{\left(\omega_{1}+\omega_{2}\right)}{2} \mathrm{t} \cos \left(\dfrac{\omega_{1}-\omega_{2}}{2}\right) \mathrm{t}$

$\mathrm{y}=\mathrm{A}_{1} \sin \omega_{1} \mathrm{t}$

$\mathrm{w}_{1}=\left(\dfrac{\omega_{1}+\omega_{2}}{2}\right)$

$\mathrm{A}_{1}=2 \mathrm{~A} \cos \left(\dfrac{\omega_{1}-\omega_{2}}{2}\right) \mathrm{t}$

• We know that frequency $(n)$ is directly proportional to the angular frequency $(\omega)$.

Here, the amplitude varies as $\left(\dfrac{\omega_{1}-\omega_{2}}{2}\right)$.

Thus, the amplitude varies as $\dfrac{{{n}_{1}}-{{n}_{2}}}{2}$, here $n_{1}$ and $\mathrm{n}_{2}$ are frequencies.

Doppler Effect

• In physics, the Doppler effect is defined as a rise (or reduction) in the frequency of sound, light, or other waves as the source and observer move closer (or further) apart.

• The apparent difference in the frequency at which sound or light waves leave a source and that at which they reach an observer produced by relative motion of the observer and the wave source is known as the Doppler effect. This effect is used in astronomical observations, Mössbauer effect research, radar, and modern navigation. Christian Doppler, an Austrian physicist, described it for the first time in 1842.

The Apparent Change in Frequency:

If the source is in motion and the observer is at rest

If source moving towards observer $f={{v}_{0}}\left( \dfrac{V}{V-{{V}_{S}}} \right)$

If source moving away from observer$f'={{v}_{0}}\left( \dfrac{V}{V+{{V}_{S}}} \right)$ Where $V=$ velocity of sound${{V}_{S}}=\text{ velocity of source ,}{{v}_{0}}=\text{ source frequency}\text{. }$

If the source is at rest and the observer in motion

• If observer moving on the way to source $f=\left( \dfrac{V+{{V}_{0}}}{V} \right){{v}_{0}}$

• If observer moving away since source and $V_{0}=$ velocity of observer:$f'=\left( \dfrac{V-{{V}_{0}}}{V} \right){{v}_{0}}$

If the source and observer both are in motion

• If either the source or the observer moves in relation to the medium, the frequency observed may differ from the frequency of the source.

• The Doppler Effect refers to the apparent shift in frequency of the wave caused by the motion of the source or the observer.

• When the observer is stationary and the source is moving, the apparent frequency of the sound experienced by the observer is

$f^{\prime}=\left(\dfrac{v}{v \pm v_{S}}\right) f$

• When the source is stationary and the observer is moving, the apparent frequency of the sound experienced by the observer is

$f^{\prime}=\left(\dfrac{v \pm v_{O}}{v}\right) f$

Here, $v=$ speed of sound in the medium,

$f^{\prime}=$ apparent frequency,

$f=$ natural frequency, ${{v}_{s}}\text{,}{{v}_{0}}=$ speed of the source & observer respectively.

• Doppler's Law is the appropriate law for determining the apparent change in frequency when a source and an observer are in motion.

Stationary of Standing Waves

A standing wave is a combination of two waves flowing in opposite directions that have the same amplitude and frequency. Interference causes the phenomenon; when waves are overlaid, their energies are either added together or wiped out. Interference causes a travelling wave when two waves move in the same direction. Interference produces an oscillating wave fixed in space for opposingly travelling waves.

Formation of Stationary Waves

Stationary Waves

• The image given above depicts two waves travelling in opposite directions via a medium. Assume the blue wave moves to the right and the green wave moves to the left. Interference occurs when two waves collide while travelling through the same medium. The blue and green waves collide to create a new wave pattern known as the resulting wave. According to the principle of superposition, the resultant is the outcome of two distinct waves.

• The resulting wave pattern is known as a standing wave pattern.

• These waves are created when two waves of the same frequency collide while travelling in opposite directions. Standing waves are generated in this manner.

• The wave patterns are distinguished by some stationary points that do not move. These points are referred to as nodes. The position of nodes is denoted by N in the preceding diagram.

• Furthermore, certain sites experience the most displacement. These points are located between the successive nodal points. AN represents the position of antinodes. These positions alternate between maximum positive displacement and maximum negative displacement.

Stationary Waves in an Organ Pipe:

• An organ pipe is a pipe filled with air with rigid walls and a diameter less than its length. By forcing air into the pipe, such pipes produce melodic sound. The best example of an organ pipe is the flute. When the pipe is open at both ends, it is referred to as an open organ pipe. A closed organ pipe has one end open and the other end closed.

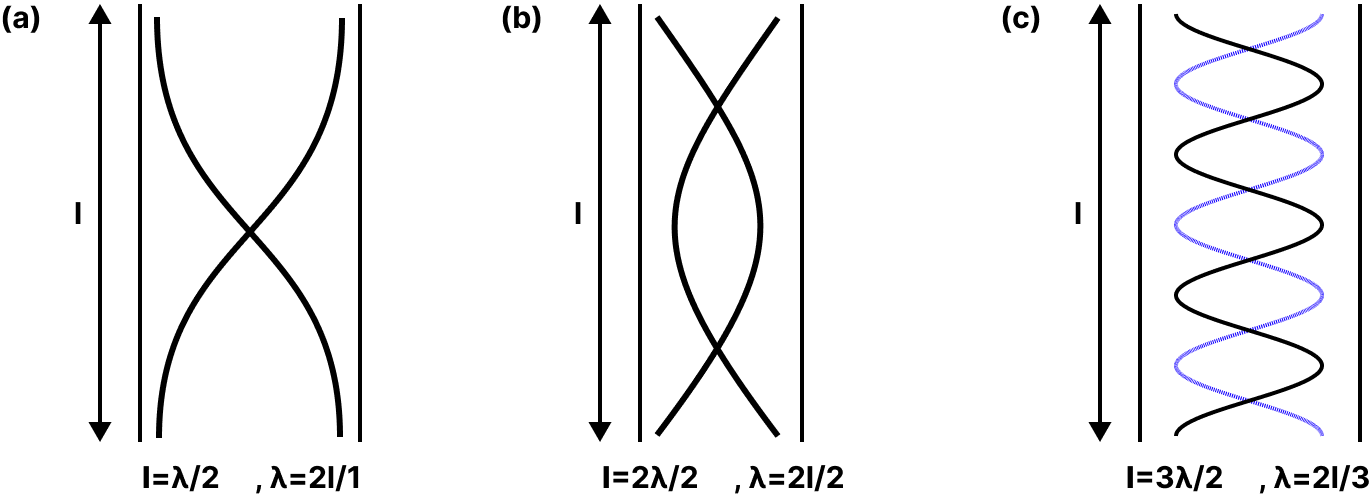
Stationary Waves in an Organ Pipe

The frequency of the basic note or first harmonic in an open organ pipe is

$n_{1}=v / 2 l$

Here $v$ is velocity of sound and $l$ is the length of the pipe. The frequency of second harmonic or first overtone is

${{n}_{2}}\text{ }=2v/2l=v/l=2{{n}_{1}}$

The subsequent harmonic/ overtones are $n_{3}=3 n_{1}$ and so on.

The basic note or first harmonic frequency in a closed organ pipe is $\mathrm{n}_{1}{ }^{\prime}=v / 4 l$

Frequency of first overtone or third harmonic is

$n_{2}^{\prime}=3 v / 4 l=3 n_{1}^{\prime}$

Frequency of second overtone or fifth harmonic is

$n_{3}{ }^{\prime}=5 v / 4 l=5 n_{1}{ }^{\prime} \text { and so on. }$

End Correction

End correction: An antinode is not generated exactly at the open end of an organ pipe. Rather, the antinode is produced a small distance (x) outside the open end. This (x) is referred to as the end correction. Its value is determined by the pipe's internal radius (r). Typically, x=0.6 r

End correction in an open organ pipe is 2 x for the two open ends of the pipe. End correction is x in a closed organ pipe since there is only one open end.

Applying end correction, frequency of fundamental note in open organ pipe is

$\mathrm{n}=v / 2(l+2 x)=v / 2(1+1.2 r)$

And frequency of fundamental note in closed organ pipe is

$n^{\prime}=v / 4(l+x)=v /(l+0.6 r)$

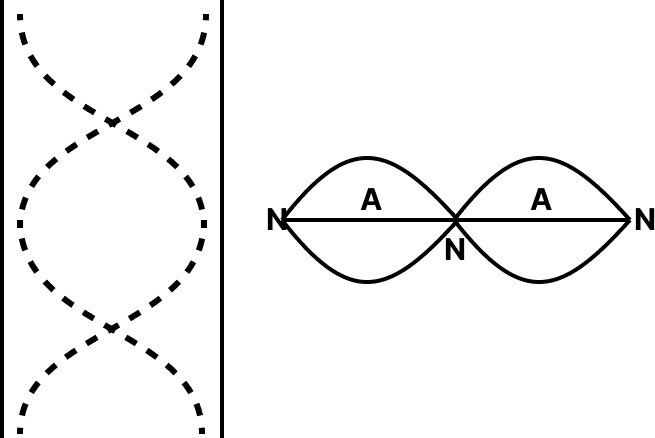
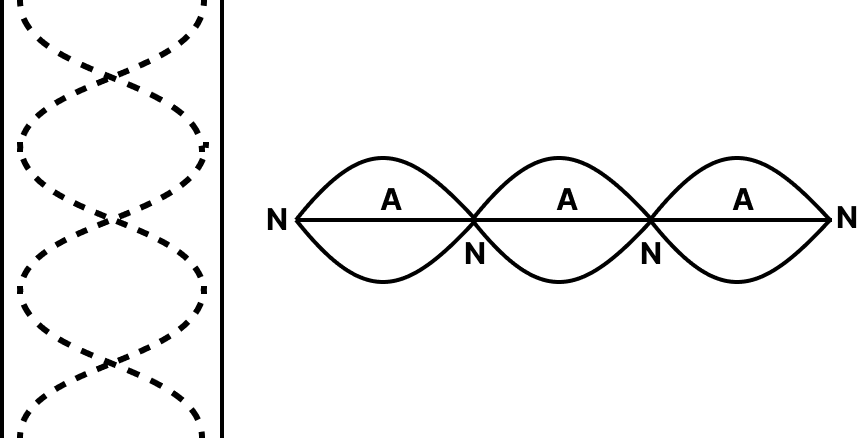
	For Vibrating Strings / Open Organ Pipes
Mode of vibration	First or Fundamental	Second	Third
Harmonic	First	Second	Third
Tone	Fundamental tone	First overtone	Second overtone
Frequency	$v=\dfrac{\mathrm{v}}{2 l}$	2v	3v
Wavelength	\[2l\]	$\dfrac{2 l}{2}$	$\dfrac{2 l}{3}$
Shape for string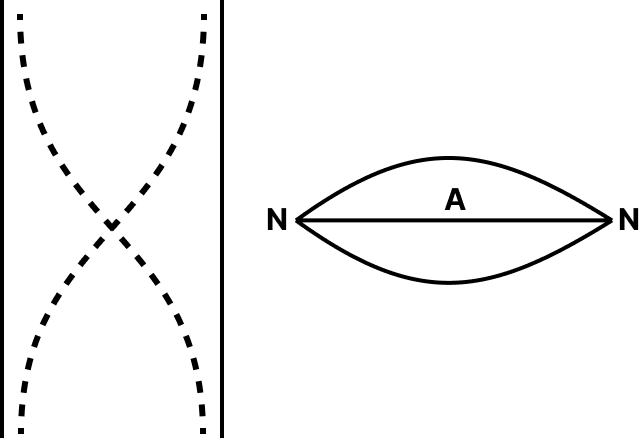

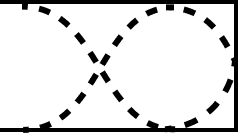
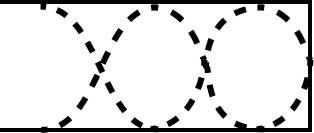
	For closed organ pipe
Mode of vibration	First or Fundamental	Second	Third
Harmonic	First	Second	Third
Tone	Fundamental tone	First overtone	Second overtone
Frequency	$v=\dfrac{\mathrm{V}}{4 l}$	3v	5v
Wavelength	\[4l\]	$\dfrac{4l}{3}$	$\dfrac{4 l}{5}$
Shape for string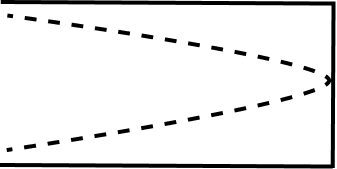

Characteristics of Sound

• A musical sound consists of rapid, predictable, and periodic compressions and rarefactions that are separated by brief amplitude changes.

• A noise is made up of slow, erratic, and periodic compressions and rarefactions that occasionally have abrupt amplitude changes.

• The characteristics of musical sound are (i) pitch, (ii) loudness, and (iii) quality.

• The relationship between pitch and frequency, loudness and intensity, and quality is influenced by the quantity and strength of overtones.

• The interval between two notes is defined as the ratio of the two notes' frequencies. Interval, for instance, between two notes of different frequencies $512 \mathrm{~Hz}$ and $1024 \mathrm{~Hz}$ is 1: 2$(or$1 / 2).

• If the frequencies of two notes are equal, or if their distance from one another is one to one, then two notes are said to be in unison.

Other frequent intervals that are useful in creating musical sound include the following

Octave $(1: 2)$, majortone $(8: 9)$, minortone $(9: 10)$ and semitone $(15: 16)$

Formula Chart:

Examples:

Q1. Consider two organ pipes of same length in which one organ pipe is closed and another organ pipe is open. If the fundamental frequency of a closed pipe is $250 \mathrm{~Hz}$. Calculate the fundamental frequency of the open pipe.

(1) $700~\text{Hz}$

(2) $500~\text{Hz}$

(3) $600~\text{Hz}$

(4) $800~\text{Hz}$

Answer: 2

Hint: The lowest frequency of a periodic waveform is known as the fundamental frequency, also known as just the fundamental. The musical pitch of a note that is heard as the lowest partial present in music is referred to as the fundamental.

Step by Step solution:

Fundamental frequency of closed organ pipe

$\gamma_{x}=\dfrac{V}{4 l}=250 \mathrm{~Hz}$(According to given question)

Fundamental frequency of closed organ pipe

We need to find${{\gamma }_{0}}\text{ }=\dfrac{V}{2l}=?$

$\dfrac{{{\gamma }_{c}}}{{{\gamma }_{o}}}=\dfrac{V}{4l}\times \dfrac{2l}{~\text{V}}=\dfrac{1}{2}$

${{\gamma }_{0}}\text{ }=2{{\gamma }_{c}}$

${{\gamma }_{0}}\text{ }=2 \times 250$

${{\gamma }_{0}}\text{ }=500 \mathrm{~Hz}$

${{\gamma }_{0}}\text{ }=500~\text{Hz}$

Therefore, the fundamental frequency of the open pipe is $500~\text{Hz}$

Q2. A source, approaching with speed u towards the open end of a stationary pipe of length $L$, is emitting a sound of frequency $\mathrm{f}_{\mathrm{s}}$. The farther end of the pipe is closed. The speed of sound in air is $v$ and $\mathrm{f}_{0}$ is the fundamental frequency of the pipe. For which of the following combination(s) of $u$ and $\mathrm{f}_{\mathrm{s}}$, will the sound reaching the pipe lead to a resonance?

(1) $\mathrm{u}=0.8 \mathrm{v}$ and $\mathrm{f}_{\mathrm{s}}=\mathrm{f}_{0}$

(2) $\mathrm{u}=0.8 \mathrm{v}$ and $\mathrm{f}_{\mathrm{s}}=2 \mathrm{f}_{0}$

(3) $\mathrm{u}=0.8 \mathrm{v}$ and $\mathrm{f}_{\mathrm{S}}=0.5 \mathrm{f}_{0}$

(4) $\mathrm{u}=0.5 \mathrm{v}$ and $\mathrm{f}_{\mathrm{S}}=1.5 \mathrm{f}_{0}$

Answer: 1,4

Hint: The lowest frequency of a periodic waveform is known as the fundamental frequency, also known as just the fundamental. The musical pitch of a note that is heard as the lowest partial present in music is referred to as the fundamental.

Step by Step solution:

Natural frequency of closed pipe,

$f=(2 n+1) f_{0}$

$\mathrm{f}_{0}$ is fundamental frequency

$n=0,1,2 \ldots \ldots$

Frequency of source received by pipe,

$f^{\prime}=f_{s}\left[\dfrac{v-0}{v-u}\right]$

For resonance,

$f^{\prime}=f$

$f_{s}\left[\dfrac{v}{v-u}\right]=(2 n+1) f_{0}$

If $u=0.8 v, f_{s}=f_{0}$

$f^{\prime}=\dfrac{v}{0.2 v} f_{0}=5 f_{0}$

For $\mathrm{n}=2$ pipe can be in resonance

Hence, option (a) is correct.

If $u=0.8 v, f_{s}=2 f_{0}$

$f^{\prime}=\dfrac{v}{0.2 v} \times 2 f_{0}=10 f_{0}$

If $u=0.8 v, f_{s}=0.5 f_{0}$

$f^{\prime}=\dfrac{v}{0.2 v} \times 0.5 f_{0}=2.5 f_{0}$

Not possible.

If $u=0.5 v, f_{s}=1.5 f_{0}$

$f^{\prime}=\dfrac{v}{0.5 v} \times 1.5 f_{0}=3 f_{0}$

For $n=1 \mathrm{f}=3 \mathrm{f}_{0}$

Pipe can be in resonance.

Common Errors or Mistakes that Should be Avoided by the Students Keeping the Exam Point of View:

• Students forget to write the working formula and not read definitions properly.

• Students also write improper units without checking their compatibility.

• Calculation errors when doing problems

• Students forget to put in the correct data they used in the working formula, which is used by teachers to check how effective the students' learning is.

• A  law stated by someone cannot be restructured, it should be reiterated like how it was stated.

• While drawing a graph, students forget to state the variables of the graph and just plot the graph.

• For questions which require the reason for a certain condition, firstly students are required to state the cause of the condition and then the consequence of the condition.

Importance of Class 11 Physics Waves

Students have studied oscillatory and simple harmonic motions in the previous chapters. In this chapter, they will be introduced to the advanced concepts of waves and the characteristics shown by the particles in the medium. They will learn how a wave propagates in a medium and what happens to it.

In this chapter, students will learn that waves do not transfer mass but it transfers the energy from one particle to the adjacent one following a rhythm. This energy can be calculated using the specific formulas used to interpret the scientific principles of waves.

The undulating motion of the particles seen in a waving medium can be used to explain the propagation of wave energy in a medium. In the Waves notes for NEET, this chapter will explain what waveforms are and how they differ from each other.

On proceeding further, it will explain what group velocity and phase velocity are in such periodic motions. The features and types of waves will also be described using specific examples. These examples will help you understand how transverse and longitudinal waves vary from each other.

This chapter is important as it teaches the basic concepts of waves and their types. It helps to understand how sound, light, and other types of energies propagate through or without mediums. Use the Waves Class 11 notes to make it easier for you to understand these fundamental concepts.

Benefits of Vedantu’s NEET Revision Notes for Waves Physics

• The revision notes prepared by the subject matter experts have the prime aim of delivering a convenient medium to describe these fundamental concepts in a simpler version.

• The simpler version will enable you to understand and revise the chapter faster. There is no need to turn the pages of your physics textbook once you are done preparing this chapter. Simply referring to these notes to recall what you have studied will save time.

• This format has been scientifically developed to offer more convenience to you for remembering the concepts. The format used by the experts will help students to memorise the concepts of waves and recall them during the NEET exam.

Download Waves Chapter of Class 11 Notes PDF

Now that you have understood the importance of this chapter and the benefit of these NEET revision notes, download its free PDF version right away. Perform Waves Class 11 notes PDF download and complete your NEET Study Materials for this chapter and prepare it excellently. Use these notes to revise and recall the fundamental principles linked to waves and score well in the exams.

Other Important Links

NEET Physics Revision Notes - Chapter Pages