Revision Notes on Electromagnetic Waves for NEET 2024

Displacement Current:

During the process of charging of capacitor, current flows through the connecting wires, known as conduction current ${I_C}$. As the charge accumulates on the plates of capacitor, a changing electric field is produced across the gap between its two plates, which produces magnetic fields. Maxwell assumed that a current also flows in the gap between the two plates of capacitor, during the process of charging, known as displacement current${I_D}$ . This displacement  current originates due to time varying electric field between the plates of capacitor and is given by

${I_D} = {\varepsilon _0}\dfrac{{d{\phi _\varepsilon }}}{{dt}}$ 

Where ${\phi _\varepsilon }$  gives the electric flux linked with the space between the two plates of the capacitor.

• Thus , displacement current ${I_D}$  is the electric current which flows in the gap between the plates of the capacitor during its charging , which originates due to the time varying electric field in  the space between the two plates of capacitor.

• So, using the concept of displacement current ${I_D}$ , Ampere’s circuital law can be modified as,

$\oint {\vec B.d\vec l = {\mu _0}\left( {{I_C} + {I_D}} \right)}$ which is also called Ampere-Maxwell’s circuital law.

• The displacement current ${I_D}$  is precisely equal to the conduction current ${I_C}$ , when the two are present in different parts of the circuit. These currents are individually discontinuous, but the two currents together possess the property of continuity through any closed circuit. For example, during charging of capacitor, in connection wires, conduction current ${I_C}$ is continuous whereas displacement current ${I_D}$  is discontinuous .So, by Amperes-Maxwell’s circuital law

$\oint {\vec B.d\vec l = {\mu _0}{I_C}}$

• Whereas, in the space between the two plates of the charging capacitor, conduction current ${I_C}$  is discontinuous, but displacement current ${I_D}$  is continuous. So by Ampere –Maxwell’s circuital law, 

$\oint {\vec B.d\vec l = {\mu _0}{I_D}}$ 

• As ${I_D}$ and ${I_C}$ are numerically equal, so together they are continuous in the circuit during the charging of the capacitor.

• Modified Ampere-Maxwell Law: The line integral of the magnetic field around any closed path is determined by the sum of the net conduction current through the path and the rate of change of electric flux through any surface bounded by the path.

$\oint {\vec B.d\vec l = {\mu _0}I + {\varepsilon _o}{\mu _o}\dfrac{{d{\phi _e}}}{{dt}}}$ 

Electromagnetic Waves:

• These are those waves in which there is a sinusoidal variation of electric and magnetic field at right angles to each other as well as at right angles to the direction wave propagation. For a plane progressive electromagnetic wave propagating along the +z direction, the electric and magnetic fields can be written as, 

${E_x} = {E_0}\sin (kz - \omega t)$ 

${B_y} = {B_0}\sin (kz - \omega t)$ 

• In electromagnetic waves, the electric and magnetic fields vary with space and time and have the same frequency and are in the same phase.

• The amplitudes of electric and magnetic fields in free space , in electromagnetic waves are related by 

${E_0} = c{B_0}$   Or    ${B_0} = \dfrac{{{E_0}}}{c}$ 

• The speed of electromagnetic wave in free space is 

$c = \dfrac{1}{{\sqrt {{\mu _0}{\varepsilon _0}} }}$  

where ${\mu _0}$  and ${\varepsilon _0}$  are the permeability and permittivity of free space.

• The speed of electromagnetic wave in a medium is,

$\upsilon  = \dfrac{1}{{\sqrt {\mu \varepsilon } }}$ 

where $\mu$  and $\varepsilon$  are permeability and permittivity of medium.

$\upsilon  = \dfrac{1}{{\sqrt {{\mu _0}{\mu _r}{\varepsilon _0}{\varepsilon _r}} }} = \dfrac{c}{{\sqrt {{\mu _r}{\varepsilon _r}} }}$ 

where  $\mu_r$  and $\varepsilon_r$ are relative permeability and relative permittivity.

Characteristics of Electromagnetic Waves:

• These waves do not carry any charge.

• These waves are not deflected by electric and magnetic fields.

• They travel with the speed of light c $\left( { = 3 \times {{10}^8}m{s^{ - 1}}} \right)$ in vacuum.

• The frequency of an electromagnetic wave does not change when it goes from one medium to another but its wavelength changes.

• These waves are transverse in nature, hence they can be polarised.

Nature of Electromagnetic Waves:

• The equation of an electric field along X-axis is given as

${E_x} = {E_0}\sin ({k_Z} - \omega t)$ 

The equation of a magnetic field along Y-axis is given as

${B_y} = {B_0}\sin ({k_Z} - \omega t)$ 

Here k is propagation constant and is equal to $\dfrac{{2\pi }}{\lambda }$ 

ω is that angular frequency = $\dfrac{{2\pi }}{T}$ 

• Electromagnetic waves are transverse in nature as the electric and magnetic fields are perpendicular to each other and to the direction of propagation of EM waves.

• When an electromagnetic wave advances, the electromagnetic energy flows in the direction. The total energy flowing perpendicularly per second unit area into the space in free space is called a pointing vector.

$\overrightarrow S  = \dfrac{{\overrightarrow E  \times \overrightarrow B }}{{{\mu _o}}}$ 

• If the $\vec E$ electric field vector is along the y-axis and magnetic field vector$\vec B$  is along the z-axis, the direction of propagation is along$\vec E \times \vec B$ . I.e. along the x-axis. So, electric field vectors.

$\vec E = {E_y}\hat j$ 

$\vec E = {E_0}\sin (kx - \omega t)\hat j$

$\vec E = {E_0}\sin \left[ {2\pi \left( {\dfrac{x}{\lambda } - \dfrac{t}{T}} \right)} \right]\hat j$ 

$\vec E = {E_0}\sin \left[ {\dfrac{{2\pi }}{\lambda }\left( {x - ct} \right)} \right]\hat j$

Here ${E_X} = {E_Z} = 0$ and magnetic field vector

$\vec B = {B_z}\hat k$

$\vec B = {B_0}\sin (kx - \omega t)\hat k$ 

$\vec B = {B_0}\sin \left[ {2\pi \left( {\dfrac{x}{\lambda } - \dfrac{t}{T}} \right)} \right]\hat k$ 

$\vec B = {B_0}\sin \left[ {\dfrac{{2\pi }}{\lambda }\left( {x - ct} \right)} \right]\hat k$ 

Here ${{\vec B}_x} = {{\vec B}_y} = 0$

• In case the EM wave is propagating in z direction the equation may be

$\vec E = {E_0}\sin \dfrac{{2\pi }}{\lambda }\left[ {z - ct} \right]\hat i$

$\vec B = {B_0}\sin \dfrac{{2\pi }}{\lambda }\left[ {z - ct} \right]\hat j$

• Energy density due to an electric field is \[u=\dfrac{1}{2}{{\varepsilon }_{o}}{{E}^{2}}\]

• Energy density due to magnetic field is \[u=\dfrac{1}{2{{\mu }_{o}}}{{B}^{2}}\]

• Energy density of an Electromagnetic wave is \[u=\dfrac{1}{2}{{\varepsilon }_{o}}{{E}^{2}}+\dfrac{1}{2}{{\varepsilon }_{o}}{{\mu }_{o}}{{E}^{2}}\]

Electromagnetic Spectrum:

• Electromagnetic waves include radio waves, microwaves, visible light waves, infrared rays, UV rays, X-rays and gamma rays.

•  The classifications of electromagnetic waves done according to the frequency are called electromagnetic spectrum.

•  The basic difference between various types of electromagnetic waves lies in their wavelength or frequency since all of them travel through vacuum with the same speed. Also, the waves differ in their mode of interaction with matter.

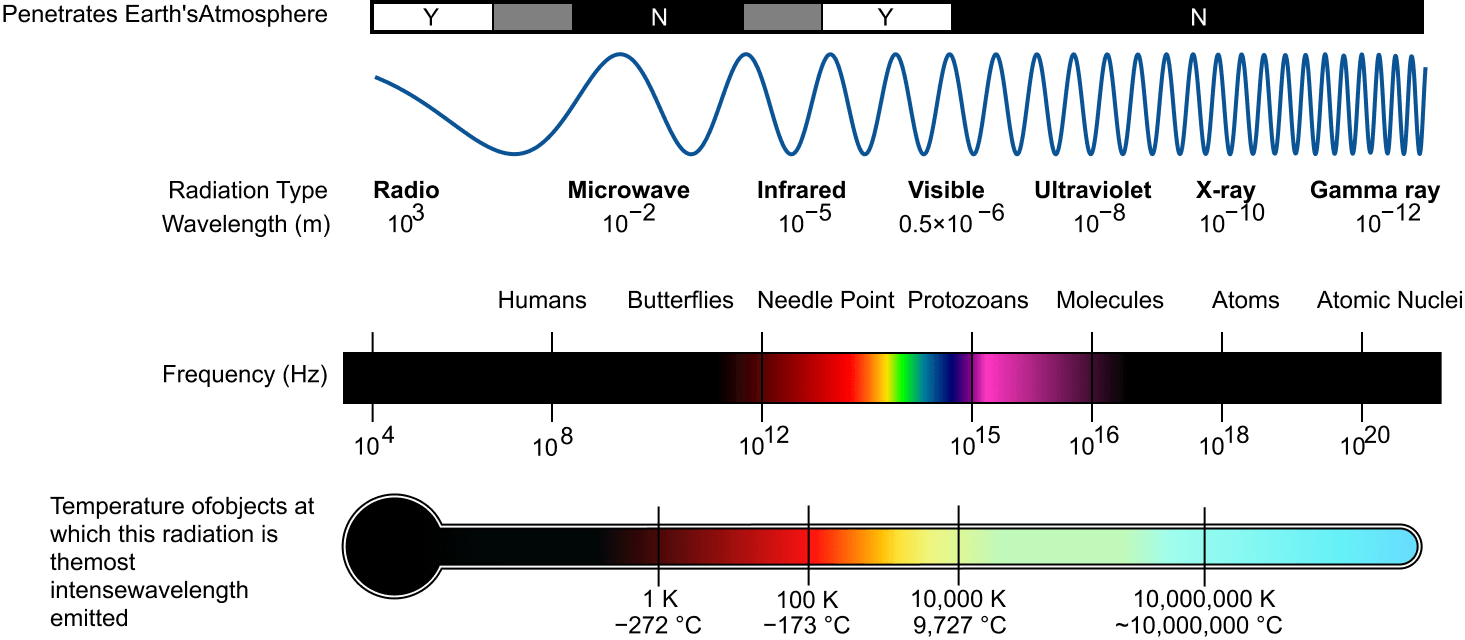
Electromagnetic Spectrum

Radio Waves

• They are generally in a frequency range 500 kHz 1000 MHz.

• The AM (amplitude modulated) band used for short distance radio transmission is from 530 kHz to 1710 kHz the SW (short wave) band involves frequencies between 1500 kHz to 50 MHz and is used for long range radio broadcast.

• TV transmission uses VHF (very high frequency) band and frequency modulation is done. The VHF band extends from 50 MHz to 900 MHz.

• Cellular phones use radio waves to transmit voice communication in the UHF (ultra high frequency) band. The UHF band extends from 900 MHz to 5000 MHz.

• Radio waves are produced by oscillating electric circuits having inductor and capacitor.

Microwaves

• Microwaves are high frequency radio waves of frequency range 1 GHz to 300 GHz.

• Microwaves are produced by special vacuum tubes e.g. klystrons, magnetrons.

• Microwaves are used in

• Radar system used in aircraft navigation.

• Speed guns to determine the speed of moving an automobile, cricket ball, tennis ball, etc.

1. In the study of atomic and molecular structure.

2. In communication via satellite.

3. In the microwave oven for cooking.

Infrared Waves

• Infrared waves are heat radiations also known as heat waves and are of frequency range $3 \times {10^{11}}$  to $4 \times {10^{14}}$ Hz and of wavelength $8 \times {10^{ - 7}}$ m to $3 \times {10^{ - 4}}m$ .

• Infrared waves are produced by hot bodies and molecules.

• Infrared waves do heating because water molecules present in most of the materials readily absorb infrared waves and their thermal motion increases, so they heat up themselves and also heat up the surroundings.

Infrared Waves are Used in

• Physical therapy to treat muscular strain.

• Taking photographs during conditions of fog, smoke, etc.

• Keeping earth's surface warm by greenhouse effect.

• To provide electrical energy by using solar cells.

• Used in remote switches for household electronic systems.

Ultraviolet Rays

• Ultraviolet rays are of frequency range $8 \times {10^{14}}$ to $5 \times {10^{16}}$ Hz of wavelength $3 \times {10^{ - 8}}$ to$4 \times {10^{ - 7}}m$ .

• Ultraviolet rays are produced by special lamps to mercury and from arc lamps and by very hot bodies like the sun.

• Ultraviolet rays in solar radiations on reaching the earth are absorbed by the ozone layer present in the atmosphere. Ultraviolet radiation has large quantities of harmful effects on humans.

Ultraviolet Rays are Used in

• Study of molecular structure.

• In sterilisation to destroy bacteria.

• In burglar alarms etc as they can cause photoelectric effect.

• U.V radiation is absorbed by ordinary glass. Hence, glass windows can protect us from UV rays.

X-rays

• X-rays are of frequency range $8 \times {10^{16}}$ to $3 \times {10^{21}}$ Hz.

• X-rays are produced by Coolidge X-ray tubes by bombarding a metal target by high energy electrons.

X - rays are Used in

• Medical applications like detection of fracture, formation of stones, etc in human bodies.

• Radiotherapy to cure skin disease and certain forms of cancer.

• To scan luggage for explosives, guns, etc.

• Engineering for detection of faults, cracks, etc in finished metal products.

• To study the crystal structure of solids.

• Overexposure of X-rays damages tissues and organisms.

Gamma Rays

• Belmont race are of frequency range $3 \times {10^{18}}$ to $5 \times {10^{22}}$ Hz and our wavelength $6 \times {10^{ - 13}}$ to${10^{ - 18}}m$ .

• Gamma rays are produced in nuclear reactions and are also emitted by radioactive nuclei.

Gamma Rays are in

• Radiotherapy to treat certain cancers and tumours.

• To produce nuclear reactions.

Wavelengths and Their Photon Energy:

So, for emission of $\lambda$ rays the energy difference among energy levels should be of the order of MeV, where for visible radiation it should be of the order of eV.

Points to Remember:

• Maxwell assumed that a current also flows in the gap between the two plates of capacitor, during the process of charging, known as displacement current ${I_D}$ . This displacement  current originates due to time varying electric field between the plates of capacitor and is given by

${I_D} = {\varepsilon _0}\dfrac{{d{\phi _\varepsilon }}}{{dt}}$ 

Where ${\phi _\varepsilon }$  gives the electric flux linked with the space between the two plates of the capacitor.

• Thus , displacement current ${I_D}$  is the electric current which flows in the gap between the plates of the capacitor during its charging , which originates due to the time varying electric field in  the space between the two plates of capacitor.

• So, using the concept of displacement current ${I_D}$ , Ampere’s circuital law can be modified as 

$\oint {\vec B.d\vec l = {\mu _0}\left( {{I_C} + {I_D}} \right)}$ Which is also called Ampere-Maxwell’s circuital law.

Modified Ampere-Maxwell Law: 

• The line integral of the magnetic field around any closed path is determined by the sum of the net conduction current through the path and the rate of change of electric flux through any surface bounded by the path.

$\oint {\vec B.d\vec l = {\mu _0}I + {\varepsilon _o}{\mu _o}\dfrac{{d{\phi _e}}}{{dt}}}$ 

• Electromagnetic waves are those waves in which there is a sinusoidal variation of electric and magnetic field at right angles to each other as well as at right angles to the direction wave propagation. For a plane progressive electromagnetic wave propagating along the +z direction, the electric and magnetic fields can be written as 

${E_x} = {E_0}\sin (kz - \omega t)$ 

${B_y} = {B_0}\sin (kz - \omega t)$ 

• The amplitudes of electric and magnetic fields in free space , in electromagnetic waves are related by 

${E_0} = c{B_0}$   Or    ${B_0} = \dfrac{{{E_0}}}{c}$ 

• Electromagnetic waves are transverse in nature as the electric and magnetic fields are perpendicular to each other and to the direction of propagation of EM waves.

• When an electromagnetic wave advances, the electromagnetic energy flows in the direction. The total energy flowing perpendicularly per second unit area into the space in free space is called a pointing vector.

$\overrightarrow S  = \dfrac{{\overrightarrow E  \times \overrightarrow B }}{{{\mu _o}}}$ 

• Characteristics - transverse, not deflected by any electric and magnetic fields, travel with speed of light (c) etc...

• Electromagnetic waves include radio waves, microwaves, visible light waves, infrared rays, UV rays, X-rays and gamma rays.

•  The classifications of electromagnetic waves done according to the frequency are called electromagnetic spectrum.

•  The basic difference between various types of electromagnetic waves lies in their wavelength or frequency since all of them travel through vacuum with the same speed. Also, the waves differ in their mode of interaction with matter.

• All electromagnetic waves have separate uses, wavelength, and frequency accordingly as shown in the figure and in above statements.

Important Formulae:

Questions:

1. The condition for which a microwave oven heats up a food item containing water molecules most efficiently is 

(a) Microwaves are heat waves, so always produce heating

(b) Infrared waves produce heating in a microwave oven

(c) The frequency of microwaves must match the resonant frequency of the molecules

(d)  The frequency of microwaves has no relation with the resonant frequency of the molecules

Ans: (c) 

The frequency of microwaves must match the resonant frequency of the molecules.

In a microwave oven the frequency of the microwaves must match the resonant frequency of water molecules so that energy from the waves is transferred efficiently to the kinetic energy of the molecules.

So, the frequency of microwaves must match the resonant frequency of the molecules

2. A radiation of energy E falls normally on a perfectly reflecting surface. The momentum transferred to the surface is (C is Velocity of light):

(a) $\dfrac{{2E}}{{{C^2}}}$

(b) $\dfrac{E}{{{C^2}}}$

(c) $\dfrac{E}{{{C^{}}}}$

(d) $\dfrac{{2E}}{C}$ 

Ans: (d) $\dfrac{{2E}}{C}$ 

Energy,  $E = h\nu  = \dfrac{{hC}}{\lambda }$

Momentum,

$p = \dfrac{h}{\lambda } = \dfrac{E}{C} = {p_i}$

${p_r} =  - {p_i} =  - \dfrac{E}{C}$

Surface momentum,

$S = {p_i} - {p_r} = \dfrac{E}{C} - \left( { - \dfrac{E}{C}} \right) = \dfrac{{2E}}{C}$ 

Therefore, the momentum on its surface is $\dfrac{{2E}}{C}$ .

List of Common Mistakes and Points to Remember:

• All of the previously stated significant issues are equally asked as numerical problems and derivations. 

• It is advised to have a conceptual understanding of each topic. 

• Practice the more and more numerical questions from each as well.

• Go over the chapter's relationships between the physical quantities again.

• Create a table or chart to show the moment of inertia for various items and forms.

Importance of the Class 12 Physics Chapter Electromagnetic Waves

Electromagnetic waves are the result of a couple time with varying magnetic and electric fields. They propagate in space and have different ranges of wavelengths. These waves prove the direct relationship between magnetism and electricity.

Maxwell was the first scientist to prove that a varying electric field with respect to time can generate fields of magnetism. It also happens due to an EMF induced in a circuit due to the fluctuating magnetic field in an opposite case. This phenomenon can be proved using Faraday and Lenz laws.

Maxwell proceeded to find some inconsistencies in Ampere’s law of circuits. He found that this law was correct for specific cases. This chapter will explain what Maxwell observed that led to the foundation of electromagnetic waves.

Different cases will be explained with proper mathematical interpretation. Students will learn what happens to the magnetic field with various Ampere surfaces and understand the concept of electromagnetic waves. To make it easier to understand, students can download the Electromagnetic Waves notes.

They will also learn how Maxwell corrected Ampere’s Law and reinstated the results of a magnetic field closer to an electric circuit. He established the shortcomings and described how a current is present in the capacitor plates.

This chapter is important as it establishes the concept and scientific principles of electromagnetic waves. Students will learn about these derivations using mathematical expressions deduced from the definitions of the scientific terms used in electricity and magnetism.

Benefits of Class 12 Physics Chapter Electromagnetic Waves Notes

• These revision notes are the ideal addition to your study material for this chapter. You will find a simpler and concise explanation of all the terms, scientific principles, laws, and findings of scientists in a single file.

• This file can be downloaded for free and used at your convenience. Refer to this file to make your study sessions more productive. When you are done preparing the chapter, you can use these notes to take a quick glance at the formulae and derivations of this chapter.

• Check your preparation level by using these notes to recall the definitions, formulae, and laws of electromagnetic waves.

• Proceed to solve the sample questions of the Electromagnetic Waves NEET notes and evaluate your preparation level. You can learn from the techniques used by the experts to answer such questions to become more efficient.

Download Electromagnetic Waves Class 12 Notes PDF

You can download the free PDF version of the revision notes. You will no longer need to read the entire chapter in detail before the NEET exam when you can use these notes to revise. Save your time preparing notes and use this file to revise this chapter. Use the easy-to-remember format of this file to recall all the terms, laws, and fundamental principles of electromagnetic waves and glance over the solved question before an exam.

Other Important Links

NEET Physics Revision Notes - Chapter Pages