Revision Notes on Ray Optics and Optical Instruments for NEET 2024

Reflection of Light:

Reflection is the phenomenon by virtue of which a light beam, after interacting with a surface separating the two different media, bounces back into the same medium.

Laws of Reflection:

• First law of reflection: states that the incident ray, reflected ray and normal to the surface lie in the same plane.

• Second law of reflection: states that angle of reflection is equal to angle of incidence.

• This law of reflection holds true for regular reflection at all surfaces, i.e., plane or curved.

• For angle of incidence $i$, angle of reflection $r$ is also the same i.e.,$i=r$.

Laws of Reflection

Reflection of Plane Mirror: 

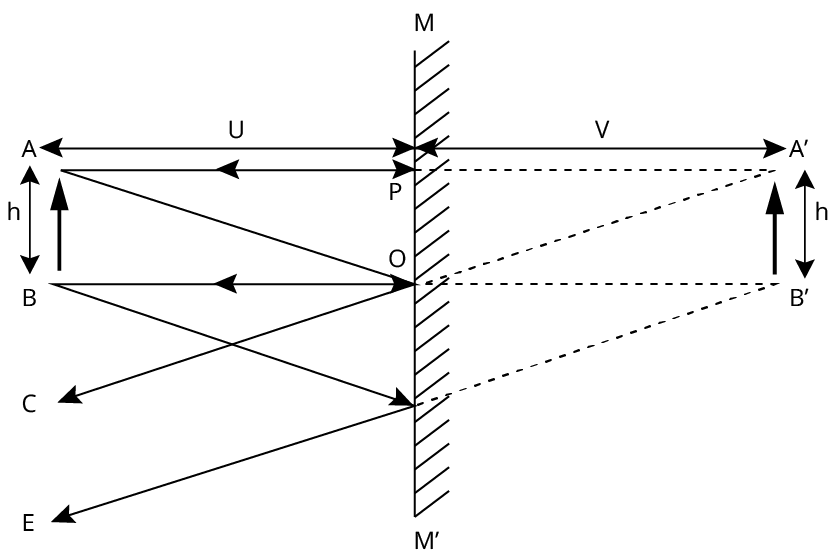
Ray Formation of Image in Plane Mirror 

• The image formed by a plane mirror is virtual, erect, of size and is formed at same distance from the mirror and the object i.e., u = v

• The image formed by the plane mirror is laterally inverted on the right side of the object and appears as the left side of the image and vice-versa.

• A plane mirror can form a real image only when a conversion beam of light falls on the plane mirror.

• On keeping the incident ray fixed, if the mirror is to through an angle θ, then the reflected ray turns by angle 2θ from its initial path.

• To view a full image, a person needs a plane mirror length equal to half the person's height.

Image Formation in Plane Mirror when a Person Stands Before it

• So, to observe the complete image of a person of height 2(H + h) the minimum height of the mirror required is (H + h).

• If there are two plane mirrors perpendicular to each other, then the ray of light after suffering reflection from both the mirrors becomes anti parallel.

• If two plane mirrors are parallel to each other, then infinite images of an object placed between them are formed. If the first image is d distance behind the mirror, then all other consecutive images are 2d distance apart.

• If there are two plane mirror inclined at angle with each other, then the number of possible images of a point object are: 

• If n = m-1, $m = \dfrac{{{{360}^0}}}{\theta }$ is an even number.

For example, if $\theta  = {60^0}$ then $m = \dfrac{{{{360}^0}}}{{{{60}^0}}} = 6$

Images: n = 6 – 1 = 5 

• If n = m, $m = \dfrac{{{{360}^0}}}{\theta }$ is an odd number.

For example, if $\theta  = {72^0}$ then $m = \dfrac{{{{360}^0}}}{{{{72}^0}}} = 5$

And n = 5

• If n = Int[m], $m = \dfrac{{{{360}^0}}}{\theta }$ is a fractional number.

View of an Image in a Plane Mirror

• If the reflecting surface is smooth, then the regular reflection takes place and images can be formed, but if the surface is rough, diffused reflection takes place where the reflected rays scatter in different directions so, the image cannot be formed by such reflection. This is why we can see our image while looking into a steel container but we do not observe the image while reading a newspaper.

Spherical Mirror

A spherical mirror is part of a spherical reflecting surface. Spherical mirror is of two types: 

• Concave mirror

• Convex mirror

Concave mirror: When the reflection takes place from the inner surface and outer surface is polished, the mirror is known as concave mirror.

Convex mirror: When the reflection takes place from the outer surface and inner surface is polished, then the mirror is known as convex mirror.

Where:

• P = Pole of mirror

• F = Principal focus

• C = Centre of curvature

• PC = R = Radius of curvature

• PF = f = Focal length

Sign Conventions:

• All distances have to be measured from the pole of the mirror.

• Distances measured in the direction of incident light are positive, and those measured in opposite directions are taken as negative.

• Heights measured upwards and normal to the principal axis of the mirror are taken as positive, while those measured downwards are taken as negative.

Spherical Mirror Formula:

• The focal length of a spherical mirror of radius R is given by $f = \dfrac{R}{2}$

• F (or R) is negative for concave or converging mirrors and positive for convex or diverging mirrors.

• Traverse or linear magnification is: 

$m =  - \dfrac{{{\text{image size}}}}{{{\text{object size}}}} =  - \dfrac{v}{u}$

Here -ve magnification implies that the image is inverted with respect to the object while +ve magnification means that the image is erect with respect to the object.

Magnification of a Mirror

• Longitudinal Magnification: When an object lies along the principal axis, its magnification is known as longitudinal. For small objects, it is given by,

${m_L} =  - \dfrac{{dv}}{{du}}$

• Superficial Magnification: When a two-dimensional object is placed with its plane perpendicular to the principal axis, then its magnification is known as superficial magnification or a real magnification and is given by,

${m_s} = \dfrac{{{\text{area of image}}}}{{{\text{area of object}}}} = {m^2}$.

• Mirror Formula: $\dfrac{1}{u} + \dfrac{1}{v} = \dfrac{1}{f}$

Where, u = distance of object from the pole of the mirror.

v = distance of image from the pole of the mirror.

• Newton’s formula is ${f^2} = xy$, where x is distance of object from the focus and y is distance of image from the focus of the mirror.

Refraction of Light:

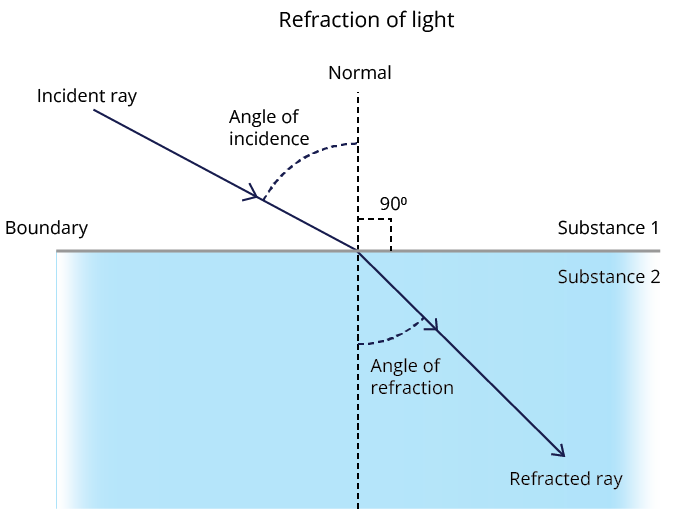
• When a ray of light passes from one medium to another, in which it has a different velocity, there occurs a change in the direction of propagation of light except when it strikes the surface of separation of two media normally. This bending of a ray of light is known as refraction.

• The angles made by the incident ray and the refracted ray with the normal to the separating surface at the point of incidence are known as the angle of incidence and of refraction, respectively.

Laws of Refraction:

The two Laws of refraction or as follows:

• The incident ray, the normal and the refracted ray all lie in the same plane.

•  The ratio of the sine of angle of incidence to the sine of angle of refraction for any two media is constant for a light of definite colour. This constant is denoted by ${}^1{\mu _2}$ or ${\mu _{21}}$ called the refractive index of the second medium with respect to the first, the subscripts 1 and 2 indicating that the light passes from medium 1 to medium 2.

$\dfrac{{\sin (i)}}{{\sin (r)}} = {}^1{\mu _2}$

where i = angle of incidence, r = angle of refraction.

This is also known as Snell’s law.

• ${}^1{\mu _2}$ Is a characteristic of the pair of media and also depends on the wavelength of light but is independent of the angle of incidence.

${}^2{\mu _1} = \dfrac{1}{{{}^1{\mu _2}}}$Or${}^2{\mu _1} \times {}^1{\mu _2} = 1$

• Absolute refractive index: Refractive index of a medium with respect to vacuum (or in practice air) is known as the absolute refractive index of the medium.

$\mu  = \dfrac{c}{v} = \dfrac{{{\text{speed of light in vacuum}}}}{{{\text{speed of light in medium}}}}$

• General expression for Snell’s law: 

${}^1{\mu _2} = \dfrac{{{\mu _2}}}{{{\mu _1}}} = \dfrac{{\left( {\dfrac{c}{{{v_2}}}} \right)}}{{\left( {\dfrac{c}{{{v_1}}}} \right)}} = \dfrac{{{v_1}}}{{{v_2}}}$

Where c is the light of speed in air, ${v_1}$and ${v_2}$ is the speed of light in medium 1 and medium 2 respectively.

• According to Snell’s law,

${}^1{\mu _2} = \dfrac{{\sin i}}{{\sin r}};$ $\dfrac{{{\mu _2}}}{{{\mu _2}}} = \dfrac{{\sin i}}{{\sin r}}$ or ${\mu _1}\sin i = {\mu _2}\sin r$

• When a light travels from one medium to another, its frequency remains constant but its wavelength as well as velocity changes.

Refraction of Light

Optical Density:

It is a measure of a refractive index of a medium. A medium with a relatively high refractive index is said to have a high optical density while one with a low refractive index is set to have a low optical density.

Optical Path:

It is defined as the product of geometrical distance and the refractive index of the medium.

${\text{optical path}}  =  \mu d$, Where d is the distance travelled by the light in the medium.

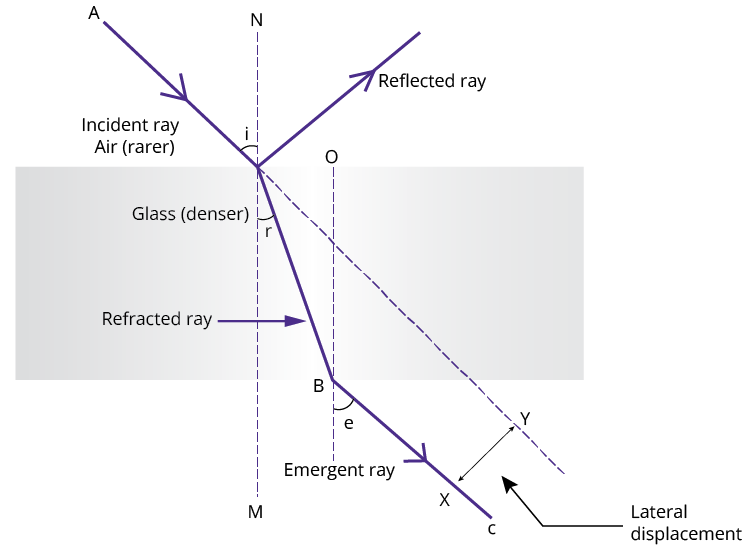
Lateral Shift:

• When the medium is the same on both sides of a glass slab, then the deviation of the emergent ray is zero. That is the emergent ray is parallel to the incident ray but it does suffer lateral displacement/shift with respect to the incident ray and is given by

• Lateral shift,   $d = t\dfrac{{\sin \left( {i - r} \right)}}{{\cos r}}$

where t is the thickness of the slab.

Lateral Shift Condition

Real Depth and Apparent Depth:

• When one looks into a pool of water, it does not appear to be as deep as it really is. Also when one looks into a slab of glass, the material does not appear to be as thick as it really is. This all happens due to the refraction of light.

• If a beaker is filled with water and a point lying at its bottom is absorbed by someone located in the air, then the bottom point appears raised. The apparent depth is less than the real depth. It can be shown that

${\text{apparent depth  = }}\dfrac{{{\text{real depth}}}}{{{\text{refractive index}(\mu )}}}$

• If there is an ink spot at the bottom of a glass slab, it appears to be raised by a distance

$d = t - \dfrac{t}{\mu } = t\left( {1 - \dfrac{1}{\mu }} \right)$

Where t is the thickness of the glass slab, and μ is its refractive index.

• If a beaker is filled with immiscible transparent liquids of refractive indices ${\mu _1},{\mu _2},{\mu _3}$ and individual depth ${d_1},{d_2},{d_3}$ respectively, then the apparent depth of the beaker is, 

$\dfrac{{{d_1}}}{{{\mu _1}}} + \dfrac{{{d_2}}}{{{\mu _2}}} + \dfrac{{{d_3}}}{{{\mu _3}}}$

Refraction effects at Sunrise and Sunset:

The sun is visible a little before the actual sunrise and until a little after the actual sunset due to the refraction of light through the atmosphere.

Refraction of Sun Rays Viewed by an Observer

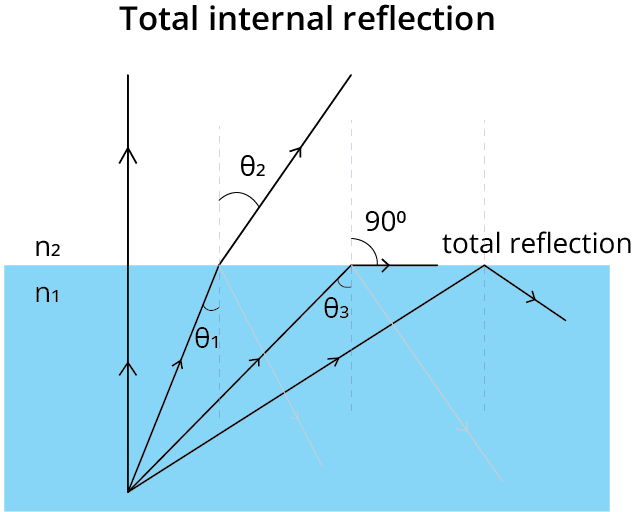
Total Internal Reflection: 

When a ray is an incident from a denser medium to a rarer medium, it bends away from the normal. The angle of incidence of a certain ray that refracts at an angle of ${90^0}$ is called the critical angle ${\theta _c}$.

When the incident angle is greater than ${\theta _c}$, the ray cannot refract, but instead reflects totally. This phenomenon is called total internal reflection.

For ${\theta _c}$, Snell’s law is ${\mu _D}\sin {\theta _c} = {\mu _R}\sin {90^0}$

$ \Rightarrow \sin {\theta _c} = \dfrac{{{\mu _R}}}{{{\mu _D}}}$  or  ${\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{{{\mu _R}}}{{{\mu _D}}}} \right)$

Usually, ${\mu _R} = {\mu _{air}} = 1$  and${\mu _D} = \mu $.

Then, ${\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right)$. 

Total Internal Reflection Phenomenon 

Refraction From a Spherical Surface:

• The portion of a refracting medium, whose curved surface form’s the part of a sphere, is known as spherical refracting surface.

• Spherical refracting surface are of two types:

• Convex refracting spherical surface

• Concave refracting spherical surface

• Sign conventions for spherical refracting surfaces are the same as those for spherical mirrors.

• When the object is situated in rare medium, the relation between ${\mu _1}$ (refractive index of rarer medium), ${\mu _2}$ (refractive index of the spherical refracting surface)and R(radius of curvature)with the object and image distance is given by,

$ - \dfrac{{{\mu _1}}}{u} + \dfrac{{{\mu _2}}}{v} = \dfrac{{{\mu _2} - {\mu _1}}}{R}$

• When the object is situated in denser medium, the relation between ${\mu _1},{\mu _2},R,u$ and $v$ can be obtained by interchanging ${\mu _1}$ and ${\mu _2}$. In that case, the relation becomes,

$ - \dfrac{{{\mu _2}}}{u} + \dfrac{{{\mu _1}}}{v} = \dfrac{{{\mu _1} - {\mu _2}}}{R}$ And $ - \dfrac{{{\mu _1}}}{u} + \dfrac{{{\mu _2}}}{v} = \dfrac{{{\mu _2} - {\mu _1}}}{R}$

• These formulae are valid for both convex and concave spherical surfaces.

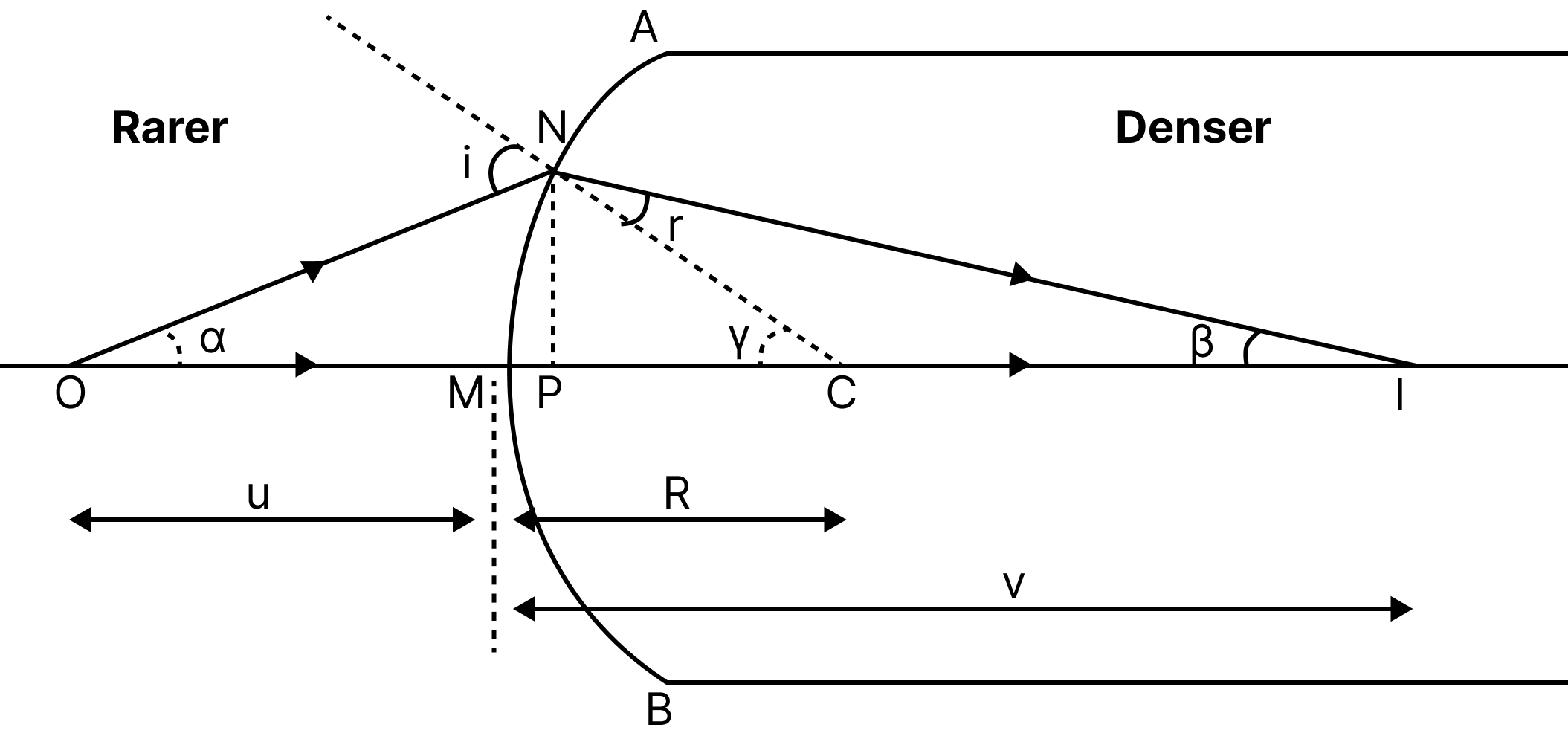
Refraction in a Spherical Surface of Two Refractive Index

Lens:

• A lens is a portion of a transparent refracting medium bound by two spherical surfaces or one spherical surface and the other plane surfaces.

• Lenses are divided into two classes:

• Convex lens or converging lens

• Concave lens or diverging lens

Convex lens or converging lens: When a lens is thicker in the middle than at the edges it is known as convex lens or converging lens. These are of three types:

• Double convex lens or biconvex lens

• Plano convex lens

• Concavo convex lens

Concave lens or diverging lens:  when the lens is thicker at the edge than in the middle it is known as concave lens or diverging lens. These are of three types:

• Double concave lens or biconcave lens

• Plano concave lens

• Convex concave lens

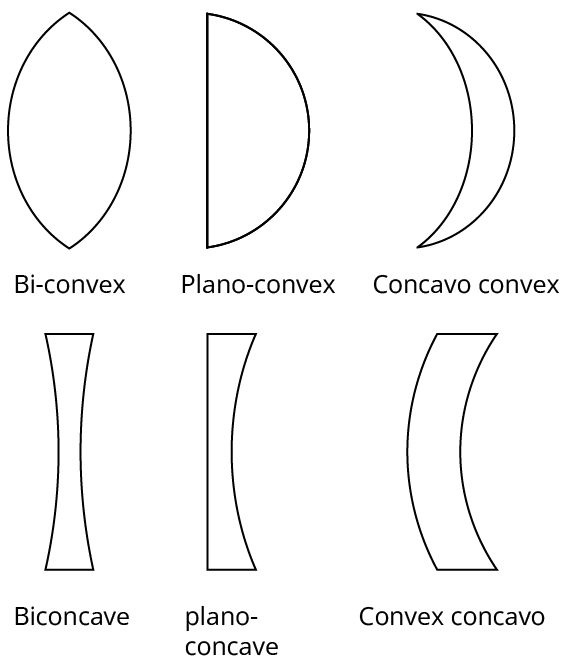
Types of Lens

Sign Conventions:

The sign conventions for thin lenses are the same as those of spherical mirrors except that instead of the pole of the mirror, we now use the optical centre of the lens.

Lens Maker’s Formula: 

$\dfrac{1}{f} = \left( {\mu  - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$

Where ${R_1}$ and ${R_2}$ are radii of curvature of the two surfaces of the lens and μ is refractive index of material of lens w.r.t. medium in which lens is placed.

• This formula is valid for thin lenses. It is valid for both convex and concave lenses.

• As per sign convention, for a convex lens, ${R_1}$ is positive and ${R_2}$ is negative and for a concave lens. ${R_1}$ is negative and ${R_2}$ is positive.

•  When the refractive index of the material of the lens is greater than that of the surroundings, then a biconvex lens acts as a converging lens and a biconcave lens acts as a diverging lens.

• When the refractive index of the material of the lens is smaller than that of the surrounding medium, then a biconvex lens acts as a diverging lens and a biconcave lens as a converging lens.

Lens Maker’s Equation Ray Diagram for a Bi-Convex Lens 

Thin Lens Formula 

$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$

Where

u = distance of the object from the optical centre of the lens

v = distance of the image from the optical centre of the lens

f = focal length of a lens

f is positive for converging or convex lenses and f is negative for diverging or concave lenses.

Linear Magnification:

$m = \dfrac{{{\text{size of image(I)}}}}{{{\text{size of object(O)}}}} = \dfrac{v}{u}$

m is positive for an erect image and m is negative for an inverted image.

Power of a Lens:

$P = \dfrac{1}{\text{focal length}}$

The SI unit of power of the lens is dioptre (D). $1D = 1{m^{ - 1}}$.

For a convex lens, P is positive.

For a concave lens, P is negative.

When focal length (f) of lens is in cm, then

$P = \dfrac{{100}}{{f(in\,cm)}}dioptre$.

Combination of Thin Lenses in Contact:

• When a number of thin lenses of focal length ${f_1},{f_2},{f_3}....$ etc. are placed in contact coaxially, the equivalent focal length F of the combination is given by,

$\dfrac{1}{F} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}} + \dfrac{1}{{{f_3}}} + ....$

• The total power of the combination is given by

$P = {P_1} + {P_2} + {P_3} + .....$

• The total magnification of the combination is given by

$m = {m_1} \times {m_2} \times {m_3}.....$

• When two thin lenses of focal lengths ${f_1}$ and ${f_2}$ are placed coaxially and separated by a distance d, the focal length of a combination is given by

$\dfrac{1}{F} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}} - \dfrac{d}{{{f_1}{f_2}}}$.

• In terms of power, $P = {P_1} + {P_2} - d{P_1}{P_2}$.

Refraction Through a Prism:

• Prism: It is a homogeneous, transparent medium enclosed by two plane surfaces inclined at an angle. These surfaces are called the refracting surfaces; the angle between them is known as the refracting angle or the prism angle.

• The angle between the incident ray and the emergent ray is known as the angle of deviation.

• For refraction through a prism it is found that

$\delta  = i + e - A$   Where $A = {r_1} + {r_2}$

When A and I are small

$\therefore \delta  = \left( {\mu  - 1} \right)A$

In a position of minimum deviation, $\delta  = {\delta _m},i = e$and ${r_1} = {r_2} = r$

$\therefore i = \left( {\dfrac{{A + {\delta _m}}}{2}} \right)$And $r = \dfrac{A}{2}$

• The refractive index of the material of the prism is,

$\mu  = \dfrac{{\sin \left[ {\left( {\dfrac{{A + {\delta _m}}}{2}} \right)} \right]}}{{\sin \left( {\dfrac{A}{2}} \right)}}$

Where A is the angle of prism and ${\delta _m}$ is the angle of minimum deviation. This is known as the prism formula.

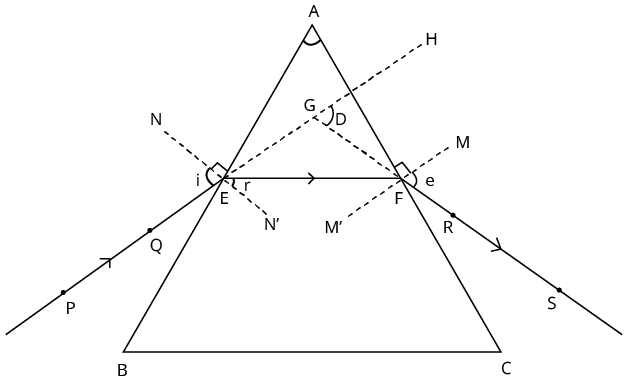
Refraction happening in a prism of angle A

Dispersion of Light:

It is the phenomenon of splitting of white light into its constituent colours on passing through a prism. This is because different colours have different wavelengths $\left( {{\lambda _R} > {\lambda _V}} \right)$.

According to Cauchy's formula

$\mu  = A + \dfrac{B}{{{\lambda ^2}}} + \dfrac{C}{{{\lambda ^4}}}$

Where A, B, C are arbitrary constants. Therefore, μ of material of prism for different colours is different $\left( {{\lambda _V} > {\lambda _R}} \right)$. As $\delta  = \left( {\mu  - 1} \right)A$, therefore different colours turn through different angles on passing through the prism. This is the cause of dispersion.

Dispersion and its Constituent Colours Formed

Angular Dispersion:

The difference is deviation between any two colours is known as angular dispersion. Angular dispersion,  ${\delta _V} - {\delta _R} = \left( {{\mu _V} - {\mu _R}} \right)A$

Where ${\mu _V}$and ${\mu _R}$ are the refractive index for violet and red rays.

Mean deviation,  $\delta  = \dfrac{{{\delta _V} - {\delta _R}}}{2}$

Dispersive power,  $\omega  = \dfrac{{{\text{angle dispersion(}}{{{\delta }}_{\text{V}}}{\text{ -  }}{{{\delta }}_{\text{R}}}{\text{)}}}}{{{\text{mean deviation}(\delta )}}}$

$\omega  = \dfrac{{{\mu _V} - {\mu _R}}}{{\left( {\mu  - 1} \right)}},$

Where $\mu  = \dfrac{{{\mu _V} - {\mu _R}}}{2}$= mean refractive index.

Dispersion Without Deviation:

• Suppose we combine two prisms of refractive angles A and $A'$, and dispersive powers $\omega $ and $\omega '$ respectively in such a way that their refracting angles are reversed with respect to each other.

• For no deviation, the condition is

$\delta  + \delta ' = 0$

$\left( {\mu  - 1} \right)A + \left( {\mu ' - 1} \right)A' = 0$  or  $A' = \dfrac{{\left( {\mu  - 1} \right)A}}{{\left( {\mu ' - 1} \right)}}$

Under this condition, net angular dispersion produced by the combination

$ = \left( {{\delta _V} - {\delta _R}} \right) + \left( {{\delta _V}^\prime  - {\delta _R}^\prime } \right) = \left( {{\mu _V} - {\mu _R}} \right)A + \left( {{{\mu '}_V} - {{\mu '}_R}} \right)A'$

Deviation Without Dispersion:

The condition for no dispersion is:

$\left( {{\mu _V} - {\mu _R}} \right)A + \left( {{{\mu '}_V} - {{\mu '}_R}} \right)A' = 0$  or   $A' =  - \dfrac{{\left( {{\mu _V} - {\mu _R}} \right)A}}{{\left( {{{\mu '}_V} - {{\mu '}_R}} \right)}}$

Under this condition, net deviation produced by the combination is

$\delta  + \delta ' = \left( {\mu  - 1} \right)A + \left( {\mu ' - 1} \right)A'$

Scattering of Light:

As sunlight travels through the earth’s atmosphere it gets scattered (changes its direction) by the atmospheric particles. Light of shorter wavelengths is scattered much more than light of longer wavelengths. The amount of scattering is inversely proportional to the fourth power of the wavelength. This is known as Rayleigh scattering.

Illustrations of scattering of light:

• Blue colour of sky

• White colour clouds

• The sun looks reddish at the time of Sunrise and sunset

• Danger signals are red.

Rainbow:

• Rainbow is a beautiful arc of seven colours seen in the sky after rainfall.

•  The rainbow is an example of the dispersion of sunlight by the water drops in the atmosphere. This is a phenomenon due to the combined effect of dispersion, refraction and reflection of sunlight by spherical water droplets of rain.

• To observe the rainbow, the back of the observer must be towards the sun.

• Generally, there are two kinds of rainbows

• Primary rainbow

• Secondary rainbow

• Primary rainbow: Primary rainbow occurs due to one internal reflection and two refractions from the water drops suspended in air. Violet colour is on the inner edge and red colour is on the outer edge.

• Secondary rainbow: secondary rainbow occurs due to two total internal reflection and two refractions from the water drops suspended in air. Red colour is on the inner edge and violet colour is on the outer edge. 

The secondary rainbow is fainter than the primary rainbow.

Optical Instruments:

Human Eye:

Eye is one of the most important optical biological instruments fitted within us.

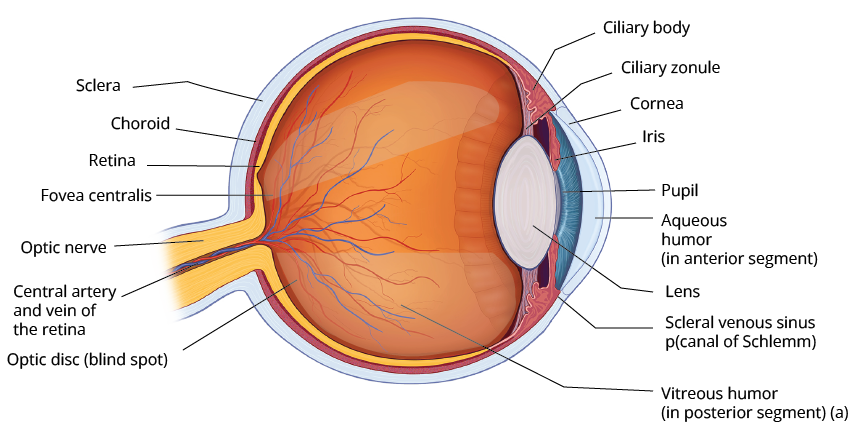
Diagrammatic View of a Human Eye

• Light enters through the curved front surface called the cornea. Then it passes through the pupil, the central hole in the iris. The size of the pupil can change under the control of muscles. Thus, the amount of light or intensity of light entering the eye is controlled by pupil size.

• Ciliary muscles control the curvature of the lens in the eye and change the effective focal length of the eye's crystalline lens. When muscles are fully relaxed, focal length is maximum, decreasing when muscles are strained.

• The eye lens focuses light on the retina. The retina is a film of nerve fibres covering the curved back surface of the eye. It contains cells in the shapes of rods and cones, which sense light intensity and colour respectively and transmit electrical signals via the optic nerve to the brain, which finally processes this information.

• For an image to be clear it must be formed on the retina. Thus, image distance is fixed for clear vision and is equal to the distance of the retina from the eye lens. It is about 2.5 cm for a grown up person.

• The closest distance for which the lens can focus light on the retina is called the least distance of distinct vision D, or the near point, which is 25 cm for normal vision. So, focal length of eye lens is minimum when Ciliary muscles are fully strained and object is at near point.

• So, when ${u_{\min }} =  - 25cm$ and v = +2.5 cm

Then   $\dfrac{1}{{{f_{\min }}}} = \dfrac{1}{v} - \dfrac{1}{{{u_{\min }}}} = \dfrac{1}{{2.5}} + \dfrac{1}{{25}} = \dfrac{{11}}{{25}}$

Or  ${f_{\min }} = \dfrac{{25}}{{11}} =  + 2.27cm$

• So, focal length of eye lens can change within the range of 2.27 cm to 2.5 cm by the action of ciliary muscles, to maintain the same image distance. This property of the eye is called accommodation. The ability of the eye by which it can adjust its focal length to see objects at Infinity to at a closest distance of 25 cm from it, is called the power of accommodation.

• Visual angle is the angle subtended by the object at the eye lens.

• The resolving power of the eye is the reciprocal of the smallest angle θ subtended by two close objects so that they appear separately visible when absorbed through the eye. This angle θ is called the limit of resolution of the eye and is less than 1 minute.

• Persistence of vision: If the time interval between two consecutive light pulses is less than 1.16s, then the eye cannot distinguish between them and the light pulses are then observed to be continuous. This is called persistence of vision.

Defects of Eye:

Defects of eye are mainly of four types:

• Myopia

• Hypermetropia

• Presbyopia and

• Astigmatism 

1) Myopia or (nearsightedness): In this eye defect, the eye lens becomes too thick and cannot focus the image of distant objects on the retina, due to which the eye cannot observe distant objects clearly. 

Far point P of a myopic eye is the farthest distance of the object from the eye, of which a clear image is focused on the retina.

2) Hypermetropia (Farsightedness): In this defect the eye lens becomes too thin and cannot focus the image of nearby objects on the retina, due to which the eye is not able to observe nearby objects clearly. This defect is removed by interposing an appropriate convex lens between the eye and the object.

3) Presbyopia: It is an old age disease. At old age, ciliary muscles lose their elasticity and cannot change the focal length of eye lens effectively. Due to this eye lens loses its power of accommodation, and a person can then suffer from both myopia and Hypermetropia. This can be overcome either by using two separate spectacles, one for myopia and another for Hypermetropia or by using a single spectacle having bifocal lens.

4) Astigmatism: it is the defect of the eye which occurs when the cornea is not spherical in shape.

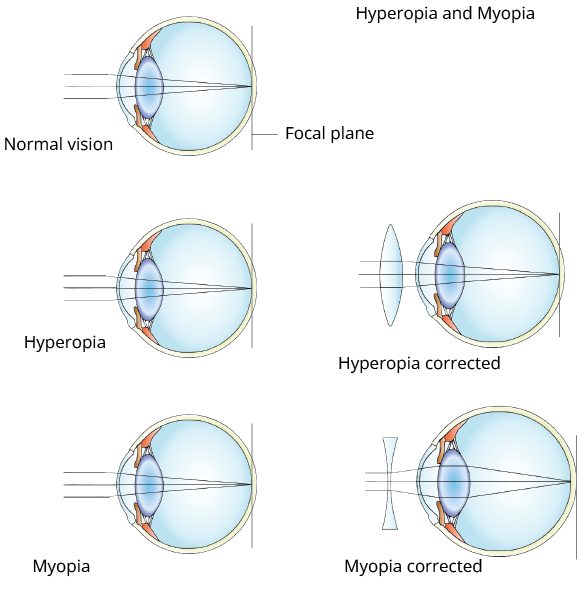
Showing Eye Defects and their Corrections

Simple Microscope:

It is also known as magnifying glass or simple magnifier. It consists of a convergent lens with an object between its focus and optical centre and eye close to it. The image formed by it is erect, virtual, enlarged and on the same side of the lens between object and Infinity.

• Magnifying power:

$M = \dfrac{{{\text{angle subtended by image at the eye}}}}{{{\text{angle subtended by the object at the eye}}}} = \dfrac{{\tan \beta }}{{\tan \alpha }} = \dfrac{\beta }{\alpha }$

Where both the object and image are situated at the least distance of distinct vision.

• When the image is formed at Infinity (far point),

$M = \dfrac{D}{f}$

• When the image is formed at the least distance of distinct vision D (near point),

$M = 1 + \dfrac{D}{f}$

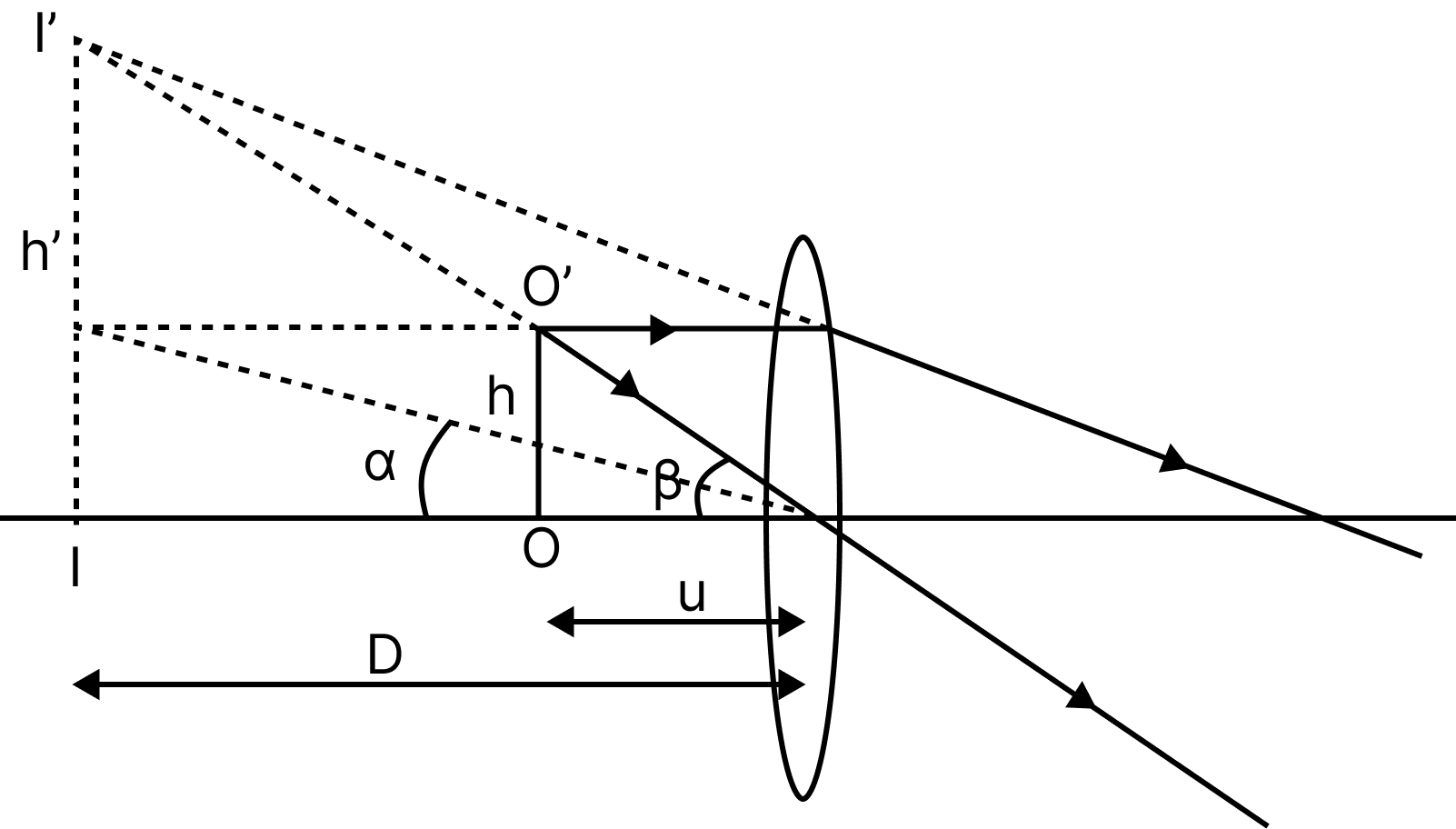
Ray Diagram of a Simple Microscope

Compound Microscope:

It consists of two convergent lenses of short focal length and apertures arranged coaxially. Lens (of focal length${f_0}$) facing the object is known as objective or field lens while the lens (of focal length${f_e}$) facing the eye, is known as eye-piece or ocular. The objective has a smaller aperture and smaller focal length than eye-piece. 

• Magnifying power of a compound microscope

$M = {m_0} \times {m_e}$

•  When the final image is formed at Infinity (normal adjustment),

$M = \dfrac{{{v_0}}}{{{u_0}}}\left( {\dfrac{D}{{{f_e}}}} \right)$

Length of tube, $L = {v_0} + {f_e}$

• When the final image is formed at least distance of distinct vision,

$M = \dfrac{{{v_0}}}{{{u_0}}}\left( {1 + \dfrac{D}{{{f_e}}}} \right)$

Where ${u_0}$ and ${v_0}$ represent the distance of object and image from the objective lens, ${f_e}$ is the focal length of an eye lens.

 Length of the tube,  $L = {u_0} + \left( {\dfrac{{{f_e}D}}{{{f_e} + D}}} \right)$

Compound Microscope Ray Diagram 

Astronomical Telescope (Refracting type):

It consists of two converging lenses. The one facing the object is known as objective or field lens and has larger focal length and aperture while the other facing the eye is known as eye-piece or ocular and has small focal length and aperture.

• When the final image is formed at Infinity (normal adjustment),

$M = \dfrac{{{f_0}}}{{{f_e}}}$

Length of tube,  $L = {f_0} + {f_e}$

• When the final image is formed at least distance of distinct vision,

$M = \dfrac{{{f_0}}}{{{f_e}}}\left( {1 + \dfrac{{{f_e}}}{D}} \right)$ and Length of tube, $L = {f_0} + \left( {\dfrac{{{f_e}D}}{{{f_e} + D}}} \right)$

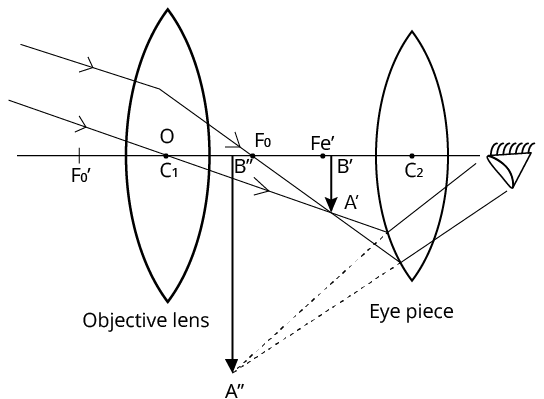
Construction of Astronomical Telescope (ray diagram)

Reflecting Type Telescope:

• Reflecting type telescopes were designed by Newton in order to overcome the drawbacks of refracting type telescopes. In a reflecting type telescope, a concave mirror of large aperture is used as an objective in place of a convex lens. It possesses a large light gathering power and a high resolving power. Due to this, it enables us to see even faint stars and observe their minute details.

• In normal adjustment

Magnifying power,  $M = \dfrac{{{f_0}}}{{{f_e}}} = \dfrac{{\left( {\dfrac{R}{2}} \right)}}{{{f_e}}}$

Where R is the radius of curvature of a concave mirror.

• Reflecting-type telescopes are free from chromatic aberration because light does not undergo refraction. Paraboloidal mirrors allow spherical aberrations to be eliminated in reflecting-type telescopes.

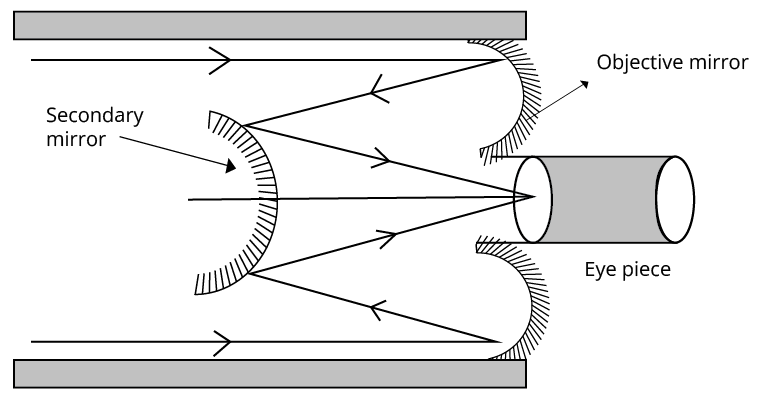
Reflecting Type Telescope

Important Formula:

• If there are two plane mirror inclined at angle with each other, then the number of possible images of a point object are: 

• If n = m-1, $m = \dfrac{{{{360}^0}}}{\theta }$ is an even number.

• If n = m, $m = \dfrac{{{{360}^0}}}{\theta }$ is an odd number.

• If n = Int[m], $m = \dfrac{{{{360}^0}}}{\theta }$ is a fractional number.

• The focal length of a spherical mirror of radius R is given by $f = \dfrac{R}{2}$

• Traverse or linear magnification is:  

• $m =  - \dfrac{{{\text{image size}}}}{{{\text{object size}}}} =  - \dfrac{v}{u}$

• Here -ve magnification implies that the image is inverted with respect to the object while +ve magnification means that the image is erect with respect to the object.

• Longitudinal magnification: ${m_L} =  - \dfrac{{dv}}{{du}}$

• Superficial magnification: ${m_s} = \dfrac{{{\text{area of image}}}}{{{\text{area of object}}}} = {m^2}$.

• Mirror formula: $\dfrac{1}{u} + \dfrac{1}{v} = \dfrac{1}{f}$

• $\dfrac{{\sin (i)}}{{\sin (r)}} = {}^1{\mu _2}$

• ${}^2{\mu _1} = \dfrac{1}{{{}^1{\mu _2}}}$Or${}^2{\mu _1} \times {}^1{\mu _2} = 1$

• Absolute refractive index: $\mu  = \dfrac{c}{v} = \dfrac{{{\text{speed of light in vacuum}}}}{{{\text{speed of light in medium}}}}$

• General expression for Snell’s law: 

• ${}^1{\mu _2} = \dfrac{{{\mu _2}}}{{{\mu _1}}} = \dfrac{{\left( {\dfrac{c}{{{v_2}}}} \right)}}{{\left( {\dfrac{c}{{{v_1}}}} \right)}} = \dfrac{{{v_1}}}{{{v_2}}}$

• Where c is the light of speed in air, ${v_1}$and ${v_2}$ is the speed of light in medium 1 and medium 2 respectively

• Optical path: ${\text{optical path}}  =  \mu d$, 

• Lateral shift,   $d = t\dfrac{{\sin \left( {i - r} \right)}}{{\cos r}}$

• where t is the thickness of the slab.  

• If a beaker is filled with water and a point lying at its bottom is absorbed by someone located in the air, then the bottom point appears raised. The apparent depth is less than the real depth. It can be shown that

• ${\text{apparent depth  = }}\dfrac{{{\text{real depth}}}}{{{\text{refractive index}(\mu )}}}$

• If there is an ink spot at the bottom of a glass slab, it appears to be raised by a distance

• $d = t - \dfrac{t}{\mu } = t\left( {1 - \dfrac{1}{\mu }} \right)$

• If a beaker is filled with immiscible transparent liquids of refractive indices ${\mu _1},{\mu _2},{\mu _3}$ and individual depth ${d_1},{d_2},{d_3}$ respectively, then the apparent depth of the beaker is, 

• $\dfrac{{{d_1}}}{{{\mu _1}}} + \dfrac{{{d_2}}}{{{\mu _2}}} + \dfrac{{{d_3}}}{{{\mu _3}}}$

• For ${\theta _c}$, Snell’s law is ${\mu _D}\sin {\theta _c} = {\mu _R}\sin {90^0}$

• $ \Rightarrow \sin {\theta _c} = \dfrac{{{\mu _R}}}{{{\mu _D}}}$  or  ${\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{{{\mu _R}}}{{{\mu _D}}}} \right)$

• Usually, ${\mu _R} = {\mu _{air}} = 1$  and${\mu _D} = \mu $.

• Then, ${\theta _c} = {\sin ^{ - 1}}\left( {\dfrac{1}{\mu }} \right)$. 

• When the object is situated in rare medium, the relation between ${\mu _1}$ (refractive index of rarer medium), ${\mu _2}$ (refractive index of the spherical refracting surface)and R(radius of curvature)with the object and image distance is given by,

$ - \dfrac{{{\mu _1}}}{u} + \dfrac{{{\mu _2}}}{v} = \dfrac{{{\mu _2} - {\mu _1}}}{R}$

• When the object is situated in denser medium, the relation between ${\mu _1},{\mu _2},R,u$ and $v$ can be obtained by interchanging ${\mu _1}$and${\mu _2}$. In that case, the relation becomes

$ - \dfrac{{{\mu _2}}}{u} + \dfrac{{{\mu _1}}}{v} = \dfrac{{{\mu _1} - {\mu _2}}}{R}$ And $ - \dfrac{{{\mu _1}}}{u} + \dfrac{{{\mu _2}}}{v} = \dfrac{{{\mu _2} - {\mu _1}}}{R}$

• Lens Maker’s Formula: $\dfrac{1}{f} = \left( {\mu  - 1} \right)\left( {\dfrac{1}{{{R_1}}} - \dfrac{1}{{{R_2}}}} \right)$

• Thin Lens Formula : $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$

• Power of a Lens:$P = \dfrac{1}{\text{focal length}}$

• When a number of thin lenses of focal length ${f_1},{f_2},{f_3}....$ etc. are placed in contact coaxially, the equivalent focal length F of the combination is given by,

$\dfrac{1}{F} = \dfrac{1}{{{f_1}}} + \dfrac{1}{{{f_2}}} + \dfrac{1}{{{f_3}}} + ....$

• The total power of the combination is given by

$P = {P_1} + {P_2} + {P_3} + .....$

• For refraction through a prism it is found that

$\delta  = i + e - A$   Where $A = {r_1} + {r_2}$

$\therefore \delta  = \left( {\mu  - 1} \right)A$

In a position of minimum deviation, $\delta  = {\delta _m},i = e$and ${r_1} = {r_2} = r$

$\therefore i = \left( {\dfrac{{A + {\delta _m}}}{2}} \right)$And $r = \dfrac{A}{2}$

• The refractive index of the material of the prism is,

$\mu  = \dfrac{{\sin \left[ {\left( {\dfrac{{A + {\delta _m}}}{2}} \right)} \right]}}{{\sin \left( {\dfrac{A}{2}} \right)}}$

Where A is the angle of prism and ${\delta _m}$ is the angle of minimum deviation. This is known as the prism formula.

• Dispersion of light: $\mu  = A + \dfrac{B}{{{\lambda ^2}}} + \dfrac{C}{{{\lambda ^4}}}$

• Angular dispersion,  ${\delta _V} - {\delta _R} = \left( {{\mu _V} - {\mu _R}} \right)A$

• Mean deviation,  $\delta  = \dfrac{{{\delta _V} - {\delta _R}}}{2}$

• Dispersive power,  $\omega  = \dfrac{{{\text{angle dispersion(}}{{{\delta }}_{\text{V}}}{\text{ -  }}{{{\delta }}_{\text{R}}}{\text{)}}}}{{{\text{mean deviation}(\delta )}}}$

• $\omega  = \dfrac{{{\mu _V} - {\mu _R}}}{{\left( {\mu  - 1} \right)}},$

where $\mu  = \dfrac{{{\mu _V} - {\mu _R}}}{2}$= mean refractive index.

• For no deviation, the condition is

$\delta  + \delta ' = 0$

$\left( {\mu  - 1} \right)A + \left( {\mu ' - 1} \right)A' = 0$  or  $A' = \dfrac{{\left( {\mu  - 1} \right)A}}{{\left( {\mu ' - 1} \right)}}$

Under this condition, net angular dispersion produced by the combination

$ = \left( {{\delta _V} - {\delta _R}} \right) + \left( {{\delta _V}^\prime  - {\delta _R}^\prime } \right) = \left( {{\mu _V} - {\mu _R}} \right)A + \left( {{{\mu '}_V} - {{\mu '}_R}} \right)A'$

• The condition for no dispersion is:

$\left( {{\mu _V} - {\mu _R}} \right)A + \left( {{{\mu '}_V} - {{\mu '}_R}} \right)A' = 0$  or   $A' =  - \dfrac{{\left( {{\mu _V} - {\mu _R}} \right)A}}{{\left( {{{\mu '}_V} - {{\mu '}_R}} \right)}}$

• Under this condition, net deviation produced by the combination is

$\delta  + \delta ' = \left( {\mu  - 1} \right)A + \left( {\mu ' - 1} \right)A'$

• Simple microscope:

• Magnifying Power:

$M = \dfrac{{{\text{angle subtended by image at the eye}}}}{{{\text{angle subtended by the object at the eye}}}} = \dfrac{{\tan \beta }}{{\tan \alpha }} = \dfrac{\beta }{\alpha }$

Where both the object and image are situated at the least distance of distinct vision.

• When the image is formed at Infinity (far point), $M = \dfrac{D}{f}$

• When the image is formed at the least distance of distinct vision D (near point), $M = 1 + \dfrac{D}{f}$

• Compound Microscope:

• Magnifying power of a compound microscope

$M = {m_0} \times {m_e}$

•  When the final image is formed at Infinity (normal adjustment),

$M = \dfrac{{{v_0}}}{{{u_0}}}\left( {\dfrac{D}{{{f_e}}}} \right)$

Length of tube, $L = {v_0} + {f_e}$

• When the final image is formed at least distance of distinct vision,

$M = \dfrac{{{v_0}}}{{{u_0}}}\left( {1 + \dfrac{D}{{{f_e}}}} \right)$

Where ${u_0}$ and ${v_0}$ represent the distance of object and image from the objective lens, ${f_e}$ is the focal length of an eye lens.

• Length of the tube,  $L = {u_0} + \left( {\dfrac{{{f_e}D}}{{{f_e} + D}}} \right)$

• Astronomical Telescope (Refracting type):

• When the final image is formed at Infinity (normal adjustment),

• $M = \dfrac{{{f_0}}}{{{f_e}}}$

• Length of tube,  $L = {f_0} + {f_e}$

• When the final image is formed at least distance of distinct vision,

• $M = \dfrac{{{f_0}}}{{{f_e}}}\left( {1 + \dfrac{{{f_e}}}{D}} \right)$ and Length of tube, $L = {f_0} + \left( {\dfrac{{{f_e}D}}{{{f_e} + D}}} \right)$ 

• Reflecting Type Telescope:

In normal adjustment, Magnifying power:  $M = \dfrac{{{f_0}}}{{{f_e}}} = \dfrac{{\left( {\dfrac{R}{2}} \right)}}{{{f_e}}}$ where R is the radius of curvature of a concave mirror.

Questions:

1. An astronomical telescope has an objective and eyepiece of focal lengths 40 cm and 4 cm respectively. To view an object, the lenses must be separated by a distance:

1. 50 cm

2. 54 cm

3. 37.3 cm

4. 46 cm

Answer: Option (b) 54 cm

Here, 

${f_o} = 40cm$

${f_e} = 4cm$

$l = {v_o} + {f_e}$ 

We need to find the tube length (l).

For, objective lens:

${u_o} =  - 200cm,{v_o} = ?$

$\dfrac{1}{{{v_o}}} - \dfrac{1}{{{u_o}}} = \dfrac{1}{{{f_0}}}$

$\dfrac{1}{{{v_o}}} - \dfrac{1}{{ - 200}} = \dfrac{1}{{40}}$

$\dfrac{1}{{{v_o}}} = \dfrac{1}{{40}} - \dfrac{1}{{200}}$

$\dfrac{1}{{{v_o}}} = \dfrac{4}{{200}}$

${v_0} = 50cm$

$l = 50 + 4 = 54cm$ 

Thus, separation is 54 cm.

2. Given the focal length of an objective lens is 50 cm then which of the following statements are true?

1. Magnifying power of microscope increases

2. Magnifying power of microscope decreases

3. Magnifying power of telescope increases

4. Magnifying power of telescope decreases

Ans: Option (b) and (c)

Magnifying power of a microscope is given by, $m = \dfrac{{LD}}{{{f_o}{f_e}}}$.

Magnifying power of a microscope is given by, $m = \dfrac{{{f_o}}}{{{f_e}}}$.

Since focal length of objective is directly proportional to magnification of a telescope, m increases. But for microscopes it decreases as it is inversely proportional.

3. An equiconvex crown glass lens has a focal length 20 cm for violet rays. Its focal length for red rays is:

Given: Refractive index of red and violet rays is 1.47 and 1.5 

1. 20.82 cm

2. 21.28 cm

3. 22.85 cm

4. 24.85 cm

Ans: Option b) 21.28 cm

For an equiconvex lens, $\dfrac{1}{f} = (\mu  - 1)\dfrac{2}{R}$.

For violet ray: $\dfrac{1}{{20}} = (1.5 - 1)\dfrac{2}{R}$

For red ray: $\dfrac{1}{{{f_r}}} = (1.47 - 1)\dfrac{2}{R}$

Dividing both equations to get f,

$\dfrac{{{f_r}}}{{20}} = \dfrac{{0.5}}{{0.47}}$

${f_r} = 0.235 \times 20 = 21.28cm$ 

Therefore, the focal length is 21.28 cm for red rays.

Importance of Physics Ray Optics and Optical Instruments

This chapter explains the features of light rays using scientific derivations. Students will find out how a light ray travels in a transparent medium and correlate its features. They will also learn how a light ray reflects on a reflecting surface.

It will explain what spherical mirrors and lenses are and how they are used in different ways. The optical instruments designed follow the fundamental principles of rectilinear propagation of light. The deviation of a light ray’s path is studied and used to make such instruments.

The different terms related to spherical mirrors and lenses such as principal axis, normal, the centre of curvature, pole, and radius of curvature will be explained elaborately in this chapter. All these terms will be described with their symbols and formulas. These formulas are used to calculate these scientific terms related to the optical instruments.

On proceeding further, the laws related to the refraction of light will be derived using scientific derivations. Students will find out how these derivations are done using mathematical principles to build formulas for calculating the refractive index, focal length, and radius of curvature.

This chapter holds immense importance as students will find out the proper explanation of reflecting and refraction of light. They will also find out optical instruments like microscopes, spectacles, telescopes and even the human eye functions. The use of Ray Optics and Optical Instruments notes will aid students to remember these concepts easily.

Benefits of Ray Optics and Optical Instruments Revision Notes

• The sole aim of preparing these revision notes is to offer a concise format of the entire chapter. Students will get a simpler explanation of all the definitions, formulas, laws, and concepts of optical instruments in a consolidated way.

• This easier format will enable students to revise this chapter faster. They will also be able to comprehend the implications of the concepts and understand the importance of the optical instruments.

• You can also reduce the time of revising this chapter. Ray Optics and Optical Instruments revision notes will also help you to recall what you have studied during the exam and formulate accurate answers to the fundamental questions.

Download Ray Optics and Optical Instruments Class 12 Revision Notes PDF

Ray Optics and Optical Instruments revision notes help students to revise the chapter quickly and in-depth. Students can download this PDF file for free and resolve doubts about this chapter on their own. They can find the relevance of the concepts related to the reflection and refraction of light and the scientific principles behind the optical instruments in easy-to-understand language. We hope these notes will help you to answer NEET questions related to ray optics and score well in the exam.

NEET Physics Revision Notes - Chapter Pages

Other Important Links