NEET 2024 Revision Notes for Physics Motion in a Straight Line

Kinematics:

Kinematics is the study of the motion of a system of bodies without directly considering the forces or potential fields affecting the motion.

The frame of reference:

The frame of reference is a system of coordinates axes attached to an observer having a clock with him, concerning which the observer can describe the position, displacement, acceleration etc., of a moving body.

Types of Frame of References:

• Inertial frame of reference: In which Newton’s first law of motion does not hold good. It means that no external force is acting on a body; it will stay at rest or remain in uniform motion.

Example: A car at a standstill, A Bus moving with constant speed

• Non-Inertial frame of reference: In which Newton’s first law of motion does not hold good. It means that it undergoes acceleration concerning an inertial frame.

Example: A car accelerating during signals, Earth rotating the sun

Motion

A body is said to be in motion if it changes its position with time, with respect to its surroundings, e.g. a bird flying in the air. Rest and motion are relative terms.

Types of motion:

• Motion in one dimension is defined as a particle moving in a single direction throughout its journey. For example, an ant moving along X-axis. Motion is described in terms of displacement(x), time (t), velocity (v) and acceleration (a).

• Motion in two dimensions: It is defined as a particle moving in a plane, i.e. a two-dimensional motion has happened in a plane of X-Y axis. For example, an ant moving on the top surface of a desk. Motion is described in terms of the projectile and circular motion.

• Motion in three dimensions: It is defined as a particle moving in space, i.e. a three-dimensional motion has happened in a plane of the X-Y-Z axis. For example, the movement of the gyroscope. 

Scalar Quantities

The physical quantities which have only magnitude but no direction are known as scalar quantities, e.g., mass, work etc.

Vector Quantities

The physical quantities which have both magnitudes and direction are known as vector quantities, e.g., force, velocity etc.

Difference Between Scalars and Vectors

Distance and Displacement

• Distance: The length of the actual path traversed by a body during its motion in a given interval is called the distance travelled by the body. Its SI unit is meters (m), and its dimension is L. Displacement is independent of the path, but distance is dependent on the path travelled.

• Displacement: Displacement is defined as the shortest distance travelled by the body. Its SI unit is meters (m), and its dimension is L. Distance is a scalar quantity, whereas displacement is a vector quantity.

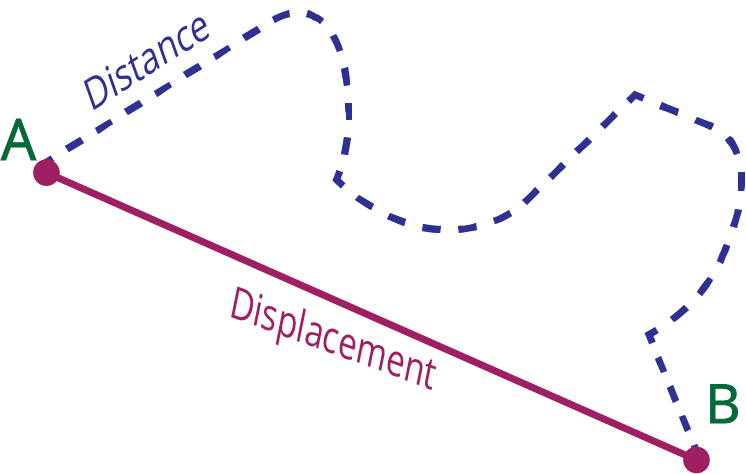
Difference Between Distance and Displacement

Speed

Speed of a body is defined as the rate of change of position of the body with time in any direction.

i.e., ${\text{speed  = }}\dfrac{{{\text{distance}}}}{{{\text{time}}}}$ 

Average Speed

Average speed is defined as the ratio of the total distance travelled by the body to the total time taken.

i.e., ${\text{Average speed  = }}\dfrac{{{\text{Average distance}}}}{{{\text{time taken}}}}$

$[{M^0}L{T^{ - 1}}]$

Instantaneous Speed

The limit of the ratio of distance and time i.e. the rate of change of distance with respect to time is called instantaneous speed.

i.e. $spee{d_{(i)}} = \dfrac{{ds}}{{dt}}$ where ds is the rate of change in distance.

Velocity

• Velocity of a body is defined as the rate of change of displacement of the body with time i.e., ${\text{velocity  =  }}\dfrac{{{\text{displacement}}}}{{{\text{time taken}}}}$ Both the speed and velocity have the same unit and same dimension formula $[{M^0}L{T^{ - 1}}]$ .

• Average velocity: Average velocity is defined as the ratio of the displacement to the time interval for which the motion takes place.

i.e., ${\text{average velocity  =  }}\dfrac{{{\text{total displacement}}}}{{{\text{total time taken}}}}$

• Instantaneous velocity: The velocity of a body at a given instant of time during motion is known as instantaneous velocity

i.e., Instantaneous velocity = $\mathop {\lim }\limits_{\vartriangle t \to 0} $  $\dfrac{{\Delta \vec r}}{{\Delta t}} = \dfrac{{d\vec r}}{{dt}}$

Acceleration

• Acceleration of a body is defined as the rate of change of velocity of a body with time. i.e. ${\text{acceleration  = }}\dfrac{{{\text{velocity}}}}{{{\text{time}}}}$ 

• Average acceleration: Average acceleration is defined as the ratio of the change in velocity to the time interval during which the change occurs

i.e. ${\text{avgerage acceleration = }}\dfrac{{{\text{total velocity}}}}{{{\text{total time}}}}$

• Instantaneous acceleration: The acceleration of a body at a given instant of time is known as instantaneous acceleration.

i.e. $a = \mathop {\lim }\limits_{t \to 0} \dfrac{{\Delta v}}{{\Delta t}} = \dfrac{{dv}}{{dt}}$ 

• If a body is speeding up, acceleration is in the direction of velocity, if its speed is decreasing, acceleration is in the direction opposite to that of the velocity.

• The zero-velocity of a body at any instant does not necessarily imply zero acceleration at that instant. A body may be momentarily at rest and yet have non-zero acceleration.

• When the acceleration is uniform instantaneous acceleration equals average acceleration over that period.

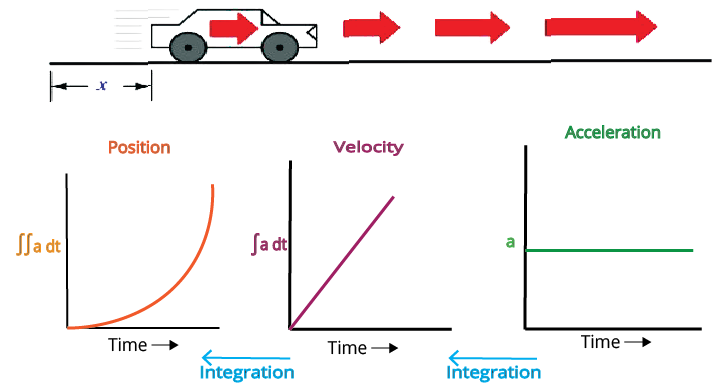
Variations of Speed, Velocity and Acceleration

Graphs on Kinematics:

Kinematic situations happening in our day-to-day life can be represented in the form of graphs that vary with time and are called kinematic graphs.

Generally, there are three kinds of graphs:

• Displacement time graph

• Velocity time graph

• Acceleration time graph

Displacement-Time Graph:

If a graph is plotted by taking displacement on the y-axis and time on the x-axis, then it is called a displacement-time graph.

• If the graph is a straight line parallel to the time-axis, the body is at rest, i.e., velocity=zero like in fig. (a).

• If the graph is a straight line inclined to time-axis shows that body is moving with a constant velocity like in fig. (b).

• If the graph obtained is a curve whose slope decreases with time, the velocity decreases, i.e., motion is retarded.

• If the graph obtained is a curve whose slope increases with time, the velocity increases, i.e., motion is accelerated like in fig. (c).

Different Variations of Displacement

Velocity-Time Graph:

• If the graph is a straight line parallel to the time axis, the body is moving with a constant velocity or acceleration of zero.

• If the graph is a straight line inclined to the time axis with a positive slope it means that the body is moving with constant acceleration.

• If the graph obtained is a curve whose slope decreases with time, the acceleration goes on decreasing.

• If the graph obtained is a curve whose slope increases with time, the acceleration goes on increasing.

• The area of the velocity-time graph with the time axis represents the displacement of that body.

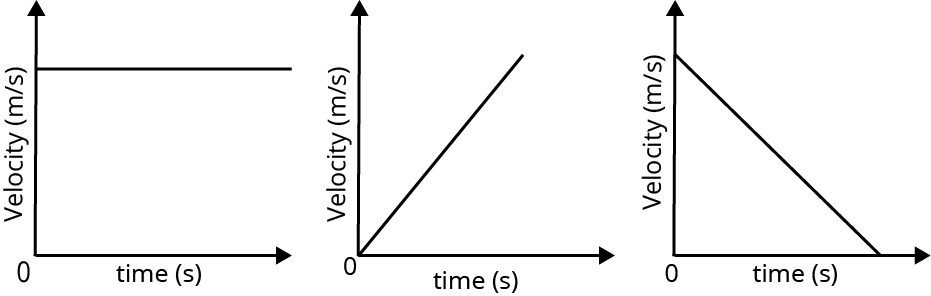
Different Variations of Velocity

Acceleration-Time Graph:

• When the graph is a straight line and parallel to time axis then acceleration is constant.

• When the graph is oblique straight line having positive slope, then acceleration is uniformly increasing.

• When the graph is an oblique straight line having negative slope, then acceleration is uniformly decreasing.

Different Variations of Acceleration

Example: Consider a body moving with a constant velocity of \[5m{{s}^{-1}}\] and thus moves with uniformly decreasing velocity of \[4m{{s}^{-1}}\]. Represent the following situations graphically using a v-t graph and explain the nature of acceleration.

Solution:

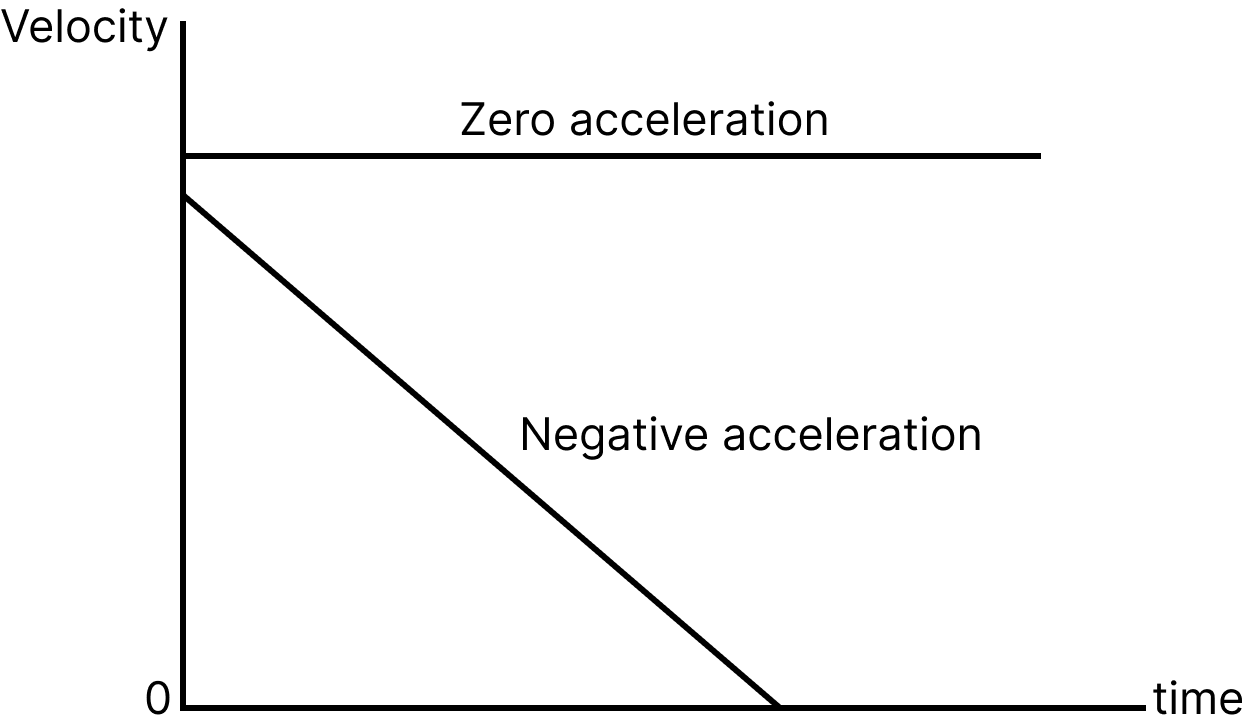
Example

From this graph we can observe that a v-t graph is drawn with velocity at y-axis and acceleration at x-axis. Considering the body moving with constant velocity of \[5m{{s}^{-1}}\] shown in the horizontal line which indicates there is 0 acceleration as the velocity is constant. 

For a body whose velocity is decreasing i.e. here \[4m{{s}^{-1}}\] the body is said to have deceleration i.e. negative acceleration.

Equations of Motion for a Uniformly Accelerated Body:

Study of kinematics is a deep study about nature of moving body and how one quantity is related to the other. Since we learned about the quantities of a one-dimensional motion, let us see how they are related.

Uniformly accelerating body is defined as a body whose acceleration is said to be uniform. For a uniformly accelerating body, the standard quantities of one-dimensional motion (velocity, acceleration…) are related as follows:

1. $v = u + at$

2. $s = ut + \dfrac{1}{2}a{t^2}$ 

3. ${v^2} = {u^2} + 2as$ 

4. ${s_n} = u + \dfrac{1}{2}a(2n - 1)$ 

Here, u is the initial velocity, v is the final velocity, a is the acceleration, s is the distance travelled or height at time interval t.

Equations of Motion for a Freely Falling Body Under Gravity:

Freely falling body is defined as the body falling freely i.e. under the action of gravitational force. The equations of motion is similar to the above but here acceleration is given by “g” which is called as acceleration due to gravity i.e. its value is \[g=9.8m{{s}^{-2}}\] . The equations of motion can be generalized as:

1. $v = u + gt$ 

2. $s = ut + \dfrac{1}{2}g{t^2}$ 

3. ${v^2} = {u^2} + 2gs$ 

4. ${s_n} = u + \dfrac{1}{2}g(2n - 1)$ 

Relative Velocity:

• Relative velocity of a body is defined as the velocity of a body applied on another body.

• ${V_r} = {V_a} - {V_b}$  is the equation for relative velocity of one body A on another body B.

• It depends on the direction, i.e. for towards motion it is negative and for away motion it is positive.

Important formulae:

• ${\text{speed  = }}\dfrac{{{\text{distance}}}}{{{\text{time}}}}$

• ${\text{Average speed  = }}\dfrac{{{\text{Average distance}}}}{{{\text{time taken}}}}$

• $spee{d_{(i)}} = \dfrac{{ds}}{{dt}}$ where ds is the rate of change in distance.

• ${\text{velocity  =  }}\dfrac{{{\text{displacement}}}}{{{\text{time taken}}}}$

• ${\text{average velocity  =  }}\dfrac{{{\text{total displacement}}}}{{{\text{total time taken}}}}$

• Instantaneous velocity = $\mathop {\lim }\limits_{\vartriangle t \to 0} $  $\dfrac{{\Delta \vec r}}{{\Delta t}} = \dfrac{{d\vec r}}{{dt}}$

• ${\text{acceleration  = }}\dfrac{{{\text{velocity}}}}{{{\text{time}}}}$ 

• ${\text{avgerage acceleration = }}\dfrac{{{\text{total velocity}}}}{{{\text{total time}}}}$

• Instantaneous acceleration: $a = \mathop {\lim }\limits_{t \to 0} \dfrac{{\Delta v}}{{\Delta t}} = \dfrac{{dv}}{{dt}}$ 

• Equations of Motion for A Uniformly Accelerated Body:

• $v = u + at$

• $s = ut + \dfrac{1}{2}a{t^2}$ 

• ${v^2} = {u^2} + 2as$ 

• ${s_n} = u + \dfrac{1}{2}a(2n - 1)$ 

• Equations of Motion for A Freely Falling Body Under Gravity:

• $v = u + gt$ 

• $s = ut + \dfrac{1}{2}g{t^2}$ 

• ${v^2} = {u^2} + 2gs$ 

• ${s_n} = u + \dfrac{1}{2}g(2n - 1)$ 

Points to remember:

• Kinematics is the study of motion of a system of bodies without directly considering the forces or potential fields affecting the motion.

• The frame of reference is a system of coordinates axes attached to an observer having a clock with him, concerning which the observer can describe a moving body's position, displacement, and acceleration.

• Types of frames of reference: Inertial and Non-Inertial

• A body are said to be in motion if it changes its position with time, concerning its surroundings, e.g. a bird flying in the air. Rest and motion are relative terms.

• Types of motion: Motion in one dimension, Motion in two, and Motion in three.

• The physical quantities which have only magnitude but no direction are known as scalar quantities, e.g., mass, work etc.

• The physical quantities which have both magnitudes and direction are known as vector quantities, e.g., force, velocity etc.

• Distance: The length of the actual path traversed by a body during its motion in a given interval of time is called distance travelled by the body. Its SI unit is meters (m), and its dimension is L.

• Displacement: Displacement is defined as the shortest distance travelled by the body. Its SI unit is meters (m), and its dimension is L.

• Speed of a body is defined as the rate of change of body position with time in any direction.

• Average speed is the ratio of the total distance travelled by the body to the total time taken.

• The limit of the ratio of distance and time, i.e. the rate of change of distance with respect to time, is called instantaneous speed.

• Velocity of a body is defined as the rate of change of displacement of the body with time

• Average velocity is defined as the ratio of the displacement to the time interval for which the motion takes place.

• The velocity of a body at a given instant of time during motion is known as instantaneous velocity

• Acceleration of a body is defined as the rate of change of velocity of a body with time.

• Average acceleration is the ratio of the change in velocity to the time interval during which the change occurs.

• The acceleration of a body at a given instant of time is known as instantaneous acceleration.

• Different types of graphs on kinematics, i.e. motion in one dimension is a position-time graph, Velocity-time graph, acceleration-time graph.

• Relative velocity of a body is defined as the velocity of a body applied to another.

Questions:

1. Given a velocity-time graph whose slope is negative. Which of the following statements are true?

1. Acceleration is negative

2. Acceleration is positive

3. Displacement is negative

4. Displacement is positive

Ans: Option a and c

In a velocity graph, the slope of the velocity graph always gives acceleration. Thus for a v-t graph, if the slope is negative, then acceleration and displacement must be negative to make the slope negative.

Thus, options a) and c) are correct

2. Which of the following equations are true for acceleration?

1. $acceleration =\dfrac{\text { velocity }}{\text { time }}$

2. $a=\lim _{t \rightarrow 0} \dfrac{\Delta v}{\Delta t}=\dfrac{d v}{d t}$

3. $s=u t+\dfrac{1}{2} a t^{2}$

4. None of these

Ans: a, b and c

Acceleration is defined as the ratio of velocity with time taken. Since the given options 

a) define acceleration,

b) defines instantaneous acceleration

c) define acceleration for some distance s

Hence, all these equations are related to acceleration.

Importance of NEET Physics Motion in a Straight

This chapter is a fundamental part of Physics where students come to know how a body behaves when it moves in a straight line. The scientific principles related to the velocity of a body will also be explained using the laws of motion.

The derivation of the laws and their mathematical interpretation will also be explained in this chapter. Students will also learn how to mould and use these formulae to seek the right answers to fundamental questions.

They will be introduced to kinematics, statics, and dynamics in this chapter elaborately. Previously, they have learnt these physics topics superficially. Now, they will be introduced to the prime concepts of kinematics along with the formulae to represent them.

This chapter is of utmost importance as the fundamental concepts of motion in a straight line will be clarified. It is the basis for advanced study in kinematics that students will learn in the upcoming years. In fact, it will also create a strong conceptual foundation for physics to score well in the NEET exam.

Benefits of Vedantu’s Motion in a Straight Line Notes

• These revision notes are prepared by the top subject matter experts to simplify the concepts and make them easier for you to comprehend. Use these notes to complete your study material for this chapter.

• Find out the easiest description of the definitions, laws, scientific principles, and fundamental concepts from the Motion in a Straight Line NEET notes at your convenience. Learn how the experts have used these concepts to decode the conceptual NEET questions.

• Use these notes to revise and recall what you have studied in this chapter. It will become a lot easier to remember the concepts using the easier and more concise format of these notes. It will help you to solve problems using the right principles during an exam.

• Use the sample questions to test your preparation level and find out where you need to focus more. Learn how the experts have answered these questions and adapt their ideas to score well in the competitive exam.

Download Motion in a Straight Line Notes PDF

Get the free PDF version of these notes and make your study sessions more fruitful. There is no need to scout the entire chapter to remember the core concepts of this chapter when you can easily do it using these notes. Find out how to score by using the answering styles developed by the experts. Use the simpler explanation of the Motion in a Straight Line notes for NEET to strengthen fundamental concepts for this chapter easily.

NEET Physics Revision Notes - Chapter Pages

Other Important Links