Revision Notes on Thermodynamics for NEET 2024

System:

A system refers to a portion of the universe, which is to be investigated or studied. For example, if a chemical reaction is taking place inside a beaker, then everything inside the beaker forms a system.

Surrounding:

The entire universe except for the system itself is termed as the surrounding. In other words, everything which lies outside the boundaries of a system is termed the surrounding

In general, it can be stated as the “Universe is the sum of the system and surrounding”.

Boundaries: 

A boundary is a closed surface that is surrounding a system, from which mass and energy may enter or leave the system. For example, the surface of any apparatus like a beaker

Types of the system:

1. Open system:  It is described as a system that may exchange matter and energies with its surroundings. For example, a beaker filled with water.

2. Closed system: A system that can only share energy with its surroundings but not matter is what is meant by a closed system. For example, a beaker of water covered by a lid.

3. Isolated system: It is characterized as a system that is incapable of exchanging matter and energy with its surroundings. For example, a thermos flask.

State of the system:

With respect to changes in the state variables, namely P, V, T, and n, the system's state can be defined and altered. These variables specify the parameters of the system, and altering any one of them will alter the system's conditions.

Properties of the system:

1. Intensive property: 

An intensive property is the property of a system that is independent of the amount of substance present in the system. For example, temperature, pressure, density, etc.

2. Extensive property: 

An extensive property is a system’s property that is dependent on the amount of substance available in the system. For example, mass, energy, and volume.

State and path function:

State function: 

A state function or point function is a property whose values are independent of the path taken to attain a particular value. In other words, it is defined as the substance which depends on the state of a substance. 

A few examples of state function variables are pressure, temperature, mass, volume, internal energy, Gibbs free energy, etc.

Path function:

The method used to introduce system changes will determine how the function turns out. For instance, heat, effort, etc.

Thermodynamic Equilibrium:

When the state variables stay the same and the three types of equilibrium listed below are met, the system remains in equilibrium.

• Mechanical Equilibrium:

Mechanical equilibrium is created when there is no mechanical motion and when the pressure and volume remain constant.

• Thermal Equilibrium:

Thermal equilibrium is created by the heat and temperature being constant throughout time.

• Chemical Equilibrium:

Chemical equilibrium is reached when the rate of the forward reaction equals the rate of the backward reaction. 

Internal Energy: It is defined as the summation of all forms of energy of its constituent atoms or molecules. It is a state function and an extensive property. It is denoted by 'U'. The energy can be determined from the relation given below

$\Delta U = q + W$ 

Here, q is the heat transferred by the system and W is the work done on the system.

Modes of Energy Transport:

• Heat: Heat is the energy that is transmitted as a result of temperature variations between a system and its surroundings (Q). When a system is heated, the molecules' kinetic energy rises, increasing the system's internal energy.

• Work: Work is the energy expended to withstand the external forces acting on the system (W). The internal energy of a system decreases as it expands. However, when the system contracts, its internal energy increases.   

The First Law of Thermodynamics:

According to the first law of thermodynamics, energy cannot be generated or destroyed.

The expression can be shown below.

$\Delta U = q + W$ 

The sign conventions are shown below;

Work done by the system = $ - W$ 

Work done on the system = $ + W$ 

Heat flows into the system = $ + q$ 

Heat flows out of the system = $ - q$ 

Expansion work:

Expansion work is the term for the work carried out as a result of changes in the system's volume. Be aware that whether compression or expansion occurs, we consider external pressure to be the driving force.

It can be modeled mathematically as;

$W =  - \int {{P_{{\rm{ex}}}}dV}$ 

External pressure is taken into account to be equivalent to the gas pressure for reversible processes. Thus,

$W =  - \int {{P_{{\rm{gas}}}}dV}$ 

When a P – V graph is drawn, work done is represented as the area covered under it as shown;

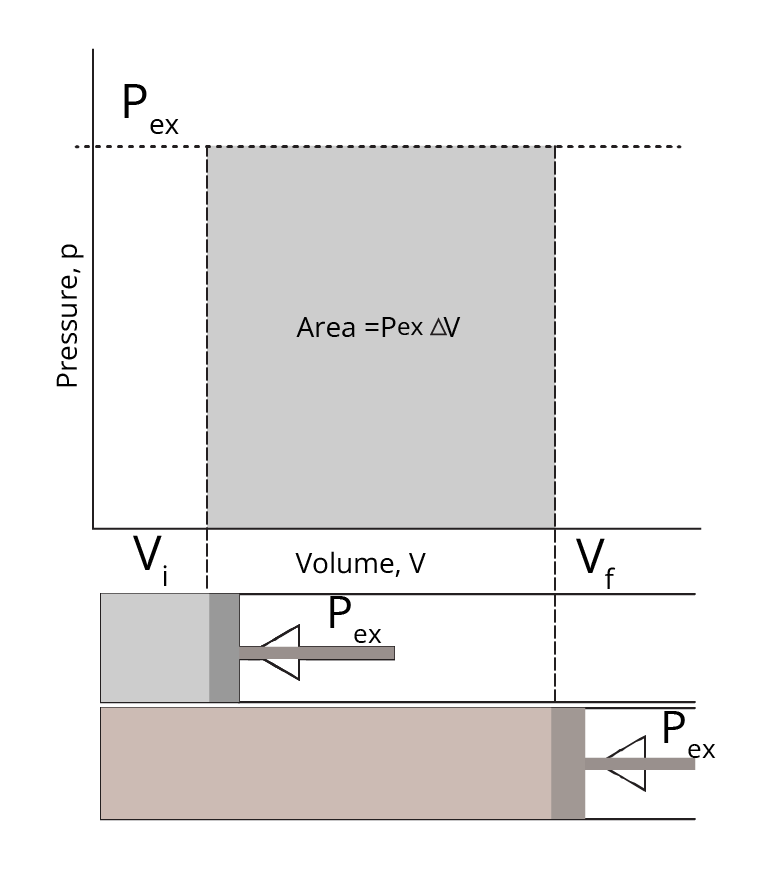
Pressure-Volume Graph

Sign Conventions:

$W:$ When the system's volume is decreasing, the value is positive; when it is rising, it is negative.

$\Delta U:$ When a system's temperature, pressure, or volume is decreasing, it is negative; otherwise, it is positive.

  $q:$ The first law of thermodynamics must be used to ascertain this.

Cyclic Process:

A cyclic process is one that continually loops back to its starting point. This method is determined by a closed graph, and here,

${q_{{\rm{net}}}} =  - {W_{{\rm{net}}}}$ 

Enthalpy:

The sum of the total amount of energy in the system and the energy in performing work is referred to as the thermodynamic state function. It can be modeled mathematically as;

$\Delta H = U + P \Delta V$  

•    At constant P, $\Delta H = {q_p}.$ 

•   At constant V, $\Delta H = {q_v}.$ 

Molar heat capacity:

At constant Pressure –

The quantity of heat required to raise a mole of gas' temperature by one degree at constant pressure. It may be expressed as;

${C_p} = \dfrac{{{q_p}}}{{n\Delta T}}$  

At constant Volume –

The quantity of heat required to raise a mole of gas' temperature by one degree at constant volume. It may be expressed as;

${C_v} = \dfrac{{{q_v}}}{{n\Delta T}}$ 

We can now say that, $\Delta H = n{C_p}\Delta T$  and $\Delta U = n{C_v}\Delta T$ 

Types of thermodynamic processes:

1. Isothermal process: Isothermal process is a thermodynamic process, wherein the volume and pressure of a system change while the temperature remains constant. In such a process, it should be noted that the exchange of heat takes place between the system and the surrounding.

For example, Carnot's engine, refrigerator.

$\begin{array}{c}W =  - 2.303nRT\log \dfrac{{{V_2}}}{{{V_1}}}\\ =  - 2.303nRT\log \dfrac{{{P_1}}}{{{P_2}}}\end{array}$ 

$\begin{array}{c}q = 2.303nRT\log \dfrac{{{V_2}}}{{{V_1}}}\\ = 2.303nRT\log \dfrac{{{P_1}}}{{{P_2}}}\end{array}$ 

2. Adiabatic process: In an adiabatic process, changes in volume, pressure and temperature occur without any heat entering or leaving the system. It should be noted that the total heat of a system, undergoing an adiabatic change, always remains constant. 

For example: ice in an icebox, compressors.

$T{V^{\gamma  - 1}} = C,{\rm{ }}P{V^\gamma } = C$ 

Here, C is constant.

$\begin{array}{l}q = o\\W = \Delta U\end{array}$ 

Now,

$\begin{array}{c}\Delta U = n{C_v}\Delta T\\ = \dfrac{{\left( {{P_2}{V_2} - {P_1}{V_1}} \right)}}{{\gamma  - 1}}\\ = \dfrac{{nR\Delta T}}{{\gamma  - 1}}\end{array}$ 

3. Isochoric process:

In an isochoric process, volume is always constant. Here, $W = 0$ and $\Delta U = n{C_{\rm{V}}}\Delta T = {q_v}.$ 

4. Isobaric process:

In isobaric process, pressure is always constant.

Here, $W =  - P\Delta V =  - nR\Delta T,{\rm{ }}\Delta H = n{C_p}\Delta T = {q_p}$. 

Graphs:

It should be noted that while the P-V graphs for the isothermal and adiabatic processes are similar, the latter's is steeper.

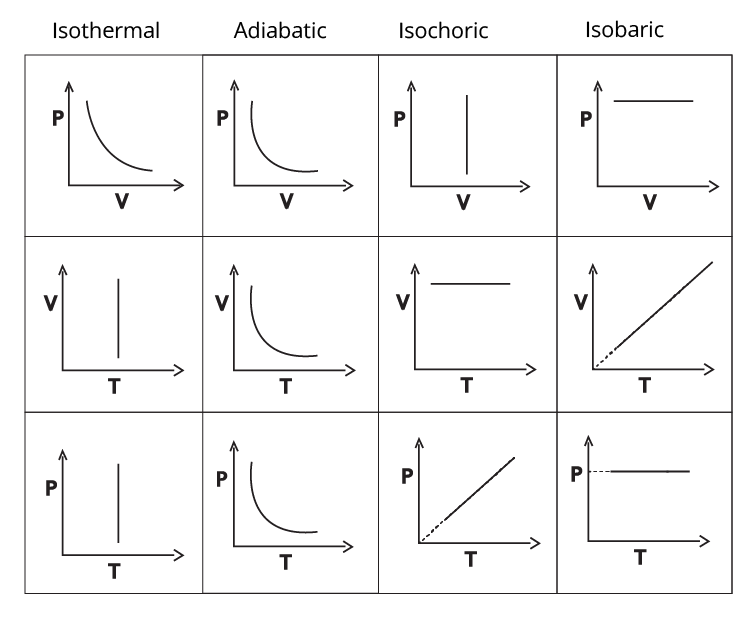
P-V graph for all Processes

Reversible process: A process, wherein a previous or initial stage can be acquired by making changes to several parameters, is called a reversible process. For example, adiabatic compression and expansion of gases.

Irreversible process: A process, wherein the previous or initial stage of the system cannot be acquired by making changes to several parameters, such as temperature and pressure, is termed an irreversible process. For example, rusting of iron.

Free expansion:

In a free expansion, the gas's external pressure is zero, meaning that the energy expended by the gas expanding against the vacuum is zero. As a result, it can be an adiabatic and isothermal process.

Polytropic process:

Any thermodynamic process can be depicted as having the following generalised form:

$P{V^{\rm{n}}} = {\rm{constant}}$  

For the isothermal process, $n = 1.$ 

For adiabatic process, $n = \gamma .$ 

Thermochemical equation:

A thermochemical equation is a chemical formula that includes all the relevant data, including the phases of the reactants and products in the reaction as well as the energy changes involved.

Types of Reaction:

1.  Endothermic reaction:

Endothermic reactions are those that chemically absorb energy. Enthalpy has increased in this case.

2. Exothermic reaction:

Exothermic reactions are those chemical processes that produce heat. Enthalpy has decreased in this situation.

For any chemical reaction, 

$\Delta {H_{{\rm{reaction}}}} = \Delta {H_{{\rm{products}}}} - \Delta {H_{{\rm{reactants}}}}$ 

This change in enthalpy takes place due to making and breaking of bonds.

Hess law of constant heat summation:

The enthalpy changes in each stage can be used to compute the overall change in enthalpy for a reaction that takes place in stages. The guiding idea is Hess's law of constant heat summation.

Enthalpy of reactions:

Enthalpy of bond dissociation:

Enthalpy of bond dissociation is the term used to describe the amount of energy required to dissociate a single molecular bond. Per mole of the molecule, it is defined.

Enthalpy of combustion:

Enthalpy of combustion is the term used to describe the amount of heat that is either absorbed or released when a mole of substance burns in the presence of oxygen. 

Enthalpy of formation:

Enthalpy of formation refers to the heat produced or absorbed when a mole of a compound is created from its component elements in their standard elemental forms.

Enthalpy of atomization:

The enthalpy of atomization is the amount of energy needed to break down any substance into gaseous atoms. Per mole of gaseous atoms, it is defined.

Enthalpy of sublimation:

Enthalpy of sublimation is the amount of heat needed to transform a mole of a substance from its solid state to its gaseous state at STP.

Enthalpy of phase transition:

The enthalpy of phase transition is a specific standard enthalpy that is released or absorbed during a phase transition from one phase to another.

Enthalpy of ionization: 

The amount of energy needed for a gaseous atom to lose an electron from its ground state is measured by the enthalpy of ionisation.

Enthalpy of the solution:

The amount of heat that is either emitted or absorbed when a mole of a substance dissolves in excess of a solvent, most frequently water, is known as the enthalpy of the solution.

Enthalpy of dilution:

Enthalpy of dilution is the term used to describe the enthalpy shift that occurs when a component is diluted in a solution while maintaining a constant pressure. Energy per mass or quantity of a substance is how it is defined.

The Second Law of Thermodynamics:

The second law of thermodynamics states that the entropy of the entire universe will always increase over time as an isolated system.

Need: The first law of thermodynamics indicates that energy is converted during a process, but it leaves out an explanation of how this is possible. The second law of thermodynamics was necessary because of this reason.

Types of processes:

Spontaneous process:

The spontaneous process tends to occur naturally and doesn't require any outside effort to complete.

Non-spontaneous process:

A non-spontaneous process is one that is influenced by outside work and is not capable of occurring organically.

Entropy:

The entropy of a process in a body is a measurement of randomness or disorder. It is a state function, denoted by the letter S.

The universe's overall randomness tends to increase during the spontaneous process. Thus,

$\Delta S = \dfrac{{{q_{{\rm{rev}}}}}}{T}$ 

For spontaneous change, $\Delta {S_{{\rm{Total}}}} = \Delta {S_{{\rm{System}}}} + \Delta {S_{{\rm{Surrounding}}}} > 0$ 

For reversible processes where the universe's entropy is constant, $\Delta {S_{{\rm{Total}}}} = 0.$ 

Entropy Changes in Thermodynamic Processes:

Any thermodynamic process' entropy changes can be quantitatively expressed as;

• Isothermal process:

• $\Delta S = nR\ln \dfrac{{{V_2}}}{{{V_1}}}$ 

•  Isochoric process:

• $\Delta S = n{C_v}\ln \dfrac{{{T_2}}}{{{T_1}}}$ 

•  Isobaric process:

• $\Delta S = n{C_p}\ln \dfrac{{{T_2}}}{{{T_1}}}$ 

•  Adiabatic process:

$\Delta S = 0$ (for reversible process)

$\Delta S = n{C_v}\ln \dfrac{{{T_2}}}{{{T_1}}} + nR\ln \dfrac{{{V_2}}}{{{V_1}}}$ (for irreversible process)

Gibbs Free Energy:

This provides us with the most practical metric to assess the process's spontaneity from the viewpoint of the system. It can be modeled as follows at constant temperature:

$\Delta {G_{{\rm{sys}}}} = \Delta H - T\Delta {S_{{\rm{sys}}}}$ 

At constant temperature and pressure, the reaction can be written as,

$\Delta {G_{{\rm{sys}}}} =  - T\Delta {S_{{\rm{Total}}}}$ 

For the process to be spontaneous, the reaction can be written as,

$\Delta {G_{{\rm{sys}}}} < 0.$ 

Third law of thermodynamics:

The third law of thermodynamics states that as a system's temperature approaches absolute zero, its entropy will tend to approach a constant value.

Solved Example: 

1. The enthalpies of elements in their standard states are taken as zero. The enthalpy of the formation of a compound

(A) Is always negative

(B) Is always positive

(C) Maybe positive or negative

(D) Is never negative

Ans: Option (C)

It is the amount of internal energy contained in a compound. The reaction by which a compound is formed can be an exothermic or endothermic reaction. The enthalpy of formation is positive for an endothermic reaction and negative for an exothermic reaction. So, the enthalpy of formation of a compound may be positive or negative depending upon the type of the reaction.

2. Which of the following is not correct?

(A) $\Delta G$ is zero for a reversible reaction

(B) $\Delta G$ is positive for a spontaneous reaction

(C) $\Delta G$ is negative for a spontaneous reaction

(D) $\Delta G$ is positive for a non-spontaneous reaction

Ans: Option (B)

(A) For a reversible reaction the change in Gibbs free energy ($\Delta G$) will be zero. This statement is correct. It states that the system is in equilibrium.

(B) The change in the Gibbs free energy is negative for a spontaneous reaction, and the reaction may proceed in the forward direction. So, the statement gave “$\Delta G$is positive for a spontaneous reaction.” is not correct.

(C) A reaction that favors the formation of products is called a spontaneous reaction. The change in the Gibbs free energy is negative for a spontaneous reaction since it is an exothermic reaction. So, this statement is correct.

(D) In a non-spontaneous reaction, the energy is absorbed and the Gibbs free energy is always positive. So, this statement is correct.

Importance of Physics Thermodynamics

The behaviour of heart energy in a system can be measured by using the concept of thermodynamics. This chapter explains how the changes in energy occur due to work done in a system. The ideal conditions to measure the internal energy, work done, and heat will be explained in different systems.

The chapter describes the different types of systems with proper definitions and mathematical expressions. Students will learn to differentiate and identify the common systems such as open systems, closed systems, and isolated systems. This chapter will also explain state variables and state functions. The correlation of the state variables such as temperature, surface area, volume, pressure, and mass with the state functions such as internal energy, entropy, enthalpy, etc will be explained in detail.

The laws of thermodynamics will be explained elaborately. Students will learn how these laws have been framed and what conditions have been considered to derive their mathematical expressions. These laws enable us to define the energy state of a system and changes in energy level due to work done.

This chapter is of utmost importance as it explains how the internal energy, heat, and work done are interrelated to each other. to make it easier, you can refer to the Thermodynamics notes prepared by the subject experts.

Benefits of Vedantu’s Thermodynamics NEET Notes

• The main objective of developing these notes is to offer a concise format of the entire chapter in a few pages. You will find it very easy to revise this chapter within a short span of time.

• Students can download these notes for free and can refer to them at their convenience. Using these notes to prepare and revise this chapter according to your study schedule will become much easier.

• You can resolve doubts based on this chapter on your own by using the revision notes and proceed to completely learn it.

• The precise format of these notes will also help you to memorize the definitions, formulas, principles, and mathematical expressions of the chapter terminologies easily. With the help of an easier description of the important terms, you can easily recall and answer fundamental questions during the exam.

Download Thermodynamics Notes PDF

Preparing and revising this chapter has never been easier for you. You can now download the PDF version of Thermodynamics Class 11 Physics NEET notes for free and complete your study material for this chapter. Add these benefits to your study sessions and become more confident in solving the fundamental problems of thermodynamics in the NEET exam.

Other Important Links