NEET 2024 Revision Notes for Electric Charges and Fields

Electric Charge:

Charge is the property associated with matter due to which it produces and experiences electrical and magnetic effects. The excess or deficiency of electrons in a body gives the concept of charge.

Properties of Charge:

• Charge is a scalar quantity.

• Charge is transferable: If a charged body is put in contact with an uncharged body, the uncharged body becomes charged due to transfer of electrons from one body to the other.

• Charge is always associated with mass, i.e., charge cannot exist without mass though mass can exist without charge. So, the presence of charge itself is a convincing proof of the existence of mass.

Quantization of charge: Total charge on a body is always an integral multiple of a basic unit of charge denoted by e and is given by q = ne,

where n is any integer, positive or negative and e =$1.6 \times {10^{ - 19}}C$ 

• The quantization of charge was first suggested by Faraday. It was experimentally demonstrated by Millikan in 1912.

• The basic unit of charge is the charge that an electron or proton carries. By convention the charge on electrons is -e (-$1.6 \times {10^{ - 19}}C$) and charge on protons is +e ($1.6 \times {10^{ - 19}}C$). 

• Additivity of Charge: Total charge of a system is the algebraic sum (i.e. Sum is taken into account with proper signs) of all individual charges in the system.

• Conservation of Charge: Total charge of an isolated system remains unchanged with time.

• Charge is Invariant: Charge is independent of the frame of reference.

• Like charges repel each other while unlike charges attract each other.

• Methods of Charging: A body can be charged by

• Friction: This is the process of charging two non-conducting bodies by rubbing them vigorously. This transfer of electrons takes place between the charged bodies.

• Induction: This method of charging charges an object without actually touching the object.

• Conduction: This method of charging charges a neutral object with a charged object.

Coulomb’s Law:

It states that “The electrostatic force of interaction (repulsion or attraction) between two electric charges ${q_1}$ and ${q_2}$ separated by a distance R is directly proportional to the product of the charges and inversely proportional to the square of the distance between them and act along the straight line joining two charges.”  

i.e.,  $F = K\dfrac{{{q_1}{q_2}}}{{{r^2}}}$

where  $K = \dfrac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}N{m^2}{C^{ - 2}}$ is the proportionality constant and

$E = \dfrac{\sigma }{{{\varepsilon _0}}}$ ,${\varepsilon _0} = 8.854 \times {10^{ - 12}}{C^2}{N^{ - 1}}{m^{ - 1}}$ is permittivity of free space.

Coulomb’s Law in Vector Form:

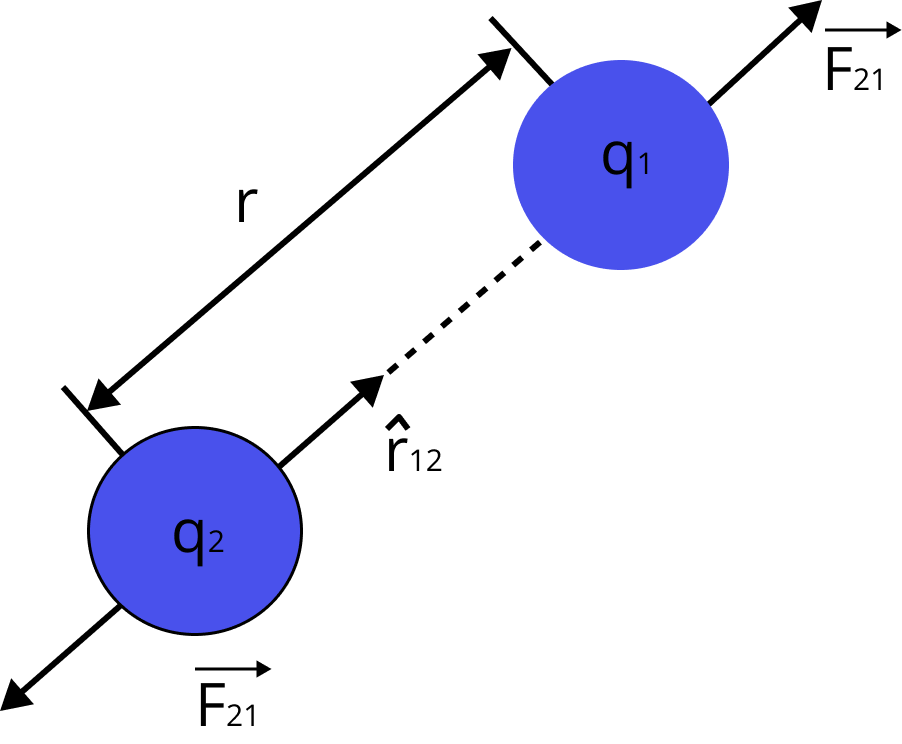
Coulomb’s Law in Vector Form

${{\vec F}_{12}} =$ force on ${q_1}$ due to ${q_2}$

$= K\dfrac{{{q_1}{q_2}}}{{{r^2}}}{\hat r_{21}}$

${{\vec F}_{21}} = K\dfrac{{{q_1}{q_2}}}{{{r^2}}}{{\hat r}_{21}}$

= force on ${q_2}$ due to ${q_1}$.

Here, ${\hat r_{12}}$ is unit vector from ${q_1}$to${q_2}$.

Coulomb’s Law in Terms of Positive Vector: ${{\vec F}_{21}} = K\dfrac{{{q_1}{q_2}}}{{{{\left| {{{\vec r}_1} - {{\vec r}_2}} \right|}^3}}}\left( {{{\vec r}_1} - {{\vec r}_2}} \right)$

The comparison Between Coulomb Force and Gravitational Force is as Follows:

Coulomb force and gravitational force follow the same inverse square law. Coulomb force can be attractive or repulsive while gravitational force is always attractive. Coulomb force between the two charges depends on the medium between two charges while gravitational force is independent of the medium between the two bodies.

The ratio of Coulomb force to the gravitational force between two protons at a same distance apart is $\dfrac{{{e^2}}}{{4\pi {\varepsilon _0}G{m_P}{m_p}}} = 1.3 \times {10^{36}}$

Principle of Superposition of Charges:

It states that, when a number of charges are interacting with each other, the total force on a given charge is vector sum of forces exerted on it by all other charges;

i.e., $F = K\dfrac{{{q_0}{q_1}}}{{r_1^2}} + K\dfrac{{{q_0}{q_2}}}{{r_2^2}} + ........ + K\dfrac{{{q_0}{q_n}}}{{r_n^2}}$

In vector form, \[\vec F = K{q_0}\sum\limits_{i = 1}^n {\dfrac{{{q_i}{{\vec r}_i}}}{{r_i^2}}}\]

Continuous Charge Distribution:

• Linear Charge Density: Charge per unit length is known as linear charge density. It is denoted by the symbol

$\lambda  = \dfrac{{Ch\arg e}}{{Length}}$. Its SI unit is $C{m^{ - 1}}$.

• Surface Charge Density: Charge per unit area is known as surface charge density. It is denoted by the symbol

$\sigma  = \dfrac{{Ch\arg e}}{{Area}}$. Its SI unit is $C{m^{ - 2}}$.

Electric Field:

The region surrounding a charge (or charge distribution) in which its electric effects are perceptible is called the electric field of the given charge.

Electric Field due to Point Charge:

$\vec E = \mathop {\lim }\limits_{{q_0} \to 0} \dfrac{{\vec F}}{{{q_0}}} = \dfrac{{kq}}{{{r^3}}}\vec r$

Here, test charge is a fictitious charge that exerts no force on hereby changes but experiences force due to them.

Electric Field Lines:

• An electric field can be represented and so visualized by electric field lines. These are drawn so that, the field lines at a point, (or the tangent to it if it is curved) gives the direction of \[\overrightarrow E \] at that point, i.e., the direction in which of positive charge would move and the number of lines per unit cross-section area is proportional to E. The field lines are imaginary but the field it represents is real.

• Electric field due to a positive point charge is represented by straight lines originating from the charge.

• The electric field due to a negative point charge is represented by straight lines terminating at the charge.

• The lines of force are purely a geometrical construction which helps us to visualize the nature of the electric field in the region. They have no physical existence.

• The number of lines originating or terminating on a charge is proportional to the magnitude of the charge. In rationalized MKS system:

The number of lines originating or terminating on a charge is proportional to the magnitude of charge. In a rationalized MKS system $\left(1 / \varepsilon_{0}\right)$ electric lines are associated with unit charge. So if a body encloses a charge $q$, total lines of force associated with it (called flux) will be $q / \varepsilon_{0}$.

Electric Dipole:

It is a pair of two equal and opposite charges separated by a small distance.

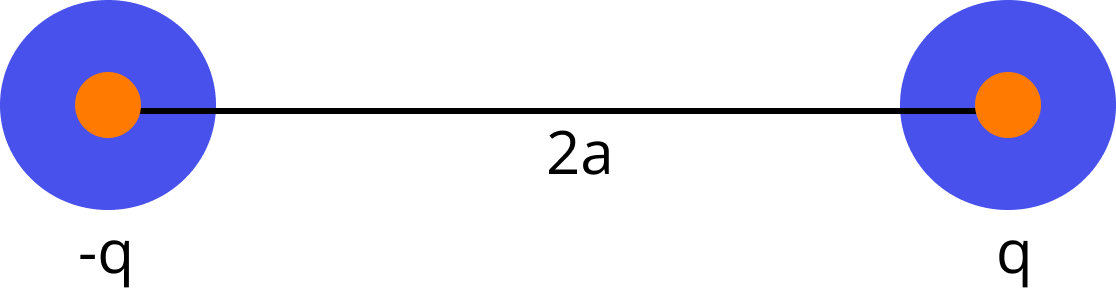
Electric Dipole

Electric Dipole Moment:

• It is a vector quantity whose magnitude is equal to the product of the magnitude of both charge and distance between the charges. i.e. $\left| {\vec p} \right|$ = q x 2a

• By convention the direction of the dipole moment is from negative charge to positive charge.

• The SI unit of electric dipole moment is C meter and its dimensional formula is   $\left[ {{M^0}LAT} \right]$. The practical unit of electric dipole moment is debye.

• Electric Field Intensity on Axial Line (End on Position) of the Electric Dipole:

• At the distance r from the center of the electric dipole, 

$E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2pr}}{{{{({r^2} - {a^2})}^2}}}$

• At very large distance i.e., (r >> a), $E = \dfrac{{2pr}}{{4\pi {\varepsilon _0}{r^3}}}$

• The direction of the electric field on the axial line of the electric dipole is along the direction of the dipole moment (i.e. from -q to q).

• Electric Field Intensity on Equatorial Line (Board on Position) of Electric Dipole:

• At the point at distance r from the center of electric dipole,

$E=\dfrac{1}{4 \pi \varepsilon_{0}} \frac{q r}{\left(r^{2}+a^{2}\right)^{3 / 2}}$

At very large distance i.e., $r \gg>$ a,

$E=\frac{1}{4 \pi \varepsilon_{0}} \dfrac{q}{r^{2}} $

• The direction of the electric field on the Equatorial line of the electric dipole is opposite to the direction of the dipole moment.

(i.e. from q to -q)

• Electric Field Intensity at any point due to an Electric Dipole:

The electric field intensity at point P due to an electric dipole,

$E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{p}{{{r^3}}}\sqrt {1 + 3{{\cos }^2}\theta } $

Electric Field Intensity due to a Charged Ring At a point on its axis at distance r from its center,

$E=\dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{q r}{\left(r^{2}+a^{2}\right)^{3 / 2}}$

Where q is the charge on the ring and a is the radius of the ring.

At very large distance i.e. r >>a, 

At the center of the ring, i.e. r = 0, E = 0.

• Torque on an Electric Dipole placed in a uniform Electric Field

When an electric dipole of dipole moment $\vec p$is placed in a uniform electric field $\vec E$, it will experience a torque and it is given by

$\vec \tau  = \vec p \times \vec E$

$\tau  = pE\sin \theta $

Where $\theta $ is the angle between p and E.

• Torque acting on a dipole is maximum$({\tau _{\max }} = pE)$When the dipole is perpendicular to the field and minimum(x = 0) when the dipole is parallel or antiparallel to the field.

• When a dipole is placed in a uniform electric field, it will experience only torque and the net force on the dipole is zero while when it is placed in a non-uniform electric field, it will experience both torque and net force.

Electric Flux:

• If the lines of force pass through a surface then the surface is set to have flux linked with it. Mathematically, it can be formulated as follows:

The flux linked with small area element on the surface of the body

$d\phi  = \vec E.\overrightarrow {ds} $

where$d\vec s$is the area vector of the small area element. The area vector of a closed surface is always in the direction of outward drawn normal. The total flux is linked with the whole of the body$\phi  = \oint {\vec E.d\vec s} $.

• Gauss’s Theorem: The total flux linked with a closed surface is $\frac{1}{\in }$ times the charge enclosed by the closest surface (Gaussian surface) i.e., $\oint {\vec E.d\vec s}  = \dfrac{q}{{{\varepsilon _0}}}$.

This law is applicable for symmetrical charge distribution and valid for all vector fields obeying inverse square law.

Gauss Theorem

• Gaussian Surface:

• It is an imaginary surface.

• It is spherical for an infinite sheet of charge, conducting and non conducting spheres.

• It is cylindrical for an infinite sheet of charge, conducting charge surfaces, infinite line of charges, charged cylindrical conductors etc. 

Application of Gauss Law:

• Electric field due to an infinitely long thin uniformly charged straight wire:

Electric field due to thin infinitely long straight wire of uniform linear charge density is 

$E = \dfrac{\lambda }{{2\pi {\varepsilon _0}r}}$where r is the perpendicular distance of the observation point from the wire.

• Electric field due to uniformly charged thin spherical shell:

Electric field due to uniformly charged thin spherical shell or uniform surface charge density$\sigma $and radius R at a point distance r from the center of the shell is given as follows:

• At a point outside the shell i.e., r > R

$E = \dfrac{1}{{2\pi {\varepsilon _0}r}}\dfrac{q}{{{r^2}}}$

• At a point on the surface of the shell i.e., r = R

$E = \dfrac{1}{{2\pi {\varepsilon _0}r}}\dfrac{q}{{{R^2}}}$

• At a point inside the shell i.e., r < R

E = 0

Here, $q = 4\pi {R^2}\sigma $

The variation of E with r for a uniformly charged thin spherical shell is as shown in the figure.

• Electric field due to a uniformly charged non-conducting solid sphere:

Electric field due to a uniformly charged non-conducting solid sphere of uniform volume charge density $\rho $and radius R at a point distant r from the center of the sphere is given as follows:

• At a point outside the sphere i.e., r > R

$E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{r^2}}}$

• At a point on the surface of the sphere i.e., r = R

$E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{R^2}}}$

• At a point inside the sphere i.e., r < R

$E = \dfrac{{\rho r}}{{3{\varepsilon _0}}} = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{qr}}{{{R^3}}}$, for r < R

Here,

The variation of E with r for a uniformly charged non-conducting sphere is as shown in the figure.

• Electric field due to uniformly charged infinite thin plane sheet:

Electric field due to an infinite thin plane sheet of uniformly charged surface density is:

$E = \dfrac{\sigma }{{2{\varepsilon _0}}}$

E is independent of r, the distance of the point from the sheet.

• Electric field due to two thin infinite parallel sheets of equal and opposite charges:

Electric field due to two thin infinite parallel sheets of uniform surface density is given as follows:

• At a point anywhere in the space between the two sheets

$E = \dfrac{\sigma }{{{\varepsilon _0}}}$

• At points outside the sheets, E = 0.

Points to Remember:

• Charge is the property associated with matter due to which it produces and experiences electrical and magnetic effects. The excess or deficiency of electrons in a body gives the concept of charge.

• Charge is a scalar quantity.

• Charge is transferable

• Charge is always associated with mass

• Quantization of charge : Total charge on a body is always an integral multiple of a basic unit of charge denoted by e and is given by q = ne,

where n is any integer, positive or negative and e =$1.6 \times {10^{ - 19}}C$ 

• The basic unit of charge is the charge that an electron or proton carries. By convention the charge on electrons is -e (-$1.6 \times {10^{ - 19}}C$) and charge on protons is +e ($1.6 \times {10^{ - 19}}C$). 

• Additivity of charge: Total charge of a system is the algebraic sum (i.e. Sum is taken into account with proper signs) of all individual charges in the system.

• Conservation of charge: Total charge of an isolated system remains unchanged with time.

• The charge is invariant: Charge is independent of the frame of reference.

• Like charges repel each other while unlike charges attract each other.

• Methods of charging include friction, induction and conduction.

Coulomb’s law:

• It states that “The electrostatic force of interaction (repulsion or attraction) between two electric charges ${q_1}$and ${q_2}$separated by a distance R is directly proportional to the product of the charges and inversely proportional to the square of the distance between them and act along the straight line joining two charges.” 

• The ratio of Coulomb force to the gravitational force between two protons at a same distance apart is $\dfrac{{{e^2}}}{{4\pi {\varepsilon _0}G{m_P}{m_p}}} = 1.3 \times {10^{36}}$

• It states that, when a number of charges are interacting with each other, the total force on a given charge is vector sum of forces exerted on it by all other charges;

• The region surrounding a charge (or charge distribution) in which its electric effects are perceptible is called the electric field of the given charge.

• The types of charge distribution are linear and surface charge distribution.

• An electric field can be represented and so visualized by electric field lines. 

• Electric field due to a positive point charge is represented by straight lines originating from the charge.

• The electric field due to a negative point charge is represented by straight lines terminating at the charge.

• Dipole is a pair of two equal and opposite charges separated by a small distance.

• Dipole moment is a vector quantity whose magnitude is equal to the product of the magnitude of both charge and distance between the charges. i.e. $\left| {\vec p} \right|$ = q x 2a

• The SI unit of electric dipole moment is C meter and its dimensional formula is   $\left[ {{M^0}LAT} \right]$. The practical unit of electric dipole moment is debye.

• If the lines of force pass through a surface then the surface is set to have flux linked with it.

• Gauss’s Theorem: The total flux linked with a closed surface is $\frac{1}{\in }$ times the charge enclosed by the closest surface (Gaussian surface) i.e., $\oint {\vec E.d\vec s}  = \dfrac{q}{{{\varepsilon _0}}}$.

Important Formulae:

• Quantization of Charge: q = ne

• Coulomb’s Law: $F = K\dfrac{{{q_1}{q_2}}}{{{r^2}}}$

• Coulomb’s Law in Vector Form: ${{\vec F}_{21}} = K\dfrac{{{q_1}{q_2}}}{{{{\left| {{{\vec r}_1} - {{\vec r}_2}} \right|}^3}}}\left( {{{\vec r}_1} - {{\vec r}_2}} \right)$

• Superposition of Charges: \[\vec F = K{q_0}\sum\limits_{i = 1}^n {\dfrac{{{q_i}{{\vec r}_i}}}{{r_i^2}}} \]

• Electric Field: $\vec E = \mathop {\lim }\limits_{{q_0} \to 0} \dfrac{{\vec F}}{{{q_0}}} = \dfrac{{kq}}{{{r^3}}}\vec r$

• Electric Dipole: $\left| {\vec p} \right|$ = q x 2a

• At the distance r from the center of the electric dipole,  $E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{{2pr}}{{{{({r^2} - {a^2})}^2}}}$

• At the point at distance r from the center of electric dipole,

$E=\dfrac{1}{4 \pi \varepsilon_{0}} \dfrac{q r}{\left(r^{2}+a^{2}\right)^{3 / 2}}$

• The electric field intensity at point P due to an electric dipole,

$E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{p}{{{r^3}}}\sqrt {1 + 3{{\cos }^2}\theta } $

• Electric Torque: $\vec \tau  = \vec p \times \vec E$

• Gauss Law: $\oint {\vec E.d\vec s}  = \dfrac{q}{{{\varepsilon _0}}}$

• $E = \dfrac{\sigma }{{2{\varepsilon _0}}}$: Application of gauss law in an infinite plane sheet

• $E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{r^2}}}$: Electric field in a uniform thin wire

Questions:

1) The electric field at a distance \[\dfrac{{3R}}{2}\]from the centre of a charged conducting shell of radius R is E. The electric field at distance \[\dfrac{R}{2}\] is:

a) Zero b) E c) \[\dfrac{E}{2}\] d) 3E

Answer: option a) zero

Solution:

WKT: Electric field is given by: $\vec E = \mathop {\lim }\limits_{{q_0} \to 0} \dfrac{{\vec F}}{{{q_0}}} = \dfrac{{kq}}{{{r^3}}}\vec r$

Here, inside a charged conductor electric field is always zero. So that the electric field between two plates had been reduced.

Therefore, the electric field is zero.

2) An electric dipole is placed at an angle 30 degrees with electric field intensity\[2 \times {10^5}NC\]. It experiences a torque equal to 4Nm. The charge on the dipole if length of the dipole is?

(a) 8mC

(b) 2mC

(c) 19mC

(d) 10mC

Answer: option b) 2mC

Solution: 

$\theta  = {30^ \circ },E = 2 \times {10^5}NC$

$\tau  = 4Nm,l = 2cm = 0.02m$ 

q = ?

Electric torque is defined as: When an electric dipole of dipole moment $\vec p$ is placed in a uniform electric field $\vec E$, it will experience a torque and it is given by $\vec \tau  = \vec p \times \vec E$

$\tau  = pE\sin \theta $

where $\theta $ is the angle between p and E.

WKT, $\tau  = pE\sin \theta$

$q = \dfrac{\tau }{{E\sin \theta }}$

$= \dfrac{4}{{2 \times {{10}^5} \times 0.02 \times 0.5}}$

$= 2 \times {10^{ - 3}} = 2mC$

Therefore, the electric field is 2mC.

Importance of NEET Physics Electric Charges and Fields 

This chapter is one of the fundamental topics of Physics that introduces the concepts of electrical charge and electricity to the students. They will learn how electricity flows in a conductor and how an insulator opposes it. Students will also learn how a body can be charged using various means.

It will teach the properties of an electric charge and how a body retains it. It will also explain how these charges are formed and transferred from one body to the other. By using the Electric Charges and Fields notes, students will also understand the difference between static electricity and current electricity.

Various laws related to electric charge will be explained elaborately using the specific scientific derivation developed by the scientists. The mathematical explanations of these laws and principles will enable students to determine their implications.

This chapter is very important for the NEET preparation as its fundamental questions test the aptitude of students. They will be asked conceptual questions related to the prime topics of this chapter.

Benefits of Vedantu’s Physics Chapter 1 Electric Charges and Fields Notes

These notes have been prepared by the experts of Vedantu to offer a simpler explanation of all the concepts described in this chapter. You will get a concise explanation of definitions, laws, derivations, and scientific principles related to electric fields and charges to complete preparing this chapter.

You can add to your own notes on electric charges and fields by easily downloading the PDF version of these concise revision notes. Refer to these notes and make your preparation level more efficient. You can also recall what you have studied within a shorter time span by using these notes.

Develop a strong foundation of these concepts using Physics Chapter 1 Electric Charges and Fields notes and proceed to answer the sample questions given here. Learn how the experts have answered these questions accurately and develop your answering skills.

Revise this descriptive chapter and get help from the concise format of these notes to recall what you have studied in no time. Your accuracy level will increase remarkably.

Download Electric Charges and Fields NEET Notes Free PDF

Add the free PDF version of these revision notes to your study material and make your study sessions more productive. Get a quick glimpse of the entire chapter before a crucial exam and become more confident. Learn the concepts of electric charges and fields faster by checking out the YouTube lectures of the subject experts of Vedantu.

NEET Physics Revision Notes - Chapter Pages

Other Important Links