Revision Notes on Oscillations for NEET 2024

Oscillatory or Vibratory Motion:

Oscillatory motion is that motion in which a body moves to and fro or back and forth repeatedly about a fixed point (called mean position), in a definite interval of time.

In such a motion, the body is confined within well-defined limits (called extreme positions) on either side of the mean position. Thus a periodic and bounded motion of a body about a fixed point is called an oscillatory or vibratory motion.

Types of Motion:

Periodic Motion:

When a body or a moving particle repeats its motion along a definite path after regular intervals of time, its motion is said to be Periodic Motion, and the interval of time is called time or harmonic motion period (T). The path of periodic motion may be linear, circular, elliptical, or any other curve.

Oscillatory Motion:

To and Fro' type of motion is called an Oscillatory Motion. It need not be periodic and need not have fixed extreme positions. The force/torque acting in oscillatory motion (directed towards the equilibrium point) is called restoring force/torque.

Simple Harmonic Motion (SHM):

Simple harmonic motion is the motion in which the restoring force is proportional to the displacement from the mean position and opposes its increase.

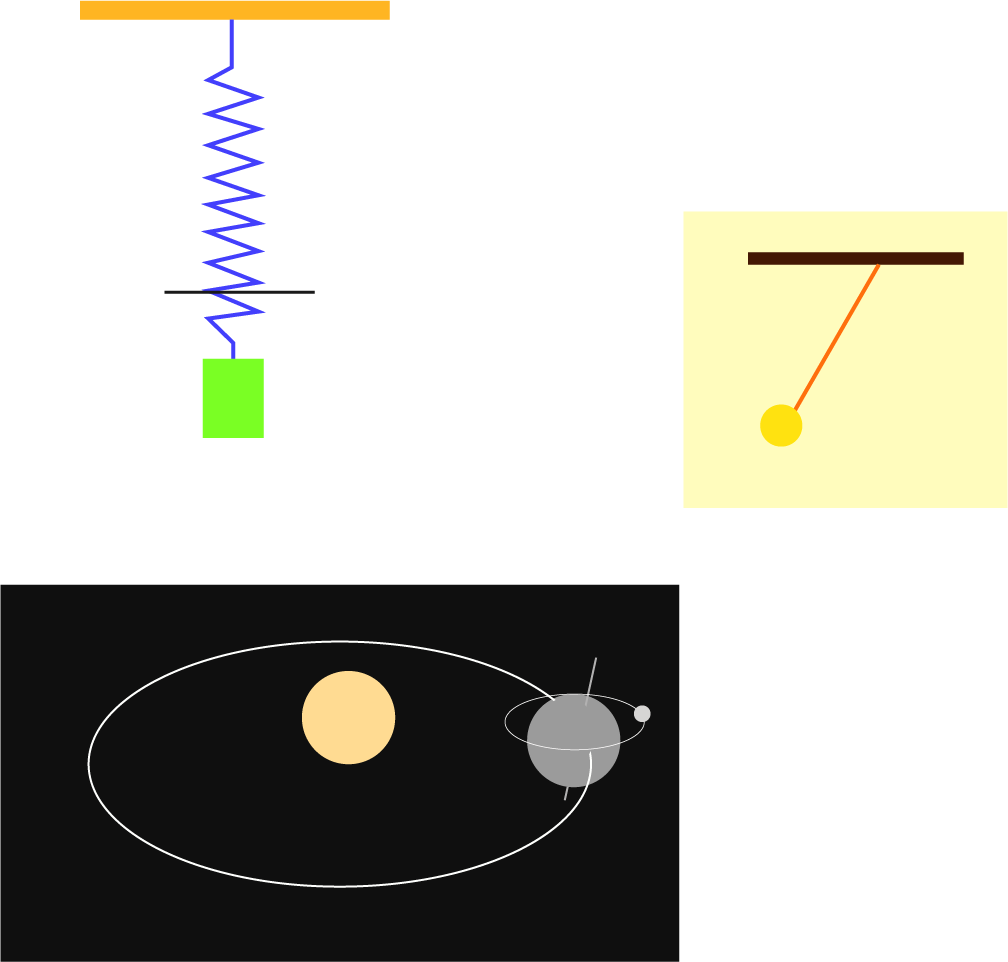
Simple Harmonic Motion

Simple Harmonic Motion (SHM):

A particle is said to move in SHM if its acceleration is proportional to the displacement and is always directed towards the mean position

Conditions of Simple Harmonic Motion:

For SHM to occur, three conditions must be satisfied.

• There must be a position of stable equilibrium

At the stable equilibrium potential energy is minimum.

So, $\dfrac{{dU}}{{dx}} = 0$ And $\dfrac{{{d^2}U}}{{d{y^2}}} > 0$

•  There must be no dissipation of energy.

•  The acceleration is proportional to the displacement and opposite in direction, that is $a =  - {\omega ^2}y$

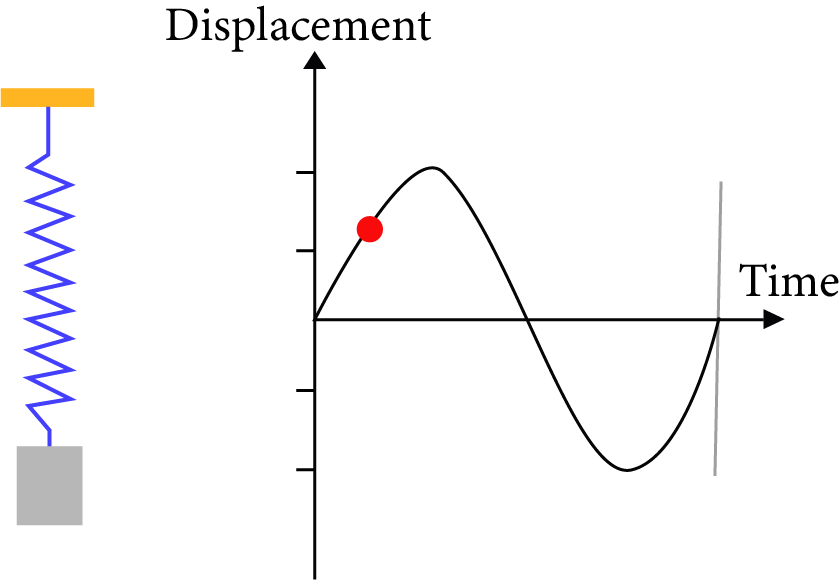
Conditions for Simple Harmonic Motion

Equation of SHM:

$f =  - ky$

$\dfrac{{{d^2}y}}{{d{t^2}}} + {\omega ^2}y = 0$

Here $\omega  = \dfrac{{\sqrt k }}{m}$ (k is the force constant)

Displacement (y):

Displacement of a particle vibrating in SHM, at any instant, is defined as its distance from the mean position at that instant.

$y = r\sin \left( {\omega t + \phi} \right)$

Here r is the radius of the circle.

Conditions

Condition:

When, $\phi=0$ , then, $y=r \sin \omega t$

and

When, $\phi=\dfrac{\pi}{2}$ , then, $y=r \cos \omega t$

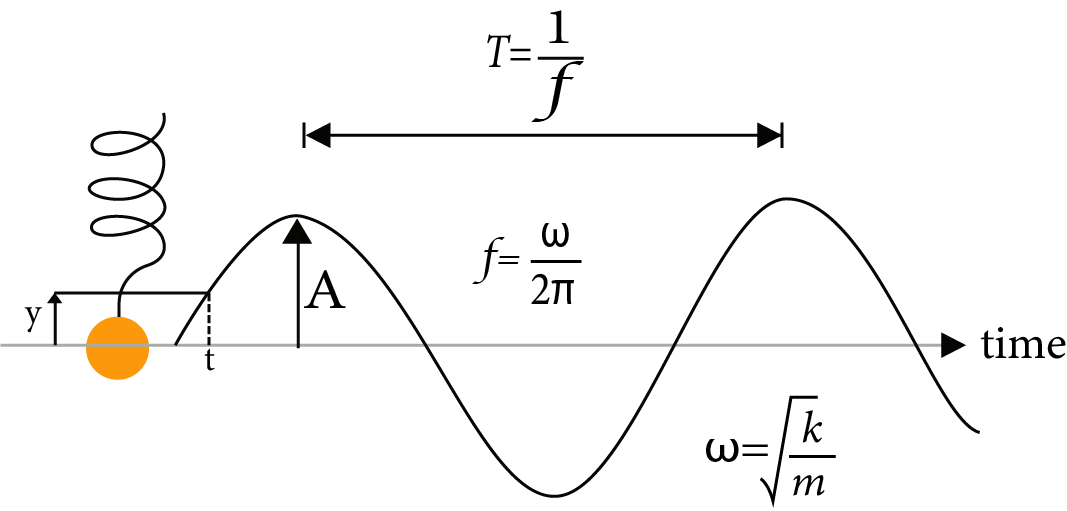
Amplitude (r):

The amplitude of a particle, vibrating in SHM, is defined as its maximum displacement on either side of the mean position. 

As the extreme value of$\omega t =  \pm 1,$thus $y =  \pm r$

Velocity (V):

$V = \dfrac{{dy}}{{dt}} = r\omega \cos \left( {\omega t + \phi} \right) = v\cos \left( {\omega t + \phi} \right) = \omega \sqrt {{r^2}}  - {y^2}$

Here v is the linear velocity of the particle. $\phi$ is any angle and t is the time.

Condition:

When, y = 0, then, V = v = rω

and

When, y = ±r, then, V=0

A particle vibrating in SHM passes with maximum velocity through the mean position and is at rest at the extreme positions.

$\dfrac{{{y^2}}}{{{r^2}}} + \dfrac{{{y^2}}}{{{\omega ^2}{r^2}}} = 1$

Acceleration 

$(a):a = \dfrac{{dV}}{{dt}} = \left( {\dfrac{{ - {v^2}}}{r}} \right)\sin \omega t =  - {\omega ^2}y$

Condition:

When, y = 0, then, a = 0

And,

When, y = ±r, then, a = ±ω2r

A particle vibrating in SHM has zero acceleration while passing through the mean position and maximum acceleration at extreme positions.

•  Acceleration is directly proportional to y (displacement).

•  Acceleration is always directed towards the mean position.  

Time period (T):

It is the time taken by the particle to complete one vibration.

$T = \dfrac{{2\pi }}{\omega }$

$\mathrm{T}=2 \pi \sqrt{\dfrac{\mathrm{displacement}}{\mathrm{acceleration}}}$

$T = \dfrac{{2\pi \sqrt m }}{k}$

Frequency (f):

It is the number of vibrations made by the body in one second.

$f = \dfrac{1}{T}$

$f = \dfrac{1}{{2\pi }}\dfrac{{\sqrt k }}{m}$

Angular frequency (ω):

$\omega  = \dfrac{{2\pi }}{T}$

${\omega}= \sqrt{\dfrac{\mathrm{acceleration}}{\mathrm{Displacement}}}$

Relation between Angular frequency (ω) and Frequency (f):

${\omega}= 2\pi f = \sqrt{\dfrac{\mathrm{k}}{\mathrm{m}}}$

Phase:

• The phase of a particle is defined as its state as regards its position and direction of motion.

•  It is measured by the fraction of time period that has elapsed since the particle crossed its mean position in the positive direction.

•  Phase can also be measured in terms of the angle, expressed as a fraction of 2π radian, traversed by the radius vector of the circle of reference while the initial position of the radius vector is taken to be that which corresponds to the instant when the particle in SHM is about to cross mean position in a positive direction.  

Energy in SHM:

(a) Kinetic Energy (Ek):

${E_k} = \dfrac{1}{2}m{\omega ^2}\left( {{r^2} - {y^2}} \right) = \dfrac{1}{2}m{\omega ^2}{r^2}co{s^2}\omega t$

When, y = 0, then,${\left( {{E_k}} \right)_{\max }} = \dfrac{1}{2}m{\omega ^2}{r^2}$ ( maximum)

and

when $y =  \pm r$, then ,${\left( {{E_k}} \right)_{\min }} = 0$ (minimum)

(b) Potential Energy (Ep):

${E_p} = \dfrac{1}{2}m{\omega ^2}{r^2} = \dfrac{1}{2}m{\omega ^2}{r^2}si{n^2}\omega t$

${({E_p})_{max}} = {\text{ }}\dfrac{1}{2}m{\omega ^2}{r^2}$ 

(c)Total Energy (E):

$E = {E_k} + {E_p} = \dfrac{1}{2}m{\omega ^2}{r^2}$  = consereved

$E = {\text{ }}{({E_k})_{max}} = {({E_p})_{max}}$ 

Average Kinetic Energy:

$< {E_k} > {\text{ }} = \left( {\dfrac{1}{4}} \right)m{\omega ^2}{r^2}$

Average Potential Energy:

$< {E_p} > {\text{ }} = \left( {\dfrac{1}{4}} \right)m{\omega ^2}{r^2}$ 

$< E/2 > {\text{ }} =  < {E_k} > {\text{ }} =  < {E_p} >$ 

Spring-Mass System: $mg = k{x_0}$ 

Period,$T = 2\pi \dfrac{{\sqrt m }}{k} = 2\pi \dfrac{{\sqrt {{x_0}} }}{g}$

Massive Spring:

Period, $T = {\text{ }}2\pi \surd [m + ({m_s}/3)]/k$ 

Cutting a Spring:

Time,$T' = \dfrac{{{T_0}}}{{\sqrt n }}$

Frequency, f' = \[ \sqrt{n} \] f₀

Spring constant, k' = nk 

If spring is cut into two pieces of length l₁ and l₂ such that, l₁= nl₂, then,

${k_1} = \left( {\dfrac{{n + 1}}{n}} \right)k,$

${k_2} = \left( {n + 1} \right)k$

and

${k_1}{l_1} = {k_2}{l_2}$

Spring in Parallel Connection:

Total  spring constant,$k = {k_1} + {k_2}$  

Time period, $T = {\text{ }}2\pi \surd [m/({k_1} + {k_2})]$ 

If ${T_1} = {\text{ }}2\pi \surd m/{k_1}$  and ${T_2} = {\text{ }}2\pi \surd m/{k_2}$  then 

$T = {T_1}{T_2}/\surd {T_1}^2 + {T_1}^2$ and ${\omega ^2} = {\omega _1}^2 + {\omega _2}^2$ 

Spring in Series Connection:

Total  spring constant, $\dfrac{1}{k} = \dfrac{1}{{{k_1}}} + \dfrac{1}{{{k_2}}}$or $k = \dfrac{{{k_1}{k_2}}}{{{k_1} + {k_2}}}$

Time period,${T^2} = {T_1}^2 + {T_2}^2$ 

$T = {\text{ }}2\pi \surd [m({k_1} + {k_2})/{k_1}{k_2}]$ 

$\dfrac{1}{{{\omega ^2}}} = \dfrac{1}{{\omega _1^2}} + \dfrac{1}{{\omega _2^2}}$

$f{\text{ }} = 1/2\pi {\text{ }}\surd [{k_1}{k_2}/m({k_1} + {k_2})]{\text{ }}$ 

Laws of the Simple Pendulum:

Laws of Isochronisms: Its states that (≤ 4^o), the time period of a simple pendulum is independent of its amplitude.

Laws of Length: It states that the time period of a simple pendulum varies directly as the square root of its length.

$T \propto \surd l$ 

Law of acceleration due to gravity:- It states that the time period of a simple pendulum varies inversely as the square root of acceleration due to gravity at that place.

$T \propto 1/\surd g$ 

So, the Time period of a simple pendulum $T = {\text{ }}{\mathbf{2\pi }}\surd l/g$ 

• When placed inside a lift being accelerated upwards, the effective value of g increases. Thus the time period of the pendulum decreases.

•  When placed inside a lift being accelerated downwards, the effective value of g decreases. Thus the time period of the pendulum increases.

•  The time period of the pendulum increases at higher altitudes due to a decrease in g.

•  The period of the pendulum at a place below the surface of the earth decreases due to an increase in g.

•  At the center of the earth (g = 0). So the period is infinite.

•  The time period is greater at the equator than at the poles.

•  Due to a decrease in the value of g due to the rotation of the earth, the period of the pendulum increases as the earth rotates about its axis.                                       

Equation of Motion:

$\dfrac{{{d^2}\theta }}{{d{t^2}}} + \left( {\dfrac{g}{l}} \right)\theta  = 0$

Frequency,

$f{\text{ }} = 1/2\pi {\text{ }}\surd (g/l)$ 

Angular frequency, 

$\omega  = \surd (g/l)$

Second Pendulum: A second’s pendulum is a pendulum whose time period is two seconds.

T = 2 sec

l = 0.9925 m  

Mass-less loaded spring in the horizontal alignment:

Force, F = -kx

Acceleration, a = -kx/m

Time period, T = 2π \[ \sqrt{\frac{m}{k}} \]

Frequency, f = 1 / 2π \[ \sqrt{\frac{m}{k}} \] 

The Time Period of Mass-less Loaded Spring in the Vertical Alignment:

$T{\text{ }} = {\text{ }}2\pi \surd m/k{\text{ }}and{\text{ }}T{\text{ }} = {\text{ }}2\pi \surd l/g$ 

The time period of the bar pendulum:

$T= 2 \pi \sqrt{\dfrac{I}{mgI}}$

Here l is the rotational inertia of the pendulum.

and

$T= 2 \pi \sqrt{\dfrac{L}{g}}$

Here, L = ( \[ \frac{k^{2}}{I} \] + I )

The Time Period of the Torsion Pendulum:

•  $T= 2 \pi \sqrt{\dfrac{I}{C}}$

• Here I is the rotational inertia of the pendulum and C is the restoring couple per unit angular twist. 

• Equation of motion:- $\dfrac{\mathrm{d}^{2} \theta}{\mathrm{dt}^{2}}+\dfrac{C}{I}\theta=0$

• Here, $\theta=\theta_{0} \sin (\omega t+\phi)$

• Angular frequency, $\omega=\sqrt{\dfrac{C}{I}}$

• Frequency, $f=\dfrac{1}{2} \pi \sqrt{\dfrac{C}{I}}$

Conical Pendulum:

Time period,$T = {\text{ }}2\pi \sqrt {\dfrac{{Lcos\theta }}{g}}$ 

Velocity, V$= \sqrt {gRtan\theta } {\text{ }}$ 

Restoring couple (τ) : $\tau  = c\theta$ 

Here C is the restoring couple per unit angular twist and θ is the twist produced in the wire.

The liquid contained in a U-tube:

Time period, $T = 2\pi \dfrac{{\sqrt l }}{g}$ 

Electrical Oscillating Circuit:

Time period, T =2π \[ \sqrt{LC} \]

Here, L is the inductance and C is the capacitance.

Angular frequency, $\omega  = \dfrac{1}{{\sqrt {LC} }}$

Ball in a bowl: Time period, $T = {\text{ }}2\pi \sqrt {\left[ {\dfrac{{R - r}}{g}} \right]}$

Free Vibrations:

A body's vibrations are termed free vibrations if it vibrates in the absence of any constraint.

Damped Vibrations:

Equation is $\dfrac{{{d^2}y}}{{d{t^2}}} + 2\mu \dfrac{{dy}}{{dt}} + {\omega ^2}y = 0$

Here amplitude, $R= Ae^{-\mu t}$

And

$\omega ’ = \sqrt{{\omega}^2 - {\mu}^2}$  

µ << ω signifies the body will show oscillatory behavior with gradually decreasing amplitude.

• µ >> ω signifies the amplitude may decrease from maximum to zero without showing the oscillatory behavior.

• In between the above two cases, the body is in the state of critically damped.

• Time period of oscillation, $T’ = \dfrac{2 \pi}{\omega}’ = \dfrac{2 \pi}{\sqrt{{\omega}^2 - {\mu}^2}}$. Thus, the presence of the damping factor µ in the denominator indicates an increase in the time period due to damping.  

Forced Vibrations:

Forced vibrations are the phenomenon of setting a body into vibrations by a strong periodic force whose frequency differs from the body's natural frequency.

Resonance: Resonance is the phenomenon of setting a body into vibrations by a strong periodic force whose frequency coincides with the natural frequency of the body.

Examples:

Q1. If the length of second pendulum is increased by $21 \%$. How many oscillations it will lose per day

(A) 3927

(B) 3722

(C) 34273

(D) None of these

Ans: 

$\mathrm{T} \propto \sqrt{\ell}$

$\dfrac{\mathrm{T}_{2}}{\mathrm{~T}_{1}}=\sqrt{\dfrac{\ell_{2}}{\ell_{1}}}$

$\Rightarrow \mathrm{T}_{2}=1.1, \mathrm{~T}_{1}=2.2 \mathrm{sec}$

Initial no. of oscillation $=\dfrac{86400}{2}=43200$ 

Final no. of oscillation $=\dfrac{86400}{2.2}=39273$

No. of lost oscillations $=43200-39273=3927$

Q2. A particle at the end of a spring executes simple harmonic motion with a period $t_{1}$, while the corresponding period for another spring is $\mathrm{t}_{2}$. If the period of oscillation with the two springs in series is $\mathrm{T}$, then -

(A) $\mathrm{T}=\mathrm{t}_{1}+\mathrm{t}_{2}$

(B) $\mathrm{T}^{2}=\mathrm{t}_{1}{ }^{2}+\mathrm{t}_{2}{ }^{2}$

(C) $\mathrm{T}^{-1}=\mathrm{t}_{1}^{-1}+\mathrm{t}_{2}^{-1}$

(D) $\mathrm{T}^{-2}=\mathrm{t}_{1}^{-2}+\mathrm{t}_{2}^{-2}$

Ans: B

$\mathrm{t}_{1} =2 \pi \sqrt{\dfrac{\mathrm{m}}{\mathrm{k}_{1}}}\ldots(\mathrm{i})$

$\mathrm{t}_{2} =2 \pi \sqrt{\dfrac{\mathrm{m}}{\mathrm{k}_{2}}}$

when springs are in series then

$\mathrm{T}=2 \pi \sqrt{\dfrac{\mathrm{m}}{\dfrac{\mathrm{k}_{1} \mathrm{k}_{2}}{\mathrm{k}_{1}+\mathrm{k}_{2}}}}=2 \pi \sqrt{\dfrac{\mathrm{m}\left(\mathrm{k}_{1}+\mathrm{k}_{2}\right)}{\mathrm{k}_{1} \mathrm{k}_{2}}}$

squaring and adding (i) and (ii) we get

$\mathrm{t}_{1}^{2}+\mathrm{t}_{2}^{2}=4 \pi^{2} \dfrac{\mathrm{m}}{\mathrm{k}_{1}}+4 \pi^{2} \dfrac{\mathrm{m}}{\mathrm{k}_{2}}$

$=4 \pi^{2} \mathrm{~m}\left(\dfrac{\mathrm{k}_{1}+\mathrm{k}_{2}}{\mathrm{k}_{1} \mathrm{k}_{2}}\right) \quad \text { or } \quad \mathrm{t}_{1}^{2}+\mathrm{t}_{2}^{2}=\mathrm{T}^{2}$

Important Formulas:

Points to Remember:

1. From this chapter lots of questions are aksed based on the numerical basis, so while solving such numerical we should take care of calculation part.

2. This oscillations chapter is a scoring chapter in terms of NEET exam. So if formula and concept is good, you can easily score full marks from this chapter.

3. Some of the important topics are Simple pendulum (Period), Damped Force, Equation of damped S.H.M, Angular frequency of damped oscillation, Time period of damped oscillation.

4. In formulas $\phi$ and $\omega$ are used at most places, so we should avoid such confusions where $\phi$ and $\omega$ will come.

5. Concept of spring mass system is also required to understand this chapter more clearly. 

Importance of Physics Oscillations

As mentioned earlier, this chapter in the NEET Physics syllabus explains how an object performs an oscillatory motion. It also explains the difference between oscillations and other periodic motions.

It will explain the harmony in an oscillatory motion that can be tracked and expressed using mathematical tools. In the same context, simple harmonic motion and period motions can also be expressed using particular formulas. Hence, this chapter is important as it explains how an oscillatory motion is different from the rest and how the formulas can be derived.

This chapter will also explain how a stable equilibrium can be achieved in simple harmonic motion and oscillations. The use of derivatives will help students understand how no dissipation of energy can enable a body to achieve a stable equilibrium.

One of the most challenging parts of oscillations is to determine the displacement of an object within a particular time period. It will lead to the calculation of the instantaneous velocity of an object performing an oscillatory motion. Here, the displacement of an oscillating body can be traced in a graph to find out the amplitude, velocity, time period, and frequency at any given condition.

To understand these scientific principles related to oscillatory motion, prefer using the Oscillation notes prepared by the Vedantu experts. This chapter explains the different types of energies in an oscillating body and how to calculate those using particular formulas.

Benefits of Vedantu’s Oscillation NEET Notes

These revision notes have been compiled with the sole purpose of offering an easier version of the scientific principles, definitions, derivations, and formulas of the terms mentioned in this chapter. You will be able to revise this chapter faster using these notes and complete the Physics NEET syllabus before the exam.

Understand the advanced concepts of motion in this chapter. Oscillations are not similar to rectilinear motion or velocity and their formulas are different too. Hence, students will need an easier explanation of these concepts. Worry not as the revision notes will offer the perfect explanation of all these concepts in a proper format.

This convenient format of the Oscillation NEET notes will enable you to complete and recall the meaningful terms related to the scientific theories and principles of this chapter. You will easily remember the formulas and accurately solve problems without facing any difficulty.

Download Oscillations Class 11 Notes PDF

Get the free PDF version of the NEET Oscillations note and complete your study material. Focus on how the experts have explained the prime topics of this chapter and get a good medium to revise it. Use the simpler version and format of these notes to recall the topics at the right time and save a lot of your time during the competitive exam.

Other Important Links

NEET Physics Revision Notes - Chapter Pages