NEET Revision Notes for Class 11 Physics Motion in a Plane

Vectors:

The physical quantities with both magnitudes and direction are known as vector quantities or vectors.

Example: force, velocity etc.

Representation of a vector: 

A vector is represented by a straight line with an arrowhead on it. The length of the line represents the magnitude of a vector and the arrowhead tells the direction of the vector.

Types of vectors:

• Polar vectors: A polar vector involves a displacement or virtual displacement Example: velocity, force etc.

• Axial vectors or Pseudo vectors: A pseudo vector or axial vector involves the orientation of an axis in space.

            Example: angular velocity, torque, angular momentum, etc.

• Equal vectors: Two vectors are said to be equal if they have the same magnitude and direction regardless of their initial position.

• Negative vector: It is a vector having the same magnitude but direction opposite to that of a given vector.

• Unlike vectors: Two vectors whose magnitude and direction are different are called unlike vectors.

• Orthogonal vectors: Two vectors are said to be orthogonal if they are perpendicular to each other

• Null vector: It is a vector whose magnitude is zero but its direction is not defined.

• Properties of a null vector:

$\vec A + \vec 0 = \vec A$ 

$\lambda \vec 0 = \vec 0$  Were λ is a scalar.

$\vec 0\vec A = \vec 0$

• Unit vector: A vector having magnitude equal to unity. To find the unit vector in the direction A, we divide the given vector by its magnitude.

            Formula for unit vector: $\hat A = \dfrac{{\vec A}}{{\left| {\vec A} \right|}}$

• Co-initial vectors: The vectors are said to be co-initial, if there initial point is common.

• Collinear vectors: These are those vectors which are having equal or unequal magnitudes and are acting along the parallel straight lines.

• Coplanar vectors: These are those vectors which are acting in the same plane.

LAWS OF VECTOR ALGEBRA:

 If $\vec A$, $\vec B$ and $\vec C$ are Vectors, and m and n are scalars, then

• Commutative law of addition

$\vec A + \vec B = \vec B + \vec A$ 

• Associative law of multiplication

$m(n\vec A) = (mn)\vec A = n(m\vec A)$

• Distributive law

$(m + n)\vec A = m\vec A + n\vec A$

$m(\vec A + \vec B) = m\vec A + m\vec B$

Triangle law of vector addition: 

It states that if two vectors can be represented both in magnitude and direction by the two sides of a triangle taken in the same order, then the resultant is represented completely (both in magnitude and direction) by the third side of the triangle taken in the opposite order.

R is the resultant of $\vec A$ and $\vec B$ then:

$R = \sqrt {{A^2} + {B^2} + 2AB{{\cos }^{}}\theta }$

$\tan \beta  = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$

Parallelogram law of vector addition: 

It states that if two vectors acting simultaneously at a point can be represented both in magnitude and direction by the two adjacent sides of a parallelogram, then the resultant is represented completely (both in magnitude and direction) by the diagonal of the parallelogram passing through that point.

If $\vec R$ is the resultant of $\vec A$ and $\vec B$ then,

$R = \sqrt {{A^2} + {B^2} + 2AB{{\cos }^{}}\theta } $ 

$\tan \beta  = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$

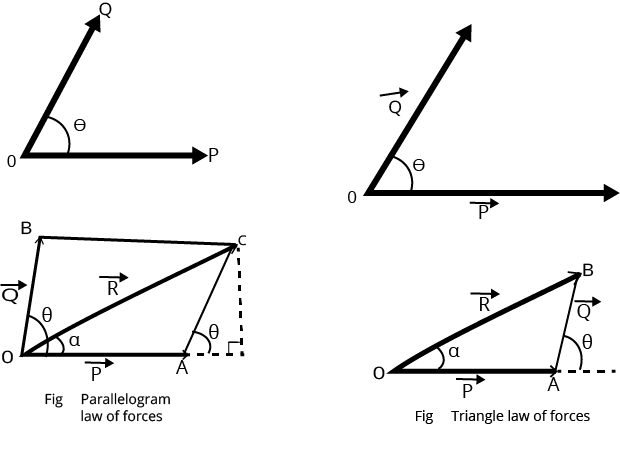
Parallelogram and Triangular Law of Vector Addition

Polygon law of vector addition: 

It states that if a number of vectors can be represented both in magnitude and direction by the sides of a Polygon taken in the same order, then their resultant is represented (both in magnitude and direction) by the closing side of the Polygon takes in the opposite order.

Rectangular component of a vector in a plane: 

When a vector is spitted into two component vectors at right angles to each other, the component vectors are called rectangular components of a vector. If A makes an angle with X-axis, and A and A be the rectangular components of A along X-axis respectively, then

$\vec A = {A_x}\hat i + {A_y}\hat j$

Here

${A_x} = A\cos \theta $ and ${A_y} = A\sin \theta $.

$\therefore $ ${A_x}^2 +{A_y}^2 = {A^2}({\cos ^2}\theta  + si{n^2}\theta )$

Or 

$A = \sqrt {{A_x}^2 +{A_y}^2 }$ and  $\tan \theta  = \dfrac{{{A_y}}}{{{A_x}}}$

Resolution of a vector in a space: 

Let α, β, and γ are the angles between $\vec A$  and the x, y and z-axis, respectively as shown in the figure, then

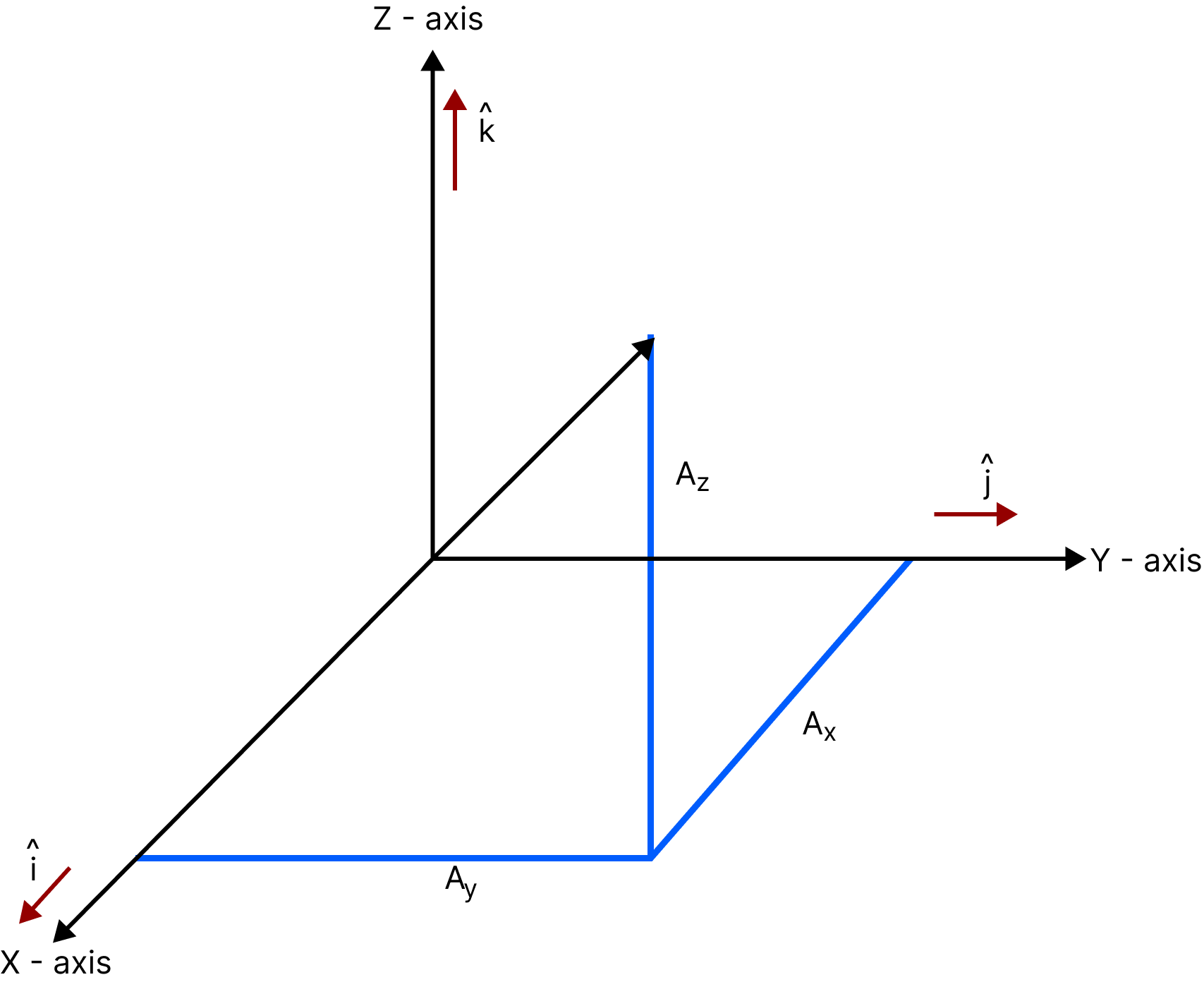
Image Showing how a Vector is Resolved

${\vec A_x} = A\cos \alpha $, ${\vec A_y} = A\cos \beta $, ${\vec A_z} = A\cos \gamma $

In general, we have $\vec A = {A_x}\hat i + {A_y}\hat j + {A_z}\hat k$

The magnitude of $\vec A$ is

$\vec A = \sqrt {A_x^2 + A_y^2 + A_z^2} $

Dot or scalar product of two vectors:

The dot or scalar product of two vectors $\vec A$and $\vec B$denoted by $\vec A.\vec B$(read $\vec A$ and$\vec B$) is defined as the product of the magnitude of $\vec A$ and $\vec B$ and the cosine of the angle between them. In symbols,$\vec A.\vec B = AB\cos \theta $,     0≤θ≤π where $\vec A.\vec B$ is a scalar and not a vector.

Properties of dot product:

• $\vec A.\vec B = \vec B.\vec A$

• $\vec A.(\vec B + \vec C) = \vec A.\vec B + \vec A.\vec C$

• $m(\vec A.\vec B) = (m\vec A).\vec B = \vec A.(m\vec B) = (\vec A.\vec B)m$, where m is a scalar.

• $\hat i.\hat j = \hat j.\hat i = \hat k.\hat k = 1,\hat i.\hat j = \hat j.\hat k = \hat k.\hat i = 0$

• If $\vec A = {A_1}\hat i + {A_2}\hat j + {A_3}\hat k$ and $\vec B = {B_1}\hat i + {B_2}\hat j + {B_3}\hat k$ then,

• $\vec A.\vec B = {A_1}{B_1} + {A_2}{B_2} + {A_3}{B_3}$

• $\vec A.\vec A = {A^2} ={A_1}^2 +{A_2}^2 +{A_3}^2$

• $\vec B.\vec B = {B^2} ={B_1}^2 +{B_2}^2 +{B_3}^2$

• If $\vec A.\vec B$=0 and $\vec A$ and $\vec B$ are not null vectors, then $\vec A$ and $\vec B$  are perpendicular.

Cross or Vector Product of two vectors:

The cross or vector product of $\vec A$ and $\vec B$is a vector $\vec C = \vec A \times \vec B$(read $\vec A$ cross$\vec B$). The magnitude of $\vec A \times \vec B$ is defined as the product of the magnitude of $\vec A$ and $\vec B$ and $\vec B$ the sine of the angle between them. 

The direction of the vector $\vec C = \vec A \times \vec B$ is perpendicular to the plane containing $\vec A$ and $\vec B$ and such that$\vec A$, $\vec B$ and $\vec C$ form a right-handed system. In symbol,$\vec A \times \vec B = AB\sin \theta \hat n$ , 0≤θ≤π where $\hat n$ is a unit vector indicating the direction of $\vec A \times \vec B$.

Examples of vector product:

• Torque    $(\vec \tau ) = \vec r \times \vec F$

• Angular momentum   $(\vec L) = \vec r \times \vec p$

• Velocity  $(\vec V) = \vec \omega  \times \vec r$

• Acceleration   $(\vec a) = \vec \alpha  \times \vec r$

Here $\vec r$ is position vector or radius vector and $\vec F$,$\vec p$,$\vec \omega$ and $\vec \alpha $ are force, linear momentum, angular velocity and angular acceleration respectively.

Properties of vector product:

• $\vec A \times \vec B =  - \vec B \times \vec A$

• $\vec A \times (\vec B + \vec C) = \vec A \times \vec B + \vec A \times \vec C$

• $m(\vec A \times \vec B) = (m\vec A) \times \vec B = \vec A \times (m\vec B) = (\vec A \times \vec B)m$, where m is a scalar.

• $\hat i \times \hat j = \hat j \times \hat i = \hat k \times \hat k = 0,\hat i \times \hat j = \hat k,\hat j \times \hat k = \hat i,\hat k \times \hat i = \hat j$

• If $\vec A = {A_1}\hat i + {A_2}\hat j + {A_3}\hat k$ and $\vec B = {B_1}\hat i + {B_2}\hat j + {B_3}\hat k$, then $\overrightarrow A  \times \overrightarrow B  = \left[{\begin{array}{*{20}{c}}i&j&k \\{{A_1}}&{{A_2}}&{{A_3}} \\{{B_1}}&{{B_2}}&{{B_3}}\end{array}} \right]$ 

• A $= \dfrac{1}{2}\left| {\vec A \times \vec B} \right|\therefore $= the area of a triangle with sides $\vec A$ and$\vec B$.

• If $\vec A \times \vec B = 0$ and $\vec A$ and $\vec B$ are not null vectors, then $\vec A$ and $\vec B$are parallel.

Area of ΔPOQ $= \dfrac{{base \times height}}{2}$

$= \dfrac{{A \times B\sin \theta }}{2}$

$= \dfrac{1}{2}\left| {\vec A \times \vec B} \right|$

$\therefore$ Area of parallelogram OPRQ = 2[area of ΔOPQ]

$= \left| {\vec A \times \vec B} \right|$

Lami’s theorem:

When three forces acting at a point are in equilibrium, then force is proportional to the sine of the angle between the other two forces. 

Mathematically: 

$\dfrac{A}{\sin \alpha}=\dfrac{B}{\sin \beta}=\dfrac{C}{\sin \theta}$

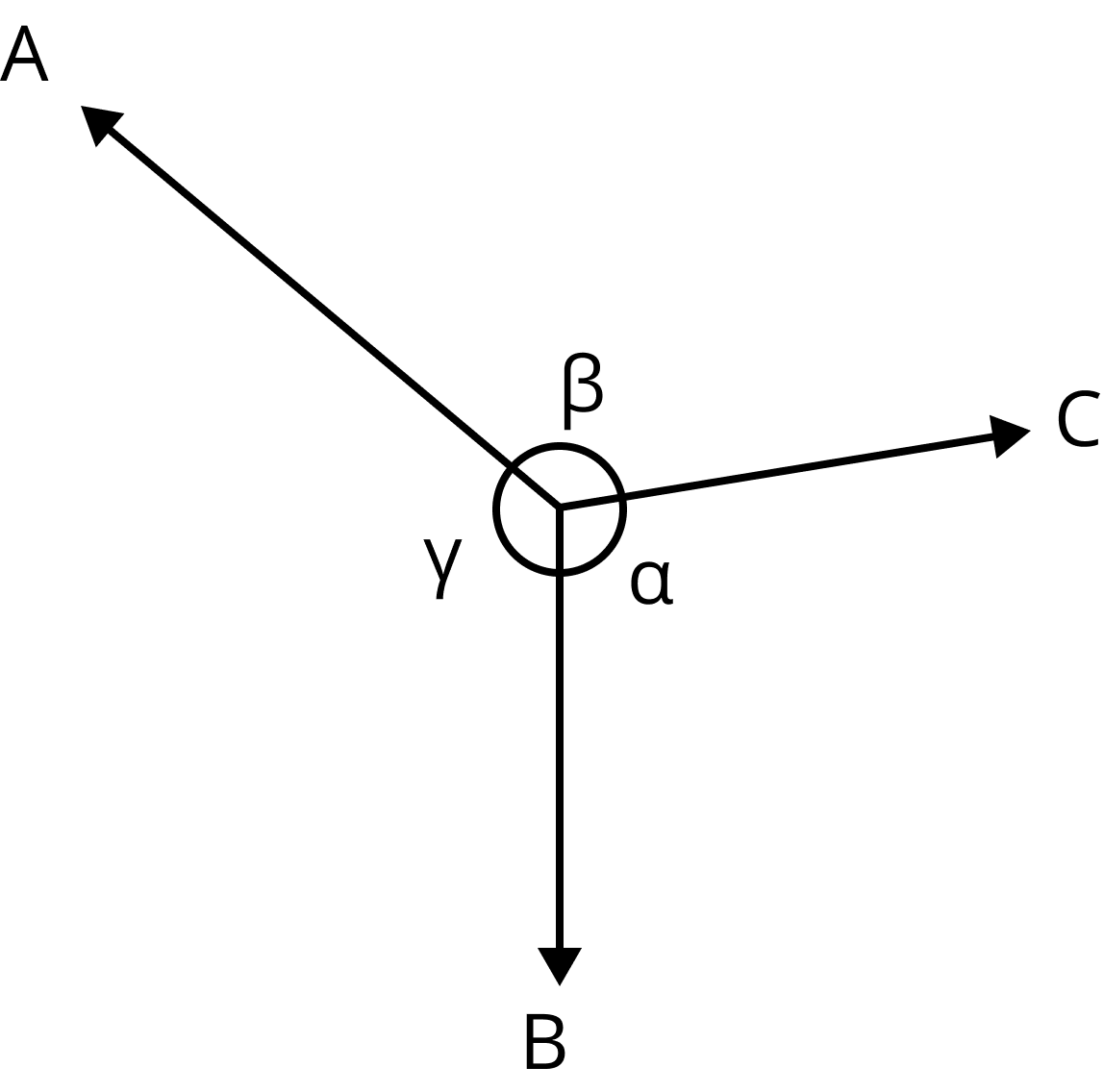
Lami’s Theorem

RELATIVE MOTION:

• There is no meaning of motion without reference or observer. If reference is not mentioned then we take the ground as a reference of motion. 

• Velocity or displacement of the particle w.r.t. the ground is called actual velocity or actual displacement of the body. 

• If we describe the motion of a particle w.r.t. an object which is also moving w.r.t ground then the velocity of particle w.r.t ground is its actual velocity( ${\vec \nu _{act}}$ ) and velocity of the particle w.r.t. moving object is its relative velocity ( ${\vec \nu _{rel}}$ ) and the velocity of moving object (w.r.t. ground) is the reference velocity ( ${\vec \nu _{ref}}$ ). 

According to vector law of addition relative displacement is:  ${\vec r_{ps}} = {\vec r_{ps'}} + {\vec r_{s's}}$ 

Differentiating the equation w.r.t. time, we get

$\dfrac{{{{\vec r}_{ps}}}}{{dt}} = \dfrac{{{{\vec r}_{ps'}}}}{{dt}} + \dfrac{{{{\vec r}_{s's}}}}{{dt}}$ 

So that,  ${\overrightarrow v _{ps}} = {\overrightarrow v _{ps'}} + {\overrightarrow v _{s's}}$  

Differentiating again, we get ${\vec a_{ps}} = {\vec a_{ps'}} + {\vec a_{s's}}$ .

SHORTCUT FORMULAS:

• Relative velocity of a body A with respect to body B, when they are moving  in the same direction is given by

                                          ${\vec \nu _{AB}} = {\vec \nu _A} - {\vec \nu _B}$ .

• Relative velocity of a body A with respect to body B when they are moving in the opposite direction is given by

${\vec \nu _{AB}} = {\vec \nu _A} - {\vec \nu _B}$ .

$\tan \beta  = \dfrac{{({\nu _B})\sin ({{180}^0} - \theta )}}{{({\nu _A}) + ({\nu _B})\cos ({{180}^0} - \theta )}} = \dfrac{{{\nu _B}\sin \theta }}{{{\nu _A} + {\nu _B}\cos \theta }}$ 

Rain man problem: 

If rain is falling vertically with a velocity  ${\vec \nu _r}$ and a man is moving horizontally with speed ${\vec \nu _m}$ , the man can protect himself from the rain if he holds his umbrella in the direction of relative velocity of rain w.r.t. man. If θ is the angle which the direction of relative velocity of rain w.r.t. man makes with the vertical, then  $\tan \theta  = \dfrac{{{\nu _m}}}{{{\nu _r}}}$ 

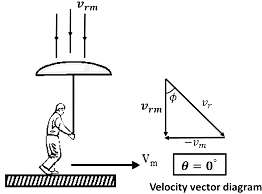
Rain-man Issue

Boat-river problem: 

Let  ${\vec \nu _1}$  = velocity of boat in still water,  ${\vec \nu _2}$  = velocity of flow of water in river, d = width of river.

The cross the river in the shortest path: 

Here it is required that the boat starting from A must reach the opposite point B along the shortest path AB. For the shortest path, the boat should be rowed upstream making an angle θ with AB such that AB gives the direction of resultant velocity.

So,   $\sin \theta  = \dfrac{{{\nu _2}}}{{{\nu _1}}}$ 

And    ${\vec \nu _{}} = {\vec \nu _1} - {\vec \nu _2}$ 

Also,   $t = \dfrac{d}{{{\nu _{}}}} = \dfrac{d}{{\sqrt {\nu _1^2 - \nu } _2^2}}$  

To cross the river in the shortest time: 

For the boat to cross the river in the shortest time, the boat should be directed along AB. Let ν be the resultant velocity making an angle θ with AB. 

Then  $\tan \theta  = \dfrac{{{\nu _2}}}{{{\nu _1}}}$  and $\nu _{}^2 = \nu _1^2 + \nu _2^2$ . 

Time of crossing:  $t = \dfrac{d}{{{\nu _1}}}$ .

Now the boat reaches the point C rather than reaching point B.

If BC = x, then

$\tan \theta  = \dfrac{{{\nu _2}}}{{{\nu _1}}} = \dfrac{x}{d}$ 

$x = d \times \left( {\dfrac{{{\nu _2}}}{{{\nu _1}}}} \right)$ 

If a man travels downstream in a river, then the time taken by the man to cover a distance d is ${t_1} = \dfrac{d}{{{\nu _1} + {\nu _2}}}$ . If a man swims upstream in a river, then the time taken by him to cover a distance d is  ${t_1} = \dfrac{d}{{{\nu _1} - {\nu _2}}}$ and thus:  

$\dfrac{{{t_1}}}{{{t_2}}} = \dfrac{{{\nu _1} - {\nu _2}}}{{{\nu _1} + {\nu _2}}}$ .

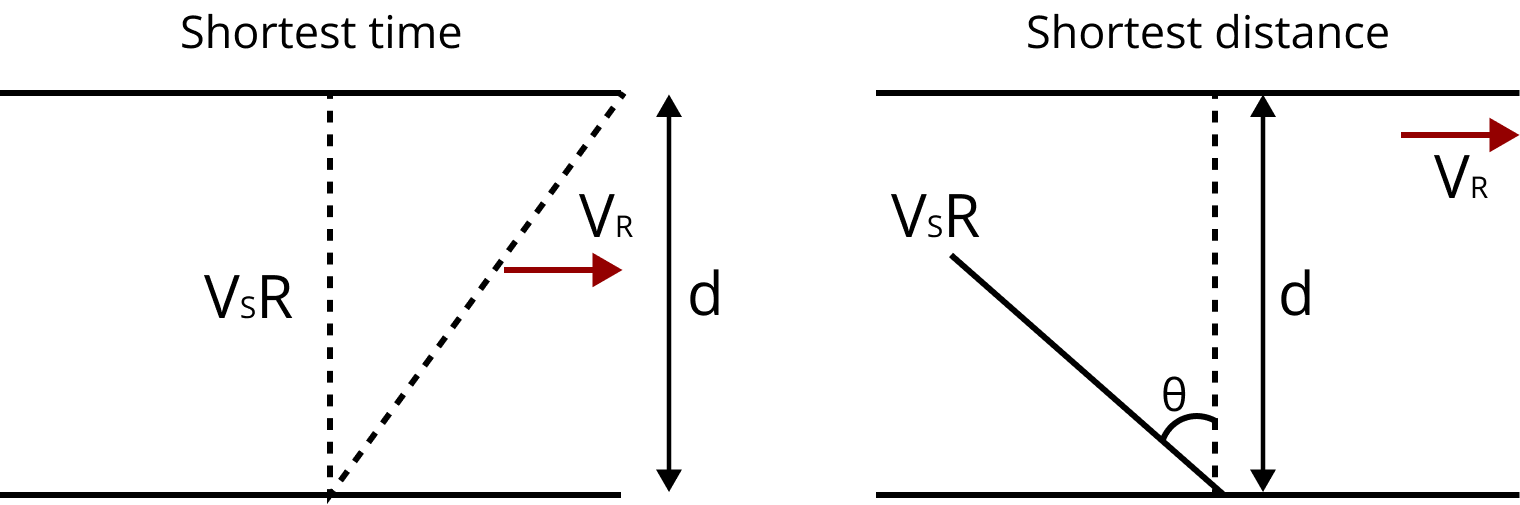
Boat Problem

PROJECTILE:

Any body given an initial velocity moves freely in space under the influence of gravity is called a projectile.

Example: 

A javelin thrown by an athlete and a ball kicked from the ground. 

The path followed by a projectile is called its trajectory. Trajectory of a projectile is a parabola. Projectile motion is a two dimensional motion.

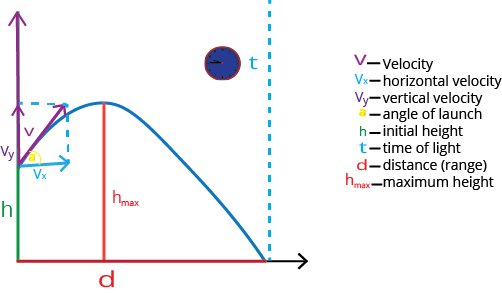
Projectile Motion with Its Parameters

Different variations and parameters in projectile motion:

A Projectile Projected Horizontally from a Height h with Velocity u:

• Time taken by the projectile to reach the ground is:  $\sqrt[{}]{{\dfrac{{2h}}{g}}}$ .

• Time taken by the projectile to reach the ground does not depend upon the velocity of projection. i.e., u.

• Horizontal range:  $x = ut = u\sqrt[{}]{{\dfrac{{2h}}{g}}}$ .

• Equation of trajectory is:  $y = \dfrac{g}{{2{u^2}}}{x^2}$ .

• Resultant velocity of the projectile at any time t is $v = \sqrt {{u^2} + {g^2}{t^2}} $ .

• Angle made by the resultant velocity with the horizontal is $\tan \beta  = \dfrac{{gt}}{u}$ .

• Velocity of the projectile on striking the ground $ = \sqrt {{u^2} + 2{g^{}}{h^{}}} $.

A Projectile Projected with Velocity u at an Angle θ with the horizontal:

• $x = u\cos \theta t$ 

• $y = u\sin \theta t - \dfrac{1}{2}g{t^2}$ 

• Equation of trajectory is $y = x\tan \theta  - \dfrac{{g{x^2}}}{{2{u^2}{{\cos }^2}\theta }}$ .

• Velocity of the projectile at any time t is $v = {\sqrt {{{\left( {u\cos \theta } \right)}^2} + {{\left( {u\sin \theta  - gt} \right)}^2}} ^{}}$ 

• $= {\sqrt {{u^2} + {g^2}{t^2} - 2gtu\sin {\theta ^{}}} ^{}}$. This velocity makes angle β with horizontal.

• $\tan \beta  = \dfrac{{u\sin \theta  - gt}}{{u\cos \theta }}$ .

• Horizontal range,  $R = \dfrac{{{u^2}\sin 2\theta }}{g}$ .

• For maximum horizontal range,  $\theta  = {45^0}$ .

• ${R_m} = \dfrac{{{u^2}}}{g}$ 

• Time of a ascent = time of descent =  $\dfrac{{u\sin \theta }}{g}$ .

• Time of flight,  $T = \dfrac{{2u\sin \theta }}{g}$ .

• Maximum height:  $H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ .

• When horizontal range is n times the maximum height, then $\tan \theta  = \dfrac{4}{n}$ .

Motion of projectile along an inclined plane:

• Range of projectile along the inclined plane is $R = \dfrac{{{u^2}}}{{g{{\cos }^2}{\theta _0}}}\left[ {\sin \left( {2\theta  - {\theta _0}} \right) - \sin {\theta _0}} \right]$ 

• Time of flight on the inclined plane is $T = \dfrac{{2u\sin \left( {\theta  - {\theta _0}} \right)}}{{g\cos {\theta _0}}}$ 

• The maximum range on inclined plane is $R = \dfrac{{{u^2}}}{{g\left( {1 + \sin {\theta _0}} \right)}}$ 

• The angle at which the horizontal range on the inclined plane becomes maximum is given as,  $\theta  = \dfrac{\pi }{4} + \dfrac{{{\theta _0}}}{2}$ .

Circular Motion

• Circular motion is a two dimensional motion.

• The motion of a body along a circular path is called as circular motion.

Angular displacement: 

The angular displacement of an object moving around a circular path is defined as the angle traced out by the radius vector at the center of the circular path in a given time. It is denoted by symbol θ.

Angular velocity: 

• Angular velocity of an object in circular motion is defined as the rate of change of its angular displacement with time. It is generally denoted by symbol ω(omega) and it is given by $\omega  = \dfrac{{d\theta }}{{dt}}$.

• SI unit of angular velocity is $rad{s^{ - 1}}$ and its dimensional formula is  $\left[ {{M^0}{L^0}{T^{ - 1}}} \right]$ .

Angular acceleration: 

Angular acceleration of an object in circular motion is defined as the rate of change of its angular velocity with time. It is generally denoted by symbol α and it is given by $\alpha  = \dfrac{{d\omega }}{{dt}}$ 

SI unit of angular acceleration is $rad{s^{ - 2}}$ and its dimensional formula is $\left[ {{M^0}{L^0}{T^{ - 2}}} \right]$ .

Uniform circular motion: 

When an object is moving on a circular path with a constant speed then the motion of an object is said to be a uniform circular motion.

• Time period: In circular motion, the time period is defined as the time taken by an object to complete one revolution on its circular path. It is generally denoted by symbol T and is expressed in second.

• Frequency: In circular motion, the frequency is defined as the number of revolutions completed by an object on its circular path in a unit time. It is generally denoted by u.

• Its unit is $S{^-1}$ or hertz (Hz).

• Relation between time and frequency $T = \dfrac{1}{\upsilon }$    Or    $\upsilon  = \dfrac{1}{T}$ 

• Relation between angular velocity, frequency and time period $\omega  = \dfrac{{2\pi }}{T} = 2\pi \upsilon$ 

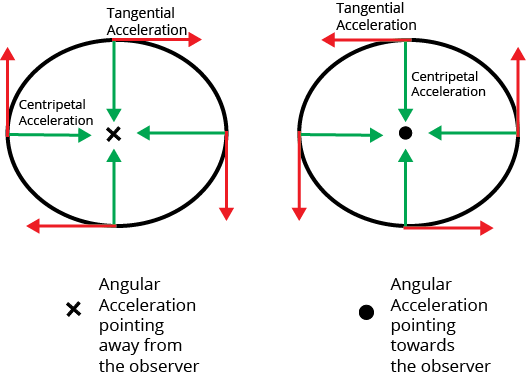
Centripetal and Tangential Acceleration

• Centripetal acceleration: Acceleration acting on an object undergoing uniform circular motion is known as centripetal acceleration. It is given by Centripetal acceleration,   ${a_c} = \dfrac{{{\upsilon ^2}}}{r} = {\omega ^2}r$ 

where r is the radius of the circle.

• Tangential acceleration : The tangential acceleration arises from the change in the speed of an object and has a magnitude given by

 ${a_t} = \dfrac{{d{{\left| {\vec \upsilon } \right|}^{}}}}{{dt}}$ 

• Radial acceleration : The radial acceleration is due to the change in direction of the velocity and is given by

 ${a_r} = \dfrac{{{\upsilon ^2}}}{r} = {\omega ^2}r$ .

Points to remember:

• Vectors: The physical quantities which have both magnitudes, as well as direction, are known as vector quantities or vectors. Example: force, velocity etc.

• Representation of a vector: a vector is represented by a straight line with an arrowhead on it. The length of the line represents the magnitude of a vector and the arrowhead tells the direction of the vector

• Types of vector are polar, non-polar, collinear, orthogonal, unit, null vectors etc… and many others.

• Vectors follow the basic laws such as commutative, associative etc…

• The cross or vector product of $\vec A$ and $\vec B$is a vector $\vec C = \vec A \times \vec B$(read $\vec A$ cross$\vec B$). 

• When three forces acting at a point are in equilibrium, then force is proportional to the sine of the angle between the other two forces is called the lamis theorem.

• Any body given an initial velocity moves freely in space under the influence of gravity is called a projectile.

• Example: A javelin thrown by an athlete and a ball kicked from the ground. 

• Using lami’s theorem and projectile motion we can solve many kinematics issues like rain-man and boat problem.

• Projectile varies according to height, angle, and along a inclined plane.

• Circular motion is a two dimensional motion.

• The motion of a body along a circular path is called as circular motion.

• Angular displacement: The angular displacement of an object moving around a circular path is defined as the angle traced out by the radius vector at the center of the circular path in a given time. It is denoted by symbol θ.

• Angular velocity: Angular velocity of an object in circular motion is defined as the rate of change of its angular displacement with time.

• Uniform circular motion: When an object is moving on a circular path with a constant speed then the motion of an object is said to be a uniform circular motion.

• Centripetal acceleration: Acceleration acting on an object undergoing uniform circular motion is known as centripetal acceleration. It is given by: Centripetal acceleration,   ${a_c} = \dfrac{{{\upsilon ^2}}}{r} = {\omega ^2}r$ where r is the radius of the circle.

• Tangential acceleration : The tangential acceleration arises from the change in the speed of an object and has a magnitude given by  ${a_t} = \dfrac{{d{{\left| {\vec \upsilon } \right|}^{}}}}{{dt}}$ 

• Radial acceleration : The radial acceleration is due to the change in direction of the velocity and is given by  ${a_r} = \dfrac{{{\upsilon ^2}}}{r} = {\omega ^2}r$ .

Numerical Examples

1. A particle moves so that its postion vector is given by $\overrightarrow r  = \cos \omega t\widehat x + \sin \omega t\widehat y$, where $\omega $is a constant. Which of the following is true? 

1. Velocity is perpendicular to $\overrightarrow r $ and acceleration is directed towards the origin

2. Velocity is perpendicular to $\overrightarrow r $ and acceleration is directed away from the origin

3. Acceleration is given by$a =  - {\omega ^2}\overrightarrow r $.

4. Velocity is directed away from origin and acceleration is equal to zero

Answer: option (a) & (c)

Complete solution:

Given, 

$\overrightarrow r  = \cos \omega t\widehat x + \sin \omega t\widehat y$

$\overrightarrow v  = \dfrac{{d\overrightarrow r }}{{dt}} =  - \omega \sin \omega t\widehat x + \omega \cos \omega t\widehat y$

$\overrightarrow a  = \dfrac{{d\overrightarrow v }}{{dt}} =  - {\omega ^2}\cos \omega t\widehat x - {\omega ^2}\sin \omega t\widehat y =  - {\omega ^2}y$ 

Thus we get 

$\overrightarrow a  =  - {\omega ^2}\overrightarrow r $.

Since the given position vector is directed away from the origin as it is a non-zero value. We have, acceleration is directed towards the origin.

Also, 

$\overrightarrow r .\overrightarrow v  = (\sin \omega t\widehat y + \cos \omega t\widehat x).( - \omega \sin \omega t\widehat x + \omega \cos \omega t\widehat y)$

$=  - \omega \sin \omega t\cos \omega t + \omega \sin \omega t\cos \omega t = 0$

$\overrightarrow r  \bot \overrightarrow v$ 

Thus, Velocity vector is perpendicular with the position vector.

2. Given a particle which is projected from a horizontal plane with a velocity of $8\sqrt 2 m{s^{ - 1}}$ at an angle x. At the highest point its velocity is found to be $8m{s^{ - 1}}$. Which of these following statements are true?

1. Angle x is $45^\circ $.

2. Horizontal range is 12.8m

3. Range is maximum at larger velocity

4. None of these values are correct.

Answer: Options (a) & (b) & (c)

Complete Solution:

At highest point, velocity of projectile is:

$v = u\cos x$

$8 = 8\sqrt 2 \cos x$

$\cos x = \dfrac{1}{{\sqrt 2 }}$

$x = 45^\circ$ 

Thus angle subtended is $45^\circ $.

$range = \dfrac{{{u^2}\sin 2\theta }}{g}$

$r = \dfrac{{{{(8\sqrt 2 )}^2}\sin (2 \times 45)}}{{10}}$

$r = \dfrac{{64 \times 2}}{{10}} = 12.8m$ 

Thus range is 12.8m.

And also it is maximum at maximum velocity as at v=8 R=6.4m.

Important formulae:

• Properties of a null vector:

1. $\vec A + \vec 0 = \vec A$ 

2. $\lambda \vec 0 = \vec 0$  Were λ is a scalar.

3. $\vec 0\vec A = \vec 0$

• Laws of Vector Algebra:

If $\vec A$, $\vec B$ and $\vec C$ are Vectors, and m and n are scalars, then

• Commutative law of addition

$\vec A + \vec B = \vec B + \vec A$ 

• Associative law of multiplication

$m(n\vec A) = (mn)\vec A = n(m\vec A)$

• Distributive law

• $(m + n)\vec A = m\vec A + n\vec A$

• $m(\vec A + \vec B) = m\vec A + m\vec B$

• Triangle law of vectors: $R = \sqrt {{A^2} + {B^2} + 2AB{{\cos }^{}}\theta } $

$\tan \beta  = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$

• Parallelogram law of vectors: If $\vec R$ is the resultant of $\vec A$ and $\vec B$ then, $R = \sqrt {{A^2} + {B^2} + 2AB{{\cos }^{}}\theta } $ 

$\tan \beta = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$

• $\vec A.\vec B = AB\cos \theta $,     0≤θ≤π for dot product

• $\vec A \times \vec B = AB\sin \theta \hat n$ , 0≤θ≤π for cross product

• Relative velocity of a body A with respect to body B, when they are moving  in the same direction is given by ${\vec \nu _{AB}} = {\vec \nu _A} - {\vec \nu _B}$ .

• Relative velocity of a body A with respect to body B when they are moving in the opposite direction is given by  

${\vec \nu _{AB}} = {\vec \nu _A} - {\vec \nu _B}$ .$\tan \beta  = \dfrac{{({\nu _B})\sin ({{180}^0} - \theta )}}{{({\nu _A}) + ({\nu _B})\cos ({{180}^0} - \theta )}} = \dfrac{{{\nu _B}\sin \theta }}{{{\nu _A} + {\nu _B}\cos \theta }}$ 

• $\tan \theta  = \dfrac{{{\nu _m}}}{{{\nu _r}}}$ for rain man problem 

• Formulas on projectiles are based on the conditions curtained above, please go through one condition and read all formulas.

• $\omega  = \dfrac{{d\theta }}{{dt}}$

• $\alpha  = \dfrac{{d\omega }}{{dt}}$ 

• ${a_c} = \dfrac{{{\upsilon ^2}}}{r} = {\omega ^2}r$ 

• ${a_r} = \dfrac{{{\upsilon ^2}}}{r} = {\omega ^2}r$ 

• ${a_t} = \dfrac{{d{{\left| {\vec \upsilon } \right|}^{}}}}{{dt}}$

Since each topic in this contains all important formulas, at least knowing at which situation to apply this formula will help in reducing the mistakes in the numerical.

Importance of NEET Physics Motion in a Plane

The Motion in a Plane chapter will explain what vectors and scalars are. You will learn how the motion of a body can be termed as a vector or a scalar quantity. In fact, you will advance to a new stage where you will gain deeper concepts related to motion in a plane. Here, the principles of coordinate geometry and trigonometry will also be used.

There are different types of vectors that students will study in this chapter. Every vector will be explained using pictorial illustrations and mathematical derivations. This chapter will also teach the basic algebraic operations followed for calculating the vectors such as addition, subtraction and multiplication. To understand these concepts, one has to be adept at using mathematical tools too.

Motion is a fundamental topic in kinematics and mechanics. This chapter holds the key to understanding the advanced concepts of other topics included in the NEET Physics syllabus. Clarifying the doubts using Motion in a Plane notes for NEET will become a crucial point for preparing this chapter.

Benefits of Vedantu’s Motion in a Plane Class 11 Notes for NEET

• These notes have been composed by the subject experts of Vedantu to offer a simpler explanation of all the concepts. It will enable you to focus on the fundamental principles of vectors and the mathematical operations done. Your conceptual foundation will become stronger when you refer to these notes during your study sessions.

• Learn from the experts how to explain the formulae of vector operations and answer questions accurately. They have described all the topics in an easier way giving you a better medium to comprehend them. Use these notes to revise and recall what you have studied and make your preparation full proof.

• Get the best description of the laws, derivations, and impressions given in this chapter. Proceed to solve the sample questions given in the exercises and learn how the experts have solved them efficiently. Increase your answering and logical reasoning skills by developing a conceptual foundation using these notes.

Download Motion in a Plane Class 11 Notes PDF

Perform Motion in a Plane notes PDF download for free and complete your study material for this important chapter. Make your NEET preparation better by seeking knowledge and clarifying doubts using the simpler explanation of the concepts from the experts. You can also get proper elaboration of the concepts from YouTube lectures of these experts on vectors and motion in a plane.

Other Important Links

NEET Physics Revision Notes - Chapter Pages