States of Matter Class 11 Notes NEET Chemistry (Free PDF Download)

Introduction:

The substance that contains mass and occupies space is known as Matter. Atoms and molecules constitute matter. It has various physical and chemical properties. Matters are classified into solid, liquid and gas. The force of interaction present in them varies which gives rise to their physical properties. Gases have the least force of interaction, while solids have the highest force of interaction.

Intermolecular Forces:

The molecules like solid, liquid or gas exhibit forces of attraction which are called intermolecular forces. Van der Waal forces are the collective of dipole-dipole, dipole-induced dipole and dispersion forces. Ion-dipole and ion-induced dipole are not Van der Waal forces. Hydrogen bonding is the strongest force of attraction.

The different types of intermolecular forces are:

1. Dipole-Dipole Interaction:

• Polar molecules exhibit dipole-dipole interactions. They have permanent dipole moments. The positive pole and negative pole are attracted in the molecule. 

• For example, ${\text{HCl}}{\text{.}}$

• In ${\text{HCl}}$ molecule, ${\text{Cl}}$ is more electronegative than hydrogen. So, the chlorine atom acquires negative charge while, hydrogen atom acquires positive charge. Thus, dipole-dipole interaction takes place among them.
  
  

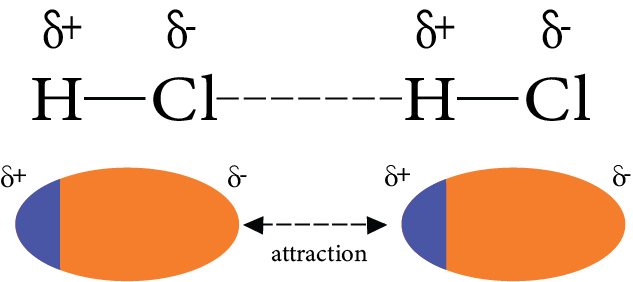
Dipole-dipole Interaction

2. Ion-Dipole Interaction:

• The attraction between the cation, anion, and a polar molecule is known as ion-dipole interaction. For example, ${\text{NaCl}}{\text{.}}$

• The polar water molecules are attracted towards ${\text{N}}{{\text{a}}^ + }$ and ${\text{C}}{{\text{l}}^ - }$ on dissolving ${\text{NaCl}}$ in water.
  
  

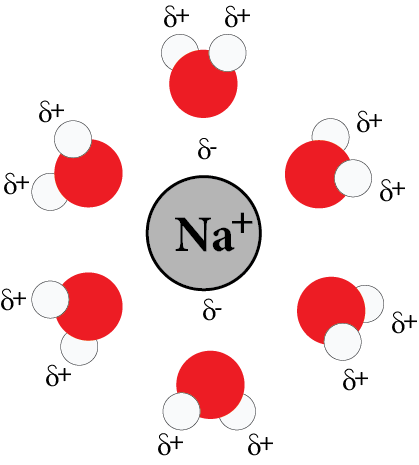
Ion-Dipole Interaction

3. Ion-induced Dipole Interaction:

The interaction between the non-polar molecules when a polarized ion is brought near to it is known as ion-induced dipole interaction. For example, an iodine molecule which is not polar gets polarized in the presence of a nitrate ion.

4. Dipole-induced Dipole Interaction:

The interaction between the non-polar molecules when a polarized dipole is brought near to it is known as dipole-induced dipole interaction. For example, in the presence of polar molecules, noble gases get polarized.

Dipole-induced Dipole Interaction

5. London Forces or Dispersion Forces:

For instance, the electron cloud of the molecule gets distorted for the generation of an instantaneous dipole. The momentary dipole is produced in the molecule in which one part of the molecule is more negative than the other part. The momentary dipole produced induces a dipole in the other molecule. Thus, the force of attraction between the induced momentarily dipole is known as London dispersion forces.

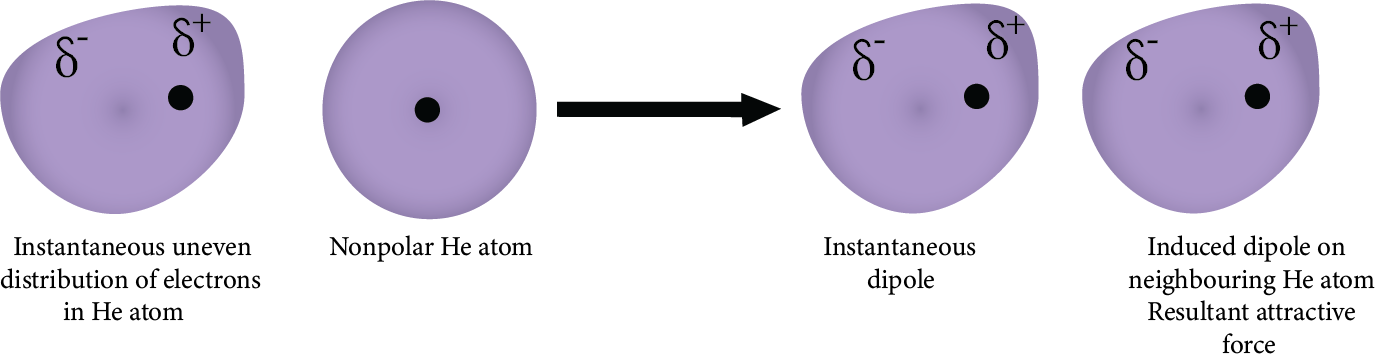
London Forces or Dispersion Forces

Intermolecular Forces Versus Thermal Energy

• The force of interaction tries to bring the molecules closer. That is, the solid possesses the strongest intermolecular force of attraction, while the gases possess the least intermolecular force of attraction. The decreasing order is,

${\text{Solid}} > {\text{Liquid}} > {\text{Gas}}$

• The thermal energy is possessed by the molecule. The kinetic energy helps in the movement of particles. The gas possesses the highest thermal energy, while the solid possesses the least thermal energy. The decreasing order is,

${\text{Gas}} > {\text{Liquid}} > {\text{Solid}}$

Ideal Gas

• An ideal gas is a hypothetical concept. There are various assumptions of an ideal gas. Some of them are:

• The force of interaction between the molecules is zero.

• The volume of the molecules is very small. The molecules of the gas collide with each other and with the walls of the container.

State of a Gas and State Variable:

The physical condition of the system is the state of a gas. The variables which are used to denote the physical condition of a gas are known as state variables. They are pressure, volume and temperature $\left( {P,V{\text{ and }}T} \right).$

Pressure

The force exerted on an object per unit area is known as pressure. The force applied is always perpendicular to the object. The unit of pressure is the pascal. Pressure can be measured by various instruments. Barometer and manometer are used to measure pressure.

Volume

The volume of the gas is the same as the volume of the container in the case of rigid containers. For non-rigid containers, the volume of the gas is determined by the number of moles and other state functions.

Temperature

The amount of heat contained in the gas can be measured by the physical term temperature. No heat flows in and out of the gas when the temperature of the gas is equal to the surrounding temperature. The thermometer is used to measure the temperature of the gas. The units of temperature are Celsius, kelvin, and Fahrenheit.

Ideal Gas Law

The laws relate the state variable of the gas in two states.

Boyle’s Law:

It gives the relation between pressure-volume. At a constant temperature, the pressure of a fixed amount of gas is inversely proportional to its volume. The value of the proportionality constant for each curve corresponds to a different constant temperature and is known as isotherm. Mathematically, it can be written as,

$P \propto {\dfrac{1}{V}}$

$P = {\dfrac{k}{V}}$

${PV} = k$ 

As, $PV$ increases, the corresponding temperature will also increase.

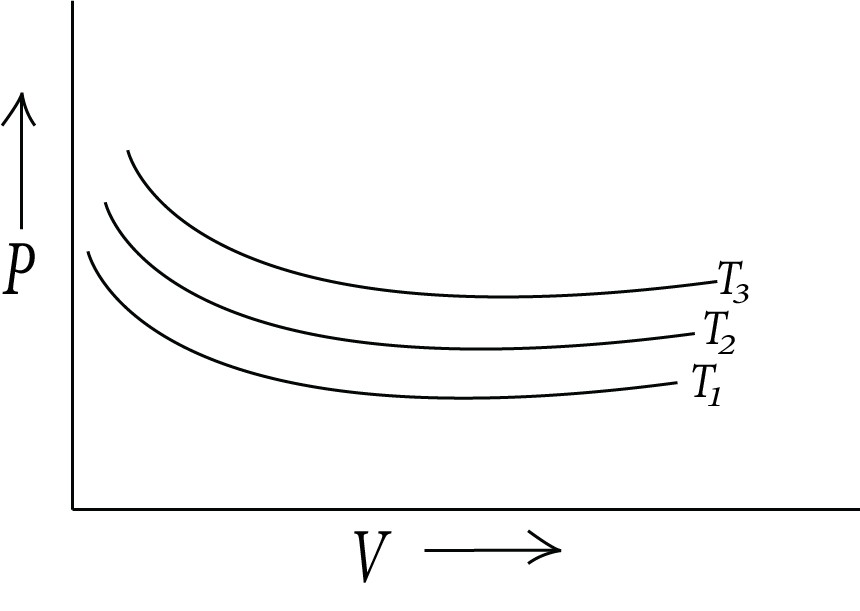
Boyles law

Charles's Law:

It gives the relation between temperature-volume. At constant pressure, the volume of a fixed mass of gas is directly proportional to the absolute temperature. Mathematically, it can be written as,

$V \propto T$ 

$V = {kT}$

$k = {\dfrac{V}{T}}$

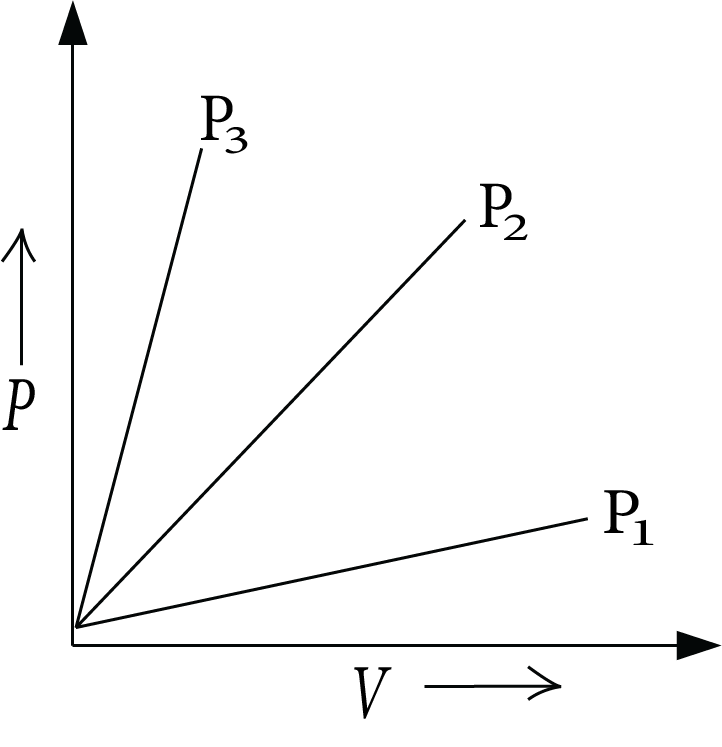
Charle’s law

Gay-Lussac’s Law:

It gives the pressure-temperature relationship. At fixed volume, the pressure of a fixed mass of gas is directly proportional to the absolute temperature. Mathematically, it can be written as,

$P \propto T$ 

$P = {kT}$

$k = {\dfrac{P}{T}}$

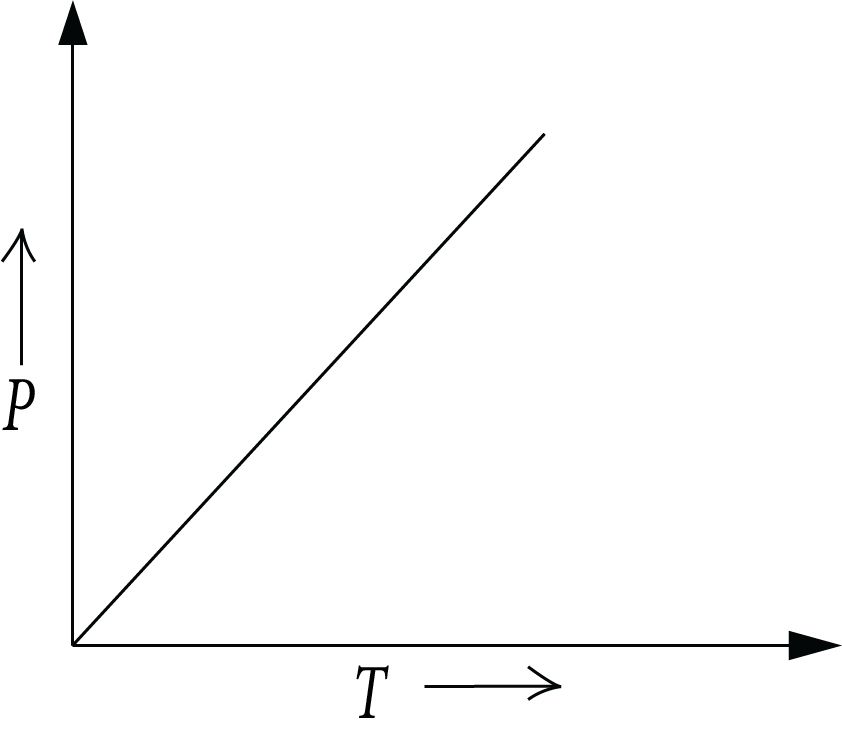
Gay-Lussac’s Law

Avogadro’s Law:

It gives the relation between the amount of gas and volume. It states that all the gases of equal volume under the same condition of temperature and pressure contain an equal number of molecules.

$V \propto n$

Ideal Gas Equation:

Combining all the three laws,

Boyle’s law: $P \propto \dfrac{1}{V}$

Charle’s law: $V \propto T$

Avogardo’s law: $V \propto n$

All the above laws when combined together give an equation, known as an ideal gas equation. Combining all the equations,

$V \propto \dfrac{{nT}}{P}$

$V = \dfrac{{nRT}}{P}$

$PV = nRT$

The above equation is known as an ideal gas equation. Here, $P$ is the pressure, $V$ is the volume, $n$ is the amount of gas, $T$ is temperature and $R$ is the universal gas constant.

The values of $R$ vary with different units. The values of $R$ are:

$R = 8.314{\text{ J }}{{\text{K}}^{ - 1}}{\text{ mo}}{{\text{l}}^{ - 1}}$

$R = 0.0821{\text{ L atm }}{{\text{K}}^{ - 1}}{\text{mo}}{{\text{l}}^{ - 1}}$

$R = 2{\text{ cal }}{{\text{K}}^{ - 1}}{\text{ mo}}{{\text{l}}^{ - 1}}$

$nR = \dfrac{{{P_1}{V_1}}}{{{T_1}}}$ and,

$nR = \dfrac{{{P_2}{V_2}}}{{{T_2}}}$

On combining the equation,

$\dfrac{{{P_1}{V_1}}}{{{T_1}}} = \dfrac{{{P_2}{V_2}}}{{{T_2}}}$

The above equation is known as Combined Gas Law.

Variation of the Ideal Gas Equation:

The ideal gas equation is written as,

$PV = nRT$

On rearranging the above equation,

$\dfrac{n}{V} = \dfrac{P}{{RT}}$

Here, $n$ is the number of moles which is equal to the given mass divided by molar mass.

The above equation can be written as,

$\dfrac{m}{{MV}} = \dfrac{P}{{RT}}$

$\dfrac{d}{M} = \dfrac{P}{{RT}}\left( {d = \dfrac{m}{V}} \right)$

On rearranging the above equation,

$PM = dRT$

Dalton’s Law of Partial Pressure:

At constant temperature and volume, the total pressure exerted by a mixture of non-reactive gases equals the sum of their partial pressures. The pressure exerted by individual gases is known as partial pressure. Mathematically, it can be shown as,

${p_{total}} = {p_1} + {p_2} + {p_3} +  \cdots  \cdots$

Here, ${p_{total}}$ is the total pressure and ${p_1},{p_2},{p_3}$ are the partial pressure of the gases.

Partial pressure can also be expressed in terms of mole fraction. If there are three gases which exerts partial pressure as, ${p_1},{p_2},{p_3}$ at constant temperature and volume, then the relation between ideal gas equation and partial pressure can be shown as,

${p_1} = \dfrac{{{n_1}RT}}{V}$

${p_2} = \dfrac{{{n_2}RT}}{V}$

${p_3} = \dfrac{{{n_3}RT}}{V}$

${p_1},{p_2},{p_3}$ are the number of moles of gases respectively.

The total pressure exerted can be calculated as,

${p_{{\text{total}}}} = {p_1} + {p_2} + {p_3}$

${p_{{\text{total}}}} = \dfrac{{{n_1}RT}}{V} + \dfrac{{{n_2}RT}}{V} + \dfrac{{{n_3}RT}}{V}$

${p_{{\text{total}}}} = \dfrac{{RT}}{V}\left( {{n_1} + {n_2} + {n_3}} \right)$

On dividing ${P_i}$ by ${P_{total}}$

$\dfrac{{{p_i}}}{{{p_{{\text{total}}}}}} = \left( {\dfrac{{{n_1}}}{{{n_1} + {n_2} + {n_3}}}} \right)\dfrac{{RTV}}{{RTV}} = \left( {\dfrac{{{n_1}}}{{{n_1} + {n_2} + {n_3}}}} \right) = \dfrac{{{n_1}}}{n} = {x_1}$

${p_1} = {x_1} \times {p_{{\text{total}}}}$

Similarly, for the other gases,

${p_2} = {x_2} \times {p_{{\text{total}}}}$ and ${p_3} = {x_3} \times {p_{{\text{total}}}}$

Thus, the general equation is,

${p_i} = {x_i} \times {p_{{\text{total}}}}$

Graham’s Law of Diffusion:

• The process of intermixing gases is known as the diffusion of gases. Gases can mix with each other even without the difference in pressure. The diffusion process becomes faster if the pressure difference increases between the gases. Due to pressure differences, gas flows through small openings. The flow of gas is effusion. 

• According to Graham’s law of diffusion, the rate of diffusion depends on two factors-partial pressure and the molecular weight of a gas. The rate of diffusion is directly proportional to the partial pressure and inversely proportional to the square root of the molar mass of the gas.

• The movement of molecules is faster when the molecules are lighter, and slower when the molecules are heavier.

Mathematically, the rate of partial pressure is shown as,

$Rate \propto \dfrac{P}{{\sqrt M }}$

• The rate of diffusion can be explained in various ways like it may be defined as many moles traveled per unit time, distance traveled per unit time, volume transferred per unit time. The rate of diffusion for the two gases can be calculated by the given formula:

$\dfrac{{{r_2}}}{{{r_1}}} = \dfrac{{{P_2}}}{{{P_1}}}\sqrt {\dfrac{{{M_1}}}{{{M_2}}}}$

Kinetic Theory of Gases

The postulates of the kinetic-molecular theory of gases are given below.

(i) Gases are made up of many similar particles (atoms or molecules). They are so small in size that the actual volume of the molecules is negligible.

(ii) At normal temperature and pressure, there is no force of attraction between the particles.

(iii) Particles of a gas are always in constant and random motion. They collide with one other and the container walls during their erratic mobility. The collision of the particles with the walls of the container is the total pressure exerted by the gas.

(iv) The collisions of gas molecules are perfectly elastic. This means that the total energy of molecules remains the same before and after a short-range collision.

(v) At any particular time, different particles in the gas have different speeds and hence different kinetic energies.

The distribution of speed remains constant even on changing the individual speeds of gases. If the gases will have variable speed, they must also have variable kinetic energy. The average kinetic energy of the gas molecule is directly proportional to the absolute temperature of the gas. Mathematically, the relation is shown as,

${\text{K}}{\text{.E per mole}} = \dfrac{3}{2}nRT$

${\text{K}}{\text{.E per molecule}} = \dfrac{3}{2}KT$

Here, $K$ is known as Boltzmann’s constant.

Molecular Distribution of Speed (Maxwell Boltzmann Distribution)

A plot of the fraction of molecules in the gas vs the speed of the gas molecule is the Maxwell Boltzmann distribution curve. The graph is shown below.

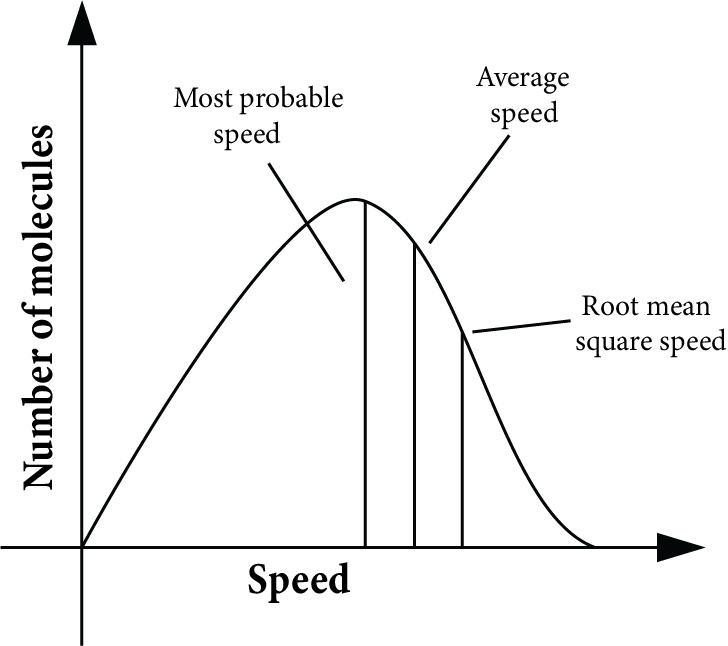
Maxwell Boltzmann Distribution

Salient Features of Graphs are:

(a) The percentage of molecules with a very high or very low speed is extremely small.

(b) Mostly, the molecules possess speed in the middle, which is known as the most probable speed.

(c) The total area covered by the graph gives the total number of molecules in the sample.

(d) There are two more speeds, root means square speeds and average speeds. Mathematically, they are shown as,

${\mu _{{\text{rms}}}} = \sqrt {\dfrac{{3RT}}{M}}$

${\mu _{{\text{mp}}}} = \sqrt {\dfrac{{2RT}}{M}}$

${\mu _{{\text{avg}}}} = \sqrt {\dfrac{{8RT}}{{\pi M}}}$

Note: Take molecular mass always in kilograms.

The ratio for the speeds of the gas at fixed temperature is,

${\mu _{{\text{mp}}}}:{\mu _{{\text{avg}}}}:{\mu _{{\text{rms}}}} = 1:1.128:1.224.$

Real Gases:

The assumption taken for ideal gases becomes invalid in case of real gases.

(i) We thought that in an ideal gas, there are no interactions between molecules.

(ii) The volume of a gas’s molecules is negligible compared to the entire volume of gases.

The molecular interaction cannot be ignored in real gases. They are:

• Attractive forces with a long range and repulsive forces with a short range.

• The interactive forces present in real gases are negligible when they are far apart. But, when the molecules are brought closer attractive forces start to develop. On bringing the molecules closer, they start repelling each other.

Compressibility Factor

The compressibility factor is the measurement of the deviation from ideal behavior. It is denoted by $Z.$ It is represented as,

Following are the Key Points:

(a) There is no contact between the molecules when the pressure is exceedingly low. At that point, the value of $Z$ is 1.

(b) When the pressure is low or moderate, attractive forces take over, compressing a real gas to a larger volume. In that case, the value of $Z$ is less than one.

(c) When the pressure is high, repulsions take over, making it difficult to compress the real gas, resulting in a smaller volume. At that point, the value of $Z$ is greater than 1.

For an ideal gas, the value of $Z$ is always one.

For real gases, $Z = \dfrac{{PV}}{{nRT}}$

Variation of $Z$ with $P$ and $T$

The graph is a straight line curve for an ideal gas of compressibility factor $Z$ with pressure. However, at low pressure, for real gases the value of $Z$ is < 1. As pressure increases, $Z$ becomes > 1. keeps on increasing. On further increasing the temperature the graph tends more towards $Z$ = 1 i.e. ideal gas.

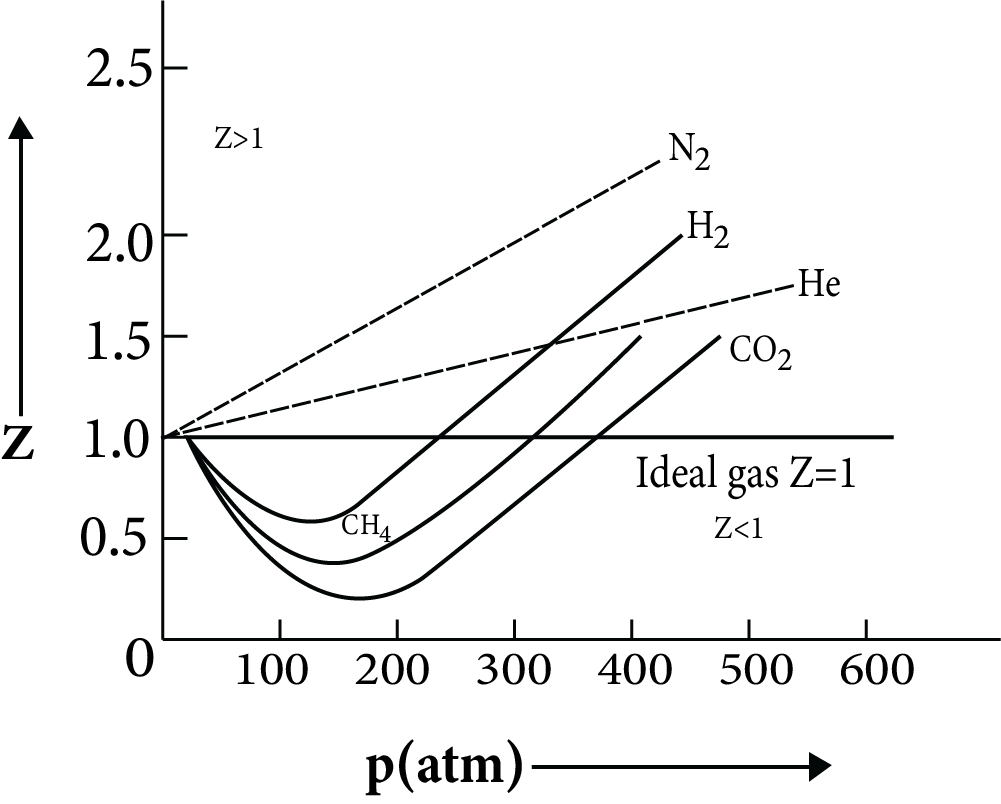
Variation of Z with P and T

• It can be concluded that real gas follows ideal behavior only at low pressure and high temperature. The main point to be noted is that on increasing and further increasing the temperature, a real gas will not convert to an ideal gas.

• There is a characteristic temperature at which a gas follows ideal behavior. The temperature at which gas follows ideal behavior is called Boyle’s temperature.

Van Der Waals Equation:

After correction of pressure and volume terms, the ideal gas equation can be formulated as,

$\left( {P + \dfrac{{a{n^2}}}{{{V^2}}}} \right) + \left( {V - nb} \right) = nRT$

Here, $a$ and $b$ are Van der Waals constants.

$a$ is the attractive force between the gases. As the attractive forces between the molecules increases, the value of $a$ increases. Whereas, $b$ is the volume occupied by the molecule.

The Van der Waal constant $a$ is always greater than $b$ for a given gas.

The higher the value of $a$, the more easily liquefaction can occur.

Applicability of Van Der Waal Equation:

• At high temperature and low pressure, the compressibility factor is equal to 1, and equation is reduced to, $P{V_m} = RT$

• At low/Moderate Pressure:

Here, the volume correction factor can be ignored. When $Z$ < 1, attractive force dominates. The equation is reduced to, $Z = \left( {1 - \dfrac{a}{{VRT}}} \right)$

• At High Pressure:

Here, a pressure correction factor can be ignored. When $Z$ > 1, the repulsion force dominates over attractive forces. The equation is reduced to, $Z = \left( {1 + \dfrac{{Pb}}{{RT}}} \right)$

Liquefaction of Gases:

When the attractive forces between the molecules increase, molecules of gas come closer to each other. A stage reaches when gas changes to a liquid. This phenomenon is known as the Liquefaction of gases.

Critical Temperature:

The critical temperature is the temperature above which a gas cannot be liquified. It is denoted as ${T_c}.$ It is represented as,

${T_c} = \dfrac{{8a}}{{27Rb}}$

Critical Pressure:

The pressure required during the liquefaction of gas is its critical pressure. It is denoted as ${P_c}.$ It is represented as,

${P_c} = \dfrac{a}{{27{b^2}}}$

Critical volume:

• Under critical temperature and pressure, the volume occupied by a gas is its critical volume. It is denoted as ${V_c}.$ It is represented as,

${V_c} = 3b$

• Note: At critical points, the value of the compressibility factor is constant and has the value of $0.375.$

• The Liquefaction of gases can be achieved in two ways:

• Either increase the pressure or decrease the temperature of the gas. The dominant factor is temperature.

Liquid State

Properties of Liquid

• There are very few empty spaces present in liquids. 

• The interactive forces present in liquid are more than gases and less than solids. 

• Liquids have a definite volume. 

• The molecules in the liquid move so fast with one another. They, therefore, acquire the shapes of the container.

Vapor Pressure

The pressure exerted by the vapor present above the liquid in equilibrium with the liquid at a given temperature is known as vapor pressure. The vapor pressure depends on two factors-nature of the liquid and temperature.

• Nature of Liquid 

The molecules leave the liquid phase and shift to the gaseous phase if the intermolecular attraction is weak. Thus, the vapor pressure becomes higher.

• Effect of Temperature: Vapor pressure increases with an increase in temperature. 

Boiling Point

• The temperature at which the vapor pressure of the liquid becomes equal to the atmospheric pressure is known as the boiling point. When the external pressure is ${\text{760 mm Hg}}$, boiling point is said to be a normal boiling point. When the external pressure is ${\text{1 bar}}$,  boiling point is said to be the standard boiling point.

• The influence of external pressure on the boiling point is applied as follows:

• Higher will be the external pressure, higher will be the boiling point. Because more heat will be required to make the vapor pressure equal to the external pressure and hence higher will be the boiling point. In hospitals, surgical instruments are sterilized in autoclaves, which raise the boiling point of water by covering the vent with a weight.

• Similarly, lower will be the external pressure, lower will be the boiling point. Therefore, on the top of a mountain, a liquid boils at a lower temperature (where pressure is low) than on the seashore.

Surface Tension

• The surface tension arises because the molecules of the liquid at the surface and in the interior portion are in a different situation.

• The force acting at right angles to the surface along the one-centimeter length of the surface is surface tension. The units of surface tension are dynes per cm or Newtons per meter.

The important results of surface tension are:

1. Minimal Surface Area: why the spherical shape drops the lowest energy state of a liquid. The surface area of the liquid is decreased to the minimum due to the surface tension. The drops of a liquid are spherical because a sphere has a minimum surface area.

2. Rise of a Liquid in a Capillary Tube: The liquid is pushed into the capillary tube by the inward pull of surface tension acting on the surface, and so the liquid rises.

3. Effect of Nature of the Liquid on Surface Tension: Surface tension arises due to the intermolecular forces of attraction among the molecules. Greater will be the intermolecular forces of attraction, higher is the surface tension of that liquid.

4. Effect of Temperature on Surface Tension: As the temperature increases, surface tension decreases. At the critical temperature, surface tension becomes zero. This is because as temperature increases, the kinetic energy of the molecules increases and, therefore, the intermolecular attraction decreases.

Viscosity 

• Viscosity is a measure of resistance to flow which arises due to the internal friction between layers of fluid as they slip past one another while liquid flows. 

• The SI unit of viscosity is ${\text{1 Ns}}{{\text{m}}^{ - 2}}.$There is a regular gradation of velocity inflowing of the water from one layer to another. 

• Such flowing of water is known as laminar flow. A force is required to maintain the flow of layers. 

This force is proportional to the area of contact of layers and velocity gradient. Mathematically, it is related as,

$F \propto A\dfrac{{du}}{{dz}}$ 

$F = \gamma A\dfrac{{du}}{{dz}}$

Here, A is the area of contact and $\dfrac{{du}}{{dz}}$ is the velocity gradient gamma is the constant and is known as the coefficient of viscosity.

The factors that cause more viscosity are hydrogen bonding and Van der Waals force. Slowly the liquid flows, greater is the viscosity. As the temperature increases, viscosity decreases. This is due to the fact that as temperature increases, the kinetic energy of the molecules increases and they overcome the intermolecular forces between the layers.

Measurement of the Pressure of the Gas

• A common arrangement to measure the pressure of a gas is called a “Barometer”.

• The height of a mercury column supported in a sealed glass tube is used to determine atmospheric pressure in a mercury barometer. The pressure of a gas can be measured by various methods. The most common method of measuring pressure is in terms of height.

• Assume a liquid of density $d$ is filled in a tube with a cross-sectional area $A$ of height $h$. A vacuum has been placed over it. The liquid exerts pressure on the bottom of a container due to gravity.

${\text{Volume of liquid}} = A \times h$

Then, ${\text{Mass of liquid}} = d \times A \times h$

Force applied is equal to the weight of the liquid which is equal to $g \times d \times A \times h$

Pressure is given as,

$P = \dfrac{F}{A}$

$P = d \times g \times h$

$P = dgh \times \sin \theta$

Important Formula:

• ${\text{Boyle's law: }}{P_1}{V_1} = {P_2}{V_2}$

• ${\text{Charle's law: }}\dfrac{{{V_1}}}{{{T_1}}} = \dfrac{{{V_2}}}{{{T_2}}}$

• ${\text{Gay Lussac law: }}\dfrac{{{P_1}}}{{{T_1}}} = \dfrac{{{P_2}}}{{{T_2}}}$

• Avogadro’s law: $V \propto n$

• For U-tube nanometer: ${O_h} = \dfrac{{{P_1} - {P_2}}}{{qg}}$

• ${\text{Ideal gas equation: }}PV = nRT$

• Variation of ideal gas equation: $PM = dRT$

• Rate of diffusion: $\dfrac{{{r_2}}}{{{r_1}}} = \dfrac{{{P_2}}}{{{P_1}}}\sqrt {\dfrac{{{M_1}}}{{{M_2}}}}$

• Dalton’s Law of partial pressure: ${p_i} = {x_i} \times {p_{{\text{total}}}}$

• ${\mu _{{\text{rms}}}} = \sqrt {\dfrac{{3RT}}{M}}$

• ${\mu _{{\text{mp}}}} = \sqrt {\dfrac{{2RT}}{M}}$

• ${\mu _{{\text{avg}}}} = \sqrt {\dfrac{{8RT}}{{\pi M}}}$

• ${\mu _{{\text{mp}}}}:{\mu _{{\text{avg}}}}:{\mu _{{\text{rms}}}} = 1:1.128:1.224.$

• Compressibility factor: $Z = \dfrac{{{V_{{\text{real}}}}}}{{{V_{{\text{ideal}}}}}}$

• Van der Waal’s equation: $\left( {P + \dfrac{{a{n^2}}}{{{V^2}}}} \right) + \left( {V - nb} \right) = nRT$

• Van der Waal’s constant: $b = 4 \times \left( {\dfrac{4}{3}\pi {r^3}} \right)N$

• At low pressure: $Z = \left( {1 - \dfrac{a}{{VRT}}} \right)$

• At high pressure: $Z = \left( {1 + \dfrac{{Pb}}{{RT}}} \right)$

• Critical temperature: ${T_c} = \dfrac{{8a}}{{27Rb}}$

• Critical pressure: ${P_c} = \dfrac{a}{{27{b^2}}}$

• Critical volume: ${V_c} = 3b$
  
  

Importance of States of Matter

This chapter focuses on explaining the advanced concepts related to the different states of matter. It describes how the three different states of matter form and what their different properties are.

It introduces the concepts of intermolecular forces existing between the particles of matter. The strength and nature of such forces determine the states of matter. Proceeding further, it also explains what dipole-dipole and ion-dipole interactions are with proper examples. The other interactions between the molecules of matter are also described here with examples.

This chapter explains what happens when heat is applied to matter. These intermolecular forces start to weaken due to the stronger movement of the particles. It results in the change of state of matter when a particular temperature is attained.

The concepts of an ideal gas, the state variable, and the state of gas are explained using the combined gas laws in this chapter. It will also define pressure, temperature, and volume in the universal gas laws.

In the Class 11 Chemistry States of Matter notes, students will find a thorough explanation of the kinetic theory of gases. The proper mathematical derivations of the laws will help students understand the characteristics of gases in different conditions.

Benefits of States of Matter Class 11 Notes for NEET

• These NEET revision notes have been prepared to provide concise definitions, derivations, explanations, and correlations of all the scientific terms covered in this chapter. By going through these notes, you will find that every state of matter is interrelated and can be inter-converted.

• The features of solids, liquids, and gases are well explained in an easier format for your exam preparation. Once you have studied this chapter elaborately, you can use these notes to revise it.

• Your preparation time before the exam for this chapter will reduce considerably. You can revise all topics in a better way when you have these revision notes for this chapter.

• Solve the sample questions of Class 11 Chemistry States of Matter and evaluate your preparation level. Refer to these notes to find how the experts have solved the sample questions and enhance your answering skills.

Download Free States of Matter Class 11 Notes PDF

These revision notes are available in a free PDF version. You can download and refer to them at your convenience. Save your time preparing topic-wise notes from this chapter as our experts have already done it for you. Download the States of Matter NEET notes PDF for free from Vedantu for your exam preparation.

Other Important Links