Revision Notes on Physics Magnetism and Matter for NEET 2024

Natural Magnets: Natural magnets are minerals or metals that can produce a magnetic field on their own without the aid of an outside energy source. Those things should not be confused with man-made artificial magnets. While artificial magnets can be either temporary or permanent, natural magnets are always permanent.

Magnet

• Lodestone, a naturally occurring black-colored material, can attract iron items maintained nearby.

• In early days, the Greeks observed this property of loadstone an oxide called magnetite$\left( \text{F}{{\text{e}}_{3}}{{\text{O}}_{4}} \right)$. This type of substance is called magnet.

Magnet is of two types:

• Natural Magnet Natural magnets are substances found in nature that attract small bits of iron, known as magnetism.

• Artificial Magnets Artificial magnets are magnets that have been created artificially. It has a set shape and size. for example , Horseshoe magnet

Properties of Magnets:

We already know that the magnetic material is what makes up magnets. There are certain crucial characteristics of magnets. As follows:

1. Attractive Property – Magnet attracts ferromagnetic materials like iron, cobalt, and nickel.

2. Repulsive Properties – Like magnetic poles repel each other and unlike magnetic poles attract each other.

3. Directive Property – A freely suspended magnet always points in a north-south direction.

• We can see that when a magnet is covered in iron filings, the iron filings stick to the end of the magnet because there is the strongest attraction. These points are referred to as the magnets' poles.

• There are always two magnetic poles.Anytime a magnet is carried freely in midair, it always faces north and south. The pole pointing northward in space is referred to as the North Pole, and the pole pointing southward in space is referred to as the South Pole.

• While unlike poles attract, like poles repel.When the two magnets are closer together, the magnetic force between them is larger.

Important Facts Related to Magnet

• The life of an artificial magnet is short, whereas the life of a natural magnet is long.

• The earth's magnetism lasts an endless amount of time.

• An induced magnet is an unstable magnet.

• Magnets can be found in electric bells, fans, and washing machines, among other things.

Pole Strength

• We know that, The ability of magnetic poles to attract magnetic material is known as pole strength. It is denoted by $m$. The pole strength of the North and South pole is represented by $+m$ and $-m$.

• Pole strength $(m)=\dfrac{\text{ Magnetic force }}{\text{ Magnetic induction }}=\dfrac{F}{m}$

• Ampere-metre or Newton/Tesla is the unit of pole strength.

Magnetic Axis

• The magnetic axis is the line that connects a magnet's north and south poles.

Effective Length of Magnet

• The effective length of a magnet is defined as the distance between the North Pole and the South Pole.

Magnetic Dipole

• A magnetic dipole is a magnetic north and south poles separated by a short distance.

Magnetic Dipole

Magnetic Moment

• A bar magnet's magnetic moment is equal to the product of its length and pole strength. It is symbolised by  $M$ because $M=(2l)\times m$.

• Unit of magnetic moment is ampere-metre$^{2}$.

Magnetic Field

• A magnetic field is an area surrounding a magnet in which another magnet exerts a force on it.

Magnetic Field Lines

• Magnetic field lines are imaginary lines that depict the direction of a magnetic field. Some properties of magnetic field lines are given below.

• Magnetic line of force is always from closed curves.

• They leave the North Pole and enter the South Pole externally.

• They move from the South Pole to the North Pole within the magnet.

• They tend to contract laterally.

• The magnetic field lines never intersect each other.

Bar Magnet

• A bar magnet is a rectangular section of an object that exhibits persistent magnetic qualities. It can be constructed of steel, iron, or any other ferromagnetic material.

• When suspended freely, the magnet's two poles—a north pole and a south pole—align themselves such that the northern pole faces the magnetic north pole of the earth.

Torque on Bar Magnet in Magnetic Field:

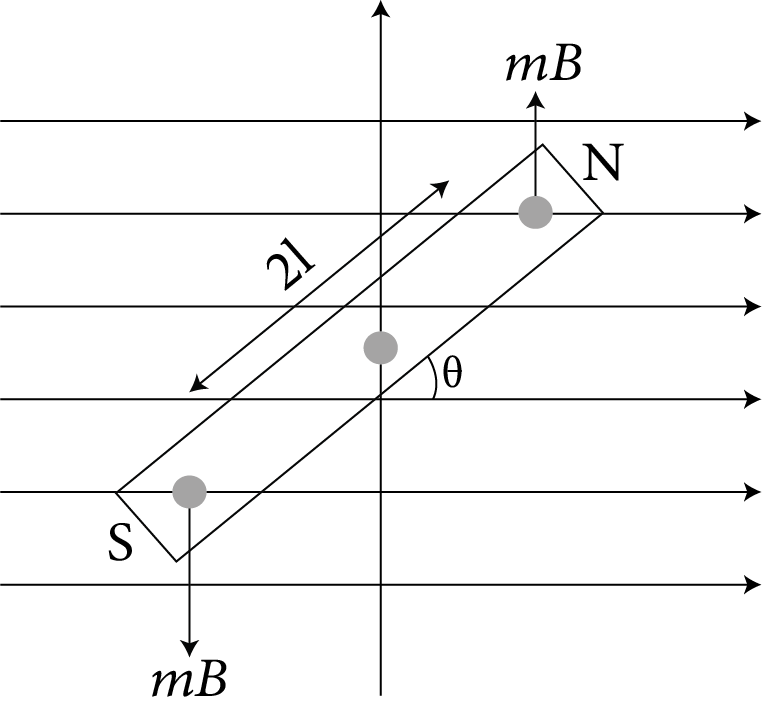
Torque on Bar Magnet in Magnetic Field

• In figure, a uniform magnetic field $B$ is represented by an equidistant parallel line. N S is a bar magnet of length $2l$ and strength of each pole is $m$. 

• The magnet is held at angle $\theta $ with the direction of $B$ Torque$(\tau )=mBl\sin \theta +mBl\sin \theta $

$\tau =2mBl\sin \theta =MB\sin \theta $

In vector, $\tau =\vec{M}\times \vec{B}$

Work Done in Rotating a Dipole in a Magnetic Field:

• The total work done in deflecting the dipole through an angle $\theta $ from ${{0}^{{}^\circ }}$ is $W=MB(1-\cos \theta )$

• If $\theta ={{0}^{{}^\circ }}$, then $W=MB[1-1]=0$

• If $\theta ={{90}^{{}^\circ }}$, then $W=MB$

• If $\theta ={{180}^{{}^\circ }}$, then $W=2MB$, Where, $M$ is magnetic dipole moment.

What is Earth’s Magnetic Field?

• The geomagnetic field is another name for Earth's magnetic field. The earth's magnetic field stretches millions of kilometres into space and resembles a bar magnet. 

• The magnetic south pole of the planet is located near the North Pole, while the magnetic north pole is located in Antarctica! This is why the North Pole of a compass magnet points north (north and south poles attract). 

• The Earth's magnetic field stretches far and broad, yet its field strength is quite modest. A refrigerator magnet has a strength of 10 times that of a 40,000 nT magnet.

Theory of Earth’s Magnetism:

There is one idea that explains the origins of the earth's magnetism:

The Dynamo Effect: The presence of metallic fluids in the outer and inner cores gives the earth its magnetic field lines. The molten iron makes up the outer core, while the solidified components make up the inner core.

What Causes Earth’s Magnetism?

• Earth's magnetism is created by molten iron and nickel convection currents in the earth's core. 

• Magnetic fields are generated by these currents, which convey streams of charged particles. This magnetic field deflects ionising charged particles from the sun, preventing them from entering our atmosphere (known as solar wind). 

• Without this magnetic shield, the solar wind would have gradually destroyed our atmosphere, making life on Earth impossible. 

• Because it lacks a magnetic field, Mars does not have a robust atmosphere capable of supporting life.

• The earth's magnetic poles are not aligned with the geographic north and south poles. Instead, Canada is home to the magnetic South Pole, while Antarctica is home to the magnetic North Pole. 

• The magnetic poles are around 10 degrees off-kilter with the earth's spinning axis. So your compass had been pointing to Canada instead of the true North all this time!

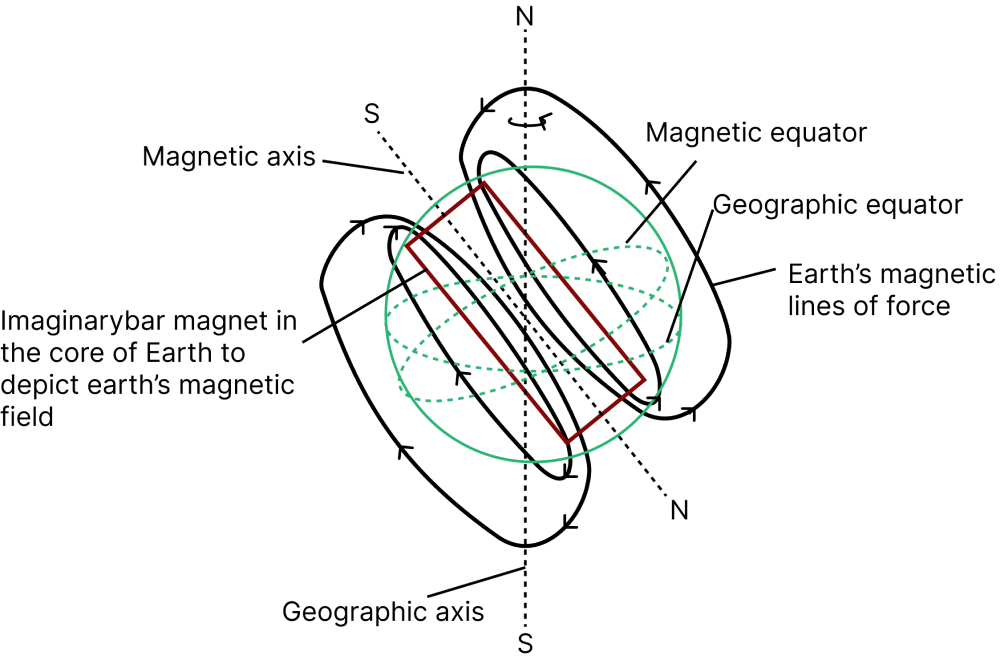
Earth’s Magnetism

The magnetic North Pole is hundreds of miles away, near the coast, in Northern Canada; the geographic South Pole is in the middle of the Antarctic continent, while the magnetic pole is hundreds of miles away, near the coast. Compasses are practically ineffective in areas near the magnetic poles.

Components of Earth’s Magnetic Field

• The size as well as the direction of the earth's magnetic field are determined by three components: 

Magnetic Declination (\[\phi\]):

• The angle between true north and magnetic north is known as magnetic declination. 

• On the horizontal plane, true north is never in the same place and varies based on the location on the earth's surface and the passage of time.

Magnetic Inclination

• The angle of dip is another name for the magnetic inclination. It's the angle formed by the horizontal plane on the earth's surface. At the magnetic poles, the magnetic inclination is 90 degrees, and at the magnetic equator, it is zero degrees. 

• At the magnetic equator, the angle of dip is ${{0}^{{}^\circ }}$ and at the magnetic poles, the angle of dip is ${{90}^{{}^\circ }}$.

Angle of Inclination or Dip (\[\theta\]):

It is the angle between the magnetic field of earth and the horizontal at that place. It is zero at the magnetic equator and 90˚ at the poles. In the magnetic northern hemisphere, the vertical component of earth's field points downward.

Horizontal Component of the Earth's Magnetic Field

• The intensity of the earth's magnetic field is explained by two factors:

1. Horizontal component (H)

2. Vertical component (v)

• Some important expressions:

$\tan \delta =\dfrac{{{B}_{v}}}{{{B}_{H}}}$

$\sin \delta =\dfrac{{{B}_{v}}}{B}$

$\cos \delta =\dfrac{{{B}_{H}}}{B}$

${{\sin }^{2}}\delta +{{\cos }^{2}}\delta =\dfrac{B_{H}^{2}}{{{B}^{2}}}+\dfrac{B_{v}^{2}}{{{B}^{2}}}$

$1=\dfrac{B_{H}^{2}}{{{B}^{2}}}+\dfrac{B_{v}^{2}}{{{B}^{2}}}$

$B=\sqrt{B_{H}^{2}+B_{v}^{2}}$

Uniform and Non-Uniform Magnetic Field

• If the magnetic field in that area of space has a consistent magnitude and consistently points in the same direction, we refer to it as being uniform. The field is non-uniform whenever its magnitude or direction varies.

Atom as Magnetic Dipole

• In an atom, the electron travels in a tight orbit around the nucleus. An electron's orbit around the nucleus is comparable to a current loop because it is a charged particle. 

• The current flows clockwise when an electron rotates counterclockwise. The lower face of the electron loop serves as the North Pole and the higher face as the South Pole. An atom acts like a magnetic dipole.

           $M=\dfrac{n e h}{4 \pi m}=n \mu_{B}$

Relation Between Magnetic Moment and Angular Momentum

$\vec{M}=\dfrac{q}{2 m} \vec{L}$

Here q is the total charge on a body of mass m rotating about a fixed axis

Some Terms Related to Magnetism

Magnetic poles are the areas where the magnetic attraction is strongest and appears to be concentrated. Means that a magnet's pole is not placed at a single spot but rather spread out over a wide area. There are pairs of magnetic poles. There is no distinct magnetic pole (north or south). When a magnet is split into two halves, each of the two sections behaves as a full magnet rather than producing distinct N- and S-poles.

Magnetic Axis: A magnet's magnetic axis is the path that runs across its poles.

Magnetic Equator: The magnetic equator of the magnet is the line that runs through its centre and perpendicular to its magnetic axis.

Magnetic Length: The magnetic length of a magnet is the smallest distance between its two poles. It is shorter than the magnet's geometric length. Effective length is another name for this magnetic length.

Coulomb’s Law of Magnetism:

• According to Coulomb, the magnetic force between two magnetic poles ${m_1}$ and ${m_2}$ placed at a separation r is given by $F = \dfrac{{{\mu _0}}}{{4\pi }}\left( {\dfrac{{{m_1}{m_2}}}{{{r^2}}}} \right)$.

Magnetic Field Due to Magnetic Pole:

• If F is the force exerted by another magnetic charge m, then magnetic field at a distance r from m can be defined as$B = \dfrac{{{\mu _0}}}{{4\pi }}\left( {\dfrac{m}{{{r^2}}}} \right)$.

Magnetic Potential:

• For a pole strength m, the field at a distance r is and radially away from the pole. The potential at a distance r is given by $V = \dfrac{{{\mu _0}}}{{4\pi }}\left( {\dfrac{m}{r}} \right)$.

Work Done in Rotating the Magnet:

• The torque exerted by the agent for any angle θ is MBsinθ. Thus, work done in rotating the magnet from ${\theta _1}$ to ${\theta _2}$ is given by $\;W =  - MB(\cos {\theta _2} - \cos {\theta _1})$.

Intensity of Magnetisation:

• Each substance contains a large number of atoms. In general, the magnetic moments of these atoms are randomly oriented and there is no net magnetic moment in any volume of the material that contains thousands of atoms. However, when the material is kept in an external magnetic field, atomic dipoles try to align parallel to the field. 

• The degree of alignment increases if the intensity of the applied field increases and the temperature decreases. With a sufficiently strong field, the alignment is nearly perfect. 

• We then say that the material is magnetically saturated. When the atomic dipoles are partially or wholly aligned, there is a net magnetic moment in the field's direction in any small material volume.

Magnetic Susceptibility:

• Magnetic susceptibility is defined as the intensity of magnetisation per unit magnetising field. Thus, $\chi  = \dfrac{I}{H}$where χ is a dimensionless quantity and may be positive or negative.

Magnetic Permeability:

• Magnetic permeability of the material is the measure of degree to which the material can be permeated by magnetic field and is defined as the ratio of magnetic field in the material to the magnetising field. Thus, $\mu  = \dfrac{B}{H}$.

Relationship between ${\mu _r}$ and χ: ${\mu _r} = 1 + \chi$

Classification of Magnetic Materials:

Diamagnetic Material:

• Suppose a material in which an individual atom does not have a net magnetic moment. When such a material is placed in a magnetic field, the applied field induces dipole moments in the atoms. 

• Magnetic moments are induced in all materials when a magnetic field is applied. Thus, the resultant field is smaller than the applied field. This type of material is called diamagnetic material. 

• Thus, all materials have the property of diamagnetism. However, if there is a permanent atomic magnetic moment, then paramagnetism or ferromagnetism is much stronger than diamagnetism and the material does not show diamagnetic properties.

• A diamagnetic substance's magnetic susceptibility has a negative value and is temperature-independent, meaning it does not change regardless of changes in temperature.

Paramagnetic Material:

• Now consider a material whose individual atoms have a net magnetic moment. When such a substance is placed in a magnetic field, an extra magnetic field produces in the material in the direction of the field. The material's resultant magnetic field is greater than the applied field. 

• The tendency to increase the magnetic field due to magnetisation of material is called paramagnetism, and material is called paramagnetic material.

• A paramagnetic material's magnetic susceptibility changes inversely with temperature. In other words, they tend to lose their magnetic properties as temperature rises.

Ferromagnetic Material:

• In some materials, the permanent atomic magnetic moments have a strong tendency to align themselves, even without any external field. These materials are called ferromagnetic materials. 

• In every unmagnetised ferromagnetic material, the atoms form domains inside the material. Different domains, however, have different directions of magnetic moment; hence, the materials remain unmagnetised. On applying an external field, these domains rotate and align in the direction of the magnetic field.

• An inverse relationship exists between temperature and susceptibility for ferromagnetic materials. Prior to the Curie temperature, there is no drop in susceptibility, but following this, it begins to decline as temperature increases.

Hysteresis:

• Only ferromagnetic materials exhibit hysteresis. In ferromagnetic materials, when the external field is removed, some domains' magnetic moments stay aligned in the direction of the previously applied magnetising field, leaving behind residual magnetism.The lagging of intensity of magnetisation (I) to magnetising field (H) is known as hysteresis.

OA: Retentivity or residual magnetism

OB: Coercivity

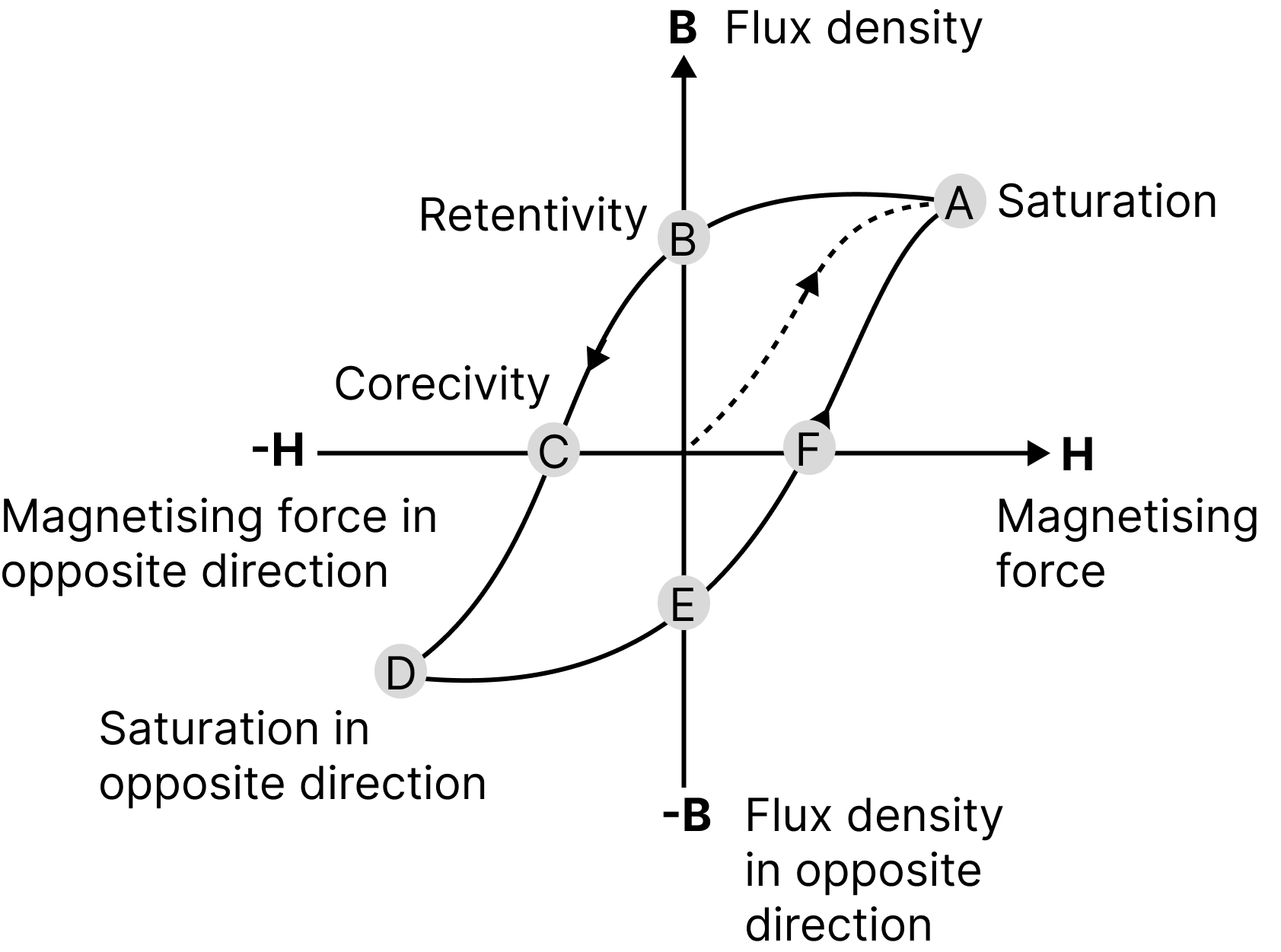
Graph of the Intensity of Magnetisation (I) and Magnetising Field is (H)

Properties of Soft Iron and Steel:

Compared to steel, soft iron exhibits higher levels of susceptibility, permeability, and retention while having lower levels of coercivity and hysteresis loss each cycle.

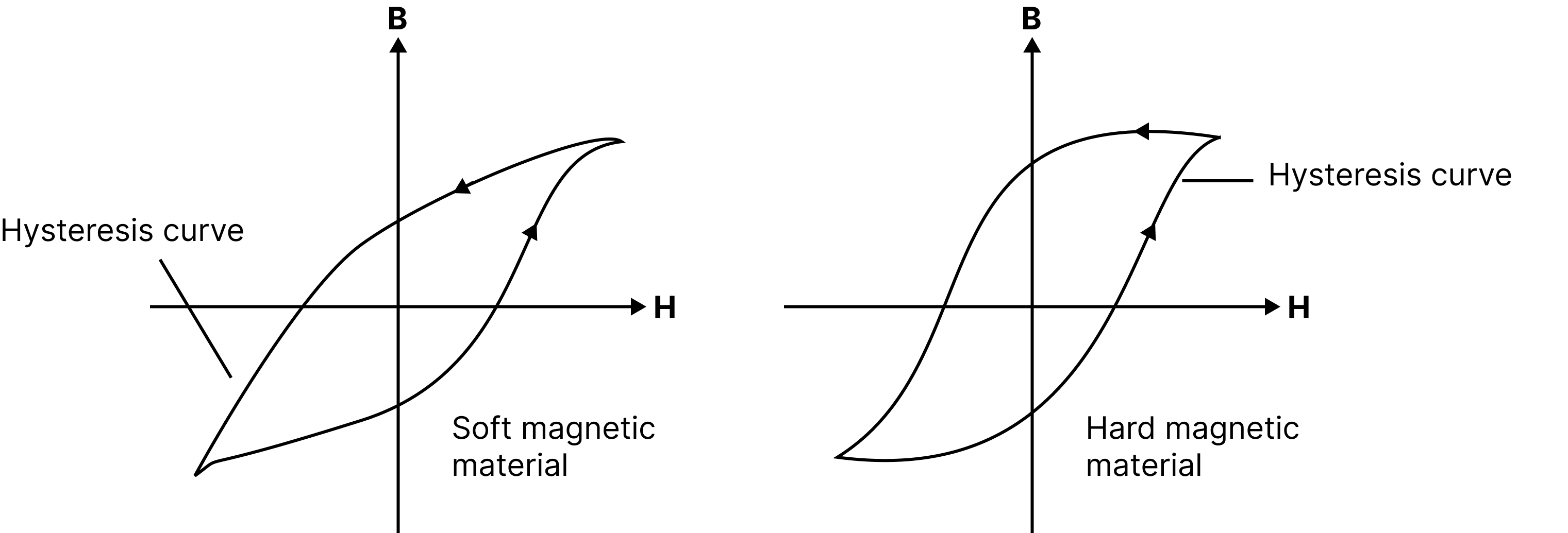
Hysteresis Curve Comparison

Curie's Law

• The magnetic susceptibility of a paramagnetic substance is inversely proportional to the absolute temperature, according to Curie's Law. i.e.

          $\chi \propto \dfrac{1}{T}$

Curie Temperature

• When a substance reaches a specific temperature, it loses its ferromagnetic properties and behaves like a paramagnetic substance. 

• This temperature is referred to as the substance's curie temperature.

Magnetic Flux

• It's the total number of magnetic lines of force that pass through any surface regularly.

• When the surface of area $A$ is placed perpendicular to the uniform magnetic field $B$. Then, magnetic flux $\phi =BA$.

• Its unit is Wb (weber) or $\text{kg}-{{\text{m}}^{2}}/{{\text{s}}^{2}}~\text{A}$.

• No flux link will pass via a plane that is parallel to the magnetic field, and the magnetic flux link with the coil will be zero. 

• If the coil is rotated through ${{90}^{{}^\circ }}$ in the magnetic field, then magnetic flux linked with the coil is zero.

Important Points

• At any place, angle of dip is $\theta $ and magnetic meridian is $\alpha $, then

$\tan \theta =2\tan \alpha $

• Intensity of Earth magnetic field

$I={{I}_{0}}\sqrt{1+3{{\sin }^{2}}\alpha }$

Where, $R=$ Radius of Earth

• At magnetic equator line $\lambda =0$ and at poles$\lambda ={{90}^{{}^\circ }}$, then ${{I}_{\text{pole }}}=2{{I}_{\text{equator }}}$

Force on a Moving Charge in Magnetic Field:

• In a magnetic field, the force on a moving charge is given by,

${{F}_{m}}=qvB\sin \theta =q(\mathbf{v}\times \mathbf{B})$

where,  $v=$ magnitude of charge, $B=$ intensity of charge, and $\quad \theta =$ angle between direction of velocity and direction of magnetic field

• Lorentz force is another name for it.

• Neutral and big substances are affected by electromagnetic and gravitational forces.

• The kinetic energy of a moving charge that moves perpendicular to the magnetic field remains constant.

• The force that acts in the presence of an electric and magnetic field simultaneously. $F=q(E+v\times B)$

Rules to Find the Direction of Force:

• The Palm Rule for the Right Hand: the fingertips of a linear conductor clasped in the palm of the right hand with the thumb pointing in the direction of the current will point in the direction of lines of force.

• The rule of Fleming's left hand If we spread our left hand's forefinger, middle finger, and thumb in such a way that they are perpendicular to each other, the first forefinger will represent the magnetic field, the second central finger will represent the current, and the thumb will represent the force.

Expression of Magnetic Field at Axial & Equatorial Point of a Bar Magnet:

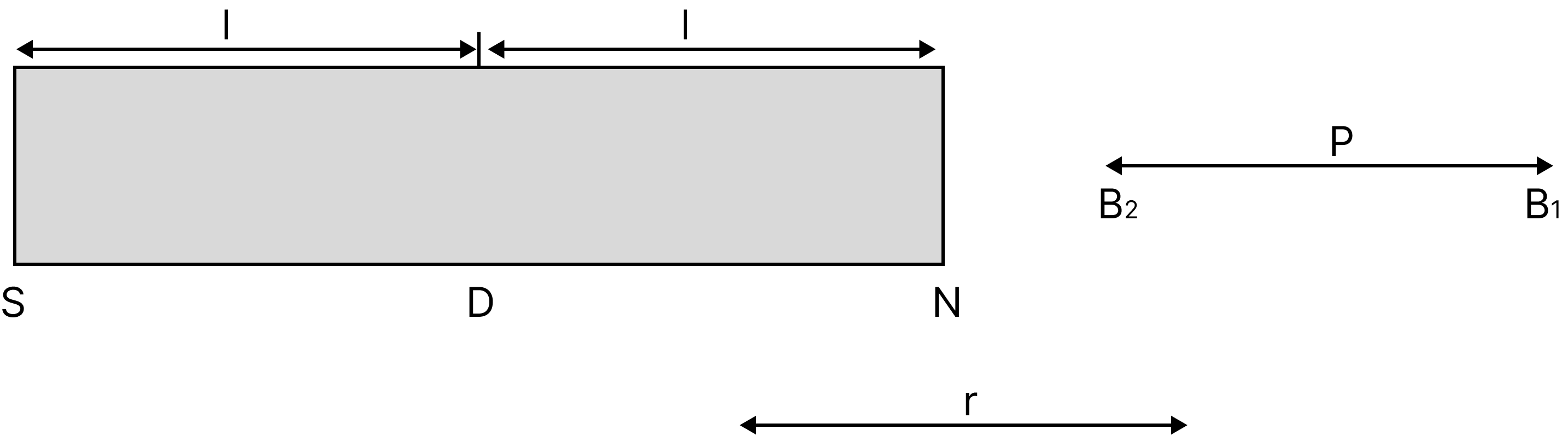
Expression of the Magnetic Field at Axial & Equatorial Point of a Bar Magnet

Let NS be a bar magnet with poles that are each of magnetic strength m and magnetic length 2l. The magnetic field must be measured at a point on an axial line called P that is located r distance from the magnet's centre, O.

The magnetic field $B_{1}$ at $P$ due to $N$ pole of magnet,

$\mathrm{B}_{1}=\dfrac{\mu_{0}}{4 \pi} \cdot \dfrac{\mathrm{m}}{\mathrm{NP}^{2}}$

or $B_{1}=\dfrac{\mu_{0}}{4 \pi} \cdot \dfrac{\mathrm{m}}{(\mathrm{r}-1)^{2}}$ (along $\mathrm{PX}$ ) ......................eq 1

And , the magnetic field $B_{2}$ at $P$ due to $S$ pole of magnet,

$\mathrm{B}_{2}=\dfrac{\mu_{0}}{4 \pi} \cdot \dfrac{\mathrm{m}}{\mathrm{SP}^{2}}$

or $B_{2}=\dfrac{\mu_{0}}{4 \pi} \cdot \dfrac{\mathrm{m}}{(\mathrm{r}+1)^{2}}$ (along PS) .....................eq 2

Therefore, resultant magnetic field at point $P$,

$\mathrm{B}=\mathrm{B}_{1}-\mathrm{B}_{2}$ (-ive sign is due to opposite directionS of $\mathrm{B}_{1}$ and $\mathrm{B}_{2}$ )

It is clear from eq1 and eq2 that $B_{1}>B_{2}$, therefore the direction of $B$ will be along PX .

or $B=\dfrac{\mu_{0}}{4 \pi} \cdot \dfrac{m}{(r-1)^{2}}-\dfrac{\mu_{0}}{4 \pi} \cdot \dfrac{m}{(r+1)^{2}} \quad$ (alongPX)

or $B=\dfrac{\mu_{0}}{4 \pi} \cdot \dfrac{m(4 r 1)}{\left(r^{2}-1^{2}\right)^{2}} \quad$ (alongPX)

Now, $\mathrm{m}(21)=\mathrm{M}$ (magnetic dipole moment of magnet)

Hence,$B=\dfrac{\mu_{0}}{4 \pi} \cdot \dfrac{2 \mathrm{Mr}}{\left(r^{2}-1^{2}\right)^{2}}$ (along PX)

Tangent Galvanometer:

A particular galvanometer with a vertical wire coil and a horizontal magnetic needle in the middle. The coil receives the current to be measured, which creates a proportionate magnetic field that causes the needle to deflect.

If the magnetic needle held at the centre of the coil of a tangent galvanometer with n turns and a mean radius of r creates a deflection when a current flows through it, then

$I=\left(\dfrac{2 \mathrm{rH}}{\mu_{0} \mathrm{n}}\right) \tan \theta ; \mathrm{I}=\mathrm{K} \tan \theta $

$\text { where } \mathrm{K}=\dfrac{2 \mathrm{rH}}{\mu_{0} \mathrm{n}} \text { and is called the reduction factor. }$

Formula Chart:

1. For bar magnet $\mathrm{L}_{\mathrm{e}}=21$ and $\mathrm{L}_{\mathrm{e}}=(5 / 6) \mathrm{L}_{\mathrm{g}}$.

For semi-circular magnet $\mathrm{L}_{\mathrm{g}}=\pi R$ and $\mathrm{L}_{\mathrm{e}}=2 \mathrm{R}$.

2. Law of magnetic poles: $\oint \vec{B} \cdot d \vec{s}\left(\right.$ or $\left.\int \vec{B} \cdot d \vec{s}\right)=0$.

3. Atom as a magnetic dipole: $M=\dfrac{n e h}{4 \pi m}=n \mu_{B}$

Where $n=1,2,3 \ldots .$ denotes the no. of orbits and $\mu_{B}=\dfrac{e h}{4 \pi m}$. Least value of dipole moment of atom $=9.27 \times 10^{-24}$ $\mathrm{Am}^{2}$.

4. Magnetic moment: $\overrightarrow{\mathrm{M}}=\mathrm{m} \times 2 l \times(\overrightarrow{\mathrm{n})} \Rightarrow|\overrightarrow{\mathrm{M}}|=2 \mathrm{~m} \ell$

5. Circular current loop as a magnet: $\vec{M}=\mathrm{I} A \hat{n}$

6. Relation between magnetic moment and angular momentum: $\vec{M}=\dfrac{q}{2 m} \vec{L}$

7. Coulomb’s Law of magnetic force: $F=\dfrac{\mu_{0}}{4 \pi} \cdot \dfrac{m_{1} m_{2}}{r^{2}}$

8. Torque on a magnet in a magnetic field: $\vec{\tau}=\vec{M} \times \vec{B} ; \tau=M B \sin \theta$

9. Work done by external agent in rotating the magnet: $W_{e x t}=\int_{\theta_{0}}^{\theta}(M B \sin \theta) d \theta$

10. Work done in rotating a uniform magnetic dipole in a magnetic field: 

$\mathrm{W}=\mathrm{MB}(1-\cos \theta)$

If $\theta=0, \cos \theta=1$ then $W=M B(1-1)=0$

If $\theta=90^{\circ}, \cos \theta=0$ then $\mathrm{W}=\mathrm{MB}$

If $\theta=180^{\circ}, \cos \theta=-1$, then $W=2 \mathrm{MB}$

11. Gauss law in magnetism: $\oint_{S} \vec{B} \cdot \overrightarrow{d a}=0$

12. Magnetic intensity: $H=\dfrac{B}{\mu}$

13. Intensity of Magnetisation (I): $\mathrm{I}_{\mathrm{m}}=\dfrac{M}{V}$

14. Magnetic susceptibility (χ): $\chi=\dfrac{\mathrm{I}_{\mathrm{m}}}{H}$

15. Magnetic Permeability (μ): $\mu=\dfrac{B}{H}$

Example 1: If the number of atoms in the domain in ferromagnetic iron, in the form of a cube of side length $1\mu m$, is 8.65 X ${{10}^{10}}$ atoms and dipole moment of each iron atom is $9.27\times {{10}^{-24}}\text{A}{{\text{m}}^{2}}$, what is the maximum Magnetization of the domain?

(a) $6\times {{10}^{5}}~\text{A}/\text{m}$

(b) $7\times {{10}^{5}}~\text{A}/\text{m}$

(c) $8\times {{10}^{5}}~\text{A}/\text{m}$

(d) $9\times {{10}^{5}}~\text{A}/\text{m}$

Solution: Correct option is ‘c’.

Explanation:

we know that, the maximum dipole moment $=\text{N}\times \text{m}$

${{\text{M}}_{\max }}=8.65\times {{10}^{10}}\times 9.27\times {{10}^{-24}}$

$=8\times {{10}^{-13}}\text{A}{{\text{m}}^{2}}$

Volume $={{\left( {{10}^{-6}} \right)}^{3}}={{10}^{-18}}~{{\text{m}}^{3}}$

Therefore, Magnetization $={{\text{M}}_{\max }}/$ Volume

$=8\times {{10}^{-13}}\text{A}{{\text{m}}^{2}}/{{10}^{-18}}~{{\text{m}}^{3}}$

$=8\times {{10}^{5}}~\text{A}/\text{m}$

Hence, the maximum magnetization of the domain is $8\times {{10}^{5}}~\text{A}/\text{m}$.

Example 2: The earth's magnetic field at a given point is $0.5\times {{10}^{-5}}\text{Wb}{{\text{m}}^{-2}}$. This field is to be annulled by magnetic induction at the centre of a circular conducting loop of radius $5.0~\text{cm}$. The current required to be flown in the loop is nearly:

(a) $0.2~\text{A}$

(b) $0.4~\text{A}$

(c) $4~\text{A}$

(d) $40~\text{A}$

Solution: Correct option is ‘b’.

Explanation:

According to the question given that, Earth's magnetic field at a point

${{B}_{E}}=0.5\times {{10}^{-5}}\text{Wb}{{\text{m}}^{-2}}$

The radius of a circular ring, $r=5~\text{cm}$

Hence, for the field to be annulled by magnetic induction at the centre of the circular conducting loop of radius $5~\text{cm}$, then ${{\text{B}}_{\text{E}}}={{\text{B}}_{\text{R}}}$ [Magnetic field at ring centre]

$0.5\times {{10}^{-5}}=\dfrac{{{\mu }_{0}}i}{2r}$

$0.5\times {{10}^{-5}}=\dfrac{{{\mu }_{0}}i\times 2\pi }{2r\times 2\pi }$

$\dfrac{{{\mu }_{0}}}{\mu \pi }={{10}^{-7}}$

$0.5\times {{10}^{-5}}={{10}^{7}}\times \dfrac{i\times 2\pi }{5\times {{10}^{-2}}}$

$0.5\times {{10}^{-5}}=\dfrac{2\times 3.14\times {{10}^{-7}}}{5\times {{10}^{-2}}}\times i$

$\text{i}=0.4~\text{A}$

Hence, the current required to be flown in the loop is nearly 0.4A.

Common Errors or Mistakes that should be Avoided by the Students Keeping the Exam Point of View:

• Calculation errors when doing problems. Students forget to write the working formula.

• Students also write improper units without checking their compatibility.

• Students forget to put in the correct data they used in the working formula, which teachers use to check how effective the students are learning.

• A  law stated by someone cannot be restructured; it should be reiterated like how it was stated.

• While drawing a graph, students forget to state the variables of the graph and just plot the graph.

• For questions requiring the reason for a certain condition, first, students are required to state the cause and then the consequence of the condition.

Importance of the NEET Physics Chapter Magnetism and Matter

This is one of the crucial chapters of the Class 12 Physics syllabus for NEET preparation. It introduces students to magnetism and its advanced concepts related to the effects of magnetic force in different cases.

When you refer to the Magnetism and Matter notes, you will find out the special cases where a unit charge travels maintaining a unit velocity in different cases of magnetic fields. All the implications and derivations will be shown in the form of mathematical expressions.

This chapter explains all these concepts using the fundamental principles of vector, force, magnetic force, and magnetism of electrical conductors. Understand these cases with proper explanation and learn how things change when the parameters change.

Find out how you can calculate these effects on an electric charge travelling in a magnetic field. The dimensions and units will be calculated using specific formulae derived from various laws.

Get the idea of the vector components calculated to find out the results accurately. The description and derivation of terms and formulae following the laws will help you understand the implications.

Benefits of Vedantu’s Magnetism and Matter NEET Notes

• These revision notes have been prepared by the subject matter experts to address the critical portions of this chapter. The simpler explanation of the scientific principles related to matter and magnetism will help you grab the objective of learning them and to answer fundamental questions faster.

• These Magnetism and Matter NEET notes have been prepared in a simpler format so that students can easily correlate and remember them. All the concepts, formulae, definitions, and derivations have been simplified so that you can revise and remember them easily even during the crucial hours of the NEET exam.

• Once you are done preparing this chapter, proceed to solve ample questions to evaluate your preparation level. Find out which sections of this chapter you need to work on more and make your preparation better.

• Find out how the experts have framed the solutions to the fundamental questions designed following the NEET level. Learn how to answer such questions accurately and score more in the exams.

Download Magnetism and Matter NEET Notes PDF

Get the free PDF version of these notes to complete your study material for magnetism and matter. Use the easiest and most concise explanation of all the concepts given to reduce your preparation time considerably. Revise these notes to remember all that you have studied in this chapter at a glance and progress to complete the syllabus in no time.

Other Important Links