Revision Notes on Kinetic Theory of Gases for NEET 2024

Ideal Gas

An ideal gas or a perfect gas is a gas which strictly obeys the gas laws.

Following are the Characteristic of the Ideal Gas:

• The size of the molecule of a gas is zero, i.e., each molecule of a gas is a point mass with no dimensions.

• There is no force of attraction or repulsion amongst the molecules of the gas.

Equation of an Ideal Gas:   $PV = nRT = {K_B}NT$

Where n is the number of moles and N is the number of molecules, R is the universal gas constant and ${K_B}$ is the Boltzmann constant.

${K_B} = \dfrac{R}{{{N_A}}}$

${N_A}$ is Avogadro's number.

Here,    $n = \dfrac{m}{M} = \dfrac{N}{{{N_A}}}$

Where m is the mass of the gas containing N molecules, M is the molar mass.

Another Form of an Ideal Gas Equation: $p = \dfrac{{\rho RT}}{M}$ where ρ is the density of the gas.

Gas Laws:

• Boyle’s Law: It states that at a constant temperature, the volume of a given mass of a gas is inversely proportional to the pressure.

$V \propto \dfrac{1}{P}$    Or   PV = constant.

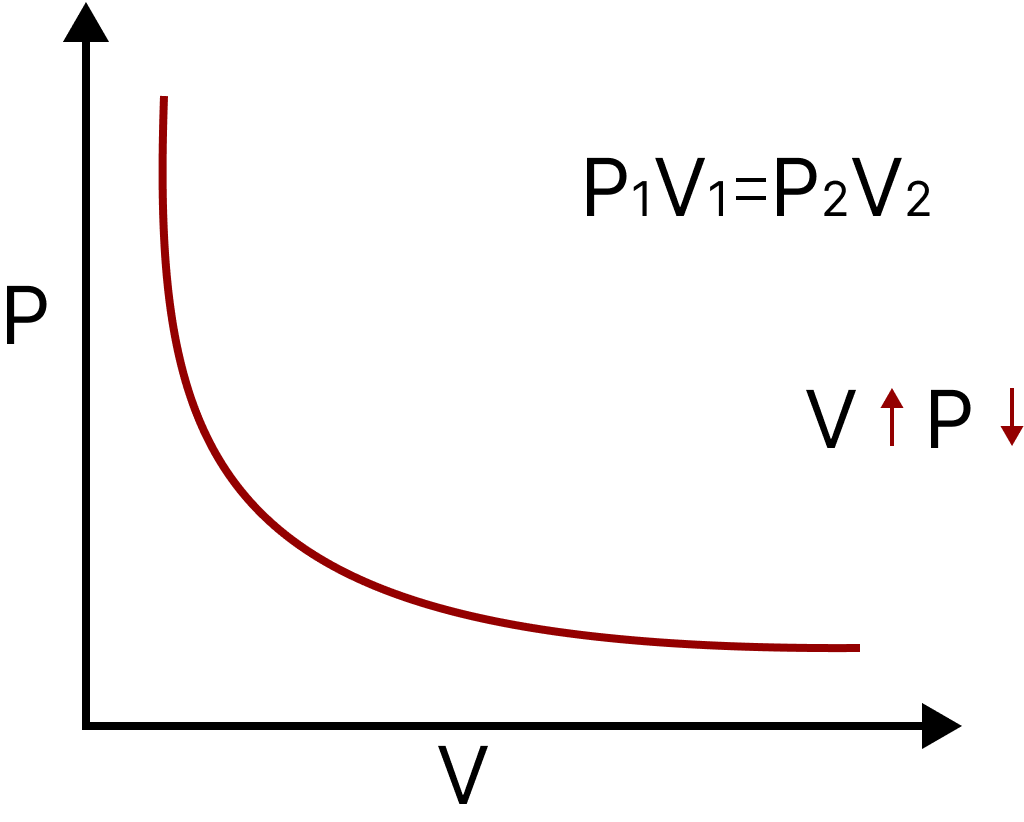
Boyle’s Law

• Charles’s Law: It states that at constant pressure, the volume of a given mass of gas is directly proportional to its absolute temperature.

$V \propto T$   Or   $\dfrac{V}{T} = K$ 

Charles Law

• Gay Lussac’s Law or Renault’s Law: It states that at a constant volume, pressure of a given mass of a gas is directly proportional to its absolute temperature.

$P \propto T$ Or  $\dfrac{P}{T} = K$ 

Gay-lussacc Law

• Avogadro’s Law: It states that at same temperature and pressure equal volumes of all the gases contain equal number of molecules.

${N_1} = {N_2}$  if P, V and T are the same.

• Graham’s Law of Diffusion: It states that at a constant pressure and temperature, the rate of diffusion of a gas is inversely proportional to the square root of its density.

Rate of diffusion$ \propto \dfrac{1}{{\sqrt \rho  }}$,   if P and T = constant.

• Dalton’s Law of Partial Pressure: It states that the total pressure exerted by a mixture of non-reactive ideal gases is equal to the sum of the partial pressure which each would exert, if it alone occupies the same volume at the given temperature.

$P = {P_1} + {P_2} + {P_3} + ......$

Work Done in Compressing a Gas

• Work done in compressing a gas from volume ${V_1}$ to volume ${V_2}$ is given by

$W =  - \int\limits_{{V_1}}^{{V_2}} {PdV}  = \int\limits_{{V_2}}^{{V_1}} {PdV} $

Where P is the pressure exerted by the gas enclosed. If the compression takes place at constant temperature P, then work done is

$W = P({V_1} - {V_2})$

Equation of a Real Gas

Real gases are gases which are non-ideal and whose molecules occupy space and have interactions; i.e. they don’t obey ideal gas law.

• Real gas obey Vander Waals equation,

$\left( {P + \dfrac{{{n^2}a}}{{{V^2}}}} \right)\left( {V - nb} \right) = nRT$

Where a, b are the Vander Waals constants.

• Critical Temperature: It is defined as the maximum temperature at which a gas can be liquefied by the increase of pressure alone. Above this temperature, the gas cannot be liquefied however large the pressure is applied. It is given by

${T_C} = \dfrac{{8a}}{{27Rb}}$

• Critical pressure: The pressure necessary to liquefy a gas at critical temperature is called the critical pressure. It is given by

${P_C} = \dfrac{a}{{27{b^2}}}$

• Critical Volume: It is the volume which unit mass of a gas occupies at a critical temperature and critical pressure.

${V_C} = 3b$

• Real gas behaves as an ideal gas at low pressure and high temperature.

Kinetic Theory of Gases

Postulates:

• A gas consists of a very large number of molecules which are perfect elastic Spheres. They are identical in all respects for a given gas and are different for different gases.

• The molecules of a gas are moving in all directions with different speeds.

• The size of the gas molecules is very small as compared to the distance between them. Hence volume occupied by the molecules is negligible in comparison to the volume of the gas.

• The molecule does not exert any force of attraction or repulsion on each other, except during collision.

• The collisions of the molecules within themselves and with the walls of the vessel are perfectly elastic.

• A molecule moves along a straight line between two successive collisions and the average straight distance covered between two successive collisions is called the mean free path of the molecules.

• The collisions are almost instantaneous i.e. the time of collision of two molecules is negligible as compared to time travel between two successive collisions.

Pressure of a Gas using Kinetic Theory:

$P=\dfrac{1}{3}\left( \dfrac{mNc_{i}^{2}}{V} \right)$ or $P=\dfrac{1}{3}\left( \rho {c_{i}}^{2} \right)$ 

Where,

• M is the mass of the gas

• N is the number of molecules

• $c_{i}^{2}$ Is the root-mean square velocity

• V is the volume of the gas

• $\rho $ is the density i.e. $\rho =\dfrac{mN}{V}$ 

Keeping this in mind for a gas with$P=\dfrac{1}{3}\left( \rho c_{i}^{2} \right)$ , we have its energy to be

$E=\dfrac{1}{2}\rho c_{i}^{2}$ When$P=\dfrac{2}{3}E$ .

Kinetic Interpretation of Temperature:

• Average kinetic energy per molecule of a gas is,

$E = \dfrac{1}{2}m{v^{ - 2}} = \dfrac{3}{2}{k_B}T$

• Here v is the root mean square velocity, m is the mass of the gas, $k_B$ is called Boltzmann constant (${{k}_{B}}=1.38\times {{10}^{-23}}$ ) and T is the absolute temperature.

• Average kinetic energy per molecule of a gas depends only on its absolute temperature. It is independent of the pressure, volume and nature of the ideal gas.

• At a given temperature, the average kinetic energy per molecule of all the gases is the same.

• Average kinetic energy per mole of a gas is $E = \dfrac{3}{2}RT$

Absolute Zero of Temperature: Absolute zero of temperature may be defined as that temperature at which the velocities of the gas molecules become zero. In other words, all molecular motion ceases at absolute zero of temperature. The value of absolute zero for an ideal gas is -273 Celsius. This definition is true only in the case of an ideal gas.

$PV = \dfrac{2}{3}E$

Maxwell-Boltzmann Distribution law:

According to this law, “All the molecules in the gas move with different velocity in different directions”.

Mathematically: $\dfrac{1}{N}\dfrac{du}{dN}=4\pi {{u}^{2}}{{\left( \dfrac{m}{2\pi {{k}_{b}}T} \right)}^{\dfrac{3}{2}}}{{e}^{\left( -\dfrac{m{{u}^{2}}}{2{{k}_{b}}T} \right)}}$ 

This is called the Maxwell-Boltzmann Distribution equation.

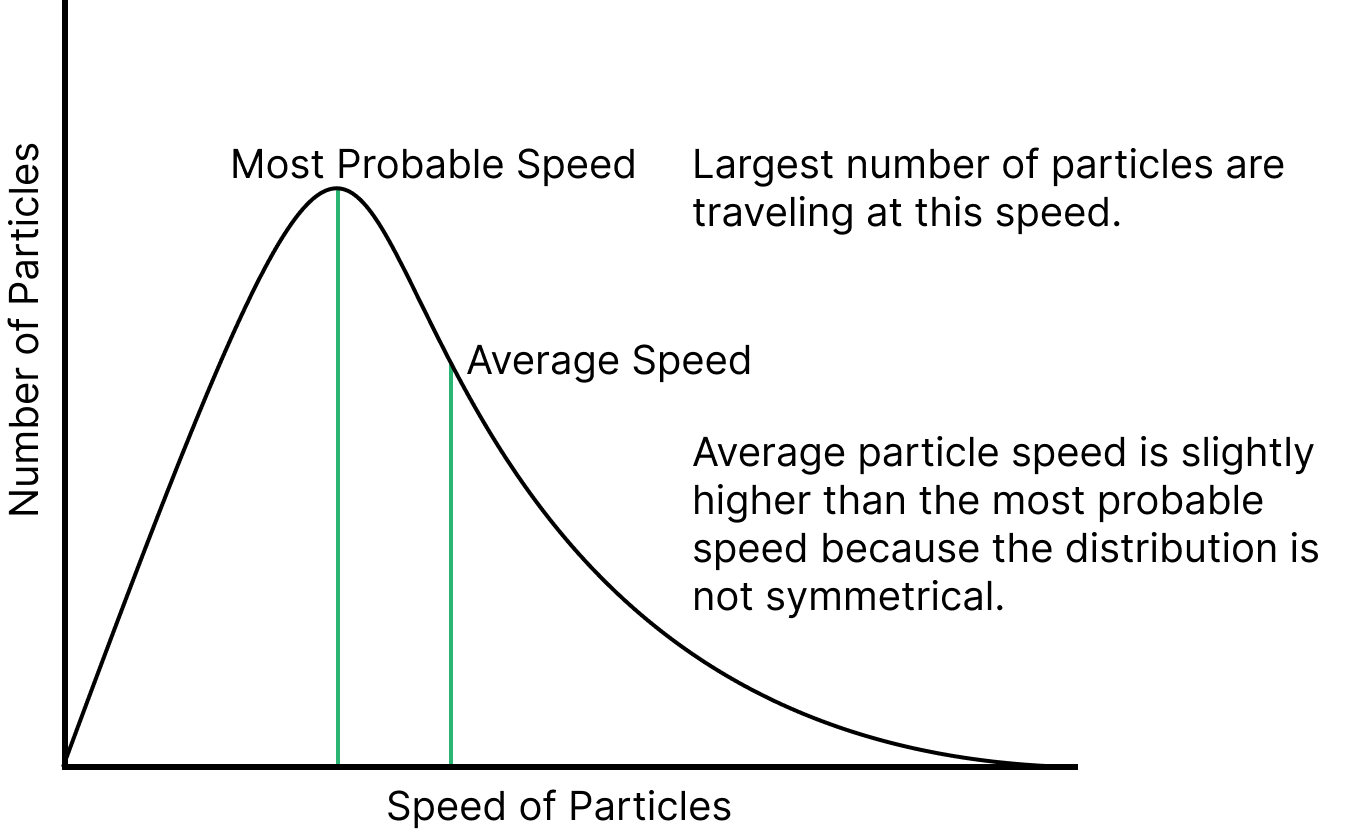
 Maxwell-Boltzmann Distribution Curve

Most Probable Speed: Speed acquired by most of the molecules of the gas at constant temperature is called most-probable speed.

${{v}_{mp}}=\sqrt{\dfrac{2{{k}_{B}}T}{M}}$ 

Average Speed: It is defined as the mean (or) average speed of all the speed of molecules.

${{v}_{av}}=\sqrt{\dfrac{8{{k}_{B}}T}{\pi M}}$ 

Root Mean Square Speed: It is defined as the value of square root of the sum of the squares of the stacking velocity values divided by the number of values.

${{v}_{rms}}=\sqrt{\dfrac{3{{k}_{B}}T}{m}}$ or ${{v}_{rms}}=\sqrt{\dfrac{v_{1}^{2}+v_{2}^{2}+......+v_{n}^{2}}{n}}$ 

Degrees of Freedom

The number of degrees of freedom of a gas molecule is defined as the no of molecules aligned to move freely in the space given by formula F= 3N-K

Where, 

N = Number of atoms in the molecule

K = Number of independent relations between atoms of a molecule

Relation between 𝛄 and degree of freedom (f) $\gamma  = 1 + \dfrac{2}{f}$

Table Showing Degrees of Freedom for Different Gases:

Law of Equipartition of Energy: 

It states that “If a system is in equilibrium at absolute temperature T, the total energy is distributed equally in different energy modes of absorption, the energy in each mode being equal to $\left( {\dfrac{1}{2}} \right){k_b}T$”.

For molecules to move freely in space, it requires three coordinates to specify its location i.e. three translational degrees of freedom ($a_x,a_y,a_z$) respectively. The position holds its centre of mass where these three ($a_x,a_y,a_z$) translational degrees of freedom rotate accordingly from a. Depending on the type of gas, and this rotation the total energy of gas is calculated which includes translational and rotational energy.

Each translational and rotational degree of freedom corresponds to one energy mode of absorption and has energy $\left( {\dfrac{1}{2}} \right){k_b}T$. 

Each vibration frequency has two modes of energy (kinetic and potential) with corresponding energy equal to $2 \times \dfrac{1}{2}{k_B}T = {k_B}T$.

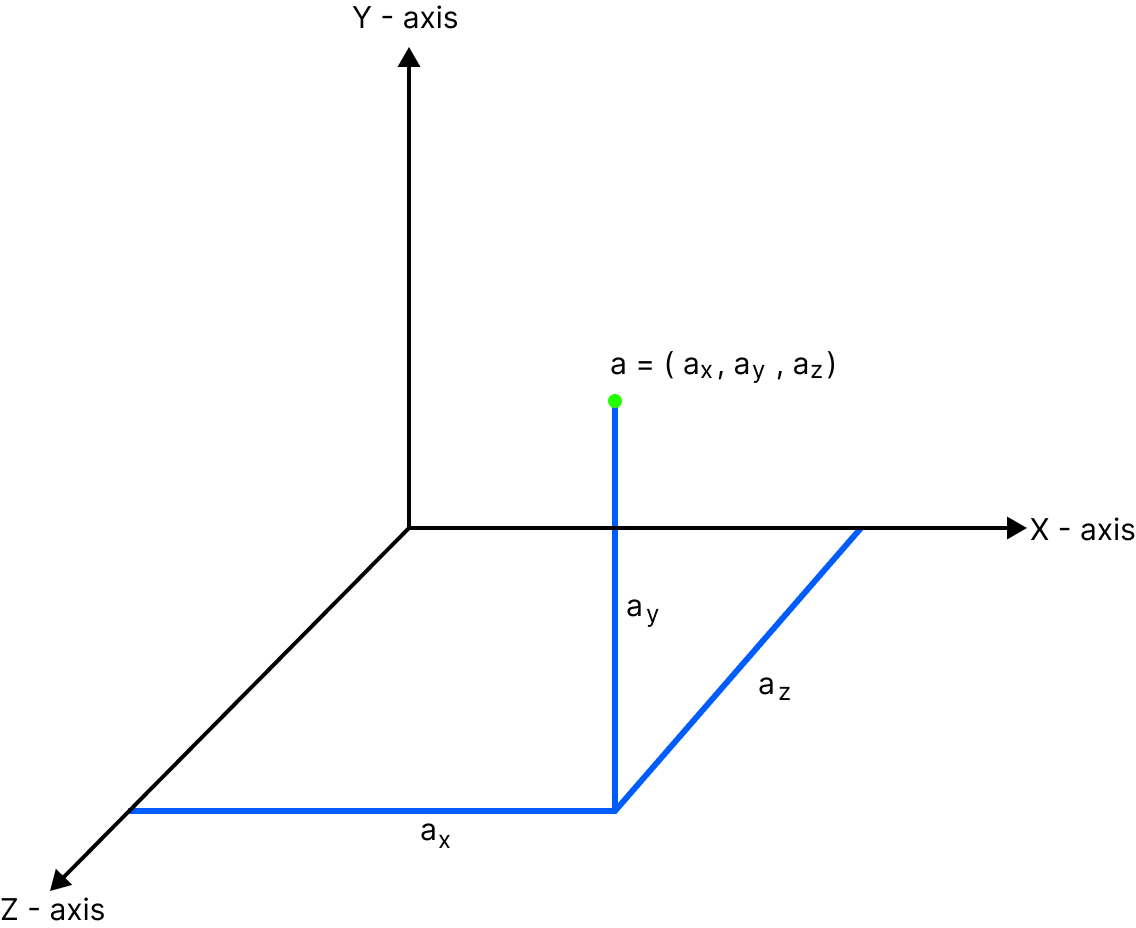
Law of Equipartition of Energy

Specific Heat Capacity:

Specific heat capacity of a gas is defined as the heat capacity which is required for the expansion of a gas.

Monatomic Gases: The molecule of a monatomic gas has only three translational degrees of freedom.

• The total internal energy of a mole of such a gas is given by $U = \dfrac{3}{2}{k_B}T \times {N_A} = \dfrac{3}{2}RT$

• The molar specific heat at constant volume, ${C_V}$ is ${C_V} = \dfrac{{dU}}{{dT}} = \dfrac{3}{2}R$

• The molar specific heat at constant pressure, ${C_P}$ is ${C_P} = \dfrac{5}{2}R$$(\because {C_P} - {C_V} = R)$

• Ratio of molar specific heats,  $\gamma  = \dfrac{{{C_P}}}{{{C_V}}} = \dfrac{5}{3}$

Diatomic Gases: A diatomic gas molecule treated as a rigid rotor like a dumbbell as 5 degrees of freedom three translational and rotational.

•  The total internal energy of a mole of such a gas is given by

$U = \dfrac{5}{2}{k_B}T \times {N_A} = \dfrac{5}{2}RT$

• The molar specific heats are given by

${C_V}$(rigid diatomic) =  $\dfrac{5}{2}R$

${C_P}$(rigid diatomic) =  $\dfrac{7}{2}R$

γ (rigid diatomic) = $\dfrac{7}{5}$

• If the diatomic molecule is not rigid but as in addition a vibrational mode, then

$U = \left( {\dfrac{5}{2}{k_B}T + {k_B}T} \right){N_A} = \dfrac{7}{2}RT$

${C_V} = \dfrac{7}{2}R,{C_P} = \dfrac{9}{2}R,\gamma  = \dfrac{9}{7}$

Polyatomic Gases: In general, a polyatomic gas molecule has 3 translational, 3 rotational degrees of freedom and a certain number (f) of vibrational mode. The total internal energy of a mole of such a gas is given by

$U = \left( {\dfrac{3}{2}{k_B}T + \dfrac{3}{2}{k_B}T + f{k_B}T} \right){N_A} = (3 + f)RT$

The molar specific heats are given by

${C_V} = \left( {3 + f} \right)R,{C_P} = (4 + f)R$

$\gamma  = \dfrac{{(4 + f)}}{{(3 + f)}}$

Note: ${C_P} - {C_V} = R$ This relation is known as Mayer’s Relation.

Mean Free Path

It is the average distance covered by a molecule between two successive collisions and is given by

$\lambda  = \dfrac{1}{{\sqrt 2 n\pi {d^2}}}$

Where n is the number density and d is the diameter of the molecule.

Mean free path related to the temperature (T) and pressure (P) as $\lambda  = \dfrac{{{k_B}T}}{{\sqrt 2 \pi {d^2}p}}$

Points to Remember:

• An ideal gas or a perfect gas is a gas which strictly obeys the gas laws.

• Equation of an ideal gas:   $PV = nRT = {K_B}NT$

• Boyle’s Law: It states that at a constant temperature, the volume of a given mass of a gas is inversely proportional to the pressure.

• Charles’s Law: It states that at a constant pressure, volume of a given mass of gas is directly proportional to its absolute temperature.

• Avogadro’s Law: It states that at same temperature and pressure equal volumes of all the gases contain equal number of molecules.

• Work done in compressing a gas from volume ${V_1}$ to volume ${V_2}$ is given by

$W =  - \int\limits_{{V_1}}^{{V_2}} {PdV}  = \int\limits_{{V_2}}^{{V_1}} {PdV} $

Where P is the pressure exerted by the gas enclosed. If the compression takes place at constant temperature P, then work done is

$W = P({V_1} - {V_2})$

• Critical Temperature: It is defined as the maximum temperature at which a gas can be liquefied by the increase of pressure alone. Above this temperature, the gas cannot be liquefied however large the applied pressure may be. It is given by

${T_C} = \dfrac{{8a}}{{27Rb}}$

• Critical Pressure: The pressure necessary to liquefy a gas at critical temperature is called the critical pressure. It is given by

${P_C} = \dfrac{a}{{27{b^2}}}$

• Critical Volume: It is the volume which unit mass of a gas occupies at a critical temperature and critical pressure.

${V_C} = 3b$

• Average kinetic energy per molecule of a gas is

$E = \dfrac{1}{2}m{v^{ - 2}} = \dfrac{3}{2}{k_B}T$

• Law of Equipartition of energy: It states that “If a system is in equilibrium at absolute temperature T, the total energy is distributed equally in different energy modes of absorption, the energy in each mode being equal to $\left( {\dfrac{1}{2}} \right){k_b}T$”.

• Specific heat capacity of a gas is defined as the heat capacity which is required for the expansion of a gas.

• Absolute zero of temperature may be defined as that temperature at which the velocities of the gas molecules become zero. In other words, all molecular motion ceases at absolute zero of temperature. The value of absolute zero for an ideal gas is -273 Celsius.

• Types of gases are: monatomic gas, diatomic gas , triatomic gas, polyatomic gas.

• Maxwell-Boltzmann Distribution Law:

According to this law, “All the molecules in the gas move with different velocity in different directions”. Mathematically: $\dfrac{1}{N}\dfrac{du}{dN}=4\pi {{u}^{2}}{{(\dfrac{m}{2\pi {{k}_{b}}T})}^{\dfrac{3}{2}}}{{e}^{\left( -\dfrac{m{{u}^{2}}}{2{{k}_{b}}T} \right)}}$ 

• Mean free path: It is the average distance covered by a molecule between two successive collisions and is given by

$\lambda  = \dfrac{1}{{\sqrt 2 n\pi {d^2}}}$

Example:

1. A gas mixture consists of 2 moles of oxygen and 4 moles of argon at temperature T. Neglecting all vibration modes, the total internal energy of the system is:

a) 15RT b) 9RT         c) 11RT       d) depends on value of n

Answer: c) and d)

Solution: 

The internal energy of 2 moles of oxygen atom is: ${U_o} = \dfrac{{nf}}{2}RT = 2 \times \dfrac{5}{2}RT = 5RT$ 

The internal energy of 4 moles of argon atom is: ${U_{Ar}} = \dfrac{{nf}}{2}RT = 4 \times \dfrac{3}{2}RT = 6RT$ 

Total energy is: 5RT + 6RT = 11RT

This internal energy is calculated by the formula ${U_g} = \dfrac{{nf}}{2}RT$ which depends on n.

Thus options c) and d) are correct options.

2. The pressure of a gas kept in an isothermal container is 200 kPa. Which of the following statements is true?

a) Pressure of the gas can be calculated using Ideal gas equation

b) Value of pressure, if half of the gas is removed, is 100 kPa

c) Degrees of freedom depend on the pressure of the gas

d) Avogadro number of particles is inversely proportional to the pressure exerted by the gas.

Answer: a), b) and d)

Solution:

We know that the Ideal gas equation: $PV = nRT$ i.e. we can calculate the pressure of gas using this equation.

For n moles of gas and Avogadro number of particles, we have: $PV = \left( {\dfrac{N}{{{N_A}}}} \right)RT$ 

By the above equation, we can conclude that$P\alpha {\dfrac{1}{N}_A}$ .

Since P is inversely proportional to ${N_A}$  we have its pressure when half of the gas particles to be removed would be:

$P = \dfrac{{200}}{2} = 100kPa$ .

Hence options a), b) and d) options are correct.

Importance of Kinetic Theory of Gases

This chapter will explain the definitions of different terminologies used to explain the kinetic theory of gases. Students will learn what the speed of molecules of a gas is and how it can be calculated. They will learn how to calculate the kinetic energy of a gas.

They will find out what pressure is and how it can be correlated to the kinetic theory. The chapter will explain how the pressure of a gas increases when the kinetic energy of the molecules increases.

This chapter is important as it explains the various physical properties of gases in terms of kinetic theory. The average energy of the gases can be linked to the different terms. The scientific principles of this chapter can also be linked to thermodynamics and other fundamental chapters of physics.

On proceeding further, this chapter will introduce the concepts of specific heat capacities of gases using the kinetic theory. Students will learn to calculate the amount of heat a gas can hold at a particular temperature.

Using the Kinetic Theory of Gases notes as a reference will help students to complete preparing this chapter easily. They will also understand the application of laws related to the kinetic theory without any difficulty.

Benefits of Vedantu’s Kinetic Theory of Gases Notes for NEET

• These notes offer a consolidated study material where all the concepts, laws, scientific terms, and principles have been defined and described in a concise format. This accurate format will help you reduce your time to prepare and revise this chapter.

• You can use these notes for free. Your study sessions will become more productive when you use these notes to check the definitions and formulas of various scientific terms related to the kinetic theory of gases.

• Comprehending and correlating the scientific principles related to the theories and laws in this chapter will become a lot easier when they are explained in a simpler way. Students preparing for NEET will get immense help from these notes to complete the NEET syllabus in no time.

• You can check the mathematical derivation of all the scientific terms and laws at a glance and recall them during an exam. These notes make these concepts easier to remember.

Download Free Kinetic Theory of Gases Class 11 Notes PDF

The addition of the revision notes for this chapter will give you a better way to study the fundamental concepts related to the kinetic theory of gases. Find out how the experts have correlated the gas laws, diffusion law, law of partial gases, law of pressure, etc and prepare this chapter confidently. You can also check how the experts have answered sample questions. Revise this chapter using these notes and complete your syllabus faster.

Other Important Links

NEET Physics Revision Notes - Chapter Pages