Revision Notes on System of Particles and Rotational Motion for NEET 2024

Rigid Body:

• A rigid body is one in which the distances between different particles of the body do not change even though forces are acting on them.

• Axis of rotation: The line along which the body is fixed is known as the axis of rotation. Examples for rotation about an axis are a ceiling fan and a merry-go-round etc.

• In pure rotation of a rigid body about a fixed axis, every particle of the rigid body moves in a circle which lies in a plane perpendicular to the axis and has its centre on the axis. Every point in the rotating rigid body has the same angular velocity at any time.

Linkage of a Rigid Body

Centre of Mass:

• The centre of mass of a body is a point where the entire mass of the body can be supposed to be concentrated. The nature of motion executed by the body shall remain unaffected if all the forces acting on the body were applied directly at this point.

• For a system of two particles of masses ${m_1}$ and ${m_2}$ having their position vector has ${\vec r_1}$ and ${\vec r_2}$ respectively, with respect to origin of the coordinate system, the position vector ${\vec R_{CM}}$ of the centre of mass is given by

${\vec R_{CM}} = \dfrac{{{m_1}{{\vec r}_1} + {m_2}{{\vec r}_2}}}{{{m_1} + {m_2}}}$

If ${m_1} = {m_2} = m$ , then ${\vec R_{CM}} = \dfrac{{{{\vec r}_1} + {{\vec r}_2}}}{2}$

Thus, the centre of a mass of two equal masses lies exactly at the centre of the line joining the two masses.

• For a system of N-particles of masses  ${m_1},{m_2},{m_3}...{m_N}$ having their position vectors as  ${\vec r_1},{\vec r_2},{\vec r_3},...,{\vec r_N}$ respectively, with respect to the origin of the coordinate system, the position vector ${\vec R_{CM}}$ of the centre of mass is given by

${\vec R_{CM}} = \dfrac{{{m_1}{{\vec r}_1} + {m_2}{{\vec r}_2} + ... + {m_N}{{\vec r}_N}}}{{{m_1} + {m_2} + ...{m_N}}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec r}_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec r}_i}} }}{M}$

• The coordinates of centre of mass for a 3-D object is given as:

${X_{CM}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{x_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{x_i}} }}{M}$

${Y_{CM}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{y_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{y_i}} }}{M}$

${Z_{CM}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{z_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{z_i}} }}{M}$

• For a continuous distribution of mass, the coordinates of centre of mass are given by

${X_{CM}} = \dfrac{1}{M}\int {xdm;}$  ${Y_{CM}} = \dfrac{1}{M}\int {ydm;}$  ${Z_{CM}} = \dfrac{1}{M}\int {zdm}$ 

• Velocity of centre of mass

${\vec v_{CM}} = \dfrac{{{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + ... + {m_N}{{\vec v}_N}}}{{{m_1} + {m_2} + ...{m_N}}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec v}_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec v}_i}} }}{M}$

• Acceleration of centre of mass

${\vec a_{CM}} = \dfrac{{{m_1}{{\vec a}_1} + {m_2}{{\vec a}_2} + ... + {m_N}{{\vec a}_N}}}{{{m_1} + {m_2} + ...{m_N}}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec a}_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec a}_i}} }}{M}$

Angular Velocity and Acceleration:

• Angular velocity: It is defined as the time rate of change of angular displacement and is given by,

$\omega  = \dfrac{{d\theta }}{{dt}}$ 

• Angular velocity is directed along the axis of rotation. Angular velocity is a vector quantity. Its SI unit is rad/s and its dimensional formula is $\left[ {{M^0}{L^0}{T^{ - 1}}} \right]$ .

• Relationship between linear velocity and angular velocity

The linear velocity of a particle of a rigid body rotating about a fixed axis is given by,

$\vec v = \vec \omega  \times \vec r$ 

where   $\vec r$  is the position vector of the particle with respect to an origin along the fixed axis.

• As in pure translational motion, all body particles have the same linear velocity at any instant. Similarly, in pure rotational motion, all body particles have the same angular velocity at any instant.

• Angular acceleration: It is defined as the time rate of change of angular velocity, and it is given by

$\vec \alpha  = \dfrac{{d\vec \omega }}{{dt}}$ 

• Angular acceleration is a vector quantity. Its SI unit is  $rad{s^{ - 2}}$ and its dimensional formula is $\left[ {{M^0}{L^0}{T^{ - 2}}} \right]$ .

Equation of Rotational Motion:

After a brief introduction to angular velocity and angular acceleration, let us see how they are related to the kinematic equations.

For a certain initial angular velocity, final angular velocity ( ${\omega _o},\omega$ ) with time t, the kinematic equations of rotational motion is given as:

 ${\omega _0} = {\omega _0} + \alpha t$ 

 $\theta  = {\omega _0}t + \dfrac{1}{2}\alpha {t^2}$ 

 ${\omega ^2} - \omega _0^2 = 2\alpha \theta$ 

These equations are valid for uniform angular acceleration.

Moment of Inertia:

• Moment of inertia of a rigid body about a given axis of rotation is defined as the sum of the product of masses of all the particles of the body and the square of their respective perpendicular distances from the axis of rotation. It is denoted by symbol I and is given by,

$I = \sum\limits_{i = 1}^N {{m_i}r_i^3}$ 

• Moment of inertia is a scalar quantity. Its SI unit is  $kg{m^2}$ and its dimensional formula is $\left[ {{M^1}{L^2}{T^0}} \right]$ . It depends upon

• Position of the axis of rotation

• Orientation of the axis of addition

• Shape of the body

• Size of the body

• Distribution of mass of the body about the axis of rotation.

• Radius of gyration: It is defined as the distance from the axis of rotation at which, if the whole mass of the body were concentrated, the moment of inertia of the body would be the same as the actual distribution of the mass of the body. It is denoted by the symbol K.

• Radius of gyration of a body about an axis of rotation may also be defined as the root mean square distance of the particles from the axis of rotation.

i.e.,     $K = \sqrt {\dfrac{{r_1^2 + r_2^2 + ... + r_N^2}}{N}}$ 

• The moment of inertia of a body about a given axis is equal to the product of the mass of the body and square of its radius of gyration about that axis.

i.e.,  $I = M{K^2}$ .

• The SI unit of radius of gyration is metre and its dimensional formula is  $\left[ {{M^0}{L^1}{T^0}} \right]$ .

• Theorem of perpendicular axes: The moment of inertia of a planar lamina about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axis concurrent with a perpendicular axis and lying in the plane of the body.

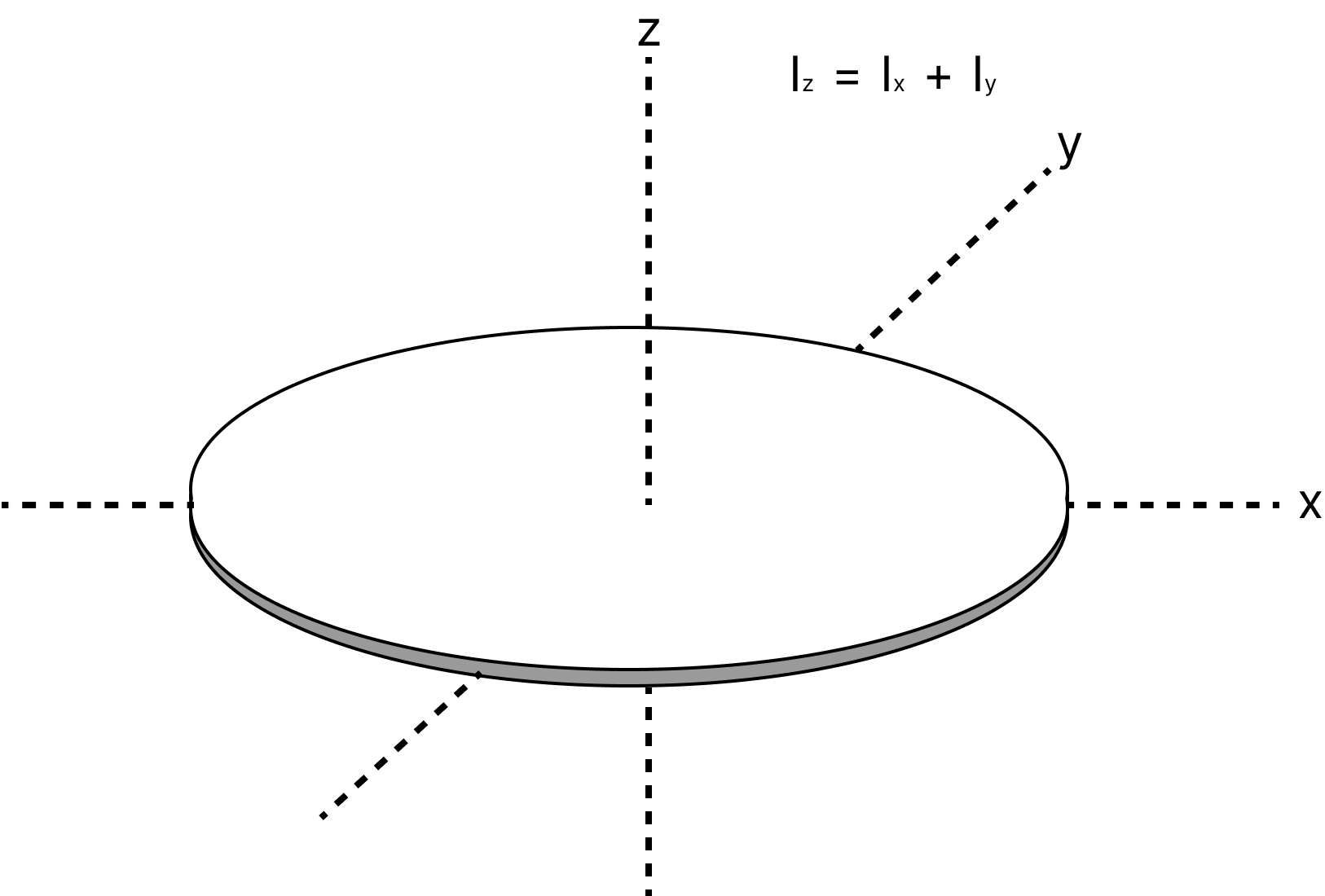
Theorem of Perpendicular Axes

 ${I_z} = {I_x} + {I_y}$ 

Where x and y are two perpendicular axes in the plane, and the z-axis is perpendicular to its plane.

• Theorem of parallel axes:  The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axis.

(Image will be uploaded soon)

Parallel Axis Theorem

$I = {I_{CM}} + M{d^2}$ 

Where  ${I_{CM}}$ is the moment of inertia of the body about an axis(z) passing through the centre of mass, and d is the perpendicular distance between two parallel axes.

The moment of inertia and radius of gyration of some regular bodies about a specific axis are given below

Sl. No	Body	Axis of Rotation	Moment of inertia (I)	Radius of Gyration (k)	Diagram
1	Uniform circular ring of mass M and radius R	About an axis passing through its centre and perpendicular to its plane	$M{R^2}$	R
		About its diameter	$\dfrac{1}{2}M{R^2}$	$\dfrac{R}{{\sqrt 2 }}$
		About a tangent in its own plane	$\dfrac{3}{2}M{R^2}$	$\sqrt {\dfrac{3}{2}} R$
		About a tangent perpendicular to its plane	$2M{R^2}$	$R\sqrt 2$
2	Uniform circular disc of mass M and radius R	About an axis passing through its centre and perpendicular to its plane	$\dfrac{1}{2}M{R^2}$	$\dfrac{R}{{\sqrt 2 }}$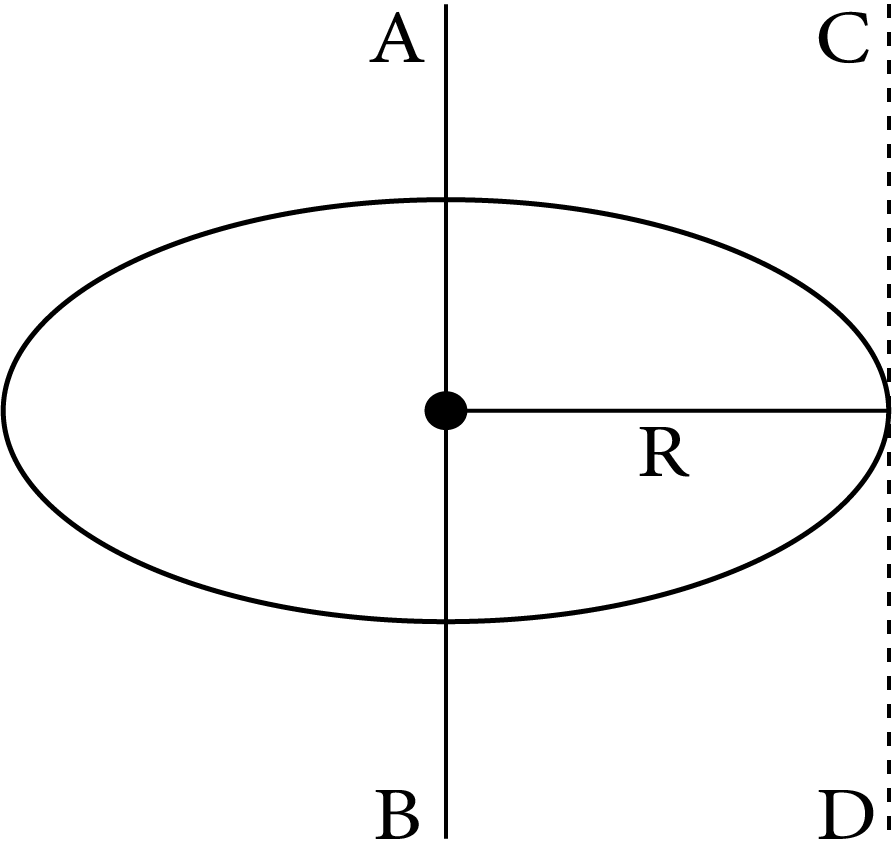
		About its diameter	$\dfrac{1}{4}M{R^2}$	$\dfrac{R}{2}$
		About a tangent in its own plane	$\dfrac{5}{4}M{R^2}$	$\sqrt 5 \dfrac{R}{2}$
		About a tangent perpendicular to its plane	$\dfrac{3}{2}M{R^2}$	$\sqrt {\dfrac{3}{2}} R$
3	Solid sphere of radius R and mass M	About its diameter	$\dfrac{2}{5}M{R^2}$	$\sqrt {\dfrac{2}{5}} R$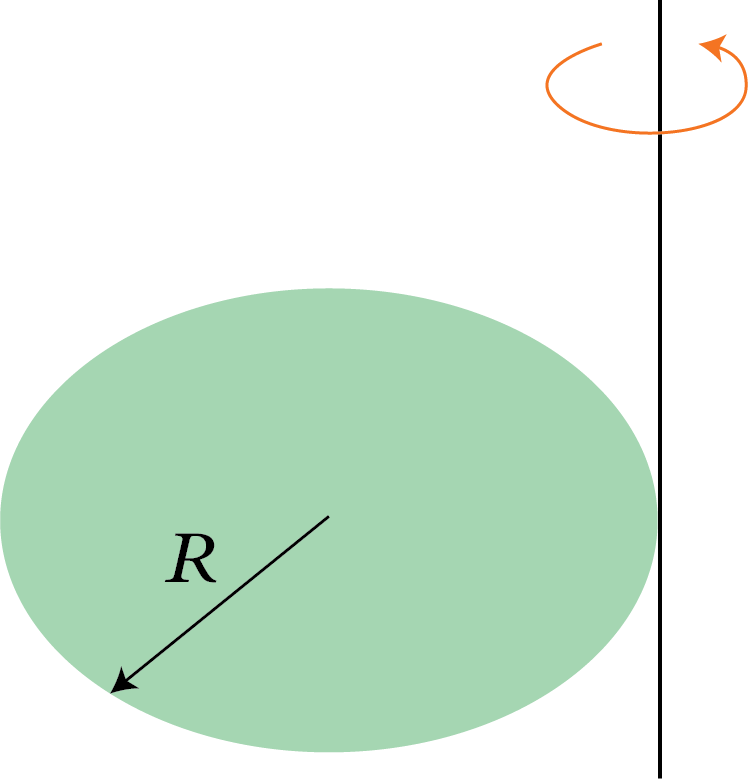
		About a tangential axis	$\dfrac{7}{5}M{R^2}$	$\sqrt {\dfrac{7}{5}} R$
4	Hollow sphere of radius R and mass M	About its diameter	$\dfrac{2}{3}M{R^2}$	$\sqrt {\dfrac{2}{3}} R$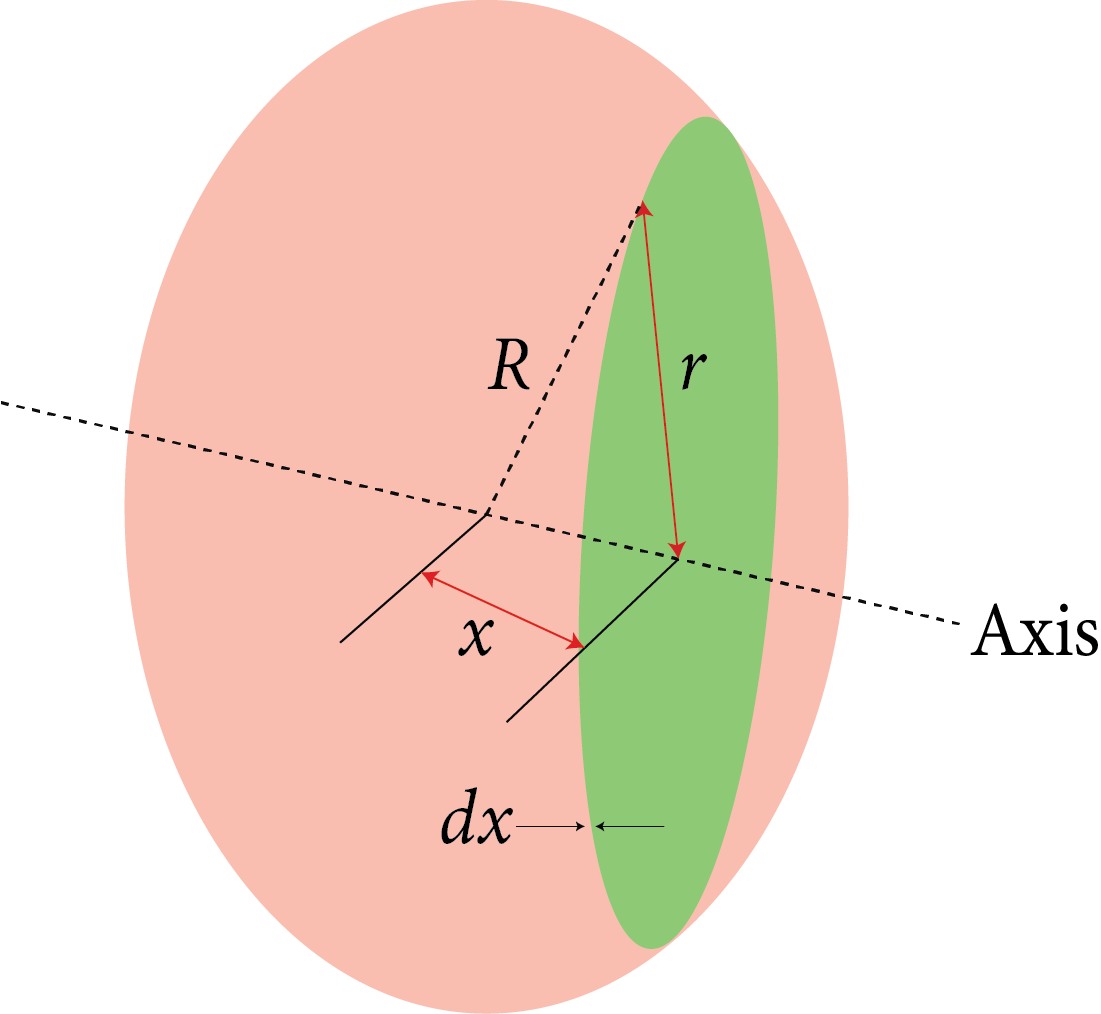
		About a tangential axis	$\dfrac{5}{3}M{R^2}$	$\sqrt {\dfrac{5}{3}} R$
5	Solid cylinder of length l, radius R and mass M	About its own axis	$\dfrac{1}{2}M{R^2}$	$\dfrac{R}{{\sqrt 2 }}$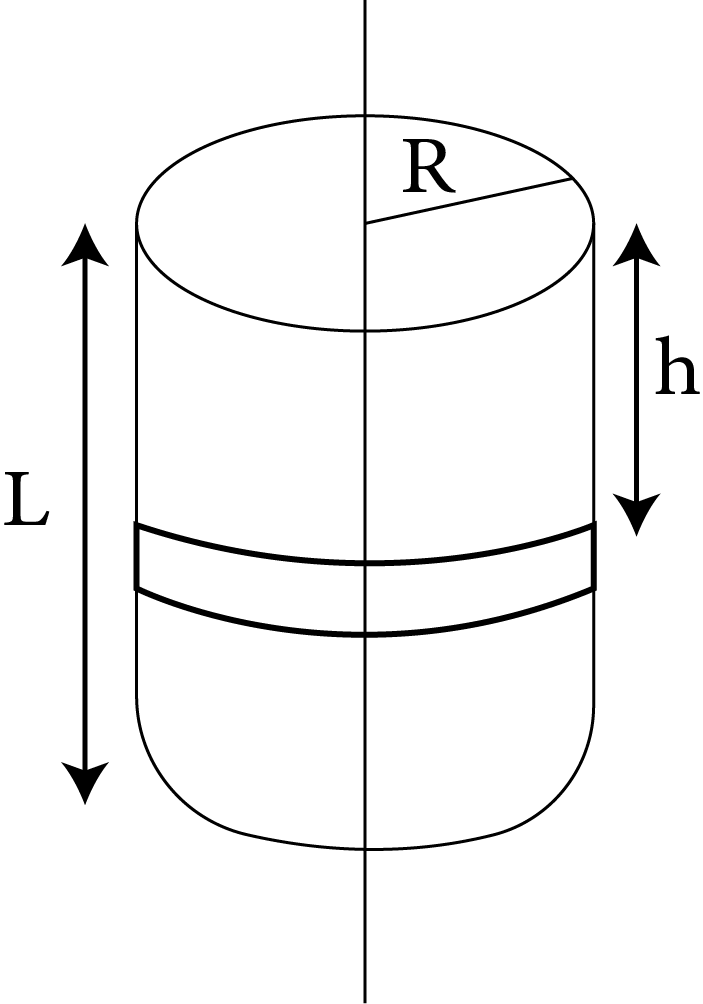
		About an axis passing through its centre and perpendicular to its own axis	$M\left[ {\dfrac{{{l^2}}}{{12}} + \dfrac{{{R^2}}}{4}} \right]$	$\sqrt {\dfrac{{{l^2}}}{{12}} + \dfrac{{{R^2}}}{4}}$
		About the diameter of one of the faces of cylinder	$M\left[ {\dfrac{{{l^2}}}{3} + \dfrac{{{R^2}}}{4}} \right]$	$\sqrt {\dfrac{{{l^2}}}{3} + \dfrac{{{R^2}}}{4}}$
6	Hollow, cylinder of mass M, length l and radius R	About its own axis	$M{R^2}$	R
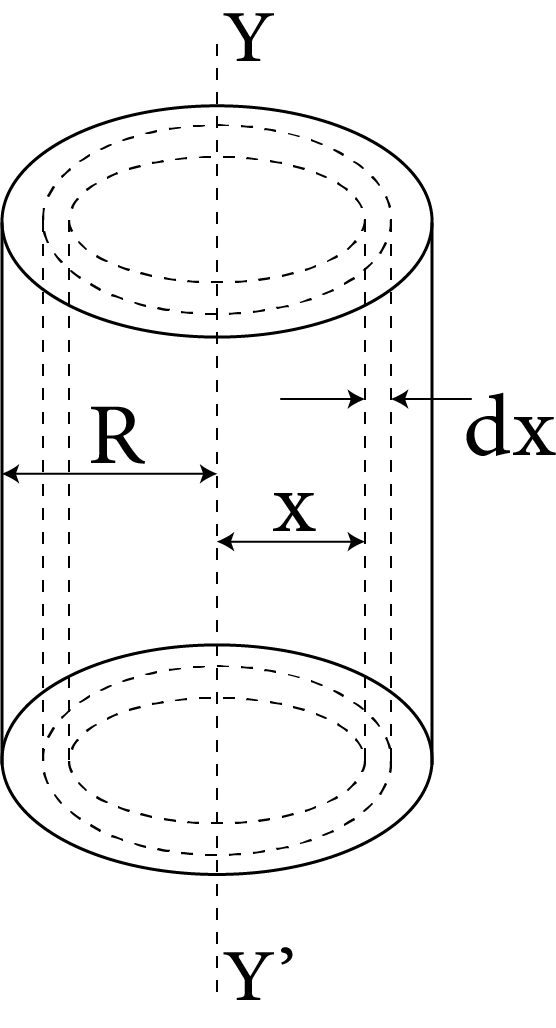
		About an axis passing through its centre and perpendicular to its own axis	$M\left( {\dfrac{{{R^2}}}{2} + \dfrac{{{l^2}}}{{12}}} \right)$	$\sqrt {\dfrac{{{R^2}}}{2} + \dfrac{{{l^2}}}{{12}}}$
7	Thin rod of length L	About an axis passing through its centre and perpendicular to the rod	$\dfrac{{M{L^2}}}{{12}}$	$\dfrac{L}{{\sqrt {12} }}$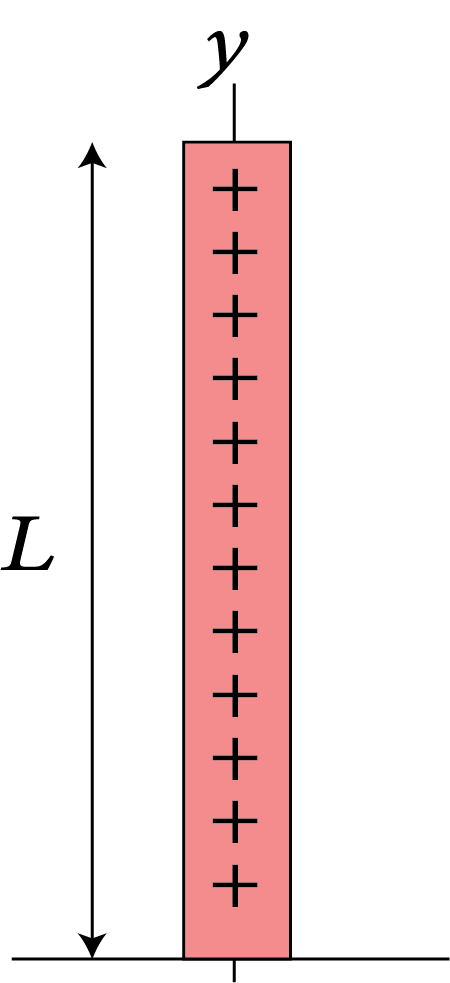
		About an axis passing through one end and perpendicular to the rod	$\dfrac{{M{L^2}}}{3}$	$\dfrac{L}{{\sqrt 3 }}$
8	Rectangular lamina of length l and breadth b	About an axis passing through its centre and perpendicular to its plane	$M\left[ {\dfrac{{{l^2} + {b^2}}}{{12}}} \right]$	$\sqrt {\dfrac{{{l^2} + {b^2}}}{{12}}}$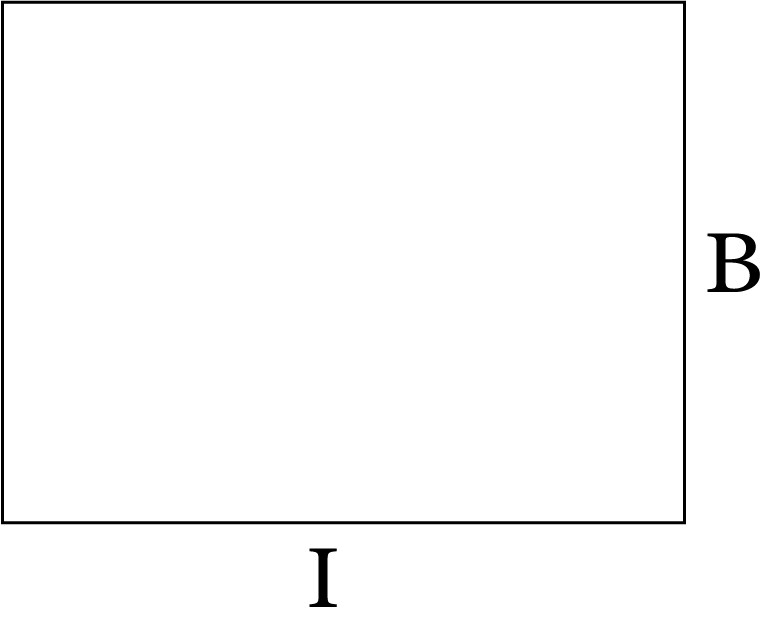
9	Uniform cone of radius R and height h	About an axis passing through its centre and joining its vertex to the centre of base	$\dfrac{3}{{10}}M{R^2}$	$R\sqrt {\dfrac{3}{{10}}}$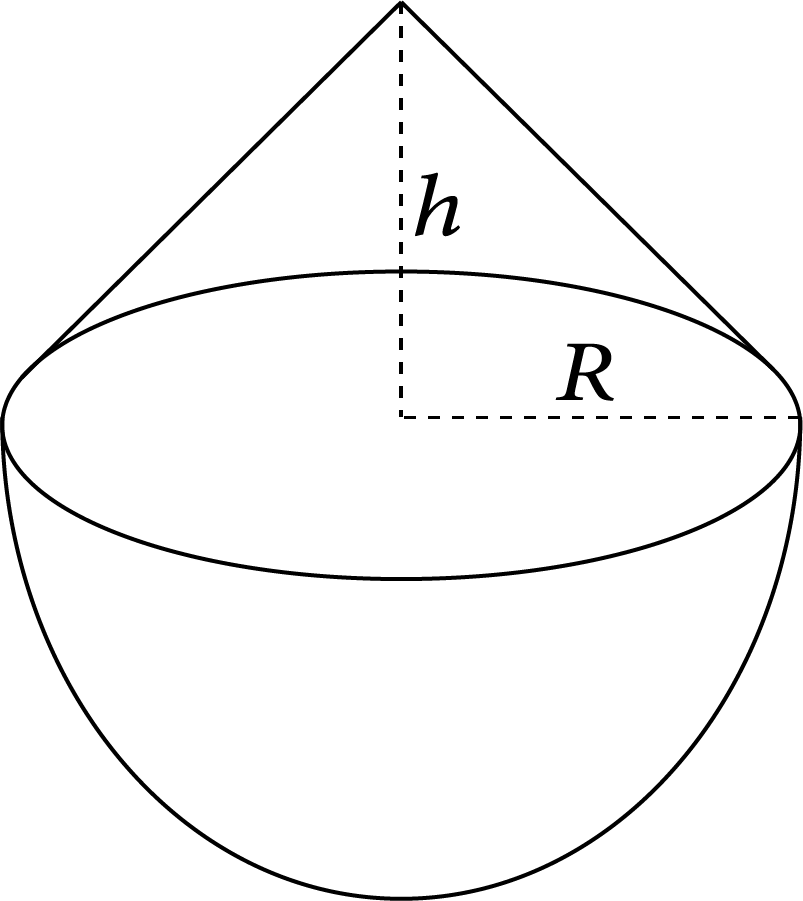
10	Parallelepiped of length l, breadth b and height h, mass M	About its central axis	$M\left( {\dfrac{{{l^2} + {b^2}}}{{12}}} \right)$	\[\sqrt{\frac{l^{2}+b^{2}}{12}}\]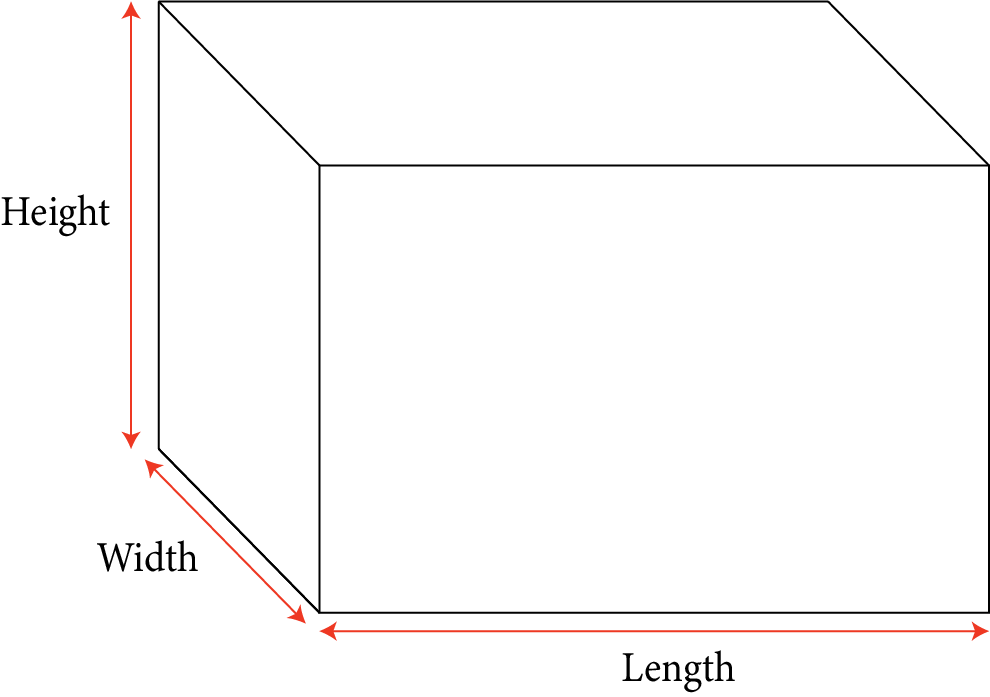

Torque:

• The torque or moment of force is a measure of the turning effect of force about the axis of rotation. It is denoted by the symbol $\vec \tau$.

Torque  $\vec \tau  = \vec r \times \vec F$ 

In magnitude,  $\tau  = rF\sin \theta$ 

Where θ is the angle between r and F.

• Principle of moments: According to the principle of moments, a body will be in rotational equilibrium if the algebraic sum of the movements of all forces acting on the body about a fixed point is zero.

• Centre of gravity: The center of gravity of a body is that point where the total gravitational torque on the body is zero.

• Angular momentum: Angular momentum of a particle about a given axis is the moment of linear momentum of the particle about that axis. It is denoted by the symbol L.

 $\overrightarrow L  = \overrightarrow r  \times \overrightarrow p$  i.e.  $L = rp\sin \theta$ 

It is a vector quantity. Its SI unit is  $kg{m^2}{s^{ - 1}}$ and dimensions are $M{L^2}{T^{ - 1}}$ .

• Relationship between torque and angular momentum:  $\overrightarrow \tau   = \dfrac{{d\overrightarrow L }}{{dt}}$ 

• Change in angular momentum is called angular impulse (J).

 $J = {L_2} - {L_1}$ .

Law of conservation of angular momentum: If no external torque acts on a system, then the total angular momentum is said to be conserved.

i.e.  $\overrightarrow \tau   = 0$ then  $\dfrac{{d\overrightarrow L }}{{dt}} = 0$  or L = constant

• A rigid body is said to be in equilibrium when:

1. It is in translational equilibrium i.e. the total external force acting on it is zero. i.e.  $\sum {{F_i} = 0}$ .

2. It is in rotational equilibrium, i.e. the total external torque acting on it is zero. i.e.  $\sum {{{\overrightarrow \tau  }_i} = 0}$ .

Relation Between Angular Momentum and Moment of Inertia: 

Angular momentum,  $L = I\omega$.

Important Points:

•  Kinetic energy of rotational motion,  ${K_R} = \dfrac{1}{2}I{\omega ^2}$ .

• For a redistribution of masses in a system:  ${I_1}{\omega _1} = {I_2}{\omega _2}$ 

• Work energy theorem in rotational motion:  $\dfrac{1}{2}{I_2}\omega _2^2 - \dfrac{1}{2}{I_1}\omega _1^2$ .

• Types of motion include Translational motion, rotational motion, and rolling motion.

• Translational motion is also known as kinematics.

• Rolling motion is the motion which happens when a body is rolling on a surface or an inclined plane.

• Kinetic energy of a rolling body = translational kinetic energy + rotational kinetic energy i.e.  $\dfrac{1}{2}M{v^2} + \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}M{v^2}\left[ {1 + \dfrac{{{K^2}}}{{{R^2}}}} \right]$ 

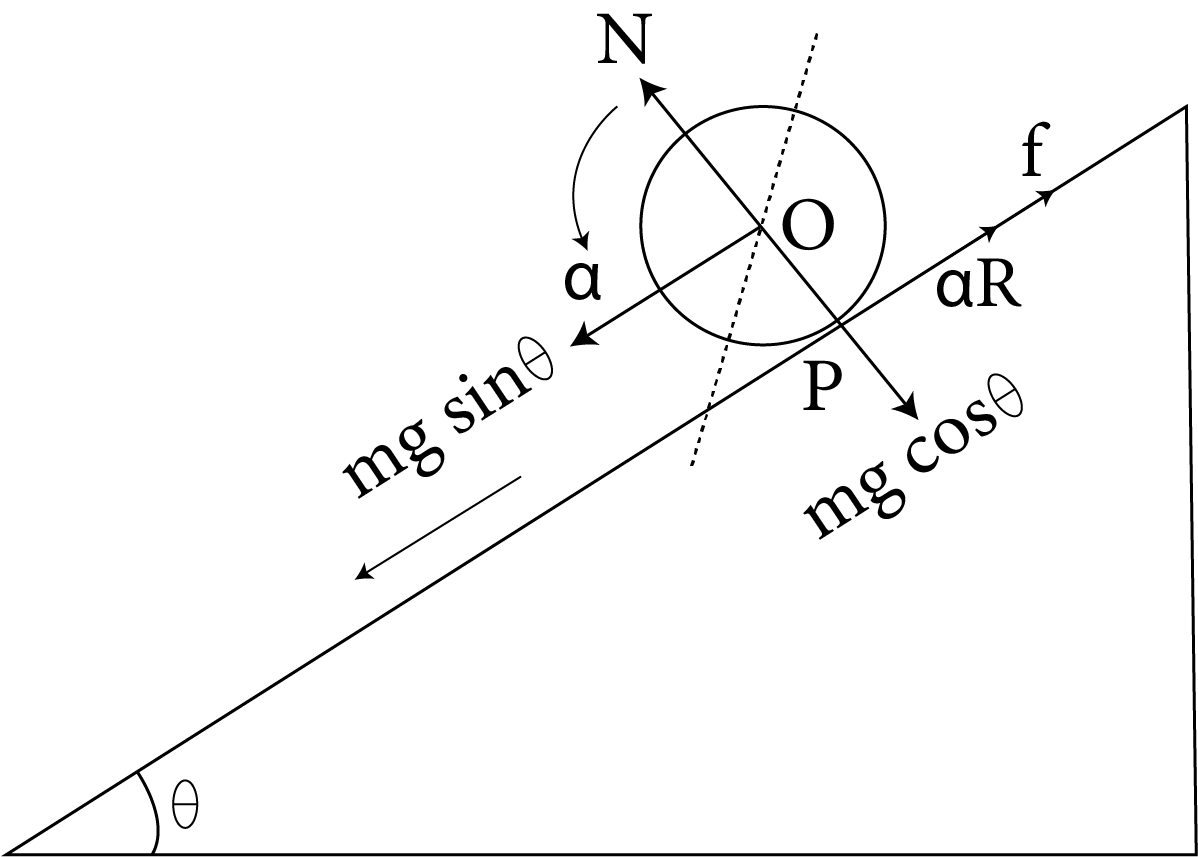
Body Rolling Down on an Inclined Plane

• When a body rolls down on an inclined plane of inclination without slipping its velocity at the bottom of incline is given by:  $v = \sqrt {\dfrac{{2gh}}{{1 + \dfrac{{{K^2}}}{{{R^2}}}}}}$ .

• When a body rolls down on an inclined plane without slipping its acceleration at the bottom of incline is given by:  $a = \dfrac{{g\sin \theta }}{{1 + \dfrac{{{K^2}}}{{{R^2}}}}}$ .

• When a body rolls down on an inclined plane without slipping its time at the bottom of incline is given by:  $t = \sqrt {\dfrac{{2l\left( {1 + \dfrac{{{K^2}}}{{{R^2}}}} \right)}}{{g\sin \theta }}}$ .

The Analogy Between Translational Motion and Rotational Motion:

Points to Remember:

• A rigid body is one in which the distances between different particles of the body do not change even though there are forces acting on them.

• Axis of rotation: The line along which the body is fixed is known as axis of rotation. Examples for rotation about an axis are a ceiling fan and a merry-go-round etc.

• The centre of mass of a body is a point where the entire mass of the body can be supposed to be concentrated. In fact, the nature of motion executed by the body shall remain unaffected if all the forces acting on the body were applied directly at this point.

• For a system of N-particles of masses  ${m_1},{m_2},{m_3}...{m_N}$ having their position vectors as  ${\vec r_1},{\vec r_2},{\vec r_3},...,{\vec r_N}$ respectively, with respect to the origin of the coordinate system, the position vector ${\vec R_{CM}}$ of the centre of mass is given by

${\vec R_{CM}} = \dfrac{{{m_1}{{\vec r}_1} + {m_2}{{\vec r}_2} + ... + {m_N}{{\vec r}_N}}}{{{m_1} + {m_2} + ...{m_N}}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec r}_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec r}_i}} }}{M}$

• Angular velocity: It is defined as the time rate of change of angular displacement and is given by

 $\omega  = \dfrac{{d\theta }}{{dt}}$ 

• Relationship between linear velocity and angular velocity

The linear velocity of a particle of a rigid body rotating about a fixed axis is given by,

$\vec v = \vec \omega  \times \vec r$ 

where   $\vec r$  is the position vector of the particle with respect to an origin along the fixed axis.

• Angular acceleration: It is defined as the time rate of change of angular velocity and it is given by,

$\vec \alpha  = \dfrac{{d\vec \omega }}{{dt}}$ 

• Moment of inertia of a rigid body about a given axis of rotation is defined as the sum of the product of masses of all the particles of the body and square of their respective perpendicular distances from the axis of rotation. It is denoted by symbol I and is given by,

$I = \sum\limits_{i = 1}^N {{m_i}r_i^3}$ 

• Moment of inertia is a scalar quantity. Its SI unit is  $kg{m^2}$ and its dimensional formula is $\left[ {{M^0}{L^1}{T^0}} \right]$ . It depends upon

• Position of the axis of rotation

• Orientation of the axis of addition

• Shape of the body

• Size of the body

• Distribution of mass of the body about the axis of rotation.

• Radius of gyration: It is defined as the distance from the axis of rotation at which the whole mass of the body was concentrated, the moment of inertia of the body would be the same as the actual distribution of the mass of the body. It is denoted by the symbol K.

• Theorem of perpendicular axes: The moment of inertia of a planar lamina about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axis concurrent with a perpendicular axis and lying in the plane of the body.  ${I_z} = {I_x} + {I_y}$ .

• Theorem of parallel axes:  The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axis.  $I = {I_{CM}} + M{d^2}$ 

• The torque or moment of force is a measure of the turning effect of force about the axis of rotation. It is denoted by the symbol $\vec \tau$.

Torque  $\vec \tau  = \vec r \times \vec F$ 

In magnitude,  $\tau  = rF\sin \theta$ 

Where θ is the angle between r and F.

• Principle of moments: According to the principle of moments, a body will be in rotational equilibrium if the algebraic sum of the movements of all forces acting on the body about a fixed point is zero.

• Centre of gravity: The center of gravity of a body is that point where the total gravitational torque on the body is zero.

• Angular momentum: Angular momentum of a particle about a given axis is the moment of linear momentum of the particle about that axis. It is denoted by the symbol L.

$\overrightarrow L  = \overrightarrow r  \times \overrightarrow p$  i.e.  $L = rp\sin \theta$ 

It is a vector quantity. Its SI unit is  $kg{m^2}{s^{ - 1}}$ and dimensions are $M{L^2}{T^{ - 1}}$ .

• Relationship between torque and angular momentum:  $\overrightarrow \tau   = \dfrac{{d\overrightarrow L }}{{dt}}$ 

• Change in angular momentum is called angular impulse (J).

$J = {L_2} - {L_1}$ .

• Law of conservation of angular momentum: If no external torque acts on a system then the total angular momentum is said to be conserved.

i.e.  $\overrightarrow \tau   = 0$ then  $\dfrac{{d\overrightarrow L }}{{dt}} = 0$  or L = constant

• A rigid body is said to be in equilibrium when:

• It is in translational equilibrium i.e. the total external force acting on it is zero. i.e.  $\sum {{F_i} = 0}$ .

• It is in rotational equilibrium i.e. the total external torque acting on it is zero. i.e.  $\sum {{{\overrightarrow \tau  }_i} = 0}$ .

Important Formulae:

• For a system of two particles of masses${m_1}$ and ${m_2}$ having their position vector has ${\vec r_1}$and ${\vec r_2}$ respectively, with respect to origin of the coordinate system, the position vector ${\vec R_{CM}}$ of the centre of mass is given by

${\vec R_{CM}} = \dfrac{{{m_1}{{\vec r}_1} + {m_2}{{\vec r}_2}}}{{{m_1} + {m_2}}}$

If ${m_1} = {m_2} = m$ , then ${\vec R_{CM}} = \dfrac{{{{\vec r}_1} + {{\vec r}_2}}}{2}$

• For n particles: ${\vec R_{CM}} = \dfrac{{{m_1}{{\vec r}_1} + {m_2}{{\vec r}_2} + ... + {m_N}{{\vec r}_N}}}{{{m_1} + {m_2} + ...{m_N}}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec r}_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec r}_i}} }}{M}$

• The coordinates of centre of mass for a 3-D object is given as:

${X_{CM}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{x_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{x_i}} }}{M}$

${Y_{CM}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{y_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{y_i}} }}{M}$

${Z_{CM}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{z_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{z_i}} }}{M}$

• For a continuous distribution of mass, the coordinates of centre of mass are given by,

${X_{CM}} = \dfrac{1}{M}\int {xdm;}$  ${Y_{CM}} = \dfrac{1}{M}\int {ydm;}$  ${Z_{CM}} = \dfrac{1}{M}\int {zdm}$ 

• Velocity of centre of mass

${\vec v_{CM}} = \dfrac{{{m_1}{{\vec v}_1} + {m_2}{{\vec v}_2} + ... + {m_N}{{\vec v}_N}}}{{{m_1} + {m_2} + ...{m_N}}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec v}_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec v}_i}} }}{M}$

• Acceleration of centre of mass

${\vec a_{CM}} = \dfrac{{{m_1}{{\vec a}_1} + {m_2}{{\vec a}_2} + ... + {m_N}{{\vec a}_N}}}{{{m_1} + {m_2} + ...{m_N}}} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec a}_i}} }}{{\sum\limits_{i = 1}^N {{m_i}} }} = \dfrac{{\sum\limits_{i = 1}^N {{m_i}{{\vec a}_i}} }}{M}$

• Relationship between linear velocity and angular velocity

The linear velocity of a particle of a rigid body rotating about a fixed axis is given by,

$\vec v = \vec \omega  \times \vec r$ 

where   $\vec r$  is the position vector of the particle with respect to an origin along the fixed axis.

• $I = \sum\limits_{i = 1}^N {{m_i}r_i^3}$ for moment of inertia.

• Radius of gyration of a body about an axis of rotation:

i.e.,  $K = \sqrt {\dfrac{{r_1^2 + r_2^2 + ... + r_N^2}}{N}}$ , $I = M{K^2}$ .

• ${I_z} = {I_x} + {I_y}$ for perpendicular axis. 

• $I = {I_{CM}} + M{d^2}$ 

• Torque $\vec \tau  = \vec r \times \vec F$ . In magnitude,  $\tau  = rF\sin \theta$  where θ is the angle between r and F.

• $\overrightarrow L  = \overrightarrow r  \times \overrightarrow p$  i.e.  $L = rp\sin \theta$ for angular momentum.

• $\overrightarrow \tau   = \dfrac{{d\overrightarrow L }}{{dt}}$ is the relationship between torque and angular momentum.

• Relation between angular momentum and moment of inertia:

Angular momentum,  $L = I\omega$ .

•  Kinetic energy of rotational motion,  ${K_R} = \dfrac{1}{2}I{\omega ^2}$ .

• For a redistribution of masses in a system:  ${I_1}{\omega _1} = {I_2}{\omega _2}$ 

• Work energy theorem in rotational motion:  $\dfrac{1}{2}{I_2}\omega _2^2 - \dfrac{1}{2}{I_1}\omega _1^2$ .

• Kinetic energy of a rolling body = translational kinetic energy + rotational kinetic energy i.e.  $\dfrac{1}{2}M{v^2} + \dfrac{1}{2}I{\omega ^2} = \dfrac{1}{2}M{v^2}\left[ {1 + \dfrac{{{K^2}}}{{{R^2}}}} \right]$ 

• When a body rolls down on an inclined plane of inclination without slipping its velocity at the bottom of incline is given by:  $v = \sqrt {\dfrac{{2gh}}{{1 + \dfrac{{{K^2}}}{{{R^2}}}}}}$ .

• When a body rolls down on an inclined plane without slipping its acceleration at the bottom of incline is given by:  $a = \dfrac{{g\sin \vartheta }}{{1 + \dfrac{{{K^2}}}{{{R^2}}}}}$ .

• When a body rolls down on an inclined plane without slipping its time at the bottom of incline is given by:  $t = \sqrt {\dfrac{{2l\left( {1 + \dfrac{{{K^2}}}{{{R^2}}}} \right)}}{{g\sin \theta }}}$ .

Questions:

1. A circular platform is mounted on a frictionless vertical axle. Its radius R = 2 m and its moment of inertia about the axis is 200 kg ${m^2}$ . It is initially at rest. A 50 kg man stands on the edge of the platform and begins to walk along the edge at the speed of 1  $m{s^{ - 1}}$ relative to the ground. Time taken by the man to complete one revolution is:

(a)  $\pi$  s                     

(b)  $\dfrac{{3\pi }}{2}s$ 

(c)  $2\pi s$ 

(d)  $\dfrac{\pi }{2}s$ 

Answer: option c)  $2\pi s$ 

Solution: As the system is initially at rest therefore, initial angular momentum ${L_i} = 0$.

According to the principle of conservation of angular momentum, final angular momentum,  ${L_f} = 0$ 

$\therefore$  Angular momentum = Angular momentum of man of platform in opposite direction

i.e.,  $mvR = I\omega$ 

Or   $\omega  = \dfrac{{mvR}}{I} = \dfrac{{50 \times 1 \times 2}}{{200}} = \dfrac{1}{2}rad{s^{ - 1}}$   

Angular velocity of man relative to platform is

${\omega _r} = \omega  + \dfrac{v}{R} = \dfrac{1}{2} + \dfrac{1}{2} = 1rad{s^{ - 1}}$ 

Time taken by the man to complete one revolution is

$T = \dfrac{{2\pi }}{{{\omega _r}}} = \dfrac{{2\pi }}{1} = 2\pi s$ 

Therefore, option c)  $2\pi s$ is the correct answer.

2. A rod of weight W is supported by two parallel knife edges A and B and is equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is:

(a)  $\dfrac{{W\left( {d - x} \right)}}{x}$ 

(b)  $\dfrac{{W\left( {d - x} \right)}}{d}$ 

(c)  $\dfrac{{Wx}}{d}$ 

(d)  $\dfrac{{Wd}}{x}$ 

Answer: option b)  $\dfrac{{W\left( {d - x} \right)}}{d}$ 

Solution: Given situation is shown in figure:

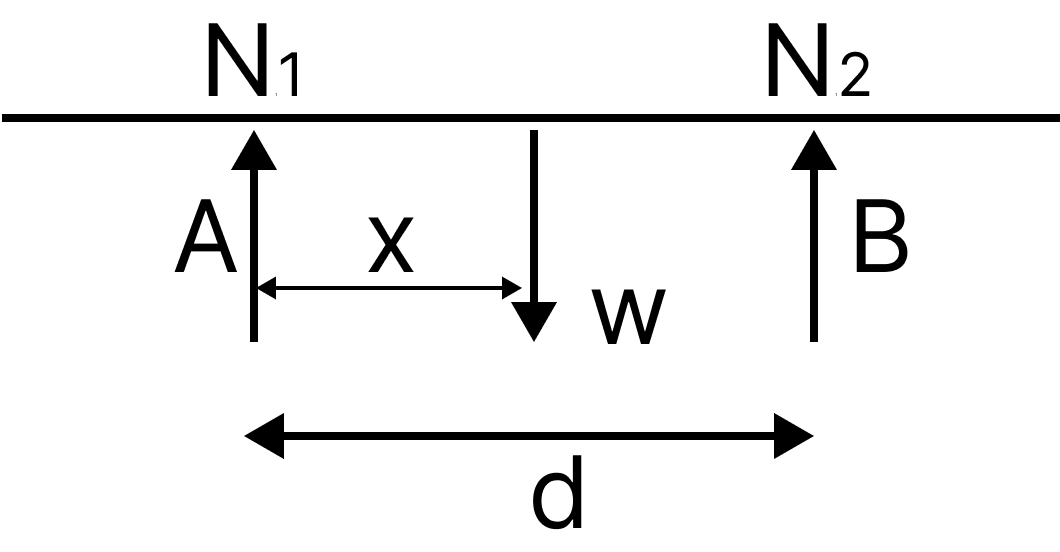
Example N1, N2

${N_1}$  = Normal reaction on A

${N_2}$  = Normal reaction on B

W = Weight of the rod

The vertical equilibrium,

${N_1} + {N_2} = W$ 

Torque balance about centre of mass of the rod,

${N_1}x = {N_2}\left( {d - x} \right)$ 

Putting the value of  ${N_2}$ from equation (1)

${N_1}x = (W - {N_1})\left( {d - x} \right)$ 

${N_1}x = Wd - Wx - {N_1}d + {N_1}x$ 

${N_1}d = W(d - x)$ 

$\therefore {N_1} = \dfrac{{W(d - x)}}{d}$ 

Hence, the normal reaction on A is $\dfrac{{W(d - x)}}{d}$.

List of Common Mistakes and Points to Remember:

• All of the previously stated significant issues are equally asked as numerical problems and derivations. 

• It is advised to have a conceptual understanding of each topic. 

• Practice the more and more numerical questions from each as well.

• Keep in mind that a rolling motion can occur both with and without slipping.

• Go over the chapter's relationships between the physical quantities again.

• Create a table or chart to show the moment of inertia for various items and forms.

Importance of the Physics Chapter System of Particles and Rotational Motion

Class 11 System of Particles and Rotational Motion is a fundamental chapter that introduces students to angular velocity and rotational momentum. Students have studied rectilinear motion and have learned how to calculate the various physical quantities. In this chapter, they will use the same concepts to understand the meaning of new terms such as the centre of mass, angular momentum, rotational motion, torque, etc.

They will also learn how to derive the formulae of these terminologies and how they are correlated. This chapter in NEET Physics Class 11 syllabus will explain what the centre of mass is in a solid. It will explain what systems of particles stand for.

Students will learn scientific principles of how the centre of mass of a body is considered for its translation and rotational motion. It is considered that the entire mass of a solid is concentrated in this region.

NEET aspirants will also learn the meaning of torque, angular momentum, rotational motion, gyration, and the theorem of parallel and perpendicular axes here. This is why this chapter is very important for the development of a conceptual foundation of kinematics and mechanics. Using the Class 11 System of Particles and Rotational Motion notes will help students to understand all these scientific terms, definitions, and derivations of formulas easily.

Benefits of Vedantu’s System of Particles and Rotational Motion NEET Notes

• These revision notes have been prepared by the experts focusing on the needs of students aspiring to appear in the NEET exam. The experts have taken great care to explain the fundamental concepts in a simpler way. Students will be able to resolve doubts on their own and proceed to complete preparing this chapter.

• The aggregation of definitions, derivations, and formulae of all the scientific terms related to rotational motion and systems of particles in these notes will help students to revise and remember them perfectly. They will be able to grab the concepts faster and recall what they have studied during the competitive medical entrance exam.

• The concise format of these notes is ideal to take a quick glance at the fundamental principles. They will also be able to check the formulae before solving the sample questions in these notes and exercise problems in this chapter.

Download System of Particles and Rotational Motion Notes PDF

You can download these revision notes in PDF version for free and complete your study material related to Rotational Motion and Systems Of Particles. Make your study sessions more convenient and productive by referring to these notes and learning about the centre of mass, angular velocity, angular momentum, torque, etc. faster.

Other Important Links

NEET Physics Revision Notes - Chapter Pages