




Core Vector Terms, Properties & Real-Life Applications Explained
A vector is a quantity in physics that has both magnitude and direction. It is frequently depicted as an arrow with a length proportional to the magnitude and a direction matching the magnitude of the quantity. A vector has both magnitude and direction.
Scalars are regular quantities with a magnitude but no direction. For instance, speed (the amount of velocity), time, and mass are scalars. Examples for vectors: displacement, velocity, momentum, and acceleration are vector quantities.
History of Inventor
Late in the 19th century, American and British physicists Josiah Willard Gibbs and Oliver Heaviside separately created vector analysis to represent the new electromagnetic principles found by Scottish scientist James Clerk Maxwell. This is when vectors first took on their current shape.
Pictures of Josiah Willard Gibbs and Oliver Heaviside
Vector Representation
How to represent a vector? A vector has a Tail as the initial point and a tip as the terminal point. You can represent the vector as \[\vec a\] (vector a). The magnitude of the vector is represented by the length of the line AB denoted as \[\left| a \right|\]. Any line can be represented as an AB line segment but an arrow mark represents the vector \[\overrightarrow {AB} \].
Vector Diagram
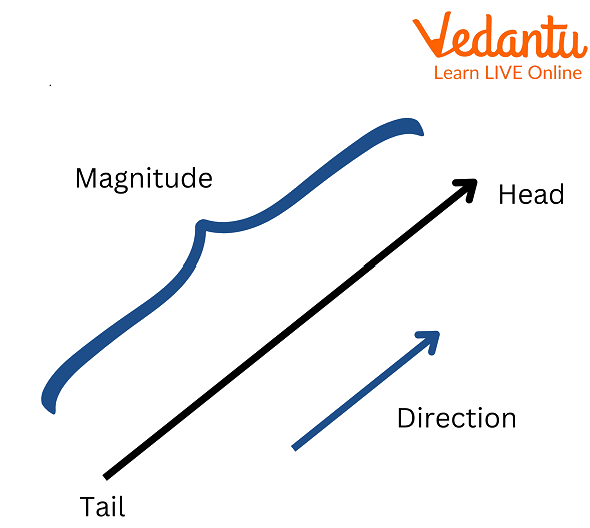
Vector diagram
This is the vector diagram in which length is the magnitude and one end is the head and one is the tail.
Representation of Vector Graphically
Graphically a vector is represented by an arrow. When a vector is represented visually, the length of the arrow serves as a reference for the vector's magnitude, and the arrow's direction serves as a reference for the vector's direction.
Magnitude of a Vector
The length of a vector represents its magnitude and is denoted as \[\left| a \right|\]. The magnitude is always positive, it cannot be negative. This magnitude of a vector formula provides a summary of the individual vector measurements along the x, y, and z axes.
Magnitude of a Vector Formula
If one point is the origin and another point is (x, y) of any vector \[\vec a\] then we can calculate the magnitude as \[\left| a \right|\]=\[\sqrt {{x^2} + {y^2}} \]
If both points are known \[({x_1},{y_1})\]and \[({x_2},{y_2})\] then the magnitude is \[\left| a \right|\]=\[\sqrt {{{({x_2} - {x_1})}^2} + ({y_2} - } {y_1}{)^2}\]
If the vector is given in \[\vec a\]= \[{x_1}i + {y_1}j + {z_1}k\] then the magnitude \[\left| a \right|\]=\[\sqrt {{x_1}^2 + {y_1}^2 + {z_1}^2} \]
Direction of a Vector
The direction of a vector is the slope of that vector with the horizontal axis. How to find the direction of a vector? Let’s say we have a vector starting from the origin, and the endpoint is (x, y) then we can calculate the direction by using its slope, that’s tan θ = y/x.
Graph showing the direction of a vector
To calculate the angle, we use θ = tan-1 (y/x).
If two points are given for any vector \[({x_1},{y_1})\]and \[({x_2},{y_2})\]then the formula to find \[(x,y)\] = \[({x_2} - {x_1},{y_2} - {y_1})\]and then we can use the same formula to calculate the angle θ = tan-1 (y/x).
Components of Vector
In a two-dimensional coordinate system, the component of a vector is the x-component (x-axis)and y-component (y-axis). Vx and Vy are the components of the x-axis and y-axis for a given vector V.
Graph showing the components of a vector V and O is the origin
If angle θ is formed between vector V and the x-component for any right triangle then we can use trigonometric ratios to find the components of the given vector.
sin θ = \[\dfrac{{Perpendicular}}{{Hypotenuse}}\]
cos θ = \[\dfrac{{Base}}{{Hypotenuse}}\]
If we use for the components Vx and Vy.:
sin θ = \[\dfrac{{{V_y}}}{V}\]
Vy =V sin θ
cos θ = \[\dfrac{{{V_x}}}{V}\]
Vy= V cos θ
Interesting Facts
Vectors are used for navigation in both the air and on boats. To establish how long they must fly before turning or landing, planes are assigned a vector to follow.
Vector is also used in a series of instructions or mathematical assertions that arrange lines and shapes in a two-dimensional or three-dimensional space to produce vector graphics, which are computer pictures.
Solved Problem
1. Find the magnitude of the vector \[\overrightarrow {AB} \] if the initial point is (3, 6) and the endpoint is (8, 12).
Sol.
Given: Initial point (3,6) and endpoint (8, 12)
We can use the magnitude formula to solve this vector.
Magnitude formula for a given vector = \[\sqrt {{{({x_2} - {x_1})}^2} + ({y_2} - } {y_1}{)^2}\]
\[\Rightarrow \text{Magnitude of a vector}= \sqrt {{{(8 - 3)}^2} + {{(12 - 6)}^2}} \]
\[\Rightarrow \text{Magnitude of a vector}=\sqrt {{{(5)}^2} + {{(6)}^2}} \]
\[\Rightarrow \text{Magnitude of a vector}=\sqrt {25 + 36} \]
\[\therefore \text{Magnitude of a vector}=\sqrt {61} \] =7.81(approx.)
Therefore, the approximate value of the magnitude of a vector is 7.81.
2. Find the direction of a vector if the initial point is (2, 6) and the endpoint is (4, 9).
Sol.
Given: Initial point is (2, 6) and the Endpoint is (4, 9).
To calculate the angle, we use θ = tan-1 (y/x).
\[(x,y)\] = \[({x_2} - {x_1},{y_2} - {y_1})\]
\[\Rightarrow (x,y)\]= \[(4 - 2,9 - 6)\]
\[\Rightarrow (x,y)\]= (2,3)
\[\Rightarrow\] θ = tan-1 (y/x)
\[\Rightarrow\] θ = tan-1 (3/2)
\[\therefore\] θ = 56.3 degrees
Hence the direction of a given vector is 56.3 degrees.
Summary
Vector has both magnitude and direction with its help. We can use it in physics numerical problems and also in real-world scenarios. Vectors can be represented graphically or we can also find the direction if we have coordinated the points. The component of the vector will help us to show the vector on the two-dimensional coordinate system.
List of Related Articles
- Components of Vector
- Vector Formulas
FAQs on Vectors in Physics: Complete Guide for Students
1. What defines a physical quantity as a vector?
A physical quantity is defined as a vector if it requires both magnitude (a numerical value) and a specific direction to be completely described. Simply stating its size is not enough. For example, saying "a force of 10 Newtons" is incomplete without specifying the direction in which the force is applied.
2. What are some common examples of vector quantities in Physics?
Many fundamental quantities in Physics are vectors. Some common examples include:
- Displacement: The shortest distance from the initial to the final point, in a specific direction.
- Velocity: The rate of change of displacement (speed in a direction).
- Acceleration: The rate of change of velocity.
- Force: A push or pull on an object, acting in a certain direction.
- Momentum: The product of mass and velocity.
- Torque: The rotational equivalent of force.
3. How do scalar and vector quantities differ, and why is this distinction important in Physics?
The fundamental difference lies in their definitions. A scalar quantity is fully described by its magnitude alone (e.g., mass, speed, distance, temperature). A vector quantity requires both magnitude and direction (e.g., force, velocity, displacement). This distinction is crucial because the mathematical operations for scalars and vectors are different. For instance, adding 5 kg and 2 kg always gives 7 kg. However, adding a 5 N force and a 2 N force can result in anything from 3 N to 7 N, depending on the angle between them. Using vectors correctly ensures accurate predictions of motion and interactions in physical systems.
4. What are the different types of vectors students should know?
In Physics, understanding different types of vectors is essential for solving problems. Key types include:
- Zero Vector (Null Vector): A vector with zero magnitude and an arbitrary direction.
- Unit Vector: A vector with a magnitude of one, used purely to specify a direction. It is denoted by a cap or hat (e.g., â).
- Equal Vectors: Two vectors are equal if they have the same magnitude and the same direction.
- Collinear Vectors: Vectors that act along the same line or parallel lines. They can be in the same direction (parallel) or opposite directions (anti-parallel).
- Position Vector: A vector that represents the position of a point in space with respect to a fixed origin.
5. How is the Parallelogram Law used to find the resultant of two vectors?
The Parallelogram Law of Vector Addition is a graphical method to find the sum (or resultant) of two vectors. The method involves representing the two vectors as the adjacent sides of a parallelogram, with their tails joined at a common point. The resultant vector is then represented by the diagonal of the parallelogram that starts from the same common point. The magnitude of the resultant is given by the formula R = √(A² + B² + 2ABcosθ), where θ is the angle between the two vectors.
6. What is the magnitude of a vector and how is it calculated?
The magnitude of a vector, also known as its length or norm, represents its numerical value or size, independent of its direction. It is always a non-negative scalar quantity. For a vector represented in a 2D Cartesian system as V = Vₓî + Vᵧĵ, its magnitude |V| is calculated using the Pythagorean theorem: |V| = √(Vₓ² + Vᵧ²). For a 3D vector V = Vₓî + Vᵧĵ + Vᶻk̂, the magnitude is |V| = √(Vₓ² + Vᵧ² + Vᶻ²).
7. What is a unit vector and what is its primary importance in Physics?
A unit vector is a vector that has a magnitude of exactly one and points in a specific direction. Its primary importance is not to represent a physical quantity's value but to specify direction in space. By multiplying a scalar magnitude by a unit vector, we can create a full vector quantity. For example, the unit vectors î, ĵ, and k̂ are used to define the positive x, y, and z axes, respectively, which simplifies the representation and manipulation of vectors in multi-dimensional space.
8. What is the resolution of a vector into its components?
The resolution of a vector is the process of splitting a single vector into two or more vectors, called its components, which, when added together, produce the original vector. Typically, a vector is resolved into perpendicular components along the x and y-axes. If a vector R makes an angle θ with the x-axis, its horizontal component is Rₓ = R cos(θ) and its vertical component is Rᵧ = R sin(θ). This technique is extremely useful for analysing forces and motion in complex situations.
9. What is the key difference between the dot product and the cross product of two vectors?
The key difference lies in the nature of their result.
- The dot product (scalar product) of two vectors results in a scalar quantity (a single number with no direction). It represents the projection of one vector onto another and is used to calculate work done or power.
- The cross product (vector product) of two vectors results in a new vector that is perpendicular to the plane containing the original two vectors. It is used to calculate quantities like torque and angular momentum.
10. Why is the concept of a zero vector (null vector) necessary in vector algebra?
The zero vector, or null vector, is a vector with zero magnitude and an arbitrary direction. It is necessary for mathematical consistency in vector algebra. For example, when two equal and opposite vectors are added (A + (-A)), the result must be a vector, which is the zero vector. It can also represent the physical state of an object with zero velocity (at rest) or zero displacement (returning to the start), making the vector system complete.























