NEET Important Chapter - Motion in a Plane

Let us first understand, what is motion in a plane? Motion in a plane means the motion of the body in two dimensions, i.e., a plane. In this chapter, we will establish concepts for position, displacement, velocity, and acceleration that are needed to describe the motion in a plane. 

In the last chapter, Motion in a Straight Line, the concepts were developed for straight-line motion where directional aspects can be taken care of by using + and - signs. The discussion about motion in a plane is much more complicated because in this we have to define directional terms in two different axes, namely, the x and y-axes. So, we need to use vectors to describe motion in two dimensions. Going further in this chapter, we will learn about vectors and how to apply mathematical operators like addition, subtraction, and multiplication on vector quantities.  

In this chapter, students will also learn about relative velocity in two dimensions, projectile motion, and circular motion by using vectors. Now, let us move on to the important concepts and formulae related to the NEET exam along with a few solved examples.

Important Topics of Motion in a Plane

• Vectors

• Addition and Subtraction of Vectors.

• Resolution of Vectors.

• Motion in a plane with constant acceleration.

• Relative Velocity in Two dimensions.

• Projectile Motion.

• Projectile motion in horizontal direction from a height.

• Projectile Motion on an inclined plane.

• Uniform Circular Motion.

Important Concepts of Motion in a Plane

List of Important Formulae

Solved Examples

1. Two Vectors have magnitudes 6 units and 8 units respectively. What should be the angle between the vectors if the magnitude of resultant is:

1. 14 units

2. 10 units

3. 2 units

Sol: 

Let, 

Magnitude of A vector = 6 units,

Magnitude of B vector = 8 units, 

Resultant of A and B = R, 

(a) The Resultant (R) of A and B is given as 14 units. Let the angle between A and B is $angle \theta$. Then, 

R = $\sqrt{A^{2}+B^{2}+2AB\cos\theta}$

14 = $\sqrt{6^{2}+8^{2}+2\times6\times8\cos\theta}$

Putting squares on both the sides, we get,

196 = $36+64+96\cos\theta$

196 = $100+96\cos\theta$

$\cos\theta$ = 1

$\theta$ = 0°

This means that the vectors A and B are parallel vectors. 

(b) Now, the Resultant (R) of A and B is given as 10 units. Let the angle between A and B is $angle \theta$. Then, 

R = $\sqrt{A^{2}+B^{2}+2AB\cos\theta}$

10 = $\sqrt{6^{2}+8^{2}+2\times6\times8\cos\theta}$

Putting squares on both the sides, we get,

100 = $36+64+96\cos\theta$

100 = $100+96\cos\theta$

$\cos\theta$ = 0

$\theta$ = 90°

This means that the vectors A and B are perpendicular vectors. 

(c) Now, the Resultant (R) of A and B is given as 2 units. Let the angle between A and B is $angle \theta$. Then, 

R = $\sqrt{A^{2}+B^{2}+2AB\cos\theta}$

2 = $\sqrt{6^{2}+8^{2}+2\times6\times8\cos\theta}$

Putting squares on both the sides, we get,

4 = $36+64+96\cos\theta$

4 = $100+96\cos\theta$

-96 = $96\cos\theta$

$\cos\theta$ = -1

$\theta$ = 180°

This means that the vectors A and B are antiparallel vectors. 

Key point: Maximum value of resultant occurs when vectors are parallel and minimum value of resultant occurs when vectors are antiparallel. 

2. At a height 45 m from the ground velocity of the projectile is, v = $(30\hat{i} +40\hat{j})$ m/s. Find the initial velocity of the projectile. 

Sol: 

Given, 

• $v_{x} = 30 m/s$, 

• $v_{y} = 40 m/s$, 

Now, given below is the pictorial representation of the given situation:

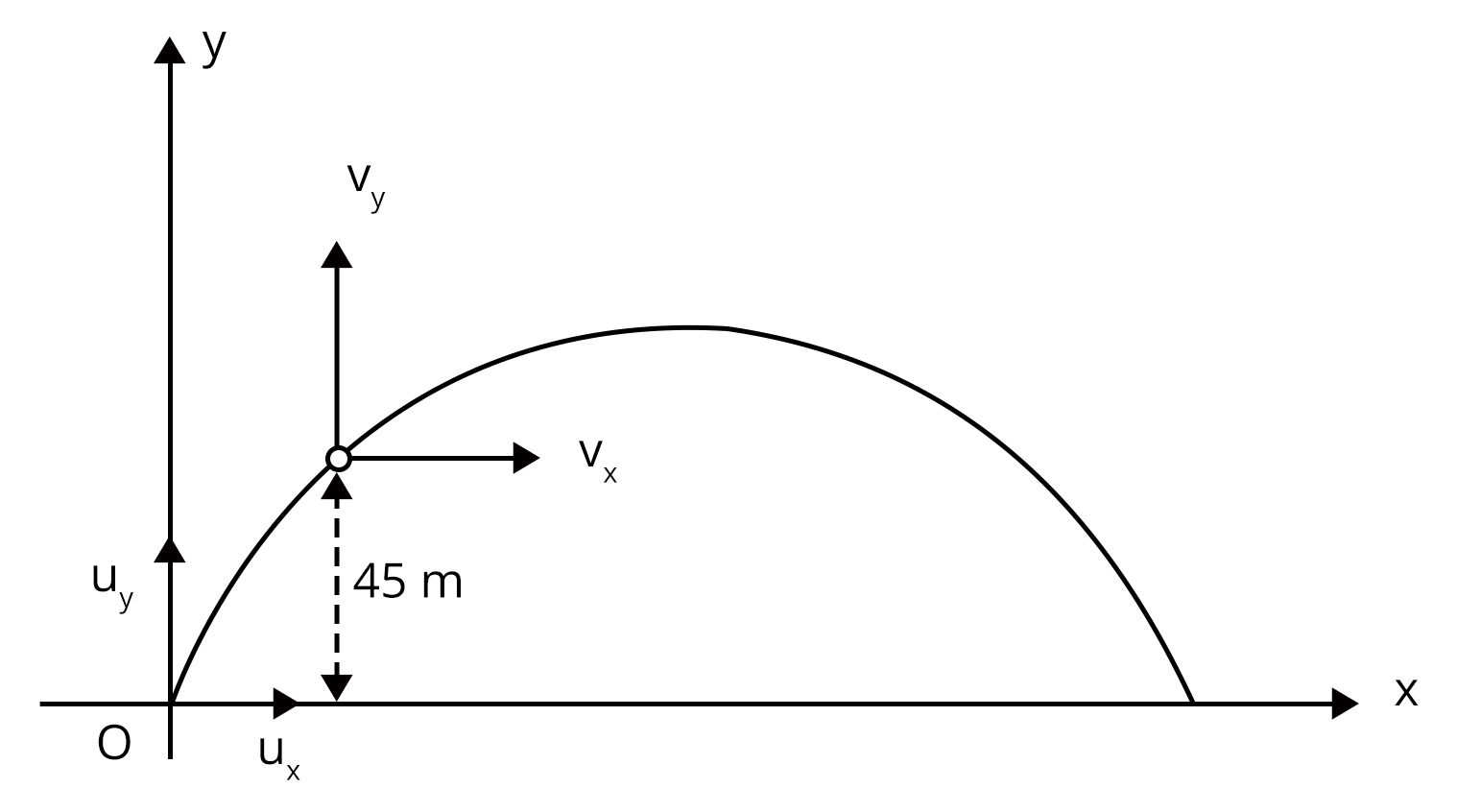
As there is no acceleration along x- direction, then velocity along x- direction will not change. therefore,  $v_{x} = u_{x} = 30 m/s$.

Now, the vertical component of the velocity will decrease as it reaches the height of 45m as the acceleration due to gravity is always in the downward direction. Using kinematic equations of motion, 

$v_{y}^{2} = u_{y}^{2}-2gy$

$30^{2} = u_{y}^{2}-2\times10\times45$

$u_{y} = 50 m/s$

So, the initial velocity, u will be given by:

$u = \sqrt{u_{x}^{2}+u_{y}^{2}}$

$u = \sqrt{30^{2}+50^{2}}$

$u = 10\sqrt{34}$

Hence, the initial velocity is $10\sqrt{34}$

Key Point: Always remember that during projectile motion, horizontal velocity doesn’t change because there is no acceleration in horizontal direction.  

Previous Year Questions from NEET Paper

1. If the magnitude of sum of two vectors is equal to the magnitude of difference of two vectors, the angle between these vectors is (NEET 2016)

1. 90°

2. 45°

3. 180°

4. 0°  

Sol:

Let the two vectors be A and B. It is given in the question that the magnitude of sum of the two vectors is equal to the magnitude of the difference between the two vectors. Therefore, 

$|A+B\lvert=|A-B\lvert$

$\sqrt{A^{2}+B^{2}+2AB\cos\theta}$ = $\sqrt{A^{2}+B^{2}-2AB\cos\theta}$

$4AB\cos\theta = 0$

$\theta = 90°$

Hence, the correct answer is option (a)

Trick: Magnitude of sum of two vectors is always equal to difference of two vectors when the two vectors are perpendicular. 

1. Two bullets are fired simultaneously towards each other from the rooftops of two buildings 100 m apart and of the same height, 200 m with the same velocity of 25 m/s. When and where will the bullets collide (NEET 2019)

1. At 2s at height of 180 m

2. At 2s at a height of 20 m

3. At 4s at a height of 120 m

4. They will not collide                                              

Sol. 

Let the bullets collide at time, t and a point whose distance from one building is x1 and other building is x2, as shown in figure, 

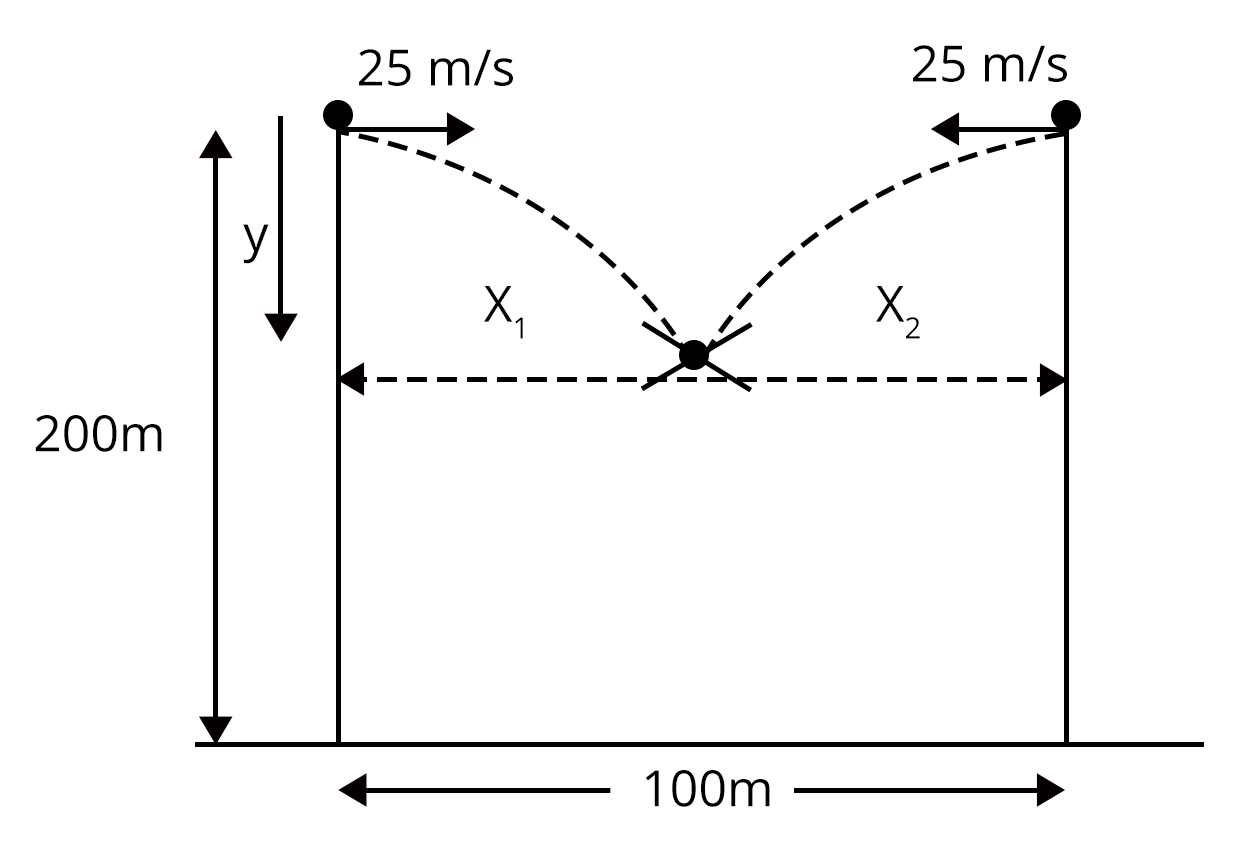
Therefore, 

x1 + x2 = 100 m, 

Also, 

x1 = ut = 25t, 

x2 = ut = 25t, 

Then, 

x1 + x2 = 100 m

25t + 25t = 100m, 

50t = 100, 

t = 2s, 

Now, the vertical distance is given by, 

y = $\dfrac{1}{2}gt^{2}$ 

y = $\dfrac{1}{2}\times10\times 2^{2}$

y = 20 m

So, the height from the ground will be (200m - 20m) = 180 m

Therefore, the bodies will collide at time 2 secs at the distance of 180 m from the ground. Hence, option (a) is the correct answer.

Trick: In any type of case, when the two particles are projected simultaneously, they will meet at the same time and position. 

Practice Questions

• A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If $\alpha$ and $\beta$ be the base angles and $\theta$ the angle of projection, prove that $\tan\theta= \tan\alpha+\tan\beta$

• The resultant of two forces, one double the other in magnitude, is perpendicular to the smaller of the two forces. Then what is the angle between the two forces? (Ans. 120°)

Conclusion

In this article we have provided important information regarding the chapter motion in a plane such as important concepts, formulae, etc.. Students should work on more solved examples for securing good grades in the NEET exam.