Revision Notes on Mechanical Properties of Solids for NEET 2025 - Free PDF Download
Studying the properties of matter is the basic foundation of Physics. The chapter Mechanical Properties of Solids deals with the different properties of solids. It explains the aspects and implications of force, elasticity, plasticity, stress, strain, tension, etc that constitute the mechanical properties of different types of solids. All these scientific terms will be explained using mathematical expressions and proper examples. To understand the concepts of these properties deeply while preparing for the NEET, refer to the Mechanical Properties of Solids Class 11 notes prepared by the subject matter experts of Vedantu.
These notes have been formulated in a simpler way to offer consolidated study material for NEET aspirants. Referring to these notes will enable students to understand, revise, and recall the concepts, formulas, definitions, and derivations easily.
Note: 👉Get a Head Start on Your Medical Career with the NEET Rank and College Predictor 2025.
Access NEET Revision Notes Physics Properties of Solids
Some Terms Related to Elasticity:
Rigid body: It is the body which does not show any deformation when any external forces are applied to it. There is no perfect rigid body, but a diamond is the nearest approach to a rigid body.
Deformation force: It is the force when applied, changes the configuration of the body.
Elasticity: It is the property of the body by which the body regains its original configuration (length, volume or shape) when the deforming forces are removed.
Perfectly elastic body: It is the body which regains its original configuration immediately and completely after removing deforming force.
Perfectly plastic body: It is that body that does not regain its original configuration at all on removing deforming force, however small the deforming force may be. In fact nobody is either perfectly elastic or perfectly plastic, and the behaviour of actual bodies lies between the two extremes.
Elastic limit: It is the upper limit of deforming force up to which, if deforming force is removed, the body regains its original form completely and behind which, if deforming force is increased, the body loses its property of elasticity and gets permanently deformed. Elastic limit is the property of a body, whereas elasticity is the property of the material of a body.
Stress:
When a body is subjected to a deforming force, a restoring force is developed in the body. This restoring force is equal in magnitude but opposite in direction to the applied force. The restoring force per unit area is known as stress. If F is the force applied and A is the area of cross-section of the body, then
$\text{Stress} =\dfrac{F}{A}$
The unit of stress in the SI system is $N{m^{ - 2}}$ or Pascal (pa) and in the CGS system is dyne $c{m^{ - 2}}$. The dimensional formula of stress is same as that of pressure i.e. $ML^{-1}T^{-2}$
Types of Stress:
Stresses are of two types:
Normal stress
Tangential or shearing stress
Normal stress: When a deforming force acts normally over an area of a body, then the internal restoring force set up per unit area of the body is called normal stress.
Normal stress can be subdivided into following categories:
Tensile stress: If there is an increase in the length of extension of the body in the direction of force applied, the stress setup is called tensile stress.
Compressive stress: If there is a decrease in length or compression of the body due to force applied, the stress set up is called compressive stress.
Hydraulic stress: When a solid body undergoes a change in volume without any change in its geometrical shape or applying the force perpendicular to every point on the surface of a body, then the restoring force per unit area in the body is called hydraulic stress. Hydraulic stress is generally possible when a solid spherical body is placed in a fluid under high pressure.
Note: Tensile or compressive stress can also be termed as longitudinal stress.
Tangential or shearing stress: When a deforming force, acting tangentially to the surface of a body produces a change in the body's shape without any volume change, then the stress set up in the body is called as tangential stress or shearing stress.
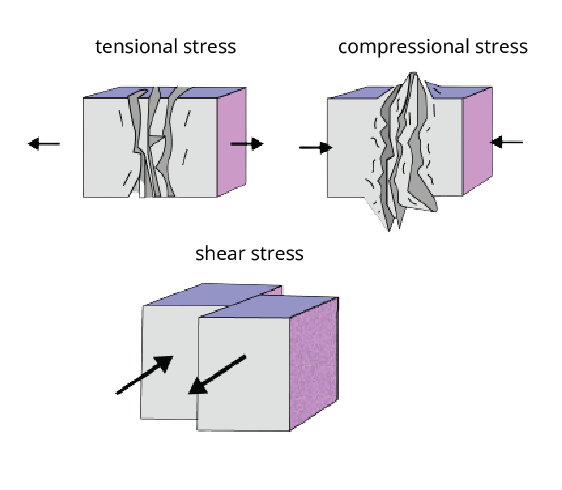
Types of Stress
Strain:
Strain is the ratio of two similar quantities; hence it is a unitless and dimensionless quantity.
$Strain =\dfrac{{{\text{Change in dimension}}}}{{{\text{Original dimension}}}}$
Strains are of three types:
Longitudinal strain = $ =\dfrac{{{\text{Change in length}}}}{{{\text{Original length}}}} =\dfrac{{\Delta L}}{L}$
Volumetric strain $ =\dfrac{{{\text{Change in volume}}}}{{{\text{Original volume}}}} =\dfrac{{\Delta V}}{V}$
Shearing strain $ = \theta =\dfrac{l}{L}$
Hooke’s Law:
According to Hooke’s law, “Within the elastic limit, the stress applied to a body is directly proportional to the corresponding strain”.
$Stress = E \times Strain$ Or $\dfrac{{Stress}}{{Strain}} = E$
Where E is the constant of proportionality and is known as coefficient of elasticity or modulus of elasticity.
Hooke’s law is an empirical law and is found to be valid for most materials. However, there are some materials which do not exhibit this linear relationship.
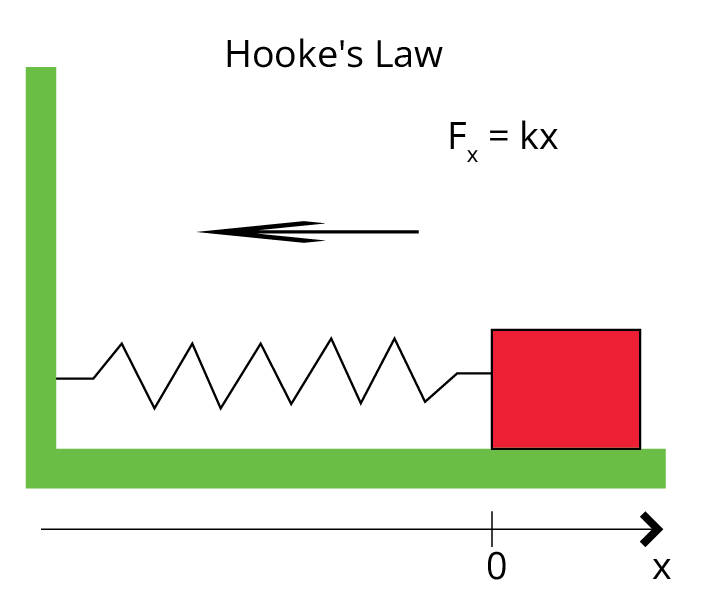
Hooke’s Law
Stress-Strain Curve:
The stress-strain curves vary from material to material. These curves help us to understand how a given material deforms with increasing loads. A typical stress-strain curve for a ductile metal is shown below.
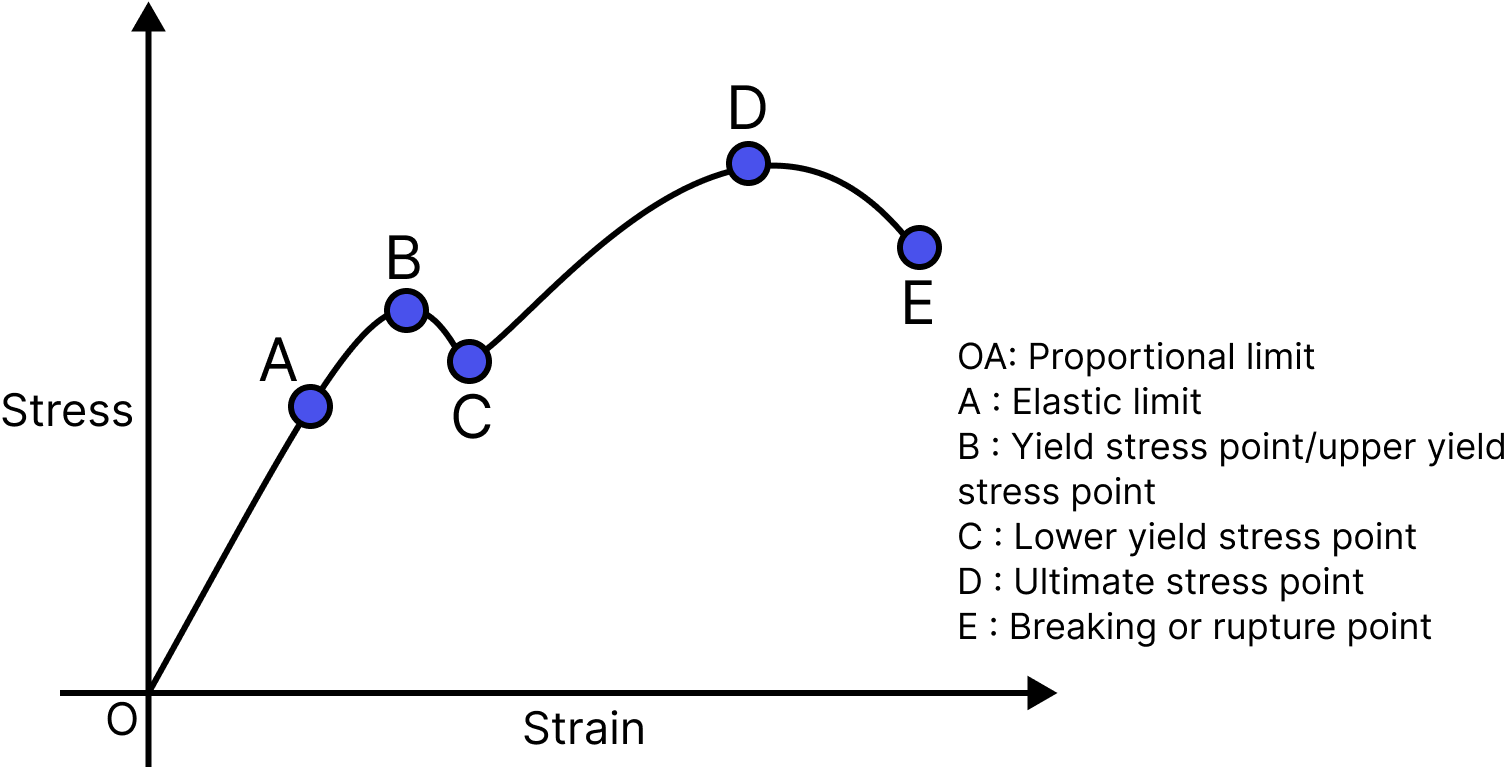
Typical Stress-Strain Curve
Here, different regions such as the elastic and plastic regions showcase the point when the body is either elastic or not. The elastic limit is the maximum point where the body can be elastic. The breaking point is the maximum stress point in which the stress value decreases. The ultimate stress point is the maximum value of stress. The proportional limit is the region where stress is proportional to strain i.e. elastic region.
Elastomers: Substances like tissue of the aorta, rubbers etc., which can be stretched to cause large strains, are called Elastomers.
Modulus of Elasticity:
It is defined as the ratio of stress to the corresponding strain produced within the elastic limit. Modulus of elasticity is of three types:
Young’s modulus: $Y=\dfrac{\text{Normal stress}}{\text{Longitudinal strain}}$
$Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta L}{L}}=\dfrac{FL}{A\Delta L}=\dfrac{FL}{\pi {{r}^{2}}\Delta L}$
Bulk modulus: $B=\dfrac{\text{Normal stress}}{\text{Volumetric strain}}$
$=\dfrac{\dfrac{-F}{A}}{\dfrac{\Delta V}{V}}=-\dfrac{PV}{\Delta V}$ where -ve sign shows that with an increase in pressure, a decrease in volume occurs.
Modulus of rigidity: $G =\dfrac{{{\text{translational stress}}}}{{{\text{shearing strain}}}} =\dfrac{F}{{A\theta }}$
The modulus of rigidity is also called the shear modulus of rigidity.
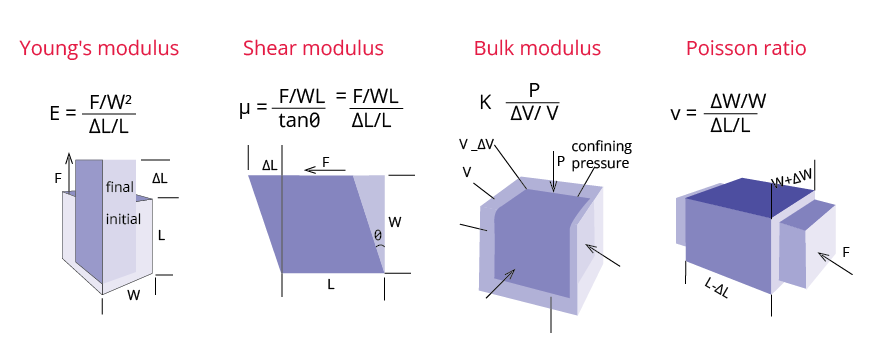
Types of Modulus of Elasticity
The modulus of elasticity has the same dimensional formula and units as that of stress since the strain is dimensionless, i.e., the dimensional formula for Y, B and G is $M{L^{ - 1}}{T^{ - 2}}$ while the SI unit of Y, B and G is $N{m^{ - 2}}$or pa and the CGS unit of Y, B and G is dyne $c{m^{ - 2}}$.
Points to Remember:
Young’s modulus is defined only for solids, but not for liquids and gases.
Young’s modulus of a perfect rigid body is infinity.
Greater the value of Young’s modulus of a material, larger Is it’s elasticity. Therefore steel is more elastic than copper.
The reciprocal of bulk modulus is known as compressibility.
Compressibility $ =\dfrac{1}{B}$
The SI unit of compressibility is ${N^{ - 1}}{m^2}$ and the CGS unit is $dyn{e^{ - 1}}c{m^2}$.
Bulk modulus is relevant for solids, liquids and gases.
Bulk modulus for gases are very low while that for liquids and solids are very high.
${B_{solid}} > {B_{liquid}} > {B_{gas}}$
For gases, bulk modulus are of two types:
Isothermal bulk modulus, ${B_{iso}} = P$(pressure exerted by the gas)
Adiabatic bulk modulus, ${B_{ad}} = \gamma P$
Where $\gamma =\dfrac{{{C}_{p}}}{{{C}_{v}}}$
$\dfrac{{{B_{ad}}}}{{{B_{iso}}}} = \gamma > 1$; ${B_{ad}} > {B_{iso}}$
Therefore adiabatic bulk modulus is greater than isothermal bulk modulus.
Shear modulus is defined for solids only. The shear modulus (or modulus of rigidity) for a solid is generally less than Young's modulus. For most the solid materials, the value of the shear modulus is 1/3 of the young modulus, i.e. $G=\dfrac{Y}{3}$
Poisson’s ratio ($\sigma$):
Poisson’s ratio, $\sigma =\dfrac{\text{Lateral strain}}{\text{Longitudinal strain}}=\dfrac{-\dfrac{\Delta r}{r}}{\dfrac{\Delta L}{L}}$
Negative sign shows that if the length increases, then the radius of the wire decreases. It has no units and dimensions. Theoretically, $\sigma $lies between -1 and $ +\dfrac{1}{2}$. Practically $\sigma $lies between zero and $ +\dfrac{1}{2}$.
Important Relationships Between Modulus of Elasticity and Poisson’s Ratio:
$Y = 3B(1 - 2\sigma )$
$Y = 2G(1 + \sigma )$
$\sigma =\dfrac{{3B - 2G}}{{2G + 6B}}$
$\dfrac{9}{Y} =\dfrac{1}{B} +\dfrac{3}{G}$
Elastic Potential Energy Stored in a Stretched Wire and Breaking Force:
Elastic potential energy stored in a stretched wire: $\dfrac{1}{2} \times Load \times extension$
$U =\dfrac{1}{2}F \times \Delta L =\dfrac{1}{2}\dfrac{F}{A} \times\dfrac{{\Delta L}}{L} \times AL$
$U =\dfrac{1}{2} \times stress \times strain \times volume$
Elastic potential energy stored per unit volume of a stretched wire
$u =\dfrac{1}{2} \times stress \times strain =\dfrac{1}{2} \times Y \times {(strain)^2}$
$ =\dfrac{1}{2} \times\dfrac{1}{Y} \times {(stress)^2}$
Breaking force: Breaking stress × Area of cross section of the wire.
Some Facts about Elasticity:
Young’s modulus is numerically equal to the normal stresses which will double the length of a wire.
Elongation in a wire by its own weight: If a wire of length L and cross-sectional area A is stretched by a force F, then by the definition of Y,
$\Delta L =\dfrac{{FL}}{{AY}}$ [As $Y =\dfrac{{FL}}{{A\Delta L}}$]
In case of elongation by its own weight, (F = Mg) will act at centre of gravity of the wire, so that length of wire which is stretched is (L/2).
$\therefore \Delta L=\dfrac{Mg\dfrac{L}{2}}{AY}=\dfrac{MgL}{2AY}=\dfrac{\rho g{{L}^{2}}}{2Y}$ [As $M = \rho AL$]
Thermal stress: If a rod is fixed between 2 rigid supports, due to change in temperature its length will change and so it will exert a normal stress on the supports. This stress is called thermal stress.
Thermal stress $= Y\alpha \Delta T$
Where $\alpha $ is the coefficient of linear expansion and $\Delta T$ is the change in temperature.
Interatomic force constant (k)
$k =\dfrac{{{\text{Interatomic force}}}}{{{\text{Change in inter atomic distance}}}} =\dfrac{{{F_0}}}{{\Delta r}}$
If the Young’s modulus for a material is Y and the equilibrium distance between the atoms is , ${r_0}$ then ${k_0} = Y{r_0}$
In case of twisting of a cylinder ( or wire) of length L and radius r, elasticity couple per unit twist is given by
$C =\dfrac{{\pi G{r^4}}}{{2L}}$
Where G is the modulus of rigidity of the material of wire.
Depression of a beam loaded at the middle by a load W and support at the end is
$\delta =\dfrac{{W{L^3}}}{{48Y{I_g}}}$
Where L is the length of a beam, Y is Young’s modulus for the material of the beam, and I is the geometrical moment of inertia.
For a beam of circular cross-section of radius r,
${I_g} =\dfrac{{\pi {r^2}}}{4}$
For a beam of rectangular cross-section of breath b and thickness d,${I_g} =\dfrac{{b{d^3}}}{{12}}$
Important Formula:
$\text{Stress} =\dfrac{F}{A}$
$\text{Strain} =\dfrac{{{\text{Change in dimension}}}}{{{\text{Original dimension}}}}$
Longitudinal strain = $ =\dfrac{{{\text{Change in length}}}}{{{\text{Original length}}}} =\dfrac{{\Delta L}}{L}$
Volumetric strain $ =\dfrac{{{\text{Change in volume}}}}{{{\text{Original volume}}}} =\dfrac{{\Delta V}}{V}$
Shearing strain $ = \theta =\dfrac{l}{L}$
Hooke’s law: $Stress = E \times Strain$ Or $\dfrac{{Stress}}{{Strain}} = E$
Young’s modulus: $Y=\dfrac{\text{Normal stress}}{\text{Longitudinal strain}}$
$Y=\dfrac{\dfrac{F}{A}}{\dfrac{\Delta L}{L}}=\dfrac{FL}{A\Delta L}=\dfrac{FL}{\pi {{r}^{2}}\Delta L}$
Bulk modulus: $B=\dfrac{\text{Normal stress}}{\text{Volumetric strain}}$
$B=\dfrac{\dfrac{-F}{A}}{\dfrac{\Delta V}{V}}=-\dfrac{PV}{\Delta V}$ where -ve sign shows that with an increase in pressure, a decrease in volume occurs.
Modulus of rigidity: $G =\dfrac{{{\text{translational stress}}}}{{{\text{shearing strain}}}} =\dfrac{F}{{A\theta }}$
Important relationships between Modulus of elasticity and Poisson’s ratio:
$Y = 3B(1 - 2\sigma )$
$Y = 2G(1 + \sigma )$
$\sigma =\dfrac{{3B - 2G}}{{2G + 6B}}$
$\dfrac{9}{Y} =\dfrac{1}{B} +\dfrac{3}{G}$
$U =\dfrac{1}{2}F \times \Delta L =\dfrac{1}{2}\dfrac{F}{A} \times\dfrac{{\Delta L}}{L} \times AL$
$U =\dfrac{1}{2} \times stress \times strain \times volume$
Thermal stress $= Y\alpha \Delta T$
Interatomic force constant (k)
$k =\dfrac{{{\text{Interatomic force}}}}{{{\text{Change in inter atomic distance}}}} =\dfrac{{{F_0}}}{{\Delta r}}$
In case of twisting of a cylinder ( or wire) of length L and radius r, elasticity couple per unit twist is given by
$C =\dfrac{{\pi G{r^4}}}{{2L}}$
Where G is the modulus of rigidity of the material of wire.
Depression of a beam loaded at the middle by a load W and support at the end is
$\delta =\dfrac{{W{L^3}}}{{48Y{I_g}}}$
Where L is the length of a beam, Y is Young’s modulus for the material of the beam, and I is the geometrical moment of inertia.
For a beam of circular cross-section of radius r,
${I_g} =\dfrac{{\pi {r^2}}}{4}$
For a beam of rectangular cross-section of breath b and thickness d,${I_g} =\dfrac{{b{d^3}}}{{12}}$
Examples:
1. The bulk modulus of a spherical object is ‘B’. If it is subjected to uniform pressure p, then its fractional decrease in radius would be:
Inversely proportional to pressure
Inversely proportional to bulk modulus
Value of the radius is $\dfrac{B}{{3p}}$
Value of the radius is $\dfrac{p}{{3B}}$
Ans: Option b) and d)
Bulk modulus B is given by: $ -\dfrac{{PV}}{{\Delta V}}$
We know that, the volume of sphere is $V =\dfrac{4}{3}\pi {r^3}$
As, there is change in radius we have:
${r^3} = 3{r^2}dr$
$V =\dfrac{4}{3}\pi (3{r^2})dr$
$\dfrac{V}{{dV}} =\dfrac{r}{{3dr}}$
$B =\dfrac{{ - pr}}{{3dr}}$
$\dfrac{{dr}}{r} =\dfrac{{ - p}}{{3B}}$
Thus
$dr =\dfrac{p}{{3B}}$
Thus, we change the radius to be $\dfrac{p}{{3B}}$and it is inversely proportional to B.
2. A metallic rod of length is elongated at y amount whose length is l and area A. It is made up of a material whose young’s modulus is Y. The work done during elongation is directly proportional to:
y
$\dfrac{1}{y}$
${y^2}$
${y^3}$
Answer: Option c)
$Volume = area \times length$
$V = A \times l$
$strain =\dfrac{y}{l}$
$Y =\dfrac{{stress}}{{strain}}$
We know that
$\text{Work Done}(W) =\dfrac{1}{2} \times stress \times {(strain)^2} \times volume$
$W =\dfrac{1}{2} \times Y \times {\left( {\dfrac{y}{l}} \right)^2} \times Al$
$W =\dfrac{1}{2} \times \left( {\dfrac{{YA}}{l}} \right){y^2}$
$\therefore W\,\alpha \,{y^2}$
Thus, Work done is directly proportional to the square of the elongation length.
List of common mistakes and points to remember:
All of the previously stated significant issues are equally asked as numerical problems and derivations.
It is advised to have a conceptual understanding of each topic.
Practice the more and more numerical questions from each as well.
Go over the chapter's relationships between the physical quantities again.
Create a table or chart to show the moment of inertia for various items and forms.
Importance of Mechanical Properties of Solids
This is a crucial chapter that teaches students preparing for NEET about the different physical properties of solids. Here, students will learn what types of mechanical properties are there and how to define them. They will find out how these terms are mathematically defined. Every formula in this chapter will be explained by interpreting the physical quantities with their dimensions and units.
They will be introduced to new scientific terms related to solids such as elasticity, elasticity, types of stresses, tensile strength, plasticity, strain etc. They will learn to equate a mathematical formula for all these terms to calculate the mechanical properties of particular solids.
This chapter will describe Hooke’s Law to correlate stress and strain. Apart from explaining the different types of stress and strain, it will teach how this law has been formulated and what we can imply from it. The Mechanical Properties of Solids notes will guide students to understand this law and its mathematical interpretation.
On progressing further, NEET aspirants will learn what the modulus of rigidity is. We can clearly understand how this chapter explains the effect of different kinds of forces on solids. This knowledge will be used further in learning the advanced concepts of mechanics, kinematics, and the behaviour of solids in different conditions.
Benefits of Vedantu’s Mechanical Properties of Solids Revision Notes for NEET
These notes are compiled by the subject experts to offer a simpler version of all the scientific terms, their definitions, derivation of formulas, units, and applications. Students will be able to comprehend the concepts behind these terms. They will become confident in using these terms to answer questions related to the mechanical properties of solids accurately.
The concise version of this chapter in these notes will also guide students to study and remember the fundamental principles.
Students will also find the sample Mechanical Properties of Solids NEET questions an ideal tool to check their progress. They can use these questions to evaluate their preparation level. Also, check how the experts have solved these questions to solve questions accurately and speedily.
Download Mechanical Properties of Solids Revision Notes PDF
These revision notes are available in a free PDF version to download. You can add these notes to your study material and prepare this chapter efficiently. Once done preparing, use these notes to revise the mechanical properties of solids faster. Use the simpler version of Mechanical Properties of Solids Notes PDF to recall the scientific principles and formulas right away during an exam and score well in the exams.
NEET Physics Revision Notes - Chapter Pages
NEET Physics Chapter-wise Revision Notes | |
FAQs on Revision Notes on Mechanical Properties of Solids for NEET 2025
1. What are solids?
A state of matter where the constituent particles are very closely packed resulting in a proper shape and lack of fluidity is called solid.
2. What is stress?
The intensity of an internal force applied to the cross-sectional area of a solid is called stress.
3. What is strain?
The deformation of a solid due to the application of stress is called strain.
4. How can we relate stress and strain in solids?
Stress is the cause and strain is the effect. It means when a solid is under stress or an internal force, a deformity is observed in a solid. This deformity is called strain.



















