Physics Mathematical Tools for NEET
As far as the NEET aspirants are concerned, one of the challenges they face while studying physics for the NEET exam is the mathematical operations and tools used at the time of solving numerical problems. However, this can be made easier if we learn the basic mathematical tools required in physics for the NEET exam.
In this article discussing the new and old mathematical tools in physics, we will see different physical constants and conversion coefficients that will come in handy while solving numerical problems. The importance of mathematics of tools like trigonometric functions of angles and their applications are discussed here. The application of differentiation and integration plays an important role in solving most of the physics problems in several chapters.
Now, let us move on to the important concepts and formulae of mathematical tools required in physics for the NEET exam, along with a few solved mathematical tools examples.
Important Topics of Mathematical Tools
Quadratic equation
Binomial expansion
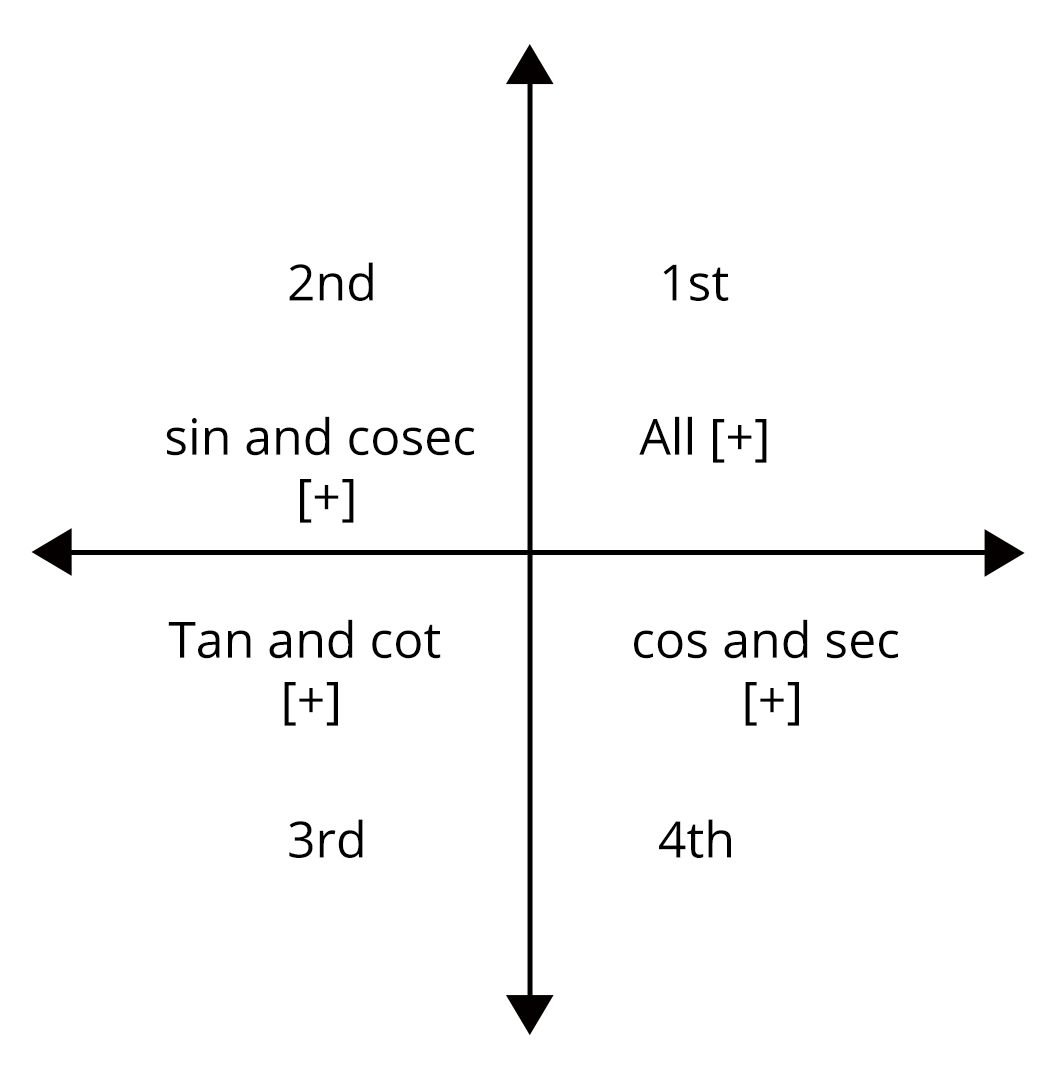
Important trigonometric identities.
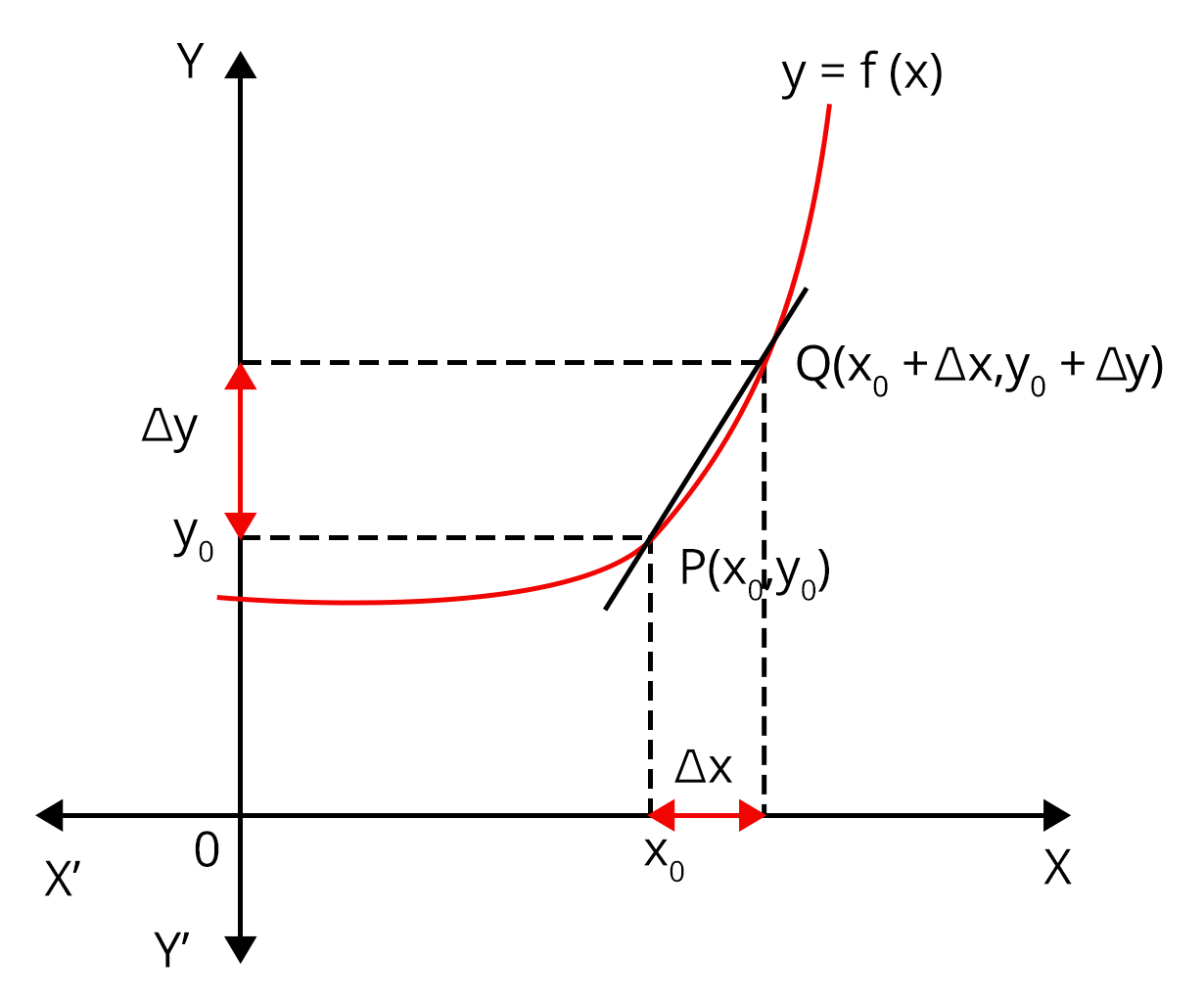
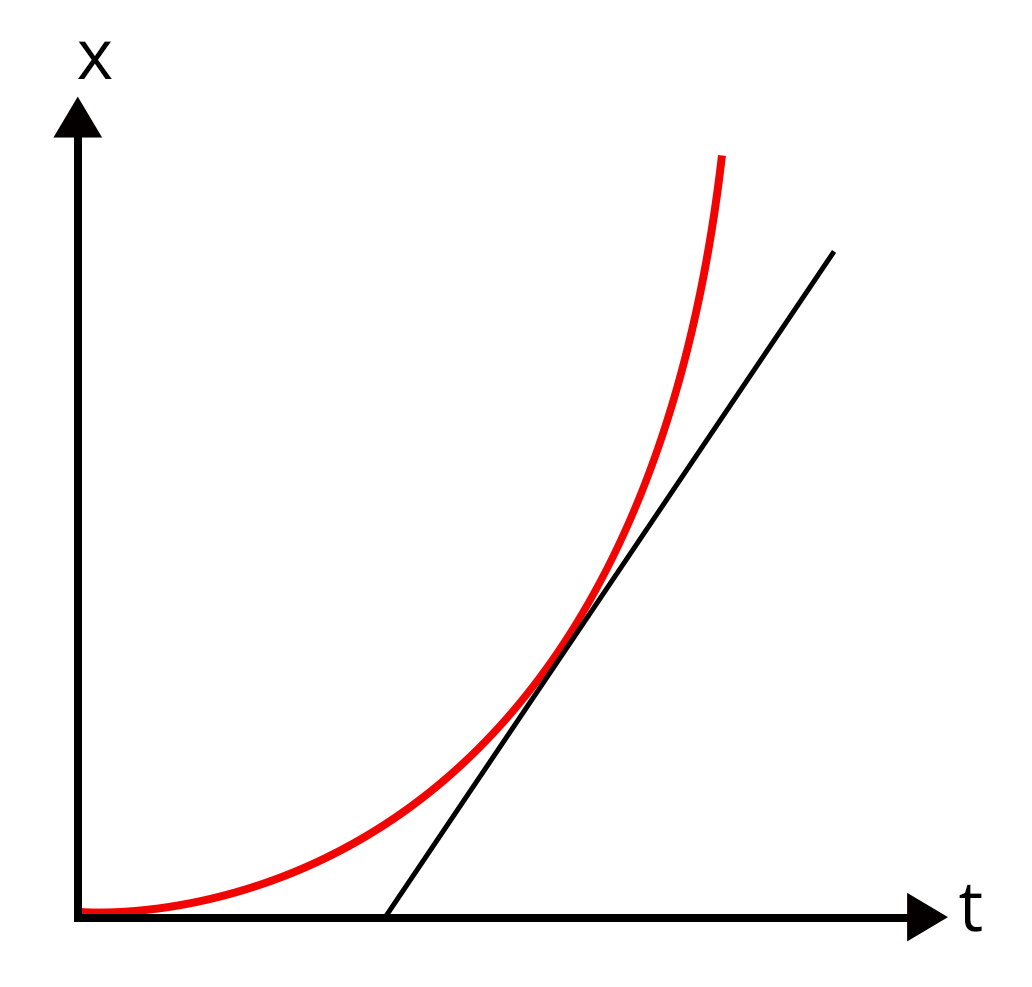
Differentiation
Rules of differentiation
Applications of differentiation
Integration and its application
Definite integral
Integration Formulae
Important Concepts of Mathematical Tools
List of Important Formulae
Solved Examples
1. The position of a particle on x-axis that varies with time is given as x=3t^2+2t+1. Find the velocity of the particle at t=2 s.
Sol:
Given,
The position of the particle ,x=3t2+2t+1
The velocity of particle at t=2 s can be found by differentiating the displacement and substituting the value of t as 2 sec
$v=\dfrac{dx}{dt}$
$v=\dfrac{d}{dt}(3t^2+2t+1)$
$v=3\times2t+2$
$v=6t+2$
Put t=2 to calculate the velocity at that instant.
$v=6t+2$
$v=6\times2+2$
$v=14~m/s$
Therefore, the velocity of the particle at t=2 s is 14 m/s.Key point: Differentiating
displacement with respect to time gives velocity.
2. The variable force acting on a body of mass 1 kg depends on the displacement on x -axis as F=3x2+2. Find the work done by the variable force from x=0 to x= 2m.
Sol:
Given,
The variable force acting on the body, F=3x2+2
We can calculate the work done by the force by integrating force from x=0 m to x= 2m
$W=\int_{0}^{2} F.dx$
$W=\int_{0}^{2} (3x^2+2).dx$
$W=3\dfrac{[x^3]^2_0}{3}+2[x]^2_0$
$W=12~J$
Thus, the work done by the variable force from x=0 to x= 2m is 12J.
Key Point: The work done by a variable force can be obtained by integration of the variable force with respect to displacement.
Previous Year Questions from NEET Paper
1. A particle moves along a straight line OX. At a time t (in seconds), the distance x (in metres) is given by x=40+12t-t3. How long would the particle travel before coming to rest? (NEET 2006)
a. 24 m
b. 40 m
c. 56 m
d. 16 m
Sol:
The speed of the particle can be obtained by differentiating the distance with respect to time.
$v=\dfrac{dx}{dt}$
$v=\dfrac{d}{dt}(40+12t-t^3)$
$v=0+12-3\times t^2$
$v=-3t^2+12$
When particle comes to rest, the speed of the particle becomes zero
$0=-3t^2+12$
$t^2=4$
$t=2~s$
Now, the distance travelled by the particle is
$x=40+12t-t^3$
$x=40+12\times2-2^3$
$x=56~m$
Therefore, correct answer is option (c)
Trick: Speed of the particle can be obtained by differentiating the expression for distance with respect to time.
2. The displacement of a particle moving in a straight line is given by s=2t2+2t+4, where s is in metres and t is in seconds. The acceleration of the particle is (NEET 2001)
2 m/s2
4 m/s2
6 m/s2
8 m/s2
Sol:
The speed of the particle can be obtained by
$v=\dfrac{dx}{dt}$
$v=\dfrac{d}{dt}(2t^2+2t+4)$
$v=4t+2$
The acceleration of the particle is calculated as follows
$a=\dfrac{dv}{dt}$
$a=\dfrac{d}{dt}(4t+2)$
$v=4~m/s^2$
Therefore, correct answer is option (b)
Trick: When displacement of any object is given second-order differentiation will
be the acceleration of the object.
Practice Questions
1. Find the work done to elongate a spring having a spring constant of 2000N/m from an extension of 1 cm to 2 cm.
Ans: 0.3 J
2. If v=x2-5x+4, find the acceleration of the particle when the velocity of the particle is zero.
Ans: 0 m/s2
Conclusion
In this article, we have provided important information under several mathematical tool names necessary for solving numerical problems in Physics. Students should have a better understanding of the mathematical operations so that students can score good marks in Physics for the NEET exam.
NEET Important Topic - Physics Mathematical Tools

 Share
ShareFAQs on NEET Important Topic - Physics Mathematical Tools
1. What are the main mathematical tools required in Physics for the NEET exam?
The main mathematical tools required for Physics in the NEET exam are differentiation and its applications, indefinite and definite integrations, trigonometric functions and their identities, measurement of positive and negative angles etc. You can download the mathematics tool pdf from Vedantu for easy reference.
2. Is Calculus required for NEET?
Some of the problems in Physics require a basic understanding of Calculus to solve problems in chapters like electrostatics, the system of particles, magnetic effects of current, etc. Even though students don't have to memorise all the Calculus formulas, they must know how to apply Calculus in a given situation to find the solution to the problems.
3. How to score good marks in Physics for the NEET exam?
First of all, understand all the concepts in depth and practise all the numerical problems in the NCERT textbook as well as other good study materials. Then, work out all the questions in the previous year's question papers. These will ensure that you will get good marks in physics for the NEET exam.




















 Watch Video
Watch Video