NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives

• Exercise 6.1: This exercise deals with finding the rate of change of a quantity using derivatives. It covers problems related to finding the instantaneous rate of change, average rate of change, and marginal cost and revenue.

• Exercise 6.2: In this exercise, you will learn about increasing and decreasing functions, and how to find the intervals of increase or decrease of a function.

• Exercise 6.3: This exercise is about finding the maximum and minimum values of a function using derivatives. It covers problems related to finding the maximum and minimum values of a function on an interval, as well as optimization problems.

• Miscellaneous Exercise: This exercise contains additional problems related to the application of derivatives.

Access NCERT Solutions for Class 12 Maths Chapter 6 – Application of Derivatives

Exercise 6.1

1. Find the rate of change of the area of a circle with respect to its radius $r$ when

a. $r = 3\;{\text{cm}}$ (b) $r = 4\;{\text{cm}}$

Ans: We know that $A = \pi {r^2}$Differentiate w.r.t r

$\therefore \dfrac{{dA}}{{dr}} = \dfrac{d}{{dr}}\left( {\pi {r^2}} \right) = 2\pi r$

(a) When $r = 3\;{\text{cm}}$,

$\dfrac{{dA}}{{dr}} = 2\pi (3) = 6\pi$

The area is changing at $6\;{\text{c}}{{\text{m}}^2}/{\text{s}}$ when radius is $3\;{\text{cm}}$.

b. When $r = 4\;{\text{cm}}$,

$\dfrac{{dA}}{{dr}} = 2\pi (4) = 8x$

The area is changing at $8\;{\text{c}}{{\text{m}}^2}/{\text{s}}$ when radius is $4\;{\text{cm}}$.

2. The volume of a cube is increasing at the rate of $8\;{\text{c}}{{\text{m}}^3}/{\text{s}}$ How fast is the surface area increasing when the length of its edge is $12\;{\text{cm}}$ ?

Ans: Let the side length, volume and surface area respectively be equal to x,v and $S$. $V = {x^3}$

$S = 6{x^2}$

$\dfrac{{dV}}{{dt}} = 8\;{\text{c}}{{\text{m}}^3}/{\text{s}}$

$\therefore 8 = \dfrac{{dV}}{{dt}} = \dfrac{d}{{dt}}\left( {{x^3}} \right)$

$= \dfrac{d}{{dx}}\left( {{x^3}} \right)\dfrac{{dx}}{{dt}} = 3{x^2}\dfrac{{dx}}{{dt}}$

$\therefore 8 = \dfrac{{dV}}{{dt}} = \dfrac{d}{{dt}}\left( {{x^3}} \right) = \dfrac{d}{{dx}}\left( {{x^3}} \right)\dfrac{{dx}}{{dt}} = 3{x^2}\dfrac{{dx}}{{dt}} \Rightarrow \dfrac{{dx}}{{dt}} = \dfrac{8}{{3{x^2}}}$

$\dfrac{{dS}}{{dt}} = \dfrac{d}{{dt}}\left( {6{x^2}} \right)$

$= \dfrac{d}{{dx}}\left( {6{x^2}} \right)\dfrac{{dx}}{{dt}}$

$\dfrac{{dS}}{{dt}} = \dfrac{d}{{dt}}\left( {6{x^2}} \right) = \dfrac{d}{{dx}}\left( {6{x^2}} \right)\dfrac{{dx}}{{dt}} = 12x\dfrac{{dx}}{{dt}} = 12x\left( {\dfrac{8}{{3{x^2}}}} \right) = \dfrac{{32}}{x}$

So, when $x = 12\;{\text{cm}},$

$\dfrac{{dS}}{{dt}} = \dfrac{{32}}{{12}}\;{\text{c}}{{\text{m}}^2}/{\text{s}}$

$x = 12\;{\text{cm}},\dfrac{{dS}}{{dt}} = \dfrac{{32}}{{12}}\;{\text{c}}{{\text{m}}^2}/{\text{s}} = \dfrac{8}{3}\;{\text{c}}{{\text{m}}^2}/{\text{s}}.$

3. The radius of a circle is increasing uniformly at the rate of $3\;{\text{cm}}/{\text{s}}$. Find the rate at which the area of the circle is increasing when the radius is $10\;{\text{cm}}/{\text{s}}$

Ans: We know that $A = \pi {r^2}$ $\therefore \dfrac{{dA}}{{dt}} = \dfrac{d}{{dr}}\left( {\pi {r^2}} \right)\dfrac{{dr}}{{dt}} = 2\pi r\dfrac{{dr}}{{dt}}$

$\dfrac{{dr}}{{dt}} = 3\;{\text{cm}}/{\text{s}}$

$\therefore \dfrac{{dA}}{{dt}} = 2\pi r(3) = 6\pi r$

So, when $r = 10\;{\text{cm}}$,

$\dfrac{{dA}}{{dt}} = 6\pi (10) = 60\pi {\text{c}}{{\text{m}}^2}/{\text{s}}$

4. An edge of a variable cube is increasing at the rate of $3\;{\text{cm}}/{\text{s}}$. How fast is the volume of the cube increasing when the edge is $10\;{\text{cm}}$ long? 

Ans: Let the length and the volume of the cube respectively be $x$ and $V$.

$V = {x^3}$

$\therefore \dfrac{{dV}}{{dt}} = \dfrac{d}{{dt}}\left( {{x^3}} \right) = \dfrac{d}{{dx}}\left( {{x^3}} \right)\dfrac{{dx}}{{dt}}$

$= 3{x^2}\dfrac{{dx}}{{dt}}$

$\dfrac{{dx}}{{dt}} = 3\;{\text{cm}}/{\text{s}}$

$\therefore \dfrac{{dV}}{{dt}} = 3{x^2}(3) = 9{x^2}$

So, when $x = 10\;{\text{cm}}$,

$\dfrac{{dV}}{{dt}} = 9{(10)^2} = 900\;{\text{c}}{{\text{m}}^3}/{\text{s}}$

5. A stone is dropped into a quiet lake and waves move in circles at the speed of $5\;{\text{cm}}/{\text{s}}.$ At the instant when the radius of the circular wave is $8\;{\text{cm}}$, how fast is the enclosed area increasing?

Ans: We know that $A = \pi {r^2}$ 

$\dfrac{{dA}}{{dt}} = \dfrac{d}{{dt}}\left( {\pi {r^2}} \right) = \dfrac{d}{{dr}}\left( {\pi {r^2}} \right)\dfrac{{dr}}{{dt}} = 2\pi r\dfrac{{dr}}{{dt}}$

$\dfrac{{dr}}{{dt}} = 5\;{\text{cm}}/{\text{s}}$

So, when $r = 8\;{\text{cm}}$, 

$\dfrac{{dA}}{{dt}} = 2\pi (8)(5)$

$= 80\pi {\text{c}}{{\text{m}}^2}/{\text{s}}.$

6. The radius of a circle is increasing at the rate of $0.7\;{\text{cm}}/{\text{s}}$. What is the rate of increase of its circumference?

Ans: We know that $C = 2\pi r$.

$\therefore \dfrac{{dC}}{{dt}} = \dfrac{{dC}}{{dr}}\dfrac{{dr}}{{dt}} = \dfrac{d}{{dr}}(2\pi r)\dfrac{{dr}}{{dt}} = 2\pi \dfrac{{dr}}{{dt}}$

$\dfrac{{dr}}{{dt}} = 0.7\;{\text{cm}}/{\text{s}}$

$\therefore \dfrac{{dC}}{{dt}} = 2\pi (0.7) = 1.4\pi {\text{cm}}/{\text{s}}$

7. The length $x$ of a rectangle is decreasing at the rate of $5\;{\text{cm}}/$ minute and the width $y$ is increasing at the rate of $4\;{\text{cm}}/$ minute. When $x = 8\;{\text{cm}}$ and $y = 6\;{\text{cm}}$, find the rates of change of $(a)$ the perimeter, and $(b)$ the area of the rectangle. 

Ans: It is given that $\dfrac{{dx}}{{dt}} =  - 5\;{\text{cm}}/{\text{min}},$$\dfrac{{dx}}{{dt}} = 4\;{\text{cm}}/{\text{min}},$ $x = 8\;{\text{cm}}$and $y = 6\;{\text{cm}}$,

1. The perimeter of a rectangle is given by $P = 2(x + y)$

$\therefore \dfrac{{dP}}{{dt}} = 2\left( {\dfrac{{dx}}{{dt}} + \dfrac{{dy}}{{dt}}} \right) = 2( - 5 + 4) =  - 2\;{\text{cm}}/{\text{min}}$

2. The area of a rectangle is given by $A = xy$ 

3. $\therefore \dfrac{{dA}}{{dt}} = \dfrac{{dx}}{{dt}}y + x\dfrac{{dy}}{{dt}} =  - 5y + 4x$

When $x = 8\;{\text{cm}}$ and $y = 6\;{\text{cm}},$

$\dfrac{{dA}}{{dt}} = ( - 5 \times 6 + 4 \times 8){\text{c}}{{\text{m}}^2}/{\text{min}} = 2\;{\text{c}}{{\text{m}}^2}/{\text{min}}$

8. A balloon, which always remains spherical on inflation, is being inflated by pumping in 900 cubic centimeters of gas per second. Find the rate at which the radius of the balloon increases when the radius is $15\;{\text{cm}}$.

Ans: We know that $V = \dfrac{4}{3}\pi {r^3}$ 

$\therefore \dfrac{{dV}}{{dt}} = \dfrac{{dV}}{{dr}}\dfrac{{dr}}{{dt}} = \dfrac{d}{{dr}}\left( {\dfrac{4}{3}\pi {r^2}} \right)\dfrac{{dr}}{{dt}} = 4\pi {r^2}\dfrac{{dr}}{{dt}}$

$\dfrac{{dV}}{{dt}} = 900\;{\text{c}}{{\text{m}}^2}/{\text{s}}$

$\therefore 900 = 4\pi {r^2}\dfrac{{dr}}{{dt}}$

$\Rightarrow \dfrac{{dr}}{{dt}} = \dfrac{{900}}{{4\pi {r^2}}} = \dfrac{{225}}{{\pi {r^2}}}$

So, when radius $= 15\;{\text{cm}}$,

 $\dfrac{{dr}}{{dt}} = \dfrac{{225}}{{\pi {{(15)}^2}}} = \dfrac{1}{\pi }{\text{cm}}/{\text{s}}$

9. A balloon, which always remains spherical has a variable radius. Find the rate at which its volume is increasing with the radius when the latter is $10\;{\text{cm}}$. 

Ans: We know that $V = \dfrac{4}{3}\pi {r^2}$

$\therefore \dfrac{{dV}}{{dr}} = \dfrac{d}{{dr}}\left( {\dfrac{4}{3}\pi {r^3}} \right) = \dfrac{4}{3}\pi \left( {3{r^2}} \right) = 4\pi {r^2}$

So, when radius $= 10\;{\text{cm}},\dfrac{{dV}}{{dr}} = 4\pi {(10)^2} = 400\pi $

Thus, the volume of the balloon is increasing at the rate of $400\pi {\text{c}}{{\text{m}}^3}/{\text{s}}$.

10. A ladder $5\;{\text{m}}$ long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of $2\;{\text{cm}}/{\text{s}}$. How fast is its height on the wall decreasing when the foot of the ladder is $4\;{\text{m}}$ away from the wall? 

Ans: Let the heigt of the wall at which the ladder is touching it be $y\;{\text{m}}$ and the distance of its foot from the wall on the ground be $x\;{\text{m}}$.

$\therefore {x^2} + {y^2} = {5^2} = 25$

$\Rightarrow y = \sqrt {25 - {x^2}}$

$\therefore \dfrac{{dy}}{{dt}} = \dfrac{d}{{dt}}\left( {\sqrt {25 - {x^2}} } \right) = \dfrac{d}{{dx}}\left( {\sqrt {25 - {x^2}} } \right)\dfrac{{dx}}{{dt}} = \dfrac{{ - x}}{{\sqrt {25 - {x^2}} }}\dfrac{{dx}}{{dt}}$

$\dfrac{{dx}}{{dt}} = 2\;{\text{cm}}/{\text{s}}$

$\therefore \dfrac{{dy}}{{dt}} = \dfrac{{ - 2x}}{{\sqrt {25 - {x^2}} }}$

So, when $x = 4m$,

 $\dfrac{{dy}}{{dt}} = \dfrac{{ - 2 \times 4}}{{\sqrt {25 - 16} }} =  - \dfrac{8}{3}$

11. A particle is moving along the curve $6y = {x^3} + 2.$ Find the points on the curve at which the $Y$ coordinate is changing 8 times as fast as the ${\text{X}}$ coordinate. 

Ans: The equation of the curve is $6y = {x^3} + 2$. Differentiating with respect to time, we have, $6\dfrac{{dy}}{{dt}} = 3{x^2}\dfrac{{dx}}{{dt}}$

$\Rightarrow 2\dfrac{{dy}}{{dt}} = {x^2}\dfrac{{dx}}{{dt}}$

According to the question, $\left( {\dfrac{{dy}}{{dt}} = 8\dfrac{{dx}}{{dt}}} \right)$

$\therefore 2\left( {8\dfrac{{dx}}{{dt}}} \right) = {x^2}\dfrac{{dx}}{{dt}} \Rightarrow 16\dfrac{{dx}}{{dt}} = {x^2}\dfrac{{dx}}{{dt}}$

$\Rightarrow \left( {{x^2} - 16} \right)\dfrac{{dx}}{{dt}} = 0$

$\Rightarrow {x^2} = 16$

$\Rightarrow x =  \pm 4$

When $x = 4,$

$y = \dfrac{{{4^3} + 2}}{6} = \dfrac{{66}}{6} = 11$

When $x =  - 4,$

$y = \dfrac{{\left( { - {4^3}} \right) + 2}}{6} =  - \dfrac{{62}}{6} =  - \dfrac{{31}}{3}$

Thus, the points on the curve are $(4,11)$ and $\left( { - 4,\dfrac{{ - 31}}{3}} \right)$

12. The radius of an air bubble is increasing at the rate of $\dfrac{1}{2}\;{\text{cm}}/{\text{s}}$. At what rate is the volume of the bubble increasing when the radius is $1\;{\text{cm}}$ ? 

Ans: Assuming that the air bubble is a sphere, $V = \dfrac{4}{3}\pi {r^2}$

$\therefore \dfrac{{dV}}{{dt}} = \dfrac{d}{{dt}}\left( {\dfrac{{4\pi }}{3}{r^3}} \right) = \dfrac{d}{{dr}}\left( {\dfrac{{4\pi }}{3}{r^3}} \right)\dfrac{{dr}}{{dt}} = 4\pi {r^2}\dfrac{{dr}}{{dt}}$

$\dfrac{{dr}}{{dt}} = \dfrac{1}{2}\;{\text{cm}}/{\text{s}}$

So, when $r = 1\;{\text{cm}},$

$\dfrac{{dV}}{{dt}} = 4\pi {(1)^2}\left( {\dfrac{1}{2}} \right) = 2\pi {\text{c}}{{\text{m}}^3}/{\text{s}}$

13. A balloon, which always remains spherical, has a variable diameter $\dfrac{3}{2}(2x + 1)$. Find the rate of change of its volume with respect to $x$. 

Ans: We know that $V = \dfrac{4}{3}\pi {r^3}$

$d = \dfrac{3}{2}(2x + 1)$

$\Rightarrow r = \dfrac{3}{4}(2x + 1)$

$\therefore V = \dfrac{4}{3}\pi {\left( {\dfrac{3}{4}} \right)^3}{(2x + 1)^3} = \dfrac{9}{{16}}\pi {(2x + 1)^3}$

$\therefore \dfrac{{dV}}{{dx}} = \dfrac{9}{{16}}\pi \dfrac{d}{{dx}}{(2x + 1)^3} = \dfrac{{27}}{8}\pi {(2x + 1)^3}.$

14. Sand is pouring from a pipe at the rate of $12\;{\text{c}}{{\text{m}}^3}/{\text{s}}$. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is $4\;{\text{cm}}$ ?

Ans: We know that $V = \dfrac{1}{3}\pi {r^2}h$ 

$h = \dfrac{1}{6}r$

$\Rightarrow r = 6h$

$\therefore V = \dfrac{1}{3}\pi {(6h)^2}h = 12\pi {h^3}$

$\therefore \dfrac{{dV}}{{dt}} = 12\pi \dfrac{d}{{dt}}\left( {{h^3}} \right)\dfrac{{dh}}{{dt}}$

$= 12\pi \left( {3{h^2}} \right)\dfrac{{dh}}{{dt}} = 36\pi {h^2}\dfrac{{dh}}{{dt}}$

$\dfrac{{dV}}{{dt}} = 12\;{\text{c}}{{\text{m}}^2}/{\text{s}}$

So, when $h = 4\;{\text{cm}}$,

$12 = 36\pi {(4)^2}\dfrac{{dh}}{{dt}}$

$\Rightarrow \dfrac{{dh}}{{dt}} = \dfrac{{12}}{{36\pi (16)}}$

$= \dfrac{1}{{48\pi }}{\text{cm}}/{\text{s}}$

15. The total cost $C(x)$ in Rupees associated with the production of $x$ units of an item is given by $C(x) = 0.007{x^3} - 0.003{x^2} + 15x + 4000$. Find the marginal cost when 17 units are produced.

Ans: Marginal cost is the rate of change of the total cost with respect to the output.

$\therefore $ Marginal cost $MC = \dfrac{{dC}}{{dx}} = 0.007\left( {3{x^2}} \right) - 0.003(2x) + 15 = 0.021{x^2} - 0.006x + 15$

When $x = 17,MC = 0.021\left( {{{17}^2}} \right) - 0.006(17) + 15$

$= 0.021(289) - 0.006(17) + 15$

$= 6.069 - 0.102 + 15$

$= 20.967$

So, when 17 units are produced, the marginal cost is Rs.20.967

16. The total revenue in Rupees received from the sale of $x$ units of a product is given by $R(x) = 13{x^2} + 26x + 15$. Find the marginal revenue when $x = 7$.

Ans: Marginal revenue is the rate of change of the total revenue with respect to the number of units sold.

$\therefore $ Marginal Revenue $MR = \dfrac{{dR}}{{dx}} = 13(2x) + 26 = 26x + 26$

When $x = 7,MR = 26(7) + 26 = 182 + 26 = 208$

Thus, the marginal revenue is Rs.208.

17. The rate of change of the area of a circle with respect to its radius $r$ at $r = 6\;{\text{cm}}$ is

(A) 10$\pi$

(B) 12$\pi$

(C) 8$\pi$

(D) 11$\pi$

Ans: We know that $A = \pi {r^2}$ 

$\therefore \dfrac{{dA}}{{dr}} = \dfrac{d}{{dr}}\left( {\pi {r^2}} \right) = 2\pi r$

So, when $r = 6\;{\text{cm}},$

$\dfrac{{dA}}{{dr}} = 2\pi  \times 6 = 12\pi {\text{c}}{{\text{m}}^2}/{\text{s}}$

Thus, the rate of change of the area of the circle is $12\pi {\text{c}}{{\text{m}}^2}/{\text{s}}$. 

The correct answer is option ${\mathbf{B}}$.

18. The total revenue in Rupees received from the sale of $x$ units of a product is given by $R(x) = 3{x^2} + 36x + 5$. The marginal revenue, when $x = 15$ is

1. 116

2. 96

3. 90

4. 126 

Ans: Marginal revenue is the rate of change of the total revenue with respect to the number of units sold.

$\therefore $ Marginal Revenue $MR = \dfrac{{dR}}{{dx}} = 3(2x) + 36$

$= 6x + 36$

So, when $x = 15,$

$MR = 6(15) + 36 = 90 + 36 = 126$

Hence, the marginal revenue is Rs.126. 

The correct answer is option D.

Exercise 6.2

1. Show, that the function given by $f(x) = 3x + 17$ is strictly increasing on ${\mathbf{R}}$.

Ans: Let ${x_1}$ and ${x_2}$, be any two numbers in $\mathbb{R}$.

${x_1} < {x_2} \Rightarrow 3{x_1} + 17 < 3{x_2} + 17 = f\left( {{x_1}} \right) < f\left( {{x_2}} \right)$

Thus, $f$ is strictly increasing on $\mathbb{R}$.

Alternate Method:

${f^\prime }(x) = 3 > 0$ on $\mathbb{R}$.

Thus, $f$ is strictly increasing on $\mathbb{R}$.

2. Show, that the function given by $f(x) = {e^{2x}}$ is strictly increasing on $\mathbb{R}$.

Ans: Let ${x_1}$ and ${x_2}$ be any two numbers in $\mathbb{R}$. 

${x_1} < {x_2}$

$\Rightarrow 2{x_1} < 2{x_2}$

$\Rightarrow {e^{2{x_1}}} < {e^{2{x_2}}}$

$\Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)$

Thus, $f$ is strictly increasing on $\mathbb{R}$

3. Show that the function given by $f(x) = \sin x$ is

1. Strictly increasing in $\left( {0,\dfrac{\pi }{2}} \right)$

2. Strictly decreasing $\left( {\dfrac{\pi }{2},\pi } \right)$

3. Neither increasing nor decreasing in $(0,\pi )$

Ans: $f(x) = \sin x \Rightarrow {f^\prime }(x) = \cos x$

1. $x \in \left( {0,\dfrac{\pi }{2}} \right)$

$\Rightarrow \cos x > 0 \Rightarrow {f^\prime }(x) > 0$

Thus, $f$ is strictly increasing in $\left( {0,\dfrac{\pi }{2}} \right)$.

2. $x \in \left( {\dfrac{\pi }{2},\pi } \right)$

$\Rightarrow \cos x < 0 \Rightarrow {f^\prime }(x) < 0$

Thus, $f$ is strictly decreasing in $\left( {\dfrac{\pi }{2},\pi } \right)$.

3. The results obtained in (A) and (B) are sufficient to state that $f$ is neither increasing nor decreasing in $(0,\pi )$.

4. Find the intervals in which the function $f$ given by $f(x) = 2{x^2} - 3x$ is

1. Strictly increasing

2. Strictly decreasing 

Ans: $f(x) = 2{x^2} - 3x \Rightarrow {f^\prime }(x) = 4x - 3$

$\therefore {f^\prime }(x) = 0 \Rightarrow x = \dfrac{3}{4}$

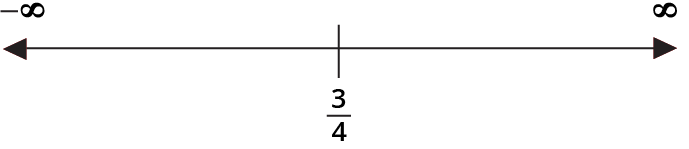
In $\left( { - \infty ,\dfrac{3}{4}} \right),$${f^\prime }(x) = 4x - 3 < 0$

Hence, $f$ is strictly decreasing in $\left( { - \infty ,\dfrac{3}{4}} \right)$

In $\left( {\dfrac{3}{4},\infty } \right),$${f^\prime }(x) = 4x - 3 > 0$

Hence, $f$ is strictly increasing in $\left( {\dfrac{3}{4},\infty } \right)$

5. Find the intervals in which the function $f$ given $f(x) = 2{x^2} - 3{x^2} - 36x + 7$ is

1. Strictly increasing 

2. Strictly decreasing 

Ans: $f(x) = 2{x^3} - 3{x^2} - 36x + 7$

${f^\prime }(x) = 6{x^2} - 6x - 36 = 6\left( {{x^2} - x - 6} \right) = 6(x + 2)(x - 3)$

$\therefore {f^\prime }(x) = 0 \Rightarrow x =  - 2,3$

In $( - \infty , - 2)$ and $(3,\infty ),{f^\prime }(x) > 0$

In $( - 2,3),{f^\prime }(x) < 0$

Hence, $f$ is strictly increasing in $( - \infty , - 2)$ and $(3,\infty )$ and strictly decreasing in $( - 2,3)$.

6. Find the intervals in which the following functions are strictly increasing or decreasing.

1. ${x^2} + 2x - 5$

2. $10 - 6x - 2{x^2}$

3. $- 2{x^3} - 9{x^2} - 12x + 1$

4. $6 - 9x - {x^2}$

5. ${(x + 1)^3}{(x - 3)^3}$

Ans: 

1. $f(x) = {x^2} + 2x - 5$

$\Rightarrow {f^\prime }(x) = 2x + 2$

$\Rightarrow {f^\prime }(x) = 0 \Rightarrow x =  - 1$

$x =  - 1$ divides the number line into intervals $( - \infty , - 1)$ and $( - 1,\infty ).$

In $( - \infty , - 1),{f^\prime }(x) = 2x + 2 < 0$

$\therefore f$ is strictly decreasing in $( - \infty , - 1)$

In $( - 1,\infty ),{f^\prime }(x) = 2x + 2 > 0,$

$\therefore {f^\prime }(x) = 2x + 2 > 0$

$\therefore f$ is strictly decreasing in $( - 1,\infty )$

2. $f(x) = 10 - 6x - 2{x^2}$

$\Rightarrow {f^\prime }(x) =  - 6 - 4x$

$\Rightarrow {f^\prime }(x) = 0 \Rightarrow x =  - \dfrac{3}{2}$

$x =  - \dfrac{3}{2}$ divides the number line into two intervals $\left( { - \infty , - \dfrac{3}{2}} \right)$ and $\left( { - \dfrac{3}{2},\infty } \right)$

In $\left( { - \infty , - \dfrac{3}{2}} \right),$${f^\prime }(x) =  - 6 - 4x < 0$

$\therefore f$ is strictly increasing for $x <  - \dfrac{3}{2}$

In $\left( { - \dfrac{3}{2},\infty } \right),{f^\prime }(x) =  - 6 - 4x > 0$.

$\therefore f$ is strictly increasing for $x >  - \dfrac{3}{2}$

3. $f(x) =  - 2{x^3} - 9{x^2} - 12x + 1$

$\therefore {f^\prime }(x) =  - 6{x^2} - 18x - 12 =  - 6\left( {{x^2} + 3x + 2} \right) =  - 6(x + 1)(x + 2)$

${f^\prime }(x) = 0 \Rightarrow x =  - 1,2$

$x =  - 1$ and $x =  - 2$ divide the number line into intervals $( - \infty , - 2),( - 2, - 1)$ and $( - 1,\infty )$

In $( - \infty , - 2)$ and $( - 1,\infty ),{f^\prime }(x) =  - 6(x + 1)(x + 2) < 0$

$\therefore f$ is strictly decreasing for $x <  - 2$ and $x >  - 1$.

In $( - 2, - 1),{f^\prime }(x) =  - 6(x + 1)(x + 2) > 0$

$\therefore f$ is strictly increasing for $ - 2 < x <  - 1$

4. $f(x) = 6 - 9x - {x^2}$

$\Rightarrow {f^\prime }(x) =  - 9 - 2x$

${f^\prime }(x) = 0 \Rightarrow x = \dfrac{{ - 9}}{2}$

$\operatorname{In} \left( { - \infty , - \dfrac{9}{2}} \right),{f^\prime }(x) > 0$

$\therefore f$ is strictly increasing for $x <  - \dfrac{9}{2}$

$\operatorname{In} \left( { - \dfrac{9}{2},\infty } \right),{f^\prime }(x) < 0$

$\therefore f$ is strictly decreasing for $x >  - \dfrac{9}{2}$

5. $f(x) = {(x + 1)^3}{(x - 3)^3}$

${f^\prime }(x) = 3{(x + 1)^2}{(x - 3)^3} + 3{(x - 3)^2}{(x + 1)^3}$

$= 3{(x + 1)^2}{(x - 3)^2}[x - 3 + x + 1]$

$= 3{(x + 1)^2}{(x - 3)^2}(2x - 2)$

$= 6{(x + 1)^2}{(x - 3)^2}(x - 1)$

${f^\prime }(x) = 0$

$\Rightarrow x =  - 1,3,1$

$x =  - 1,3,1$ divides the number line into four intervals $( - \infty , - 1),( - 1,1),(1,3)$ and $(3,\infty )$

In $( - \infty , - 1)$ and $( - 1,1),{f^\prime }(x) = 6{(x + 1)^2}{(x - 3)^2}(x - 1) < 0$

$\therefore f$ is strictly decreasing in $( - \infty , - 1)$ and $( - 1,1)$

In $(1,3)$ and $(3,\infty ),{f^\prime }(x) = 6{(x + 1)^2}{(x - 3)^2}(x - 1) > 0$

$\therefore f$ is strictly increasing in $(1,3)$ and $(3,\infty )$

7. Show that $y = \log (1 + x) - \dfrac{{2x}}{{2 + x}},x >  - 1$, is an increasing function throughout its domain. 

Ans: $y = \log (1 + x) - \dfrac{{2x}}{{2 + x}}$

$\therefore \dfrac{{dy}}{{dx}} = \dfrac{1}{{1 + x}} - \dfrac{{(2 + x)(2) - 2x(1)}}{{{{(2 + x)}^2}}} = \dfrac{1}{{1 + x}} - \dfrac{4}{{{{(2 + x)}^2}}} = \dfrac{{{x^2}}}{{(1 + x){{(2 + x)}^2}}}$

$\dfrac{{dy}}{{dx}} = 0$

$\Rightarrow \dfrac{{{x^2}}}{{{{(2 + x)}^2}}} = 0$

$\Rightarrow {x^2} = 0$

$\Rightarrow x = 0$

Because $x >  - 1,x = 0$ divides domain $( - 1,\infty )$ in two intervals $ - 1 < x < 0$ and $x > 0$. When $ - 1 < x < 0$, $x < 0 \Rightarrow {x^2} > 0$

$x >  - 1 \Rightarrow (2 + x) > 0$

$\Rightarrow {(2 + x)^2} > 0$

$\therefore {y^\prime } = \dfrac{{{x^2}}}{{{{(2 + x)}^2}}} > 0$

When $x > 0$, 

$\Rightarrow {x^2} > 0,{(2 + x)^2} > 0$

$\therefore {y^\prime } = \dfrac{{{x^2}}}{{{{(2 + x)}^2}}} > 0$

Hence, $f$ is increasing throughout the domain.

8. Find the values of $x$ for which $y = {[x(x - 2)]^2}$ is an increasing function.

Ans: $y = {[x(x - 2)]^2} = {\left[ {{x^2} - 2x} \right]^2}$

$\therefore \dfrac{{dy}}{{dx}} = {y^\prime } = 2\left( {{x^2} - 2x} \right)(2x - 2) = 4x(x - 2)(x - 1)$

$\therefore \dfrac{{dy}}{{dx}} = 0$

$\Rightarrow x = 0,x = 2,x = 1$

$x = 0,x = 1$ and $x = 2$ divide the number line into intervals $( - \infty ,0),(0,1),(1,2)$ and $(2,\infty )$ In $( - \infty ,0)$ and $(1,2),\dfrac{{dy}}{{dx}} < 0$

$\therefore y$ is strictly decreasing in intervals $( - \infty ,0)$ and $(1,2)$ In intervals $(0,1)$ and $(2,\infty ),\dfrac{{dy}}{{dx}} > 0$

$\therefore y$ is strictly increasing in intervals $(0,1)$ and $(2,\infty )$

9. Prove that $y = \dfrac{{4\sin \theta }}{{(2 + \cos \theta )}} - \theta $ is an increasing function of $\theta $ in $\left[ {0,\dfrac{\pi }{2}} \right]$. 

Ans: $y = \dfrac{{4\sin \theta }}{{(2 + \cos \theta )}} - \theta $

$\therefore \dfrac{{dy}}{{d\theta }} = \dfrac{{(2 + \cos \theta )(4\cos \theta ) - 4\sin \theta ( - \sin \theta )}}{{{{(2 + \cos \theta )}^2}}} - 1$

$= \dfrac{{8\cos \theta  + 4{{\cos }^2}\theta  + 4{{\sin }^2}\theta }}{{{{(2 + \cos \theta )}^2}}} - 1$

$= \dfrac{{8\cos \theta  + 4}}{{{{(2 + \cos \theta )}^2}}} - 1$

$\dfrac{{dy}}{{d\theta }} = 0$

$\Rightarrow \dfrac{{8\cos \theta  + 4}}{{{{(2 + \cos \theta )}^2}}} = 1$

$\Rightarrow 8\cos \theta  + 4 = 4 + {\cos ^2}\theta  + 4\cos \theta $

$\Rightarrow {\cos ^2}\theta  - 4\cos \theta  = 0$

$\Rightarrow \cos \theta (\cos \theta  - 4) = 0$

$\Rightarrow \cos \theta  = 0$ or $\cos \theta  = 4$

Because $\cos \theta  \ne 4,\cos \theta  = 0$

$\cos \theta  = 0 \Rightarrow \theta  = \dfrac{\pi }{2}$

$\dfrac{{dy}}{{d\theta }} = \dfrac{{8\cos \theta  + 4 - \left( {4 + {{\cos }^2}\theta  + 4\cos \theta } \right)}}{{{{(2 + \cos \theta )}^2}}} = \dfrac{{4\cos \theta  - {{\cos }^2}\theta }}{{{{(2 + \cos \theta )}^2}}} = \dfrac{{\cos \theta (4 - \cos \theta )}}{{{{(2 + \cos \theta )}^2}}}$

In $\left[ {0,\dfrac{\pi }{2}} \right],\cos \theta  > 0$,

$4 > \cos \theta  \Rightarrow 4 - \cos \theta  > 0.$

$\therefore \cos \theta (4 - \cos \theta ) > 0$

${(2 + \cos \theta )^2} > 0$

$\Rightarrow \dfrac{{\cos \theta (4 - \cos \theta )}}{{{{(2 + \cos \theta )}^2}}} > 0$

$\Rightarrow \dfrac{{dy}}{{d\theta }} > 0$

So, $y$ is strictly increasing in $\left( {0,\dfrac{\pi }{2}} \right)$ The function is continuous at $x = 0$ and $x = \dfrac{\pi }{2}$.

So, $y$ is increasing in $\left[ {0,\dfrac{\pi }{2}} \right]$.

10. Prove that the logarithmic function is strictly increasing on $(0,\infty )$.

Ans: $f(x) = \log x$

$\therefore {f^\prime }(x) = \dfrac{1}{x}$

For $x > 0,{f^\prime }(x) = \dfrac{1}{x} > 0$

Thus, the logarithmic function is strictly increasing in interval $(0,\infty )$.

11.Prove that the function $f$ given by $f(x) = {x^2} - x + 1$ is neither strictly increasing nor strictly decreasing on $( - 1,1)$.

Ans: $f(x) = {x^2} - x + 1$

$\therefore {f^\prime }(x) = 2x - 1$

${f^\prime }(x) = 0 \Rightarrow x = \dfrac{1}{2}$

$x = \dfrac{1}{2}$ divides $( - 1,1)$ into $\left( { - 1,\dfrac{1}{2}} \right)$ and $\left( {\dfrac{1}{2},1} \right)$.

In $\left( { - 1,\dfrac{1}{2}} \right),$

${f^\prime }(x) = 2x - 1 < 0$

So, $f$ is strictly decreasing in $\left( { - 1,\dfrac{1}{2}} \right)$

$\operatorname{In} \left( {\dfrac{1}{2},1} \right),$

${f^\prime }(x) = 2x - 1 > 0$

So, $f$ is strictly increasing in interval $\left( {\dfrac{1}{2},1} \right)$. 

Thus, $f$ is neither strictly increasing nor strictly decreasing in interval $( - 1,1)$.

12. Which of the following functions are strictly decreasing on $\left( {0,\dfrac{\pi }{2}} \right)$ ?

1. $\cos x$

2. $\cos 2{\text{x}}$

3. $\cos 3x$

4. $\tan {\text{x}}$

Ans: 

1. ${f_1}(x) = \cos x$.

$\therefore f_1^\prime (x) =  - \sin x$

$\operatorname{In} \left( {0,\dfrac{\pi }{2}} \right),f_1^\prime (x) =  - \sin x < 0.$

$\therefore {f_1}(x) = \cos x$ is strictly decreasing in $\left( {0,\dfrac{\pi }{2}} \right)$.

2. ${f_2}(x) = \cos 2x$

$\therefore f_2^\prime (x) =  - 2\sin 2x$

$0 < x < \dfrac{\pi }{2}$

$\Rightarrow 0 < 2x < \pi $

$\Rightarrow \sin 2x > 0 \Rightarrow  - 2\sin 2x < 0$

$\therefore f_2^\prime (x) =  - 2\sin 2x < 0$ in $\left( {0,\dfrac{\pi }{2}} \right)$

$\therefore {f_2}(x) = \cos 2x$ is strictly decreasing in $\left( {0,\dfrac{\pi }{2}} \right)$.

3. ${f_3}(x) = \cos 3x$

$\therefore f_3^\prime (x) =  - 3\sin 3x$

$f_3^\prime (x) = 0$

$\Rightarrow \sin 3x = 0 \Rightarrow 3x = \pi $, as $x \in \left( {0,\dfrac{\pi }{2}} \right)$

$\Rightarrow x = \dfrac{\pi }{3}$

$x = \dfrac{\pi }{3}$ divides $\left( {0,\dfrac{\pi }{2}} \right)$ into $\left( {0,\dfrac{\pi }{3}} \right)$ and $\left( {\dfrac{\pi }{3},\dfrac{\pi }{2}} \right)$.

In $\left( {0,\dfrac{\pi }{3}} \right),{f_3}(x) =  - 3\sin 3x < 0\quad \left[ {0 < x < \dfrac{\pi }{3} \Rightarrow 0 < 3x < \pi } \right]$

$\therefore {f_3}$ is strictly decreasing in $\left( {0,\dfrac{\pi }{3}} \right)$.

$\operatorname{In} \left( {\dfrac{\pi }{3},\dfrac{\pi }{2}} \right),{f_3}(x) =  - 3\sin 3x > 0\quad \left[ {\dfrac{\pi }{3} < x < \dfrac{\pi }{2} \Rightarrow \pi  < 3x < \dfrac{{3\pi }}{2}} \right]$

$\therefore {f_3}$ is strictly increasing in $\left( {\dfrac{\pi }{3},\dfrac{\pi }{2}} \right)$.

So, ${f_3}$ is neither increasing nor decreasing in interval $\left( {0,\dfrac{\pi }{2}} \right)$.

4. ${f_4}(x) = \tan x$

$\therefore f_4^\prime (x) = {\sec ^2}x$

In $\left( {0,\dfrac{\pi }{2}} \right),f_4^\prime (x) = {\sec ^2}x > 0.$

$\therefore {f_4}$ is strictly increasing in $\left( {0,\dfrac{\pi }{2}} \right)$.

So, the correct answers are ${\mathbf{A}}$ and ${\mathbf{B}}$.

13. On which of the following intervals is the function $f$ is given by $f(x) = {x^{100}} + \sin x - 1$ strictly decreasing?

1. $(0,1)$

2. $\left( {\dfrac{\pi }{2},\pi } \right)$

3. $\left( {0,\dfrac{\pi }{2}} \right)$

4. None of these

Ans: $f(x) = {x^{100}} + \sin x - 1$

$\therefore {f^\prime }(x) = 100{x^{99}} + \cos x$

In $(0,1),\cos x > 0$ and $100{x^{99}} > 0$

$\therefore {f^\prime }(x) > 0$

So, $f$ is strictly increasing in $(0,1)$.

In $\left( {\dfrac{\pi }{2},\pi } \right),\cos x < 0$ and $100{x^{99}} > 0$

$100{x^{99}} > \cos x$

$\therefore {f^\prime }(x) > 0$ in $\left( {\dfrac{\pi }{2},\pi } \right)$

So, $f$ is strictly increasing in interval $\left( {\dfrac{\pi }{2},\pi } \right)$. In interval $\left( {0,\dfrac{\pi }{2}} \right),\cos x > 0$ and $100{x^{99}} > 0$. $\therefore 100{x^{99}} + \cos x > 0$

$\Rightarrow {f^\prime }(x) > 0$ on $\left( {0,\dfrac{\pi }{2}} \right)$

$\therefore f$ is strictly increasing in interval $\left( {0,\dfrac{\pi }{2}} \right)$. Hence, $f$ is strictly decreasing in none of the intervals. 

The correct answer is ${\mathbf{D}}$.

14. Find the least value of $a$ such that the function $f$ given $f(x) = {x^2} + ax + 1$ is strictly increasing on $(1,2)$.(This question has to be solved)

Ans: $f(x) = {x^2} + ax + 1$

$\therefore {f^\prime }(x) = 2x + a$

${f^\prime }(x) > 0$ in $(1,2)$

$\Rightarrow 2x + a > 0$

$\Rightarrow 2x >  - a$

$\Rightarrow x > \dfrac{{ - a}}{2}$

So, we need to find the smallest value of a such that

$x > \dfrac{{ - a}}{2}$, when $x \in (1,2)$.

$\Rightarrow x > \dfrac{{ - a}}{2}($ when $1 < x < 2)$

$\dfrac{{ - a}}{2} = 1 \Rightarrow a =  - 2$

Hence, the required value of $a$ is $ - 2$.

15. Let ${\mathbf{I}}$ be any interval disjoint from $( - 1,1)$, prove that the function $f$ given by $f(x) = x + \dfrac{1}{x}$ is strictly increasing on I. 

Ans: $f(x) = x + \dfrac{1}{x}$

$\therefore {f^\prime }(x) = 1 - \dfrac{1}{{{x^2}}}$

${f^\prime }(x) = 0$

$\Rightarrow \dfrac{1}{{{x^2}}}$

$\Rightarrow x =  \pm 1$

$x = 1$ and $x =  - 1$ divide the real line in intervals $( - \infty ,1),( - 1,1)$ and $(1,\infty )$. In $( - 1,1)$, $ - 1 < x < 1$

$\Rightarrow {x^2} < 1$

$\Rightarrow 1 < \dfrac{1}{{{x^2}}},x \ne 0$

$\Rightarrow 1 - \dfrac{1}{{{x^2}}} < 0,x \ne 0$

$\therefore {f^\prime }(x) = 1 - \dfrac{1}{{{x^2}}} < 0$ on $( - 1,1) $.

In $( - \infty , - 1)$ and $(1,\infty )$,

$x <  - 1$ or $1 < x$

$\Rightarrow {x^2} > 1$

$\Rightarrow 1 > \dfrac{1}{{{x^2}}}$

$\Rightarrow 1 - \dfrac{1}{{{x^2}}} > 0$

$\therefore {f^\prime }(x) = 1 - \dfrac{1}{{{x^2}}} > 0$ on $( - \infty , - 1)$ and $(1,\infty )$.

$\therefore f$ is strictly increasing on $( - \infty ,1)$ and $(1,\infty )$. 

Hence, $f$ is strictly increasing in ${\mathbf{I}} - ( - 1,1)$.

16. Prove that the function $f$ given by $f(x) = \log \sin x$ is strictly increasing on $\left( {0,\dfrac{\pi }{2}} \right)$ and strictly decreasing on $\left( {\dfrac{\pi }{2},\pi } \right)$

Ans: $f(x) = \log \sin x$

$\therefore {f^\prime }(x) = \dfrac{1}{{\sin x}}\cos x = \cot x$

$\operatorname{In} \left( {0,\dfrac{\pi }{2}} \right),{f^\prime }(x) = \cot x > 0$

$\therefore f$ is strictly increasing in $\left( {0,\dfrac{\pi }{2}} \right)$. $\operatorname{In} \left( {\dfrac{\pi }{2},\pi } \right),{f^\prime }(x) = \cot x < 0$

$\therefore f$ is strictly decreasing in $\left( {\dfrac{\pi }{2},\pi } \right)$.

17. Prove that the function $f$ given by $f(x) = \log \cos x$ is strictly decreasing on $\left( {0,\dfrac{\pi }{2}} \right)$ and strictly increasing on $\left( {\dfrac{\pi }{2},\pi } \right)$

Ans: $f(x) = \log \cos x$

$\therefore {f^\prime }(x) = \dfrac{1}{{\cos x}}( - \sin x) =  - \tan x$

$\operatorname{In} \left( {0,\dfrac{\pi }{2}} \right),\tan x > 0 \Rightarrow  - \tan x < 0$.

$\therefore {f^\prime }(x) =  < 0$ on $\left( {0,\dfrac{\pi }{2}} \right)$

$\therefore f$ is strictly decreasing on $\left( {0,\dfrac{\pi }{2}} \right)$.

In $\left( {\dfrac{\pi }{2},\pi } \right),\tan x < 0$

$\Rightarrow  - \tan x > 0$

$\therefore {f^\prime }(x) > 0$ on $\left( {\dfrac{\pi }{2},\pi } \right)$

$\therefore f$ is strictly increasing on $\left( {\dfrac{\pi }{2},\pi } \right)$.

18. Prove that the function given by $f(x) = {x^3} - 3{x^2} + 3x = 100$ is increasing in ${\mathbf{R}}$. 

Ans: $f(x) = {x^3} - 3{x^2} + 3x = 100$

${f^\prime }(x) = 3{x^2} - 6x + 3$

$= 3\left( {{x^2} - 2x + 1} \right)$

$= 3{(x - 1)^2}$

For $x \in {\mathbf{R}}{(x - 1)^2} \geqslant 0$.

So ${f^\prime }(x)$ is always positive in ${\mathbf{R}}$.

So, the $f$ is increasing in ${\mathbf{R}}$.

19. The interval in which $y = {x^2}{e^{ - x}}$ is increasing is

1. $( - \infty ,\infty )$

2. $( - 2,0)$

3. $(2,\infty )$

4. $(0,2)$ 

Ans: $y = {x^2}{e^{ - x}}$

$\therefore \dfrac{{dy}}{{dx}} = 2x{e^{ - x}} - {x^2}{e^{ - x}} = x{e^{ - x}}(2 - x)$

$\dfrac{{dy}}{{dx}} = 0$

$\Rightarrow x = 0$ and $x = 2$

In $( - \infty ,0)$ and $(2,\infty ),{f^\prime }(x) < 0$ as ${e^{ - x}}$ is always positive. 

$\therefore f$ is decreasing on $( - \infty ,0)$ and $(2,\infty )$. In $(0,2),{f^\prime }(x) > 0$.

$\therefore f$ is strictly increasing on $(0,2)$. So, $f$ is strictly increasing in $(0,2)$. 

The correct answer is ${\mathbf{D}}$.

Exercise 6.3

1. Find the maximum and minimum values, if any, of the following given by

(i) $f(x) = {(2x - 1)^2} + 3$

(ii) $f(x) = 9{x^2} + 12x + 2$

(iii) $f(x) =  - {(x - 1)^2} + 10$

(iv)$g(x) = {x^3} + 1$

Ans: (i) $f(x) = {(2x - 1)^2} + 3$

${(2x - 1)^2} \geqslant 0$ for every $x \in {\mathbf{R}}$.

$f(x) = {(2x - 1)^2} + 3 \geqslant 3$ for $x \in {\mathbf{R}}$.

The minimum value of $f$ occurs when when $2x - 1 = 0$.

$2x - 1 = 0,x = \dfrac{1}{2}$

Min value of $f\left( {\dfrac{1}{2}} \right) = {\left( {2 \cdot \dfrac{1}{2} - 1} \right)^2} + 3 = 3$.

The function $f$ does not have a maximum value.

(ii) $f(x) = 9{x^2} + 12x + 2 = {\left( {3{x^2} + 2} \right)^2} - 2$.

${\left( {3{x^2} + 2} \right)^2} \geqslant 0$ for $x \in {\mathbf{R}}$.

$f(x) = {\left( {3{x^2} + 2} \right)^2} - 2 \geqslant  - 2$ for $x \in {\mathbf{R}}$.

minimum value of $f$ is when $3x + 2 = 0$. 

$3x + 2 = 0 = 0,$

$x = \dfrac{{ - 2}}{3}$

Minimum value of $f\left( { - \dfrac{2}{3}} \right) = {\left( {3\left( {\dfrac{{ - 2}}{3}} \right) + 2} \right)^2} - 2 =  - 2$

$f$ does not have a maximum value.

(iii) $f(x) =  - {(x - 1)^2} + 10$

${(x - 1)^2} \geqslant 0$ for $x \in {\mathbf{R}}$.

$f(x) =  - {(x - 1)^2} + 10 \leqslant 10$ for $x \in {\mathbf{R}}$.

maximum value of $f$ is when $(x - 1) = 0$.

$(x - 1) = 0,x = 0$

Maximum value of $f = f(1) =  - {(1 - 1)^2} + 10 = 10$

$f$ does not have a minimum value.

(iv) $g(x) = {x^3} + 1.$

$g$ neither has a maximum value nor a minimum value.

2. Find the maximum and minimum values, if any, of the following functions given by

(i) $f(x) = |x + 2| - 1$

(ii) $g(x) =  - |x + 1| + 3$

(iii) $h(x) = \sin (2x) + 5$

(iv) $f(x) = |\sin 4x + 3|$

(v) $h(x) = x + 4,x \in ( - 1,1)$

Ans:  (i) $f(x) = |x + 2| - 1$

$|x + 2| \geqslant 0$ for $x \in {\mathbf{R}}$.

$f(x) = |x + 2| - 1 \geqslant  - 1$ for $x \in {\mathbf{R}}$.

minimum value of $f$ is when $|x + 2| = 0$.

$|x + 2| = 0$

$\Rightarrow x =  - 2$

Minimum value of $f = f( - 2) = | - 2 + 2| - 1 =  - 1$

 $f$ does not have a maximum value.

(ii) $g(x) =  - |x + 1| + 3$

$ - |x + 1| \leqslant 0$ for $x \in {\mathbf{R}}$.

$g(x) =  - |x + 1| + 3 \leqslant 3$ for $x \in {\mathbf{R}}$.

maximum value of $g$ is when $|x + 1| = 0$.

$|x + 1| = 0$

$\Rightarrow x =  - 1$

Maximum value of $g = g( - 1) =  - | - 1 + 1| + 3 = 3$

g does not have a minimum value.

(iii) $h(x) = \sin 2x + 5$

$- 1 \leqslant \sin 2x \leqslant 1$

$- 1 + 5 \leqslant \sin 2x + 5 \leqslant 1 + 5$

$4 \leqslant \sin 2x + 5 \leqslant 6$

maximum and minimum values of $h$ are 6 and 4 respectively.

(iv) $f(x) = |\sin 4x + 3|$

$ - 1 \leqslant \sin 4x \leqslant 1$

$2 \leqslant \sin 4x + 3 \leqslant 4$

$2 \leqslant |\sin 4x + 3| \leqslant 4$

maximum and minimum values of $f$ are 4 and 2 respectively.

(v) $h(x) = x + 4,x \in ( - 1,1)$

Here, if a point ${x_0}$ is closest to $ - 1$, then we find $\dfrac{{{x_0}}}{2} + 1 < {x_0} + 1$ for all ${x_0} \in ( - 1,1)$.

Also, if ${x_1}$ is closet to $ - 1$, then we find ${x_1} + 1 < \dfrac{{{x_1} + 1}}{2} + 1$ for all ${x_0} \in ( - 1,1)$. 

function has neither maximum nor minimum value in $( - 1,1)$.

3. Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:

(i) $f(x) = {x^2}$

(ii) $g(x) = {x^3} - 3x$

(iii) $h(x) = \sin x + \cos .0 < x < \dfrac{\pi }{2}$

(iv) $f(x) = \sin x - \cos x,0 < x < 2\pi $ 

(v) $f(x) = {x^3} - 6{x^2} + 9x + 15$

(vi) $g(x) = \dfrac{x}{2} + \dfrac{2}{x},x > 0$

(vii) $g(x) = \dfrac{1}{{{x^2} + 2}}$

(vii) $f(x) = x\sqrt {1 - x} ,x > 0$

Ans: (i) $f(x) = {x^2}$

$\therefore {f^\prime }(x) = 2x$

${f^\prime }(x) = 0 \Rightarrow x = 0$

We have ${f^\prime }(0) = 2$,

by second derivative test, $x = 0$ is a point of local minima and local minimum value of $f$

at $x = 0$ is $f(0) = 0$.

(ii) $g(x) = {x^3} - 3x$

$\therefore {g^\prime }(x) = 3{x^2} - 3$

${g^\prime }(x) = 0 \Rightarrow 3{x^2} = 3$

$\Rightarrow x =  \pm 1$

${g^\prime }(x) = 6x$

${g^\prime }(1) = 6 > 0$

${g^\prime }( - 1) =  - 6 < 0$

By second derivative test, $x = 1$ is a point of local minima and local minimum value of $g$

At $x = 1$ is $g(1) = {1^3} - 3 = 1 - 3 =  - 2$.

$x =  - 1$ is a point of local maxima and local maximum value of $g$ at

$x =  - 1$ is $g(1) = {( - 1)^3} - 3( - 1) =  - 1 + 3 =  - 2$.

(iii) $h(x) = \sin x + \cos .0 < x < \dfrac{\pi }{2}$

$\therefore {h^\prime }(x) = \cos x + \sin x$

${h^\prime }(x) = 0 \Rightarrow \sin x = \cos x$

$\Rightarrow \tan x = 1$

$\Rightarrow x = \dfrac{\pi }{4} \in \left( {0,\dfrac{\pi }{2}} \right)$

${h^\prime }(x) = \sin x - \cos x =  - (\sin x + \cos x)$

$h\left( {\dfrac{\pi }{4}} \right) =  - \left( {\dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }}} \right) =  - \dfrac{2}{{\sqrt 2 }} =  - \sqrt 2  < 0$

Therefore, by second derivative test, $x = \dfrac{\pi }{4}$ is a point of local maxima and the local Maximum value of $h$ at $x = \dfrac{\pi }{4}$ is $h\left( {\dfrac{\pi }{4}} \right) = \sin \dfrac{\pi }{4} + \cos \dfrac{\pi }{4}$

$= \dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }} = \sqrt 2 $

(iv) $f(x) = \sin x - \cos x,0 < x < 2\pi $

$\therefore {f^\prime }(x) = \cos x + \sin x$

${f^\prime }(x) = 0 \Rightarrow \cos x =  - \sin x \Rightarrow \tan x =  - 1$

$\Rightarrow x = \dfrac{{3\pi }}{4},\dfrac{{7\pi }}{4} \in (0,2\pi )$

${f^{\prime \prime }}(x) =  - \sin x + \cos x$

$=  - \dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{\sqrt 2 }} =  - \sqrt 2  > 0$

$= \dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }} = \sqrt 2  > 0$

by second derivative test, $x = \dfrac{{3\pi }}{4}$ is a point of local maxima and the local maximum value of

$f$ at $x = \dfrac{{3\pi }}{4}$ is

$f\left( {\dfrac{{3\pi }}{4}} \right) = \sin \dfrac{{3\pi }}{4}\cos \dfrac{{3\pi }}{4}$

$= \dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }} = \sqrt 2 $

$x = \dfrac{{7\pi }}{4}$ is a point of local minima and the local minimum value of $f$ at $x = \dfrac{{7\pi }}{4}$ is $f\left( {\dfrac{{7\pi }}{4}} \right) = \sin \dfrac{{7\pi }}{4} - \cos \dfrac{{7\pi }}{4}$

$=  - \dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{\sqrt 2 }} =  - \sqrt 2 $

(v) $f(x) = {x^3} - 6x + 9x + 15$

$\therefore {f^\prime }(x) = 3{x^2} - 12x + 9$

$f(x) = 0 \Rightarrow 3\left( {{x^2} - 4x + 3} \right) = 0$

$\Rightarrow 3(x - 1)(x - 3) = 0$

$\Rightarrow x = 1,3$

${f^{\prime \prime }}(x) = 6x - 12 = 6(x - 2)$

${f^{\prime \prime }}(1) = 6(1 - 2) =  - 6 < 0$

${f^{\prime \prime }}(3) = 6(3 - 2) = 6 > 0$

by second derivative test, $x = 1$ is a point of local maxima and the local maximum value of $f$ at

$x = 1$ is $f(1) = 1 - 6 + 9 + 15 = 19$.

$x = 3$ is a point of local minima and the local minimum value of $f$ at $x = 3$ is

$f(3) = 27 - 54 + 27 + 15 = 15$.

(vi) $g(x) = \dfrac{x}{2} + \dfrac{2}{x},x > 0$

$\therefore {g^\prime }(x) = \dfrac{1}{2} - \dfrac{2}{{{x^2}}}$

${g^\prime }(x) = 0 \Rightarrow \dfrac{2}{{{x^2}}} = \dfrac{1}{2} \Rightarrow {x^3} = 4$

$x > 0,x = 2$.

${g^{\prime \prime }}(x) = \dfrac{4}{{{x^3}}}$

${g^{\prime \prime }}(2) = \dfrac{4}{{{2^3}}} = \dfrac{1}{2} > 0$

by second derivative test, $x = 2$ is a point of local minima and the local minimum value of $g$ at

$x = 2$ is $g(2) = \dfrac{2}{2} + \dfrac{2}{2} = 1 + 1 = 2.$

(vii) $g(x) = \dfrac{1}{{{x^2} + 2}}$

$\therefore {g^\prime }(x) = \dfrac{{ - (2x)}}{{{{\left( {{x^3} + 2} \right)}^2}}}$

${g^\prime }(x) = 0 \Rightarrow \dfrac{{ - 2x}}{{{{\left( {{x^3} + 2} \right)}^2}}} = 0$

$\Rightarrow x = 0$

for values close to $x = 0$ and left of $0,{g^1}(x) > 0$ for values close to $x = 0$ and to right of $0{g^1}(x) < 0$

by first derivative test $x = 0$ is a point of local maxima and the local maximum value of $g(0)$ is $\dfrac{1}{{0 + 2}} = \dfrac{1}{2}$

(viii) $f(x) = x\sqrt {1 - x} ,x > 0$

$\therefore {f^\prime }(x) = x\sqrt {1 - x}  + x \cdot \dfrac{1}{{2\sqrt {1 - x} }}( - 1) = \sqrt {1 - x}  - \dfrac{x}{{2\sqrt {1 - x} }}$

$= \dfrac{{2(1 - x) - x}}{{2\sqrt {1 - x} }} - \dfrac{{2 - 3x}}{{2\sqrt {1 - x} }}$

${f^\prime }(x) = 0 \Rightarrow \dfrac{{2 - 3x}}{{2\sqrt {1 - x} }} = 0 \Rightarrow 2 - 3x = 0$

$\Rightarrow x = \dfrac{2}{3}$

${f^{\prime \prime }}(x) = \dfrac{1}{2}\left[ {\dfrac{{\sqrt {1 - x} ( - 3) - (2 - 3x)\left( {\dfrac{{ - 1}}{{2\sqrt {1 - x} }}} \right)}}{{1 - x}}} \right]$

$= \dfrac{{\sqrt {1 - x} ( - 3) + 2(2 - 3x)\left( {\dfrac{1}{{2\sqrt {1 - x} }}} \right)}}{{2(1 - x)}}$

$= \dfrac{{ - 6(1 - x) + 2(2 - 3x)}}{{4{{(1 - x)}^{\dfrac{3}{2}}}}}$

$= \dfrac{{3x - 4}}{{4{{(1 - x)}^{\dfrac{3}{2}}}}}$

${f^{\prime \prime }}\left( {\dfrac{2}{3}} \right) = \dfrac{{3\left( {\dfrac{2}{3}} \right) - 4}}{{4{{\left( {1 - \dfrac{2}{3}} \right)}^{\dfrac{3}{2}}}}} = \dfrac{{2 - 4}}{{4{{\left( {\dfrac{1}{3}} \right)}^{\dfrac{3}{2}}}}} = \dfrac{{ - 1}}{{2{{\left( {\dfrac{1}{3}} \right)}^{\dfrac{3}{2}}}}} < 0$

by second derivative test, $x = \dfrac{2}{3}$ is a point of local maxima and the local maximum value of $f$

$x = \dfrac{2}{3}$

$f\left( {\dfrac{2}{3}} \right) = \dfrac{2}{3}\sqrt {1 - \dfrac{2}{3}}  = \dfrac{2}{3}\sqrt {\dfrac{1}{3}}  = \dfrac{2}{{3\sqrt 3 }} = \dfrac{{2\sqrt 3 }}{9}$

4. Prove that the following functions do not have maxima or minima:

(i) $f(x) = {e^x}$

(ii) $g(x) = \log x$

(iii) $h(x) = {x^3} + {x^2} + x + 1$

Ans: (i) $f(x) = {e^x}$

$\therefore {f^\prime }(x) = {e^x}$

if ${f^\prime }(x) = 0,{e^x} = 0.$ But exponential function can never be 0 for any value of $x$.

There is no $c \in {\mathbf{R}}$ such that ${f^\prime }(c) = 0$.

$f$ does not have maxima or minima.

(ii) We have, $g(x) = \log x$

$\therefore {g^\prime }(x) = \dfrac{1}{x}$

$\log x$ is defined for positive $x,{g^\prime }(x) > 0$ for any $x$.

there does not exist $c \in {\mathbf{R}}$ such that ${g^\prime }(c) = 0$

function $g$ does not have maxima or minima.

(iii) We have, $h(x) = {x^3} + {x^2} + x + 1$

$\therefore {h^\prime }(x) = 3{x^2} + 2x + 1$

there does not exist $c \in {\mathbf{R}}$ such that ${h^\prime }(c) = 0$. function $h$ does not have maxima or minima.

5. Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:

(i) $f(x) = {x^3},x \in [ - 2,2]$

(iii) $f(x) = 4x - \dfrac{1}{2}{x^2},x \in \left[ { - 2,\dfrac{9}{2}} \right]$

(ii) $f(x) = \sin x + \cos x,x \in [0,\pi ]$

(iv) $f(x) = {(x - 1)^2} + 3,x \in [ - 3,1]$

Ans: (i) $f(x) = {x^3}$. $\therefore {f^\prime }(x) = 3{x^2}$

${f^\prime }(x) = 0 \Rightarrow x = 0$

$f(0) = 0$

$f( - 2) = {( - 2)^3} =  - 8$

$f(2) = {(2)^3} = 8$

Hence, the absolute maximum of $f$ on $[ - 2,2]$.is 8 at $x =  - 2$.

the absolute minimum of $f$ on $[ - 2,2]$ is $ - 8$ at $x =  - 2$.

(ii) $f(x) = \sin x + \cos x.$

$\therefore {f^\prime }(x) = \cos x - \sin x$

${f^\prime }(x) = 0 \Rightarrow \sin x = \cos x$

$\Rightarrow \tan x = 1 \Rightarrow x = \dfrac{\pi }{4}$

$f\left( {\dfrac{\pi }{4}} \right) = \sin \dfrac{\pi }{4} + \cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }} = \dfrac{2}{{\sqrt 2 }} = \sqrt 2 $

$f(0) = \sin 0 + \cos 0 = 0 + 1 = 1$

$f(\pi ) = \sin \pi  + \cos \pi  = 0 - 1 = 1$

the absolute maximum of $f$ on $[0,\pi ]$ is $\sqrt 2 $ at $x = \dfrac{\pi }{4}$

the absolute minimum of $f$ on $[0,\pi ]$ is $ - 1$ at $x = \pi $.

(iii) $f(x) = 4x - \dfrac{1}{2}{x^2}$

$\therefore {f^\prime }(x) = 4x - \dfrac{1}{2}(2x) = 4 - x$

${f^\prime }(x) = 0 \Rightarrow x = 4$

$f(4) = 16 - \dfrac{1}{2}(16) = 16 - 8 = 8$

$f( - 2) =  - 8 - \dfrac{1}{2}(4) =  - 8 - 2 =  - 10$

$f\left( {\dfrac{9}{2}} \right) = 4\left( {\dfrac{9}{2}} \right) - \dfrac{1}{2}{\left( {\dfrac{9}{2}} \right)^2} = 18 - \dfrac{{81}}{8}$

$= 18 - 10.125 = 7.875$

the absolute maximum of $f$ on $\left[ { - 2,\dfrac{9}{2}} \right]$ is 8 at $x = 4$

the absolute minimum of $f$ on $\left[ { - 2,\dfrac{9}{2}} \right]$ is $ - 10$ at $x =  - 2$.

(iv) $f(x) = {(x - 1)^2} + 3$

$\therefore {f^\prime }(x) = 2(x - 1)$

${f^\prime }(x) = 0 \Rightarrow 2(x - 1) = 0,x = 1$

$f(1) = {(1 - 1)^2} + 3 = 0 + 3 = 3$

$f( - 3) = {( - 3 - 1)^2} + 3 = 16 + 3 = 19$

absolute maximum value of $f$ on $[ - 3,1]$ is 19 at $x =  - 3$

minimum value of $f$ on $[ - 3,1]$ is at $x = 1$.

6. Find the maximum profit that a company can make, if the profit function is given by $p(x) = 41 - 24x - 18{x^2}$

Ans: $p(x) = 41 - 24x - 18{x^2}.$

$\therefore {p^\prime }(x) =  - 24 - 36x$

${p^{\prime \prime }}(x) =  - 36$

${p^\prime }(x) = 0 \Rightarrow x = \dfrac{{ - 24}}{{36}} =  - \dfrac{2}{3}$

${p^{\prime \prime }}\left( {\dfrac{{ - 2}}{3}} \right) =  - 36 < 0$

By second derivative test, $x =  - \dfrac{2}{3}$ is the point of local maximum of $p$.

$\therefore $ Maximum profit $= p = \left( { - \dfrac{2}{3}} \right)$

$= 41 - 24\left( { - \dfrac{2}{3}} \right) - 18{\left( { - \dfrac{2}{3}} \right)^2} = 41 + 16 - 8$

7. Find the intervals in which the function $f$ given by $f(x) = {x^3} + \dfrac{1}{{{x^3}}},x \ne 0$ is

(i) Increasing

(ii) Decreasing 

Ans: $f(x) = {x^3} + \dfrac{1}{{{x^3}}}$

$\therefore {f^\prime }(x) = 3{x^2} - \dfrac{3}{{{x^4}}} = \dfrac{{3{x^6} - 3}}{{{x^4}}}$

${f^\prime }(x) = 0 \Rightarrow 3{x^6} - 3 = 0$

$\Rightarrow {x^6} = 1 \Rightarrow x =  \pm 1$

In $( - \infty , - 1)$ and $(1,\infty ),{f^\prime }(x) > 0.$

when $x <  - 1$ and $x > 1,f$ is increasing.

In $( - 1,1),{f^\prime }(x) < 0$.

when $ - 1 < x < 1,f$ is decreasing.

8. At what points in the interval $[0,2\pi ]$, does the function $\sin 2x$ attain, its maximum value? 

Ans: $f(x) = \sin 2x$.

$\therefore {f^\prime }(x) = 2\cos 2x$

${f^\prime }(x) = 0 \Rightarrow \cos 2x = 0$

$\Rightarrow 2x = \dfrac{\pi }{2},\dfrac{{3\pi }}{2},\dfrac{{5\pi }}{2},\dfrac{{7\pi }}{2}$

$\Rightarrow x = \dfrac{\pi }{4},\dfrac{{3\pi }}{4},\dfrac{{5\pi }}{4},\dfrac{{7\pi }}{4}$

$f\left( {\dfrac{\pi }{4}} \right) = \sin \dfrac{\pi }{2} = 1,$$f\left( {\dfrac{{3\pi }}{4}} \right) = \sin \dfrac{{3\pi }}{2} =  - 1$

$f\left( {\dfrac{{5\pi }}{4}} \right) = \sin \dfrac{{5\pi }}{2} = 1,$$f\left( {\dfrac{{7\pi }}{4}} \right) = \sin \dfrac{{7\pi }}{2} =  - 1$

$f(0) = \sin 0 = 0,f(2\pi ) = \sin 2\pi  = 0$

absolute maximum value of $f[0,2\pi ]$ is at $x = \dfrac{\pi }{4}$ and $x = \dfrac{{5\pi }}{4}$.

9. What is the maximum value of the function $\sin x + \cos x$ ?

Ans: $f(x) = \sin x + \cos x$

$\therefore {f^\prime }(x) = \cos x - \sin x$

${f^\prime }(x) = 0 \Rightarrow \sin x = \cos x \Rightarrow \tan x = 1 \Rightarrow x = \dfrac{\pi }{4},\dfrac{{5\pi }}{4} \ldots $

${f^\prime }(x) =  - \sin x - \cos x =  - (\sin x + \cos x)$

${f^{\prime \prime }}(x)$ will be negative when $(\sin x + \cos x)$ is positive

we know that $\sin x$ and $\cos x$ are positive in the first quadrant ${f^{\prime \prime }}(x)$ will be negative when $x \in \left( {0,\dfrac{\pi }{2}} \right)$.

consider $x = \dfrac{\pi }{4}$. ${f^{\prime \prime }}\left( {\dfrac{\pi }{4}} \right) =  - \left( {\sin \dfrac{\pi }{4} + \cos \dfrac{\pi }{4}} \right) =  - \left( {\dfrac{2}{{\sqrt 2 }}} \right) =  - \sqrt 2  < 0$

By second derivative test, $f$ will be the maximum at $x = \dfrac{\pi }{4}$ and the maximum value of $f$ is

$f\left( {\dfrac{\pi }{4}} \right) = \sin \dfrac{\pi }{4} + \cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }} \times \dfrac{1}{{\sqrt 2 }} = \dfrac{2}{{\sqrt 2 }} = \sqrt 2 $

10. Find the maximum value of $2{x^3} - 24x + 107$ in the interval $[1,3]$. Find the maximum value of the same function in $[ - 3, - 1]$.

Ans: $f(x) = 2{x^3} - 24x + 107$

$\therefore {f^\prime }(x) = 6{x^2} - 24 = 6\left( {{x^2} - 4} \right)$

${f^\prime }(x) = 0 \Rightarrow 6\left( {{x^2} - 4} \right) = 0 \Rightarrow {x^2} = 4 \Rightarrow x =  \pm 2$

consider\[[1,3]\]. 

$f(2) = 2(8) - 24(2) + 107 = 16 - 48 + 107 = 75$

$f(1) = 2(1) - 24(1) + 107 = 2 - 24 + 107 = 85$

$f(3) = 2(27) - 24(3) + 107 = 54 - 72 + 107 = 89$

absolute maximum of $f(x)$ in the \[[1,3]\] is 89 at $x = 3$.

consider $[ - 3, - 1]$. 

$f( - 3) = 2( - 27) - 24( - 3) + 107 = 54 + 72 + 107 = 125$

$f( - 1) = 2( - 1) - 24( - 1) + 107 = 2 + 24 + 107 = 129$

$f( - 2) = 2( - 8) - 24( - 2) + 107 =  - 16 + 48 + 107 = 139$

absolute maximum of $f(x)$ in $[ - 3, - 1]$ is 139 at $x =  - 2$.

11. It is given that at $x = 1$, the function ${x^4} - 62{x^2} + ax + 9$ attains its maximum value, on the interval $[0,2]$. Find the value of $a$.

Ans: $f(x) = {x^4} - 62{x^2} + ax + 9.$

$\therefore {f^\prime }(x) = 4{x^2} - 124x + a$

$\therefore {f^\prime }(1) = 0$

$\Rightarrow 4 - 124 + a = 0$

$\Rightarrow a = 120$

the value of $a$ is 120.

12. Find the maximum and minimum values of $x + \sin 2x$ on $[0,2\pi ]$.

Ans: $f(x) = x + \sin 2x$

$\therefore {f^\prime }(x) = 1 + 2\cos 2x$

${f^\prime }(x) = 0 \Rightarrow \cos 2x =  - \dfrac{1}{2} =  - \cos \dfrac{\pi }{3} = \cos \left( {\pi  - \dfrac{\pi }{3}} \right) = \cos \dfrac{{2\pi }}{3}$

$2x = 2\pi  \pm \dfrac{{2\pi }}{{{3^\prime }}}n \in {\mathbf{Z}}$

$\Rightarrow x = \pi  \pm \dfrac{\pi }{3},n \in {\mathbf{Z}}$

$\Rightarrow x = \dfrac{\pi }{3},\dfrac{{2\pi }}{3},\dfrac{{4\pi }}{3},\dfrac{{5\pi }}{3} \in [0,2\pi ]$

$f\left( {\dfrac{\pi }{3}} \right) = \dfrac{\pi }{3} + \sin \dfrac{{2\pi }}{3} = \dfrac{\pi }{3} + \dfrac{{\sqrt 3 }}{2}$

$f\left( {\dfrac{{2\pi }}{3}} \right) = \dfrac{{2\pi }}{3} + \sin \dfrac{{4\pi }}{3} = \dfrac{{2\pi }}{3} - \dfrac{{\sqrt 3 }}{2}$

$f\left( {\dfrac{{4\pi }}{3}} \right) = \dfrac{{4\pi }}{3} + \sin \dfrac{{8\pi }}{3} = \dfrac{{4\pi }}{3} + \dfrac{{\sqrt 3 }}{2}$

$f\left( {\dfrac{{5\pi }}{3}} \right) = \dfrac{{5\pi }}{3} + \sin \dfrac{{10\pi }}{3} = \dfrac{{5\pi }}{3} - \dfrac{{\sqrt 3 }}{2}$

$f(0) = 0 + \sin 0 = 0$

$f(2\pi ) = 2\pi  + \sin 4\pi  = 2\pi  + 0 = 2\pi $

absolute maximum value of $f(x)$ in $[0,2\pi ]$ is $2\pi $ at $x = 2\pi $ 

absolute minimum value of $f(x)$ in $[0,2\pi ]$ is 0 at $x = 0$.

13. Find two numbers whose sum is 24 and whose product is as large as possible. 

Ans: Let number be $x$. The other number is $(24 - x)$. $p(x)$ denote the product of the two numbers.

$P(x) = x(24 - x) = 24x - {x^2}$

$\therefore {P^\prime }(x) = 24 - 2x$

${P^{\prime \prime }}(x) =  - 2$

${P^\prime }(x) = 0 \Rightarrow x = 12$

${P^{\prime \prime }}(12) =  - 2 < 0$

$x = 12$ is point of local maxima of $P$. 

Product of the numbers is the maximum when numbers are 12 and $24 - 12 = 12$.

14. Find two positive numbers $x$ and $y$ such that $x + y = 60$ and $x{y^3}$ is maximum. 

Ans: numbers are $x$ and $y$ such that $x + y = 60$. $y = 60 - x$

$f(x) = x{y^3}$

$\Rightarrow f(x) = x{(60 - x)^3}$

$\therefore {f^\prime }(x) = {(60 + x)^3} - 3x{(60 - x)^2}$

$= {(60 + x)^3}[60 - x - 3x]$

$= {(60 + x)^3}(60 - 4x)$

${f^{\prime \prime }}(x) =  - 2(60 - x)(60 - 4x) - 4{(60 - x)^2}$

$=  - 2(60 - x)[60 - 4x + 2(60 - x)]$

$=  - 2(60 - x)(180 - 6x)$

$=  - 12(60 - x)(30 - x)$

${f^\prime }(x) = 0 \Rightarrow x = 60$ or $x = 15$

$x = 60,{f^{\prime \prime }}(x) = 0$

$x = 15,$${f^{\prime \prime }}(x) =  - 12(60 - 15)(30 - 15) = 12 \times 45 \times 15 < 0$

$x = 15$ is a point of local maxima of $f$.

function $x{y^3}$ is maximum when $x = 15$ and $y = 60 - 15 = 45$.

Required numbers are 15 and 45.

15. Find two positive numbers $x$ and $y$ such that their sum is 35 and the product ${x^2}{y^5}$ is a maximum

Ans: one number be $x$. other number is $y = (35 - x)$.

$p(x) = {x^2}{y^5}$

$P(x) = {x^2}{(35 - x)^5}$

$\therefore {P^\prime }(x) = 2x{(35 - x)^5} - 5{x^2}{(35 - x)^4}$

$= x{(35 - x)^4}[2(35 - x) - 5x]$

$= x{(35 - x)^4}(70 - 7x)$

$= 7x{(35 - x)^4}(10 - x)$

And, ${P^{\prime \prime }}(x) = 7{(35 - x)^4}(10 - x) + 7x\left[ { - {{(35 - 5)}^4} - 4{{(35 - x)}^3}(10 - x)} \right]$

$= 7{(35 - x)^4}(10 - x) - 7x{(35 - x)^4} - 28x{(35 - x)^3}(10 - x)$

$= 7{(35 - x)^3}[(35 - x)(10 - x) - x(35 - x) - 4x(10 - x)]$

$= 7{(35 - x)^3}\left[ {350 - 45x + {x^2} - 35x + {x^2} - 40x + 4{x^2}} \right]$

$= 7{(35 - x)^3}\left( {6{x^2} - 120x + 350} \right)$

${P^\prime }(x) = 0 \Rightarrow x = 0,x = 35,x = 10$

$x = 35,{f^\prime }(x) = f(x) = 0$ and $y = 35 - 35 = 0.$

$x = 0,y = 35 - 0 = 35$ and product ${x^2}{y^2}$ will be 0 .

 $x = 0$ and $x = 35$ cannot be the possible values of $x$. 

$x = 10$, 

${P^{\prime \prime }}(x) = 7{(35 - 10)^3}(6 \times 100 - 120 \times 10 + 350)$

$= 7{(25)^3}( - 250) < 0$

$P(x)$ will be the maximum when $x = 10$ and $y = 35 - 10 = 25$. the numbers are 10 and 25.

16. Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.

Ans: one number be $x$. the other number is $(16 - x)$. sum of cubes of these numbers be denoted by $S(x)$. $S(x) = {x^3} + {(16 - x)^3}$

$\therefore {S^\prime }(x) = 3{x^2} - 3{(16 - x)^2},$

${S^{\prime \prime }}(x) = 6x + 6(16 - x)$

${S^\prime }(x) = 0 \Rightarrow 3{x^2} - 3{(16 - x)^2} = 0$

$\Rightarrow {x^2} - {(16 - x)^2} = 0$

$\Rightarrow {x^2} - 256 - {x^2} + 32x = 0$

$\Rightarrow x = \dfrac{{256}}{{32}} = 8$

${S^{\prime \prime }}(8) = 6(8) + 6(16 - 8) = 48 + 48 = 96 > 0$

By second derivative test, $x = 8$ is point of local minima of $S$. sum of the cubes of the numbers is minimum when the numbers are 8 and $16 - 8 = 8$.

17. A square piece of tin od side $18\;{\text{cm}}$ is to made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible? 

Ans: side of the square to be cut off be $x\;{\text{cm}}$.

The length and breath of the box will be $(18 - 2x){\text{cm}}$ each and the height of the box is $x\;{\text{cm}}$.

$V(x) = x{(18 - 2x)^2}$

$\therefore {V^\prime }(x) = {(18 - 2x)^2} - 4x(18 - 2x)$

$= (18 - 2x)[18 - 2x - 4x]$

$= (18 - 2x)(18 - 6x)$

$= 6 \times 2(9 - x)(3 - x)$

$= 12(9 - x)(3 - x)$

${V^{\prime \prime }}(x) = 12[ - (9 - x) - (3 - x)]$

$=  - 12(9 - x + 3 - x)$

$=  - 12(12 - 2x)$

$=  - 24(6 - x)$

${v^\prime }(x) = 0 \Rightarrow x = 9$ or $x = 3$

$x = 9$, then the length and the breadth will become $0 .$

$\therefore x \ne 9$.

$\Rightarrow x = 3$.

${V^{\prime \prime }}(3) =  - 24(6 - 3) =  - 72 < 0$

$\therefore $ By second derivative test, $x = 3$ is the point of maxima of $V$.

18. A rectangular sheet of tin $45\;{\text{cm}}$ by $24\;{\text{cm}}$ is to be made into a box without top, by cutting off square from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible? 

Ans: side of the square to be cut be $x\;{\text{cm}}$.

height of the box is $x$, the length is $45 - 2x$,

breadth is $24 - 2x$.

$V(x) = x(45 - 2x)(24 - 2x)$

$= x\left( {1080 - 90x - 48x + 4{x^2}} \right)$

$= 4{x^3} - 138{x^2} + 1080x$

\[\therefore V'(x) = 12{x^2} - 276 + 1080\]

\[ = 12\left( {{x^2} - 23x + 90} \right)\]

$= 12(x - 18)(x - 5)$ 

${V^{\prime \prime }}(x) = 24x - 276 = 12(2x - 23)$

${V^\prime }(x) = 0 \Rightarrow x = 18$ and $x = 5$

not possible to cut a square of side $18\;{\text{cm}}$ from each corner of rectangular sheet, $x$ cannot ${\text{b}}$.

equal to 18. 

$x = 5$

${V^{\prime \prime }}(5) = 12(10 - 23) = 12( - 13) =  - 156 < 0$

$x = 5$ is the point of maxima.

19. Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.

Ans: A rectangle of length $l$ and breadth $b$ be inscribed in the given circle of radius $a$ . The diagonal passes through the center and is of length $2a\;{\text{cm}}$.

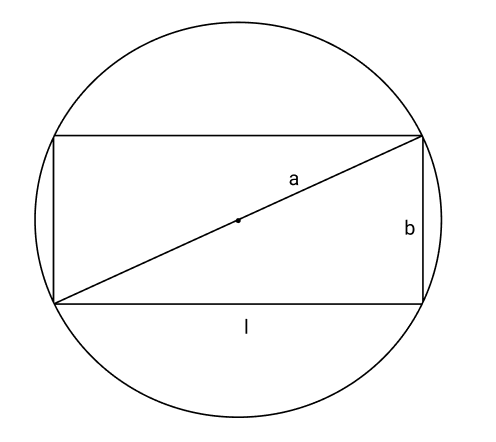
${(2a)^2} = {l^2} + {b^2}$

$\Rightarrow {b^2} = 4{a^2} - {l^2}$

$\Rightarrow b = \sqrt {4{a^2} - {l^2}} $

$A = l\sqrt {4{a^2} - {l^2}} $

$\therefore \dfrac{{dA}}{{dl}} = \sqrt {4{a^2} - {l^2}}  + l\dfrac{1}{{2\sqrt {4{a^2} - {l^2}} }}( - 2l) = \sqrt {4{a^2} - {l^2}}  - \dfrac{1}{{\sqrt {4{a^2} - {l^2}} }}$

$= \dfrac{{4{a^2} - {l^2}}}{{\sqrt {4{a^2} - {l^2}} }}$

$\dfrac{{{d^2}A}}{{d{l^2}}} = \dfrac{{\sqrt {4{a^2} - {l^2}} ( - 4l) - \left( {4{a^2} - 2{l^2}} \right)\dfrac{{( - 2l)}}{{2\sqrt {4{a^2} - {l^2}} }}}}{{\left( {4{a^2} - {l^2}} \right)}}$

$= \dfrac{{\left( {4{a^2} - {l^2}} \right)( - 4l) + 1\left( {4{a^2} - 2{l^2}} \right)}}{{{{\left( {4{a^2} - {l^2}} \right)}^{\dfrac{3}{2}}}}}$

$= \dfrac{{ - 12{a^2}l + 2{l^3}}}{{{{\left( {4{a^2} - {l^2}} \right)}^{\dfrac{3}{2}}}}} = \dfrac{{ - 2l\left( {6{a^2} - {l^2}} \right)}}{{{{\left( {4{a^2} - {l^2}} \right)}^{\dfrac{3}{2}}}}}$

$\dfrac{{dA}}{{dl}} = 0$ gives $4{a^2} = 2{l^2} \Rightarrow l = \sqrt {2a} $

$\Rightarrow b = \sqrt {4{a^2} - 2{a^2}}  = \sqrt {2{a^2}}  = \sqrt {2a} $

when $l = \sqrt {2a} $,

$\dfrac{{{d^2}A}}{{d{l^2}}} = \dfrac{{ - 2(\sqrt {2a} )\left( {6{a^2} - 2{a^2}} \right)}}{{2\sqrt {2{a^3}} }} = \dfrac{{ - 8\sqrt {2{a^3}} }}{{2\sqrt {2{a^3}} }} =  - 4 < 0$

when $l = \sqrt {2a} $, then area of rectangle is maximum. Since $l = b = \sqrt {2a} $, rectangle is a square.

20. Show that the right circular cylinder of given surface and maximum volume is such that is heights is equal to the diameter of the base. 

Ans: $S = 2\pi {r^2} + 2\pi rh$

$\Rightarrow h = \dfrac{{S - 2\pi {r^2}}}{{2\pi r}}$

$\quad  = \dfrac{S}{{2\pi }}\left( {\dfrac{1}{r}} \right) - r$

$V = \pi {r^2}h = \pi {r^2}\left[ {\dfrac{S}{{2\pi }}\left( {\dfrac{1}{r}} \right) - r} \right] = \dfrac{{Sr}}{2} =  - \pi {r^3}$

$\dfrac{{dV}}{{dr}} = \dfrac{S}{2} - 3\pi {r^2},\dfrac{{{d^2}V}}{{d{r^2}}} =  - 6\pi r$

$\dfrac{{dV}}{{dr}} = 0 \Rightarrow \dfrac{S}{2} = 3\pi {r^2} \Rightarrow {r^2} = \dfrac{S}{{6\pi }}$

${r^2} = \dfrac{S}{{6\pi }},\dfrac{{{d^2}V}}{{d{r^2}}} =  - 6\pi \left( {\sqrt {\dfrac{S}{{6\pi }}} } \right) < 0$

volume is maximum when ${r^2} = \dfrac{S}{{6\pi }}$. when ${r^2} = \dfrac{S}{{6\pi }}$, 

then $h = \dfrac{{6\pi {r^2}}}{{2\pi }}\left( {\dfrac{1}{r}} \right) - r = 3r - r = 2r$.

21. Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimeters,

find the dimensions of the can which has the minimum surface area?

Ans: $V = \pi {r^2}h = 100$

$\therefore h = \dfrac{{100}}{{\pi {r^2}}}$

$S = 2{\pi ^2} + 2\pi rh = 2\pi {r^2} + \dfrac{{200}}{r}$

$\therefore \dfrac{{dS}}{{dr}} = 4\pi r - \dfrac{{200}}{{{r^2}}},\dfrac{{{d^2}S}}{{d{r^2}}} = 4\pi  + \dfrac{{400}}{{{r^3}}}$

$\dfrac{{dS}}{{dr}} = 0 \Rightarrow 4\pi r = \dfrac{{200}}{{{r^2}}}$

$\Rightarrow {r^3} = \dfrac{{200}}{{4\pi }} = \dfrac{{50}}{\pi }$

$\Rightarrow r = {\left( {\dfrac{{50}}{\pi }} \right)^{\dfrac{1}{3}}}$

when $r = {\left( {\dfrac{{50}}{\pi }} \right)^{\dfrac{1}{3}}},\dfrac{{{d^2}S}}{{d{r^2}}} > 0$.

the surface area is the minimum when the radius of the cylinder is ${\left( {\dfrac{{50}}{\pi }} \right)^{\dfrac{1}{3}}}\;{\text{cm}}$. $r = {\left( {\dfrac{{50}}{\pi }} \right)^{\dfrac{1}{3}}},h = 2{\left( {\dfrac{{50}}{\pi }} \right)^{\dfrac{1}{3}}}\;{\text{cm}}$.

22. A Wire of length $28 m$ is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the circle is minimum? 

Ans: Piece of length $l$ be cut from wire to make square. other piece of wire to be made into circle is $(28 - l)m$. side of square $= \dfrac{l}{4}$

$2\pi r = 28 - l \Rightarrow r = \dfrac{1}{{2\pi }}(28 - l).$

$A = \dfrac{{{l^2}}}{{16}} + \pi {\left[ {\dfrac{1}{{2\pi }}(28 - l)} \right]^2}$

$= \dfrac{{{l^2}}}{{16}} + \dfrac{1}{{4\pi }}{(28 - l)^2}$

$\therefore \dfrac{{dA}}{{dl}} = \dfrac{{2l}}{{16}} + \dfrac{2}{{4\pi }}(28 - l)( - 1) = \dfrac{l}{8} - \dfrac{1}{{2\pi }}(28 - l)$

$\dfrac{{{d^2}A}}{{d{l^2}}} = \dfrac{1}{8} + \dfrac{1}{{2\pi }} > 0$

$\dfrac{{dA}}{{dl}} = 0 \Rightarrow \dfrac{l}{8} - \dfrac{l}{{2\pi }}(28 - l) = 0$

$\Rightarrow \dfrac{{\pi l - 4(28 - l)}}{{8\pi }} = 0$

$(\pi  + 4)l - 112 = 0$

$\Rightarrow l = \dfrac{{112}}{{\pi  + 4}}$

when $l = \dfrac{{112}}{{\pi  + 4}},\dfrac{{{d^2}A}}{{d{l^2}}} > 0$.

the area is minimum when $l = \dfrac{{112}}{{\pi  + 4}}$.

23. Prove that the volume of the largest cone that can be inscribed in a sphere of radius $R$ is $\dfrac{8}{{27}}$ of the volume of the sphere. 

Ans: Let $r$ and $h$ be the radius and height of the cone respectively inscribed in a sphere of radius $R$.

$V = \dfrac{1}{3}\pi {r^2}h$

$h = R + AB = R + \sqrt {{R^2} - {r^2}} $

$\therefore V = \dfrac{1}{3}\pi {r^2}\left( {R + \sqrt {{R^2} - {r^2}} } \right)$

$= \dfrac{1}{3}\pi {r^2}R + \dfrac{1}{3}\pi {r^2}\sqrt {{R^2} + {r^2}} $

$\dfrac{{dV}}{{dr}} = \dfrac{2}{3}\pi rR + \dfrac{2}{3}\pi r\sqrt {{R^2} - {r^2}}  + \dfrac{1}{3}\pi {r^2} \cdot \dfrac{{( - 2r)}}{{2\sqrt {{R^2} - {r^2}} }}$

$= \dfrac{2}{3}\pi rR + \dfrac{2}{3}\pi r\sqrt {{R^2} - {r^2}}  - \dfrac{1}{3}\pi \dfrac{{{r^3}}}{{\sqrt {{R^2} - {r^2}} }}$

$= \dfrac{2}{3}\pi rR + \dfrac{{2\pi r\left( {{R^2} - {r^2}} \right) - \pi {r^3}}}{{3\sqrt {{R^2} - {r^2}} }}$

$= \dfrac{2}{3}\pi rR + \dfrac{{2\pi r{R^2} - 3\pi {r^3}}}{{3\sqrt {{R^2} - {r^2}} }}.$

$\dfrac{{{d^2}V}}{{d{r^2}}} = \dfrac{{2\pi R}}{3} + \dfrac{{3\sqrt {{R^2} - {r^2}} \left( {2\pi {R^2} - 9\pi {r^2}} \right) - \left( {2\pi r{R^2} - 3\pi {r^3}} \right) \cdot \dfrac{{( - 2r)}}{{6\sqrt {{R^2} - {r^2}} }}}}{{9\left( {{R^2} - {r^2}} \right)}}$

$= \dfrac{2}{3}\pi rR + \dfrac{{9\left( {{R^2} - {r^2}} \right)\left( {2\pi {R^2} - 9\pi {r^2}} \right) + 2\pi {r^2}{R^2} + 3\pi {r^4}}}{{27{{\left( {{R^2} - {r^2}} \right)}^{\dfrac{3}{2}}}}}$

$\dfrac{{dV}}{{dr}} = 0 \Rightarrow \pi \dfrac{2}{3}rR = \dfrac{{3\pi {r^3} - 2\pi {R^2}}}{{3\sqrt {{R^2} - {r^2}} }}$

$\Rightarrow 2R = \dfrac{{3\pi {r^3} - 2\pi {R^2}}}{{\sqrt {{R^2} - {r^2}} }} = 2R\sqrt {{R^2} - {r^2}}  = 3{r^2} - 2{R^2}$

$\Rightarrow 4{R^2}\left( {{R^2} - {r^2}} \right) = {\left( {3{r^2} - 2{R^2}} \right)^2}$

$\Rightarrow 4{R^4} - 4{R^2}{r^2} = 9{r^4} + 4{R^4} - 12{r^2}{R^2}$

$\Rightarrow 9{r^4} = 8{R^2}{r^2}$

$\Rightarrow {r^2} = \dfrac{8}{9}{R^2}$

${r^2} = \dfrac{8}{9}{R^2},\dfrac{{{d^2}V}}{{d{r^2}}} < 0$

volume of the cone is the maximum when ${r^2} = \dfrac{8}{9}{R^2}$.

${r^2} = \dfrac{8}{9}{R^2},h = R + \sqrt {{R^2} - \dfrac{8}{9}{R^2}}  = R + \sqrt {\dfrac{1}{9}{R^2}}  = R + \dfrac{R}{3} = \dfrac{4}{3}R$.

$= \dfrac{1}{3}\pi \left( {\dfrac{8}{9}{R^2}} \right)\left( {\dfrac{4}{3}R} \right)$

$= \dfrac{8}{{27}}\left( {\dfrac{4}{3}\pi {R^3}} \right)$

$= \dfrac{8}{{27}}{\text{x}}($ volume of the sphere)

24. Show that he right circular cone of least curved surface and given volume has an altitude equal to $\sqrt 2 $ time the radius of the base.

Ans: $V = \dfrac{1}{{3\pi }}\pi {r^2}h \Rightarrow h = \dfrac{{3V}}{{{r^2}}}$

$S = \pi rl$

$= \pi r\sqrt {{r^2} + {h^2}} $

$= \pi r\sqrt {{r^2} + \dfrac{{9{V^2}}}{{{\pi ^2}{r^4}}}} \pi \dfrac{{r\sqrt {{9^2}{r^6} + {V^2}} }}{{\pi {r^2}}}$

$= \dfrac{1}{r}\sqrt {{\pi ^2}{r^6} + 9{V^2}} $

$\therefore \dfrac{{dS}}{{dr}} = \dfrac{{r \cdot \dfrac{{6{\pi ^2}{r^5}}}{{2\sqrt {{\pi ^2}{r^6} + 9{V^2}} }} - \sqrt {{\pi ^2}{r^6} + 9{V^2}} }}{{{r^2}}}$

$= \dfrac{{3{\pi ^2}{r^6} - {\pi ^2}{r^6} - 9{V^2}}}{{{r^2}\sqrt {{\pi ^2}{r^6} + 9{V^2}} }}$

$= \dfrac{{2{\pi ^2}{r^6} - 9{V^2}}}{{{r^2}\sqrt {{\pi ^2}{r^6} + 9{V^2}} }}$

$= \dfrac{{2{\pi ^2}{r^6} - 9{V^2}}}{{{r^2}\sqrt {{\pi ^2}{r^6} + 9{V^2}} }}$

$\dfrac{{dS}}{{dr}} = 0 \Rightarrow 2{\pi ^2}{r^6} = 9{V^2} \Rightarrow {r^6} = \dfrac{{9{V^2}}}{{2{\pi ^2}}}$

${r^6} = \dfrac{{9{V^2}}}{{2{\pi ^2}}},\dfrac{{{d^2}S}}{{d{r^2}}} > 0$

surface area of the cone is least when ${r^6} = \dfrac{{9{V^2}}}{{2{\pi ^2}}}$

${r^6} = \dfrac{{9{V^2}}}{{2{\pi ^2}}},h = \dfrac{{3V}}{{\pi {r^2}}} = \dfrac{{3V}}{{\pi {r^2}}}{\left( {\dfrac{{2{\pi ^2}{r^6}}}{9}} \right)^{\dfrac{1}{2}}} = \dfrac{3}{{\pi {r^2}}} \cdot \dfrac{{\sqrt {2\pi {r^3}} }}{3} = \sqrt 2 r.$

25. Show that the semi-vertical angle of the cone of the maximum volume and of given slant heigh is ${\tan ^{ - 1}}\sqrt 2 $.

Ans: Let $\theta $ be semi-vertical angle of cone. $\theta  \in \left[ {0,\dfrac{\pi }{2}} \right]$

$r = l\sin \theta $ and $h = l\cos \theta $

$V = \dfrac{1}{3}\pi {r^2}h$

$= \dfrac{1}{3}\pi \left( {{l^2}{{\sin }^2}\theta } \right)(l\cos \theta )$

$= \dfrac{1}{3}\pi {l^3}{\sin ^2}\theta \cos \theta $

$\therefore \dfrac{{dV}}{{d\theta }} = \dfrac{{{l^3}\pi }}{3}\left[ {{{\sin }^2}\theta ( - \sin \theta ) + \cos \theta (2\sin \theta \cos \theta )} \right]$

\[ = \dfrac{{{l^3}\pi }}{3}\left[ { - {{\sin }^3} + 2\sin \theta {{\cos }^2}\theta } \right]\]

\[\dfrac{{{d^2}V}}{{d{\theta ^2}}} = \dfrac{{{l^3}\pi }}{3}\left[ { - 3{{\sin }^2}\theta \cos \theta  + 2{{\cos }^3}\theta  - 4{{\sin }^2}\theta \cos \theta } \right]\]

\[ = \dfrac{{{l^3}\pi }}{3}\left[ {2{{\cos }^2}\theta  - 7{{\sin }^2}\theta \cos \theta } \right]\]

\[\dfrac{{dV}}{{d\theta }} = 0\]

$\Rightarrow {\sin ^3}\theta  = 2\sin \theta {\cos ^2}\theta $

$\Rightarrow {\tan ^2}\theta  = 2$

$\Rightarrow \tan \theta  = \sqrt 2 $

$\Rightarrow \theta  = {\tan ^{ - 1}}\sqrt 2 $

when $\theta  = {\tan ^{ - 1}}\sqrt 2 $, then ${\tan ^2}\theta  = 2$ or ${\sin ^2}\theta  = 2{\cos ^2}\theta $.

$\dfrac{{{d^2}V}}{{d{\theta ^2}}} = \dfrac{{{l^3}\pi }}{3}\left[ {2{{\cos }^3}\theta  - 14{{\cos }^3}\theta } \right] =  - 4\pi {l^3}{\cos ^3}\theta  < 0$ for $\theta  \in \left[ {0,\dfrac{\pi }{2}} \right]$

volume is the maximum when $\theta  = {\tan ^{ - 1}}\sqrt 2 $. 

26. Show that the semi-vertical angle of the right circular cone of given surface area and maximum volume is ${\tan ^{ - 1}}\frac {1} {3}$.

Ans: Consider x be the radius and y be the height of the cone and semi-vertical angle be $\theta $.  And, Total Surface area of cone (S) = $\pi x\sqrt{{{x}^{2}}+{{y}^{2}}}+\pi {{x}^{2}}$

$\pi x\sqrt{{{x}^{2}}+{{y}^{2}}}+\pi {{x}^{2}}=\frac{S}{\pi }=k$ (say)

$\pi x\sqrt{{{x}^{2}}+{{y}^{2}}}=k-{{x}^{2}}$

${{x}^{2}}({{x}^{2}}+{{y}^{2}})={{(k-{{x}^{2}})}^{2}}$

${{x}^{4}}+{{x}^{2}}{{y}^{2}}={{k}^{2}}+{{x}^{4}}-2k{{x}^{2}}$

${{x}^{2}}{{y}^{2}}={{k}^{2}}-2k{{x}^{2}}$

${{x}^{2}}=\frac{{{k}^{2}}}{{{y}^{2}}+2k}$……….(1) 

Volume of cone (V) =  $\frac{1}{3}\pi {{x}^{2}}y$

=  $\frac{1}{3}\pi \left( \frac{{{k}^{2}}}{{{y}^{2}}+2k} \right)y$

= $\frac{1}{3}\pi {{k}^{2}}\left( \frac{y}{{{y}^{2}}+2k} \right)$

$\frac{dV}{dy}=\frac{1}{3}\pi {{k}^{2}}\frac{d}{dy}\left( \frac{y}{{{y}^{2}}+2k} \right)$

= $\frac{1}{3}\pi {{k}^{2}}\left( \frac{({{y}^{2}}+2k).1-y.2y}{{{({{y}^{2}}+2k)}^{2}}} \right)$[Using quotient rule]

$\frac{dV}{dy}=\frac{1}{3}\pi {{k}^{2}}\left( \frac{2k-{{y}^{2}}}{{{({{y}^{2}}+2k)}^{2}}} \right)$……….(2)

Now $\frac{dV}{dy}=0$

$\frac{1}{3}\pi {{k}^{2}}\left( \frac{2k-{{y}^{2}}}{{{({{y}^{2}}+2k)}^{2}}} \right)=0$

$2k-{{y}^{2}}=0$

${{y}^{2}}=2k$

$y=\pm \sqrt{2k}$

$y=\sqrt{2k}$[height can’t be negative]

Here $y=\sqrt{2k}$ is the turning point.

As, \[\frac{dV}{dy}>0\], therefore, Volume is maximum at $y=\sqrt{2k}$  

From equation (1),

${{x}^{2}}=\frac{{{k}^{2}}}{2k+2k}=\frac{{{k}^{2}}}{4k}=\frac{k}{4}$

$x=\frac{\sqrt{k}}{2}$

Now Semi-vertical angle of the cone

\[\sin \theta =\frac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}}}=\frac{\frac{\sqrt{k}}{2}}{\sqrt{\frac{k}{4}+2k}}=\frac{\sqrt{k}}{2}\times \sqrt{\frac{4}{9k}}=\frac{1}{3}\]

Which implies $\theta ={{\sin }^{-1}}\frac{1}{3}$

27. The point on the curve ${x^2} = 2y$ which is nearest to the point $(0,5)$ is

${{\text{ (A) }}(2\sqrt 2 ,4)}{{\text{ (B) }}(2\sqrt 2 ,0)}{{\text{ (C) }}(0,0)}{{\text{ (D) }}(2,2)}$

Ans: position of point is $\left( {x,\dfrac{{{x^2}}}{2}} \right)$. 

distance $d(x)$ between points $\left( {x,\dfrac{{{x^2}}}{2}} \right)$ and $(0,5)$ is $d(x) = \sqrt {{{(x - 0)}^2} + {{\left( {\dfrac{{{x^2}}}{2} - 5} \right)}^2}}  = \sqrt {{x^2} + \dfrac{{{x^4}}}{4} + 25 - 5{x^2}}  = \sqrt {\dfrac{{{x^4}}}{4} - 4{x^2} + 25} $

$\therefore {d^\prime }(x) = \dfrac{{\left( {{x^3} - 8x} \right)}}{{2\sqrt {\dfrac{{{x^4}}}{4} - 4{x^2} + 25} }} = \dfrac{{\left( {{x^3} - 8x} \right)}}{{\sqrt {{x^4} - 16{x^2} + 100} }}$

${d^\prime }(x) = 0 \Rightarrow {x^3} - 8x = 0$

$\Rightarrow x\left( {{x^2} - 8} \right) = 0$

$\Rightarrow x = 0, \pm 2\sqrt 2 $

\[ = \dfrac{{\left( {{x^4} - 16{x^2} + 100} \right)\left( {3{x^2} - 8} \right) - 2\left( {{x^3} - 8x} \right)\left( {{x^3} - 8x} \right)}}{{{{\left( {{x^4} - 16{x^2} + 100} \right)}^{\dfrac{3}{2}}}}}\]

\[ = \dfrac{{\left( {{x^4} - 16{x^2} + 100} \right)\left( {3{x^2} - 8} \right) - 2{{\left( {{x^3} - 8x} \right)}^2}}}{{{{\left( {{x^4} - 16{x^2} + 100} \right)}^{\dfrac{3}{2}}}}}\]

$x = 0$, then ${d^{\prime \prime }}(x) = \dfrac{{36( - 8)}}{{{6^3}}} < 0.$

$x =  \pm 2\sqrt 2 ,{d^{\prime \prime }}(x) > 0$

$d(x)$ is the minimum at $x =  \pm 2\sqrt 2 $. $x =  \pm 2\sqrt 2 ,y = \dfrac{{{{(2\sqrt 2 )}^2}}}{2} = 4.$

The correct answer is A. 

28. For all real values of $x$, the minimum value of $\dfrac{{1 - x + {x^2}}}{{1 + x + {x^2}}}$ is

1. 0 (B) $1({\mathbf{C}})3$ (D) $\dfrac{1}{3}$

Ans: $f(x) = \dfrac{{1 - x + {x^2}}}{{1 + x + {x^2}}}$

$\therefore {f^\prime }(x) = \dfrac{{\left( {1 - x + {x^2}} \right)( - 1 + 2x) - \left( {1 - x + {x^2}} \right)(1 + 2x)}}{{{{\left( {1 + x + {x^2}} \right)}^2}}}$

$= \dfrac{{ - 1 + 2x - x + 2{x^2} - {x^2} + 2{x^2} - 1 - 2x + x + 2{x^2} - {x^2} - 2{x^3}}}{{{{\left( {1 + x + {x^2}} \right)}^2}}}$

$= \dfrac{{2{x^2} - 2}}{{{{\left( {1 + x + {x^2}} \right)}^2}}} = \dfrac{{2\left( {{x^2} - 1} \right)}}{{{{\left( {1 + x + {x^2}} \right)}^2}}}$

$\therefore {f^\prime }(x) = 0 \Rightarrow {x^2} = 1 \Rightarrow x =  \pm 1$

${f^{\prime \prime }}(x) = \dfrac{{2\left[ {\left( {1 + x + {x^2}} \right)(2x) - \left( {{x^2} - 1} \right)(2)\left( {1 + x + {x^2}} \right)(1 + 2x)} \right]}}{{{{\left( {1 + x + {x^2}} \right)}^4}}}$

$= \dfrac{{4\left( {1 + x + {x^2}} \right)\left[ {\left( {1 + x + {x^2}} \right)x - \left( {{x^2} - 1} \right)(1 + 2x)} \right]}}{{{{\left( {1 + x + {x^2}} \right)}^4}}}$

$= 4\dfrac{{\left[ {x + {x^2} + {x^3} - {x^2} - 2{x^3} + 1 + 2x} \right]}}{{{{\left( {1 + x + {x^2}} \right)}^3}}}$

$= \dfrac{{4\left( {1 + 3x - {x^3}} \right)}}{{{{\left( {1 + x + {x^2}} \right)}^3}}}$

${f^{\prime \prime }}(1) = \dfrac{{4(1 + 3 - 1)}}{{{{(1 + 1 + 1)}^3}}} = \dfrac{{4(3)}}{{{{(3)}^3}}} = \dfrac{4}{9} > 0$

${f^{\prime \prime }}( - 1) = \dfrac{{4(1 - 3 + 1)}}{{{{(1 + 1 + 1)}^3}}} = 4( - 1) = 4 < 0$

$f$ is the minimum at $x = 1$ and the minimum value is given by

$f(1) = \dfrac{{1 - 1 + 1}}{{1 + 1 + 1}} = \dfrac{1}{3}$.

The correct answer is ${\mathbf{D}}$.

29. The maximum value of ${[x(x + 1) + 1]^{\dfrac{1}{3}}},0 \leqslant x \leqslant 1$ is

1. ${\left( {\dfrac{1}{3}} \right)^{\dfrac{1}{3}}}$ 

2. $\dfrac{1}{2}$

$({\mathbf{C}})1{\kern 1pt} \,$

$({\mathbf{D}})0$

Ans: $f(x) = {[x(x + 1) + 1]^{\dfrac{1}{3}}}$

$\therefore {f^\prime }(x) = \dfrac{{2x - 1}}{{3{{[x(x + 1) + 1]}^{\dfrac{2}{3}}}}}$

${f^\prime }(x) = 0 \Rightarrow x = \dfrac{1}{2}$

$f(0) = {[0(0 - 1) + 1]^{\dfrac{1}{3}}} = 1$

$f(1) = {[1(1 - 1) + 1]^{\dfrac{1}{3}}} = 1$

$f\left( {\dfrac{1}{2}} \right) = {\left[ {\dfrac{1}{2}\left( {\dfrac{{ - 1}}{2}} \right) + 1} \right]^{\dfrac{1}{3}}} = {\left( {\dfrac{3}{4}} \right)^{\dfrac{1}{3}}}$

Maximum value of $f$ in \[[0,1]\]is 1. 

The correct answer is ${\mathbf{C}}$.

Miscellaneous Solutions

1. Show that the function given by $f(x) = \dfrac{{\log x}}{x}$ has maximum at $x = e$.

Ans: $f(x) = \dfrac{{\log x}}{x}$

${f^\prime }(x) = \dfrac{{x\left( {\dfrac{1}{x}} \right) - \log x}}{{{x^2}}} = \dfrac{{1 - \log x}}{{{x^2}}}$

${f^\prime }(x) = 0$

$\Rightarrow 1 - \log x = 0$

$\Rightarrow \log x = 1$

$\Rightarrow \log x = \log e$

$\Rightarrow x = e$

${f^{\prime \prime }}(x) = \dfrac{{{x^2}\left( { - \dfrac{1}{x}} \right) - (1 - \log x)(2x)}}{{{x^4}}}$

$= \dfrac{{ - x - 2x(1 - \log x)}}{{{x^4}}}$

$= \dfrac{{ - 3 + 2\log x}}{{{x^3}}}$

${f^{\prime \prime }}(e) =  = \dfrac{{ - 3 + 2\log e}}{{{e^3}}} = \dfrac{{ - 3 + 2}}{{{e^3}}} = \dfrac{{ - 1}}{{{e^3}}} < 0$

$f$ is the maximum at $x = e$

2. The two equal sides of an isosceles triangle with fixed base $b$ are decreasing at the rate of $3\;{\text{cm}}$ per second. How fast is the area decreasing when the two equal sides are equal to the base? 

Ans: Let $\vartriangle ABC$ be isosceles where \[BC\]is the base of fixed length $b$. 

Let the length of the two equal sides of $\vartriangle ABC$ be $a$. 

Draw $AD \bot BC$.

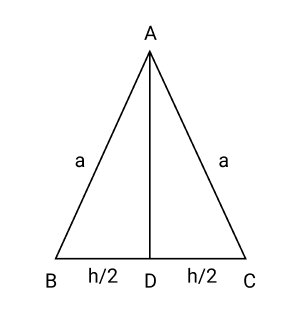
$AD = \sqrt {{a^2} - \dfrac{{{b^2}}}{4}} $

Area of triangle $= \dfrac{1}{2}b\sqrt {{a^2} - \dfrac{{{b^2}}}{4}} $

$\dfrac{{dA}}{{dt}} = \dfrac{1}{2}b \cdot \dfrac{{2a}}{{2\sqrt {{a^2} - \dfrac{{{b^2}}}{4}} }}\dfrac{{da}}{{dt}} = \dfrac{{ab}}{{\sqrt {4{a^2} - {b^2}} }}\dfrac{{da}}{{dt}}$

$\dfrac{{da}}{{dt}} =  - 3\;{\text{cm}}/{\text{s}}$

$\therefore \dfrac{{da}}{{dt}} = \dfrac{{ - 3ab}}{{\sqrt {4{a^2} - {b^2}} }}$

when $a = b$

$\dfrac{{dA}}{{dt}} = \dfrac{{ - 3{b^2}}}{{\sqrt {4{b^2} - {b^2}} }} = \dfrac{{ - 3{b^2}}}{{\sqrt {3{b^2}} }} =  - \sqrt {3b}$

3. Find the intervals in which the function $f$ given by $f(x) = \dfrac{{4\sin x - 2x - x\cos x}}{{2 + \cos x}}$ Is 

(i) increasing (ii) decreasing

Ans: $f(x) = \dfrac{{4\sin x - 2x - x\cos x}}{{2 + \cos x}}$

$\therefore {f^\prime }(x) = \dfrac{{(2 + \cos x)(4\cos x - 2 - \cos x + x\sin x) - (4\sin x - 2x - x\cos x)( - \sin x)}}{{{{(2 + \cos x)}^2}}}$

$= \dfrac{{(2 + \cos x)(3\cos x - 2 + x\sin x) + \sin x(4\sin x - 2x - x\cos x)}}{{{{(2 + \cos x)}^2}}}$

$= \dfrac{{6\cos x - 4 + 2x\sin x + 3{{\cos }^2}x - 2\cos x + x\sin x\cos x + 4{{\sin }^2}x - 2{{\sin }^2}x - 2x\sin x - x\sin x\cos x}}{{{{(2 + \cos x)}^2}}}$

$= \dfrac{{4\cos x - 4 + 3{{\cos }^2}x + 4{{\sin }^2}x}}{{{{(2 + \cos x)}^2}}}$

$= \dfrac{{4\cos x - {{\cos }^2}x}}{{{{(2 + \cos x)}^2}}} = \dfrac{{\cos x(4 - \cos x)}}{{{{(2 + \cos x)}^2}}}$

${f^\prime }(x) = 0$

$\Rightarrow \cos x = 0\cos x = 4$

$\cos x \ne 4$

$\cos x = 0$

$\Rightarrow x = \dfrac{\pi }{2},\dfrac{{3\pi }}{2}$

$\operatorname{In} \left( {0,\dfrac{\pi }{2}} \right)$ and $\left( {\dfrac{{3\pi }}{2},2\pi } \right),{f^\prime }(x) > 0$

$f(x)$ is increasing for $0 < x < \dfrac{x}{2}$ and $\dfrac{{3\pi }}{2} < x < 2\pi $.

$\operatorname{In} \left( {\dfrac{\pi }{2},\dfrac{{3\pi }}{2}} \right),{f^\prime }(x) < 0$

$f(x)$ is decreasing for $\dfrac{\pi }{2} < x < \dfrac{{3\pi }}{2}$.

4. Find the intervals in which the function $f$ given by $f(x) = {x^3} + \dfrac{1}{{{x^3}}},x \ne 0$ is

(i) increasing 

(ii) decreasing

Ans: $f(x) = {x^3} + \dfrac{1}{{{x^3}}}$

$\therefore {f^\prime }(x) = 3{x^2} - \dfrac{3}{{{x^4}}} = \dfrac{{3{x^6} - 3}}{{{x^4}}}$

${f^\prime }(x) = 0 \Rightarrow 3{x^6} - 3 = 0 \Rightarrow {x^6} = x =  \pm 1$

In $( - \infty ,1)$ and $(1,\infty )$ i.e.., when $x <  - 1$ and $x > 1,{f^\prime }(x) > 0.$ when $x <  - 1$ and $x > 1,f$ is increasing. In $( - 1,1)$ i.e., when $ - 1 < x < 1,{f^\prime }(x) < 0$.

Thus, when $ - 1 < x < 1,f$ is decreasing.

5. Find the maximum area of an isosceles triangle inscribed in the ellipse $\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1$ with its vertex at one end of the major axis.

Ans:

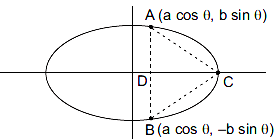
Ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$

Let $A B C$, be the triangle inscribed in the ellipse where vertex $C$ is at $(a,0)$. Since the ellipse is symmetrical with $x$-axis and $y - axis$ ${y_1} =  \pm \dfrac{b}{a}\sqrt {{a^2} - x_1^2} .$

Coordinates of $A$ are $\left( { - {x_{1,}}\dfrac{b}{a}\sqrt {{a^2} - {x^2}1} } \right)$ and coordinates of $B$ are $\left( {{x_1}, - \dfrac{b}{a}\sqrt {{a^2} - x_1^2} .} \right)$ As the point $\left( { - {x_1},{y_1}} \right)$ lies on the ellipse, the area of triangle $A B C$ is $A = \dfrac{1}{2}\mid a\left( {\dfrac{{2b}}{a}\sqrt {{a^2} - x_1^2} } \right) + \left( { - {x_1}} \right)\left( { - \dfrac{b}{a}\sqrt {{a^2} - x_1^2} } \right) + \left( { - {x_1}} \right)\left( { - \dfrac{b}{a}\sqrt {{a^2} - {x^2}1} } \right)$

$\Rightarrow A = ba\sqrt {{a^2} - {x^2}1}  + {x_1}\dfrac{b}{a}\sqrt {{a^2} - x_1^2} $

$\therefore \dfrac{{dA}}{{d{x_1}}} = \dfrac{{ - 2xb}}{{2\sqrt {{a^2} - x_1^2} }} + \dfrac{b}{a}\sqrt {{a^2} - x_1^2}  - \dfrac{{2bx_1^2}}{{{a^2}\sqrt {{a^2} - x_1^2} }}$

$= \dfrac{b}{{2\sqrt {{a^2} - x_1^2} }}\left[ { - {x_1}a + \left( {{a^2} - x_1^2} \right) - x_1^2} \right]$

$= \dfrac{{b\left( { - 2x_1^2 - x_1^2 + {a^2}} \right)}}{{a\sqrt {{a^2} - x_1^2} }}$

$\dfrac{{dA}}{{d{x_1}}} = 0$

$\Rightarrow  - 2x_1^2 - {x_1}a + {a^2} = 0$

$\Rightarrow {x_1} = \dfrac{{a \pm \sqrt {{a^2} - 4( - 2)\left( {{a^2}} \right)} }}{{2( - 2)}}$

$= \dfrac{{a \pm \sqrt {9{a^2}} }}{{ - 4}}$

$= \dfrac{{a \pm 3a}}{{ - 4}}$

$\Rightarrow {x_1} =  - a,\dfrac{a}{2}$

${x_1}$ cannot be equal to $a$. $\therefore {x_1} = \dfrac{a}{2} \Rightarrow {y_1} = \dfrac{b}{a}\sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{ba}}{{2a}}\sqrt 3  = \dfrac{{\sqrt {3b} }}{2}$

Now,$\dfrac{{{d^2}A}}{{d{x^2}1}} = \dfrac{b}{a}\left\{ {\dfrac{{\sqrt {{a^2} - x_1^2} \left( { - 4{x_1} - a} \right) - \left( { - 2x_1^2 - {x_1}a + {a^2}} \right)\dfrac{{\left( { - 2{x_1}} \right)}}{{2\sqrt {{a^2} - x_1^2} }}}}{{{a^2} - x_1^2}}} \right\}$

$= \dfrac{b}{a}\left\{ {\dfrac{{\left( {{a^2} - x_1^2} \right)\left( { - 4{x_1} - a} \right) + {x_1}\left( { - 2x_1^2 - {x_1}a + {a^2}} \right)}}{{{{\left( {{a^2} - x_1^2} \right)}^{\dfrac{2}{3}}}}}} \right\}$

$= \dfrac{b}{a}\left\{ {\dfrac{{2{x^3} - 3{a^2}x - {a^3}}}{{{{\left( {{a^2} - x_1^2} \right)}^{\dfrac{3}{2}}}}}} \right\}$

when ${x_1} = \dfrac{a}{2}$,

$\dfrac{{{d^2}A}}{{dx_1^2}} = \dfrac{b}{a}\left\{ {\dfrac{{2\dfrac{{{a^3}}}{8} - 3\dfrac{{{a^3}}}{2} - {a^3}}}{{{{\left( {\dfrac{{3{a^2}}}{4}} \right)}^{\dfrac{3}{2}}}}}} \right\} = \dfrac{b}{a}\left\{ {\dfrac{{\dfrac{{{a^3}}}{4} - \dfrac{3}{2}{a^3} - {a^3}}}{{{{\left( {\dfrac{{3{a^2}}}{4}} \right)}^{\dfrac{3}{2}}}}}} \right\}$

$= \dfrac{b}{a}\left\{ {\dfrac{{\dfrac{9}{4}{a^3}}}{{{{\left( {\dfrac{{3{a^2}}}{4}} \right)}^{\dfrac{3}{2}}}}}} \right\} < 0$

Area is the maximum when ${x_1} = \dfrac{a}{2}$. Maximum area of the triangle is $A = b\sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  + \left( {\dfrac{a}{2}} \right)\dfrac{b}{a}\sqrt {{a^2} - \dfrac{{{a^2}}}{4}} $

$= ab\dfrac{{\sqrt 3 }}{2} + \left( {\dfrac{a}{2}} \right)\dfrac{b}{a} \times \dfrac{{a\sqrt 3 }}{2}$

$= \dfrac{{ab\sqrt 3 }}{2} + \dfrac{{ab\sqrt 3 }}{4} = \dfrac{{3\sqrt 3 }}{4}ab$

6. A tank with a rectangular base and rectangular sides, open at the top is to be constructed so that its depth is \[2m\]and volume is $8{m^3}$. If the building of tank costs Rs 70 per sq meters for the base and Rs 45 per sq meters for sides. What is the cost of the least expensive tank?

Ans: Let \[l,b\]and $h$ represent the length, breadth, and height of the tank respectively.

height $(h) = 2m$

Volume of the tank $= 8\;{{\text{m}}^3}$ Volume of the tank $= l \times b \times {\text{h}}$ $8 = l \times b \times 2$

$\Rightarrow lb = 4 \Rightarrow b = \dfrac{4}{l}$

Area of the base $= lb = 4$ 

Area of 4 walls $(A) = 2h(l + b)$

$\therefore A = 4\left( {l + \dfrac{4}{l}} \right)$

$\Rightarrow \dfrac{{dA}}{{dl}} = 4\left( {1 - \dfrac{4}{{{l^2}}}} \right)$

$Now,\dfrac{{dA}}{{dl}} = 0$

$\Rightarrow l - \dfrac{4}{{{l^2}}} = 0$

$\Rightarrow {l^2} = 4$

$\Rightarrow l =  \pm 2$

Therefore, we have $l = 4$. 

$\therefore b = \dfrac{4}{l} = \dfrac{4}{2} = 2$

$\dfrac{{{d^2}A}}{{d{l^2}}} = \dfrac{{32}}{{{l^3}}}$

$l = 2,\dfrac{{{d^2}A}}{{d{l^2}}} = \dfrac{{32}}{8} = 4 > 0.$

Area is the minimum when $l = 2$. 

We have $l = b = h = 2$.

Cost of building base \[ = \] Rs $70{\text{x}}(lb) = $ Rs$70(4) = $ Rs 280

Cost of building walls $= Rs2h(l + h) \times 45 = Rs90(2)(2 + 2) = $ 

Rs $8(90) = $ Rs 720

Required total cost $= Rs(280 + 720) = $ Rs 1000

7. The sum of the perimeter of a circle and square is $k$, where $k$ is some constant. Prove that the sum of their area is least when the side of square is double the radius of the circle. 

Ans: $2\pi r + 4a = k$ (where $k$ is constant) $\Rightarrow a = \dfrac{{k - 2\pi r}}{4}$

sum of the areas of the circle and the square $(A)$ is given by,

$A = \pi {r^2} + {a^2} = \pi {r^2} + \dfrac{{{{(k = 2\pi r)}^2}}}{{16}}$

$\therefore \dfrac{{dA}}{{dr}} = 2\pi r + \dfrac{{2(k - 2\pi r)(2\pi )}}{{16}} = 2\pi r$

$=  - \dfrac{{\pi (k - 2\pi r)}}{4}$

Now, $\dfrac{{dA}}{{dr}} = 0$

$\Rightarrow 2\pi r = \dfrac{{\pi (k - 2\pi r)}}{4}$

$8r = k - 2\pi r$

$\Rightarrow (8 + 2\pi )r = k$

$\Rightarrow r = \dfrac{k}{{8 + 2\pi }} = \dfrac{k}{{2(4 + \pi )}}$

Now, $\dfrac{{{d^2}A}}{{d{r^2}}} = 2\pi  + \dfrac{{{\pi ^2}}}{2} > 0$

$\therefore $ where $r = \dfrac{k}{{2(4 + \pi )}},\dfrac{{{d^2}A}}{{d{r^2}}} > 0.$

area is least when $r = \dfrac{k}{{2(4 + \pi )}}$ where $r = \dfrac{k}{{2(4 + \pi )}},$

$a = \dfrac{{k - 2\pi \left[ {\dfrac{k}{{2(4 + \pi )}}} \right]}}{4} = \dfrac{{8k + 2\pi k - 2\pi k}}{{2(4 + \pi ) \times 4}} = \dfrac{k}{{4 + \pi }} = 2r$

8. A window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is $10\;{\text{m}}$. Find the dimensions of the window to admit maximum light through the whole opening. 

Ans: $x$ and $y$ be length and breadth of the rectangular window.

Radius of semicircular opening $= \dfrac{x}{2}$

$\therefore x + 2y + \dfrac{{\pi {\text{x}}}}{2} = 10$

$\Rightarrow x\left( {1 + \dfrac{\pi }{2}} \right) + 2y = 10$

$\Rightarrow 2y = 10 - x\left( {1 + \dfrac{\pi }{2}} \right)$

$\Rightarrow y = 5 - x\left( {\dfrac{1}{2} + \dfrac{\pi }{4}} \right)$

$A = xy + \dfrac{\pi }{2}{\left( {\dfrac{x}{2}} \right)^2}$

$= x\left[ {5 - x\left( {\dfrac{1}{2} + \dfrac{\pi }{4}} \right)} \right] + \dfrac{\pi }{8}{\text{x}}{x^2}$

$= 5x - {x^2}\left( {\dfrac{1}{2} + \dfrac{\pi }{4}} \right) + \dfrac{\pi }{8}{\text{x}}{x^2}$

$\therefore \dfrac{{dA}}{{dx}} = 5 - 2x\left( {\dfrac{1}{2} + \dfrac{\pi }{4}} \right) + \dfrac{\pi }{4}x$

$\dfrac{{{d^2}A}}{{d{x^2}}} =  - \left( {1 - \dfrac{\pi }{2}} \right) + \dfrac{\pi }{4} =  - 1 - \dfrac{\pi }{4}$

$\dfrac{{dA}}{{dx}} = 0$

$\Rightarrow 5 - x\left( {1 + \dfrac{\pi }{2}} \right) + \dfrac{\pi }{4}x = 0$

$\Rightarrow 5 - x - \dfrac{\pi }{4}x = 0$

$\Rightarrow x\left( {1 + \dfrac{\pi }{4}} \right) = 5$

$\Rightarrow x = \dfrac{5}{{\left( {1 + \dfrac{\pi }{4}} \right)}} = \dfrac{{20}}{{\pi  + 4}}$

$x = \dfrac{{20}}{{\pi  + 4}},\dfrac{{{d^2}A}}{{d{x^2}}} < 0.$

area is maximum when length $x = \dfrac{{20}}{{\pi  + 4}}m$. 

Now, $y = 5 - \dfrac{{20}}{{\pi  + 4}}\left( {\dfrac{{2 + \pi }}{4}} \right) = 5 - \dfrac{{5(2 + \pi )}}{{\pi  + 4}} = \dfrac{{10}}{{\pi  + 4}}m$

the required dimensions length $= \dfrac{{20}}{{\pi  + 4}}m$ and breadth $= \dfrac{{10}}{{\pi  + 4}}m$.

9. A point of the hypotenuse of a triangle is at distance $a$ and $b$ from the sides of the triangle. Show that the minimum length of the hypotenuse is ${\left( {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}}} \right)^{\dfrac{3}{2}}}$ 

Ans: $\vartriangle ABC$ right-angled at $B$. $AB = x$ and $BC = y$.

$P$ be a point on hypotenuse such that ${\text{P}}$ is at a distance of a and ${\text{b}}$ from the sides \[AB\]and \[BC\]respectively.

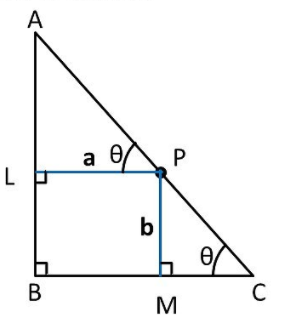
$\angle c = \theta $

$AC = \sqrt {{x^2} + {y^2}} $

$PC = b\operatorname{cosec} \theta $

$AP = a\sec \theta $

$AC = AP + PC$

$AC = b\operatorname{cosec} \theta  + a\sec \theta  \ldots ..(1)$

$\therefore \dfrac{{d(AC)}}{{d\theta }} =  - b\operatorname{cosec} \theta \cot \theta  + a\sec \theta \tan \theta $

$\therefore \dfrac{{d(AC)}}{{d\theta }} = 0$

$\Rightarrow a\sec \theta \tan \theta  = b\cos \operatorname{ec} \theta \cot \theta $

$\Rightarrow \dfrac{a}{{\cos \theta }} \cdot \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{b}{{\sin \theta }}\dfrac{{\cos \theta }}{{\sin \theta }}$

$\Rightarrow a{\sin ^3}\theta  = b{\cos ^3}\theta $

$\Rightarrow {(a)^{\dfrac{1}{3}}}\sin \theta  = {(b)^{\dfrac{1}{3}}}\cos \theta $

$\Rightarrow \tan \theta  = {\left( {\dfrac{b}{a}} \right)^{\dfrac{1}{3}}}$

$\therefore \sin \theta  = \dfrac{{{{(b)}^{\dfrac{1}{3}}}}}{{\sqrt {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}}} }}$ and $\cos \theta  = \dfrac{{{{(a)}^{\dfrac{1}{3}}}}}{{\sqrt {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}}} }}\quad  \ldots ..(2)$

clearly $\dfrac{{{d^2}(AC)}}{{d{\theta ^2}}} < 0$ when $\tan \theta  = {\left( {\dfrac{b}{a}} \right)^{\dfrac{1}{3}}}$.

the length of the hypotenuse is the maximum when $\tan \theta  = {\left( {\dfrac{b}{a}} \right)^{\dfrac{1}{3}}}$. 

Now, when $\tan \theta  = {\left( {\dfrac{b}{a}} \right)^{\dfrac{1}{3}}}$

$\tan \theta  = {\left( {\dfrac{b}{a}} \right)^{\dfrac{1}{3}}}$

$AC = \dfrac{{b\sqrt {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}}} }}{{{b^{\dfrac{1}{3}}}}} + \dfrac{{a\sqrt {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}}} }}{{{a^{\dfrac{1}{3}}}}}$

$= a\sqrt {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}}} \left( {{b^{\dfrac{2}{3}}} + {a^{\dfrac{2}{3}}}} \right)$

$= {\left( {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}}} \right)^{\dfrac{3}{2}}}$

maximum length of the hypotenuse is $= {\left( {{a^{\dfrac{2}{3}}} + {b^{\dfrac{2}{3}}}} \right)^{\dfrac{3}{2}}}$.

10. Find the points at which the function $f$ given by $f(x) = {(x - 2)^4}{(x + 1)^3}$ has

(i) local maxima

(ii) local minima

(iii) point of inflexion

Ans: $f(x) = {(x - 2)^4}{(x + 1)^3}$

$\therefore {f^\prime }(x) = 4{(x - 2)^3}{(x + 1)^3} + 3{(x + 1)^2}{(x - 2)^4}$

$= {(x - 2)^3}{(x + 1)^2}[4(x + 1) + 3(x - 2)]$

$= {(x - 2)^3}{(x + 1)^2}(7x - 2)$

${f^\prime }(x) = 0 \Rightarrow x =  - 1$ and $x = \dfrac{2}{7}$ or $x = 2$

for $x$ close to $\dfrac{2}{7}$ and to left of $\dfrac{2}{7},{f^\prime }(x) > 0$.

for $x$ close to $\dfrac{2}{7}$ and to right of $\dfrac{2}{7},{f^\prime }(x) > 0$. $x = \dfrac{2}{7}$ is point of local minima.

as the value of $x$ varies ${f^\prime }(x)$ does not changes its sign.

$x =  - 1$ is point of inflexion.

11. Find the absolute maximum and minimum values of the function $f$ given by

$f(x) = {\cos ^2}x + \sin x,x \in [0,\pi ]$

Ans: $f(x) = {\cos ^2}x + \sin x$

${f^\prime }(x) = 2\cos x( - \sin x) + \cos x$

$=  - 2\sin x\cos x + \cos x$

${f^\prime }(x) = 0{\text{ }}$

$\Rightarrow 2\sin x\cos x = \cos x \Rightarrow \cos x(2\sin x - 1) = 0$

$\Rightarrow \sin x = \dfrac{1}{2}$ or $\cos x = 0$

$\Rightarrow x = \dfrac{\pi }{6}$, or $\dfrac{\pi }{2}$ as $x \in [0,\pi ]$

$f\left( {\dfrac{\pi }{6}} \right) = {\cos ^2}\dfrac{\pi }{6} + \sin \dfrac{\pi }{6} = {\left( {\dfrac{{\sqrt 3 }}{2}} \right)^2} + \dfrac{1}{2} = \dfrac{5}{4}$

$f(0) = {\cos ^2}0 + \sin 0 = 1 + 0 = 1$

$f(\pi ) = {\cos ^2}\pi  + \sin \pi  = {( - 1)^2} + 0 = 1$

$f\left( {\dfrac{\pi }{2}} \right) = {\cos ^2}\dfrac{\pi }{2} + \sin \dfrac{\pi }{2} = 0 + 1 = 1$

absolute maximum value of $f$ is $\dfrac{5}{4}$ at $x = \dfrac{\pi }{6}$

The absolute minimum value of $f$ is 1 at $x = 0,x = \dfrac{\pi }{2}$, and $\pi $.

12. Show that the altitude of the right circular cone of maximum volume that can be inscribed in a sphere of radius $\mathrm{r}$ is $\dfrac{4 r}{3}$.

Ans: $V = \dfrac{1}{3}\pi {R^2}h$

$BC = \sqrt {{r^2} - {R^2}} $

$h = r + \sqrt {{r^2} - {R^2}} $

$\therefore V = \dfrac{1}{3}\pi {R^2}\left( {r + \sqrt {{r^2} - {R^2}} } \right) = \dfrac{1}{3}\pi {R^2}r + \dfrac{1}{3}\pi {R^2}\sqrt {{r^2} - {R^2}} $

$\therefore \dfrac{{dV}}{{dR}} = \dfrac{2}{3}\pi Rr + \dfrac{{2\pi }}{3}\pi R\sqrt {{r^2} - {R^2}}  + \dfrac{{{R^2}}}{3} \cdot \dfrac{{( - 2R)}}{{2\sqrt {{r^2} - {R^2}} }}$

$= \dfrac{2}{3}\pi Rr + \dfrac{{2\pi }}{3}\pi R\sqrt {{r^2} - {R^2}}  - \dfrac{{{R^3}}}{{3\sqrt {{r^2} - {R^2}} }}$

$= \dfrac{2}{3}\pi Rr + \dfrac{{2\pi Rr\left( {{r^2} - {R^2}} \right) - \pi {R^3}}}{{3\sqrt {{r^2} - {R^2}} }}$

$= \dfrac{2}{3}\pi Rr + \dfrac{{2\pi R{r^2} - 3\pi R{r^3}}}{{3\sqrt {{r^2} - {R^2}} }}$

$\dfrac{{dV}}{{d{R^2}}} = 0$

$\Rightarrow \dfrac{{2\pi rR}}{3} = \dfrac{{3\pi {R^2} - 2\pi R{r^2}}}{{3\sqrt {{r^2} - {R^2}} }}$

$\Rightarrow 2{\text{r}}\sqrt {{r^2} - {R^2}}  = 3{R^2} - 2{r^2}$

$\Rightarrow 4{r^2}\left( {{r^2} - {R^2}} \right) = {\left( {3{R^2} - 2{r^2}} \right)^2}$

$\Rightarrow 14{r^4} - 4{r^2}{R^2} = 9{R^4} + 4{r^4} - 12{R^2}{r^2}$

$\Rightarrow 9{R^4} - 8{r^2}{R^2} = 0$

$\Rightarrow 9{R^2} = 8{r^2}$

$\Rightarrow {R^2} = \dfrac{{8{r^2}}}{9}$

$\dfrac{{{d^2}V}}{{d{R^2}}} = \dfrac{{2\pi r}}{3} + \dfrac{{3\sqrt {{r^2} - {R^2}} \left( {2\pi {r^2} - 9\pi {R^2}} \right) - \left( {2\pi {R^3} - 3\pi {R^3}} \right)( - 6R)\dfrac{1}{{2{{\sqrt {{r^2} - R} }^2}}}}}{{9\left( {{r^2} - {R^2}} \right)}}$

$= \dfrac{{2\pi r}}{3} + \dfrac{{3\sqrt {{r^2} - {R^2}} \left( {2\pi {r^2} - 9\pi {R^2}} \right) - \left( {2\pi {R^3} - 3\pi {R^3}} \right)(3R)\dfrac{1}{{2{{\sqrt {{r^2} - R} }^2}}}}}{{9\left( {{r^2} - {R^2}} \right)}}$

when ${R^2} = \dfrac{{8{r^2}}}{9},\dfrac{{{d^2}V}}{{d{R^2}}} < 0$.

volume is the maximum when ${R^2} = \dfrac{{8{r^2}}}{9}$. ${R^2} = \dfrac{{8{r^2}}}{9}$, 

height of the cone $= r + \sqrt {{r^2} - \dfrac{{8{R^2}}}{9}}  = r + \sqrt {\dfrac{{{r^2}}}{9}}  = r + \dfrac{r}{3} = \dfrac{{4r}}{3}$

13. Let f be a function defined on $\left[ a,b \right]$such that ${{f}^{'}}(x)>0$ for all $x\in (a,b)$. Then prove that f is an increasing function on (a, b).

Ans: Consider I be the interval (a, b)

Given that ${{f}^{'}}(x)>0$for all x in an interval I. Consider ${{x}_{1}},{{x}_{1}},\in $I with ${{x}_{1}}<{{x}_{2}}$.

By Lagrange’s Mean Value Theorem, we have, 

$\frac{f({{x}_{2}})-f({{x}_{1}})}{{{x}_{2}}-{{x}_{1}}}={{f}^{'}}(c)\,$where ${{x}_{1}}<c<{{x}_{2}}$

$\Rightarrow f({{x}_{2}})-f({{x}_{1}})=({{x}_{2}}-{{x}_{1}}){{f}^{'}}(c)$where ${{x}_{1}}<c<{{x}_{2}}$

Now ${{x}_{1}}<{{x}_{2}}$

$\Rightarrow {{x}_{2}}-{{x}_{1}}>0$……….(1)

 Also, ${{f}^{'}}(x)>0$for all $x$ in an interval I

$\Rightarrow {{f}^{'}}(c)>0$

From equation (1), $f({{x}_{2}})-f({{x}_{1}})>0$

$\Rightarrow f({{x}_{1}})<f({{x}_{2}})$

Thus, for every pair of points ${{x}_{1}},{{x}_{1}},\in $I with ${{x}_{1}}<{{x}_{2}}$

$\Rightarrow f({{x}_{1}})<f({{x}_{2}})$

Therefore, f(x) is strictly increasing in I.

14. Show that the height of the cylinder of maximum volume that can be inscribed in a sphere of radius $R$ is $\dfrac{{2R}}{{\sqrt 3 }}$, also find the maximum volume.

Ans: $h = 2\sqrt {{R^2} - {r^2}} $

$V = \pi {r^2}h = 2\pi {r^2}\sqrt {{R^2} - {r^2}} $

$\therefore \dfrac{{dV}}{{dr}} = 4\pi r\sqrt {{R^2} - {r^2}}  + \dfrac{{2\pi {r^2}( - 2r)}}{{2\sqrt {{R^2} - {r^2}} }}$

$= 4\pi r\sqrt {{R^2} - {r^2}}  - \dfrac{{2\pi {r^3}}}{{\sqrt {{R^2} - {r^2}} }}$

$= \dfrac{{4\pi r\left( {{R^2} - {r^2}} \right) - 2\pi {r^3}}}{{\sqrt {{R^2} - {r^2}} }}$

$= \dfrac{{4\pi r{R^2} - 6\pi {r^3}}}{{\sqrt {{R^2} - {r^2}} }}$

Now, $\dfrac{{dV}}{{dr}} = 0 \Rightarrow 4\pi r{R^2} - 6\pi {r^3} = 0$

$\Rightarrow {r^2} = \dfrac{{2{R^2}}}{3}$

$\dfrac{{{d^2}V}}{{d{r^2}}} = \dfrac{{\sqrt {{R^2} - {r^2}} \left( {4\pi {R^2} - 18\pi {r^2}} \right) - \left( {4\pi r{R^2} - 6\pi {r^3}} \right)\dfrac{{( - 2r)}}{{2\sqrt {{R^2} - {r^2}} }}}}{{\left( {{R^2} - {r^2}} \right)}}$

$= \dfrac{{\left( {{R^2} - {r^2}} \right)\left( {4\pi {R^2} - 18\pi {r^2}} \right) + r\left( {4\pi r{R^2} - 6\pi {r^3}} \right)}}{{{{\left( {{R^2} - {r^2}} \right)}^{\dfrac{3}{2}}}}}$

$= \dfrac{{4\pi {R^4} - 22\pi {r^2}{R^2} + 12\pi {r^4} + 4\pi {r^2}{R^2}}}{{{{\left( {{R^2} - {r^2}} \right)}^{\dfrac{3}{2}}}}}$

${r^2} = \dfrac{{2{R^2}}}{3},\dfrac{{{d^2}V}}{{d{r^2}}} < 0.$

volume is maximum when ${r^2} = \dfrac{{2{R^2}}}{3}$. ${r^2} = \dfrac{{2{R^2}}}{3}$.

height of the cylinder is $2\sqrt {{R^2} - \dfrac{{2{R^2}}}{3}}  = 2\sqrt {\dfrac{{{R^2}}}{3}}  = \dfrac{{2R}}{{\sqrt 3 }}$.

volume of the cylinder is maximum when height of cylinder is $\dfrac{{2R}}{{\sqrt 3 }}$

15. Show that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height ${\text{h}}$ and semi veritical angle a is one-third that of the cone and the greatest volume of cylinder is $\dfrac{4}{{27}}\pi {h^2}{\tan^2}a$.

Ans:

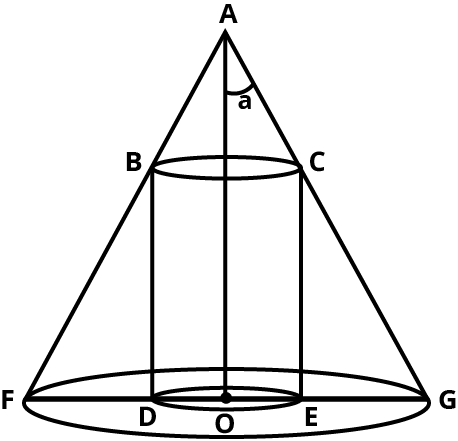
$r = h\tan a$

since $\Delta AOG$ is similar to $\Delta CEG$,

$\dfrac{{AO}}{{OG}} = \dfrac{{CE}}{{EG}}$

$\Rightarrow \dfrac{h}{r} = \dfrac{H}{{r - R}}$

$\Rightarrow H = \dfrac{h}{r}(r - R) = \dfrac{h}{{h\tan a}}(h\tan a - R) = \dfrac{1}{{\tan a}}(h\tan a - R)$

volume of the cylinder is $V = \pi {R^2}H = \dfrac{{\pi {R^2}}}{{\tan a}}(h\tan a - R)$

$= \pi {R^2}h - \dfrac{{\pi {R^3}}}{{\tan a}}$

$\therefore \dfrac{{dV}}{{dR}} = 2\pi Rh\dfrac{{3\pi {R^2}}}{{\tan a}}$

$\dfrac{{dV}}{{dR}} = 0$

$\Rightarrow 2\pi Rh = \dfrac{{3\pi {R^2}}}{{\tan a}}$

$\Rightarrow 2h\tan a = 3R$

$\Rightarrow R = \dfrac{{2h}}{3}\tan a$

$\dfrac{{{d^2}V}}{{d{R^2}}} = 2\pi Rh - \dfrac{{6\pi R}}{{\tan a}}$

And, for $R = \dfrac{{2h}}{3}\tan a$, we have:

$\dfrac{{{d^2}V}}{{d{R^2}}} = 2\pi h - \dfrac{{6\pi }}{{\tan a}}\left( {\dfrac{{2h}}{3}\tan a} \right) = 2\pi h - 4\pi h =  - 2\pi h < 0$

volume of the cylinder is greatest when $R = \dfrac{{2h}}{3}\tan a$. $R = \dfrac{{2h}}{3}\tan a,H = \dfrac{1}{{\tan a}}\left( {h\tan a - \dfrac{{2h}}{3}\tan a} \right) = \dfrac{1}{{\tan a}}\left( {\dfrac{{h\tan a}}{3}} \right) = \dfrac{h}{3}$.

the maximum volume of cylinder can be obtained as

$\pi {\left( {\dfrac{{2h}}{3}\tan a} \right)^2}\left( {\dfrac{h}{3}} \right) = \pi \left( {\dfrac{{4{h^2}}}{9}{{\tan }^2}a} \right)\left( {\dfrac{h}{3}} \right) = \dfrac{4}{{27}}\pi {h^3}{\tan ^2}a$

NCERT Solutions for Chapter 6 Maths Class 12 

6.1 Introduction

In class 12 Maths chapter 6, the introduction part will be a recap of the last chapter where you got acquainted with concepts of the derivative of a composite function, implicit functions, logarithmic functions, inverse trigonometric functions, and exponential functions. 

In this chapter, you will learn how the application of derivatives works in different disciplines like social science, engineering, science, etc. This chapter will go through how to apply the application of derivatives to find out the rate of change of quantities.

6.2 Rate of Change of Quantities

In the chapter, application of derivatives class 12 NCERT solutions - you would brush up on all the learnings from the previous class. You would be reminded that to represent the rate of change of quantity with respect to another, we use the notation dy/dx, this means that y changes when x is changed.

You would further expand this concept to find out if changes in x and y are dependent on a 3rd variable (say z)  i.e. x= f(z) and y=g(z), The Chain rule can be applied as shown below:

dy/dx = (dy/dz)/(dx/dz), given dx/dz <> =0

6.3 Increasing and Decreasing Functions

In this section of Chapter 6 Maths Class 12, you will understand what is meant by increasing and decreasing functions and how to determine whether a function is increasing or decreasing in a given range by using differentiation. You would define that a function is increasing in a range if the first derivative is positive in that range. Similarly, you would learn that a function is decreasing in a range if the derivative is negative in that range.

6.6 Maxima and Minima

This unit of NCERT class 12 application of derivatives solutions describes the minimum and maximum values of a function in the form of derivatives. You will learn about turning points on the graph of a function where the graph reaches its highest point and the lowest point locally in a domain. You would understand how these points can be used to sketch the graph of a function.

Overview of Deleted Syllabus for CBSE Class 12 Maths Chapter 6

Class 12 Maths Chapter 6: Exercises Breakdown

Conclusion 

NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives on Vedantu highlights the chapter's importance in calculus, a critical area in Class 12 mathematics. This chapter covers key concepts such as rate of change, increasing and decreasing functions, tangents and normals, approximations, and maxima and minima. These topics are essential for understanding and solving practical problems using derivatives. For exam preparation, students should focus on mastering these concepts and practicing various problems provided in the exercises. In previous years, this chapter has featured multiple questions in the CBSE exams, indicating its significant weight. Specifically, exercises from this chapter include questions ranging from short answers to long-form problems and multiple-choice questions (MCQs), ensuring comprehensive coverage of the applications of derivatives.

Other Related Links for CBSE Class 12 Maths Chapter 6

NCERT Solutions for Class 12 Maths | Chapter-wise List

Given below are the chapter-wise NCERT 12 Maths solutions PDF. Using these chapter-wise class 12th maths ncert solutions, you can get clear understanding of the concepts from all chapters.

Related Links for NCERT Class 12 Maths in Hindi

Explore these essential links for NCERT Class 12 Maths in Hindi, providing detailed solutions, explanations, and study resources to help students excel in their mathematics exams.

Important Related Links for NCERT Class 12 Maths