NCERT Exemplar for Class 12 Maths - Application Of Derivatives - Free PDF Download

Solved Examples

Short Answer Type (S.A.)

1. For the curve y =5x-2x3 if x increases at the rate of 2 units/sec, then how fast is the slope of curve changing when x = 3?

Ans: Here x is increasing at the rate of 2unit/sec, so we can write this as $\frac{\text{dx}}{\text{dt}}=2$

Now we find the slope of the curve which is $\frac{\text{dy}}{\text{dx}}\text{=5-6}{{\text{x}}^{\text{2}}}$

We have asked to find the change in slope which can we written mathematically as:

 $\frac{\text{d}}{\text{dt}}\left( \frac{\text{dy}}{\text{dx}} \right)\text{= }\!\!~\!\!\text{ -12x}\frac{\text{dx}}{\text{dt}}$                $\left[ \frac{\text{dx}}{\text{dt}}=2 \right]$(given)

$\Rightarrow \frac{\text{d}}{\text{dt}}\left( \frac{\text{dy}}{\text{dx}} \right)\text{= }\!\!~\!\!\text{ -1}2\times 3\times 2$

$\Rightarrow \frac{\text{d}}{\text{dt}}\left( \frac{\text{dy}}{\text{dx}} \right)\text{= }\!\!~\!\!\text{ -72}$unit/sec

-sign represents that slope is decreasing. Hence the slope will decrease at the rate of 72unit/sec.

2. Water is dripping out from a conical funnel of semi-vertical angle $\frac{4}{\mathbf{\pi }}$at the uniform rate of 2 cm2 /sec in the surface area, through a tiny hole at the vertex of the bottom. When the slant height of the cone is 4 cm, find the rate of decrease of the slant height of water. 

Ans: 

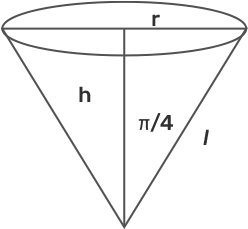
Given- $\frac{\text{ds}}{\text{dt}}=2\text{c}{{\text{m}}^{2}}/\text{sec}$Where s= surface area

and $\frac{\text{ds}}{\text{dt}}$= decrease in surface area

We know that the surface area of cone is $\text{s}=\text{ }\!\!\pi\!\!\text{ rl}$

Now we reform this relation in terms of  s and $\text{l}$only.

So, $\text{sin}\frac{\text{ }\!\!\pi\!\!\text{ }}{4}=\frac{\text{r}}{\text{l}}$

$\Rightarrow \text{r}=\frac{\text{l}}{\sqrt{2}}$

Now, $\text{s}=\frac{\text{ }\!\!\pi\!\!\text{ }{{\text{l}}^{2}}}{\sqrt{2}}$

$\Rightarrow \frac{\text{ds}}{\text{dt}}=\sqrt{2}\text{ }\!\!\pi\!\!\text{ l}\frac{\text{dl}}{\text{dt}}$

When $\text{l}=4$, $\frac{\text{ds}}{\text{dt}}=4\sqrt{2}\text{ }\!\!\pi\!\!\text{ }\frac{\text{dl}}{\text{dt}}$.

$\Rightarrow \frac{\text{dl}}{\text{dt}}=\frac{2}{4\sqrt{2}\text{ }\!\!\pi\!\!\text{ }}$    [On substituting the value of $\frac{\text{ds}}{\text{dt}}=2$]

$\Rightarrow \frac{\text{dl}}{\text{dt}}=\frac{\sqrt{2}}{4\text{ }\!\!\pi\!\!\text{ }}$cm/sec

3. Find the angle of intersection of the curves ${{\mathbf{y}}^{2}}=\mathbf{x}$and $\mathbf{y}={{\mathbf{x}}^{2}}$.

Ans: First we find the intersection points of the given curve and then find the angle between the slope of curves on the intersection points. So first we solve both the equations:

${{\text{y}}^{2}}=\text{x}$-------(1)

$\text{y}={{\text{x}}^{2}}$-------(2)

From eq. 1 and 2 

${{\text{x}}^{4}}=\text{x}\Rightarrow {{\text{x}}^{4}}-\text{x}=0$

$\Rightarrow \text{x}\left( {{\text{x}}^{3}}-1 \right)=0$

$\Rightarrow \text{x}=0,\text{ }\!\!~\!\!\text{ x}=1$Now putting these values in equation 2 we get the value of y as

$\Rightarrow \text{y}=0,\text{y}=1\text{ }\!\!~\!\!\text{ }$Hence the intersection points (0,0) and (1,1)

Now slope of tangent on curve ${{\text{y}}^{2}}=\text{x}$ is $2\text{y}\frac{\text{dy}}{\text{dx}}=1\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{1}{2\text{y}}$

and slope of tangent on curve ${{\text{x}}^{2}}=\text{y }\!\!~\!\!\text{ }$is $\frac{\text{dy}}{\text{dx}}=2\text{x}$

At (0,0) slope of ${{\text{y}}^{2}}=\text{x}$is $\frac{\text{dy}}{\text{dx}}=\infty $ which means the tangent on this curve is parallel to y-axis and slope of tangent on curve $\text{y}={{\text{x}}^{2}}$is $\frac{\text{dy}}{\text{dx}}=0$which is parallel to x-axis. That means the tangents are perpendicular on each other.

Hence angle of intersection at point (0,0) =$\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$

At point (1,1) slope of tangent on curve ${{\text{y}}^{2}}=\text{x}$ $\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{1}{2}$and that of ${{\text{x}}^{2}}=\text{y}\Rightarrow \frac{\text{dy}}{\text{dx}}=2$

Angle b/w two lines $\text{tan }\!\!\theta\!\!\text{ }=\left| \frac{{{\text{m}}_{1}}-{{\text{m}}_{2}}}{1+{{\text{m}}_{1}}{{\text{m}}_{2}}} \right|$

$\Rightarrow \text{tan }\!\!\theta\!\!\text{ }=\left| \frac{2-\frac{1}{2}}{1+2.\frac{1}{2}} \right|$

$\Rightarrow \text{tan }\!\!\theta\!\!\text{ }=\frac{3}{4}$

$\Rightarrow \text{ }\!\!\theta\!\!\text{ }=\text{ta}{{\text{n}}^{-1}}\left( \frac{3}{4} \right)$

4. Prove that the function f(x) = tanx – 4x is strictly decreasing on $\left( \frac{-\mathbf{\pi }}{3},\frac{\mathbf{\pi }}{3} \right)$.

Ans: We know that a function is strictly decreasing if f′(x)<0 in the given interval.

Given: $\frac{\text{- }\!\!\pi\!\!\text{ }}{\text{3}}\text{x}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{3}}$

Here f′(x)=$\text{se}{{\text{c}}^{2}}\text{x}-4$

For given interval

 $1<\text{secx}<2$

$\Rightarrow 1<\text{se}{{\text{c}}^{2}}\text{x}<4$

$\Rightarrow -3<\text{se}{{\text{c}}^{2}}\text{x}-4<0$

Thus for $\frac{-\text{ }\!\!\pi\!\!\text{ }}{3}<\text{x}<\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$f′(x)<0 that means function is strictly decreasing in the given interval.

5. Determine for which values of x, the function $\mathbf{y}={{\mathbf{x}}^{4}}-\frac{4{{\mathbf{x}}^{3}}}{3}$is increasing and for which values, it is decreasing. 

Ans: Here we first find the derivative of the given function as:

$\frac{\text{dy}}{\text{dx}}=4{{\text{x}}^{3}}-4{{\text{x}}^{2}}$

Now we put this value equal to 0 for finding the critical points such as:

$\Rightarrow 4{{\text{x}}^{3}}-4{{\text{x}}^{2}}=0$

$\Rightarrow 4{{\text{x}}^{2}}\left( \text{x}-1 \right)=0$

$\Rightarrow \text{x}=0,\text{x}=1$

Since f’(x) is continuous in the interval $\left( -\infty ,0 \right]$and $\left[ -\infty ,1 \right]$and f’(x)<0 in $\left( -\infty ,0 \right)\cup \left( 0,1 \right)$ Hence the function is decreasing in $\left( -\infty ,1 \right]$ and will be increasing $\left[ 1,\infty  \right)$.

6. Show that the function $\mathbf{f}\left( \mathbf{x} \right)=4{{\mathbf{x}}^{3}}-18{{\mathbf{x}}^{2}}+27\mathbf{x}-7~$has neither maxima nor minima. 

Ans: $\text{f}\left( \text{x} \right)=4{{\text{x}}^{3}}-18{{\text{x}}^{2}}+27\text{x}-7$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=12{{\text{x}}^{2}}-36\text{x}+27$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=3\left( 4{{\text{x}}^{2}}-12\text{x}+9 \right)$

For critical point $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\Rightarrow \left( 4{{\text{x}}^{2}}-12\text{x}+9 \right)=0$

$\Rightarrow {{\left( 2\text{x}-3 \right)}^{2}}=0$

$\Rightarrow \text{x}=\frac{3}{2}$ This is the critical point.

\[\text{f  }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=3\left( 8\text{x}-12 \right)\]   at $\text{x}=\frac{3}{2}\text{f  }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \frac{3}{2} \right)=3\left( 12-12 \right)=0$

$\text{f  }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \frac{3}{2} \right)=3\left( 8 \right)$

Here at  $\text{x}=\frac{3}{2}$The 2nd and 3rd derivative is constant, which means the function's value is not changing . Hence we can say the function neither has maxima nor minima.

7. Using differentials, find the approximate value of $\sqrt{0.082}$

Ans: Let $\text{f}\left( \text{x} \right)=\sqrt{\text{x}}$

We know that,

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{\text{f}\left( \text{x}+\text{ }\!\!\Delta\!\!\text{ x} \right)-\text{f}\left( \text{x} \right)}{\text{ }\!\!\Delta\!\!\text{ x}}$

Here we write 0.082 as = 0.09-0.008 =$\left( \text{x}+\text{ }\!\!\Delta\!\!\text{ x} \right),$ on comparing we get x=0.09 and $\text{ }\!\!\Delta\!\!\text{ x}=-0.008$

$\Rightarrow \text{f}\left( \text{x}+\text{ }\!\!\Delta\!\!\text{ x} \right)=\text{f}\left( \text{x} \right)+\text{ }\!\!\Delta\!\!\text{ x}.\text{ }\!\!~\!\!\text{ f }\!\!'\!\!\text{ }\left( \text{x} \right)$

$\Rightarrow \text{f}\left( 0.09-0.008 \right)=\text{f}\left( 0.09 \right)+\left( -0.008 \right).\text{ }\!\!~\!\!\text{ f }\!\!'\!\!\text{ }\left( 0.09 \right)$

$\Rightarrow \sqrt{0.082}=\sqrt{0.09}+\left( -0.008 \right).\text{ }\!\!~\!\!\text{ }\frac{1}{2\sqrt{0.09}}$                   $\left[ \text{f}\left( \text{x} \right)=\sqrt{\text{x }\!\!~\!\!\text{ }}\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{1}{2\sqrt{\text{x}}} \right]$

$\Rightarrow \sqrt{0.082}=0.3-\frac{0.008}{0.6}$

$=0.3-0.0133=0.2867$

8. Find the condition for the curves $\frac{{{\mathbf{x}}^{2}}}{{{\mathbf{a}}^{2}}}-\frac{{{\mathbf{y}}^{2}}}{{{\mathbf{b}}^{2}}}=1;\mathbf{xy}={{\mathbf{c}}^{2}}$ to intersect orthogonally. 

Ans: For the curves becoming orthogonal the slope of tangents on the curves should be perpendicular like ${{\text{m}}_{1}}\times {{\text{m}}_{2}}=-1$. 

Let the curves intersect at point(h,k). So now we find the slope of tangents on both the curves,

$\frac{{{\text{x}}^{2}}}{{{\text{a}}^{2}}}-\frac{{{\text{y}}^{2}}}{{{\text{b}}^{2}}}=1$

$\Rightarrow \frac{2\text{x}}{{{\text{a}}^{2}}}-\frac{2\text{y}}{{{\text{b}}^{2}}}\frac{\text{dy}}{\text{dx}}=0\text{ }\!\!~\!\!\text{ }$                   [On differentiating both sides]

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{{{\text{b}}^{2}}}{{{\text{a}}^{2}}}\frac{\text{x}}{\text{y}}$

$\Rightarrow {{\text{m}}_{1}}=\frac{{{\text{b}}^{2}}}{{{\text{a}}^{2}}}\frac{\text{h}}{\text{k}}$ 

Now using the curve $\text{xy}={{\text{c}}^{2}}$

$\Rightarrow \text{y}+\text{x}\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{-\text{y}}{\text{x}}$

$\Rightarrow {{\text{m}}_{2}}=\frac{-\text{k}}{\text{h}}$

For orthogonality the condition is  ${{\text{m}}_{1}}\times {{\text{m}}_{2}}=-1$

${{\text{m}}_{1}}\times {{\text{m}}_{2}}=-1$

$\Rightarrow \frac{{{\text{b}}^{2}}}{{{\text{a}}^{2}}}\frac{\text{h}}{\text{k}}\times \frac{-\text{k}}{\text{h}}=-1$

$\Rightarrow \frac{{{\text{b}}^{2}}}{{{\text{a}}^{2}}}=1$

$\Rightarrow {{\text{a}}^{2}}-{{\text{b}}^{2}}=0$

9. Find all the points of local maxima and local minima of the function $\mathbf{f}\left( \mathbf{x} \right)=-\frac{3}{4}{{\mathbf{x}}^{4}}-8{{\mathbf{x}}^{3}}-\frac{45}{2}{{\mathbf{x}}^{2}}+105$.

Ans: $\text{f}\left( \text{x} \right)=-\frac{3}{4}{{\text{x}}^{4}}-8{{\text{x}}^{3}}-\frac{45}{2}{{\text{x}}^{2}}+105$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=-3{{\text{x}}^{3}}-24{{\text{x}}^{2}}-45\text{x}$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=-3\text{x}\left( {{\text{x}}^{2}}+8\text{x}+15 \right)$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=-3\text{x}\left( \text{x}+5 \right)\left( \text{x}+3 \right)$

Now we find the critical points as $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\Rightarrow -3\text{x}\left( \text{x}+5 \right)\left( \text{x}+3 \right)=0$

$\Rightarrow \text{x}=0,\text{x}=-5,\text{x}=-3$

For Finding maxima and minima we find the second derivative as:

$\Rightarrow \text{f}''\left( \text{x} \right)=-9{{\text{x}}^{2}}-48\text{x}-45$

On substituting x=0,-5,-3 in f’’(x) the function will have local maxima if f’’(x)

<0 and will have local minima if f’’(x)>0.

$\Rightarrow \text{f}''\left( 0 \right)=-45<0$. Therefore at x=0 function has local maxima

$\Rightarrow \text{f}''\left( -5 \right)=-9{{\left( -5 \right)}^{2}}-48\left( -5 \right)-45=-30<0$. Therefore at x=-5 function has local maxima.

$\Rightarrow \text{f}''\left( -3 \right)=-9{{\left( -3 \right)}^{2}}-48\left( -3 \right)-45=18>0$. Therefore at x=-3 function has local minima.

10. Show that the local maximum value of $\mathbf{x}+\frac{1}{\mathbf{x}}$ is less than the local minimum value.

Ans: Given $\text{f}\left( \text{x} \right)=\text{x}+\frac{1}{\text{x}}$

For finding the local maxima and minima we first find out the first derivative, after solving the f’(x) we get critical points and for those critical points we check the second derivative of the function whether it is negative or positive.

$\text{f}\left( \text{x} \right)=\text{x}+\frac{1}{\text{x}}$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=1-\frac{1}{{{\text{x}}^{2}}}$

Now, $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\Rightarrow 1-\frac{1}{{{\text{x}}^{2}}}=0$

$\Rightarrow \text{x}=\pm 1$

$\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{\text{d}}{\text{dx}}\left( \text{f}\left( \text{x} \right) \right)$

 $\Rightarrow \text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{2}{{{\text{x}}^{3}}}$

 $\Rightarrow \text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( 1 \right)=\frac{2}{1}=2>0$Therefore the function has local minima at x=1and the local minimum value is $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( 1 \right)=2$

$\Rightarrow \text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( -1 \right)=\frac{2}{-1}=-2<0$ Therefore the function has local maxima at x=-1 and the local maximum value is $\text{f}\left( -1 \right)=-2$

Hence Local maximum value(-2) is less than local minimum value(2).

Long Answer Type (L.A.)

11. Water is dripping out at a steady rate of 1 cu cm/sec through a tiny hole at the vertex of the conical vessel, whose axis is vertical. When the slant height of water in the vessel is 4 cm, find the rate of decrease of slant height, where the vertical angle of the conical vessel is $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$.

Ans: 

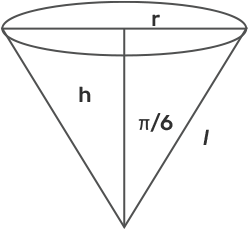
Here we are given  that the water is dripping out that means = $\frac{\text{dv}}{\text{dt}}=1\text{c}{{\text{m}}^{3}}/\text{sec}.\text{ }\!\!~\!\!\text{ }$and we have to find out $\frac{\text{dl}}{\text{dt}}=?$

We know that volume of a cone $\text{V}=\frac{1}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}\text{h}$-------------(1)

From the figure:

$\text{cos}\frac{\text{ }\!\!\pi\!\!\text{ }}{6}=\frac{\text{h}}{\text{l}}$

$\Rightarrow \text{h}=\text{l }\!\!~\!\!\text{ cos}30=\frac{\sqrt{3}\text{l}}{2}$---(2)

$\text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\frac{\text{r}}{\text{l}}$

$\Rightarrow \text{r}=\text{l }\!\!~\!\!\text{ sin}30=\frac{\text{l}}{2}$------(3)

Putting the values of r & h in eq. 1 

$\text{V}=\frac{1}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}\text{h}$

$\Rightarrow \text{V}=\frac{1}{3}\text{ }\!\!\pi\!\!\text{ }{{\left( \frac{\text{l}}{2} \right)}^{2}}\left( \frac{\sqrt{3}\text{l}}{2} \right)$

$\Rightarrow \frac{\text{dV}}{\text{dt}}=\frac{1}{3}\text{ }\!\!\pi\!\!\text{ }\frac{\sqrt{3}}{8}3{{\text{l}}^{2}}.\frac{\text{dl}}{\text{dt}}$

$\Rightarrow 1=\frac{\sqrt{3}\text{ }\!\!\pi\!\!\text{ }}{8}{{\left( 4 \right)}^{2}}.\text{ }\!\!~\!\!\text{ }\frac{\text{dl}}{\text{dt}}$

$\Rightarrow \text{ }\!\!~\!\!\text{ }\frac{\text{dl}}{\text{dt}}=\frac{1}{2\sqrt{3}\text{ }\!\!\pi\!\!\text{ }}\text{cm}/\text{sec}$

Therefore, the rate of decrease of slant height is $\Rightarrow \text{ }\!\!~\!\!\text{ }\frac{\text{dl}}{\text{dt}}=\frac{1}{2\sqrt{3}\text{ }\!\!\pi\!\!\text{ }}\text{cm}/\text{sec}$.

12. Find the equation of all the tangents to the curve $\mathbf{y}=\mathbf{cos}\left( \mathbf{x}+\mathbf{y} \right)$, –2π ≤ x ≤ 2π, that is parallel to the line $\mathbf{x}+2\mathbf{y}=0$.

Ans: 

Given: $\text{y}=\text{cos}\left( \text{x}+\text{y} \right)$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=-\text{sin}\left( \text{x}+\text{y} \right)\left\{ 1+\frac{\text{dy}}{\text{dx}} \right\}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}\left[ 1+\text{sin}\left( \text{x}+\text{y} \right) \right]=-\text{sin}\left( \text{x}+\text{y} \right)$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{-\text{sin}\left( \text{x}+\text{y} \right)}{\left[ 1+\text{sin}\left( \text{x}+\text{y} \right) \right]}$

This is the slope of the tangent to the given curve.

Now we have a line $\text{x}+2\text{y}=0$whose slope is $\text{m}=\frac{-1}{2}$and we know that if two lines are parallel then their slopes are equal. In the problem we are given that the tangent line is parallel to the $\text{x}+2\text{y}=0$.

Since we equate the slopes of line and tangent as:

$\frac{-\text{sin}\left( \text{x}+\text{y} \right)}{\left[ 1+\text{sin}\left( \text{x}+\text{y} \right) \right]}=\frac{-1}{2}$

$\Rightarrow -2\text{sin}\left( \text{x}+\text{y} \right)=-1-\text{sin}\left( \text{x}+\text{y} \right)$

$\Rightarrow \text{sin}\left( \text{x}+\text{y} \right)=1------\left( 1 \right)$ and $\text{y}=\text{cos}\left( \text{x}+\text{y} \right)\text{ }\!\!~\!\!\text{ }\left( \text{Given} \right)$-------------(2)

After squaring  on both side in eq. 1 and eq.2 and adding them

$\text{si}{{\text{n}}^{2}}\left( \text{x}+\text{y} \right)+\text{co}{{\text{s}}^{2}}\left( \text{x}+\text{y} \right)=1+{{\text{y}}^{2}}\text{ }\!\!~\!\!\text{ }$

$\Rightarrow 1=1+{{\text{y}}^{2}}$

$\Rightarrow \text{y}=0$

Now putting this value in eq.2 

$\Rightarrow \text{cosx}=0$

$\Rightarrow \text{x}=\left( 2\text{n}+1 \right)\frac{\text{ }\!\!\pi\!\!\text{ }}{2}\text{where }\!\!~\!\!\text{ n}=0,\pm 1,\pm 2.....$

Given that $-2\text{ }\!\!\pi\!\!\text{ }\le \text{x}\le 2\text{ }\!\!\pi\!\!\text{ }$. So we select only those values of x which belong into the given range. Thus $\text{x}=\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{2},\pm \frac{3\text{ }\!\!\pi\!\!\text{ }}{2}$but $\text{x}=-\frac{\text{ }\!\!\pi\!\!\text{ }}{2},\frac{3\text{ }\!\!\pi\!\!\text{ }}{2}$ does not satisfy eq. 1

Hence the points are $\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{2},0 \right),\left( \frac{-3\text{ }\!\!\pi\!\!\text{ }}{2},0 \right).$

Now the equation of tangent passing through the point $\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{2},0 \right)$and having slope $\frac{-1}{2}$is $\left( \text{y}-0 \right)=\frac{-1}{2}\left( \text{x}-\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)\Rightarrow 2\text{x}+4\text{y}-\text{ }\!\!\pi\!\!\text{ }=0$ and equation of tangent passing through the point $\left( \frac{-3\text{ }\!\!\pi\!\!\text{ }}{2},0 \right)$and having slope $\frac{-1}{2}$ is 

$\left( \text{y}-0 \right)=\frac{-1}{2}\left( \text{x}+\frac{3\text{ }\!\!\pi\!\!\text{ }}{2} \right)\Rightarrow 2\text{x}+4\text{y}+3\text{ }\!\!\pi\!\!\text{ }=0$.

13. Find the angle of intersection of the curves ${{\mathbf{y}}^{2}}=4\mathbf{ax}$ and ${{\mathbf{x}}^{2}}=4\mathbf{by}$.

Ans: Given ${{\text{y}}^{2}}=4\text{ax}$& ${{\text{x}}^{2}}=4\text{by}$

The angle of intersection of the curve means the angle between the tangents on both curves. First we find the intersection point for both the curves.

${{\left( \frac{{{\text{x}}^{2}}}{4\text{b}} \right)}^{2}}=4\text{ax}$

$\Rightarrow {{\text{x}}^{4}}=64\text{a}{{\text{b}}^{2}}\text{x}$

$\Rightarrow {{\text{x}}^{4}}-64\text{a}{{\text{b}}^{2}}\text{x}=0$

$\Rightarrow \text{x}\left( {{\text{x}}^{3}}-64\text{a}{{\text{b}}^{2}} \right)=0$

$\Rightarrow \text{x}=0,\text{ }\!\!~\!\!\text{ x}=4{{\text{a}}^{\left( \frac{1}{3} \right)}}{{\text{b}}^{\left( \frac{2}{3} \right)}}^{{}}$

Substituting these values in ${{\text{y}}^{2}}=4\text{ax}$we get $\text{y}=0,\text{ }\!\!~\!\!\text{ y}=4{{\text{a}}^{\frac{2}{3}}}{{\text{b}}^{\frac{1}{3}}}^{{}}$. Thus the intersection points are $\left( 0,0 \right)\text{ }\!\!~\!\!\text{ }\And {{(4{{\text{a}}^{\left( \frac{1}{3} \right)}}{{\text{b}}^{\left( \frac{2}{3} \right)}}^{{}},4{{\text{a}}^{\frac{2}{3}}}{{\text{b}}^{\frac{1}{3}}})}^{{}}}$

${{\text{y}}^{2}}=4\text{ax}$

$\Rightarrow 2\text{y}\frac{\text{dy}}{\text{dx}}=4\text{a}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{2\text{a}}{\text{y}}$

And ${{\text{x}}^{2}}=4\text{by}$

$\Rightarrow 2\text{x}=4\text{b}\frac{\text{dy}}{\text{dx}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{\text{x}}{2\text{b}}$

At (0,0) the slope of tangent to the curve ${{\text{y}}^{2}}=4\text{ax}$is $\infty $which means the tangent is parallel to y-axis and tangent to the curve ${{\text{x}}^{2}}=4\text{by}$is 0 which means parallel to the x-axis. Thus the angle b/w these curves = $\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$.

At ${{(4{{\text{a}}^{\left( \frac{1}{3} \right)}}{{\text{b}}^{\left( \frac{2}{3} \right)}}^{{}},4{{\text{a}}^{\frac{2}{3}}}{{\text{b}}^{\frac{1}{3}}})}^{{}}}$the slope of tangent to the curve ${{\text{y}}^{2}}=4\text{ax}$is ${{\text{m}}_{1}}=\frac{1}{2}{{\left( \frac{\text{a}}{\text{b}} \right)}^{\frac{1}{3}}}$

And the slope of tangent to the curve ${{\text{x}}^{2}}=4\text{by}$is ${{\text{m}}_{2}}=2{{\left( \frac{\text{a}}{\text{b}} \right)}^{\frac{1}{3}}}$

Therefore the angle b/w the curve is $\text{tan }\!\!\theta\!\!\text{ }=\left| \frac{2{{\left( \frac{\text{a}}{\text{b}} \right)}^{\frac{1}{3}}}-\frac{1}{2}{{\left( \frac{\text{a}}{\text{b}} \right)}^{\frac{1}{3}}}}{1+\frac{1}{2}{{\left( \frac{\text{a}}{\text{b}} \right)}^{\frac{1}{3}}}\times 2{{\left( \frac{\text{a}}{\text{b}} \right)}^{\frac{1}{3}}}} \right|=\frac{3{{\left( \text{a} \right)}^{\frac{1}{3}}}{{\left( \text{b} \right)}^{\frac{1}{3}}}}{2\left( {{\text{a}}^{\frac{2}{3}}}+{{\text{b}}^{\frac{2}{3}}} \right)}$

$\Rightarrow \text{ }\!\!\theta\!\!\text{ }=\text{ta}{{\text{n}}^{-1}}\left( \frac{3{{\left( \text{a} \right)}^{\frac{1}{3}}}{{\left( \text{b} \right)}^{\frac{1}{3}}}}{2\left( {{\text{a}}^{\frac{2}{3}}}+{{\text{b}}^{\frac{2}{3}}} \right)} \right)$

14. Show that the equation of normal at any point on the curve $\mathbf{x}=3\mathbf{cos\theta }-\mathbf{co}{{\mathbf{s}}^{3}}\mathbf{\theta },~\mathbf{y}=3\mathbf{sin\theta }-\mathbf{si}{{\mathbf{n}}^{3}}\mathbf{\theta }$is $4\left( \mathbf{yco}{{\mathbf{s}}^{3}}\mathbf{\theta }-\mathbf{xsi}{{\mathbf{n}}^{3}}\mathbf{\theta } \right)=3\mathbf{sin}4\mathbf{\theta }.$

Ans: $\text{x}=3\text{cos }\!\!\theta\!\!\text{ }-\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }$

$\Rightarrow \frac{\text{dx}}{\text{d }\!\!\theta\!\!\text{ }}=-3\text{sin }\!\!\theta\!\!\text{ }+3\text{co}{{\text{s}}^{2}}\text{ }\!\!\theta\!\!\text{ }.\text{sin }\!\!\theta\!\!\text{ }$

$\Rightarrow \frac{\text{dx}}{\text{d }\!\!\theta\!\!\text{ }}=-3\text{sin }\!\!\theta\!\!\text{ }\left( 1-\text{co}{{\text{s}}^{2}}\text{ }\!\!\theta\!\!\text{ } \right)$

$\Rightarrow \frac{\text{dx}}{\text{d }\!\!\theta\!\!\text{ }}=-3\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }$----------------(1)

Now, $\text{y}=3\text{sin }\!\!\theta\!\!\text{ }-\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }$

$\Rightarrow \frac{\text{dy}}{\text{d }\!\!\theta\!\!\text{ }}=3\text{cos }\!\!\theta\!\!\text{ }-3\text{si}{{\text{n}}^{2}}\text{ }\!\!\theta\!\!\text{ }.\text{cos }\!\!\theta\!\!\text{ }$.$\Rightarrow \frac{\text{dy}}{\text{d }\!\!\theta\!\!\text{ }}=3\text{cos }\!\!\theta\!\!\text{ }\left( 1-\text{si}{{\text{n}}^{2}}\text{ }\!\!\theta\!\!\text{ } \right)$

$\Rightarrow \frac{\text{dy}}{\text{d }\!\!\theta\!\!\text{ }}=3\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }$-----------------(2)

Now we find the slope as $\frac{\text{dy}}{\text{dx}}=\frac{\frac{\text{dy}}{\text{d }\!\!\theta\!\!\text{ }}}{\frac{\text{dx}}{\text{d }\!\!\theta\!\!\text{ }}}=-\frac{3\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }}{3\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }}$. Since the slope of the normal $=-\frac{1}{\frac{\text{dy}}{\text{dx}}}=\frac{\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }}{\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }}$

The equation of line passing through a point $\left( 3\text{cos }\!\!\theta\!\!\text{ }-\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ },\text{ }\!\!~\!\!\text{ }3\text{sin }\!\!\theta\!\!\text{ }-\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ } \right)$and having slope $\frac{\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }}{\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }}$is $\left[ \text{y}-\left( 3\text{sin }\!\!\theta\!\!\text{ }-\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ } \right) \right]=\frac{\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }}{\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }}\left[ \text{x}-\left( 3\text{cos }\!\!\theta\!\!\text{ }-\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ } \right) \right]$

$\Rightarrow \text{y}.\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }-3\text{sin }\!\!\theta\!\!\text{ }.\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }+\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }.\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }=\text{xsi}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }-3\text{cos }\!\!\theta\!\!\text{ }.\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }+\text{si}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }.\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }$

$\Rightarrow \text{y}.\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }-\text{xsi}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }=3\text{sin }\!\!\theta\!\!\text{ cos }\!\!\theta\!\!\text{ }\left( \text{co}{{\text{s}}^{2}}\text{ }\!\!\theta\!\!\text{ }-\text{si}{{\text{n}}^{2}}\text{ }\!\!\theta\!\!\text{ } \right)$

We know that $\text{cos}2\text{ }\!\!\theta\!\!\text{ }=\text{co}{{\text{s}}^{2}}\text{ }\!\!\theta\!\!\text{ }-\text{si}{{\text{n}}^{2}}\text{ }\!\!\theta\!\!\text{ }$

$\Rightarrow \text{y}.\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }-\text{xsi}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }=\frac{3}{2}\times 2\text{sin }\!\!\theta\!\!\text{ cos }\!\!\theta\!\!\text{ }\left( \text{cos}2\text{ }\!\!\theta\!\!\text{ } \right)$ [Multiply and divide by 2]

$\Rightarrow \text{y}.\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }-\text{xsi}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }=\frac{3}{2}\times \text{sin}2\text{ }\!\!\theta\!\!\text{ }\left( \text{cos}2\text{ }\!\!\theta\!\!\text{ } \right)$

$\Rightarrow \text{y}.\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }-\text{xsi}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ }=\frac{3}{4}\times \text{sin}4\text{ }\!\!\theta\!\!\text{ }$        [Multiply and divide by 2]

$\Rightarrow 4\left( \text{y}.\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }-\text{xsi}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ } \right)=3\text{sin}4\text{ }\!\!\theta\!\!\text{ }$

Hence the equation of normal on the curve is $4\left( \text{y}.\text{co}{{\text{s}}^{3}}\text{ }\!\!\theta\!\!\text{ }-\text{xsi}{{\text{n}}^{3}}\text{ }\!\!\theta\!\!\text{ } \right)=3\text{sin}4\text{ }\!\!\theta\!\!\text{ }$.

15. Find the maximum and minimum values of $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{secx}+\mathbf{log}~\mathbf{co}{{\mathbf{s}}^{2}}\mathbf{x}$, 0 < x < 2π.

Ans: Here for finding the maxima and minima, first we find the critical points.

$\text{f}\left( \text{x} \right)=\text{secx}+\text{log }\!\!~\!\!\text{ co}{{\text{s}}^{2}}\text{x}$

$\Rightarrow \text{f}\,\text{ }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{secx}.\text{ }\!\!~\!\!\text{ tan }\!\!~\!\!\text{ x}+\frac{1}{\text{co}{{\text{s}}^{2}}\text{x}}2\text{cosx}.\left( -\text{sinx} \right)$                        \[\left[ \frac{\text{d}}{\text{dx}}\text{secx}=\text{secx}.\text{tanx} \right]\]

$\Rightarrow \text{f}\,\text{ }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{tanx}\left( \text{secx}-2 \right)$

Now for critical points, $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\text{tanx}=0$ and $\left( \text{secx}-2 \right)=0\Rightarrow \text{secx}-2=0$

$\Rightarrow \text{x}=0,\text{ }\!\!\pi\!\!\text{  }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{ x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{3},\frac{5\text{ }\!\!\pi\!\!\text{ }}{3}$

$\text{f}\,\text{ }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{tanx}.\text{ }\!\!~\!\!\text{ secx}-2\text{tanx}$

$\Rightarrow \text{f}\,\text{ }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{secx}.\text{se}{{\text{c}}^{2}}\text{x}+\text{secx}.\text{ }\!\!~\!\!\text{ ta}{{\text{n}}^{2}}\text{x}-2\text{se}{{\text{c}}^{2}}\text{x}$     $\left[ On\text{ }using\frac{\text{d}}{\text{dx}}\left( \text{u}.\text{v} \right)=\text{v}.\frac{\text{du}}{\text{dx}}+\text{u}.\frac{\text{du}}{\text{dx}} \right]$

\[\Rightarrow \text{f}\,\text{ }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{se}{{\text{c}}^{3}}\text{x}+\text{secx}.\text{ }\!\!~\!\!\text{ ta}{{\text{n}}^{2}}\text{x}-2\text{se}{{\text{c}}^{2}}\text{x}\]   

Here on  putting $\text{x}=0,\text{ }\!\!\pi\!\!\text{ },\text{ }\!\!~\!\!\text{ }\frac{\text{ }\!\!\pi\!\!\text{ }}{3},\frac{5\text{ }\!\!\pi\!\!\text{ }}{3}$

Here we get the maxima when f’’(x)<0 and minima when f’’(x)<0.

$\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( 0 \right)=\text{se}{{\text{c}}^{3}}\text{x}+\text{secx}.\text{ }\!\!~\!\!\text{ ta}{{\text{n}}^{2}}\text{x}-2\text{se}{{\text{c}}^{2}}\text{x}=1+0-2=-1<0$Therefore at x=0 function has the maxima.

At x=$\text{ }\!\!\pi\!\!\text{ },$ $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{ }\!\!\pi\!\!\text{ } \right)=\text{se}{{\text{c}}^{3}}\text{x}+\text{secx}.\text{ }\!\!~\!\!\text{ ta}{{\text{n}}^{2}}\text{x}-2\text{se}{{\text{c}}^{2}}\text{x}=-1+0-2=-3<0.$Therefore function has the maxima at x=$\text{ }\!\!\pi\!\!\text{ }$.

At x=$\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$, $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{3} \right)=\text{se}{{\text{c}}^{3}}\text{x}+\text{secx}.\text{ }\!\!~\!\!\text{ ta}{{\text{n}}^{2}}\text{x}-2\text{se}{{\text{c}}^{2}}\text{x}={{\left( 2 \right)}^{3}}+2.\left( 3 \right)-2.\left( 4 \right)=6>0$. Therefore function has minima at x=$\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$.

At x=$\frac{5\text{ }\!\!\pi\!\!\text{ }}{3}$, $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \frac{5\text{ }\!\!\pi\!\!\text{ }}{3} \right)=\text{se}{{\text{c}}^{3}}\text{x}+\text{secx}.\text{ }\!\!~\!\!\text{ ta}{{\text{n}}^{2}}\text{x}-2\text{se}{{\text{c}}^{2}}\text{x}={{\left( 2 \right)}^{3}}+2.\left( 3 \right)-2.\left( 4 \right)=6$>0. 

Therefore function has minima at x=$\frac{5\text{ }\!\!\pi\!\!\text{ }}{3}$

SO from the above the maxima points are 0, $\text{ }\!\!\pi\!\!\text{ }$and minima points are $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$, $\frac{5\text{ }\!\!\pi\!\!\text{ }}{3}$. 

Now the maximum values of f(x) is f(0)=$\text{secx}+\text{log }\!\!~\!\!\text{ co}{{\text{s}}^{2}}\text{x}$=1+0=1

f($\text{ }\!\!\pi\!\!\text{ }$)=$\text{sec}\left( \text{ }\!\!\pi\!\!\text{ } \right)+\text{log }\!\!~\!\!\text{ co}{{\text{s}}^{2}}\left( \text{ }\!\!\pi\!\!\text{ } \right)=1+0=1$

Minimum value at $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$, $\frac{5\text{ }\!\!\pi\!\!\text{ }}{3}$ are f($\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$)=$\text{sec}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{3} \right)+\text{log }\!\!~\!\!\text{ co}{{\text{s}}^{2}}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{3} \right)=2+2\text{log}\left( \frac{1}{2} \right)$ and f($\frac{5\text{ }\!\!\pi\!\!\text{ }}{3}$)=$\text{sec}\left( \frac{5\text{ }\!\!\pi\!\!\text{ }}{3} \right)+\text{log }\!\!~\!\!\text{ co}{{\text{s}}^{2}}\left( \frac{5\text{ }\!\!\pi\!\!\text{ }}{3} \right)=2+2\text{log}\left( \frac{1}{2} \right)$.

16. Find the area of the greatest rectangle that can be inscribed in an ellipse $\frac{{{\mathbf{x}}^{2}}}{{{\mathbf{a}}^{2}}}+\frac{{{\mathbf{y}}^{2}}}{{{\mathbf{b}}^{2}}}=1$.

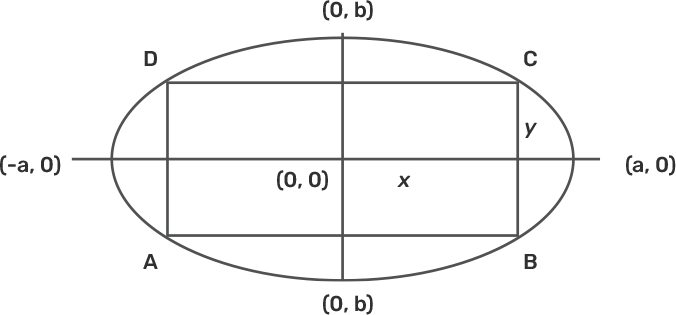
Ans: From the figure,

Let the side on the major axis is =2x, side on the minor axis = 2y. Now the area of rectangle $\text{A}=2\text{x}.2\text{y}=4\text{xy}$Squaring on both sides ${{\text{A}}^{2}}=16{{\text{x}}^{2}}{{\text{y}}^{2}}=\text{S}$

$\text{S}=16{{\text{x}}^{2}}{{\text{y}}^{2}}$

$\Rightarrow \text{S}=16{{\text{x}}^{2}}{{\text{b}}^{2}}\left\{ 1-\frac{{{\text{x}}^{2}}}{{{\text{a}}^{2}}} \right\}$

Now we have to maximise this function for getting the maximum area of a rectangle.

$\frac{\text{dS}}{\text{dx}}=16{{\text{b}}^{2}}\left\{ {{\text{x}}^{2}}-\frac{{{\text{x}}^{4}}}{{{\text{a}}^{2}}} \right\}$

$\Rightarrow \frac{\text{dS}}{\text{dx}}=16{{\text{b}}^{2}}\left\{ 2\text{x}-\frac{4{{\text{x}}^{3}}}{{{\text{a}}^{2}}} \right\}$

$\Rightarrow \frac{\text{dS}}{\text{dx}}=16\frac{{{\text{b}}^{2}}}{{{\text{a}}^{2}}}\left\{ 2{{\text{a}}^{2}}\text{x}-4{{\text{x}}^{3}} \right\}$

For critical points $\frac{\text{dS}}{\text{dx}}=0$

$2{{\text{a}}^{2}}\text{x}-4{{\text{x}}^{3}}=0$

$\Rightarrow \text{x}(2{{\text{a}}^{2}}-4{{\text{x}}^{2}}\}=0$

$\text{x}=0\text{ }\!\!~\!\!\text{ }\left( \text{Rejected} \right)\text{ }\!\!~\!\!\text{ }\And \text{ }\!\!~\!\!\text{ x}=\frac{\text{a}}{\sqrt{2}}$

On putting the value $\text{x}=\frac{\text{a}}{\sqrt{2}}$ in equation of ellipse we get $\text{y}=\frac{\text{b}}{\sqrt{2}}$

Now,  $\frac{{{\text{d}}^{2}}\text{S}}{\text{d}{{\text{x}}^{2}}}=16\frac{{{\text{b}}^{2}}}{{{\text{a}}^{2}}}\left\{ 2{{\text{a}}^{2}}-12{{\text{x}}^{2}} \right\}$

At $\text{x}=\frac{\text{a}}{\sqrt{2}}$, $\frac{{{\text{d}}^{2}}\text{S}}{\text{d}{{\text{x}}^{2}}}=16\frac{{{\text{b}}^{2}}}{{{\text{a}}^{2}}}\left\{ -4{{\text{a}}^{2}} \right\}<0.\text{ }\!\!~\!\!\text{ }$Therefore we get the maximum area. 

Hence At $\text{x}=\frac{\text{a}}{\sqrt{2}},\text{ }\!\!~\!\!\text{ y}=\frac{\text{b}}{\sqrt{2}}$. The area of rectangle ${{\text{A}}_{\text{max}}}=2\text{x}.2\text{y}=4\text{xy}=4.\frac{\text{a}}{\sqrt{2}}.\frac{\text{b}}{\sqrt{2}}=2\text{ab}.$

Maximum area $=2\text{ab}.$Sq. units

17. Find the difference between the greatest and least values of the function $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{sin}2\mathbf{x}-\mathbf{x},~\mathbf{on}~\left[ \frac{-\mathbf{\pi }}{2},\frac{\mathbf{\pi }}{2} \right]$ .

Ans: $\text{f}\left( \text{x} \right)=\text{sin}2\text{x}-\text{x}$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=2\text{cos}2\text{x}-1$

For critical points $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$2\text{cos}2\text{x}-1=0$

$\Rightarrow \text{cos}2\text{x}=\frac{1}{2}\Rightarrow 2\text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{3},\text{ }\!\!~\!\!\text{ }\frac{-\text{ }\!\!\pi\!\!\text{ }}{3}\Rightarrow \text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{6},\text{ }\!\!~\!\!\text{ }\frac{-\text{ }\!\!\pi\!\!\text{ }}{6}$

Now in interval $\frac{-\text{ }\!\!\pi\!\!\text{ }}{2}\le \text{x}\le \frac{\text{ }\!\!\pi\!\!\text{ }}{2}$we find the values at points $\frac{\text{ }\!\!\pi\!\!\text{ }}{6},$ $\frac{-\text{ }\!\!\pi\!\!\text{ }}{6}$, $\frac{-\text{ }\!\!\pi\!\!\text{ }}{2}$&$\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$

$\text{f}\left( \frac{-\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\text{sin}2\left( \frac{-\text{ }\!\!\pi\!\!\text{ }}{6} \right)-\left( \frac{-\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\frac{-\sqrt{3}}{2}+\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$

$\text{f}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\text{sin}2\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)-\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\frac{\sqrt{3}}{2}-\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$

$\text{f}\left( \frac{-\text{ }\!\!\pi\!\!\text{ }}{2} \right)=\text{sin}2\left( \frac{-\text{ }\!\!\pi\!\!\text{ }}{2} \right)-\left( \frac{-\text{ }\!\!\pi\!\!\text{ }}{2} \right)=\text{f}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$

$\text{f}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)=\text{sin}2\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)-\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)=\frac{-\text{ }\!\!\pi\!\!\text{ }}{2}$

If we compare all four value the greatest value is $\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$ and least value is $\frac{-\text{ }\!\!\pi\!\!\text{ }}{2}$. Hence the difference between them is = $\frac{\text{ }\!\!\pi\!\!\text{ }}{2}-\left( \frac{-\text{ }\!\!\pi\!\!\text{ }}{2} \right)=\text{ }\!\!\pi\!\!\text{ }.$

.18. An isosceles triangle of vertical angle 2θ is inscribed in a circle of radius a. Show that the area of triangle is maximum when $\text{ }\!\!\theta\!\!\text{ }=\frac{\mathbf{\pi }}{6}$.

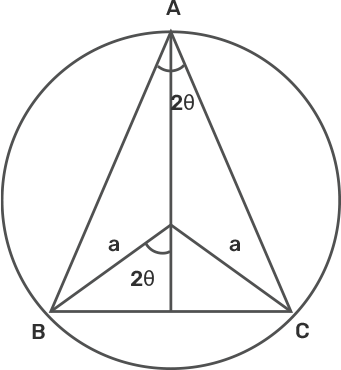
Ans: Given ABC is an isolated triangle.

We know that area of triangle = $\frac{1}{2}\times \text{Height}\times \text{Base}.$

Here Height = AD, Base = BC

BC=2BD=$2.\text{asin}2\text{ }\!\!\theta\!\!\text{ }$

AD=OA+OD where OA =Radius =a and OD=OB$\text{cos}2\text{ }\!\!\theta\!\!\text{ }$

Hence AD=$\text{a}+\text{acos}2\text{ }\!\!\theta\!\!\text{ }$

Now Area of triangle $\text{ }\!\!\Delta\!\!\text{ }=\frac{1}{2}\times \text{Height}\times \text{Base}.$

$=\frac{1}{2}\times \left( \text{a}+\text{acos}2\text{ }\!\!\theta\!\!\text{ } \right)\times 2\text{asin}2\text{ }\!\!\theta\!\!\text{ }.$

We have to maximise this area of triangle where the area depends on angle $\text{ }\!\!\theta\!\!\text{ },$So we use the 2nd derivative test for finding the maximum area. 

$\text{ }\!\!\Delta\!\!\text{ }=\frac{1}{2}\times {{\text{a}}^{2}}\left( 1+\text{cos}2\text{ }\!\!\theta\!\!\text{ } \right)\times 2\text{sin}2\text{ }\!\!\theta\!\!\text{ }$

$\Rightarrow \text{ }\!\!\Delta\!\!\text{ }=\frac{1}{2}\times {{\text{a}}^{2}}2\text{sin}2\text{ }\!\!\theta\!\!\text{ }+\frac{1}{2}\times {{\text{a}}^{2}}\times \text{sin}4\text{ }\!\!\theta\!\!\text{ }$

$\Rightarrow \frac{\text{d }\!\!\Delta\!\!\text{ }}{\text{d }\!\!\theta\!\!\text{ }}={{\text{a}}^{2}}\times 2\text{cos}2\text{ }\!\!\theta\!\!\text{ }+2{{\text{a}}^{2}}\times \text{cos}4\text{ }\!\!\theta\!\!\text{ }$

For critical points $\frac{\text{d }\!\!\Delta\!\!\text{ }}{\text{d }\!\!\theta\!\!\text{ }}=0$

${{\text{a}}^{2}}\times 2\text{cos}2\text{ }\!\!\theta\!\!\text{ }+2{{\text{a}}^{2}}\times \text{cos}4\text{ }\!\!\theta\!\!\text{ }=0$

$\Rightarrow \text{cos}2\text{ }\!\!\theta\!\!\text{ }=-\text{cos}4\text{ }\!\!\theta\!\!\text{ }$

$\Rightarrow \text{cos}2\text{ }\!\!\theta\!\!\text{ }=\text{cos}\left( \text{ }\!\!\pi\!\!\text{ }-4\text{ }\!\!\theta\!\!\text{ } \right)$       [$\text{cos}\left( \text{ }\!\!\pi\!\!\text{ }-\text{ }\!\!\theta\!\!\text{ } \right)=-\text{cos }\!\!\theta\!\!\text{ }]$

$\Rightarrow 2\text{ }\!\!\theta\!\!\text{ }=\left( \text{ }\!\!\pi\!\!\text{ }-4\text{ }\!\!\theta\!\!\text{ } \right)$

$\Rightarrow \text{ }\!\!\theta\!\!\text{ }=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$

$\frac{{{\text{d}}^{2}}\text{ }\!\!\Delta\!\!\text{ }}{\text{d}{{\text{ }\!\!\theta\!\!\text{ }}^{2}}}=-4{{\text{a}}^{2}}\text{sin}2\text{ }\!\!\theta\!\!\text{ }-8{{\text{a}}^{2}}\text{sin}2\text{ }\!\!\theta\!\!\text{ }$

$\frac{{{\text{d}}^{2}}\text{ }\!\!\Delta\!\!\text{ }}{\text{d}{{\text{ }\!\!\theta\!\!\text{ }}^{2}}}=-4{{\text{a}}^{2}}\left( \text{sin}2\text{ }\!\!\theta\!\!\text{ }+2\text{sin}2\text{ }\!\!\theta\!\!\text{ } \right)<0$

At $\text{ }\!\!\theta\!\!\text{ }=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}\frac{{{\text{d}}^{2}}\text{ }\!\!\Delta\!\!\text{ }}{\text{d}{{\text{ }\!\!\theta\!\!\text{ }}^{2}}}=-4{{\text{a}}^{2}}\left( \text{sin}\frac{\text{ }\!\!\pi\!\!\text{ }}{3}+2\text{sin}\frac{\text{ }\!\!\pi\!\!\text{ }}{3} \right)=-4{{\text{a}}^{2}}\frac{3\sqrt{3}}{2}<0$Therefore the area of triangle is maximum when $\text{ }\!\!\theta\!\!\text{ }=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$.

Objective Type Questions

Choose the correct answer from the given four options in each of the following Examples 19 to 23. 

19. The abscissa of the point on the curve $3\mathbf{y}=6\mathbf{x}-5{{\mathbf{x}}^{3}}$, the normal at which passes through origin is: 

(A) 1 

(B) $\frac{1}{3}$

(C) 2

 (D) $\frac{1}{2}$

Ans: Given: $3\text{y}=6\text{x}-5{{\text{x}}^{3}}$

Let the point on the curve is $\left( {{\text{x}}_{1}},\text{ }\!\!~\!\!\text{ }{{\text{y}}_{1}} \right)$. 

So the curve is $3{{\text{y}}_{1}}={{\text{x}}_{1}}\left( 6-5{{\text{x}}_{1}}^{2} \right)\Rightarrow \frac{{{\text{y}}_{1}}}{{{\text{x}}_{1}}}=\frac{\left( 6-5{{\text{x}}_{1}}^{2} \right)}{3}$-------------(1)

Now we find the Slope of normal at this point. 

$3\text{y}=6\text{x}-5{{\text{x}}^{3}}$

$\Rightarrow 3\frac{\text{dy}}{\text{dx}}=6-15{{\text{x}}^{2}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=2-5{{\text{x}}^{2}}$

Slope of Normal = $\frac{-1}{2-5{{\text{x}}^{2}}}$

Equation of normal Passing through origin $\left( \text{y}-0 \right)=\frac{-1}{2-5{{\text{x}}^{2}}}\left( \text{x}-0 \right)$

Now the Equation of normal on point $\left( {{\text{x}}_{1}},\text{ }\!\!~\!\!\text{ }{{\text{y}}_{1}} \right)$is ${{\text{y}}_{1}}=\frac{-{{\text{x}}_{1}}}{2-5{{\text{x}}_{1}}^{2}}\Rightarrow \frac{{{\text{y}}_{1}}}{{{\text{x}}_{1}}}=\frac{-1}{2-5{{\text{x}}_{1}}^{2}}$-----(2)

By using eq. 1 & 2

$\frac{\left( 6-5{{\text{x}}_{1}}^{2} \right)}{3}=\frac{-1}{2-5{{\text{x}}_{1}}^{2}}$

$\Rightarrow 12-30{{\text{x}}_{1}}^{2}-10{{\text{x}}^{2}}_{1}+25{{\text{x}}_{1}}^{4}=-3$

Let ${{\text{x}}_{1}}^{2}=\text{t}$

$\Rightarrow 12-30\text{t}-10\text{t}+25{{\text{t}}^{2}}=-3$

$\Rightarrow 25{{\text{t}}^{2}}-40\text{t}+15=0$

$\Rightarrow 5{{\text{t}}^{2}}-8\text{t}+3=0$

$\Rightarrow 5{{\text{t}}^{2}}-5\text{t}-3\text{t}+3=0$

$\Rightarrow 5\text{t}\left( \text{t}-1 \right)-3\left( \text{t}-1 \right)=0$

$\Rightarrow \text{t}=1\text{and }\!\!~\!\!\text{ t}=\frac{3}{5}$

$\text{ }\!\!~\!\!\text{ t}=\frac{3}{5}$(Rejected)

$\text{t}=1\Rightarrow {{\text{x}}_{1}}^{2}=1\Rightarrow {{\text{x}}_{1}}=\pm 1$

${{\text{x}}_{1}}=1$ Only satisfies the equations, Hence the option A is the correct answer.

20.The two curves ${{\mathbf{x}}^{3}}-3\mathbf{x}{{\mathbf{y}}^{2}}+2=0$ and $3{{\mathbf{x}}^{2}}\mathbf{y}-{{\mathbf{y}}^{3}}=2$

(A) touch each other 

(B) cut at right angle 

(C) cut at an angle $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$

(D) cut at an angle $\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$

Ans: First we find the slope of both the curves.

${{\text{x}}^{3}}-3\text{x}{{\text{y}}^{2}}+2=0$

Differentiating on both sides 

$3{{\text{x}}^{2}}-3{{\text{y}}^{2}}-6\text{xy}.\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow .\frac{\text{dy}}{\text{dx}}=\frac{3{{\text{x}}^{2}}-3{{\text{y}}^{2}}}{6\text{xy}}=\frac{{{\text{x}}^{2}}-{{\text{y}}^{2}}}{2\text{xy}}={{\text{M}}_{1}}$---------(1)

$\text{Curve}2:\text{ }\!\!~\!\!\text{ }3{{\text{x}}^{2}}\text{y}-{{\text{y}}^{3}}=2$

Differentiating on both sides

$6\text{xy}+3{{\text{x}}^{2}}\frac{\text{dy}}{\text{dx}}-3{{\text{y}}^{2}}\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{-6\text{xy}}{3{{\text{x}}^{2}}-3{{\text{y}}^{2}}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{-2\text{xy}}{{{\text{x}}^{2}}-{{\text{y}}^{2}}}={{\text{M}}_{2}}$---------(2)

By Eq. 1 & 2 We can write ${{\text{M}}_{1}}{{\text{M}}_{2}}=\text{ }\!\!~\!\!\text{ }-1.$Hence the curves cut at right angles.

21. The tangent to the curve given by $\mathbf{x}={{\mathbf{e}}^{\mathbf{t}}}.\mathbf{cost}$, $\mathbf{y}={{\mathbf{e}}^{\mathbf{t}}}.~\mathbf{sint}$ at $\mathbf{t}=\frac{\mathbf{\pi }}{4}$ makes with x-axis an angle: 

(A) 0 

(B) $\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$

(C) $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$ 

(D) $\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$

Ans: Slope of the tangent of the curve is $\frac{\text{dy}}{\text{dx}}$. 

$\text{x}={{\text{e}}^{\text{t}}}.\text{cost}$

$\Rightarrow \frac{\text{dx}}{\text{dt}}=\text{cost}.\text{ }\!\!~\!\!\text{ }{{\text{e}}^{\text{t}}}-{{\text{e}}^{\text{t}}}\text{sint}$

$\text{y}={{\text{e}}^{\text{t}}}.\text{ }\!\!~\!\!\text{ sint}$

$\Rightarrow \frac{\text{dy}}{\text{dt}}=\text{cost}.\text{ }\!\!~\!\!\text{ }{{\text{e}}^{\text{t}}}+{{\text{e}}^{\text{t}}}\text{sint}$

$\frac{\text{dy}}{\text{dx}}=\frac{\frac{\text{dy}}{\text{dt}}}{\frac{\text{dx}}{\text{dt}}}=\frac{{{\text{e}}^{\text{t}}}\left( \text{cost}+\text{sint} \right)}{{{\text{e}}^{\text{t}}}\left( \text{cost}-\text{sint} \right)}$

Slope at point $\text{t}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$, ${{\left( \frac{\text{dy}}{\text{dx}} \right)}_{\text{t}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}}}=\frac{\left( \text{cost}+\text{sint} \right)}{\left( \text{cost}-\text{sint} \right)}=\frac{\sqrt{2}}{0}=\infty $ Since the tangent is y-axis. 

Hence the tangent (y-axis) will make angle $\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$ with x-axis as the y-axis and x-axis are perpendicular to each other.

22. The equation of the normal to the curve y = sinx at (0, 0) is: 

(A) $\mathbf{x}=0$ 

(B) $\mathbf{y}=0$

(C) $\mathbf{x}+\mathbf{y}=0$

(D) $\mathbf{x}-\mathbf{y}=0$

Ans: Slope of the tangent = $\frac{\text{dy}}{\text{dx}}$

Slope of the Normal = $\frac{-1}{\text{slope }\!\!~\!\!\text{ of }\!\!~\!\!\text{ tangent}}=\frac{-1}{\frac{\text{dy}}{\text{dx}}}$----(1)

$\frac{\text{dy}}{\text{dx}}=\text{cosx}$

$\Rightarrow {{\left( \frac{\text{dy}}{\text{dx}} \right)}_{\left( 0,0 \right)}}=\text{cos}\left( 0 \right)=1$

Slope of the Normal = $\frac{-1}{1}=-1$

Equation of normal having slope -1, passing through (0,0) is

$\left( \text{y}-0 \right)=-1\left( \text{x}-0 \right)$

$\Rightarrow \text{x}+\text{y}=0$

Hence option c is the correct answer.

23. The point on the curve ${{\mathbf{y}}^{2}}=\mathbf{x}$, where the tangent makes an angle of $\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$with x-axis is 

(A) $\left( \frac{1}{2},\frac{1}{4} \right)$     

(B) $\left( \frac{1}{4},\frac{1}{2} \right)$   

(C) (4, 2) 

(D) (1, 1)

Ans: Given: ${{\text{y}}^{2}}=\text{x}$

Slope of the tangent of curve ${{\text{y}}^{2}}=\text{x}$is $\frac{\text{dy}}{\text{dx}}$

So on differentiating the given curve ${{\text{y}}^{2}}=\text{x}$ on both sides 

$2\text{y}.\frac{\text{dy}}{\text{dx}}=1$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{1}{2\text{y}}$

Let the point on curve is $\left( {{\text{x}}_{1}},{{\text{y}}_{1}} \right)$then ${{\text{y}}_{1}}^{2}={{\text{x}}_{1}}$and the slope on the this point is $\frac{\text{dy}}{\text{dx}}=\frac{1}{2{{\text{y}}_{1}}}$. We are given that the tangent is making the angle of  $\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$with x-axis hence the slope will be = tan$\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)$=1. 

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{1}{2{{\text{y}}_{1}}}=1$

$\Rightarrow {{\text{y}}_{1}}=\frac{1}{2}$

On Putting this value in curve equation we get ${{\text{y}}_{1}}^{2}={{\text{x}}_{1}}\Rightarrow {{\text{x}}_{1}}={{\left( \frac{1}{2} \right)}^{2}}=\frac{1}{4}$

Hence the point is $\left( \frac{1}{4},\frac{1}{2} \right).$Option B is the correct answer.

24. The values of a for which $\mathbf{y}={{\mathbf{x}}^{2}}+\mathbf{ax}+25$ touches the axis of x are______. 

Ans: The curve touches the x-axis that means the tangent on the curve will touch the x-axis. So we first find the slope and equate it with 0.

$\frac{\text{dy}}{\text{dx}}=2\text{x}+\text{a}$ 

$\Rightarrow 2\text{x}+\text{a}=0$

$\Rightarrow \text{x}=\frac{-\text{a}}{2}$

Therefore, 

Now on putting $\text{x}=\frac{-\text{a}}{2}$ in the curve then y- will be zero such as ${{\left( \frac{-\text{a}}{2} \right)}^{2}}+\text{a}\left( \frac{-\text{a}}{2} \right)+25=0$

$\Rightarrow \frac{{{\text{a}}^{2}}}{4}-\frac{{{\text{a}}^{2}}}{2}+25=0$

$\Rightarrow \frac{{{\text{a}}^{2}}-2{{\text{a}}^{2}}+25}{4}=0$

$\Rightarrow {{\text{a}}^{2}}=100$

$\Rightarrow {{\text{a}}^{{}}}=\pm 10$

Hence the values of a are $\pm 10$.

25. If $\mathbf{f}\left( \mathbf{x} \right)=\frac{1}{4{{\mathbf{x}}^{2}}+2\mathbf{x}+1}$, then its maximum value is _______.

Ans: For the function $\text{f}\left( \text{x} \right)$ to be maximum $4{{\text{x}}^{2}}+2\text{x}+1$should be minimum. Now our aim is to find the minimum value of  $4{{\text{x}}^{2}}+2\text{x}+1$.

Let $\text{g}\left( \text{x} \right)=4{{\text{x}}^{2}}+2\text{x}+1$

$\text{g }\!\!'\!\!\text{ }\left( \text{x} \right)=8\text{x}+2$

For critical points $\text{g }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\Rightarrow 8\text{x}+2=0$

$\Rightarrow \text{x}=\frac{-1}{4}$

$\text{g }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=8>0$Therefore the function $4{{\text{x}}^{2}}+2\text{x}+1$has minima at $\text{x}=\frac{-1}{4}$

Since ${{\text{g}}_{\text{min}}}\left( \text{x} \right)=4{{\text{x}}^{2}}+2\text{x}+1=4.{{\left( \frac{-1}{4} \right)}^{2}}+2\left( \frac{-1}{4} \right)+1=\frac{1}{4}-\frac{1}{2}+1=\frac{3}{4}$

Hence ${{\text{f}}_{\text{max}}}\left( \text{x} \right)=\frac{3}{4}$

26. Let f have a second derivative at c such that $\mathbf{f}'\left( \mathbf{c} \right)=0$ and $\mathbf{f}''\left( \mathbf{c} \right)>0$, then c is a point of ______.

Ans: We know that if we have a function f such that at c, $\text{f }\!\!'\!\!\text{ }\left( \text{c} \right)=0$ then c is called critical point and then if  $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{c} \right)>0$then point c is called the local minima.

27. Minimum value of f if $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{sinx}~\mathbf{in}~\left[ \frac{-\mathbf{\pi }}{2},\frac{\mathbf{\pi }}{2} \right]$ is _____.

Ans: We know that sin function 

Given: $\text{f}\left( \text{x} \right)=\text{sinx}$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{cosx}$

For critical points $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\Rightarrow \text{cosx}=0$

$\Rightarrow \text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{2},\frac{-\text{ }\!\!\pi\!\!\text{ }}{2}\in \left[ \frac{-\text{ }\!\!\pi\!\!\text{ }}{2},\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right]$

$\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=-\text{sinx}$

At $\text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$, $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=-\text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)=-1<0.\text{ }\!\!~\!\!\text{ }$Therefore function has maxima at x=$\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$

At  $\text{x}=\frac{-\text{ }\!\!\pi\!\!\text{ }}{2}$, $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=-\text{sin}\left( \frac{-\text{ }\!\!\pi\!\!\text{ }}{2} \right)=1>0$. Therefore function has maxima at x=$\frac{-\text{ }\!\!\pi\!\!\text{ }}{2}$

Hence ${{\text{f}}_{\text{min}}}\left( \text{x} \right)\text{ }\!\!~\!\!\text{ }=\text{sin}\left( {{\frac{-\text{ }\!\!\pi\!\!\text{ }}{2}}_{{}}} \right)=\text{ }\!\!~\!\!\text{ }-1.$

28. The maximum value of sinx + cosx is _____.

Ans: Let $\text{f}\left( \text{x} \right)=\text{sinx}+\text{cosx}$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{cosx}-\text{sinx}$

For critical points, $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\text{cosx}-\text{sinx}=0$

$\Rightarrow \text{cosx}=\text{sinx}$

$\Rightarrow \text{tanx}=1$

$\Rightarrow \text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$

$\Rightarrow \text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=-\text{sinx}-\text{cosx}$

At $\text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$, $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }}<0$. Therefore function has maxima at $\text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$. Hence the maximum value of the function ${{\text{f}}_{\text{max}}}\left( \text{x} \right)=\text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)+\text{cos}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}$

29. The rate of change of volume of a sphere with respect to its surface area, when the radius is 2 cm, is______. 

Ans: Volume of a sphere is V= $\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{3}}$ and surface area is S=$4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}$.

Here the rate of change of volume w.r.t surface will be = $\frac{\text{dV}}{\text{dS}}$ We know that both the quantities(area, volume) depends on radius so we write this rate of change in terms of r as $\frac{\text{dV}}{\text{dS}}$=$\frac{\frac{\text{dV}}{\text{dr}}}{\frac{\text{dS}}{\text{dr}}}$---------(1)

$\text{V}=\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{3}}\Rightarrow \frac{\text{dV}}{\text{dr}}=\frac{4}{3}.3\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}=4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}$-----(2)

S=$4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}\Rightarrow \frac{\text{dS}}{\text{dr}}=8\text{ }\!\!\pi\!\!\text{ r}$--------(2)

Using the values from Eq.(2)&(3) in Eq.(1)

$\frac{\text{dV}}{\text{dS}}$=$\frac{\frac{\text{dV}}{\text{dr}}}{\frac{\text{dS}}{\text{dr}}}=\frac{4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}{8\text{ }\!\!\pi\!\!\text{ r}}=\frac{\text{r}}{2}$

When r=2

$\frac{\text{dV}}{\text{dS}}=\frac{2}{2}=1$

EXERCISE 

Short Answer (S.A.)

1. A spherical ball of salt is dissolving in water in such a manner that the rate of decrease of the volume at any instant is proportional to the surface. Prove that the radius is decreasing at a constant rate.

Ans: Given that the rate of decrease of the volume at any instant is proportional to the surface . Let the radius of the spherical ball is r.

Volume of sphere V= $\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{3}}\Rightarrow \frac{\text{dV}}{\text{dt}}=-\frac{4}{3}.3\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}$[-sign represent that the volume is decreasing]

Surface area of sphere $\text{S}=4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}$

According to the problem $\frac{\text{dV}}{\text{dt}}\text{ }\!\!\alpha\!\!\text{  }\!\!~\!\!\text{ S}$

$\Rightarrow \frac{\text{d}}{\text{dt}}\left( \frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{3}} \right)\text{ }\!\!\alpha\!\!\text{  }\!\!~\!\!\text{ }4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}$

$\Rightarrow -\frac{4}{3}.3\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}.\text{ }\!\!~\!\!\text{ }\frac{\text{dr}}{\text{dt}}\text{ }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{  }\!\!~\!\!\text{ }4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}$

$\Rightarrow \text{ }\!\!~\!\!\text{ }\frac{\text{dr}}{\text{dt}}\text{ }\!\!\alpha\!\!\text{  }\!\!~\!\!\text{ }-\frac{4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}{4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}$

$\Rightarrow \text{ }\!\!~\!\!\text{ }\frac{\text{dr}}{\text{dt}}=-\text{ }\!\!~\!\!\text{ k}.1$   [k= proportionality constant]

Since $\frac{\text{dr}}{\text{dt}}=-\text{k}$. Hence we can say that the radius is decreasing at a constant rate.

2. If the area of a circle increases at a uniform rate, then prove that perimeter varies inversely as the radius.

Ans: Given that the area of the circle is increasing at a uniform rate as $\frac{\text{dA}}{\text{dt}}=\text{k}$-------(1) .

Let the radius of a circle =r

Area of a circle $\text{A}=\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}$

$\frac{\text{dA}}{\text{dt}}=2\text{ }\!\!\pi\!\!\text{ r}.\text{ }\!\!~\!\!\text{ }\frac{\text{dr}}{\text{dt}}$-----(2)

By Eq. 1 & 2

$\text{k}=2\text{ }\!\!\pi\!\!\text{ r}.\frac{\text{dr}}{\text{dt}}$

$\Rightarrow \frac{\text{dr}}{\text{dt}}=\frac{\text{k}}{2\text{ }\!\!\pi\!\!\text{ r}}$----(3)

Let the perimeter $\text{P}=2\text{ }\!\!\pi\!\!\text{ r}$

$\Rightarrow \frac{\text{dP}}{\text{dt}}=2\text{ }\!\!\pi\!\!\text{ }\frac{\text{dr}}{\text{dt}}$

Putting the values of $\frac{\text{dr}}{\text{dt}}$by Eq. 3 in above eq.

$\Rightarrow \frac{\text{dP}}{\text{dt}}=2\text{ }\!\!\pi\!\!\text{ }.\frac{\text{k}}{2\text{ }\!\!\pi\!\!\text{ r}}$

$\Rightarrow \frac{\text{dP}}{\text{dt}}=\frac{\text{k}}{\text{r}}$

$\Rightarrow \frac{\text{dP}}{\text{dt}}\text{ }\!\!\alpha\!\!\text{  }\!\!~\!\!\text{ }\frac{1}{\text{r}}$

Hence the perimeter varies inversely as the radius.

3. A kite is moving horizontally at a height of 151.5 meters. If the speed of the kite is 10 m/s, how fast is the string being let out; when the kite is 250 m away from the boy who is flying the kite? The height of the boy is 1.5 m. 

Ans: 

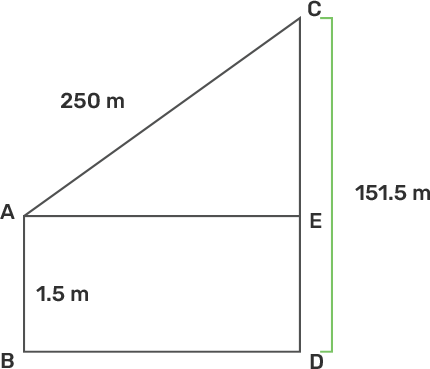
Height(h)=151.5m, Speed of kite =10m/s

From the figure, Let CD be the height of the kite and AB is the height of the boy.

Let $\text{BD}=\text{x }\!\!~\!\!\text{ m }\!\!~\!\!\text{ }=\text{EA }\!\!~\!\!\text{ and }\!\!~\!\!\text{ AC}=250\text{m}$

$\frac{\text{dx}}{\text{dt}}=10\text{m}/\text{sec}$

$\text{EC}=\text{CD}-\text{DE}=151.5-1.5=150\text{m}$

Using pythagoras theorem in $\text{ }\!\!\Delta\!\!\text{ AEC}$

$\text{A}{{\text{C}}^{2}}=\text{A}{{\text{E}}^{2}}+\text{E}{{\text{C}}^{2}}$

Here AC=250m , AE= x , EC=150m

${{\text{y}}^{2}}={{\text{x}}^{2}}+{{150}^{2}}$

When $\text{y}=250$

${{250}^{2}}={{\text{x}}^{2}}+{{150}^{2}}$

$\Rightarrow {{250}^{2}}-{{150}^{2}}={{\text{x}}^{2}}$

$\Rightarrow {{\text{x}}^{2}}=\left( 250-150 \right)\left( 250+150 \right)$

$\Rightarrow {{\text{x}}^{2}}=\left( 250-150 \right)\left( 250+150 \right)$

$\Rightarrow {{\text{x}}^{2}}=100\times 400$

$\Rightarrow \text{x}=20\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }-20$ [side can’t be negative, so x=-20 rejected]

Now , ${{\text{y}}^{2}}={{\text{x}}^{2}}+{{150}^{2}}$

Differentiating on both sides

$\Rightarrow 2\text{y}.\frac{\text{dy}}{\text{dt}}=2\text{x}.\frac{\text{dx}}{\text{dt}}$

$\Rightarrow \frac{\text{dy}}{\text{dt}}=\frac{\text{x}}{\text{y}}.\frac{\text{dx}}{\text{dt}}$

On putting the values x=20, y=250 and $\frac{\text{dx}}{\text{dt}}=10$, we get

$\frac{\text{dy}}{\text{dt}}=\frac{200}{250}.10=8\text{m}/\text{sec}$

So, the string being let out at the rate of $8\text{m}/\text{sec}$.

4. Two men A and B start with velocities v at the same time from the junction of two roads inclined at 45° to each other. If they travel by different roads, find the rate at which they are being seperated.

Ans: 

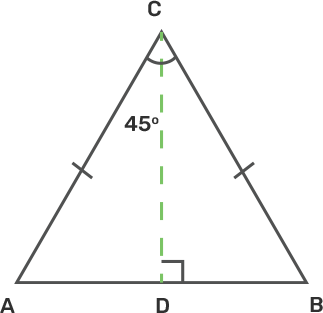
Let the men A and B start from point c with the 

Same velocities v at the same time. 

And given, $\angle \text{ACB}={{45}^{\circ }}$

Since, Men A and B moving with same velocities v at the same time , so they will cover the same distance, 

Hence AC=AB, Therefore the triangle ABC is an isosceles triangle. 

Now we draw $\text{CD}\bot \text{AB}$

Let at time t the distance b/w A and B is y and AC=x

$\because \text{ }\!\!\Delta\!\!\text{ ABC}$is an isosceles triangle, So AC=AB=x

In $\text{ }\!\!\Delta\!\!\text{ ACD}$and $\text{ }\!\!\Delta\!\!\text{ BCD}$

$\angle \text{CAB}=\angle \text{CBD}$    (∵ AC=AB)

$\angle \text{ADC}=\angle \text{BDC}={{90}^{\circ }}$

$\text{CD}=\text{CD}$ (common side)

By ASA ,  $\text{ }\!\!\Delta\!\!\text{ ACD}\text{ }\!\!\Delta\!\!\text{ BCD}$

$\therefore \angle \text{ACD}=\angle \text{DCB}$

Since, $\angle \text{ACD}+\angle \text{DCB}={{45}^{\circ }}$

 $\Rightarrow \angle \text{ACD}=\angle \text{DCB}=\frac{1}{2}.\frac{\text{ }\!\!\pi\!\!\text{ }}{4}=\frac{\text{ }\!\!\pi\!\!\text{ }}{8}$

In $\text{ }\!\!\Delta\!\!\text{ ACD}$

$\text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{8} \right)=\frac{\text{AD}}{\text{AC}}$

$\Rightarrow \text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{8} \right)=\frac{\frac{\text{y}}{2}}{\text{x}}$

$\Rightarrow \text{y}=2\text{x}.\text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{8} \right)------\left( 1 \right)$

Since distance b/w A and B is y. Hence the rate of the separation of A and B is $\frac{\text{dy}}{\text{dt}}.$ 

Differentiating the equation 1 w.r.t. t,

$\frac{\text{dy}}{\text{dt}}=2\text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{8} \right).\text{ }\!\!~\!\!\text{ }\frac{\text{dx}}{\text{dt}}$

$\Rightarrow \frac{\text{dy}}{\text{dt}}=2\text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{8} \right).\text{ }\!\!~\!\!\text{ v}$      $\left[ \frac{\text{dx}}{\text{dt}}=\text{v} \right]$

$\Rightarrow \frac{\text{dy}}{\text{dt}}=2\text{v}.\frac{\sqrt{2-\sqrt{2}}}{2}$

$\Rightarrow \frac{\text{dy}}{\text{dt}}=\text{v}.\sqrt{2-\sqrt{2}}$unit/sec

So the rate is$\text{v}.\sqrt{2-\sqrt{2}}$at which A and B are being separated.

5. Find an angle θ, $0<\mathbf{\theta }<\frac{\mathbf{\pi }}{2}$ , which increases twice as fast as its sine.

Ans: Let the angle $\text{ }\!\!\theta\!\!\text{  }\!\!~\!\!\text{ }$increases twice as fast as its sine as

$\text{ }\!\!\theta\!\!\text{ }=2\text{sin }\!\!\theta\!\!\text{ }$

Now,on differentiatingboth sides w.r.t. t, we get

$\Rightarrow \frac{\text{d }\!\!\theta\!\!\text{ }}{\text{dt}}=2\text{cos }\!\!\theta\!\!\text{ }.\frac{\text{d }\!\!\theta\!\!\text{ }}{\text{dt}}$

$\Rightarrow 1=2\text{cos }\!\!\theta\!\!\text{ }.$

$\Rightarrow \text{ }\!\!\theta\!\!\text{ }=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$

So the required angle is $\text{ }\!\!\theta\!\!\text{ }=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$

6. Find the approximate value of ${{\left( 1.999 \right)}^{5}}$

Ans: Let $\text{y}+\text{ }\!\!\Delta\!\!\text{ y}={{\left( 1.999 \right)}^{5}}$

We write 1.999 as $\text{x}+\text{ }\!\!\Delta\!\!\text{ x}=1.999$then $\text{y}+\text{ }\!\!\Delta\!\!\text{ y}={{\left( \text{x}+\text{ }\!\!\Delta\!\!\text{ x} \right)}^{2}}$

Let x=2 then $\text{ }\!\!\Delta\!\!\text{ x}=1.999-2=\text{ }\!\!~\!\!\text{ }-0.001$

$\text{y}={{\left( \text{x} \right)}^{5}}$

Differentiating on both sides w.r.t. T, we get 

$\frac{\text{dy}}{\text{dt}}=5{{\text{x}}^{4}}\frac{\text{dx}}{\text{dt}}$

$\Rightarrow \text{dy}=5{{\text{x}}^{4}}\text{dx}$

$\Rightarrow \text{ }\!\!\Delta\!\!\text{ y}=5{{\text{x}}^{4}}\text{ }\!\!\Delta\!\!\text{ x}$

$\Rightarrow \text{ }\!\!\Delta\!\!\text{ y}=5{{\left( 2 \right)}^{4}}\left( -0.001 \right)$

$\Rightarrow \text{ }\!\!\Delta\!\!\text{ y}=-0.080$

Now $\text{y}+\text{ }\!\!\Delta\!\!\text{ y }\!\!~\!\!\text{ }={{\left( 2 \right)}^{5}}-0.080$

$\text{y}+\text{ }\!\!\Delta\!\!\text{ y }\!\!~\!\!\text{ }=32-0.080=31.920$

7. Find the approximate volume of metal in a hollow spherical shell whose internal and external radii are 3 cm and 3.0005 cm, respectively. 

Ans: Let the external radius of spherical shell $\text{R}=3.0005\text{cm}$and internal radius $\text{r}=3\text{cm }\!\!~\!\!\text{ }$

Volume of hollow spherical shell $\text{V}=\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }\left( {{\text{R}}^{3}}-{{\text{r}}^{3}} \right)$ 

$\Rightarrow \text{V}=\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{({{3.0005}^{3}}-{{3}^{3}})}^{{}}}$-------(i)

We can find the value of ${{3}^{3}}$easily but the value of ${{3.0005}^{3}}$is tough to find so we use the approximation.

Let $\text{y}+\text{ }\!\!\Delta\!\!\text{ y}={{\left( 3.0005 \right)}^{3}}$ and $3.0005=\text{x}+\text{ }\!\!\Delta\!\!\text{ x}$where $\text{x}=3,\text{ }\!\!~\!\!\text{  }\!\!\Delta\!\!\text{ x}=0.0005$

Also let $\text{y}={{\left( \text{x} \right)}^{3}}$

Now we differentiate on both sides w.r.t. t, 

$\frac{\text{dy}}{\text{dt}}=3{{\text{x}}^{2}}.\frac{\text{dx}}{\text{dt}}$

$\Rightarrow \text{ }\!\!\Delta\!\!\text{ y}=3{{\text{x}}^{2}}.\text{ }\!\!\Delta\!\!\text{ x}$

$\Rightarrow \text{ }\!\!\Delta\!\!\text{ y}=27\times 0.0005=0.0135$ and $\text{y}={{\left( 3 \right)}^{3}}=27$

So now $\text{y}+\text{ }\!\!\Delta\!\!\text{ y}={{\left( 3.0005 \right)}^{3}}=27+0.0135=27.0135$

Since $\text{V}=\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }\left( 27.0135-27 \right)=\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }\times 0.0135=0.0180\text{ }\!\!\pi\!\!\text{  }\!\!~\!\!\text{ c}{{\text{m}}^{3}}$

8. A man, 2m tall, walks at the rate of $1\frac{2}{3}$m/s towards a street light which is $5\frac{1}{3}$m above the ground. At what rate is the tip of his shadow moving? At what 136 MATHEMATICS rate is the length of the shadow changing when he is $3\frac{1}{3}$ m from the base of the light?

Ans: 

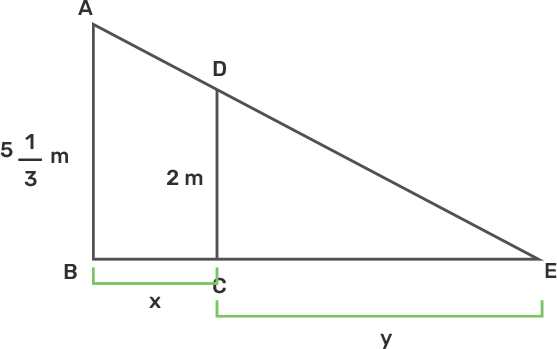
From the figure, Let AB be the height of street light source and CD be the height of man, CD=2m.

Let $\text{BC}=\text{x }\!\!~\!\!\text{ m},\text{ }\!\!~\!\!\text{ CE}=\text{y }\!\!~\!\!\text{ m}$and the man moving towards the light post so $\frac{\text{dx}}{\text{dt}}=-1\frac{2}{3}\text{m}/\text{sec}$ 

From $\text{ }\!\!\Delta\!\!\text{ ABE }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!\Delta\!\!\text{ DCE},\text{ }\!\!~\!\!\text{ }$we see that

$\frac{\text{AB}}{\text{CD}}=\frac{\text{BE}}{\text{CE}}\Rightarrow \frac{\frac{16}{3}}{2}=\frac{\text{x}+\text{y}}{\text{y}}$

$\Rightarrow \frac{16}{6}=\frac{\text{x}+\text{y}}{\text{y}}$

$\Rightarrow 10\text{y}=6\text{x}$

$\Rightarrow \text{y}=\frac{3}{5}\text{x}$

On differentiating both sides w.r.t. T

$\frac{\text{dy}}{\text{dt}}=\frac{3}{5}\frac{\text{dx}}{\text{dt}}$

$\Rightarrow \frac{\text{dy}}{\text{dt}}=\frac{3}{5}.\left( \frac{-5}{3} \right)=-1\text{m}/\text{sec}$

Let the distance of tip of shadow from the foot of street light post is Z

$\text{z}=\text{x}+\text{y}$

Now on differentiating both sides w.r.t. T, we get 

$\frac{\text{dz}}{\text{dt}}=\frac{\text{dx}}{\text{dt}}+\frac{\text{dy}}{\text{dt}}$

$\frac{\text{dz}}{\text{dt}}=\text{ }\!\!~\!\!\text{ }-\frac{5}{3}-1=\frac{-8}{3}\text{m}/\text{sec}$

Therefore the tip of shadow is moving at the rate of $\frac{-8}{3}\text{m}/\text{sec}$towards the light post and length of the shadow is decreasing at the rate of 1 m/s. 

9. A swimming pool is to be drained for cleaning. If L represents the number of litres of water in the pool t seconds after the pool has been plugged off to drain and $\mathbf{L}=200{{\left( 10-\mathbf{t} \right)}^{2}}$ . How fast is the water running out at the end of 5 seconds? What is the average rate at which the water flows out during the first 5 seconds?

Ans: Given that L represents the number of liters of water in the pool t seconds after the pool has been plugged off to drain and that is $\text{L}=200{{\left( 10-\text{t} \right)}^{2}}$

Let the rate at which water is running out = $-\frac{\text{dL}}{\text{dt}}$

 $\text{L}=200{{\left( 10-\text{t} \right)}^{2}}$

$\frac{\text{dL}}{\text{dt}}=400\left( 10-\text{t} \right)$

Rate at which the water  is running out at the t=5s 

$\frac{\text{dL}}{\text{dt}}{{|}_{\text{t}=5}}=400\left( 10-\text{t} \right)=400\left( 10-5 \right)=2000\text{L}/\text{sec}$

Since the initial Rate = $-\frac{\text{dL}}{\text{dt}}{{|}_{\text{t}=0}}$=400(10-0)=4000L/sec

Now the average rate = $\frac{\text{Initial }\!\!~\!\!\text{ Rate}+\text{Final }\!\!~\!\!\text{ Rate}}{2}$

$=\frac{4000+2000}{2}=3000\text{L}/\text{sec}$

10. The volume of a cube increases at a constant rate. Prove that the increase in its surface area varies inversely as the length of the side. 

Ans: Let the Side of a cube = x

We know the volume of a cube $\text{V}={{\text{x}}^{3}}$ and Surface area $\text{S}=6{{\text{x}}^{2}}$

Differentiating on both sides w.r.t. t,

$\frac{\text{dV}}{\text{dt}}=3{{\text{x}}^{2}}.\frac{\text{dx}}{\text{dt}}$

$\Rightarrow \text{k}=3{{\text{x}}^{2}}.\frac{\text{dx}}{\text{dt}}$ [Given volume of a cube increases at a constant rate so $\frac{\text{dV}}{\text{dt}}=\text{k}$]

$\Rightarrow \frac{\text{dx}}{\text{dt}}=\frac{\text{k}}{3{{\text{x}}^{2}}}$-------(1)

Also the surface area of cube $\text{S}=6{{\text{x}}^{2}}$

Differentiating on both sides w.r.t. t,

$\frac{\text{dS}}{\text{dt}}=12\text{x}.\frac{\text{dx}}{\text{dt}}$

Now by putting the value of $\frac{\text{dx}}{\text{dt}}$from eq. 1

$\frac{\text{dS}}{\text{dt}}=12\text{x}.\frac{\text{k}}{3{{\text{x}}^{2}}}$

$\Rightarrow \frac{\text{dS}}{\text{dt}}=\frac{4\text{k}}{\text{x}}$

$\Rightarrow \frac{\text{dS}}{\text{dt}}=4\left( \frac{\text{k}}{\text{x}} \right)$   [K= proportionality constant]

$\Rightarrow \frac{\text{dS}}{\text{dt}}\text{ }\!\!\alpha\!\!\text{  }\!\!~\!\!\text{ }\frac{1}{\text{x}}$

Hence the increase in its surface area varies inversely as the length of the side. 

11. x and y are the sides of two squares such that $\mathbf{y}=\mathbf{x}-{{\mathbf{x}}^{2}}$ . Find the rate of change of the area of the second square with respect to the area of the first square.

Ans: Given : x and y are the sides of two squares such that $\text{y}=\text{x}-{{\text{x}}^{2}}$

Let the area of first square having side x is ${{\text{A}}_{1}}={{\text{x}}^{2}}$

The area of second square having side y is ${{\text{A}}_{2}}={{\text{y}}^{2}}={{\left( \text{x}-{{\text{x}}^{2}} \right)}^{2}}$ and we have to find the rate of change of the area of the second area w.r.t.  area of the first square which mathematically can be written as =$\frac{\text{d}{{\text{A}}_{2}}}{\text{d}{{\text{A}}_{1}}}=\frac{\frac{\text{d}{{\text{A}}_{2}}}{\text{dt}}}{\frac{\text{d}{{\text{A}}_{1}}}{\text{dt}}}$

Now, ${{\text{A}}_{1}}={{\text{x}}^{2}}$

Differentiating on both sides w.r.t. t,

$\frac{\text{d}{{\text{A}}_{1}}}{\text{dt}}=2\text{x}.\text{ }\!\!~\!\!\text{ }\frac{\text{dx}}{\text{dt}}$--------(1)

And ${{\text{A}}_{2}}={{\left( \text{x}-{{\text{x}}^{2}} \right)}^{2}}$

Differentiating on both sides w.r.t. t,

$\frac{\text{d}{{\text{A}}_{2}}}{\text{dt}}=2\left( \text{x}-{{\text{x}}^{2}} \right)\left( 1-2\text{x} \right)\frac{\text{dx}}{\text{dt}}$--------(2)

Dividing Eq. 2 by Eq. 1

$\frac{\text{d}{{\text{A}}_{2}}}{\text{d}{{\text{A}}_{1}}}=\frac{\frac{\text{d}{{\text{A}}_{2}}}{\text{dt}}}{\frac{\text{d}{{\text{A}}_{1}}}{\text{dt}}}=\frac{2\left( \text{x}-{{\text{x}}^{2}} \right)\left( 1-2\text{x} \right)\frac{\text{dx}}{\text{dt}}}{2\text{x}.\text{ }\!\!~\!\!\text{ }\frac{\text{dx}}{\text{dt}}}$

$\Rightarrow \frac{\text{d}{{\text{A}}_{2}}}{\text{d}{{\text{A}}_{1}}}=\frac{2\text{x}\left( 1-\text{x} \right)\left( 1-2\text{x} \right)}{2\text{x}}$

$\Rightarrow \frac{\text{d}{{\text{A}}_{2}}}{\text{d}{{\text{A}}_{1}}}=\left( 1-\text{x} \right)\left( 1-2\text{x} \right)$

$\Rightarrow \frac{\text{d}{{\text{A}}_{2}}}{\text{d}{{\text{A}}_{1}}}=\left( 1-2\text{x}-\text{x}+2{{\text{x}}^{2}} \right)$

$\Rightarrow \frac{\text{d}{{\text{A}}_{2}}}{\text{d}{{\text{A}}_{1}}}=2{{\text{x}}^{2}}-3\text{x}+1$

12. Find the condition that the curves $2\mathbf{x}={{\mathbf{y}}^{2}}$ and $2\mathbf{xy}=\mathbf{k}$ intersect orthogonally.

Ans: Here first we find the point of intersection of given curves.

$2\text{x}={{\text{y}}^{2}}$-----(1) 

$2\text{xy}=\text{k}$----(2)

$\Rightarrow \text{y}=\frac{\text{k}}{2\text{x}}$

Now putting this value in eq. 1

$2\text{x}={{\left( \frac{\text{k}}{2\text{x}} \right)}^{2}}$

$\Rightarrow 8{{\text{x}}^{3}}={{\text{k}}^{2}}$

$\Rightarrow \text{x}=\frac{1}{2}{{\text{k}}^{\frac{2}{3}}}$

Now substituting this value in $\text{y}=\frac{\text{k}}{2\text{x}}$

$\text{y}=\frac{\text{k}}{2\frac{1}{2}{{\text{k}}^{\frac{2}{3}}}}={{\text{k}}^{\frac{1}{3}}}$

Thus the point of intersection of curves is $\left( \frac{1}{2}{{\text{k}}^{\frac{2}{3}}},{{\text{k}}^{\frac{1}{3}}}\text{ }\!\!~\!\!\text{ } \right)$

Orthogonality means the tangents on both the curves are intersecting each other at an angle of $\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$ that means ${{\text{m}}_{1}}\times {{\text{m}}_{2}}=\text{ }\!\!~\!\!\text{ }-1\text{ }\!\!~\!\!\text{ }$where ${{\text{m}}_{1}}\And \text{ }\!\!~\!\!\text{ }{{\text{m}}_{2}}$are the slopes of the curves.

$2\text{x}={{\text{y}}^{2}}$

Differentiating on both sides w.r.t. x,

$2=2\text{y}.\frac{\text{dy}}{\text{dx}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{2}{2\text{y}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}{{|}_{\left( \frac{1}{2}{{\text{k}}^{\frac{2}{3}}},{{\text{k}}^{\frac{1}{3}}} \right)}}=\frac{2}{2\left( {{\text{k}}^{\frac{1}{3}}} \right)}$  = ${{\text{m}}_{1}}\left( \text{assume} \right)$

$\text{Also},\text{ }\!\!~\!\!\text{ }2\text{xy}=\text{k}$

Differentiating on both sides w.r.t. X,

$2\left[ \text{y}+\text{x}.\frac{\text{dy}}{\text{dx}} \right]=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{-\text{y}}{\text{x}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}{{|}_{\left( \frac{1}{2}{{\text{k}}^{\frac{2}{3}}},{{\text{k}}^{\frac{1}{3}}} \right)}}=\frac{-{{\text{k}}^{\frac{1}{3}}}}{\frac{1}{2}{{\text{k}}^{\frac{2}{3}}}}=-{{\text{k}}^{\frac{-1}{3}}}$= ${{\text{m}}_{2}}\text{ }\!\!~\!\!\text{ }\left( \text{assume} \right)$

Since curves intersect orthogonally, So

${{\text{m}}_{1}}\times {{\text{m}}_{2}}=-1$

$\Rightarrow \frac{1}{\left( {{\text{k}}^{\frac{1}{3}}} \right)}\times -{{\text{k}}^{\frac{-1}{3}}}=-1$

$\Rightarrow -2{{\text{k}}^{\frac{-2}{3}}}=-1$

$\Rightarrow 2{{\text{k}}^{\frac{-2}{3}}}=1$

$\Rightarrow \frac{2}{{{\text{k}}^{\frac{2}{3}}}}=1$

$\Rightarrow {{\text{k}}^{\frac{2}{3}}}=2$

$\Rightarrow {{\text{k}}^{2}}=8$

Hence for intersecting the given curve orthogonally the required condition is ${{\text{k}}^{2}}=8$

13. Prove that the curves xy = 4 and ${{\mathbf{x}}^{2}}+{{\mathbf{y}}^{2}}={{8}_{{}}}$ touch each other.

Ans: If the curves touch each other then the slope of tangents on both curves on the touching point are the same . Since we have to prove this condition.

So first we find the touching point. 

Let we have a point (x,y) where the curves intersect.

xy = 4 $\Rightarrow \text{y}=\frac{4}{\text{x}}$---(1)

${{\text{x}}^{2}}+{{\text{y}}^{2}}={{8}_{{}}}$----(2)

Now on putting the value of $\text{y}=\frac{4}{\text{x}}$in Eq. 2 

${{\text{x}}^{2}}+{{\left( \frac{4}{\text{x}} \right)}^{2}}=8$

$\Rightarrow {{\text{x}}^{4}}+16=8{{\text{x}}^{2}}$

Let ${{\text{x}}^{2}}=\text{t}$

$\Rightarrow {{\text{t}}^{2}}-8\text{t}+16=0$

$\Rightarrow {{\left( \text{t}-4 \right)}^{2}}=0$

$\Rightarrow \text{t}=4$

$\Rightarrow {{\text{x}}^{2}}=4$

$\Rightarrow {{\text{x}}^{{}}}=\text{ }\!\!~\!\!\text{ }\pm 2$

Now from Eq. 1 

$\text{y}=\pm \frac{4}{2}$

So the touching points (2,2) & (-2,-2)

Now we find the slopes of both curves:

xy = 4

On differentiating both sides w.r.t. x, 

$\text{y}+\text{x}.\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{-\text{y}}{\text{x}}$=${{\text{m}}_{1}}\left( \text{say} \right)$

Also, ${{\text{x}}^{2}}+{{\text{y}}^{2}}={{8}_{{}}}$

Differentiating on both sides w.r.t. x,

$2\text{x}+2\text{y}.\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{-\text{y}}{\text{x}}={{\text{m}}_{2}}\left( \text{Say} \right)$

For point (2,2)

${{\text{m}}_{1}}=\frac{-2}{2}=\text{ }\!\!~\!\!\text{ }-1$

${{\text{m}}_{2}}=\frac{-2}{2}=\text{ }\!\!~\!\!\text{ }-1$

$\because \text{ }\!\!~\!\!\text{ }{{\text{m}}_{1}}={{\text{m}}_{2}}$

Also for point (-2,-2)

${{\text{m}}_{1}}=\frac{2}{2}=\text{ }\!\!~\!\!\text{ }1$

${{\text{m}}_{2}}=\frac{2}{2}=\text{ }\!\!~\!\!\text{ }1$

$\because \text{ }\!\!~\!\!\text{ }{{\text{m}}_{1}}={{\text{m}}_{2}}$

Thus, for both the intersection points,We see that the slopes of both curves are the same. Hence, the curves touch each other.

14.  Find the coordinates of the point on the curve $\sqrt{\mathbf{x}}+\sqrt{\mathbf{y}}=4~$at which tangent is equally inclined to the axes. 

Ans: Given that we have a curve $\sqrt{\text{x}}+\sqrt{\text{y}}=4$----(1)

Differentiating on both sides w.r.t. x, 

$\frac{1}{2\sqrt{\text{x}}}+\frac{1}{2\sqrt{\text{y}}}\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{-\sqrt{\text{y}}}{\sqrt{\text{x}}}$

The tangent inclined equally on both axes hence 

$\frac{\text{dy}}{\text{dx}}=\pm 1$

$\Rightarrow \frac{-\sqrt{\text{y}}}{\sqrt{\text{x}}}=\pm 1$

Squaring on both sides we get 

$\Rightarrow \frac{\text{y}}{\text{x}}=1$

$\Rightarrow \text{y}=\text{x}$----(2)

From eq. 1 , $\sqrt{\text{y}}+\sqrt{\text{y}}=4$

$\Rightarrow \sqrt{\text{y }\!\!~\!\!\text{ }}=2$

$\Rightarrow \text{y}=4$

Putting this value in eq. 2

$\Rightarrow \text{x}=4$

Hence the required coordinates of the point are (4,4).

15. Find the angle of intersection of the curves $\mathbf{y}=4-{{\mathbf{x}}^{2}}$ and $\mathbf{y}={{\mathbf{x}}^{2}}.$

Ans: Given that both curves are intersecting each other so first we find the intersection point and then find the angle b/w the tangents on both curves drawn on intersecting points.

$\text{y}=4-{{\text{x}}^{2}}$-----(1)

$\text{y}={{\text{x}}^{2}}$-------(2)

From Eq. 1 & 2

$4-{{\text{x}}^{2}}={{\text{x}}^{2}}$

$\Rightarrow 2{{\text{x}}^{2}}=4$

$\Rightarrow {{\text{x}}^{2}}=2$

$\Rightarrow \text{x}=\pm \sqrt{{}}2$

Now from eq. 1 $\text{y}={{\text{x}}^{2}}\Rightarrow \text{y}={{\left( \sqrt{2} \right)}^{2}}=2$

So the intersection points are $\left( \sqrt{2},2 \right)\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }\left( -\sqrt{2},2 \right)$.

Now we find the slopes of both curves

$\text{y}=4-{{\text{x}}^{2}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=-2\text{x}={{\text{m}}_{1}}\left( \text{Say} \right)$

$\text{y}={{\text{x}}^{2}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=2\text{x}={{\text{m}}_{2}}\left( \text{Say} \right)$

For point $\left( \sqrt{2},2 \right)$

${{\text{m}}_{1}}=-2\text{x}=-2\sqrt{2}$

${{\text{m}}_{2}}=2\text{x}=2\sqrt{2}$

So for point $\left( \sqrt{2},2 \right)$ $\text{tan }\!\!\theta\!\!\text{ }=\left| \frac{{{\text{m}}_{1}}-{{\text{m}}_{2}}}{1+{{\text{m}}_{1}}{{\text{m}}_{2}}} \right|=\left| \frac{-2\sqrt{2}-2\sqrt{2}}{1-2\sqrt{2}.2\sqrt{2}} \right|=\left| \frac{-4\sqrt{2}}{-7} \right|$

$\text{ }\!\!\theta\!\!\text{ }=\text{ta}{{\text{n}}^{-1}}\left( \frac{4\sqrt{2}}{7} \right)$

Now for point $\left( -\sqrt{2},2 \right)$

${{\text{m}}_{1}}=-2\text{x}=2\sqrt{2}$

${{\text{m}}_{2}}=2\text{x}=-2\sqrt{2}$

Here $\text{tan }\!\!\theta\!\!\text{ }=\left| \frac{{{\text{m}}_{1}}-{{\text{m}}_{2}}}{1+{{\text{m}}_{1}}{{\text{m}}_{2}}} \right|=\left| \frac{-2\sqrt{2}-2\sqrt{2}}{1-2\sqrt{2}.2\sqrt{2}} \right|=\left| \frac{-4\sqrt{2}}{-7} \right|$

$\text{ }\!\!\theta\!\!\text{ }=\text{ta}{{\text{n}}^{-1}}\left( \frac{4\sqrt{2}}{7} \right)$

Therefore, For both intersecting points we get the angle $\text{ }\!\!\theta\!\!\text{ }=\text{ta}{{\text{n}}^{-1}}\left( \frac{4\sqrt{2}}{7} \right)$.

16. Prove that the curves ${{\mathbf{y}}^{2}}=4\mathbf{x}$ and ${{\mathbf{x}}^{2}}+{{\mathbf{y}}^{2}}-6\mathbf{x}+1=0$ touch each other at the point (1, 2).

Ans: If the given curves touch each other then the slope of tangents on both curves at the intersecting point is same. 

Let the slope of curve ${{\text{y}}^{2}}=4\text{x}$is ${{\text{m}}_{1}}$and the slope of curve ${{\text{x}}^{2}}+{{\text{y}}^{2}}-6\text{x}+1$is ${{\text{m}}_{2}}$. So for these curves ${{\text{m}}_{1}}={{\text{m}}_{2}}$

 ${{\text{y}}^{2}}=4\text{x}$

Differentiating on both sides w.r.t. x,

$2\text{y}.\frac{\text{dy}}{\text{dx}}=4$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{2}{\text{y}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}{{|}_{\left( 1,2 \right)}}=\frac{2}{\text{y}}=\frac{2}{2}=1$

$\Rightarrow {{\text{m}}_{1}}=1$

And ${{\text{x}}^{2}}+{{\text{y}}^{2}}-6\text{x}+1=0$

Differentiating on both sides w.r.t. x,

$2\text{x}+2\text{y}.\frac{\text{dy}}{\text{dx}}-6=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{6-2\text{x}}{2\text{y}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}{{|}_{\left( 1,2 \right)}}=\frac{3-\text{x}}{\text{y}}=\frac{2}{2}=1$

$\Rightarrow {{\text{m}}_{2}}=1$

Thus we see that the slope of both the curves are equal toeach other i.e., ${{\text{m}}_{1}}={{\text{m}}_{2}}=1$ at the point(1,2).

17. Find the equation of the normal lines to the curve $3{{\mathbf{x}}^{2}}-{{\mathbf{y}}^{2}}=8$ which are parallel to the line x + 3y = 4. 

Ans: We are given an equation of a curve $3{{\text{x}}^{2}}-{{\text{y}}^{2}}=8$-----(1)

First we find the slope of normal on the given curve $3{{\text{x}}^{2}}-{{\text{y}}^{2}}=8$

Differentiating on both sides w.r.t. X

$6\text{x}-2\text{y}\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{3\text{x}}{\text{y}}$ 

This is the slope of tangent on the given curve but we have to find the slope of normal, and we know that $\text{slope }\!\!~\!\!\text{ of }\!\!~\!\!\text{ normal }\!\!~\!\!\text{ }=\frac{-1}{\text{slope }\!\!~\!\!\text{ of }\!\!~\!\!\text{ tangent }\!\!~\!\!\text{ }}$So the slope of normal on the given curve  = $\frac{-1}{\frac{\text{dy}}{\text{dx}}}=\frac{-\text{y}}{3\text{x}}$

It is given that the normal is parallel to the line x + 3y = 4. We know that the slope of two parallel lines are the same hence the slope of normal will be equal to the slope of the given line . So the slope of line $=\frac{-\text{a}}{\text{b}}=\frac{-1}{3}$

$\Rightarrow \frac{-\text{y}}{3\text{x}}=\frac{-1}{3}$

$\Rightarrow \text{y}=\text{x}$--------(2)

On substituting $\text{y}=\text{x}$ in eq. 1, we get 

$3{{\text{x}}^{2}}-{{\text{x}}^{2}}=8$

$\Rightarrow 2{{\text{x}}^{2}}=8$

$\Rightarrow \text{x}=2,-2$

For x=2, from eq. 2 $\text{y}=$2

For x=-2, y=-2

Hence the (2,2) and (-2,2) are the points where the normal at the given curve is parallel to line x + 3y = 4.

Now the Required equations of normals passing through points (2,2) & (-2,2) and having slope of $\frac{-1}{3}$ are

$\left( \text{y}-2 \right)=\frac{-1}{3}\left( \text{x}-2 \right)\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }\left( \text{y}+2 \right)=\frac{-1}{3}\left( \text{x}+2 \right)$

$\Rightarrow 3\left( \text{y}-2 \right)=-1\left( \text{x}-2 \right)\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{ }3\left( \text{y}+2 \right)=-1\left( \text{x}+2 \right)$

$\Rightarrow 3\text{y}+\text{x}=8\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{ }3\text{y}+\text{x}=\text{ }\!\!~\!\!\text{ }-8$

So the required equations of Normal are $3\text{y}+\text{x}=\text{ }\!\!~\!\!\text{ }\pm 8\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ }$

18.  At what points on the curve ${{\mathbf{x}}^{2}}+{{\mathbf{y}}^{2}}-2\mathbf{x}-4\mathbf{y}+1=0$, the tangents are parallel to the y-axis?

Ans: We are given an equation of the curve ${{\text{x}}^{2}}+{{\text{y}}^{2}}-2\text{x}-4\text{y}+1=0$-------(1)

Differentiating on both sides w.r.t. x,

$2\text{x}+2\text{y}.\frac{\text{dy}}{\text{dx}}-2-4\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}\left( 2\text{y}-4 \right)=2\left( 1-\text{x} \right)$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{2\left( 1-\text{x} \right)}{2\left( \text{y}-2 \right)}$

This is the slope of tangent which is parallel to y-axis and we know that the slope of y-axis is $\frac{1}{0}.$So the above slope of tangent will be equal to $\frac{1}{0}$.

 $\frac{2\left( 1-\text{x} \right)}{2\left( \text{y}-2 \right)}=\frac{1}{0}$

$\Rightarrow \left( \text{y}-2 \right)=0$

$\Rightarrow \text{y}=2$

On substituting $\text{y}=2$ in eq.1, we get 

${{\text{x}}^{2}}+4-2\text{x}-8+1=0$

$\Rightarrow {{\text{x}}^{2}}-2\text{x}-3=0$

$\Rightarrow {{\text{x}}^{2}}-3\text{x}+\text{x}-3=0$

$\Rightarrow \left( \text{x}-3 \right)\left( \text{x}+1 \right)=0$

$\Rightarrow \text{x}=3,-1$

Hence the required points are (3,2) &(-1,2) where the tangents are parallel to the y-axis.

19. Show that the line $\frac{\mathbf{x}}{\mathbf{a}}+\frac{\mathbf{y}}{\mathbf{b}}=1$, touches the curve $\mathbf{y}=\mathbf{b}.{{\mathbf{e}}^{\frac{-\mathbf{x}}{\mathbf{a}}}}$ at the point where the curve intersects the axis of y. 

Ans: Given we have given a curve $\text{y}=\text{b}.{{\text{e}}^{\frac{-\text{x}}{\text{a}}}}$and line$\frac{\text{x}}{\text{a}}+\frac{\text{y}}{\text{b}}=1$.

We know that if two curves touch each other at a point then the slope of both the curves at the meeting point should be equal i.e. ${{\text{m}}_{1}}={{\text{m}}_{2}}$where ${{\text{m}}_{1}}\And \text{ }\!\!~\!\!\text{ }{{\text{m}}_{2}}$

are slopes of curves.

The curve $\text{y}=\text{b}.{{\text{e}}^{\frac{-\text{x}}{\text{a}}}}$intersects the y-axis i.e. x=0

$\text{y}=\text{b}.{{\text{e}}^{0}}=\text{b}$

So the point of intersection is (0,b).

Now the slope of curve at point (0,b) is:

$\frac{\text{dy}}{\text{dx}}=\text{b}.{{\text{e}}^{\frac{-\text{x}}{\text{a}}}}.\left( \frac{-1}{\text{a}} \right)$

$\Rightarrow {{\left( \frac{\text{dy}}{\text{dx}} \right)}_{\left( 0,\text{b} \right)}}=\text{b}.{{\text{e}}^{0}}.\left( \frac{-1}{\text{a}} \right)=\frac{-\text{b}}{\text{a}}=\left( {{\text{m}}_{1}} \right)$---------(1)

Also slope of the line  $\frac{\text{x}}{\text{a}}+\frac{\text{y}}{\text{b}}=1$at point (0,b) is:

Differentiating the equation of line w.r.t. x,

$\frac{1}{\text{a}}+\frac{1}{\text{b}}.\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{-\text{b}}{\text{a}}=\left( {{\text{m}}_{2}} \right)$-----(2)

From eq. 1 and eq.2 

${{\text{m}}_{1}}={{\text{m}}_{2}}=\frac{-\text{b}}{\text{a}}$

Therefore, the line $\frac{\text{x}}{\text{a}}+\frac{\text{y}}{\text{b}}=1$touches the curve $\text{y}=\text{b}.{{\text{e}}^{\frac{-\text{x}}{\text{a}}}}$at the point (0,b).

20.  Show that $\mathbf{f}\left( \mathbf{x} \right)=2\mathbf{x}+\mathbf{co}{{\mathbf{t}}^{-1}}\mathbf{x}+\mathbf{log}\left( \sqrt{1+{{\mathbf{x}}^{2}}}-\mathbf{x} \right)$ is increasing in R.

Ans: Given function  $\text{f}\left( \text{x} \right)=2\text{x}+\text{co}{{\text{t}}^{-1}}\text{x}+\text{log}\left( \sqrt{1+{{\text{x}}^{2}}}-\text{x} \right)$

A function is said to be increasing function if $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)>0\text{ }\!\!~\!\!\text{ }$in its domain .

$\text{f}\left( \text{x} \right)=2\text{x}+\text{co}{{\text{t}}^{-1}}\text{x}+\text{log}\left( \sqrt{1+{{\text{x}}^{2}}}-\text{x} \right)$

Differentiating the function w.r.t. x,

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=2+\frac{-1}{1+{{\text{x}}^{2}}}+\frac{1}{\sqrt{1+{{\text{x}}^{2}}}-\text{x}}\left( \frac{1}{2\sqrt{1+{{\text{x}}^{2}}}}.2\text{x}-1 \right)$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=2-\frac{1}{1+{{\text{x}}^{2}}}+\frac{1}{\sqrt{1+{{\text{x}}^{2}}}-\text{x}}\left( \frac{\text{x}-\sqrt{1+{{\text{x}}^{2}}}}{\sqrt{1+{{\text{x}}^{2}}}} \right)$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=2-\frac{1}{1+{{\text{x}}^{2}}}-\frac{1}{\sqrt{1+{{\text{x}}^{2}}}}$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{2\left( 1+{{\text{x}}^{2}} \right)-1-\sqrt{1+{{\text{x}}^{2}}}}{1+{{\text{x}}^{2}}}$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{1+2{{\text{x}}^{2}}-\sqrt{1+{{\text{x}}^{2}}}}{1+{{\text{x}}^{2}}}$

For increasing function, $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)>0$

$\frac{1+2{{\text{x}}^{2}}-\sqrt{1+{{\text{x}}^{2}}}}{1+{{\text{x}}^{2}}}>0$

$\Rightarrow 1+2{{\text{x}}^{2}}-\sqrt{1+{{\text{x}}^{2}}}>0\text{ }\!\!~\!\!\text{ }$            [$1+{{\text{x}}^{2}}\text{ }\!\!~\!\!\text{ is }\!\!~\!\!\text{ always }\!\!~\!\!\text{ positive}$]

$\Rightarrow 1+2{{\text{x}}^{2}}>\sqrt{1+{{\text{x}}^{2}}}$

$\Rightarrow {{\left( 1+2{{\text{x}}^{2}} \right)}^{2}}>1+{{\text{x}}^{2}}$       [Squaring on both sides]

$\Rightarrow 1+4{{\text{x}}^{2}}+4{{\text{x}}^{4}}>1+{{\text{x}}^{2}}$

$\Rightarrow 4{{\text{x}}^{4}}+3{{\text{x}}^{2}}>0$

$\Rightarrow {{\text{x}}^{2}}\left( 4{{\text{x}}^{2}}+3 \right)>0$ 

This is true for every value of x, Hence the f(x) is increasing in R.

21.  Show that for a ≥ 1, $\mathbf{f}\left( \mathbf{x} \right)=\sqrt{3}\mathbf{sinx}-\mathbf{cosx}-2\mathbf{ax}+\mathbf{b}$ is decreasing in R.

Ans: We have function $\text{f}\left( \text{x} \right)=\sqrt{3}\text{sinx}-\text{cosx}-2\text{ax}+\text{b}$ 

We know that a function is said to be decreasing if $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)<0$in its domain.

Differentiating the function w.r.t. x,

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\sqrt{3}\text{cosx}+\text{sinx}-2\text{a}$

$=2\left[ \frac{\sqrt{3}}{2}\text{cosx}+\frac{1}{2}\text{sinx} \right]-2\text{a}$     [Multiplying and dividing by 2]

$=2\left[ \text{cos}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)\text{cosx}+\text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)\text{sinx} \right]-2\text{a}$

$=2\left[ \text{cos}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6}-\text{x} \right) \right]-2\text{a}$

We know that $-1\le \text{cosx}\le 1$So $-1\le \text{cos}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6}-\text{x} \right)\le 1$

$\Rightarrow -2-2\text{a}\le 2\text{cos}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6}-\text{x} \right)-2\text{a}\le 2-2\text{a}$

$\Rightarrow -2-2\text{a}\le \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)\le 2-2\text{a}$

Here we have to prove that the function is decreasing , we know that the function is decreasing if $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)<0$. For the given function we have$-2-2\text{a}\le \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)\le 2-2\text{a}$ so if the maximum value of $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)$ is $<0\text{ }\!\!~\!\!\text{ }$then the function will be decreasing in its domain.

So ,  $2-2\text{a}\le 0$

$\Rightarrow 2\text{a}\ge 2$

$\Rightarrow \text{a}\ge 1$

Therefore the function will be decreasing for $\text{a}\ge 1$.

22. Show that $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{ta}{{\mathbf{n}}^{-1}}\left( \mathbf{sinx}+\mathbf{cosx} \right)$ is an increasing function in $\left( 0,\frac{\mathbf{\pi }}{4} \right)$.

Ans: The given function  $\text{f}\left( \text{x} \right)=\text{ta}{{\text{n}}^{-1}}\left( \text{sinx}+\text{cosx} \right)$

Differentiating the function

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{1}{1+{{\left( \text{sinx}+\text{cosx} \right)}^{2}}}\left( \text{cosx}-\text{sinx} \right)$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{1}{1+{{\left( \text{sinx}+\text{cosx} \right)}^{2}}}\left( \text{cosx}-\text{sinx} \right)$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{1}{1+\text{si}{{\text{n}}^{2}}\text{x}+\text{co}{{\text{s}}^{2}}\text{x}+2\text{sinx}.\text{cosx}}\left( \text{cosx}-\text{sinx} \right)$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{1}{2\left( 1+\text{sinx}.\text{cosx} \right)}\left( \text{cosx}-\text{sinx} \right)$

For increasing function $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)>0$

$\frac{1}{2\left( 1+\text{sinx}.\text{cosx} \right)}\left( \text{cosx}-\text{sinx} \right)>0$

$\Rightarrow \left( \text{cosx}-\text{sinx} \right)>0$ [2sinx.cosx is +ve in $\left( 0,\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)$]

$\Rightarrow \text{cosx}>\text{sinx}$

$\Rightarrow \text{tanx}<1\text{ }\!\!~\!\!\text{ }$

This is true when $\text{x}\in \left( 0,\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)$

So the function is increasing in $\left( 0,\frac{\text{ }\!\!\pi\!\!\text{ }}{4} \right)$.

23. At what point, the slope of the curve $\mathbf{y}=-{{\mathbf{x}}^{3}}+3{{\mathbf{x}}^{2}}+9\mathbf{x}-27$ is maximum? Also find the maximum slope.

Ans: The curve we have: $\text{y}=-{{\text{x}}^{3}}+3{{\text{x}}^{2}}+9\text{x}-27$---------(1)

Slope of tangent on the curve $\frac{\text{dy}}{\text{dx}}=-3{{\text{x}}^{2}}+6\text{x}+9$

Now, $\frac{{{\text{d}}^{2}}\text{y}}{\text{d}{{\text{x}}^{2}}}=-6\text{x}+6$

For critical point, $\frac{{{\text{d}}^{2}}\text{y}}{\text{d}{{\text{x}}^{2}}}=0$

$\Rightarrow -6\text{x}+6=0$

$\Rightarrow \text{x}=1$

For slope to be maximum, $\frac{\text{d}}{\text{dx}}\left( \frac{{{\text{d}}^{2}}\text{y}}{\text{d}{{\text{x}}^{2}}} \right)<0$

Now , $\frac{\text{d}}{\text{dx}}\left( \frac{{{\text{d}}^{2}}\text{y}}{\text{d}{{\text{x}}^{2}}} \right)=-6<0$ Hence the slope will be maximum at x=1.

On substituting x=1 in eq. 1 we get,

$\text{y}=-{{\left( 1 \right)}^{3}}+3{{\left( 1 \right)}^{2}}+9\left( 1 \right)-27=-1+3+9-27=\text{ }\!\!~\!\!\text{ }-16$

So the point is (1, -16) at which the slope of the curve is maximum .

Slope at x=1,  $\frac{\text{dy}}{\text{dx}}{{|}_{\text{x}=1}}=-3{{\left( 1 \right)}^{2}}+6\left( 1 \right)+9=-3+6+9=12$

Hence the point is (1, -16) and the maximum slope is 12.

24. Prove that $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{sinx}+\sqrt{3}\mathbf{cosx}$ has maximum value at $\mathbf{x}=\frac{\mathbf{\pi }}{6}$.

Ans: 

The function we have : $\text{f}\left( \text{x} \right)=\text{sin }\!\!~\!\!\text{ x}+\sqrt{3}\text{cos }\!\!~\!\!\text{ x}$

Differentiating the function w.r.t. X,

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{cosx}-\sqrt{3}\text{sinx}$

For critical point $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\text{cosx}-\sqrt{3}\text{sinx}=0$

$\Rightarrow \text{tanx}=\frac{1}{\sqrt{3}}$

$\Rightarrow \text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$

For finding either function has maxima or minima, we again differentiate the $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)$. 

$\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{ }\!\!~\!\!\text{ }-\text{sinx}-\sqrt{3}\text{cosx}$

At $\text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$, $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\text{ }\!\!~\!\!\text{ }-\text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)-\sqrt{3}\text{cos}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{6} \right)=\frac{-1}{2}-\sqrt{3}.\frac{\sqrt{3}}{2}=-2<0$

Thus the function has local maxima and the point of maxima is $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$.

25. If the sum of the lengths of the hypotenuse and a side of a right angled triangle is given, show that the area of the triangle is maximum when the angle between them is $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$. 

Ans: 

Let the triangle is $\text{ }\!\!\Delta\!\!\text{ ABC }\!\!~\!\!\text{ }$in which BC=y, 

AB=x, AC=h

Given : $\text{h}+\text{x}=\text{k}$--------(1)

By using the pythagorean theorem in triangle $\text{ }\!\!\Delta\!\!\text{ ABC}$ as 

${{\text{h}}^{2}}={{\text{x}}^{2}}+{{\text{y}}^{2}}$ Here x and y are unknown.

By eq. 1 $\text{h}=\text{k}-\text{x }\!\!~\!\!\text{ }$

${{\left( \text{k}-\text{x} \right)}^{2}}={{\text{x}}^{2}}+{{\text{y}}^{2}}$

$\Rightarrow {{\text{k}}^{2}}+{{\text{x}}^{2}}-2\text{kx}={{\text{x}}^{2}}+{{\text{y}}^{2}}$

$\Rightarrow \text{y}=\sqrt{{{\text{k}}^{2}}-2\text{kx}}$------(2)

Now area of triangle $\text{ }\!\!\Delta\!\!\text{ ABC}=\frac{1}{2}\text{AB}.\text{BC}=\frac{1}{2}\text{xy}$

$\text{A}=\frac{1}{2}\text{x}.\sqrt{{{\text{k}}^{2}}-2\text{kx}}$

Now we have to maximize the area of the triangle, So we differentiate w.r.t. x, 

$\frac{\text{dA}}{\text{dx}}=\frac{1}{2}\left[ \sqrt{{{\text{k}}^{2}}-2\text{kx}}.+\text{x}\frac{1}{2\sqrt{{{\text{k}}^{2}}-2\text{kx}}}\left( 0-2\text{k} \right) \right]$

For critical points, $\frac{\text{dA}}{\text{dx}}=0$

$\frac{1}{2}\left[ \sqrt{{{\text{k}}^{2}}-2\text{kx}}.+\text{x}\frac{1}{2\sqrt{{{\text{k}}^{2}}-2\text{kx}}}\left( 0-2\text{k} \right) \right]=0$

$\Rightarrow {{\text{k}}^{2}}-2\text{kx}-\text{kx}=0$

$\Rightarrow \text{x}=\frac{\text{k}}{3}$

Again differentiating $\frac{\text{dA}}{\text{dx}}\text{ }\!\!~\!\!\text{ w}.\text{r}.\text{t}.\text{ }\!\!~\!\!\text{ x}$, we get

$\frac{{{\text{d}}^{2}}\text{A}}{\text{d}{{\text{x}}^{2}}}=\frac{1}{2}\left[ \frac{1}{2\sqrt{{{\text{k}}^{2}}-2\text{kx}}}.\left( -2\text{k} \right)-\text{k}\frac{\sqrt{{{\text{k}}^{2}}-2\text{kx}}-\text{x}.\text{ }\!\!~\!\!\text{ }\frac{1}{2\sqrt{{{\text{k}}^{2}}-2\text{kx}}}\left( -2\text{k} \right)}{{{\text{k}}^{2}}-2\text{kx}} \right]$

$=\frac{1}{2}\left[ \frac{-{{\text{k}}^{2}}\text{x}}{{{\left( {{\text{k}}^{2}}-2\text{kx} \right)}^{\frac{3}{2}}}}-\frac{2\text{k}}{\sqrt{{{\text{k}}^{2}}-2\text{kx}}} \right]$

$=\frac{-{{\text{k}}^{2}}\text{x}-2\text{k}\left( {{\text{k}}^{2}}-2\text{kx} \right)}{\left( {{\text{k}}^{2}}-2\text{kx} \right){{\frac{3}{2}}^{{}}}}$

$=\frac{3{{\text{k}}^{2}}\text{x}-2{{\text{k}}^{3}}}{\left( {{\text{k}}^{2}}-2\text{kx} \right){{\frac{3}{2}}^{{}}}}$

At $\text{x}=\frac{\text{k}}{3}$ we have $\frac{{{\text{d}}^{2}}\text{A}}{\text{d}{{\text{x}}^{2}}}=\frac{-{{\text{k}}^{3}}}{{{\text{k}}^{3}}}{{\left( 3 \right)}^{\frac{-3}{2}}}<0$ 

So area will be maximum at $\text{x}=\frac{\text{k}}{3}$.

On putting the value $\text{x}=\frac{\text{k}}{3}$in eq. 2

$\text{y}=\sqrt{{{\text{k}}^{2}}-2\text{k}.\frac{\text{k}}{3}}=\frac{\text{k}}{\sqrt{{}}3}$

So the point is $\left( \frac{\text{k}}{3},\frac{\text{k}}{\sqrt{3}} \right)$ where we get the maximum area of the triangle. At the given point the value of angle is $\text{tan }\!\!\theta\!\!\text{  }\!\!~\!\!\text{ }=\text{ }\!\!~\!\!\text{ }\frac{\text{y}}{\text{x}}=\frac{\frac{\text{k}}{\sqrt{3}}}{\frac{\text{k}}{3}}=\sqrt{3}$

$\text{tan }\!\!\theta\!\!\text{ }=\sqrt{3}\Rightarrow \text{ }\!\!\theta\!\!\text{ }=\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$

Therefore the area of triangle is maximum when the angle is $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$.

26. Find the points of local maxima, local minima and the points of inflection of the function $\mathbf{f}\left( \mathbf{x} \right)={{\mathbf{x}}^{5}}-5{{\mathbf{x}}^{4}}+5{{\mathbf{x}}^{3}}-1$. Also find the corresponding local maximum and local minimum values.

Ans: Given function $\text{f}\left( \text{x} \right)={{\text{x}}^{5}}-5{{\text{x}}^{4}}+5{{\text{x}}^{3}}-1$

Differentiating the function w.r.t. x,

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=5{{\text{x}}^{4}}-20{{\text{x}}^{3}}+15{{\text{x}}^{2}}$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=5{{\text{x}}^{2}}\left( {{\text{x}}^{2}}-4\text{x}+3 \right)$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=5{{\text{x}}^{2}}\left( {{\text{x}}^{2}}-3\text{x}-\text{x}+3 \right)$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=5{{\text{x}}^{2}}(\text{x}-1\left( \text{x}-3 \right)$

For critical points $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$5{{\text{x}}^{2}}(\text{x}-1\left( \text{x}-3 \right)=0$

$\Rightarrow \text{x}=0,1,3$

(Image will be uploaded soon)

If we see at point x=0 , the value of f’(x) is not changing that means the function has neither maxima nor minima.

At x=1, the value of f’(x) is changing from +ve to -ve so at x=1 the function has local maxima.

So the corresponding maximum value is $\text{f}\left( 1 \right)=1-5+5-1=0$

At x=3 , the value of f’(x) is changing from -ve to +ve so at x=3 the function has local minima.

Now the corresponding minimum value is 

$\text{f}\left( 3 \right)={{\left( 3 \right)}^{5}}-5{{\left( 3 \right)}^{4}}+5{{\left( 3 \right)}^{3}}-1=243-405+135-1=-28$.

27. A telephone company in a town has 500 subscribers on its list and collects fixed charges of Rs 300/- per subscriber per year. The company proposes to increase the annual subscription and it is believed that for every increase of Re 1/- one subscriber will discontinue the service. Find what increase will bring maximum profit? 

Ans: Let the company increase its annual subscription by x Rs.

So the x subscriber will discontinue the service.

Now the total revenue of the company after the increment

$\text{R}\left( \text{x} \right)=\left( 500-\text{x} \right)\left( 300+\text{x} \right)$

$\Rightarrow \text{R}\left( \text{x} \right)=150000+500\text{x}-300\text{x}-{{\text{x}}^{2}}$

On differentiating both sides w.r.t. x, 

$\text{R }\!\!'\!\!\text{ }\left( \text{x} \right)=500-300-2\text{x}$

Now, $\text{R }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$200-2\text{x}=0$

$\Rightarrow \text{x}=100$

For finding maxima and minima of the function we again differentiate $\text{R }\!\!'\!\!\text{ }\left( \text{x} \right)$

$\text{R }\!\!'\!\!\text{ }\left( \text{x} \right)=500-300-2\text{x}$

$\text{R }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=-2<0$

So the revenue will be maximum at x=100.

Hence the maximum value of revenue 

$\text{R}\left( 100 \right)=\left( 500-100 \right)\left( 300+100 \right)=400\times 400=160000$

Hence the company will earn the maximum profit at the increment of 100 Rs.

28. If the straight line x cosα + y sinα = p touches the curve $\frac{{{\mathbf{x}}^{2}}}{{{\mathbf{a}}^{2}}}+\frac{{{\mathbf{y}}^{2}}}{{{\mathbf{b}}^{2}}}=1$, then prove that ${{\mathbf{a}}^{2}}\mathbf{co}{{\mathbf{s}}^{2}}\mathbf{\alpha }+{{\mathbf{b}}^{2}}\mathbf{si}{{\mathbf{n}}^{2}}\mathbf{\alpha }={{\mathbf{p}}^{2}}$.

Ans: Given curve$\frac{{{\text{x}}^{2}}}{{{\text{a}}^{2}}}+\frac{{{\text{y}}^{2}}}{{{\text{b}}^{2}}}=1$

It is given that the line x cosα + y sinα = p touches the curve that means the slope of the line should be equal to the slope of the tangent to the curve.

$\frac{{{\text{x}}^{2}}}{{{\text{a}}^{2}}}+\frac{{{\text{y}}^{2}}}{{{\text{b}}^{2}}}=1$---------(1)

On differentiating both sides w.r.t. x, 

$\frac{2\text{x}}{{{\text{a}}^{2}}}+\frac{2\text{y}}{{{\text{b}}^{2}}}.\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{\text{b}{{2}^{{}}}}{{{\text{a}}^{2}}}\left( \frac{-\text{x}}{\text{y}} \right)$

This slope should be equal to the slope of line x cosα + y sinα = p which is $\text{slope }\!\!~\!\!\text{ of }\!\!~\!\!\text{ line }\!\!~\!\!\text{ }=\frac{-\text{coefficient }\!\!~\!\!\text{ of }\!\!~\!\!\text{ x}}{\text{coefficient }\!\!~\!\!\text{ of }\!\!~\!\!\text{ y}}=\frac{-\text{cos }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{ }}{\text{sin }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{ }}=-\text{cot }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{ }$

Now, $\frac{\text{b}{{2}^{{}}}}{{{\text{a}}^{2}}}\left( \frac{-\text{x}}{\text{y}} \right)=-\text{cot }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{ }$

$\Rightarrow \frac{\text{x}}{{{\text{a}}^{2}}\text{cos }\!\!\alpha\!\!\text{ }}=\frac{\text{y}}{{{\text{b}}^{2}}\text{sin }\!\!\alpha\!\!\text{ }}$

Let $\text{k}=\frac{\text{x}}{{{\text{a}}^{2}}\text{cos }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{ }}=\frac{\text{y}}{{{\text{b}}^{2}}\text{sin }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{ }}$

$\Rightarrow \text{x}=\text{k}{{\text{a}}^{2}}\text{cos }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{  }\!\!~\!\!\text{ },\text{ }\!\!~\!\!\text{ y}=\text{k}{{\text{b}}^{2}}\text{sin }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{ }$

So the point is ${{(\text{k}{{\text{a}}^{2}}\text{cos }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{  }\!\!~\!\!\text{ },\text{ }\!\!~\!\!\text{ k}{{\text{b}}^{2}}\text{sin }\!\!~\!\!\text{  }\!\!\alpha\!\!\text{ })}_{{}}}$where the line x cosα + y sinα = p touches the curve $\frac{{{\text{x}}^{2}}}{{{\text{a}}^{2}}}+\frac{{{\text{y}}^{2}}}{{{\text{b}}^{2}}}=1$.

On substituting the point in given curve, we get 

$\frac{{{\left( \text{k}{{\text{a}}^{2}}\text{cos }\!\!\alpha\!\!\text{ } \right)}^{2}}}{{{\text{a}}^{2}}}+\frac{{{\left( \text{k}{{\text{b}}^{2}}\text{sin }\!\!\alpha\!\!\text{ } \right)}^{2}}}{{{\text{b}}^{2}}}=1$

$\Rightarrow {{\text{k}}^{2}}{{\text{b}}^{2}}{{\text{a}}^{4}}\text{co}{{\text{s}}^{2}}\text{ }\!\!\alpha\!\!\text{ }+{{\text{k}}^{2}}{{\text{b}}^{4}}{{\text{a}}^{2}}\text{si}{{\text{n}}^{2}}\text{ }\!\!\alpha\!\!\text{ }={{\text{a}}^{2}}{{\text{b}}^{2}}$

$\Rightarrow {{\text{k}}^{2}}{{\text{b}}^{2}}{{\text{a}}^{2}}\left( {{\text{a}}^{2}}\text{co}{{\text{s}}^{2}}\text{ }\!\!\alpha\!\!\text{ }+{{\text{b}}^{2}}\text{si}{{\text{n}}^{2}}\text{ }\!\!\alpha\!\!\text{ } \right)={{\text{a}}^{2}}{{\text{b}}^{2}}$

$\Rightarrow \left( {{\text{a}}^{2}}\text{co}{{\text{s}}^{2}}\text{ }\!\!\alpha\!\!\text{ }+{{\text{b}}^{2}}\text{si}{{\text{n}}^{2}}\text{ }\!\!\alpha\!\!\text{ } \right)=\frac{1}{{{\text{k}}^{2}}}$--------(2)

Now substituting the point ${{(\text{k}{{\text{a}}^{2}}\text{cos }\!\!\alpha\!\!\text{  }\!\!~\!\!\text{ },\text{ }\!\!~\!\!\text{ k}{{\text{b}}^{2}}\text{sin }\!\!\alpha\!\!\text{ })}_{{}}}$in equation of line x cosα + y sinα = p 

$\text{k}{{\text{a}}^{2}}\text{cos }\!\!\alpha\!\!\text{ }.\text{cos }\!\!\alpha\!\!\text{ }+\text{k}{{\text{b}}^{2}}\text{sin }\!\!\alpha\!\!\text{ }.\text{ }\!\!~\!\!\text{ sin }\!\!\alpha\!\!\text{ }=\text{p}$

$\Rightarrow \text{k}\left( {{\text{a}}^{2}}\text{co}{{\text{s}}^{2}}\text{ }\!\!\alpha\!\!\text{ }+{{\text{b}}^{2}}\text{si}{{\text{n}}^{2}}\text{ }\!\!\alpha\!\!\text{ } \right)=\text{p}$

$\Rightarrow {{\text{a}}^{2}}\text{co}{{\text{s}}^{2}}\text{ }\!\!\alpha\!\!\text{ }+{{\text{b}}^{2}}\text{si}{{\text{n}}^{2}}\text{ }\!\!\alpha\!\!\text{ }=\frac{\text{p}}{\text{k}}$

Squaring on both sides

$\Rightarrow {{\left( {{\text{a}}^{2}}\text{co}{{\text{s}}^{2}}\text{ }\!\!\alpha\!\!\text{ }+{{\text{b}}^{2}}\text{si}{{\text{n}}^{2}}\text{ }\!\!\alpha\!\!\text{ } \right)}^{2}}=\frac{{{\text{p}}^{2}}}{{{\text{k}}^{2}}}$-----(3)

Now on dividing eq.(3) by eq.(2)

${{\text{a}}^{2}}\text{co}{{\text{s}}^{2}}\text{ }\!\!\alpha\!\!\text{ }+{{\text{b}}^{2}}\text{si}{{\text{n}}^{2}}\text{ }\!\!\alpha\!\!\text{ }={{\text{p}}^{2}}$(Hence proved)

29.  An open box with square base is to be made of a given quantity of card board of area ${{\mathbf{c}}^{2}}^{{}}$. Show that the maximum volume of the box is $\frac{{{\mathbf{c}}^{3}}}{6\sqrt{3}}$ cubic units.

Ans: 

Let the side of the square base is x and its height is y.

Area of base =${{\text{x}}^{2}}$

Given: The area of the metal used is ${{\text{x}}^{2}}+4\text{xy}={{\text{c}}^{2}}$

$\Rightarrow \text{y}=\frac{{{\text{c}}^{2}}-\text{x}{{2}^{{}}}}{4\text{x}}$-------(1)

Volume of the box $\text{V}={{\text{x}}^{2}}\text{y}$

On substituting the value of y from eq.1, we get

$\text{V}={{\text{x}}^{2}}\left( \frac{{{\text{c}}^{2}}-\text{x}{{2}^{{}}}}{4\text{x}} \right)$

$\Rightarrow \text{V}=\frac{\text{x}}{4}\left( {{\text{c}}^{2}}-{{\text{x}}^{2}} \right)$

$\Rightarrow \text{V}=\frac{1}{4}\left( {{\text{c}}^{2}}\text{x}-{{\text{x}}^{3}} \right)$

Now on differentiating w.r.t. x, we get

$\Rightarrow \frac{\text{dV}}{\text{dx}}=\frac{1}{4}\left( {{\text{c}}^{2}}-3{{\text{x}}^{2}} \right)$

Now, $\frac{\text{dV}}{\text{dx}}=0$

$\frac{1}{4}\left( {{\text{c}}^{2}}-3{{\text{x}}^{2}} \right)=0$

$\Rightarrow \text{x}=\pm \frac{\text{c}}{\sqrt{3}}$

Here x represents the side of the box , Hence we reject $\text{x}=\frac{-\text{c}}{\sqrt{3}}$

Hence $\text{x}=\frac{\text{c}}{\sqrt{3}}$

Again, differentiating Eq.(ii) w.r.t. X, we get

$\frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}=\frac{-3\text{x}}{2}$

$\frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}{{|}_{\text{x}=\frac{\text{c}}{\sqrt{3}}}}=\frac{-\sqrt{3}\text{c}}{2}<0$

Therefore we get the maximum value at $\text{x}=\frac{\text{c}}{\sqrt{3}}$

So the maximum volume ${{\text{V}}_{\text{max }\!\!~\!\!\text{ }}}=\frac{1}{4}\left( {{\text{c}}^{2}}\text{x}-{{\text{x}}^{3}} \right)$

${{\text{V}}_{\text{max }\!\!~\!\!\text{ }}}=\frac{1}{4}\left( \frac{{{\text{c}}^{3}}}{\sqrt{3}}-\frac{{{\text{c}}^{3}}}{3\sqrt{3}} \right)$

$\Rightarrow {{\text{V}}_{\text{max }\!\!~\!\!\text{ }}}=\frac{1}{2}\left( \frac{{{\text{c}}^{3}}}{3\sqrt{3}} \right)$

$\Rightarrow {{\text{V}}_{\text{max }\!\!~\!\!\text{ }}}=\frac{{{\text{c}}^{3}}}{6\sqrt{3}}$cu units.

30. Find the dimensions of the rectangle of perimeter 36 cm which will sweep out a volume as large as possible, when revolved about one of its sides. Also find the maximum volume.

Ans: 

Let the breadth and length of the rectangle 

be x and y respectively.

∵ Perimeter of rectangle $\text{P}=2\text{x}+2\text{y}$

Given perimeter P=36cm

So, $2\text{x}+2\text{y}=36\text{cm}$

$\Rightarrow \text{x}+\text{y}=18$

$\Rightarrow \text{y}=18-\text{x}$------(1)

Now according to the problem, let the rectangle be revolved out about its length y , then the new shape cylinder is formed.

The volume of the cylinder is $\text{V}=\text{ }\!\!\pi\!\!\text{ }{{\text{x}}^{2}}\text{y}$

On substituting $\text{y}=18-\text{x}$ from eq.1 in equation of volume , we get 

$\text{V}=\text{ }\!\!\pi\!\!\text{ }{{\text{x}}^{2}}\text{y}$

$\Rightarrow \text{V}=\text{ }\!\!\pi\!\!\text{ }{{\text{x}}^{2}}\left( 18-\text{x} \right)$

$\Rightarrow \text{V}=18\text{ }\!\!\pi\!\!\text{ }{{\text{x}}^{2}}-\text{ }\!\!\pi\!\!\text{ }{{\text{x}}^{3}}$

On differentiating w.r.t. x, we get

 $\Rightarrow \frac{\text{dV}}{\text{dx}}=36\text{ }\!\!\pi\!\!\text{ x}-3\text{ }\!\!\pi\!\!\text{ }{{\text{x}}^{2}}$

Now $\frac{\text{dV}}{\text{dx}}=0$

$36\text{ }\!\!\pi\!\!\text{ x}-3\text{ }\!\!\pi\!\!\text{ }{{\text{x}}^{2}}=0$

$\Rightarrow 3\text{ }\!\!\pi\!\!\text{ x}\left( 12-\text{x} \right)=0$

$\Rightarrow \text{x}=0,12$

Here x represents the side of a rectangle and we know that side can’t be 0. 

So, x=0(rejected)

Again, On differentiating $\frac{\text{dV}}{\text{dx}}$w.r.t. x, we get

$\Rightarrow \frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}=\text{ }\!\!\pi\!\!\text{ }\left( 36-6\text{x} \right)$

At x=12, $\Rightarrow \frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}=\text{ }\!\!\pi\!\!\text{ }\left( 36-6\text{x} \right)=-36\text{ }\!\!\pi\!\!\text{ }<0$

Hence at x=12, Cylinder has maximum volume. 

Therefore the volume at x=12, 

$\text{V}=18\text{ }\!\!\pi\!\!\text{ }{{\text{x}}^{2}}-\text{ }\!\!\pi\!\!\text{ }{{\text{x}}^{3}}$

$=18\text{ }\!\!\pi\!\!\text{ }{{\left( 12 \right)}^{2}}-\text{ }\!\!\pi\!\!\text{ }{{\left( 12 \right)}^{3}}$

$=\text{ }\!\!\pi\!\!\text{ }{{.12}^{2}}\left( 18-12 \right)$

$=864\text{ }\!\!\pi\!\!\text{  }\!\!~\!\!\text{ c}{{\text{m}}^{3}}$

.31. If the sum of the surface areas of a cube and a sphere is constant, what is the ratio of an edge of the cube to the diameter of the sphere, when the sum of their volumes is minimum? 

Ans: Let the side of a cube is x and radius of sphere is r.

Surface area of cube =$6{{\text{x}}^{2}}$

Surface area of sphere $=4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}$

And, $6{{\text{x}}^{2}}+4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}=\text{k}\left( \text{Given} \right)$[K=constant]

$\Rightarrow {{\text{x}}^{2}}=\frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}^{{}}}{6}$

$\Rightarrow \text{x}={{\left[ \frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}^{{}}}{6} \right]}^{\frac{1}{2}}}^{{}}$-------(1)

Now, the volume of cube $={{\text{x}}^{3}}$

Volume of sphere =$\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{3}}$

Le the sum  of their volume is $\text{S}={{\text{x}}^{3}}+\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{3}}$

$\text{S}={{\left[ \frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}^{{}}}{6} \right]}^{\frac{3}{2}}}{{+}^{{}}}\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{3}}$ [Substituting the value of r from eq.1]

$\frac{\text{dS}}{\text{dr}}=\frac{3}{2}{{\left[ \frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}^{{}}}{6} \right]}^{\frac{1}{2}}}\left( \frac{-8\text{ }\!\!\pi\!\!\text{ r}}{6} \right){{+}^{{}}}4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}$

$\Rightarrow \frac{\text{dS}}{\text{dr}}={{\left[ \frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}^{{}}}{6} \right]}^{\frac{1}{2}}}\left( -2\text{ }\!\!\pi\!\!\text{ r} \right){{+}^{{}}}4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}$

$\Rightarrow \frac{\text{dS}}{\text{dr}}=\text{ }\!\!~\!\!\text{ }-2\text{ }\!\!\pi\!\!\text{ r}\left[ {{\left\{ \frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}^{{}}}{6} \right\}}^{\frac{1}{2}}}-2\text{r} \right]$

For critical points, $\frac{\text{dS}}{\text{dr}}=0$

$-2\text{ }\!\!\pi\!\!\text{ r}\left[ {{\left\{ \frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}{6} \right\}}^{\frac{1}{2}}}-2\text{r} \right]=0$

$\Rightarrow \text{r}=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ r}=\frac{1}{2}{{\left( \frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}{6} \right)}^{\frac{1}{2}}}$

$\Rightarrow \text{r}=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }4{{\text{r}}^{2}}=\frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}{6}$

$\Rightarrow \text{r}=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }24{{\text{r}}^{2}}+4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}=\text{k}$

$\Rightarrow \text{r}=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }{{\text{r}}^{2}}\left( 24+4\text{ }\!\!\pi\!\!\text{ } \right)=\text{k}$

$\Rightarrow \text{r}=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }{{\text{r}}^{2}}=\frac{\text{k}}{4\left( 6+\text{ }\!\!\pi\!\!\text{ } \right)}$.

$\Rightarrow \text{r}=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ r}=\frac{1}{2}\sqrt{\frac{\text{k}}{6+\text{ }\!\!\pi\!\!\text{ }}}$

re r represents the radius and radius can’t be zero. 

Hence $\text{r}\ne 0.$

∴ $\text{r}=\frac{1}{2}\sqrt{\frac{\text{k}}{6+\text{ }\!\!\pi\!\!\text{ }}}$

On differentiating again $\frac{\text{dS}}{\text{dr}}$ w.r.t. r, we get

$\Rightarrow \frac{\text{dS}}{\text{dr}}=\text{ }\!\!~\!\!\text{ }-2\text{ }\!\!\pi\!\!\text{ r}\left[ {{\left\{ \frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}^{{}}}{6} \right\}}^{\frac{1}{2}}}-2\text{r} \right]$

 $\Rightarrow \frac{{{\text{d}}^{2}}\text{S}}{\text{d}{{\text{r}}^{2}}}=8\text{ }\!\!\pi\!\!\text{ r}-2\text{ }\!\!\pi\!\!\text{ }[\sqrt{\frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}{6}}+\text{r}.\frac{1}{2\sqrt{\frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}{6}}}\left( \frac{-8\text{ }\!\!\pi\!\!\text{ r}}{6} \right)$

$\Rightarrow \frac{{{\text{d}}^{2}}\text{S}}{\text{d}{{\text{r}}^{2}}}=2\text{ }\!\!\pi\!\!\text{ }\left[ \frac{-8\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}+12\left( \text{k}-\frac{4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}{6} \right)}{12\sqrt{\frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}{6}}} \right]+8\text{ }\!\!\pi\!\!\text{ r}$

$\Rightarrow \frac{{{\text{d}}^{2}}\text{S}}{\text{d}{{\text{r}}^{2}}}=2\text{ }\!\!\pi\!\!\text{ }\left[ \frac{-96\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}+72\text{k}}{72\sqrt{\frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}}{6}}} \right]+8\text{ }\!\!\pi\!\!\text{ r}>0$

Hence the sum of their volumes at $\text{r}=\frac{1}{2}\sqrt{\frac{\text{k}}{6+\text{ }\!\!\pi\!\!\text{ }}}$ is minimum

At $\text{r}=\frac{1}{2}\sqrt{\frac{\text{k}}{6+\text{ }\!\!\pi\!\!\text{ }}}$ the value of x from eq.1 is 

$\text{x}={{\left[ \frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}^{{}}}{6} \right]}^{\frac{1}{2}}}^{{}}$

$\Rightarrow \text{x}={{\left[ \frac{\text{k}-4\text{ }\!\!\pi\!\!\text{ }{{\left( \frac{1}{2}\sqrt{\frac{\text{k}}{6+\text{ }\!\!\pi\!\!\text{ }}} \right)}^{2}}}{6} \right]}^{\frac{1}{2}}}^{{}}$

$\Rightarrow \text{x}={{\left[ \frac{\text{k}-\text{ }\!\!\pi\!\!\text{ }\left( \frac{\text{k}}{6+\text{ }\!\!\pi\!\!\text{ }} \right)}{6} \right]}^{\frac{1}{2}}}^{{}}$

$\Rightarrow \text{x}={{\left[ \frac{\text{k}}{6+\text{ }\!\!\pi\!\!\text{ }} \right]}^{\frac{1}{2}}}=2{{\text{r}}^{{}}}$--------(2)

Now the ratio of edge of cube to the diameter of sphere is =$\frac{\text{x}}{2\text{r}}$

$=\frac{2\text{r}}{2\text{r}}=\frac{1}{1}$

Hence the ratio of edge of cube to the diameter of sphere is $1:1$

32. AB is the diameter of a circle and C is any point on the circle. Show that the area of $\text{ }\!\!\Delta\!\!\text{ }\mathbf{ABC}$ is maximum, when it is isosceles.

Ans: 

Let the sides of the triangle is $\text{AC}=\text{x}$ and $\text{BC}=\text{y}$

We have to prove that the area of the triangle is maximum and the triangle is isosceles means (x=y).

We have $\text{AB}=2\text{r}$, AB is the diameter of the circle

$\because {{\left( 2\text{r} \right)}^{2}}={{\text{x}}^{2}}+{{\text{y}}^{2}}$

$\Rightarrow {{\text{y}}^{2}}=4{{\text{r}}^{2}}-{{\text{x}}^{2}}$

$\Rightarrow \text{y}=\sqrt{4{{\text{r}}^{2}}-{{\text{x}}^{2}}}$-------(1)

Now, Area of triangle $\text{A}=\frac{1}{2}\text{x}.\text{y}$

$\text{A}=\frac{1}{2}\text{x}.(\sqrt{4{{\text{r}}^{2}}-{{\text{x}}^{2}})}$

Now,differentiating both sides w.r.t. x, we get

$\frac{\text{dA}}{\text{dx}}=\frac{1}{2}\left[ \sqrt{4{{\text{r}}^{2}}-{{\text{x}}^{2}}\text{ }\!\!~\!\!\text{ }}+\text{x}.\frac{1}{2}.{{\left( 4{{\text{r}}^{2}}-{{\text{x}}^{2}} \right)}^{\frac{-1}{2}}}\left( -2\text{x} \right) \right]$

$\Rightarrow \frac{\text{dA}}{\text{dx}}=\frac{1}{2}\left[ \sqrt{4{{\text{r}}^{2}}-{{\text{x}}^{2}}\text{ }\!\!~\!\!\text{ }}-\frac{{{\text{x}}^{2}}}{\sqrt{4{{\text{r}}^{2}}-{{\text{x}}^{2}}\text{ }\!\!~\!\!\text{ }}} \right]$

$\Rightarrow \frac{\text{dA}}{\text{dx}}=\frac{1}{2}\left[ \frac{4{{\text{r}}^{2}}-2{{\text{x}}^{2}}}{\sqrt{4{{\text{r}}^{2}}-{{\text{x}}^{2}}}} \right]$

$\Rightarrow \frac{\text{dA}}{\text{dx}}=\left[ \frac{2{{\text{r}}^{2}}-{{\text{x}}^{2}}}{\sqrt{4{{\text{r}}^{2}}-{{\text{x}}^{2}}}} \right]$

For critical point, $\frac{\text{dA}}{\text{dx}}=0$

$\frac{2{{\text{r}}^{2}}-{{\text{x}}^{2}}}{\sqrt{4{{\text{r}}^{2}}-{{\text{x}}^{2}}}}=0$

$\Rightarrow 2{{\text{r}}^{2}}-{{\text{x}}^{2}}=0$

$\Rightarrow \text{r}=\frac{1}{\sqrt{2}}\text{x}$

$\Rightarrow \text{x}=\pm \text{r}\sqrt{2}$

Here x represents the side of the triangle and the side can’t be negative. So $\text{x}=-\text{r}\sqrt{2}$(Rejected)

For finding whether the area of triangle is maximum and minimum we again differentiate $\frac{\text{dA}}{\text{dx}}$ w.r.t. x, 

$\frac{{{\text{d}}^{2}}\text{A}}{\text{d}{{\text{x}}^{2}}}=\left[ \frac{\sqrt{4{{\text{r}}^{2}}-{{\text{x}}^{2}}}\left( 0-2\text{x} \right)-\frac{2{{\text{r}}^{2}}-{{\text{x}}^{2}}}{2\sqrt{4{{\text{r}}^{2}}-{{\text{x}}^{2}}}}\left( 0-2\text{x} \right)}{4{{\text{r}}^{2}}-{{\text{x}}^{2}}} \right]$

$\Rightarrow \frac{{{\text{d}}^{2}}\text{A}}{\text{d}{{\text{x}}^{2}}}=-2\text{x}\left[ \frac{\left( 8{{\text{r}}^{2}}-2{{\text{x}}^{2}} \right)-\left( 2{{\text{r}}^{2}}-{{\text{x}}^{2}} \right)}{2{{\left( 4{{\text{r}}^{2}}-{{\text{x}}^{2}} \right)}^{\frac{3}{2}}}} \right]$

$\Rightarrow \frac{{{\text{d}}^{2}}\text{A}}{\text{d}{{\text{x}}^{2}}}=-2\text{r}\left[ \frac{6{{\text{r}}^{2}}-{{\text{x}}^{2}}}{2{{\left( 4{{\text{r}}^{2}}-{{\text{x}}^{2}} \right)}^{\frac{3}{2}}}} \right]$

At $\text{x}=\text{r}\sqrt{2}$, $\Rightarrow \frac{{{\text{d}}^{2}}\text{A}}{\text{d}{{\text{x}}^{2}}}=-2\text{r}\left[ \frac{4{{\text{r}}^{2}}}{{{2}^{\frac{5}{2}}}{{\text{r}}^{3}}} \right]<0$

Hence at $\text{x}=\text{r}\sqrt{2}$ we get the maximum area of the triangle.

For $\text{x}=\text{r}\sqrt{2}$, $\text{y}=\sqrt{4{{\text{r}}^{2}}-(\text{r}{{\sqrt{2)}}^{2}}}=\text{r}\sqrt{2}$

If we see, here $\text{x}=\text{y}=\text{r}\sqrt{2}$ . That means the two sides of the triangle are the same. Hence the triangle is isosceles. 

33. A metal box with a square base and vertical sides is to contain $1024\mathbf{c}{{\mathbf{m}}^{3}}$. The material for the top and bottom costs Rs.$5/\mathbf{c}{{\mathbf{m}}^{2}}$ and the material for the sides costs Rs $2.50/\mathbf{c}{{\mathbf{m}}^{2}}$. Find the least cost of the box. 

Ans: 

Let the side of the base be x and height is y.

Volume of the box $\text{V}={{\text{x}}^{2}}\text{y}$which is given as 1024 .

So, ${{\text{x}}^{2}}\text{y}=1024$

$\Rightarrow \text{y}=\frac{1024}{{{\text{x}}^{2}}}$. --------(1)

The cost for bottom and top = $2{{\text{x}}^{2}}\times 5$and the cost for sides material= $4\text{xy}\times 2.50$

So the total cost is denoted as $\text{C}=10{{\text{x}}^{2}}+10\text{xy}$

$\text{C}=10{{\text{x}}^{2}}+10\text{xy}$

 substituting the value of y from eq. 1

$\text{C}=10{{\text{x}}^{2}}+10\text{x}\left( \frac{1024}{{{\text{x}}^{2}}} \right)$

$\text{C}=10{{\text{x}}^{2}}+10\left( \frac{1024}{\text{x}} \right)$

On differentiating w.r.t. x, 

$\frac{\text{dC}}{\text{dx}}=20\text{x}-\frac{10240}{{{\text{x}}^{2}}}$

Now, $\frac{\text{dC}}{\text{dx}}=0$

$20\text{x}-\frac{10240}{{{\text{x}}^{2}}}=0$

$\Rightarrow 20{{\text{x}}^{3}}=10240$

$\Rightarrow {{\text{x}}^{3}}=512$

$\Rightarrow \text{x}=8$

Again, differentiating $\frac{\text{dC}}{\text{dx}}$w.r.t. x, we get

$\frac{{{\text{d}}^{2}}\text{C}}{\text{d}{{\text{x}}^{2}}}=20+\frac{20480}{{{\text{x}}^{3}}}>0$

Hence the cost at $\text{x}=8$is minimum.

The cost at $\text{x}=8$ is $\text{C}\left( 8 \right)=10{{\left( 8 \right)}^{2}}+10\left( \frac{1024}{8} \right)$

$\Rightarrow \text{C}\left( 8 \right)=640+1280=1920\text{Rs}.$

34.  The sum of the surface areas of a rectangular parallelopiped with sides x, 2x and  $\frac{\mathbf{x}}{3}$ and a sphere is given to be constant. Prove that the sum of their volumes is minimum, if x is equal to three times the radius of the sphere. Also find the minimum value of the sum of their volumes.

Ans: Given that we have the sides of a rectangular parallelopiped as $\text{x},\text{ }\!\!~\!\!\text{ }2\text{x }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }\frac{\text{x}}{3}$and the sum of the surface area of the parallelopiped and sphere is constant.

Let the sum of surface area is S

$\text{S}=2\left( \text{x}.2\text{x}+2\text{x}.\frac{\text{x}}{3}+\text{x}.\frac{\text{x}}{3} \right)+4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}=\text{k}\left( \text{Given} \right)$

$\Rightarrow 2\left( \text{x}.2\text{x}+2\text{x}.\frac{\text{x}}{3}+\text{x}.\frac{\text{x}}{3} \right)+4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}=\text{k}$

$\Rightarrow 6{{\text{x}}^{2}}+4\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{2}}=\text{k}$

$\Rightarrow \text{r}=\sqrt{\frac{\text{k}-6{{\text{x}}^{2}}}{4\text{ }\!\!\pi\!\!\text{ }}}$--------(1)

Volume of parallelopiped = $\text{x}.2\text{x}.\frac{\text{x}}{3}$

Volume of sphere = $\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{3}}$ 

Let the Sum of the volume of parallelopiped and volume of the sphere is V.

Then, $\text{V}=\text{x}.2\text{x}.\frac{\text{x}}{3}+\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{3}}$

$\text{V}=\text{x}.2\text{x}.\frac{\text{x}}{3}+\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\left( \sqrt{\frac{\text{k}-6{{\text{x}}^{2}}}{4\text{ }\!\!\pi\!\!\text{ }}} \right)}^{3}}$

$\Rightarrow \text{V}=\frac{2{{\text{x}}^{3}}}{3}+\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\left( \frac{\text{k}-6{{\text{x}}^{2}}}{4\text{ }\!\!\pi\!\!\text{ }} \right)}^{\frac{3}{2}}}$

$\Rightarrow \text{V}=\frac{2{{\text{x}}^{3}}}{3}+\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }\frac{1}{8{{\text{ }\!\!\pi\!\!\text{ }}^{\frac{3}{2}}}}{{\left( \text{k}-6{{\text{x}}^{2}} \right)}^{\frac{3}{2}}}$

On differentiating w.r.t. x, we get

$\frac{\text{dV}}{\text{dx}}=2{{\text{x}}^{2}}+\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }\frac{1}{8{{\text{ }\!\!\pi\!\!\text{ }}^{\frac{3}{2}}}}\frac{3}{2}{{\left( \text{k}-6{{\text{x}}^{2}} \right)}^{\frac{1}{2}}}\left( -12\text{x} \right)$

$\Rightarrow \frac{\text{dV}}{\text{dx}}=2{{\text{x}}^{2}}-\frac{3\text{x}}{\sqrt{\text{ }\!\!\pi\!\!\text{ }}}{{\left( \text{k}-6{{\text{x}}^{2}} \right)}^{\frac{1}{2}}}$

Now, $\frac{\text{dV}}{\text{dx}}=0$

$2{{\text{x}}^{2}}-\frac{3\text{x}}{\sqrt{\text{ }\!\!\pi\!\!\text{ }}}{{\left( \text{k}-6{{\text{x}}^{2}} \right)}^{\frac{1}{2}}}=0$

$\Rightarrow 4{{\text{x}}^{4}}=\frac{9{{\text{x}}^{2}}}{\text{ }\!\!\pi\!\!\text{ }}\left( \text{k}-6{{\text{x}}^{2}} \right)$

$\Rightarrow 4\text{ }\!\!\pi\!\!\text{ }{{\text{x}}^{4}}+54{{\text{x}}^{4}}=9\text{k}{{\text{x}}^{2}}$

$\Rightarrow {{\text{x}}^{4}}\left( 4\text{ }\!\!\pi\!\!\text{ }+54 \right)=9\text{k}{{\text{x}}^{2}}$

$\Rightarrow {{\text{x}}^{2}}=\frac{9\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}$

$\Rightarrow \text{x}=3\sqrt{\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}$----------(2)

Again differentiating $\frac{\text{dV}}{\text{dx}}$w.r.t. x, we get

$\frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}=4\text{x}-\frac{3}{\sqrt{\text{ }\!\!\pi\!\!\text{ }}}\left[ {{\left( \text{k}-6{{\text{x}}^{2}} \right)}^{\frac{1}{2}}}+\text{x}.\left( -6\text{x} \right){{\left( \text{k}-6{{\text{x}}^{2}} \right)}^{\frac{-1}{2}}} \right]$

$\Rightarrow \frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}=4\text{x}-\frac{3}{\sqrt{\text{ }\!\!\pi\!\!\text{ }}}\left[ \frac{\left( \text{k}-6{{\text{x}}^{2}} \right)+\left( -6{{\text{x}}^{2}} \right)}{{{\left( \text{k}-6{{\text{x}}^{2}} \right)}^{\frac{1}{2}}}} \right]$

$\Rightarrow \frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}=4\text{x}-\frac{3}{\sqrt{\text{ }\!\!\pi\!\!\text{ }}}\left[ \frac{\left( \text{k}-12{{\text{x}}^{2}} \right)}{{{\left( \text{k}-6{{\text{x}}^{2}} \right)}^{\frac{1}{2}}}} \right]$

At $\text{x}=3\sqrt{\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}$,

$\frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}=12\sqrt{\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}-\frac{3}{\sqrt{\text{ }\!\!\pi\!\!\text{ }}}\left[ \frac{\text{k}-12.9.\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}{\sqrt{\text{k}-\frac{6.9.\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}} \right]$

$\Rightarrow \frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}=12\sqrt{\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}-\frac{3}{\sqrt{\text{ }\!\!\pi\!\!\text{ }}}\left[ \frac{\frac{4\text{ }\!\!\pi\!\!\text{ k}+54\text{k}-108\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}{\sqrt{\frac{4\text{ }\!\!\pi\!\!\text{ k}+54\text{k}-6.9.\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}} \right]$

$\Rightarrow \frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}=12\sqrt{\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}-\frac{3}{\sqrt{\text{ }\!\!\pi\!\!\text{ }}}\left[ \frac{\frac{4\text{ }\!\!\pi\!\!\text{ k}-54\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}{\sqrt{\frac{4\text{ }\!\!\pi\!\!\text{ k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}} \right]$

$\Rightarrow \frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}}=12\sqrt{\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}-\frac{6\text{k}}{\sqrt{\text{ }\!\!\pi\!\!\text{ }}}\left[ \frac{2\text{ }\!\!\pi\!\!\text{ }-27}{\sqrt{4\text{ }\!\!\pi\!\!\text{ }+54}\sqrt{4\text{ }\!\!\pi\!\!\text{ k}}} \right]$ since $\left( 2\text{ }\!\!\pi\!\!\text{ }-27 \right)\left\langle 0\Rightarrow \frac{{{\text{d}}^{2}}\text{V}}{\text{d}{{\text{x}}^{2}}} \right\rangle 0;\text{k}>0$

For $\text{x}=3\sqrt{\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}$, the sum of volumes is minimum.

From eq. 1 , for $\text{x}=3\sqrt{\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}$

$\text{r}=\sqrt{\frac{\text{k}-6{{\text{x}}^{2}}}{4\text{ }\!\!\pi\!\!\text{ }}}$

$\Rightarrow \text{r}=\sqrt{\frac{\text{k}-6.9\left( \frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54} \right)}{4\text{ }\!\!\pi\!\!\text{ }}}$

$\Rightarrow \text{r}=\frac{1}{2\sqrt{\text{ }\!\!\pi\!\!\text{ }}}\sqrt{\frac{4\text{ }\!\!\pi\!\!\text{ k}+54\text{k}-54\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}$

$\Rightarrow \text{r}=\sqrt{\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}=\frac{\text{x}}{3}$

$\Rightarrow \text{x}=3\text{r}$

Hence x is 3 times the radius of the sphere.

Now the minimum sum of volume is

$\text{V}{{|}_{\text{x}=3\sqrt{\frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54}}}}=\frac{2{{\text{x}}^{3}}}{3}+\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\text{r}}^{3}}$

$=\frac{2{{\text{x}}^{3}}}{3}+\frac{4}{3}\text{ }\!\!\pi\!\!\text{ }{{\left( \frac{\text{x}}{3} \right)}^{3}}=18.{{\left( \frac{\text{k}}{4\text{ }\!\!\pi\!\!\text{ }+54} \right)}^{\frac{3}{2}}}\left( 1+\frac{2\text{ }\!\!\pi\!\!\text{ }}{27} \right)$

Choose the correct answer from the given four options in each of the following questions 35 to 39:

35. The sides of an equilateral triangle are increasing at the rate of 2 cm/sec. The rate at which the area increases, when side is 10 cm is: 

$\left( \mathbf{A} \right).~10\mathbf{c}{{\mathbf{m}}^{2}}/\mathbf{s}$

$\left( \mathbf{B} \right).~\sqrt{3}\mathbf{c}{{\mathbf{m}}^{2}}/\mathbf{s}$

$\left( \mathbf{C} \right).~10\sqrt{3}\mathbf{c}{{\mathbf{m}}^{2}}/\mathbf{s}$

$\left( \mathbf{D} \right).~\frac{10}{3}\mathbf{c}{{\mathbf{m}}^{2}}/\mathbf{s}$

Ans: Let the side of the equilateral triangle is $\text{xcm}.$

Area of equilateral triangle$\text{A}=\frac{\sqrt{3}}{4}{{\text{x}}^{2}}$------(1)

Given that $\frac{\text{dx}}{\text{dt}}=2\text{cm}/\text{sec}$

On differentiating the eq.(1). W.r.t. t, we get

$\frac{\text{dA}}{\text{dt}}=\frac{\sqrt{3}}{4}.2\text{x}.\frac{\text{dx}}{\text{dt}}$

When $\text{x}=10\text{cm }\!\!~\!\!\text{ }$and $\frac{\text{dx}}{\text{dt}}=2\text{cm}/\text{sec}$

$\frac{\text{dA}}{\text{dt}}=\frac{\sqrt{3}}{4}.40=10\sqrt{3}\text{c}{{\text{m}}^{2}}/\text{sec}$

Hence the area is increasing at the rate of $10\sqrt{3}\text{c}{{\text{m}}^{2}}/\text{sec}$.

36. A ladder, 5 meter long, standing on a horizontal floor, leans against a vertical wall. If the top of the ladder slides downwards at the rate of 10 cm/sec, then the rate at which the angle between the floor and the ladder is decreasing when lower end of ladder is 2 metres from the wall is:

 $\left( \mathbf{A} \right).~\frac{1}{10}\mathbf{radian}/\mathbf{sec}$ 

 $\left( \mathbf{B} \right).~\frac{1}{20}\mathbf{radian}/\mathbf{sec}$

 $\left( \mathbf{C} \right).~20~\mathbf{radian}/\mathbf{sec}$

 $\left( \mathbf{D} \right).~10~\mathbf{radian}/\mathbf{sec}$

Ans: 

Let the angle b/w floor and the ladder is $\text{ }\!\!\theta\!\!\text{ }$

And sides of the triangle are $\text{x},\text{ }\!\!~\!\!\text{ y}$where $\text{BC}=\text{y }\!\!~\!\!\text{ }\And \text{ }\!\!~\!\!\text{ AB}=\text{x}$

From the figure,

$\text{sin }\!\!\theta\!\!\text{ }=\frac{\text{x}}{500}\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{ and }\!\!~\!\!\text{ cos }\!\!\theta\!\!\text{ }=\frac{\text{y}}{500}$ 

$\Rightarrow \text{x}=500\text{sin }\!\!\theta\!\!\text{  }\!\!~\!\!\text{  }\!\!~\!\!\text{ and }\!\!~\!\!\text{ y}=500\text{cos }\!\!\theta\!\!\text{ }$-----(1)

Given that the top of the ladder slides downwards at the rate of 10cm/sec.

Hence $\frac{\text{dx}}{\text{dt}}=10\text{cm}/\text{sec}$

$\text{x}=500\text{sin }\!\!\theta\!\!\text{ }$

Differentiating on both sides w.r.t. T, we get

$\frac{\text{dx}}{\text{dt}}=500\text{cos }\!\!\theta\!\!\text{ }.\frac{\text{d }\!\!\theta\!\!\text{ }}{\text{dt}}$

$\frac{\text{d }\!\!\theta\!\!\text{ }}{\text{dt}}=\frac{10}{500\text{cos }\!\!\theta\!\!\text{ }}$

On substituting the value of $\text{cos }\!\!\theta\!\!\text{ }=\frac{\text{y}}{500}$from the eq.1

$\frac{\text{d }\!\!\theta\!\!\text{ }}{\text{dt}}=\frac{10}{500.\frac{\text{y}}{500}}$

$\frac{\text{d }\!\!\theta\!\!\text{ }}{\text{dt}}=\frac{10}{\text{y}}$

Given that lower end from the wall is 2m=200cm

Hence, $\frac{\text{d }\!\!\theta\!\!\text{ }}{\text{dt}}=\frac{10}{200}\text{rad}/\text{sec}$

$\frac{\text{d }\!\!\theta\!\!\text{ }}{\text{dt}}=\frac{1}{20}\text{rad}/\text{sec}$

Therefore option B is the correct answer.

37. The curve $\mathbf{y}={{\mathbf{x}}^{\frac{1}{5}}}$ has at (0, 0) 

(A) a vertical tangent (parallel to y-axis) 

(B) a horizontal tangent (parallel to x-axis) 

(C) an oblique tangent 

(D) no tangent

Ans: The curve we have $\text{y}={{\text{x}}^{\frac{1}{5}}}$

Now the slope of the tangent on the curve is

$\frac{\text{dy}}{\text{dx}}=\frac{1}{5}{{\left( \text{x} \right)}^{\frac{-4}{5}}}$

Slope on point (0,0) is

$\frac{\text{dy}}{\text{dx}}{{|}_{\left( 0,0 \right)}}=\frac{1}{5}{{\left( \text{x} \right)}^{\frac{-4}{5}}}=\frac{1}{5}{{\left( 0 \right)}^{\frac{-4}{5}}}=\infty $

Here slope of the tangent is $\infty $and we know that $\infty \text{ }\!\!~\!\!\text{ }$is the slope of the vertical line. So the curve $\text{y}={{\text{x}}^{\frac{1}{5}}}$has a vertical tangent at (0,0) which is parallel to y-axis. Therefore option A is the correct option.

38.  The equation of normal to the curve $3{{\mathbf{x}}^{2}}-{{\mathbf{y}}^{2}}={{8}^{{}}}$ which is parallel to the line x + 3y = 8 is :

(A) 3x – y = 8 

(B) 3x + y + 8 = 0 

(C) x + 3y ± 8 = 0 

(D) x + 3y = 0

Ans: The given curve we have $3{{\text{x}}^{2}}-{{\text{y}}^{2}}={{8}^{{}}}$and the equation of the line is x + 3y = 8.

$\text{x}+3\text{y}=8$

$\text{y}=-\frac{1}{3}\text{x}+\frac{8}{3}$

On comparison with equation $\text{y}=\text{mx}+\text{c }\!\!~\!\!\text{ }$swe get the slope as $\text{m}=\frac{-1}{3}$. This slope should be equal to the slope of normal as it is given that the line is parallel to the normal and we know that parallel lines have the same slope. 

Now, $3{{\text{x}}^{2}}-{{\text{y}}^{2}}={{8}^{{}}}$

On differentiating w.r.t. x , we get $6\text{x}-2\text{y}.\frac{\text{dy}}{\text{dx}}=0$

$\frac{\text{dy}}{\text{dx}}=\frac{3\text{x}}{\text{y}}$= slope of the curve

Now, Slope of the normal to the curve$=\frac{-1}{\text{slope }\!\!~\!\!\text{ of }\!\!~\!\!\text{ the }\!\!~\!\!\text{ curve}}=\frac{-1}{\left( \frac{\text{dy}}{\text{dx}} \right)}=\frac{-\text{y}}{3\text{x}}$

$\frac{-\text{y}}{3\text{x}}=\frac{-1}{3}$

$\Rightarrow \text{y}=\text{x}$------(1)

On substituting  this value in the given equation of thecurve, we get

$3{{\text{x}}^{2}}-{{\text{x}}^{2}}=8$

$\Rightarrow {{\text{x}}^{2}}=4$

$\Rightarrow \text{x}=\pm 2$

For $\text{x}=2$, from eq.1 ,$\text{y}=\text{x}=2$

For $\text{x}=-2$, $\text{x}=-2$

So the points are (2,2) &(-2,-2) at which normal is parallel to line x + 3y = 8 .

Now the equation of normals passing through points (2,2) &(-2,-2) and having slope $\frac{-1}{3}.$

$\left( \text{y}-2 \right)=\frac{-1}{3}\left( \text{x}-2 \right)\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }\left( \text{y}+2 \right)=\frac{-1}{3}\left( \text{x}+2 \right)$

$\Rightarrow 3\left( \text{y}-2 \right)+\left( \text{x}-2 \right)=0\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }3\left( \text{y}+2 \right)+\left( \text{x}+2 \right)=0$

$\Rightarrow 3\text{y}+\text{x}-8=0\text{ }\!\!~\!\!\text{  }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }3\text{y}+\text{x}+8=0$

Hence the equation of normals is $3\text{y}+\text{x}\pm 8=0\text{ }\!\!~\!\!\text{ }$. So option B is the correct option.

39. If the curve $\mathbf{ay}+{{\mathbf{x}}^{2}}=7$ and ${{\mathbf{x}}^{3}}=\mathbf{y}$, cut orthogonally at (1, 1), then the value of a is: 

(A).  1 

(B).  0 

(C). – 6 

(D). 6

Ans: Given that the curves cut orthogonally at point (1,1) that means the slope of both the curves should satisfy the condition ${{\text{m}}_{1}}.{{\text{m}}_{2}}=-1$where let ${{\text{m}}_{1}}$is the slope of curve $\text{ay}+{{\text{x}}^{2}}=7$ and ${{\text{m}}_{2}}$is the slope of curve${{\text{x}}^{3}}=\text{y}$.

$\text{ay}+{{\text{x}}^{2}}=7$

Differentiating on both sides w.r.t. x, we get

$\text{a}\frac{\text{dy}}{\text{dx}}+2\text{x}=0$

$\frac{\text{dy}}{\text{dx}}=\frac{-2\text{x}}{\text{a}}$

$\frac{\text{dy}}{\text{dx}}{{|}_{\left( 1,1 \right)}}=\frac{-2\text{x}}{\text{a}}=\frac{-2}{\text{a}}={{\text{m}}_{1}}\left( \text{Say} \right)$

Now, ${{\text{x}}^{3}}=\text{y}$

Differentiating on both sides w.r.t. x, 

$3{{\text{x}}^{2}}=\frac{\text{dy}}{\text{dx}}$

$\frac{\text{dy}}{\text{dx}}{{|}_{\left( 1,1 \right)}}=3\left( 1 \right)=3={{\text{m}}_{2}}\left( \text{Say} \right)$

Given that both curves cut orthogonally. So, 

${{\text{m}}_{1}}.{{\text{m}}_{2}}=-1$

$\frac{-2}{\text{a}}.3=-1$

$\Rightarrow \text{a}=6$

Therefore the correct option is D.

40.  If $\mathbf{y}={{\mathbf{x}}^{4}}-10$ and if x changes from 2 to 1.99, what is the change in y? 

(A) 0.32 

(B) 0.032 

(C) 5.68 

(D) 5.968

Ans: We have the curve $\text{y}={{\text{x}}^{4}}-10$

We know that $\frac{\text{dy}}{\text{dx}}=\frac{\text{y}+\text{ }\!\!\Delta\!\!\text{ y}-\text{y}}{\text{ }\!\!\Delta\!\!\text{ x}}$

$\Rightarrow \text{ }\!\!\Delta\!\!\text{ y}=\frac{\text{dy}}{\text{dx}}.\text{ }\!\!\Delta\!\!\text{ x}$

Now, $\text{y}={{\text{x}}^{4}}-10$

On differentiating on both sides w.r.t. x, we get

$\frac{\text{dy}}{\text{dx}}=4{{\text{x}}^{3}}$

Changes in x is $\text{ }\!\!\Delta\!\!\text{ x}=2-1.99=0.01$

Now, $\text{ }\!\!\Delta\!\!\text{ y}=\frac{\text{dy}}{\text{dx}}.\text{ }\!\!\Delta\!\!\text{ x}$

$\Rightarrow \text{ }\!\!\Delta\!\!\text{ y}=4{{\left( 2 \right)}^{3}}\times \left( 0.01 \right)$

$\Rightarrow \text{ }\!\!\Delta\!\!\text{ y}=0.32$

Hence option A is the correct answer.

41. The equation of tangent to the curve $\mathbf{y}\left( 1+{{\mathbf{x}}^{2}} \right)=2-\mathbf{x}$, where it crosses x-axis is: 

(A) x + 5y = 2 

(B) x – 5y = 2 

(C) 5x – y = 2 

(D) 5x + y = 2

Ans: Given curve $\text{y}\left( 1+{{\text{x}}^{2}} \right)=2-\text{x}$

The curve passes crosses the x-axis, hence $\text{y}=0$

$\Rightarrow 0\left( 1+{{\text{x}}^{2}} \right)=2-\text{x}$

$\Rightarrow 2-\text{x}=0$

$\Rightarrow \text{x}=2$

Hence the point where the tangent passes through is (2,0).

Now, we find the slope of the tangent on curve $\text{y}\left( 1+{{\text{x}}^{2}} \right)=2-\text{x}$

On differentiating both sides w.r.t. x, we get 

$2\text{xy}+\left( 1+{{\text{x}}^{2}} \right)\frac{\text{dy}}{\text{dx}}=-1$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{-1-2\text{xy}}{1+{{\text{x}}^{2}}}$

Slope at the point (2,0)

$\Rightarrow \frac{\text{dy}}{\text{dx}}{{|}_{\left( 2,0 \right)}}=\frac{-1-2\text{xy}}{1+{{\text{x}}^{2}}}=\frac{-1}{5}$

Now the equation of tangent passing through (2,0) and having slope $\frac{-1}{5}$

$\left( \text{y}-0 \right)=\frac{-1}{5}\left( \text{x}-2 \right)$

$\Rightarrow 5\left( \text{y}-0 \right)=-1\left( \text{x}-2 \right)$

$\Rightarrow \text{x}+5\text{y}=2$

Hence the correct option is option A.

42.  The points at which the tangents to the curve $\mathbf{y}={{\mathbf{x}}^{3}}-12\mathbf{x}+18$are parallel to x-axis are: 

(A) (2, –2), (–2, –34) 

(B) (2, 34), (–2, 0) 

(C) (0, 34), (–2, 0) 

(D) (2, 2), (–2, 34)

Ans: The given curve is $\text{y}={{\text{x}}^{3}}-12\text{x}+18$

For finding the slope of tangent on the curve we differentiate the given equation of curve w.r.t. x, 

$\frac{\text{dy}}{\text{dx}}=3{{\text{x}}^{2}}-12$

Given that the tangent is parallel to the x-axis, so the above slope will be equal to 0 as we know that the slope of the x-axis is 0 and if two lines are parallel then their slopes are to be equal. Therefore,

$\frac{\text{dy}}{\text{dx}}=0$ 

$\Rightarrow 3{{\text{x}}^{2}}-12=0$

$\Rightarrow {{\text{x}}^{2}}=4$

$\Rightarrow \text{x}=\pm 2$

For $\text{x}=2$, $\text{y}={{\left( 2 \right)}^{3}}-24+18=2$

For $\text{x}=-2$, $\text{y}={{\left( -2 \right)}^{3}}+24+18=34$

Hence the required points are (2,2) and (-2,34) where the tangents to the curve  $\text{y}={{\text{x}}^{3}}-12\text{x}+18$ are parallel to x-axis.

43.  The tangent to the curve$~\mathbf{y}={{\mathbf{e}}^{2\mathbf{x}}}$ at the point (0, 1) meets x-axis at:

 (A) (0, 1) 

(B) $\left( \frac{-1}{2},0 \right)$       

(C) (2, 0) 

(D) (0, 2)

Ans: The given curve we have $\text{y}={{\text{e}}^{2\text{x}}}$

Slope of tangent to the curve is

$\frac{\text{dy}}{\text{dx}}=2.{{\text{e}}^{2\text{x}}}$

Slope at point $\frac{\text{dy}}{\text{dx}}{{|}_{\left( 0,1 \right)}}=2.{{\text{e}}^{0}}=2$

Now, the equation of a tangent passing through the point (0,1) and having slope 2 is:

$\left( \text{y}-1 \right)=2\left( \text{x}-0 \right)$

$\Rightarrow 2\text{x}-\text{y}+1=0$

It is asked that the tangent meets x-axis , so on substituting y=0 in equation of tangent, we get

$2\text{x}-\left( 0 \right)+1=0$

$\Rightarrow \text{x}=\frac{-1}{2}$

Thus the point where tangent meets the x-axis is $\left( \frac{-1}{2},0 \right)$. So option B is the correct answer.

44. The slope of tangent to the curve $\mathbf{x}={{\mathbf{t}}^{2}}+3\mathbf{t}-8,~\mathbf{y}=2{{\mathbf{t}}^{2}}-2\mathbf{t}-5$at the point (2, –1) is: 

(A) $\frac{22}{7}$ 

(B) $\frac{6}{7}$ 

(C) $\frac{-6}{7}$ 

(D) – 6

Ans: The equation of curve we have

 $\text{x}={{\text{t}}^{2}}+3\text{t}-8\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{ y}=2{{\text{t}}^{2}}-2\text{t}-5$

Differentiating w.r.t. t,

$\frac{\text{dx}}{\text{dt}}=2\text{t}+3\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{ }\frac{\text{dy}}{\text{dt}}=4\text{t}-2$

We know that the slope is $\frac{\text{dy}}{\text{dx}}=\frac{\frac{\text{dy}}{\text{dt}}}{\frac{\text{dx}}{\text{dt}}}$

So $\frac{\text{dy}}{\text{dx}}=\frac{4\text{t}-2}{2\text{t}+3}$

Given that the curve passes through the point (2, –1) , So

$2={{\text{t}}^{2}}+3\text{t}-8\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{ }-1=2{{\text{t}}^{2}}-2\text{t}-5$

$\Rightarrow {{\text{t}}^{2}}+3\text{t}-10=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{ }2{{\text{t}}^{2}}-2\text{t}-4=0$

$\Rightarrow {{\text{t}}^{2}}+5\text{t}-2\text{t}-10=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{ }2{{\text{t}}^{2}}-4\text{t}+2\text{t}-4=0$

$\Rightarrow \text{t}\left( \text{t}+5 \right)-2\left( \text{t}+5 \right)=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{ }2\text{t}\left( \text{t}-2 \right)+2\left( \text{t}-2 \right)=0$

$\Rightarrow \left( \text{t}+5 \right)\left( \text{t}-2 \right)=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{ }\left( \text{t}-2 \right)\left( 2\text{t}+2 \right)=0$

$\Rightarrow \text{t}=-5,2\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{  }\!\!~\!\!\text{ t}=-1,2$

Here the common value of t is 2.

Now at t=2 the slope of tangent is 

$\frac{\text{dy}}{\text{dx}}{{|}_{\text{t}=2}}=\frac{4\left( 2 \right)-2}{2\left( 2 \right)+3}=\frac{6}{7}$

Therefore the slope of tangent to the curve is $\frac{6}{7}$. Hence option B is the correct answer.

45.  The two curves ${{\mathbf{x}}^{3}}-3\mathbf{x}{{\mathbf{y}}^{2}}+2=0$and $3{{\mathbf{x}}^{2}}\mathbf{y}-{{\mathbf{y}}^{3}}-2=0$ intersect at an angle of 

(A) $\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$ 

(B)   $\frac{\text{ }\!\!\pi\!\!\text{ }}{3}$

(C) $\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$

(D) $\frac{\text{ }\!\!\pi\!\!\text{ }}{6}$

Ans: The equations of curves we have 

${{\text{x}}^{3}}-3\text{x}{{\text{y}}^{2}}+2=0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }3{{\text{x}}^{2}}\text{y}-{{\text{y}}^{3}}-2=0$

On Differentiating the first curve w.r.t. x, we get 

$3{{\text{x}}^{2}}-3{{\text{y}}^{2}}-3\text{x}.2\text{y}.\frac{\text{dy}}{\text{dx}}=0$

$\frac{\text{dy}}{\text{dx}}=\frac{3{{\text{x}}^{2}}-3{{\text{y}}^{2}}}{6\text{xy}}={{\text{m}}_{1}}\left( \text{Say} \right)$

Now On differentiating the second curve $3{{\text{x}}^{2}}\text{y}-{{\text{y}}^{3}}-2=0$, we get

$6\text{xy}+3{{\text{x}}^{2}}\frac{\text{dy}}{\text{dx}}-3{{\text{y}}^{2}}\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\frac{6\text{xy}}{3{{\text{y}}^{2}}-3{{\text{x}}^{2}}}={{\text{m}}_{2}}\left( \text{Say} \right)$

If we see ${{\text{m}}_{1}}.{{\text{m}}_{2}}=\frac{3{{\text{x}}^{2}}-3{{\text{y}}^{2}}}{6\text{xy}}\times \frac{6\text{xy}}{3{{\text{y}}^{2}}-3{{\text{x}}^{2}}}=-1$

We know that if ${{\text{m}}_{1}}.{{\text{m}}_{2}}=-1$then both the curves intersect at right angle i.e. making angle $\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$with each other.  

46.  The interval on which the function $\mathbf{f}\left( \mathbf{x} \right)=2{{\mathbf{x}}^{3}}+9{{\mathbf{x}}^{2}}+12\mathbf{x}-1$ is decreasing is: 

(A) [–1, ∞ ) 

(B) [–2, –1] 

(C) (– ∞ , –2] 

(D) [–1, 1]

Ans: We have the function $\text{f}\left( \text{x} \right)=2{{\text{x}}^{3}}+9{{\text{x}}^{2}}+12\text{x}-1$

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=6{{\text{x}}^{2}}+18\text{x}+12$

$=6\left( {{\text{x}}^{2}}+3\text{x}+2 \right)$

$=6\left( {{\text{x}}^{2}}+2\text{x}+\text{x}+2 \right)$

$=6\left( \text{x}+2 \right)\left( \text{x}+1 \right)$

We know that a function is said to be decreasing if $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)\le 0$

So on drawing the points on number line 

We see that $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)<0$in interval [-2,-1]. Hence the given function is decreasing in [-2,-1], So option B is the correct answer.

47. Let the f : R → R be defined by $\mathbf{f}\left( \mathbf{x} \right)=2\mathbf{x}+\mathbf{cosx}$, then f : 

(A) has a minimum at x = π 

(B) has a maximum, at x = 0 

(C) is a decreasing function 

(D) is an increasing function

Ans: The given function is $\text{f}\left( \text{x} \right)=2\text{x}+\text{cosx}$

Differentiating the function w.r.t. x, 

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=2-\text{sinx}$

We know that  $-1\le \text{sinx}\le 1$

So, $-1+2\le 2-\text{sinx}\le 1+2$

$\Rightarrow 1\le 2-\text{sinx}\le 3$

$\Rightarrow 1\le \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)\le 3$

Since $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)>0$

Hence the function is an increasing function. Option D is the correct answer.

48. $\mathbf{y}=\mathbf{x}{{\left( \mathbf{x}-3 \right)}^{2}}$ decreases for the values of x given by : 

(A) 1 < x < 3 

(B) x < 0 

(C) x > 0 

(D) $0<\mathbf{x}<\frac{3}{2}$

Ans: The given function is $\text{y}=\text{x}{{\left( \text{x}-3 \right)}^{2}}$

Differentiating the given function w.r.t. x,

$\frac{\text{dy}}{\text{dx}}={{\left( \text{x}-3 \right)}^{2}}+\text{x}.2\left( \text{x}-3 \right)$

$={{\text{x}}^{2}}-6\text{x}+9+2{{\text{x}}^{2}}-6\text{x}$

$=3{{\text{x}}^{2}}-12\text{x}+9$

We know that the function is decreasing function if $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)<0$

$3{{\text{x}}^{2}}-12\text{x}+9<0$

$\Rightarrow {{\text{x}}^{2}}-4\text{x}+3<0$

$\Rightarrow {{\text{x}}^{2}}-\text{x}-3\text{x}+3<0$

$\Rightarrow \left( \text{x}-3 \right)\left( \text{x}-1 \right)<0$

So the function decreases for $\left( 1,3 \right)$. Hence option A is the correct answer.

49. The function $\mathbf{f}\left( \mathbf{x} \right)=4\mathbf{si}{{\mathbf{n}}^{3}}\mathbf{x}-6\mathbf{si}{{\mathbf{n}}^{2}}\mathbf{x}+12\mathbf{sinx}+100$ is strictly 

(A) increasing in \[\left( \text{ }\!\!\pi\!\!\text{ , }\!\!~\!\!\text{ }\frac{\text{3 }\!\!\pi\!\!\text{ }}{\text{2}} \right)\]       

(B) decreasing in $\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}}\text{, }\!\!\pi\!\!\text{ } \right)$    

(C) decreasing in $\left[ \frac{\text{- }\!\!\pi\!\!\text{ }}{\text{2}}\text{,}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}} \right]$  

(D) decreasing in $\left[ \text{0,}\frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}} \right]$

Ans: The given function is $\text{f}\left( \text{x} \right)=4\text{si}{{\text{n}}^{3}}\text{x}-6\text{si}{{\text{n}}^{2}}\text{x}+12\text{sinx}+100$

Differentiating the given function w.r.t. x, 

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=12\text{si}{{\text{n}}^{2}}\text{x}.\text{cosx}-12\text{sinx}.\text{cosx}+12\text{cosx}$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=12\text{cosx}\left[ \text{si}{{\text{n}}^{2}}\text{x}-\text{sinx}+1 \right]$

$\Rightarrow \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=12\text{cosx}\left[ \text{si}{{\text{n}}^{2}}\text{x}+\left( 1-\text{sinx} \right) \right]$

We know that $\because \text{si}{{\text{n}}^{2}}\text{x}\ge 0$and $-1\le \text{sinx}\le 1\Rightarrow 0\le 1-\text{sinx}\le 2$

$\text{si}{{\text{n}}^{2}}\text{x}+1-\text{sinx}\ge 0$

Hence $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)<0$if $\text{cosx}<0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ we }\!\!~\!\!\text{ know }\!\!~\!\!\text{ that }\!\!~\!\!\text{ cosx}<0\text{ }\!\!~\!\!\text{ in }\!\!~\!\!\text{ }\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{2},\text{ }\!\!\pi\!\!\text{ } \right)\text{ }\!\!~\!\!\text{ }$

So the function is decreasing function in $\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{2},\text{ }\!\!\pi\!\!\text{ } \right)$. Hence option B is the correct  answer.

50. Which of the following functions is decreasing on $\left( 0,\frac{\mathbf{\pi }}{2} \right)$      

(A) sin2x 

(B) tanx 

(C) cosx 

(D) cos 3x

Ans: We know that a function is said to be decreasing function if $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)<0\text{ }\!\!~\!\!\text{ }$in a given domain. Here the given domain is  $\left( 0,\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)$. If we see the derivative of cosx is $-\text{sinx }\!\!~\!\!\text{ }$which is $-\text{sinx}<0\text{ }\!\!~\!\!\text{ in }\!\!~\!\!\text{ }\left( 0,\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right).\text{ }\!\!~\!\!\text{ }$

So $\text{f}\left( \text{x} \right)=\text{cosx}$

Differentiating the function w.r.t. x, 

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=-\text{sinx}$

$-\text{sinx}<0\text{ }\!\!~\!\!\text{ in }\!\!~\!\!\text{ }\left( 0,\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)$

Hence option C is the correct answer.

51. The function $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{tanx}-\mathbf{x}$ 

(A) always increases 

(B) always decreases 

(C) never increases 

(D) sometimes increases and sometimes decreases.

Ans: The given function is $\text{f}\left( \text{x} \right)=\text{tanx}-\text{x}$

Differentiating the function w.r.t. x, 

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{se}{{\text{c}}^{2}}\text{x}-1$

$\Rightarrow \text{secx}\in \text{R}-\left( -1,1 \right)$

$\Rightarrow \text{se}{{\text{c}}^{2}}\text{x}-1>0$

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)>0,\forall \text{x}\in \text{R}$

Hence $\text{tanx}-\text{x}$ always an increasing function. So option A is the correct answer.

52.  If x is real, the minimum value of ${{\mathbf{x}}^{2}}-8\mathbf{x}+17$ is 

(A) –1 

(B) 0 

(C) 1 

(D) 2

Ans: The given function is $\text{f}\left( \text{x} \right)\text{ }\!\!~\!\!\text{ }=\text{ }\!\!~\!\!\text{ }{{\text{x}}^{2}}-8\text{x}+17$

Differentiating the function w.r.t. x,

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)\text{ }\!\!~\!\!\text{ }=\text{ }\!\!~\!\!\text{ }2\text{x}-8$

For critical point $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\Rightarrow 2\text{x}-8=0$

$\Rightarrow \text{x}=4$

We know that a function has local minima if f’’(x)>0. 

So here we have to find the 2nd derivative of the given function.

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)\text{ }\!\!~\!\!\text{ }=\text{ }\!\!~\!\!\text{ }2\text{x}-8$

$\Rightarrow \text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)\text{ }\!\!~\!\!\text{ }=\text{ }\!\!~\!\!\text{ }2>0\text{ }\!\!~\!\!\text{ }$

Hence  we get the minimum value at x=4. 

Now the value of function at x=4 is the minimum value of the function.

$\text{f}\left( 4 \right)=\text{ }\!\!~\!\!\text{ }{{\left( 4 \right)}^{2}}-8\left( 4 \right)+17=16-32+17=1$

Hence the option c is the correct answer.

53.  The smallest value of the polynomial ${{\mathbf{x}}^{3}}-18{{\mathbf{x}}^{2}}+96\mathbf{x}$ in [0, 9] is 

(A) 126 

(B) 0 

(C) 135 

(D) 160

Ans: The given polynomial function is $\text{f}\left( \text{x} \right)={{\text{x}}^{3}}-18{{\text{x}}^{2}}+96\text{x}$

Differentiating the function w.r.t. x, 

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=3{{\text{x}}^{2}}-36\text{x}+96$

$\because \text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=3{{\text{x}}^{2}}-36\text{x}+96$

So, $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$3{{\text{x}}^{2}}-36\text{x}+96=0$

$\Rightarrow {{\text{x}}^{2}}-12\text{x}+32=0$

$\Rightarrow {{\text{x}}^{2}}-8\text{x}-4\text{x}+16=0$

$\Rightarrow \left( \text{x}-8 \right)\left( \text{x}-4 \right)=0$

$\Rightarrow \text{x}=4,8\in \left[ 0,9 \right]$

Now we find the value of given function at points x=0,4,8,9 

$\text{f}\left( 0 \right)={{\left( 0 \right)}^{3}}-18{{\left( 0 \right)}^{2}}+96\left( 0 \right)=0$

$\text{f}\left( 4 \right)={{\left( 4 \right)}^{3}}-18{{\left( 4 \right)}^{2}}+96\left( 4 \right)=64-288+384=160$

$\text{f}\left( 8 \right)={{\left( 8 \right)}^{3}}-18{{\left( 8 \right)}^{2}}+96\left( 8 \right)=512-1152+768=128$

$\text{f}\left( 9 \right)={{\left( 9 \right)}^{3}}-18{{\left( 9 \right)}^{2}}+96\left( 9 \right)=729-1458+864=135$

If we see the minimum absolute value of the function is 0 in [0,9]. Hence the correct option is option B.

54.  The function $\mathbf{f}\left( \mathbf{x} \right)=2{{\mathbf{x}}^{3}}-3{{\mathbf{x}}^{2}}-12\mathbf{x}+4$, has 

(A) two points of local maximum 

(B) two points of local minimum 

(C) one maxima and one minima 

(D) no maxima or minima

Ans: The given function is $\text{f}\left( \text{x} \right)=2{{\text{x}}^{3}}-3{{\text{x}}^{2}}-12\text{x}+4$

Differentiating the function w.r.t. x,

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=6{{\text{x}}^{2}}-6\text{x}-12$

For critical points $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$6{{\text{x}}^{2}}-6\text{x}-12=0$

$\Rightarrow {{\text{x}}^{2}}-\text{x}-2=0$

$\Rightarrow {{\text{x}}^{2}}-2\text{x}+\text{x}-2=0$

$\Rightarrow \text{x}\left( \text{x}-2 \right)+1\left( \text{x}-2 \right)=0$

$\Rightarrow \text{x}=2,-1$

Differentiate again $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)$w.r.t. x,

$\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=12\text{x}-6$

At x=-1, $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( -1 \right)=12\left( -1 \right)-6=-18<0$. Hence the function has local maxima at x=-1.

At x=2, $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( 2 \right)=12\left( 2 \right)-6=18>0$. Hence the function has local minima at x=2.

Since the function has one maxima and one minima. So the option C is the correct answer.

55. The maximum value of sin x . cos x is 

(A) $\frac{\text{1}}{\text{4}}$

(B) $\frac{\text{1}}{\text{2}}$ 

(C) $\sqrt{\text{2}}$

(D) $\text{2}\sqrt{\text{2}}$

Ans: We have the function $\text{f}\left( \text{x} \right)=\text{sinx}.\text{cosx}=\frac{1}{2}.2\text{sinx}.\text{cosx}=\frac{1}{2}\text{sin}2\text{x}$ 

 Differentiating the function w.r.t. x,

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{1}{2}\text{cos}2\text{x}.2=\text{cos}2\text{x}$

Now, $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\Rightarrow \text{cos}2\text{x}=0$

$\Rightarrow 2\text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{2}$

$\Rightarrow \text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$

Again differentiating $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)$w.r.t. x,

$\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{1}{2}\text{cos}2\text{x}.2=-2\text{sin}2\text{x}$

${{\left[ \text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right) \right]}_{\text{at }\!\!~\!\!\text{ x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}}}=-2\text{sin}\left( \frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)=-2<0$. Hence at $\text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$, the function has local maxima.

The value of the function at $\text{x}=\frac{\text{ }\!\!\pi\!\!\text{ }}{4}$

$\text{f}\left( \text{x} \right)=\text{sinx}.\text{cosx}=\text{sin}\frac{\text{ }\!\!\pi\!\!\text{ }}{4}.\text{cos}\frac{\text{ }\!\!\pi\!\!\text{ }}{4}=\frac{1}{\sqrt{2}}.\frac{1}{\sqrt{2}}=\frac{1}{2}$. So option B is the correct answer.

56.  At $\mathbf{x}=\frac{5\mathbf{\pi }}{6}$, $\mathbf{f}\left( \mathbf{x} \right)=2\mathbf{sin}3\mathbf{x}+3\mathbf{cos}3\mathbf{x}$is: 

(A) maximum 

(B) minimum 

(C) zero 

(D) neither maximum nor minimum.

Ans: The function we have, is $\text{f}\left( \text{x} \right)=2\text{sin}3\text{x}+3\text{cos}3\text{x}$

Differentiating the function w.r.t. x,

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=6\text{cos}3\text{x}-9\text{sin}3\text{x}$

For finding, the function has minima or maxima at $\text{x}=\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$, we again differentiate $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)$w.r.t. x, 

$\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=-18\text{sin}3\text{x}-27\text{cos}3\text{x}=-9\left( 2\text{sin}3\text{x}+3\text{cos}3\text{x} \right)$

Now, ${{\left[ \text{f }\!\!'\!\!\text{ }\left( \text{x} \right) \right]}_{\text{x}=\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}}}=6\text{cos}\left( 3.\frac{5\text{ }\!\!\pi\!\!\text{ }}{6} \right)-9\text{sin}\left( 3.\frac{5\text{ }\!\!\pi\!\!\text{ }}{6} \right)$

$=6\text{cos}\left( \frac{5\text{ }\!\!\pi\!\!\text{ }}{2} \right)-9\text{sin}\left( \frac{5\text{ }\!\!\pi\!\!\text{ }}{2} \right)$

$=6\text{cos}\left( 2\text{ }\!\!\pi\!\!\text{ }+\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)-9\text{sin}\left( 2\text{ }\!\!\pi\!\!\text{ }+\frac{\text{ }\!\!\pi\!\!\text{ }}{2} \right)=0-9=-9$

At $\text{x}=\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$, $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)\ne 0$ So $\text{x}=\frac{5\text{ }\!\!\pi\!\!\text{ }}{6}$is neither point of maxima or minima. Hence option D is the correct answer.

57. Maximum slope of the curve $\mathbf{y}=-{{\mathbf{x}}^{3}}+3{{\mathbf{x}}^{2}}+9\mathbf{x}-27$is: 

(A) 0 

(B) 12 

(C) 16 

(D) 32

Ans: The curve we have, $\text{y}=-{{\text{x}}^{3}}+3{{\text{x}}^{2}}+9\text{x}-27$

Slope of the curve = $\frac{\text{dy}}{\text{dx}}=-3{{\text{x}}^{2}}+6\text{x}+9$

Now we find whether the slope of the curve is maximum or minimum.

Differentiating the slope of the curve w.r.t. X,

$\frac{{{\text{d}}^{2}}\text{y}}{\text{d}{{\text{x}}^{2}}}=-6\text{x}+6=-6\left( \text{x}-1 \right)$

For critical points, $\frac{{{\text{d}}^{2}}\text{y}}{\text{d}{{\text{x}}^{2}}}=0$ 

$-6\left( \text{x}-1 \right)=0$

$\Rightarrow \text{x}=1$

Now, $\frac{{{\text{d}}^{3}}\text{y}}{\text{d}{{\text{x}}^{3}}}=-6<0$. Hence we get the maximum slope at $\text{x}=1$.

So the slope of curve at $\text{x}=1$,

 $\frac{\text{dy}}{\text{dx}}{{|}_{\text{x}=1}}=-3{{\left( 1 \right)}^{2}}+6\left( 1 \right)+9=15-3=12$

Therefore the correct answer is option B.

58. $\mathbf{f}\left( \mathbf{x} \right)={{\mathbf{x}}^{\mathbf{x}}}$ has a stationary point at 

(A) $\mathbf{x}=\mathbf{e}$ 

(B) $\mathbf{x}=\frac{1}{\mathbf{e}}$ 

(C) $\mathbf{x}=1$ 

(D) $\mathbf{x}=\sqrt{\mathbf{e}}$

Ans: The function we have, $\text{f}\left( \text{x} \right)={{\text{x}}^{\text{x}}}$

Let $\text{y}={{\text{x}}^{\text{x}}}$

Taking log on both sides

$\text{logy}=\text{x}.\text{log}\left( \text{x} \right)$

Differentiating on both sides w.r.t. x,

$\frac{1}{\text{y}}.\frac{\text{dy}}{\text{dx}}=\text{log}\left( \text{x} \right)+\text{x}.\frac{1}{\text{x}}$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\text{y}.\left[ 1+\text{logx} \right]$

$\Rightarrow \frac{\text{dy}}{\text{dx}}={{\text{x}}^{\text{x}}}.\left[ 1+\text{logx} \right]$

For the stationary points $\frac{\text{dy}}{\text{dx}}=0$

${{\text{x}}^{\text{x}}}.\left[ 1+\text{logx} \right]=0$       [${{\text{x}}^{\text{x }\!\!~\!\!\text{ }}}$always +ve]

$\Rightarrow 1+\text{log }\!\!~\!\!\text{ x}=0$

$\Rightarrow \text{log }\!\!~\!\!\text{ x}=-1$

$\Rightarrow \text{log }\!\!~\!\!\text{ x}=\text{log}{{\text{e}}^{-1}}$

$\Rightarrow \text{ }\!\!~\!\!\text{ x}={{\text{e}}^{-1}}$

$\Rightarrow \text{ }\!\!~\!\!\text{ x}=\frac{1}{\text{e}}$

This is the stationary point. So option B is the correct answer.

59. The maximum value of  ${{\left( \frac{1}{\mathbf{x}} \right)}^{\mathbf{x}}}$is: 

(A) e 

(B) ${{\mathbf{e}}^{\mathbf{e}}}$

(C) ${{\text{e}}^{\frac{\text{1}}{\text{e}}}}$ 

(D) ${{\left( \frac{\text{1}}{\text{e}} \right)}^{\frac{\text{1}}{\text{e}}}}$   

Ans: The function we have, $\text{f}\left( \text{x} \right)={{\left( \frac{1}{\text{x}} \right)}^{\text{x}}}$

Let $\text{y}={{\left( \frac{1}{\text{x}} \right)}^{\text{x}}}$

Taking log on both sides 

$\text{logy}=\text{x}.\text{log}\left( \frac{1}{\text{x}} \right)$

Differentiating on both sides w.r.t. x,

$\frac{1}{\text{y}}.\frac{\text{dy}}{\text{dx}}=\text{log}\left( \frac{1}{\text{x}} \right)+\text{x}.\frac{1}{\frac{1}{\text{x}}}\left( \frac{-1}{{{\text{x}}^{2}}} \right)$

$\Rightarrow \frac{\text{dy}}{\text{dx}}=\text{y}\left[ \text{log}\left( \frac{1}{\text{x}} \right)-1 \right]$

$\Rightarrow \frac{\text{dy}}{\text{dx}}={{\left( \frac{1}{\text{x}} \right)}^{\text{x}}}\left[ \text{log}\left( \frac{1}{\text{x}} \right)-1 \right]$

For critical points, $\frac{\text{dy}}{\text{dx}}=0$

$\Rightarrow {{\left( \frac{1}{\text{x}} \right)}^{\text{x}}}\left[ \text{log}\left( \frac{1}{\text{x}} \right)-1 \right]=0$

$\Rightarrow \text{log}\left( \frac{1}{\text{x}} \right)=1$   {${{\left( \frac{1}{\text{x}} \right)}^{\text{x}}}$ is always +ve}

$\Rightarrow \text{log}\left( \frac{1}{\text{x}} \right)=\text{loge}$

$\Rightarrow \frac{1}{\text{x}}=\text{e}$

$\Rightarrow \text{x}=\frac{1}{\text{e}}$

Again differentiating $\frac{\text{dy}}{\text{dx}}$w.r.t. x, we get:

$\frac{\text{dy}}{\text{dx}}={{\left( \frac{1}{\text{x}} \right)}^{\text{x}}}.\text{log}\left( \frac{1}{\text{x}} \right)-{{\left( \frac{1}{\text{x}} \right)}^{\text{x}}}$

$\frac{{{\text{d}}^{2}}\text{y}}{\text{d}{{\text{x}}^{2}}}={{\left( \frac{1}{\text{x}} \right)}^{\text{x}}}.\left( \frac{-1}{\text{x}} \right)+{{\left[ \text{log}\left( \frac{1}{\text{x}} \right)-1 \right]}^{2}}{{\left( \frac{1}{\text{x}} \right)}^{\text{x}}}$

Now, $\frac{{{\text{d}}^{2}}\text{y}}{\text{d}{{\text{x}}^{2}}}{{|}_{\text{x}=\frac{1}{\text{e}}}}={{\left( \text{e} \right)}^{\frac{1}{\text{e}}}}\left( -\text{e} \right)+{{\left( 1-1 \right)}^{2}}{{\left( \text{e} \right)}^{\frac{1}{\text{e}}}}=-\text{e}.{{\left( \text{e} \right)}^{\frac{1}{\text{e}}}}<0$

Hence the function has maxima at $\text{x}=\frac{1}{\text{e}}$

So the maximum value of function at $\text{x}=\frac{1}{\text{e}}$

$\text{f}\left( \frac{1}{\text{e}} \right)={{\left( \frac{1}{\frac{1}{\text{e}}} \right)}^{\frac{1}{\text{e}}}}={{\left( \text{e} \right)}^{\frac{1}{\text{e}}}}$

Therefore option C is the correct answer.

Fill in the blanks in each of the following Exercises 60 to 64:

60. The curves $\mathbf{y}=4{{\mathbf{x}}^{2}}+2\mathbf{x}-8$ and $\mathbf{y}={{\mathbf{x}}^{3}}-\mathbf{x}+13$ touch each other at the point_____. 

Ans: The given curves are $\text{y}=4{{\text{x}}^{2}}+2\text{x}-8$and $\text{y}={{\text{x}}^{3}}-\text{x}+13$

Given that the curves touch each other so the slope of both the curves should be the same.

For slope of curves, differentiate both curves w.r.t. x, 

$\text{y}={{\text{x}}^{3}}-\text{x}+13$

Differentiating w.r.t. x,

$\frac{\text{dy}}{\text{dx}}=3{{\text{x}}^{2}}-1$-----(1)

Also, $\text{y}=4{{\text{x}}^{2}}+2\text{x}-8$

Differentiating w.r.t. X,

$\frac{\text{dy}}{\text{dx}}=8\text{x}+2$------(2)

Now equating the slopes from eq.1 and eq.2

$3{{\text{x}}^{2}}-1=8\text{x}+2$

$\Rightarrow 3{{\text{x}}^{2}}-8\text{x}-3=0$

$\Rightarrow 3{{\text{x}}^{2}}-9\text{x}+\text{x}-3=0$

$\Rightarrow 3\text{x}\left( \text{x}-3 \right)+1\left( \text{x}-3 \right)=0$

$\Rightarrow \left( 3\text{x}+1 \right)\left( \text{x}-3 \right)=0$

$\Rightarrow \text{x}=3,\frac{-1}{3}$

For $\text{x}=3,$

$\text{ }\!\!~\!\!\text{ y}=4{{\left( 3 \right)}^{2}}+2\left( 3 \right)-8=36+6-8=34$

For $\text{x}=\frac{-1}{3}$ 

$\text{ }\!\!~\!\!\text{ y}=4{{\left( \frac{-1}{3} \right)}^{2}}+2\left( \frac{-1}{3} \right)-8=\frac{4}{9}-\frac{2}{3}-8=\frac{-74}{9}$

So the required points are $\left( 3,34 \right)$and $\left( \frac{-1}{3},\frac{-74}{9} \right).$

61. The equation of normal to the curve $\mathbf{y}=\mathbf{tanx}$ at (0, 0) is ________.

Ans: The given curve is $\text{y}=\text{tanx}$

Differentiating the curve w.r.t. x,

$\frac{\text{dy}}{\text{dx}}=\text{se}{{\text{c}}^{2}}\text{x}$

Now the slope of the curve at (0,0)

$\frac{\text{dy}}{\text{dx}}{{|}_{\left( 0,0 \right)}}=\text{se}{{\text{c}}^{2}}\text{x}=1$

Slope of Normal=$\frac{-1}{\text{slope }\!\!~\!\!\text{ of }\!\!~\!\!\text{ curve}}=\frac{-1}{1}=-1$

The equation of normal passing through (0,0) and having slope -1

$\left( \text{y}-0 \right)=-1\left( \text{x}-0 \right)$

$\Rightarrow \text{y}+\text{x}=0$

So the equation of normal to the curve $\text{y}=\text{tanx}$ at (0, 0) is $\text{y}+\text{x}=0$.

62. The values of a for which the function $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{sin}~\mathbf{x}-\mathbf{ax}+\mathbf{b}$ increases on R are ______.

Ans: The given function is $\text{f}\left( \text{x} \right)=\text{sin }\!\!~\!\!\text{ x}-\text{ax}+\text{b}$

Differentiating the function w.r.t. x, 

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{cos }\!\!~\!\!\text{ x}-\text{a}$

We know that a function is increasing function if $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)>0\text{ }\!\!~\!\!\text{ }$in its domain.

Given that the function is increasing in R.

Hence $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)>0$

$\text{cos }\!\!~\!\!\text{ x}-\text{a}>0$

$\text{cos }\!\!~\!\!\text{ x}>\text{a}$

Since $\text{cos }\!\!~\!\!\text{ x}\in \left[ -1,1 \right]$

For the condition $\text{cos }\!\!~\!\!\text{ x}>\text{a}$ being true the minimum value of cosx should be greater than a i.e. $-1>\text{a}$

So the values of a should be $\left( -\infty ,-1 \right)$for which the function $\text{f}\left( \text{x} \right)=\text{sin }\!\!~\!\!\text{ x}-\text{ax}+\text{b}$ increases on R.

63. The function $\mathbf{f}\left( \mathbf{x} \right)=\frac{2{{\mathbf{x}}^{2}}-1}{{{\mathbf{x}}^{4}}},\mathbf{x}>0$, decreases in the interval _______.

Ans: The given function is $\text{f}\left( \text{x} \right)=\frac{2{{\text{x}}^{2}}-1}{{{\text{x}}^{4}}}$

Differentiating the function w.r.t. x, 

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{4\text{x}.{{\text{x}}^{4}}-\left( 2{{\text{x}}^{2}}-1 \right).4{{\text{x}}^{3}}}{{{\text{x}}^{8}}}$

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\frac{-4{{\text{x}}^{5}}+4{{\text{x}}^{3}}}{{{\text{x}}^{8}}}=\frac{4{{\text{x}}^{3}}\left( -{{\text{x}}^{2}}+1 \right)}{{{\text{x}}^{8}}}$

A function is decreasing function if $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)<0$

$\frac{4{{\text{x}}^{3}}\left( -{{\text{x}}^{2}}+1 \right)}{{{\text{x}}^{8}}}<0$

$\Rightarrow -{{\text{x}}^{2}}+1<0$        [Given that x>0, so ${{\text{x}}^{8}}>0\text{ }\!\!~\!\!\text{ and }\!\!~\!\!\text{ }4{{\text{x}}^{3}}>0$]

 $\Rightarrow {{\text{x}}^{2}}-1>0$

$\Rightarrow \left( \text{x}-1 \right)\left( \text{x}+1 \right)>0$

$\Rightarrow \text{x}>1,\text{x}<-1$

$\because \text{x}>0\left( \text{given} \right)$

$\therefore \text{ }\!\!~\!\!\text{ x}<-1\left( \text{Rejected} \right)$

So the function decreases in interval $\left( 1,\infty  \right).$

64. The least value of the function $\mathbf{f}\left( \mathbf{x} \right)=\mathbf{ax}+\frac{\mathbf{b}}{\mathbf{x}}~(\mathbf{a}>0,\mathbf{b}>0,\mathbf{x}>0)$is ______.

Ans: The given function is $\text{f}\left( \text{x} \right)=\text{ax}+\frac{\text{b}}{\text{x}}$

Differentiating the function w.r.t x,

$\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=\text{a}-\frac{\text{b}}{{{\text{x}}^{2}}}$

For critical points, $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)=0$

$\text{a}-\frac{\text{b}}{{{\text{x}}^{2}}}=0$

$\Rightarrow {{\text{x}}^{2}}=\frac{\text{b}}{\text{a}}$

$\Rightarrow \text{x}=\pm \sqrt{\frac{\text{b}}{\text{a}}}$

Since given that x>0, hence $\text{x}=-\sqrt{\frac{\text{b}}{\text{a}}}$(Rejected)

Now again differentiating $\text{f }\!\!'\!\!\text{ }\left( \text{x} \right)\text{ }\!\!~\!\!\text{ }$w.r.t. x,

$\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)=-\text{b}.\frac{-2}{{{\text{x}}^{3}}}=\frac{2\text{b}}{{{\text{x}}^{3}}}$

At $\text{x}=\sqrt{\frac{\text{b}}{\text{a}}}$, $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right){{|}_{\text{x}=\sqrt{\frac{\text{b}}{\text{a}}}}}=\frac{2\text{b}}{{{\left( \frac{\text{b}}{\text{a}} \right)}^{\frac{3}{2}}}}=2\frac{{{\text{a}}^{\frac{3}{2}}}}{{{\text{b}}^{\frac{1}{2}}}}$

Since a>0 and b>0 , Hence $\text{f }\!\!'\!\!\text{  }\!\!'\!\!\text{ }\left( \text{x} \right)>0.$therefore the function has minima at $\text{x}=\sqrt{\frac{\text{b}}{\text{a}}}$.

Now the minimum value at $\text{x}=\sqrt{\frac{\text{b}}{\text{a}}}$

$\text{f}\left( \sqrt{\frac{\text{b}}{\text{a}}} \right)=\text{a}.\sqrt{\frac{\text{b}}{\text{a}}}+\frac{\text{b}}{\sqrt{\frac{\text{b}}{\text{a}}}}$

$\Rightarrow \text{f}(\left( \sqrt{\frac{\text{b}}{\text{a}}} \right)=\sqrt{\text{ab}}+\sqrt{\text{ab}}=2\sqrt{\text{ab}}$

Therefore the least value is $2\sqrt{\text{ab}}$...

Chapter 12 - Application of Derivatives

Chapter 12 - Application of Derivatives is an important Chapter for the boards of Class 12th. The Exemplar will help students to solve the questions and strengthen important concepts and will act as a revision. Students will learn the concept of rate of change of quantitative, tangents and normal approximation, increasing and decreasing functions, maximum and minimum values of functions in closed intervals, and maxima and minima through Chapter 6. Students focusing on the strong grip on the Chapter can reach out the Vedantu’s official site and go for the exemplar for the respective Chapter. 

Vedantu also offers other online material for Chapter 6 - Application of Derivatives like notes, sample question papers, additional questions, and last year’s papers. The notes offered by the Vedantu are designed by their expert faculty for the students to understand the theoretical concepts of the Chapter. A good collection of sample papers and additional questions are also offered that will give an upper hand to students for the practice during the preparation. The PDF also consists of last year’s paper so that the students can know what type of questions are asked in the Exam. Vedantu also offers live sessions for the students, so that they can revise the topics they have learned and clear doubts from the teachers. The teaching faculty of Vedantu is a group that focuses on enhancing the results for the registered students.