Maths Notes for Chapter 13 Probability Class 12 - FREE PDF Download



FAQs on Probability Class 12 Maths Chapter 13 CBSE Notes - 2025-26
1. What are the most important concepts to revise in Class 12 Probability for quick exam preparation?
The essential concepts to cover include random experiments, sample space, events and types (simple, compound, mutually exclusive, exhaustive), probability formulas, conditional probability, Bayes’ theorem, probability distributions (binomial, Poisson), and mean and variance of random variables. Reviewing these ensures a strong grasp of the entire chapter as outlined in the CBSE Class 12 Maths syllabus.
2. How should one structure their revision for Probability in Class 12 Maths to maximise understanding?
Begin with basic definitions and properties, then move to conditional probability and independent events. Next, focus on theorems like Bayes' theorem and the Law of Total Probability, and finally, revise random variables and distributions along with solved examples and key formulas. Consistently using concept maps and summary sheets helps visualise links between topics.
3. What are the common misconceptions students have about Probability in Class 12?
Frequent misunderstandings include:
- Confusing mutually exclusive with independent events (they are not the same).
- Assuming a probability of 1 guarantees certainty or a probability of 0 means impossibility in a practical sense.
- Forgetting to check if events are exhaustive or disjoint when applying formulas.
- Miscalculating conditional probabilities when events are dependent.
4. What is the role of conditional probability in solving advanced questions in Probability Class 12?
Conditional probability helps determine the likelihood of an event given that another event has already happened. It is essential for tackling problems involving sequential events, dependent probabilities, and for applying Bayes' theorem. Mastery of this concept allows for accurate analysis in multi-step and real-world probability situations.
5. Why is it important to understand the difference between independent events and mutually exclusive events in Probability?
Independent events are those where the occurrence of one does not affect the other, allowing the multiplication rule for probabilities. Mutually exclusive events cannot occur together (their intersection is zero). Misidentifying these can lead to use of incorrect formulas and wrong answers in exams.
6. How does Bayes’ theorem support problem-solving in Class 12 Probability?
Bayes' theorem enables calculation of the likelihood of a cause, given an observed outcome. It is crucial when the problem involves revising initial probabilities based on new evidence. This concept is especially useful in problems with multiple sources or cases, as required by the syllabus.
7. What strategies can students use to quickly recall key probability formulas during revision?
Effective techniques include
- organizing formulas into thematic groups (e.g., basic, addition, multiplication, distributions),
- using flashcards,
- creating concise formula charts,
- regular self-testing, and
- practising application of formulas through solved problems
8. How are random variables and their probability distributions represented and calculated in Class 12 Probability?
A random variable assigns a real number to each outcome in the sample space. Its probability distribution lists the probabilities for each possible value. Calculations use formulas like E(X) = ∑ xi P(xi) for mean, and Var(X) = E(X2) - [E(X)]2 for variance, as outlined by CBSE guidelines.
9. What is the significance of binomial and Poisson distributions in Class 12 Probability?
These are standard probability distributions covered in the Class 12 syllabus. Binomial distribution models the probability of a fixed number of successes in repeated independent trials, while Poisson distribution applies to events happening randomly over a continuous interval. Understanding their features, formulas, and applications is vital for answering related problems accurately.
10. How does practising solved examples and subjective questions in Probability contribute to exam success?
By working through varied examples and subjective questions, students develop familiarity with question patterns, learn the application of multiple concepts in one problem, and identify frequent exam traps. This targeted practice reinforces formula use, improves speed, and builds confidence for handling any type of question in Class 12 board exams.
11. What steps can students take to avoid calculation errors in Probability problems during revision?
To minimise mistakes,
- double-check calculations,
- write down all steps clearly,
- pay attention to event types (disjoint, independent),
- read questions thoroughly, and
- verify whether to apply addition, multiplication, or conditional formulas
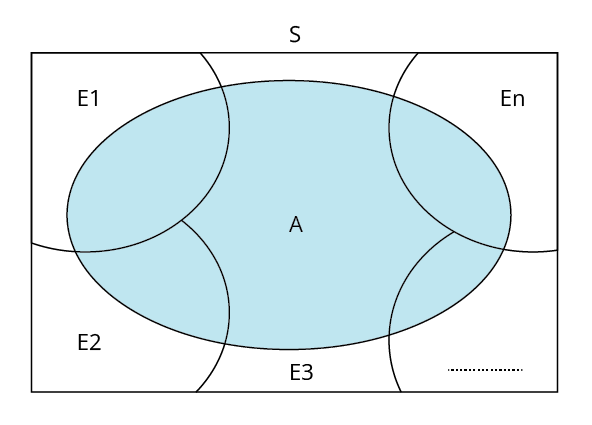
12. How can visual aids such as probability trees and diagrams help in understanding Probability concepts?
Probability trees and diagrams visually map out possible outcomes and event relations, making it easier to organize information about compound and conditional probabilities. These tools clarify paths, intersections, and unions, enhancing comprehension and accuracy—especially in multi-step problems.
13. What are the key benefits of using structured revision notes for Probability in Class 12 Maths?
Structured revision notes summarise core concepts, formulas, and application methods in an organised manner. They make last-minute reviews efficient, support quick lookup for challenging topics, and ensure that all vital points as per the CBSE curriculum are covered systematically before exams.