Vedantu's Class 12 Maths Exercise 6.2 Solutions With Expert Guidance
FAQs on NCERT Solutions For Class 12 Maths Chapter 6 Application Of Derivatives Exercise 6.2 - 2025-26
1. What type of problems are solved in NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives Exercise 6.2 as per the CBSE 2025–26 syllabus?
NCERT Solutions for Class 12 Maths Chapter 6, Exercise 6.2, cover questions focused on determining the increasing and decreasing nature of functions using derivatives. Problems involve analyzing intervals where functions are strictly increasing or decreasing by finding where the derivative is positive or negative, aligned with the latest CBSE guidelines.
2. How do NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2 help develop problem-solving strategies for calculus?
These solutions guide you through a step-by-step approach: calculate the derivative, set it to zero to find critical points, and test the sign of the derivative in different intervals. This method strengthens analytical skills in calculus and supports systematic problem solving, mirroring the CBSE examination pattern.
3. Which key concepts from the Application of Derivatives are emphasized in Exercise 6.2 solutions?
Key focus areas in Exercise 6.2 include:
- Monotonic behavior of functions (increasing/decreasing)
- Critical points and their role in interval analysis
- How to interpret the sign of the derivative
- Real-world application of calculus through function analysis
4. Why is it essential to practice the stepwise methods shown in NCERT Solutions for Class 12 Maths Chapter 6 Exercise 6.2?
Following a stepwise solution process ensures clarity in identifying intervals of monotonicity and prevents calculation errors. It helps avoid common mistakes like misinterpreting critical points or intervals, thereby boosting exam confidence and accuracy on CBSE board questions.
5. What role do derivatives play in determining whether a function is increasing or decreasing?
The sign of the derivative (positive or negative) at a point or over an interval directly indicates the increasing or decreasing nature of a function. If the derivative is positive in an interval, the function is increasing; if negative, it is decreasing within that interval.
6. How does Exercise 6.2 support preparation for higher mathematical studies and competitive exams?
This exercise builds a strong foundational understanding of function behavior and rate of change, which are crucial in advanced calculus, engineering, and entrance exams like JEE. Mastery of these stepwise solutions makes tackling complex problems easier in higher studies.
7. What are some common misconceptions students have about analyzing increasing and decreasing functions using derivatives?
Students often:
- Assume a function is always increasing if its derivative is positive at some point, ignoring interval analysis
- Forget to test all intervals created by critical points
- Miss checking endpoints for closed intervals
8. In NCERT Class 12 Maths Chapter 6 Exercise 6.2, how are intervals of monotonicity identified for a given function?
Intervals are identified by:
- Finding the derivative and all values where it is zero or undefined (critical points)
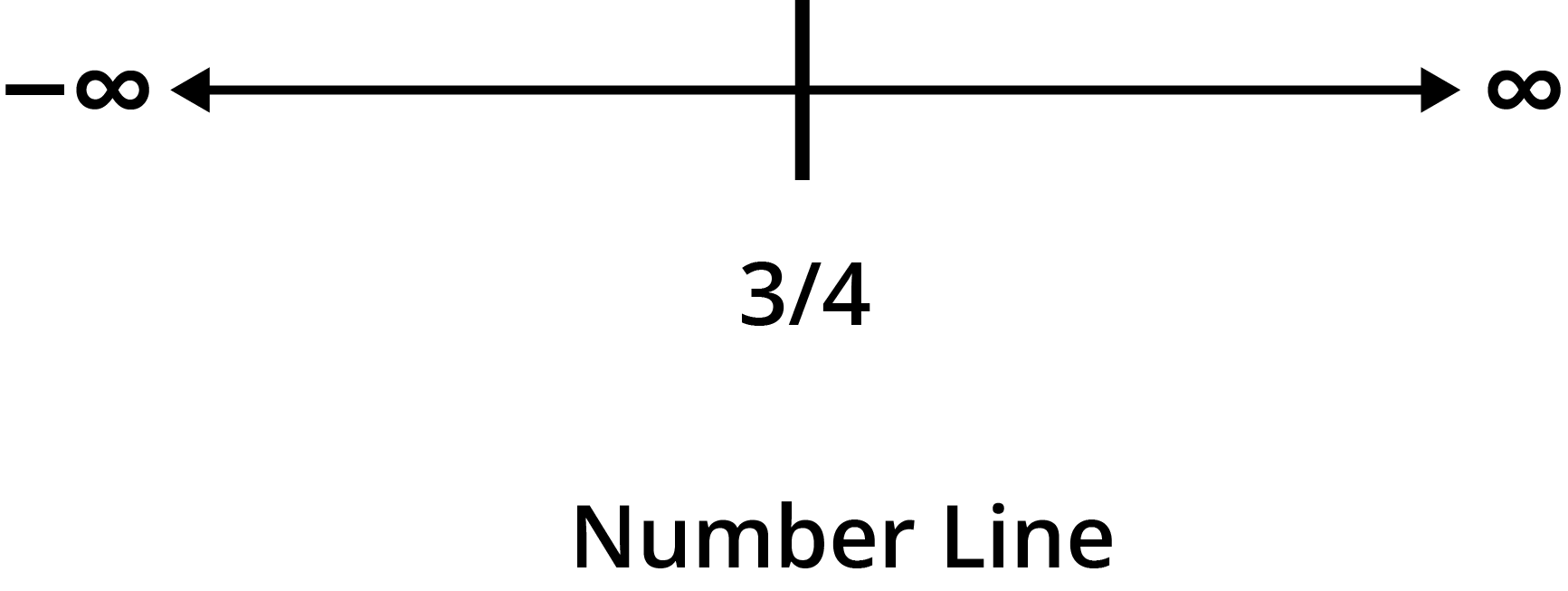
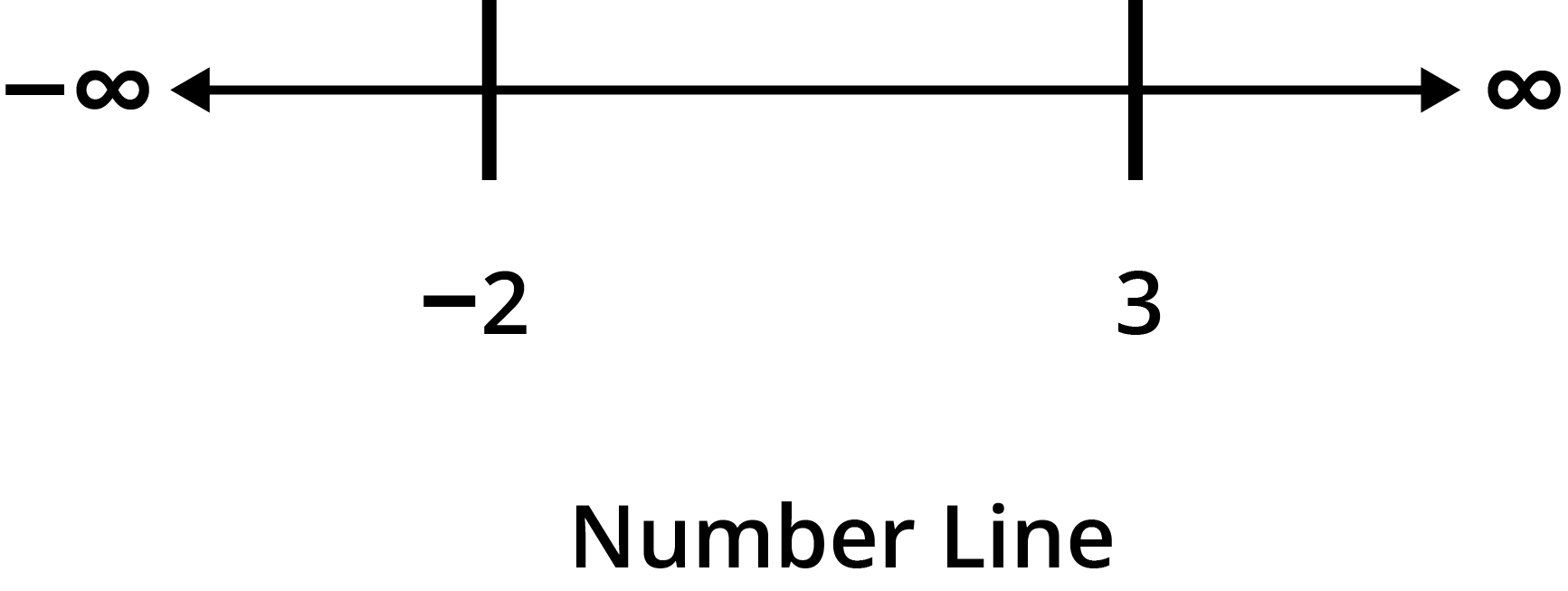
- Dividing the number line at these points
- Testing the sign of the derivative within each interval to classify them as increasing or decreasing
9. How does understanding increasing and decreasing functions help in optimization problems?
Knowing where a function increases or decreases allows you to pinpoint local maxima and minima, key for solving real-life optimization problems in economics, physics, and engineering, as emphasized in the CBSE syllabus for Class 12.
10. What is the importance of following the latest CBSE 2025–26 marking scheme while practicing NCERT Solutions for Application of Derivatives?
Practicing according to the CBSE 2025–26 marking scheme ensures you:
- Structure answers stepwise, as required in board exams
- Allocate time and steps for full marks
- Present solutions as expected by CBSE evaluators