Maths Notes for Chapter 5 Continuity and Differentiability Class 12 - FREE PDF Download



FAQs on CBSE Notes Class 12 Maths Chapter 5 - Continuity and Differentiability - 2025-26
1. What are the essential points to remember for quick revision of Continuity and Differentiability in Class 12 Maths?
Focus on these core ideas:
- Definition and conditions of continuity and differentiability at a point
- Types of discontinuities—removable and non-removable
- All main derivative rules—power, product, quotient, and chain rule
- Important formulas for trigonometric, exponential, and logarithmic derivatives
- How to verify continuity and differentiability using limits and derivatives
- Practice of typical sample problems and understanding graphical differences between continuity and differentiability
2. How should students structure their revision for Chapter 5 to maximise understanding before exams?
Start with a concise summary of formulas and derivative rules. Then, review solved examples focusing on various types of discontinuities and differentiability problems. Next, practice graphical questions that visually compare continuity and differentiability, and finish by tackling advanced application problems, especially with composite and piecewise functions.
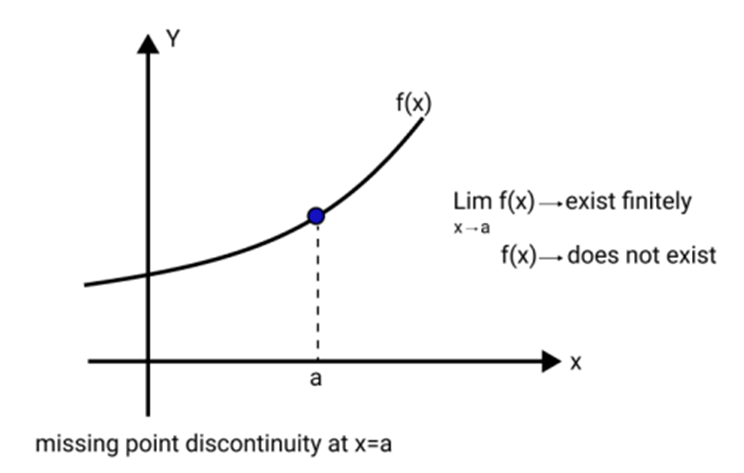
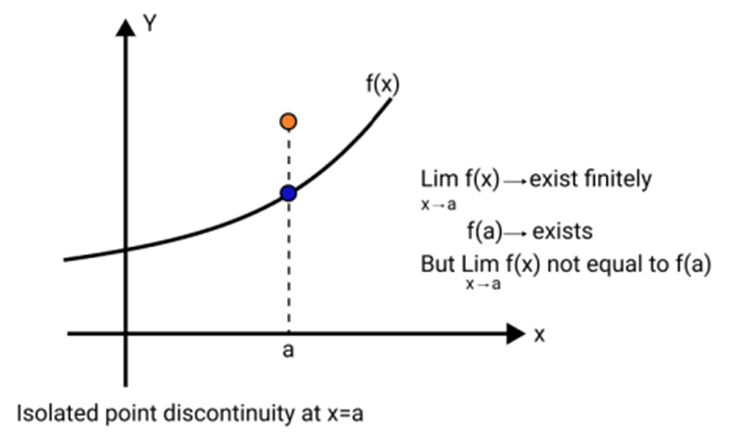
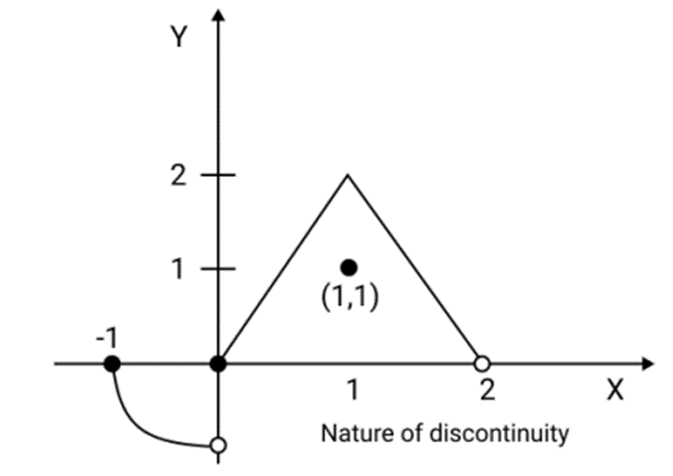
3. What is meant by removable and non-removable discontinuity, and why is this distinction important during revision?
Removable discontinuity occurs when the limit of a function exists at a point, but the function's value is either undefined or different from the limit. It can be fixed by redefining the function at that point. Non-removable discontinuity means the limit does not exist, so continuity cannot be restored by redefining the point. Understanding this distinction helps in correctly classifying and solving related questions in board exams.
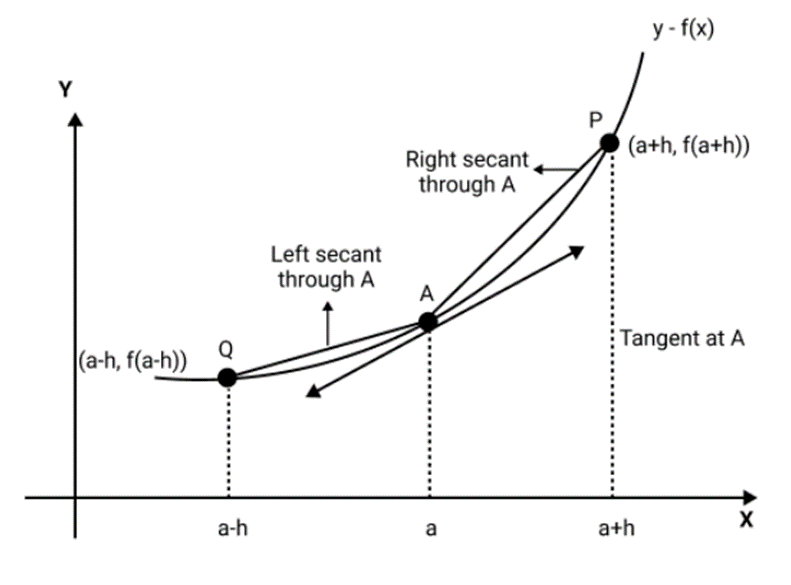
4. Why is differentiability considered a stronger condition than continuity for Class 12 board preparation?
Every function that is differentiable at a point is also continuous there, but the reverse is not always true. Differentiability requires both continuity and the existence of a unique tangent (no sharp corners or cusps), so if a function is not continuous at a point, it cannot be differentiable there. This is crucial to avoid common misconceptions in board questions.
5. Which derivative rules should be prioritised for last-minute revision in Continuity and Differentiability?
Ensure you have memorised the following:
- Power Rule: d/dx(xn) = n·xn-1
- Product Rule: d/dx[u·v] = u'·v + u·v'
- Quotient Rule: d/dx[u/v] = [u'·v - u·v']/v2
- Chain Rule: dy/dx = dy/du · du/dx
- Standard derivatives for trigonometric, exponential, and logarithmic functions
6. How can using graphs help clarify the difference between continuity and differentiability during revision?
By sketching or analysing the graph of a function, you can see that continuity means there are no breaks or jumps at a point, while differentiability also requires the graph to be smooth—meaning there are no sharp turns or corners. For example, y = |x| is continuous everywhere but not differentiable at x = 0 due to its sharp corner.
7. What common misconceptions should students avoid while revising this chapter?
One main misconception is assuming that every continuous function is differentiable. The correct view is that while differentiability implies continuity, the converse is not always true. Functions can be continuous but not differentiable at certain points. Always check both conditions separately during exams.
8. How should piecewise functions be revised for continuity and differentiability checks?
When revising piecewise functions, always check the left-hand and right-hand limits and the left-hand and right-hand derivatives at the junction points where the function's definition changes. A function is only continuous and differentiable at those points if these respective limits and derivatives are equal.
9. What role do higher order derivatives play in Class 12 Chapter 5, and how should they be revised?
Higher order derivatives, such as the second derivative (f''(x)), are obtained by differentiating the first derivative multiple times. They help in analysing the shape and curvature of graphs, finding points of inflexion and extremum. Revise standard results and formulas for second and third derivatives, as these often feature in advanced exam questions.
10. How do these revision notes prepare students for future competitive exams in addition to board exams?
The notes strengthen foundational concepts like derivative rules, conditions for continuity and differentiability, and logical problem-solving, which are all essential for exams such as JEE and NEET. They also help develop the analytical thinking and revision habits required for advanced study in mathematics, engineering, and physics.
11. What revision strategy should be used when short on time before a Class 12 Maths exam?
Prioritise the following sequence:
- Review key formulas and essential differentiation rules
- Quickly skim through solved examples and typical board-style problems
- Practice crucial questions on visual (graphical) and application-based continuity and differentiability
- Give special attention to composite and piecewise functions for potential tricky questions
12. How can worked examples in the notes enhance a student's conceptual clarity?
Worked examples show the step-wise application of formulas to diverse problems, clarifying common doubts and strengthening understanding of how concepts like continuity, differentiability, and derivative rules are actually applied. They bridge the gap between memorisation and real problem-solving, an essential skill for board exams.
13. Why is the chain rule particularly important for students revising for this chapter?
The chain rule is crucial for solving problems involving the differentiation of composite functions (functions within functions). Mastering it enables students to efficiently tackle complex derivatives that frequently appear in both board and competitive examinations.
14. What kinds of problems should students practice most to build confidence in Chapter 5 during revision?
Prioritise problems involving:
- Checking continuity and differentiability at specific points and intervals
- Applying all derivative rules (power, product, quotient, chain rule)
- Classifying types of discontinuities
- Graphical interpretation of functions
- Handling piecewise and composite functions
15. How can understanding continuity and differentiability concepts help in solving real-world problems or higher mathematics?
A deep understanding of continuity ensures you can model real-world processes without sudden jumps, while differentiability allows accurate analysis of rates of change—critical in physics, engineering, and advanced calculus. These foundational concepts support success in both further studies and practical applications.