Determinants Class 12 Notes CBSE Maths Chapter 4 (Free PDF Download)

Section–A (1 Mark Questions)

1. If $A$ is invertible matrix of order $3 \times 3$, then $\left|A^{-1}\right|=\ldots \ldots$

Ans. $A A^{-1}=I$

$$\begin{aligned}& \Rightarrow\left|A A^{-1}\right|=|I| \\& \Rightarrow|A|\left|A^{-1}\right|=1 \\& \Rightarrow\left|A^{-1}\right|=\frac{1}{|A|} .\end{aligned}$$

2. If $A$ is a matrix of order $3 \times 3$, then number of minors in determinant of $A$ are

Ans. If $A$ is a matrix of order $3 \times 3$, then it has 9 elements and hence, the number of minors in determinant of $A$ are 9 .

3. The sum of the products of elements of any row with the co-factors of corresponding elements is equal to..........

Ans. The sum of products of elements of any row with the cofactors of corresponding elements is equal to value of the determinant.

Let $$\Delta=\left|\begin{array}{lll}a_{11} & a_{12} & a_{13} \\a_{21} & a_{22} & a_{23} \\a_{31} & a_{32} & a_{33}\end{array}\right|$$

Expanding along $R_1$,

$$\Delta=a_{11} A_{11}+a_{12} A_{12}+a_{13} A_{13}$$

4. Evaluate $\left|\begin{array}{cc}2 & 4 \\ -1 & 2\end{array}\right|$.

Ans. We have $\left|\begin{array}{cc}2 & 4 \\ -1 & 2\end{array}\right|=2(2)-4(-1)$

$$=4+4=8$$

5. $$\Delta=\left|\begin{array}{lll}3 & 2 & 3 \\2 & 2 & 3 \\3 & 2 & 3\end{array}\right| .$$

Ans. Here ${ }^{R_1}$ and $R_3$ are identical. Thus, value of determinant is zero.

Section–B (2 Marks Questions)

6. Prove that $\left(A^{\prime}\right)^{-1}=\left(A^{-1}\right)^{\prime}$, where $A$ is an invertible matrix.

Ans. Since $\mathrm{A}$ is an invertible matrix, so it is non-singular.

We know that $|A|=|A|$

But $|A| \neq 0$.

So $\left|A^{\prime}\right| \neq 0$ i.e. $A^{\prime}$ is invertible matrix.

Now we know that $A A^{-1}=A^{-1} A=I$.

Taking transpose on both sides, we get

$\left(A^{-1}\right)^{\prime}A^{\prime}=A^{\prime}\left(A^{-1}\right)^{\prime}=(I)^{\prime}=I$

Hence $\left(A^{-1}\right)^{\prime}$ is inverse of $A^{\prime}$, i.e $\left(A^{\prime}\right)^{-1}=\left(A^{-1}\right)^{\prime}$.

7. If $\left|\begin{array}{cc}2 x & 5 \\ 8 & x\end{array}\right|=\left|\begin{array}{cc}6 & -2 \\ 7 & 3\end{array}\right|$, then find $x$.

Ans. We have $\left|\begin{array}{cc}2 x & 5 \\ 8 & x\end{array}\right|=\left|\begin{array}{cc}6 & -2 \\ 7 & 3\end{array}\right|$

$$\begin{aligned}& \Rightarrow 2 x^2-40=18+14 \\& \Rightarrow 2 x^2=72 \\& \Rightarrow x^2=36 \\& \Rightarrow x= \pm 6\end{aligned}$$

8. The area of a triangle with vertices $(-3,0),(-3,0),(3,0)$ and $(0, k)$ is 9 sq. units. Find the value of $k$.

Ans. Area of triangle with vertices $(-3,0),(3,0)$and $(0, k)$ is 9

$$\begin{aligned}& \Delta=\left|\frac{1}{2}\right| \begin{array}{ccc}-3 & 0 & 1 \\3 & 0 &1 \\0 & k & 1\end{array} \mid=9 \quad \text { (given) } \\\therefore & \quad[-3(-k)-0+1(3 k)]= \pm 18\end{aligned}$$

$$\begin{aligned}& \Rightarrow 6 k= \pm 18 \\& \therefore k= \pm \frac{18}{6}= \pm 3\end{aligned}$$

$$\Delta=\left|\begin{array}{ccc}\sin ^2 23^{\circ} & \sin ^2 67^{\circ} & \cos 180^{\circ} \\-\sin ^2 67^{\circ} & -\sin ^2 23^{\circ} & \cos ^2 180^{\circ} \\\cos 180^{\circ} & \sin ^2 23^{\circ} & \sin ^2 67^{\circ}\end{array}\right| .$$

9. Find the value of the determinant $$\Delta=\left|\begin{array}{ccc}\sin ^2 23^{\circ} & \sin ^2 67^{\circ} & \cos 180^{\circ} \\-\sin ^2 67^{\circ} & -\sin ^2 23^{\circ} & \cos ^2 180^{\circ} \\\cos 180^{\circ} & \sin ^2 23^{\circ} & \sin ^2 67^{\circ}\end{array}\right|$$

Ans. $$=\left|\begin{array}{ccc}\sin ^2 23^{\circ} & \cos ^2 23^{\circ} & -1 \\-\sin ^2 67^{\circ} & -\cos ^2 67^{\circ} & 1 \\-1 & \sin ^2 23^{\circ} & \cos ^2 23^{\circ}\end{array}\right|$$

Apply $C_1 \rightarrow C_1+C_2+C_3$

$$=\left|\begin{array}{ccc}0 & \cos ^2 23^{\circ} & -1 \\0 & -\cos ^2 67^{\circ} & 1 \\0 & \sin ^2 23^{\circ} & \cos ^2 23^{\circ}\end{array}\right|=0$$

10. Find the value of $a$ if the value of the determinant

$$\left|\begin{array}{ccc}1 & -2 & 5 \\2 & a & 1 \\0 & 4 & 2 a\end{array}\right| \text { is} 78 .$$

Ans. We have, $$\Delta=\left|\begin{array}{ccc}1 & -2 & 5 \\2 & a & 1 \\0 & 4 & 2 a\end{array}\right|=78$$

Expanding along $\mathrm{C}_1$

$$\begin{aligned}& 1\left(2 a^2-4\right)-2(-4 a-20)+0=78 \\& \Rightarrow 2 a^2-4+8 a+40=78 \\& \Rightarrow 2 a^2+8 a-42=0 \\& \Rightarrow a^2+4 a-21=0 \\& \Rightarrow(a+7)(a-3)=0\end{aligned}$$

$\Rightarrow a=-7$ and 3

11. Solve $\left|\begin{array}{cc}x^2-x+1 & x-1 \\ x+1 & x+1\end{array}\right|$ using the properties of

Ans. We have, $\left|\begin{array}{cc}x^2-x+1 & x-1 \\ x+1 & x+1\end{array}\right|$

Applying $C_1 \rightarrow C_1-C_2$

$$\begin{aligned}& =\left|\begin{array}{cc}x^2-2 x+2 & x-1 \\0 & x+1\end{array}\right| \\& =\left(x^2-2 x+2\right) \cdot(x+1)-(x-1) \cdot 0 \\& =x^3-2 x^2+2 x+x^2-2 x+2 \\& =x^3-x^2+2 .\end{aligned}$$determinants.

12. $$\Delta=\left|\begin{array}{ccc}0 & b-a & c-a \\a-b & 0 & c-b \\a-c & b-c & 0\end{array}\right|,$$, then show that $\Delta$ is equal to zero.

Ans. Interchanging rows and columns we get

$$\Delta=\left|\begin{array}{ccc}0 & a-b & a-c \\b-a & 0 & b-c \\c-a & c-b & 0\end{array}\right|$$

Taking ' -1 ' common from $R_1, R_2$ and $R_3$, we get

$$\begin{aligned}& \Delta=(-1)^3\left|\begin{array}{ccc}0 & b-a & c-a \\a-b & 0 & c-b \\a-c & b-c & 0\end{array}\right|=-\Delta \\& 2 \Delta=0 \text { or } \Delta=0 . \\& \Rightarrow \Delta=0\end{aligned}$$

13. Evaluate: $\left|\begin{array}{ccc}0 & x y^2 & x z^2 \\ x^2 y & 0 & y z^2 \\ x z^2 & z y^2 & 0\end{array}\right|$.

Ans. Let,

$$\Delta=\left|\begin{array}{ccc}0 & x y^2 & x z^2 \\x^2 y & 0 & y z^2 \\x^2 z & z y^2 & 0\end{array}\right|$$

On simplification we get,

$$\begin{aligned}& =0\left(0-y^3 z^3\right)-x y^2\left(0-x^2 y z^3\right)+x z^2\left(x^2 y^3 z-0\right) \\& =0+x^3 y^3 z^3+x^3 y^3 z^3 \\& =2 x^3 y^3 z^3\end{aligned}$$

PDF Summary - Class 12 Maths Determinants Notes (Chapter 4)

Recollecting Concepts

When a system of algebraic equations is given to us as:

${{a}_{1}}x+{{b}_{1}}y={{c}_{1}}$

${{a}_{2}}x+{{b}_{2}}y={{c}_{2}}$

Then we can express them in the form of matrices as:

$\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right]\left[ \begin{matrix} x  \\ y  \\ \end{matrix} \right]=\left[ \begin{matrix} {{c}_{1}}  \\ {{c}_{2}}  \\ \end{matrix} \right]$

To get the solution of a system of linear equations, we find all the values of the variables satisfying all the linear equations in the system.

Definition of Determinants

• We can define the determinant of a matrix as a scalar value that can be calculated from the elements of a square matrix.

• The scalar value for a square matrix  $\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right]$ is given by ${{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}$.

• It is represented as $\left| A \right|$ or det $\left( A \right)$ or $\Delta $.

• For a matrix  $\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right]$, the determinant is written as $\left| \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right|$.

• Square matrices are those matrices that have the same number of rows and columns. Only such matrices have determinants.

Types of Determinants

1. First Order Determinant – It is the determinant of a matrix of order one. The element of the matrix will be the determinant value. 

For example,

$\left[ 2 \right]\Rightarrow \left| 2 \right|\Rightarrow 2$ 

2. Second Order Determinant - It is the determinant of a matrix of order two.

If $\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right]$, then $\left| \begin{matrix} {{a}_{1}} & {{b}_{1}}  \\ {{a}_{2}} & {{b}_{2}}  \\ \end{matrix} \right|={{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}$.

For example,

$\left[ \begin{matrix} 1 & 3  \\ 5 & 3  \\ \end{matrix} \right]\Rightarrow \left| \begin{matrix} 1 & 3  \\ 5 & 3  \\ \end{matrix} \right|$ 

$\Rightarrow \left( 1\times 3 \right)-\left( 3\times 5 \right)\Rightarrow 3-15\Rightarrow -12$

3. Third Order Determinant - It is the determinant of a matrix of order three.

Let us consider $\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}} & {{c}_{1}}  \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}}  \\ {{a}_{3}} & {{b}_{3}} & {{c}_{3}}  \\ \end{matrix} \right]$. 

We have six ways to write the determinant, i.e. three ways to expand along rows and three ways to expand along columns.

Let us consider the expansion along the first row, which is the most common method.

So, first we consider the first element, ${{a}_{11}}$ and delete the row \[1\] and column $1$. We end up with a second order matrix and so we apply the determinant for this and multiply with ${{a}_{11}}$ and also \[{{\left( -1 \right)}^{sum\text{ }of\text{ }coefficients\text{ }of\text{ }{{a}_{11}}}}\Rightarrow {{\left( -1 \right)}^{1+1}}\], here sum of coefficients indicates the sum $i+j$ for element ${{a}_{ij}}$.

${{\left( -1 \right)}^{2}}.{{a}_{1}}.\left( {{b}_{2}}{{c}_{3}}-{{b}_{3}}{{c}_{2}} \right)$ 

Then we move onto element ${{a}_{12}}$ and delete the row \[1\] and column $2$. Again, We end up with a second order matrix and so we apply the determinant for this and multiply with \[{{a}_{12}}\] and also \[{{\left( -1 \right)}^{sum\text{ }of\text{ }coefficients\text{ }of\text{ }{{a}_{12}}}}\Rightarrow {{\left( -1 \right)}^{1+2}}\].

${{\left( -1 \right)}^{3}}.{{b}_{1}}.\left( {{a}_{2}}{{c}_{3}}-{{a}_{3}}{{c}_{2}} \right)$

At last, we move onto element ${{a}_{13}}$ and delete the row \[1\] and column $3$.

Again, We end up with a second order matrix and so we apply the determinant for this and multiply with ${{a}_{13}}$ and also \[{{\left( -1 \right)}^{sum\text{ }of\text{ }coefficients\text{ }of\text{ }{{a}_{13}}}}\Rightarrow {{\left( -1 \right)}^{1+3}}\].

${{\left( -1 \right)}^{4}}.{{c}_{1}}.\left( {{a}_{2}}{{b}_{3}}-{{a}_{3}}{{b}_{2}} \right)$

Now, we add them up to get the determinant of matrix 

$\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}} & {{c}_{1}}  \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}}  \\ {{a}_{3}} & {{b}_{3}} & {{c}_{3}}  \\ \end{matrix} \right]$ as 

${{a}_{1}}\left( {{b}_{2}}{{c}_{3}}-{{b}_{3}}{{c}_{2}} \right)-{{b}_{1}}\left({{a}_{2}}{{c}_{3}}-{{a}_{3}}{{c}_{2}} \right)+{{c}_{1}}\left({{a}_{2}}{{b}_{3}}-{{a}_{3}}{{b}_{2}} \right)$.

In the same manner, we can expand along other rows and columns. We will get the same value of determinant irrespective of the kind of expansion we opt for.

A tip to keep in mind while choosing the expansion method would be to go for the row or column containing the maximum number of zeroes. If zeroes are not present, then one. This will make calculations easier.

Another interesting point to keep in mind is that if we have two square matrices $A$ and $B$ of order $n$ and $A=kB$, then $\left| A \right|={{k}^{n}}\left| B \right|$, where $n=1,2,3,....$.

Properties of Determinants

The below properties are true for determinants of all orders.

1. Property 1 - The value of the determinant remains unchanged if its rows and columns are interchanged. Let us verify with the help of an example,

The determinant ${\left| \begin{matrix} 1 & 2 & 1  \\ 3 & 4 & 1  \\ 1 & 2 & 3  \\ \end{matrix} \right|}$ is $1\left( 12-2 \right)-2\left( 9-1 \right)+1\left( 6-4 \right)\Rightarrow 10-16+2\Rightarrow -4$. 

Exchanging rows and columns, we get  $\left| \begin{matrix} 1 & 3 & 1  \\ 2 & 4 & 2  \\ 1 & 1 & 3  \\ \end{matrix} \right|$. The value of this determinant is $1\left( 12-2 \right)-3\left( 6-2 \right)+1\left( 2-4 \right)\Rightarrow 10-12-2\Rightarrow -4$.

Hence verified.

• It follows from the above property that if $A$ is a square matrix, then $det\left( A \right)=det\left( A\prime  \right)$ . Here, $A\prime $ is the transpose of $A$.

• For interchange of row and columns, say ${{R}_{i}}={{i}^{th}}$ row and ${{C}_{i}}={{i}^{th}}$ column, we represent it symbolically as ${{C}_{i}}\leftrightarrow {{R}_{i}}$.

2. Property 2 - If any two rows (or columns) of a determinant are interchanged, then sign of determinant changes. Let us verify with the help of an example,

The determinant  $\left| \begin{matrix} 1 & 2 & 1  \\ 3 & 4 & 1  \\ 1 & 2 & 3  \\ \end{matrix} \right|$ is $1\left( 12-2 \right)-2\left( 9-1 \right)+1\left( 6-4 \right)\Rightarrow 10-16+2\Rightarrow -4$.

 

Interchanging first and second rows, we get  $\left| \begin{matrix} 3 & 4 & 1  \\ 1 & 2 & 1  \\ 1 & 2 & 3  \\ \end{matrix} \right|$. The value of this determinant is $3\left( 6-2 \right)-4\left( 3-1 \right)+1\left( 2-2 \right)\Rightarrow 12-8+0\Rightarrow 4$.

Hence verified.

• For interchange of two rows/columns, say ${{R}_{i}}\text{ and }{{R}_{j}}$ rows or ${{C}_{i}}\text{ }and\text{ }{{C}_{j}}$ columns, we represent it symbolically as ${{R}_{i}}\leftrightarrow {{R}_{j}}$ or ${{C}_{i}}\leftrightarrow {{C}_{j}}$.

3. Property 3 - If any two rows (or columns) of a determinant are identical (all corresponding elements are the same), then the value of the determinant is zero. Let us verify with the help of an example,

The value of the determinant with identical columns  $\left| \begin{matrix} 1 & 3 & 1  \\ 3 & 4 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$ is $1\left( 4-6 \right)-3\left( 3-3 \right)+1\left( 6-4 \right)\Rightarrow -2+0+2\Rightarrow 0$.

Hence verified.

4. Property 4 - If each element of a row (or a column) of a determinant is multiplied by a constant $k$, then its value gets multiplied by $k$. Let us verify with the help of an example,

Consider the determinant  $\left| \begin{matrix} 1 & 2 & 3  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$. The value of this determinant is $1\left( 3-6 \right)-2\left( 1-3 \right)+3\Rightarrow -3+4-3\Rightarrow -2$.

Now, first row of the same determinant is multiplied by a constant $2$ to get 

$\left| \begin{matrix} 2 & 4 & 6  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$. The value of this determinant is $2\left( 3-6 \right)-4\left( 1-3 \right)+6\left( 2-3 \right)\Rightarrow -6+8-6\Rightarrow -4$, which is $2\left[ -2 \right]$.

Hence verified.

5. Property 5 - If some or all elements of a row or column of a determinant are expressed as sum of two (or more) terms, then the determinant can be expressed as sum of two (or more) determinants. Let us verify with the help of an example,

Consider the determinant $\left| \begin{matrix} 1 & 2 & 3  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$. The value of this determinant is $1\left( 3-6 \right)-2\left( 1-3 \right)+3\left( 2-3 \right)\Rightarrow -3+4-3\Rightarrow -2$.

Now, we add terms to the terms in the first row of the same determinant and get 

$\left| \begin{matrix} 2+1 & 2+2 & 1+3  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$. The value of this determinant is $3\left( 3-6 \right)-4\left( 1-3 \right)+4\left( 2-3 \right)\Rightarrow -9+8-4\Rightarrow -5$.

The value of this determinant is $\left| \begin{matrix} 1 & 2 & 3  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|+\left| \begin{matrix} 2 & 2 & 1  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$$\left[ 1\left( 3-6 \right)-2\left( 1-3 \right)+3\left( 2-3 \right) \right]+\left[ 2\left( 3-6 \right)-2\left( 1-3 \right)+1\left( 2-3 \right) \right]$

$\Rightarrow \left[ -3+4-3 \right]+\left[ -6+4-1 \right]$

$\Rightarrow \left[ -2 \right]+\left[ -3 \right]$

$\Rightarrow -5$

which is same as determinant value for $\left| \begin{matrix} 2+1 & 2+2 & 1+3  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$.

Hence verified.

6. Property 6 - If, to each element of any row or column of a determinant, the equimultiples of corresponding elements of other row (or column) are added, then value of determinant remains the same, i.e., the value of determinant remain same if we apply the operation ${{R}_{i}}\to {{R}_{i}}+k{{R}_{j}}$ or ${{C}_{i}}\to {{C}_{i}}+k{{C}_{j}}$. Let us verify with the help of an example,

Consider the determinant $\left| \begin{matrix} 1 & 2 & 3  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$. The value of this determinant is $1\left( 3-6 \right)-2\left( 1-3 \right)+3\left( 2-3 \right)\Rightarrow -3+4-3\Rightarrow -2$.

Now, we add term which is a multiple of third row to the terms in the first row of the same determinant and get $\left| \begin{matrix} 2+2 & 2+4 & 1+2  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$.

By using the property 5, this can be expressed as $\left| \begin{matrix} 1 & 2 & 3  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|+\left| \begin{matrix} 2 & 4 & 2  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$.

By using the property 3, since we have the first and third row as proportional, the second determinant would be zero. The value of determinant $\left| \begin{matrix} 2+2 & 2+4 & 1+2  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$ would be the same as determinant $\left| \begin{matrix} 1 & 2 & 3  \\ 1 & 3 & 3  \\ 1 & 2 & 1  \\ \end{matrix} \right|$.

Hence verified.

7. Property 7 - If each element of a row (or column) of a determinant is zero, then its value is zero. For example,  $\left| \begin{matrix} 0 & 12 & -7  \\ 0 & 8 & 1  \\ 0 & -5 & 13  \\ \end{matrix} \right|$. If we expand this along the first column, then the value will be zero.

8. Property 8 - In a determinant, if all the elements on one side of the principal diagonal are zeroes, then the value of the determinant is equal to the product of the elements in the principal diagonal. For example the determinant  $\left| \begin{matrix} 3 & -3 & 2  \\ 0 & 8 & 1  \\ 0 & 0 & 1  \\ \end{matrix} \right|$ expanded along the first column has value as $3\left( 8-0 \right)=24$. The product of the elements in principal diagonal is $3\times 8\times 1=24$. Hence, verified. (Not in the current syllabus)

Area of a Triangle

• Consider a triangle with vertices as $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$. We know that the area of the triangle can be found as $A=\dfrac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]$.

• We can represent the same using determinants as $\Delta$ =$\dfrac{1}{2}\left| \begin{matrix} {{x}_{1}} & {{y}_{1}} & 1  \\ {{x}_{2}} & {{y}_{2}} & 1  \\ {{x}_{3}} & {{y}_{3}} & 1  \\ \end{matrix} \right|$.

• We always take the absolute value of the determinant while computing the area as it is a positive quantity.

• We use both positive and negative values of the determinant in case the area is given.

• We know that three collinear points cannot form a triangle and hence we can say that the area of the triangle formed by three collinear points is zero.

Minors

• If we delete the ${{i}^{th}}$ row and \[{{j}^{th}}\] column of a determinant in which the element ${{a}_{ij}}$ lies, then we get the minor of that element.

• Minor is represented as \[{{M}_{ij}}\].

• Minor of an element of a determinant of order \[n\left( n\ge 2 \right)\] is a determinant of order \[n1\].

• If we have to find \[{{M}_{21}}\] of determinant \[\left| \begin{matrix} 1 & -4 & 0  \\ 2 & 5 & 3  \\ -1 & 2 & 1  \\ \end{matrix} \right|\], then we get it as \[{{M}_{21}}=\left| \begin{matrix} -4 & 0  \\ 2 & 1  \\ \end{matrix} \right|\Rightarrow {{M}_{21}}=-4\].

Cofactors

• We denote the cofactor of an element \[{{a}_{ij}}\] as ${{A}_{ij}}$.

• Multiplying the minor of an element with a factor \[{{\left( 1 \right)}^{i+j}}\] gives the cofactor.

• It can be defined as \[{{A}_{ij}}=\text{ }{{\left( 1 \right)}^{i+j}}{{M}_{ij}}\], where \[{{M}_{ij}}\] is minor of \[{{a}_{ij}}\].

• When the elements of a row/column are multiplied with the cofactors of any other row/column, then their sum is zero.

• If we have to find \[{{A}_{11}}\] of determinant \[\left| \begin{matrix} 1 & -4 & 0  \\ 2 & 5 & 3  \\ -1 & 2 & 1  \\ \end{matrix} \right|\], then we get it as \[{{A}_{11}}={{\left( -1 \right)}^{1+1}}\left| \begin{matrix} 5 & 3  \\ 2 & 1  \\ \end{matrix} \right|\Rightarrow {{A}_{11}}=1.\left( 5-6 \right)\Rightarrow {{A}_{11}}=-1\].

Adjoint of a Matrix

• The matrix obtained after taking the transpose of the matrix of cofactors of the given matrix is called the adjoint of that matrix.

• For example, if we have the cofactor matrix as \[\left[\begin{matrix} a & b & c  \\ d & e & f  \\ g & h & i  \\ \end{matrix} \right]\], then the adjoint would be $\left[ \begin{matrix} a & d & g  \\ b & e & h  \\ c & f & i  \\ \end{matrix} \right]$.

• For a square matrix of order two, we can use the following shortcut:

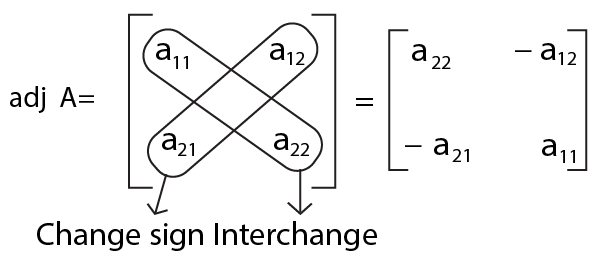
• Theorem 1 - If $A$ be any given square matrix of order $n$, then \[A\left( adj\text{ }A \right)=\left( adj\text{ }A \right)A=\left| A \right|I\], where $I$ is the identity matrix of order $n$.

If we have a matrix $\left[ \begin{matrix} a & b  \\ c & d  \\ \end{matrix} \right]$ and its adjoint as $\left[ \begin{matrix} e & f  \\ g & h  \\ \end{matrix} \right]$, then we can say that the sum of product of elements of a row/column with corresponding cofactors is equal to \[\left| A \right|\] and otherwise zero. So, we can write

$A\left( adj\text{ }A \right)=\left[ \begin{matrix} \left| A \right| & 0  \\ 0 & \left| A \right|  \\ \end{matrix} \right]=\left| A \right|I$

• Singular Matrices – If the determinant of a square matrix is zero, then it is said to be a singular matrix.

• Non-Singular Matrices – If the determinant of a square matrix is a non-zero value, then it is said to be a non-singular matrix.

• Theorem 2 - If $A$ and $B$ are nonsingular matrices of the same order, then $AB$ and $BA$ are also non-singular matrices of the same order.

• Theorem 3 - The determinant of the product of matrices is equal to the product of their respective determinants. It can be written as \[AB=\left| A \right|\left| B \right|\], where $A$ and $B$ are square matrices of the same order.

This can be verified as shown below:

From Theorem 1, we have $A\left( adj\text{ }A \right)=\left[ \begin{matrix} \left| A \right| & 0  \\ 0 & \left| A \right|  \\ \end{matrix} \right]$. 

Now taking the determinant value of matrices on both sides,

$\left| A\left( adj\text{ }A \right) \right|=\left| \begin{matrix} \left| A \right| & 0  \\ 0 & \left| A \right|  \\ \end{matrix} \right|$

$\left| A \right|\left| \left( adj\text{ }A \right) \right|={{\left| A \right|}^{2}}\left| \begin{matrix} 1 & 0  \\ 0 & 1  \\ \end{matrix} \right|$

$\left| A \right|\left| \left( adj\text{ }A \right) \right|={{\left| A \right|}^{2}}I$

$\left| \left( adj\text{ }A \right) \right|={{\left| A \right|}^{1}}$

Hence verified. This leads us to the general conclusion that if $A$ is a square matrix of order $n$, then $\left| \left( adj\text{ }A \right) \right|={{\left| A \right|}^{n-1}}$.

• Theorem 4 - A square matrix is invertible if and only if it is a non-singular matrix.

So, for a non-singular matrix $A$, we can write the inverse of the matrix as ${{A}^{-1}}=\dfrac{1}{\left| A \right|}\left( adj\text{ }A \right)$.

Looking into the proof,

Let $A$ be an invertible matrix of order $n$. Let $I$ be the identity matrix of order $n$. Then, there exists a square matrix $B$ of order $n$ such that \[AB=BA=I\].

So, we have \[AB=I\]. We can write \[\left| AB \right|=I\]. Since \[\left| I \right|=1,\left| AB \right|=\left| A \right|\left| B \right|\], it can be written as \[\left| A \right|\left| B \right|=1\].

This gives \[\left| A \right|\ne 0\] and hence $A$ is non-singular.

Conversely, if we let $A$ as a non-singular matrix, then \[\left| A \right|\ne 0\].

From Theorem 1, \[A\left( adj\text{ }A \right)=\left( adj\text{ }A \right)A=\left| A \right|I\]. Rearranging terms,

\[A\left[ \dfrac{1}{\left| A \right|}\left( adj\text{ }A \right) \right]=\left[ \left( adj\text{ }A \right)\dfrac{1}{\left| A \right|} \right]A=I\]

It is the same as $AB=BA=I$.

So, here $B=\dfrac{1}{\left| A \right|}\left( adj\text{ }A \right)$, which is the inverse of matrix $A$.

Applications of Determinants and Matrices

• They can be used for solving systems of linear equations in two or three variables. They can also be used for checking the consistency of a system of linear equations.

• Consistent system is a system of equations whose solution (one or more) exists.

• Inconsistent system is a system of equations whose solution does not exist.

• We can say that the determinant is a number that determines the uniqueness of the solution of a system of linear equations.

Solution of a System of Linear Equations Using Inverse of Matrix

Let us consider system of equations with three variables as

${{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z={{d}_{1}}$

${{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z={{d}_{2}}$

${{a}_{3}}x+{{b}_{3}}y+{{c}_{3}}z={{d}_{3}}$

Writing it in matrix form, we have

$\left[ \begin{matrix} {{a}_{1}} & {{b}_{1}} & {{c}_{1}}  \\ {{a}_{2}} & {{b}_{2}} & {{c}_{2}}  \\ {{a}_{3}} & {{b}_{3}} & {{c}_{3}}  \\ \end{matrix} \right]\left[ \begin{matrix} x  \\ y  \\ z  \\ \end{matrix} \right]=\left[ \begin{matrix} {{d}_{1}}  \\ {{d}_{2}}  \\ {{d}_{3}}  \\ \end{matrix} \right]$

This can be expressed as $AX=B$.

• Now, we look at two cases:

Case 1: If $A$ is a non-singular matrix, then its inverse exists.

From $AX=B$, we premultiply by ${{A}^{-1}}$,

${{A}^{-1}}\left( AX \right)={{A}^{-1}}B$

Using associative property,

$\left( {{A}^{-1}}A \right)X={{A}^{-1}}B$

$IX={{A}^{-1}}B$

$X={{A}^{-1}}B$

The above matrix equation provides a unique solution for the system of equations as we know that the inverse of a matrix is unique. We call this method as Matrix Method.

Case 2: If $A$ is a singular matrix, then \[\left| A \right|=0\].

For this case, first we calculate \[\left( adj\text{ }A \right)B\].

If \[\left( adj\text{ }A \right)B\] is a non-zero matrix, then the solution does not exist and the system of equations is called inconsistent.

If \[\left( adj\text{ }A \right)B\] is a zero matrix, then the system of equations may be either consistent (with infinitely many solutions) or inconsistent (with no solution).

Other Related Links for Class 12 Maths Chapter 4

• CBSE Class 12 Maths Chapter 4 Determinants Formulas

• NCERT Class 12 Maths Chapter 4 Solutions in English

• Important Questions for CBSE Class 12 Maths Chapter 4 - Determinants

• JEE Main Matrices and Determinants Important Questions