Differential Equations Class 12 Notes: CBSE Maths Chapter 9

Definition:

An equation involving the dependent variable and independent variable and also the derivatives of the dependable variable is known as differential equation. This can be mathematically written as $x\dfrac{dy}{dx}+y=0$.

The derivative $\dfrac{dy}{dx}$ can also be written as $f'(x)\text{ }or\text{ }y'(x)$. Similarly,

$ \dfrac{{{d}^{2}}y}{d{{x}^{2}}}\Rightarrow f''(x)\text{ or }y''(x) $ 

$ \dfrac{{{d}^{3}}y}{d{{x}^{3}}}\Rightarrow f'''(x)\text{ or }y'''(x) $ 

Some examples can be \[\dfrac{dy}{dx}=\dfrac{x}{{{y}^{\dfrac{1}{3}}}\left( 1+{{x}^{\dfrac{1}{3}}} \right)}\] , $\dfrac{{{d}^{2}}y}{d{{x}^{2}}}=-{{p}^{2}}y$  or \[{{x}^{2}}{{\left( \dfrac{dy}{dx} \right)}^{2}}={{y}^{2}}+1\] . 

Differential equations which involve only one independent variable are called ordinary differential equations.

Order of Differential Equations:

The order of a differential equation is the order of the highest derivative involved in the differential equation. This can be understood clearly by looking at a few examples. 

1. First order differential equation - ${{\left( \dfrac{dy}{dx} \right)}^{4}}+{{\left( \dfrac{dy}{dx} \right)}^{2}}-5x=0$. The maximum derivative of $y$ with respect to $x$ is $\dfrac{dy}{dx}$.

2. Second order differential equation - $\dfrac{{{d}^{2}}y}{d{{x}^{2}}}+7y=0$. The maximum derivative of $y$ with respect to $x$ is $\dfrac{{{d}^{2}}y}{d{{x}^{2}}}$.

3. Third order differential equation - \[{{\left( \dfrac{{{d}^{3}}y}{d{{x}^{3}}} \right)}^{2}}-3\left( \dfrac{dy}{dx} \right)+2=0\] . The maximum derivative of $y$ with respect to $x$ is \[\dfrac{{{d}^{3}}y}{d{{x}^{3}}}\].
   
   

Degree of Differential Equations:

The degree of a differential equation is the degree of the highest differential coefficient when the equation has been made rational and integral as far as the differential coefficients are concerned. This can be understood clearly by looking at a few examples.

1. First degree differential equation - \[\dfrac{dy}{dx}=\dfrac{5x}{{{y}^{\dfrac{1}{3}}}\left( 1-{{x}^{\dfrac{1}{3}}} \right)}\]. The power of the highest order derivative \[\dfrac{dy}{dx}\] is $1$.

2. Second degree differential equation - \[{{\left( \dfrac{{{d}^{3}}y}{d{{x}^{3}}} \right)}^{2}}+6\left( \dfrac{dy}{dx} \right)=-2\] . The power of the highest order derivative \[\dfrac{{{d}^{3}}y}{d{{x}^{3}}}\] is $2$.

3. Third degree differential equation - ${{\left[ 1+{{\left( \dfrac{dy}{dx} \right)}^{2}} \right]}^{{}^{1}/{}_{3}}}=3\dfrac{{{d}^{2}}y}{d{{x}^{2}}}$ . First, making it rational, $\left[ 1+{{\left( \dfrac{dy}{dx} \right)}^{2}} \right]=27{{\left( \dfrac{{{d}^{2}}y}{d{{x}^{2}}} \right)}^{3}}$. The power of highest order derivative $\dfrac{{{d}^{2}}y}{d{{x}^{2}}}$ is $3$.
   
   

Illustration 1: Find the order and degree of the following differential equations.

i. $\sqrt{\dfrac{{{d}^{2}}y}{d{{x}^{2}}}}=\sqrt[3]{\dfrac{dy}{dx}+3}$ 

Ans: Rewriting it as ${{\left( \dfrac{{{d}^{2}}y}{d{{x}^{2}}} \right)}^{3}}={{\left( \dfrac{dy}{dx}+3 \right)}^{2}}$

So, the order $=2$ and the degree $=3$.

ii. \[\dfrac{{{d}^{2}}y}{d{{x}^{2}}}={{\left\{ 1+{{\left( \dfrac{dy}{dx} \right)}^{4}} \right\}}^{{}^{5}/{}_{3}}}\] 

Ans: Rewriting it as \[{{\left( \dfrac{{{d}^{2}}y}{d{{x}^{2}}} \right)}^{3}}={{\left[ 1+{{\left( \dfrac{dy}{dx} \right)}^{4}} \right]}^{5}}\].

So, the order $=2$ and the degree $=3$.

iii. $y=px+\sqrt{{{a}^{2}}{{p}^{2}}+{{b}^{2}}}\text{ where }p=\dfrac{dy}{dx}$ 

Ans: Substituting p and then rewriting it as ${{\left( y-x\dfrac{dy}{dx} \right)}^{2}}={{a}^{2}}{{\left( \dfrac{dy}{dx} \right)}^{2}}+{{b}^{2}}$.  

So, the order $=1$ and the degree $=2$.

Formation of Ordinary Differential Equation:

There may be some arbitrary constants in an equation containing variables and constants. An ordinary differential equation is formed as a result of elimination of these arbitrary constants. 

Consider an equation containing $n$ arbitrary constants. Differentiating this equation n times we get $n$ additional equations containing n arbitrary constants and derivatives. Eliminating $n$ arbitrary constants from the above $\left( n+1 \right)$ equations, differential equations involving nth derivative are obtained. After this is complete, the resulting equation will be of the form $\phi \left( x,y,\dfrac{dy}{dx},\dfrac{{{d}^{2}}y}{d{{x}^{2}}},.....,\dfrac{{{d}^{n}}y}{d{{x}^{n}}} \right)=0$

Illustration 2: Find the differential equation of the family of all circles which pass through the origin and whose centre lie on $y-$axis.

Ans: Let the equation of the circle be 

${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ 

If it passes through $(0,0)$, then $c=0$

$\therefore $ The equation of circle is ${{x}^{2}}+{{y}^{2}}+2gx+2fy=0$

Since the centre of the circle lies on $y-$axis then $g=0$.

$\therefore $ The equation of the circle is 

${{x}^{2}}+{{y}^{2}}+2fy=0......(i)$

This represents a family of circles. 

Differentiating gives, 

$2x+2y\dfrac{dy}{dx}+2f\dfrac{dy}{dx}=0...........(ii)$ 

From $(i)\text{ and }(ii)$, 

$\left( {{x}^{2}}+{{y}^{2}} \right)\dfrac{dy}{dx}-2xy=0$ 

Hence, this is the required differential equation.

Solution of a Differential Equation:

The solution of the differential equation is a relation is a relation between the independent and dependent variable free from derivatives satisfying the given differential equation.

So, the solution of an equation given by $\dfrac{dy}{dx}=m$ can be obtained by integrating both the sides to remove the derivatives and obtain $y=mx+c$, where $c$ is an arbitrary constant.

a) General solution or primitive

The general solution of a differential equation is the relation between the variables (not involving the derivatives) which contain the same number of the arbitrary constants as the order of the differential equation. 

Thus the general solution of the differential equation 

$\dfrac{{{d}^{2}}y}{d{{x}^{2}}}=4y$ is $y=A\sin 2x+B\cos 2x$, where $A\text{ and }B$ are the constants.

b) Particular solution or integral 

A solution which is obtained by giving particular values to the arbitrary constants in the general solution is called a particular solution.

Illustration 3: Show that \[v=\dfrac{A}{r}+B\] is the general solution of the second order differential equation $\dfrac{{{d}^{2}}v}{d{{r}^{2}}}+\dfrac{2}{r}\dfrac{dv}{dr}=0$, where $A\text{ and }B$ are arbitrary constant. 

Ans: Given \[v=\dfrac{A}{r}+B\] 

Differentiating, $\dfrac{dv}{dr}=-\dfrac{A}{{{r}^{2}}}$.

Differentiating again, $\dfrac{{{d}^{2}}v}{d{{r}^{2}}}=\dfrac{2A}{{{r}^{3}}}.......(i)$ 

Rearranging the second term and substituting first derivative, 

$\dfrac{{{d}^{2}}v}{d{{r}^{2}}}=-\dfrac{2}{r}\dfrac{dv}{dr}$

$\dfrac{2A}{{{r}^{3}}}=-\dfrac{2}{r}\left( -\dfrac{A}{{{r}^{2}}} \right)$

$\dfrac{2A}{{{r}^{3}}}-\dfrac{2A}{{{r}^{3}}}=0$

Putting $A=4,B=5$ in \[v=\dfrac{A}{r}+B\] we get a particular solution of the differential equation 

$\dfrac{{{d}^{2}}v}{d{{r}^{2}}}+\dfrac{2}{r}\dfrac{dv}{dr}=0$ is $v=\dfrac{4}{r}+5$.

Illustration 4: Show that $y=a{{e}^{x}}+b{{e}^{2x}}+c{{e}^{-3x}}$ is a solution of the equation $\dfrac{{{d}^{3}}y}{d{{x}^{3}}}-7\dfrac{dy}{dx}+6y=0$.

Ans: Given that

\[y=a{{e}^{x}}+\text{ }b{{e}^{2x}}+c{{e}^{-3x}}\text{ }...\left( i \right)\] 

Differentiating, 

\[y'=a{{e}^{x}}+2b{{e}^{2x}}-3c{{e}^{-3x}}\text{ }...\left( ii \right)\] 

Differentiating \[\left( ii \right)\],

\[y''=a{{e}^{x}}+\text{ }4b{{e}^{2x}}+9c{{e}^{-3x}}\] 

Differentiating again,

$y'''=a{{e}^{x}}+8b{{e}^{2x}}-27c{{e}^{-3x}}$ 

The given differential equation is \[\dfrac{{{d}^{3}}y}{d{{x}^{3}}}-7\dfrac{dy}{dx}+6y=0\].

Considering the LHS and substituting the terms,

$\left[ a{{e}^{x}}+8b{{e}^{2x}}-27c{{e}^{-3x}} \right]-7\left[ a{{e}^{x}}+2b{{e}^{2x}}-3c{{e}^{-3x}} \right]+6\left[ a{{e}^{x}}+b{{e}^{2x}}+c{{e}^{-3x}} \right]$  

\[\Rightarrow a{{e}^{x}}+8b{{e}^{2x}}-27c{{e}^{-3x}}-7a{{e}^{x}}-14b{{e}^{2x}}+21c{{e}^{-3x}}+6a{{e}^{x}}+6b{{e}^{2x}}+6c{{e}^{-3x}}\]

\[\Rightarrow 0\] 

This is equal to RHS.

Since it satisfies the equation, $y=a{{e}^{x}}+b{{e}^{2x}}+c{{e}^{-3x}}$ is the solution for \[\dfrac{{{d}^{3}}y}{d{{x}^{3}}}-7\dfrac{dy}{dx}+6y=0\].

Method of solving an equation of the first order and first degree:

A differential equation of the first order and first degree can be written in the form $\dfrac{dy}{dx}=f\left( x,y \right)$ or, $Mdx+Ndy=0$, where $M\text{ and }N$  are functions of $x\text{ and }y$.

1. Method – 1

i. Variable Separation: 

The general form of such an equation is 

$f(x)dx+f(y)dy=0$ ...(i) 

Integrating it gives the solution as 

$\int{f(x)dx}+\int{f(y)dy}=c$

ii. Solution of differential equation of the type $\dfrac{dy}{dx}=f\left( ax+by+c \right)$:

Consider the differential equation $\dfrac{dy}{dx}=f\left( ax+by+c \right)$ ...(i) where $f\left( ax+by+c \right)$ is some function of $ax+by+c$. 

Let $z=ax+by+c$ 

$\therefore \dfrac{dz}{dx}=a+b\dfrac{dy}{dx}$ 

or, $\dfrac{dy}{dx}=\dfrac{\dfrac{dz}{dx}-a}{b}$ 

From (i), $\dfrac{\dfrac{dz}{dx}-a}{b}=f(z)$ 

or, $\dfrac{dz}{dx}=bf(z)+a$ 

or, $\dfrac{dz}{bf(z)+a}=dx$ ...(ii) 

In the differential equation (ii), the variables $x\text{ and }z$ are separated.

Integrating, we get 

 \[\int{\dfrac{dx}{bf(z)+a}=\int{dx}+c}\] 

or, \[\int{\dfrac{dx}{bf(z)+a}=x+c}\] , where $z=ax+by+c$

This represents the general solution of the differential equation (i)

Illustration 5: Solve ${{\left( x-y \right)}^{2}}\dfrac{dy}{dx}={{a}^{2}}$.

Ans: Let \[xy=v\] and differentiate it to get

$\Rightarrow \dfrac{dy}{dx}=1-\dfrac{dv}{dx}$

Substituting these in ${{\left( x-y \right)}^{2}}\dfrac{dy}{dx}={{a}^{2}}$ and rearranging terms in variable separable form,

$\Rightarrow dx=\dfrac{{{v}^{2}}}{{{v}^{2}}-{{a}^{2}}}dv$

Integrating

\[\int{dx}=\int{\dfrac{{{v}^{2}}}{{{v}^{2}}-{{a}^{2}}}dv}\] 

$x+c=\int{\dfrac{{{v}^{2}}-{{a}^{2}}+{{a}^{2}}}{{{v}^{2}}-{{a}^{2}}}}dv$ 

$x+c=\int{dv}+\int{\dfrac{{{a}^{2}}}{{{v}^{2}}-{{a}^{2}}}}dv$ 

\[x+c=v+\dfrac{{{a}^{2}}}{2a}\log \left| \dfrac{v-a}{v+a} \right|\]

$x+c=x-y+\dfrac{a}{2}\log \left| \dfrac{x-y-a}{x-y+a} \right|$

$c=-y+\dfrac{a}{2}\log \left| \dfrac{x-y-a}{x-y+a} \right|$

$y-\dfrac{a}{2}\log \left| \dfrac{x-y-a}{x-y+a} \right|=C$ 

Illustration 6: Solve, $\dfrac{dy}{dx}=\sin \left( x+y \right)+\cos \left( x+y \right)$ 

Ans: Let $z=x+y$ and differentiate it to get the variable separable form as

$\therefore \dfrac{dz}{dx}=1+\dfrac{dy}{dx}\Rightarrow \dfrac{dy}{dx}=\dfrac{dz}{dx}-1$ 

$\dfrac{dz}{dx}-1=\sin z+\cos z$  

$\dfrac{dz}{dx}=\sin z+\cos z+1$

Using identities $\sin x=2\sin \dfrac{x}{2}\text{cos}\dfrac{x}{2}\text{ }and\text{ }\cos x=2{{\cos }^{2}}\dfrac{x}{2}-1$,

$\Rightarrow \dfrac{dz}{dx}=2\sin \dfrac{z}{2}\text{cos}\dfrac{z}{2}+2{{\cos }^{2}}\dfrac{z}{2}$

Taking out $2{{\cos }^{2}}\dfrac{z}{2}$,

$\Rightarrow \dfrac{dz}{dx}=2{{\cos }^{2}}\dfrac{z}{2}\left( \tan \dfrac{z}{2}+1 \right)$

$\Rightarrow \dfrac{dz}{2{{\cos }^{2}}\dfrac{z}{2}\left( \tan \dfrac{z}{2}+1 \right)}=dx$ 

Integrating, 

$\Rightarrow \int{\dfrac{dz}{2{{\cos }^{2}}\dfrac{z}{2}\left( \tan \dfrac{z}{2}+1 \right)}}=\int{dx}$

Take $u=\tan \dfrac{z}{2}+1$.

So, $du=\dfrac{1}{2}{{\sec }^{2}}\dfrac{z}{2}dz$ 

Using identities $\sec x=\dfrac{1}{\cos x}$,

$du=\dfrac{1}{2{{\cos }^{2}}\dfrac{z}{2}}dz$

Substituting in the integral,

$\Rightarrow \int{\dfrac{du}{u}}=\int{dx}$

$\Rightarrow \log u=x+c$ 

Resubstituting back $u=\tan \dfrac{z}{2}+1$, 

$\Rightarrow \log \left( \tan \dfrac{z}{2}+1 \right)=x+c$

$\therefore \log \left( \tan \dfrac{x+y}{2}+1 \right)=x+c$  

This is the required general solution. 

i. Solution of differential equation of the type \[\dfrac{dy}{dx}=\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}},\text{ }\mathbf{where}\text{ }\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}\ne \dfrac{{{c}_{1}}}{{{c}_{2}}}\] 

Here \[\dfrac{dy}{dx}=\dfrac{{{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}}{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}},\text{ }\mathbf{where}\text{ }\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}\ne \dfrac{{{c}_{1}}}{{{c}_{2}}}\] ...(i) 

Let \[\dfrac{{{a}_{1}}}{{{a}_{2}}}=\dfrac{{{b}_{1}}}{{{b}_{2}}}=\lambda \] (say) 

$\therefore {{a}_{1}}=\lambda {{a}_{2}},{{b}_{1}}=\lambda {{b}_{2}}$   

From (i), \[\dfrac{dy}{dx}=\dfrac{\lambda {{a}_{2}}x+\lambda {{b}_{2}}y+{{c}_{1}}}{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}\] 

$=\dfrac{dy}{dx}=\dfrac{\lambda \left( {{a}_{2}}x+{{b}_{2}}y \right)+{{c}_{1}}}{{{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}}$ ...(ii) 

Let $z={{a}_{2}}x+{{b}_{2}}y$ 

$\therefore \dfrac{dz}{dx}={{a}_{2}}+{{b}_{2}}\dfrac{dy}{dx}\Rightarrow \dfrac{dy}{dx}=\dfrac{\dfrac{dz}{dx}-{{a}_{2}}}{{{b}_{2}}}$ ...(iii) 

From (ii) and (iii), we get 

$\dfrac{\dfrac{dz}{dx}-{{a}_{2}}}{{{b}_{2}}}=\dfrac{\lambda z+{{c}_{1}}}{z+{{c}_{2}}}$

or, $\dfrac{dz}{dx}=\dfrac{{{b}_{2}}\lambda z+{{c}_{1}}}{z+{{c}_{2}}}+{{a}_{2}}=\dfrac{\lambda {{b}_{2}}z+{{b}_{2}}{{c}_{1}}+{{a}_{2}}z+{{a}_{2}}{{c}_{2}}}{z+{{c}_{2}}}$ 

or $dx=\dfrac{z+{{c}_{2}}}{\lambda {{b}_{2}}+{{a}_{2}}z+{{b}_{2}}{{c}_{1}}+{{a}_{2}}{{c}_{2}}}dz$, where $x\text{ and }z$ are separated.

Integrating, we get 

$x+c=\int{\dfrac{z+{{c}_{2}}}{\lambda {{b}_{2}}+{{a}_{2}}z+{{b}_{2}}{{c}_{1}}+{{a}_{2}}{{c}_{2}}}dz\text{ where }z={{a}_{2}}x+{{b}_{2}}y}$

2. Method – 2

i. Homogeneous differential equation: 

A function $f\left( x,y \right)$ is called homogeneous function of degree n if 

$f\left( \lambda x,\lambda y \right)={{\lambda }^{n}}f\left( x,y \right)$ 

For example: 

a) $f\left( x,y \right)={{x}^{2}}{{y}^{2}}-x{{y}^{3}}$ is a homogeneous function of degree four, since 

$f\left( \lambda x,\lambda y \right)=\left( {{\lambda }^{2}}{{x}^{2}} \right)\left( {{\lambda }^{2}}{{y}^{2}} \right)-\left( \lambda x \right)\left( {{\lambda }^{3}}{{y}^{3}} \right)$  

$={{\lambda }^{4}}\left( {{x}^{2}}{{y}^{2}}-x{{y}^{3}} \right)$ 

$=\lambda f\left( x,y \right)$ 

b) $f\left( x,y \right)={{x}^{2}}{{e}^{\dfrac{x}{y}}}+\dfrac{{{x}^{3}}}{y}+{{y}^{2}}\log \left( \dfrac{y}{x} \right)$ is a homogeneous function of degree two, since

$f\left( \lambda x,\lambda y \right)=\left( {{\lambda }^{2}}{{x}^{2}} \right){{e}^{\dfrac{\lambda x}{\lambda y}}}+\dfrac{{{\lambda }^{3}}{{x}^{3}}}{\lambda y}+\left( {{\lambda }^{2}}{{y}^{2}} \right)\log \left( \dfrac{\lambda y}{\lambda x} \right)$ 

\[={{\lambda }^{2}}\left[ {{x}^{2}}{{e}^{\dfrac{x}{y}}}+\dfrac{{{x}^{3}}}{y}+{{y}^{2}}\log \left( \dfrac{y}{x} \right) \right]\] 

$={{\lambda }^{2}}f\left( x,y \right)$  

A differential equation of the form $\dfrac{dy}{dx}=f(x,y)$ , where $f\left( x,y \right)$ is a homogeneous polynomial of degree zero is called a homogeneous differential equation. Such equations are solved by substituting $v=\dfrac{y}{x}\text{ or }\dfrac{x}{y}$ and then separating the variables.

Illustration 7: Solve $\dfrac{dy}{dx}=\dfrac{y\left( 2y-x \right)}{x\left( 2y+x \right)}$ 

Ans: Each of the given functions, i.e. $y\left( 2y-x \right)$ and $x\left( 2y+x \right)$ is a homogeneous function of degree $2$. Hence, the given equation is a homogeneous differential equation.

Putting $y=vx$ and differentiating w.r.t $x$,

$\dfrac{dy}{dx}=v+x\dfrac{dv}{dx}$ 

Substituting in given equation,

$v+x\dfrac{dv}{dx}=\dfrac{vx\left( 2vx-x \right)}{x\left( 2vx+x \right)}=\dfrac{v\left( 2v-1 \right)}{2v+1}$

$\Rightarrow x\dfrac{dv}{dx}=\dfrac{v\left( 2v-1 \right)}{2v+1}-v$

After simplifying the RHS,

$\Rightarrow x\dfrac{dv}{dx}=\dfrac{-2v}{2v+1}$

$\Rightarrow \dfrac{2v+1}{2v}dv=-\dfrac{1}{x}dx$

Integrating,

$\Rightarrow \int{\dfrac{2v+1}{2v}}dv=-\int{\dfrac{1}{x}}dx$

$\Rightarrow \int{dv}+\int{\dfrac{1}{2v}}dv=-\int{\dfrac{1}{x}}dx$

\[\Rightarrow v+\dfrac{1}{2}\log v=-\log x+\log c\] 

Resubstituting $v=\dfrac{y}{x}$,

\[\Rightarrow \dfrac{y}{x}+\dfrac{1}{2}\log \dfrac{y}{x}=-\log x+\log c\]

\[\therefore y+\dfrac{x}{2}\log \dfrac{y}{x}=-x\log x+C\]

ii. Differential equation reducible to homogeneous forms:

Equation of the form $\dfrac{dy}{dx}=\dfrac{ax+by+c}{{a}'x+{b}'y+{c}'}$, where $\dfrac{a}{{{a}'}}\ne \dfrac{b}{{{b}'}}$ can be reduced to homogeneous form by changing the variables $x,y\text{ to }{x}',{y}'$ by equations $x={x}'+h\text{ and }y={y}'+k$ where $h\text{ and }k$ are constants to be chosen so as to make the given equation homogeneous.

$dx=d{x}'\text{ and }dy=d{y}'$ 

The given equation becomes 

\[\dfrac{d{y}'}{d{x}'}=\dfrac{a\left( {x}'+h \right)+b\left( {y}'+k \right)+c}{{a}'\left( {x}'+h \right)+{b}'\left( {y}'+k \right)+{c}'}\] 

$=\dfrac{a{x}'+b{y}'+\left( ah+bk+c \right)}{{a}'{x}'+{b}'{y}'+\left( {a}'h+{b}'k+{c}' \right)}$ 

Now, choose $h\text{ and }k$ so that 

$ah+bk+c=0$ 

and ${a}'h+{b}'k+{c}'=0$

From these equations, the values of $h\text{ and }k$ in terms of the coefficients are obtained. 

Then the given equation reduces to 

$\dfrac{dy}{dx}=\dfrac{a{x}'+b{y}'}{{a}'{x}'+{b}'{y}'}$   

Which is the homogeneous form.

3. Method – 3

i. Linear differential equation: 

A differential equation is said to be linear if the dependent variable y and its derivative occur in the first degree. 

An equation of the form \[\dfrac{dy}{dx}+Py=Q\] ...(i) 

where $P\text{ and }Q$ are functions of x only or constant is called a linear equation of the first order.

Similarly $\dfrac{dx}{dy}+Px=Q$ is a linear differential equation where $P\text{ and }Q$ are functions of $y$ only. 

To get the general solution of the above equations, determination of a function $R\text{ of }x$ called Integrating function (I.F) is required. So, multiply both sides of the given equation by $R$

where, $R={{e}^{\int{Pdx}}}=\text{I}\text{.F}\text{.}$ ...(iii) 

From (i) and (iii), 

${{e}^{\int{Pdx}}}\dfrac{dy}{dx}+Py{{e}^{\int{Pdx}}}=Q{{e}^{\int{Pdx}}}$ 

\[\dfrac{d}{dx}\left( y{{e}^{\int{Pdx}}} \right)=Q.{{e}^{\int{Pdx}}}\]  

Integrating, 

$y{{e}^{\int{Pdx}}}=\int{Q{{e}^{\int{Pdx}}}dx}+c$ is the required solution. 

This can also be written and memorized as 

$y\left( \text{I}\text{.F}\text{.} \right)=\int{Q\left( \text{I}\text{.F}\text{.} \right)dx}+c$

Illustration 8: Solve $2x\dfrac{dy}{dx}=y+6{{x}^{\dfrac{5}{2}}}-2\sqrt{x}$
Ans: The given equation can be written as 

$\dfrac{dy}{dx}+\left( \dfrac{-1}{2x} \right)y=3{{x}^{\dfrac{3}{2}}}-\dfrac{1}{\sqrt{x}}$ 

This is the form of \[\dfrac{dy}{dx}+Py=Q\] 

Hence $\text{I}\text{.F}\text{.}={{e}^{\int{\dfrac{-1}{2x}dx}}}={{e}^{-\dfrac{1}{2}\log x}}=\dfrac{1}{\sqrt{x}}$ 

Now using $y\left( \text{I}\text{.F}\text{.} \right)=\int{Q\left( \text{I}\text{.F}\text{.} \right)dx}+c$,

$\Rightarrow \dfrac{y}{\sqrt{x}}=\int{\left( 3{{x}^{\dfrac{3}{2}}}-\dfrac{1}{\sqrt{x}} \right)\dfrac{1}{\sqrt{x}}}dx+c$ 

$\Rightarrow \dfrac{y}{\sqrt{x}}=\int{\left( 3x-\dfrac{1}{x} \right)}dx+c$

Integrating,

$\Rightarrow \dfrac{y}{\sqrt{x}}=3\dfrac{{{x}^{2}}}{2}-\log x+c$

$\Rightarrow y=\dfrac{3}{2}{{x}^{2}}\sqrt{x}-\sqrt{x}\log x+c\sqrt{x}$

Therefore, $y=\dfrac{3}{2}{{x}^{\dfrac{5}{2}}}-\sqrt{x}\log x+c\sqrt{x}$.

i. Differential equation reducible to the linear form: 

Sometimes equations which are not linear can be reduced to the linear form by suitable transformation. 

Here, ${f}'\left( y \right)\dfrac{dy}{dx}+f(y)P(x)=Q(x)$ ...(i) 

Let, $f\left( y \right)=u\Rightarrow {f}'\left( y \right)dy=du$ 

Then (i) reduces to 

$\dfrac{du}{dx}+uP(x)=Q(x)$ Which is of the linear differential equation form.

Illustration 9: Solve \[{{\sec }^{2}}\theta d\theta +\tan \theta \left( 1-r\tan \theta  \right)dr=0\]

Ans: The given equation can be written as 

$\dfrac{d\theta }{dr}+\dfrac{\tan \theta }{{{\sec }^{2}}\theta }=\dfrac{r{{\tan }^{2}}\theta }{{{\sec }^{2}}\theta }$ 

$\left( \dfrac{{{\sec }^{2}}\theta }{{{\tan }^{2}}\theta } \right)\dfrac{d\theta }{dr}+\dfrac{1}{\tan \theta }=r$ 

${{\csc }^{2}}\theta \dfrac{d\theta }{dr}+\cot \theta =r$ ...(i) 

Let $\cot \theta =u$ 

$\Rightarrow -{{\csc }^{2}}\theta d\theta =du$ 

Then (i) reduces to 

$-\dfrac{du}{dr}+u=r\text{ or }\dfrac{du}{dr}-u=-r$ ...(ii) 

Which is a linear differential equation. 

So, $\text{I}\text{.F}\text{.}={{e}^{\int{-1dr}}}={{e}^{-r}}$

Now using $y\left( \text{I}\text{.F}\text{.} \right)=\int{Q\left( \text{I}\text{.F}\text{.} \right)dx}+c$,

$\Rightarrow u{{e}^{-r}}=\int{-r}{{e}^{-r}}dr+c$ 

$\Rightarrow u{{e}^{-r}}=-\int{r{{e}^{-r}}dr}+c$

Using integration by parts with first function as $r$ and second function as ${{e}^{-r}}$,

$\Rightarrow u{{e}^{-r}}=-\left[ r\int{{{e}^{-r}}}dr-\int{\dfrac{d}{dr}(r).\int{{{e}^{-r}}}dr} \right]$

$\Rightarrow u{{e}^{-r}}=-\left[ -r{{e}^{-r}}-\int{{{e}^{-r}}}dr \right]$

\[\Rightarrow u{{e}^{-r}}=-\left[ -r{{e}^{-r}}+{{e}^{-r}} \right]+c\]

\[\Rightarrow u{{e}^{-r}}=r{{e}^{-r}}-{{e}^{-r}}+c\]

\[\Rightarrow u=r-1+C\]

Resubstituting,

$\therefore \cot \theta =r-1+C$
 

i. Extended form of linear equations: 

Bernoulli’s equation: 

An equation of the form $\dfrac{dy}{dx}+Py=Q{{y}^{n}}$, where $P\text{ and }Q$  are function of $x$ alone or constants and $n$ is constant, other than $0\text{ and }1$, is called a Bernoulli’s equation. 

Here $\dfrac{dy}{dx}+Py=Q{{y}^{n}}$

Dividing by ${{y}^{n}}$,

$\dfrac{1}{{{y}^{n}}}\dfrac{dy}{dx}+P.\dfrac{1}{{{y}^{n-1}}}=Q$

Putting $\dfrac{1}{{{y}^{n-1}}}=v$and differentiating w.r.t $x$, 

$-\dfrac{(n-1)}{{{y}^{n}}}\dfrac{dy}{dx}=\dfrac{dv}{dx}$ 

$\dfrac{1}{{{y}^{n}}}\dfrac{dy}{dx}=\dfrac{-1}{n-1}\dfrac{dv}{dx}$ 

$\dfrac{dv}{dx}=\left( 1-n \right){{y}^{-n}}\dfrac{dy}{dx}$ 

The equation becomes 

$\dfrac{dv}{dx}+\left( 1-n \right)Pv=Q\left( 1-n \right)$ 

Which is a linear equation with $v$ as an independent variable.

Illustration 10: Solve ${{\cos }^{2}}x\dfrac{dy}{dx}-y\tan 2x={{\cos }^{4}}x$, where $\left| x \right|=\dfrac{\pi }{4}$ and $y\left( \dfrac{\pi }{4} \right)=\dfrac{3\sqrt{3}}{8}$.

Ans: The given equation can be written as 

$\dfrac{dy}{dx}-y\tan 2x{{\sec }^{2}}x={{\cos }^{2}}x$

This is the form of $\dfrac{dy}{dx}+Py=Q$ 

Here $P=-\tan 2x{{\sec }^{2}}x,Q={{\cos }^{2}}x$ 

$\int{Pdx}=-\int{\tan 2x{{\sec }^{2}}xdx}$ 

$=-\int{\dfrac{2\tan x}{1-{{\tan }^{2}}x}{{\sec }^{2}}xdx}$

$=\int{\dfrac{dt}{t}}$ 

Putting $1-{{\tan }^{2}}x=t$ 

$\therefore -2\tan x{{\sec }^{2}}xdx=dt$ 

$=\log t=\log \left( 1-{{\tan }^{2}}x \right)$ 

$\therefore \text{I}\text{.F}\text{.}={{e}^{\int{P.dx}}}={{e}^{\log \left( 1-{{\tan }^{2}}x \right)}}=1-{{\tan }^{2}}x$ 

Now using $y\left( \text{I}\text{.F}\text{.} \right)=\int{Q\left( \text{I}\text{.F}\text{.} \right)dx}+c$,

$\Rightarrow y\left( 1-{{\tan }^{2}}x \right)=\int{{{\cos }^{2}}x\left( 1-{{\tan }^{2}}x \right)dx}+c$

$\Rightarrow y\left( 1-{{\tan }^{2}}x \right)=\int{\left( {{\cos }^{2}}x-{{\sin }^{2}}x \right)dx}+c$

Using identity $\cos 2x={{\cos }^{2}}x-{{\sin }^{2}}x$,

$\Rightarrow y\left( 1-{{\tan }^{2}}x \right)=\int{\cos 2xdx}+c$

$\Rightarrow y\left( 1-{{\tan }^{2}}x \right)=\dfrac{\sin 2x}{2}+C$ …..(i)

Given that \[x=\dfrac{\pi }{6},y=\dfrac{3\sqrt{3}}{8}\]

Substituting in (i),

$\Rightarrow \dfrac{3\sqrt{3}}{8}\left( 1-{{\tan }^{2}}\dfrac{\pi }{6} \right)=\dfrac{\sin \dfrac{\pi }{3}}{2}+C$

\[\Rightarrow \dfrac{3\sqrt{3}}{8}\left( 1-\dfrac{1}{3} \right)=\dfrac{\sqrt{3}}{4}+C\]

\[\Rightarrow \dfrac{3\sqrt{3}}{8}\left( \dfrac{2}{3} \right)=\dfrac{\sqrt{3}}{4}+C\]

\[\Rightarrow \dfrac{\sqrt{3}}{4}=\dfrac{\sqrt{3}}{4}+C\]

$\therefore C=0$

Hence from (i),

$\Rightarrow y\left( 1-{{\tan }^{2}}x \right)=\dfrac{\sin 2x}{2}$

$\therefore y=\dfrac{\sin 2x}{2\left( 1-{{\tan }^{2}}x \right)}$

4. Method – 4

Exact Differential Equation: 

A differential equation is said to be exact if it can be derived from its solution (primitive) directly by differentiation, without any elimination, multiplication etc. 

For example, the differential equation $xdy+ydx=0$ is an exact differential equation as it is derived by direct differentiation for its solution, the function $xy=c$.

Illustration 11: Solve $\left( 1+xy \right)ydx+\left( 1-xy \right)xdy=0$ 

Ans: The given equation can be written as 

$ydx+x{{y}^{2}}dx+xdy-{{x}^{2}}ydy=0$ 

$\left( ydx+xdy \right)+xy\left( ydx-xdy \right)=0$ 

$d\left( xy \right)+xy\left( ydx-xdy \right)=0$  

Dividing by ${{x}^{2}}{{y}^{2}}$,

$\dfrac{d\left( xy \right)}{{{x}^{2}}{{y}^{2}}}+\dfrac{ydx-xdy}{xy}=0$ 

$\dfrac{d\left( xy \right)}{{{x}^{2}}{{y}^{2}}}+\dfrac{dx}{x}-\dfrac{dy}{y}=0$ 

Integrating,

$-\dfrac{1}{xy}+\log x-\log y=c$ 

Which is the required solution.

Application of Differential Equations: 

The below results are helpful when solving geometrical problems.

Consider the below diagram,

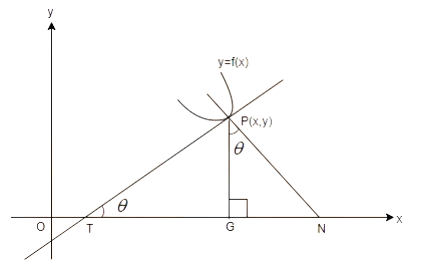
Let PT and PN be the tangent and the normal at $P(x,y)$ respectively. Let the tangent at P make an angle $\theta $ with the x-axis.

Then the slope of the tangent at P $=\tan \theta ={{\left( \dfrac{dy}{dx} \right)}_{P}}$ 

The slope of the normal at P $=-\dfrac{1}{{{\left( \dfrac{dy}{dx} \right)}_{P}}}$  

Equation of the tangent at $P(x,y)$ is

$Y-y={{\left( \dfrac{dy}{dx} \right)}_{P}}\left( X-x \right)$

Equation of the normal at $P(x,y)$ is 

$Y-y=-\dfrac{1}{{{\left( \dfrac{dy}{dx} \right)}_{P}}}\left( X-x \right)$

From $\Delta PGT,\sin \theta =\dfrac{PG}{PT}=\dfrac{y}{PT}$ 

\[\therefore \] 

And $\tan \theta =\dfrac{PG}{TG}=\dfrac{y}{TG}$ 

$\Rightarrow $ 

From $\Delta PGN,\cos \theta =\dfrac{PG}{PN}=\dfrac{y}{PN}$ 

$\Rightarrow $ 

$\tan \theta =\dfrac{GN}{y}$ 

$\Rightarrow $

Illustration 12: If the length of the sub-normal at any point P on the curve is directly proportional to $\text{O}{{\text{P}}^{2}}$, where O is the origin, then form the differential equation of the family of curves and hence find the family of curves. 

Ans: Here $\text{AB}=y\tan \theta =y\dfrac{dy}{dx}$ 

Drawing the diagram,

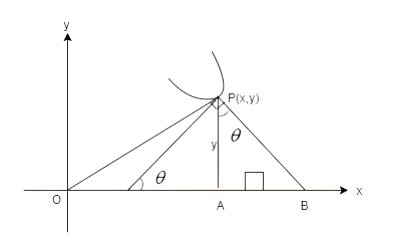
Also $\text{O}{{\text{P}}^{2}}={{x}^{2}}+{{y}^{2}}$ 

Given, length of the subnormal $=k.\text{O}{{\text{P}}^{2}}$ 

$y\dfrac{dy}{dx}=k\left( {{x}^{2}}+{{y}^{2}} \right)$ 

$2y\dfrac{dy}{dx}-2k{{y}^{2}}=2k{{x}^{2}}$ ….(i) 

Let ${{y}^{2}}=t\Rightarrow 2y\dfrac{dy}{dt}=\dfrac{dt}{dx}$ …(ii)

From (i) and (ii),

$\dfrac{dt}{dx}-2kt=2k{{x}^{2}}$ 

Which is a linear differential equation.

$\therefore \text{I}\text{.F}\text{.}={{e}^{\int{-2kdx}}}={{e}^{-2kx}}$  

The solution is 

$t.{{e}^{-2kx}}=\int{2k{{x}^{2}}{{e}^{-2kx}}dx}+c$ 

$=2k\left[ {{x}^{2}}\dfrac{{{e}^{-2kx}}}{-2k}+\dfrac{2}{2k}\int{x{{e}^{-2kx}}dx} \right]$ 

$=2k\left[ {{x}^{2}}\dfrac{{{e}^{-2kx}}}{-2k}+\dfrac{1}{k}\left\{ x\dfrac{{{e}^{-2kx}}}{-2k}+\dfrac{1}{2k}\int{{{e}^{-2kx}}dx} \right\} \right]$ 

$=-{{x}^{2}}{{e}^{-2kx}}-\dfrac{x{{e}^{-2kx}}}{k}+\dfrac{1}{k}\dfrac{{{e}^{-2kx}}}{2k}+c$ 

$\therefore {{y}^{2}}=-{{x}^{2}}-\dfrac{x}{k}+\dfrac{1}{2{{k}^{2}}}+c{{e}^{2kx}}$

Differential Equations Class 12 Notes Maths - Basic Subjective Questions

Section–A (1 Mark Questions)

1. The degree of the differential equation $\left ( \frac{d^{2}y}{dx^{2}} \right )^{2}+\left ( \frac{dy}{dx} \right )^{2}=xsin\left ( \frac{dy}{dx} \right )$  is______.

Ans. The degree of above differential equation is not defined because on solving $sin\left ( \frac{dy}{dx} \right )$  we will get an infinite series in the increasing powers of $\frac{dy}{dx}$ . Therefore, its degree is not defined.

2. The integrating factor of differential equation $cos\;x\frac{dy}{dx}+ysinx=1$  is_______.

Ans. Given, $cos\;x\frac{dy}{dx}+ysinx=1$ 

$\Rightarrow \frac{dy}{dx}+y\;tan\;x=sec\;x$

Here, P=tan x and Q=sec x 

$I.F.\;=e^{Pdx}=e^{\int tan\;x\;dx}=e^{log\;sec\;x}=sec\;x $

3. Integrating factor of the differential of the form $\frac{dy}{dx}+P_{1}x=Q_{1}$

is given by _____.

Ans. Given differential equation

$\frac{dy}{dx}+P_{1}x=Q_{1}$ 

$I.F.=e^{\int P_{1}dy}$.

4. State True or False. Correct substitution for the solution of differential equation of the type $\frac{dy}{dx}=f(x,y)$ where $f(x,y)$ is a homogeneous function of zero degree is v=xy.

Ans. False, The correct substitution is y=vx.

5. Find the degree of the differential equation $\left [ 1+\left ( \frac{dy}{dx} \right )^{2} \right ]^{\frac{3}{2}}=\frac{d^{2}y}{dx^{2}}$ .

Ans. Given is, $\left [ 1+\left ( \frac{dy}{dx} \right )^{2} \right ]^{\frac{3}{2}}=\frac{d^{2}y}{dx^{2}}$ 

On squaring both sides, we get

$\left [ 1+\left ( \frac{dy}{dx} \right )^{2} \right ]^{3}=\frac{d^{2}y}{dx^{2}}$

So, the degree of differential equation is 2.

Section–B (2 Marks Questions)

6. Find the solution of the differential equation $x \frac{d y}{d x}+2 y=x^2$.

Ans. Given differential equation is $x \frac{d y}{d x}+2 y=x^2$

$\Rightarrow \frac{d y}{d x}+\frac{2 y}{x}=x$

This equation of the form $\frac{d y}{d x}+P y=Q$

$\therefore \text { I.F. }=e^{\int_{\frac{1}{x}}^2 d x}=e^{2 \log x}=x^2$

The general solution is

$\begin{aligned}& y x^2=\int x \cdot x^2 d x+C \\& \Rightarrow y x^2=\frac{x^4}{4}+C \\& \Rightarrow y=\frac{x^2}{4}+C x^{-2} .\end{aligned}$

7. Find the order and degree of the differential equation $\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^{\frac{1}{4}}+x^{\frac{1}{5}}=0$

Ans. Given that, $\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^{\frac{1}{4}}+x^{\frac{1}{5}}=0$

$\Rightarrow\left(\frac{d y}{d x}\right)^{\frac{1}{4}}=-\left(x^{\frac{1}{5}}+\frac{d^2y}{d x^2}\right)$

On squaring both sides, we get

$\left(\frac{d y}{d x}\right)^{\frac{1}{2}}=\left(x^{\frac{1}{5}}+\frac{d^2 y}{d x^2}\right)^2$

Again, squaring both sides, we get

$\frac{d y}{d x}=\left(x^{\frac{1}{5}}+\frac{d^2 y}{d x^2}\right)^4$

Thus, order $=2$, degree $=4$.

8. Form the differential equation for $y=A \cos \alpha x+B \sin \alpha x$, where $\mathrm{A}$ and $\mathrm{B}$ are arbitrary constants.

Ans. Given, $y=A \cos \alpha x+B \sin \alpha x$

On differentiating both sides w.r.t., $x$ we get

$\frac{d y}{d x}=-\alpha A \sin \alpha x+\alpha B \cos \alpha x$

Again, differentiating both sides w.r.t. $x$, we get

$\begin{aligned}& \frac{d^2 y}{d x^2}=-A \alpha^2 \cos \alpha x-\alpha^2 B \sin \alpha x \\& \Rightarrow \frac{d^2 y}{d x^2}=-\alpha^2(A \cos \alpha x+B \sin \alpha x) \\& \Rightarrow \frac{d^2 y}{d x^2}=-\alpha^2 y \\& \Rightarrow \frac{d^2 y}{d x^2}+\alpha^2 y=0 .\end{aligned}$

9. Show that the solution of differential equation $x d y-y d x=0$ represents a straight line passing through origin.

Ans. Given is, $x d y-y d x=0$

$\begin{aligned}& \Rightarrow x d y=y d x \\& \Rightarrow \frac{d y}{y}=\frac{d x}{x}\end{aligned}$

On integrating both sides, we get

$\begin{aligned}& \Rightarrow \log y=\log x+\log C \\& \Rightarrow \log y=\log C x \\& \Rightarrow y=C x\end{aligned}$ which represents is a straight line passing through origin.

10. What is/are the number of solutions of $\frac{d y}{d x}=\frac{y+1}{x-1}$, when $y(1)=2$.

Ans. Given is, $\frac{d y}{d x}=\frac{y+1}{x-1}$

$\Rightarrow \frac{d y}{y+1}=\frac{d x}{x-1}$

On integrating both sides, we get

$\begin{aligned}& \log (y+1)=\log (x-1)-\log C \\& \Rightarrow C(y+1)=(x-1) \\& \Rightarrow C=\frac{x-1}{y+1}\end{aligned}$

When $x=1$ and $y=2$, then $C=0$

So, the required solution is $x-1=0$

Hence, only one solution exists.

11. Show that the General solution of the differential equation of the type $\frac{d x}{d y}+P_1 x=Q_1$ is given by $$x e^{\int A d y}=\int Q_1 e^{\int A d y} d y+C .$$

Ans. Given differential equation is $\frac{d x}{d y}+P_1 x=Q_1$

To get the general solution of this equation, we multiply both sides by integrating factor,

$\begin{aligned}& \text { I.F. }=e^{\int P_1 d y} \\& \Rightarrow e^{\int P_1 d y}\left(\frac{d x}{d y}+P_1 x\right)=Q_1 e^{\int P_1 d y} \\& \Rightarrow \frac{d x}{d y} e^{\int P_{d y}}+P_1 x e^{\int P_1 d y}=Q_1 e^{\int P_d d y} \\& \Rightarrow \frac{d}{d y}\left(x e^{\int P_1 d y}\right)=Q_1 e^{\int P_1 d y} \\& \Rightarrow \int \frac{d}{d y}\left(x e^{\int P_1 d y}\right) d y=\int Q_1 e^{\int P_1 d y} d y \\& \Rightarrow x e^{\int P_1 d y}=\int Q_1 e^{\int P_1 d y} d y+C\end{aligned}$

This is the required solution of the given differential equation.

12. Find the differential equation of all non-vertical lines in a plane.

Ans. The family of all non-vertical line is represented as:

$y=m x+c$, where $m \neq \tan \frac{\pi}{2}$

On differentiating above equation w.r.t. $x$, we get

$\frac{d y}{d x}=m$

Again, differentiating equation (i) w.r.t. $x$, we get

$\frac{d^2 y}{d x^2}=0$

13. Solve: $\frac{d y}{d x}-y=1, y(0)=1$.

Ans. Given is, $\frac{d y}{d x}-y=1$

$\begin{aligned}& \Rightarrow \frac{d y}{d x}=1+y \\& \Rightarrow \frac{d y}{1+y}=d x\end{aligned}$

On integrating both sides, we get

$\log (1+y)=x+C$

When $x=0$ and $y=1$, then

$\begin{aligned}& \log 0+C \\& \Rightarrow C=\log 2\end{aligned}$

The required solution is

$\begin{aligned}& \log (1+y)=x+\log 2 \\& \Rightarrow \log \left(\frac{1+y}{2}\right)=x \\& \Rightarrow \frac{1+y}{2}=e^x \\& \Rightarrow 1+y=2 e^x \\& \Rightarrow y=2 e^x-1 .\end{aligned}$

Importance of Chapter 9 Differential Equations Class 12 Notes

Understanding Chapter 9: Differential Equations in Class 12 is crucial for several reasons:

1. Foundation for Advanced Mathematics:

Differential equations form the basis for many advanced mathematical concepts and techniques used in higher studies, including physics, engineering, and applied mathematics.

2. Real-World Applications:

Differential equations are used to model and solve problems in various fields such as biology, economics, and engineering. They describe how quantities change and are essential for solving real-world problems.

3. Problem-Solving Skills:

Mastering differential equations enhances your ability to solve complex problems by applying different methods and techniques, which is important for both exams and practical applications.

4. Exam Preparation:

Differential equations are a significant part of the Class 12 syllabus. Comprehensive notes help you understand key concepts, practice solving different types of differential equations, and prepare effectively for exams.

5. Conceptual Understanding:

Detailed notes provide clear explanations and step-by-step solutions, which help in building a strong conceptual foundation and improve your ability to tackle various mathematical problems.

Important Formulas of Class 12 Chapter 9 You Shouldn’t Miss!

1. General Form of a Differential Equation:

\[F\left(x, y, \frac{dy}{dx}, \frac{d^2y}{dx^2}, \ldots \right) = 0 \]

2. First-Order Linear Differential Equation:

General form:

\[\frac{dy}{dx} + P(x)y = Q(x)\]

Solution:

\[y = e^{-\int P(x) \, dx} \left( \int Q(x) e^{\int P(x) \, dx} \, dx + C \right)\]

3. Separation of Variables:

For a differential equation of the form:

\[\frac{dy}{dx} = g(x)h(y)\]

Solution involves separating variables and integrating:

\[\int \frac{1}{h(y)} \, dy = \int g(x) \, dx\]

4. Homogeneous Differential Equation:

For the form:

\[\frac{dy}{dx} = \frac{f(x, y)}{g(x, y)}\]

If \[( f(x, y) ) and ( g(x, y) )\] are homogeneous functions of the same degree, use substitution \[( y = vx )\] to solve.

5. Exact Differential Equation:

General form:

\[M(x, y) \, dx + N(x, y) \, dy = 0\]

If \[( \frac{\partial M}{\partial y} = \frac{\partial N}{\partial x} )/], the equation is exact. The solution is found by integrating M and N.

6. Second-Order Differential Equation with Constant Coefficients:

General form:

\[a \frac{d^2y}{dx^2} + b \frac{dy}{dx} + c y = 0\]

Characteristic equation:

\[ar^2 + br + c = 0\]

7. Particular Solution using Method of Undetermined Coefficients:

For non-homogeneous differential equations:

\[y_p = A \cdot e^{mx}\]

Solve for A by substituting \[( y_p )\] into the differential equation.

8. Variation of Parameters:

For a non-homogeneous differential equation of the form:

y'' + p(x)y' + q(x)y = g(x)

Use the particular solution:

\[y_p = u_1(x) y_1 + u_2(x) y_2\]

Where \[( y_1 )\] and \[( y_2 )\] are solutions of the homogeneous equation.

9.  Laplace Transform of a Differential Equation:

For a differential equation:

\[\mathcal{L}\{y''\} = s^2 Y(s) - sy(0) - y'(0)\]

Use Laplace transforms to solve the differential equation by converting it into an algebraic equation.

10.  General Solution of a Differential Equation:

For a first-order linear differential equation:

\[y = e^{-\int P(x) \, dx} \left( \int Q(x) e^{\int P(x) \, dx} \, dx + C \right)\]

Where \[( C )\] is the constant of integration.

Tips for Learning the Class 12 Maths Chapter 9 Differential Equations

Here are some effective tips for learning Class 12 Maths Chapter 9: Differential Equations:

1. Understand Basic Concepts:

• Start by mastering the fundamental concepts of differential equations, including what they are, their types, and how they are used in various applications.

2. Learn Key Formulas:

• Memorise and understand key formulas and methods used for solving differential equations, such as separation of variables, linear equations, and exact equations.

3. Practice Different Types:

• Solve a variety of problems involving different types of differential equations. Practice solving first-order linear equations, homogeneous equations, and exact equations to build confidence.

4. Use Step-by-Step Solutions:

• Study solved examples in your textbook and notes. Pay attention to the step-by-step process used to solve each problem and try to replicate it on your own.

5. Apply Real-World Problems:

• Apply differential equations to real-world problems to see their practical applications. This can help in understanding the relevance and utility of the concepts.

6. Work on Integration Skills:

• Since solving differential equations often requires integration, ensure you are comfortable with integration techniques and formulas.

Conclusion

Mastering differential equations is crucial for solving complex problems in mathematics and its applications. By utilising the provided notes and PDFs, you gain access to clear explanations, essential formulas, and practical examples that will enhance your understanding and exam preparation. Consistent study and practice using these resources will help you excel in your Class 12 mathematics course and build a strong foundation for future studies. 

Related Study Materials for Class 12 Maths Chapter 9 Differential Equations

Students can also download additional study materials provided by Vedantu for Class 12 Maths Chapter 9 Differential Equations:

Chapter-wise Revision Notes Links for Class 12 Maths

Important Study Materials for Class 12 Maths