What Are the Four Phases of Bacterial Growth?
Bacteria are single-celled organisms that mainly reproduce by dividing into two cells, a process known as binary fission. Rather than getting bigger in size, their growth curve tracks how the number of cells increases over time. In suitable conditions, bacterial cells can divide rapidly, leading to a quick rise in their population.
A key measure here is the generation time, which is the time it takes for a bacterial cell to double in number. Different bacteria have different generation times depending on species and growing conditions:
Clostridium perfringens can double in about 10 minutes.
Escherichia coli often doubles in about 20 minutes.
Mycobacterium tuberculosis can take 12–16 hours to double.
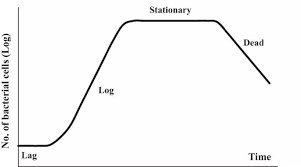
When bacteria are grown in a closed environment with limited nutrients, their population typically goes through four phases of the bacterial growth curve: lag, log (exponential), stationary, and death.
Phases of the Bacterial Growth Curve
1. Lag Phase
After being placed into a fresh nutrient medium, bacterial cells do not immediately start dividing.
They adapt to their new surroundings, synthesising the molecules (like proteins, RNA, and enzymes) needed for cell division.
Although cell numbers do not increase significantly, the cells become metabolically active and grow in size.
2. Log (Exponential) Phase
Once fully prepared, bacteria begin to divide at a constant rate, causing their numbers to multiply in a logarithmic manner (1 → 2 → 4 → 8 → 16, and so on).
This is called the exponential or log phase.
Cells are at their healthiest, and many experiments use bacteria from this phase.
The log phase lasts until nutrients start to become limited or harmful by-products build up.
3. Stationary Phase
As resources dwindle, growth slows down.
Eventually, the rate of new cell formation equals the rate of cell death.
The overall population remains constant, forming a flat (stationary) plateau on the graph.
4. Death Phase
When nutrients become scarce or toxic substances accumulate, more cells die than are formed.
The number of viable cells falls, leading to the death phase.
Generation Time Variations
Generation time depends on factors such as temperature, pH, nutrient availability, and oxygen levels.
Fast growers like Clostridium perfringens thrive in conditions that favour quick metabolism.
Slower bacteria, like Mycobacterium tuberculosis, have thicker cell walls and more complex requirements.
Quick Quiz
1. Which phase involves no increase in cell number but cells increase in size?
Answer: Lag phase.
2. In which phase do bacteria divide at a constant rate?
Answer: Log (exponential) phase.
3. Name any factor that can influence the generation time of bacteria.
Answer: Temperature, pH, nutrient availability, oxygen level, etc.
Related Topic Links


FAQs on Growth of Bacterial Populations: Phases, Curve & Examples
1. What are the four main phases of a bacterial growth curve?
A typical bacterial growth curve in a batch culture (a closed system) is divided into four distinct phases that describe the changes in a population over time:
Lag Phase: An initial period of adaptation where bacteria prepare for division, but there is no significant increase in cell number.
Log (Exponential) Phase: A period of rapid, exponential growth where the number of new bacteria appearing per unit time is proportional to the present population.
Stationary Phase: A plateau where the rate of bacterial cell growth equals the rate of cell death, often due to nutrient depletion and accumulation of toxic waste.
Death (Decline) Phase: A final phase where the death rate exceeds the growth rate, leading to a decline in the number of viable bacteria.
2. What is the key difference between the lag phase and the log phase of bacterial growth?
The key difference lies in cellular activity and population size. In the lag phase, bacteria are metabolically active and synthesising enzymes and proteins needed for growth in a new environment, but they are not yet dividing, so the population size remains stable. In contrast, the log phase is characterised by active and constant cell division, leading to a rapid, exponential increase in the bacterial population.
3. What is generation time, and does it vary between different bacterial species?
Generation time, or doubling time, is the specific time it takes for a bacterial population to double its number of cells during the exponential phase. Yes, it varies significantly among different species and is heavily influenced by environmental conditions like temperature, nutrient availability, and pH. For example, E. coli can have a generation time of just 20 minutes under ideal conditions, while other bacteria, like Mycobacterium tuberculosis, can take 15-20 hours.
4. What happens to a bacterial population when essential nutrients in the culture medium are depleted?
When essential nutrients become limited, the bacterial growth rate slows down significantly, forcing the population to transition from the log phase into the stationary phase. In this phase, the rate of cell division becomes equal to the rate of cell death. If nutrient depletion continues and toxic metabolic byproducts accumulate, the population will eventually enter the death phase, where the number of viable cells decreases.
5. Why are bacteria from the log phase preferred for use in biotechnology and industrial microbiology?
Bacteria in the log (exponential) phase are preferred for several key reasons. They are in their healthiest and most physiologically active state, exhibiting uniform metabolic activity. This uniformity is crucial for obtaining reliable and reproducible results in experiments, such as antibiotic susceptibility testing or producing metabolites like enzymes and antibiotics. Their rapid growth also ensures a high yield of biomass or desired products in a short time.
6. Besides nutrient depletion, what other factors can trigger the stationary phase in a bacterial culture?
While nutrient limitation is a primary cause, other factors can also trigger the stationary phase. These include:
Accumulation of toxic waste: As bacteria multiply, they release metabolic byproducts (e.g., organic acids) that can lower the pH and become toxic to the population.
Lack of physical space: In a confined environment, overcrowding can inhibit further growth.
Changes in oxygen levels: For aerobic bacteria, a decrease in available oxygen can limit the energy production needed for rapid growth.
7. How is the concept of the bacterial growth curve applied in food preservation?
The principles of the bacterial growth curve are fundamental to food preservation. The primary goal is to prevent spoilage bacteria from reaching the log phase of rapid growth. Methods like refrigeration and vacuum sealing extend the lag phase by creating unfavourable temperature or oxygen conditions. Adding preservatives like salt or acids can also inhibit enzyme activity, keeping bacteria in the lag phase. Conversely, sterilisation techniques like pasteurisation or canning aim to push the population directly into the death phase by killing the bacteria.
8. Is the death phase always a complete wipeout of the bacterial population?
Not necessarily. While the death phase is defined by the death rate exceeding the growth rate, the decline is logarithmic and may not lead to complete sterilisation. Some cells may be more resistant and die more slowly, a phenomenon known as 'tailing'. Furthermore, certain species can form highly resistant endospores when conditions become harsh. These spores can remain dormant for long periods and are not considered part of the viable cell count, but they can germinate if conditions improve, starting a new population.










