Physics Notes for Chapter 8 Electromagnetic Waves Class 12 - FREE PDF Download



FAQs on Electromagnetic Waves Class 12 Physics Chapter 8 CBSE Notes - 2025-26
1. What are electromagnetic waves and how are they produced according to the Class 12 syllabus?
Electromagnetic (EM) waves are disturbances composed of coupled, time-varying electric and magnetic fields that propagate through space. According to Maxwell's theory, they are produced by accelerating electric charges. When a charge oscillates, it creates a changing electric field, which in turn generates a changing magnetic field, and this self-sustaining process allows the wave to travel.
2. For a quick revision, what are the key properties of electromagnetic waves?
When revising Chapter 8, focus on these essential properties of electromagnetic waves:
- They are transverse waves, meaning the electric and magnetic fields are perpendicular to each other and to the direction of wave propagation.
- They do not require a material medium to travel and can propagate through a vacuum.
- In a vacuum, all EM waves travel at the speed of light, c = 3 x 108 m/s.
- They carry energy and momentum, which are shared between the electric and magnetic fields.
- The speed of an EM wave in a medium is given by v = 1/√(με), where μ is the permeability and ε is the permittivity of the medium.
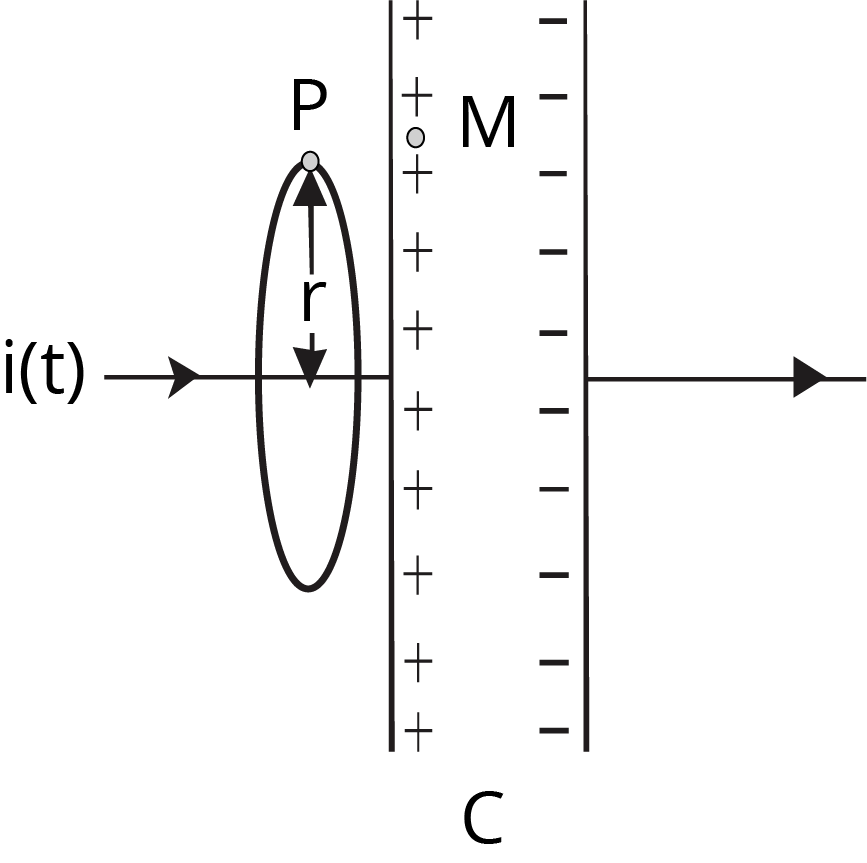
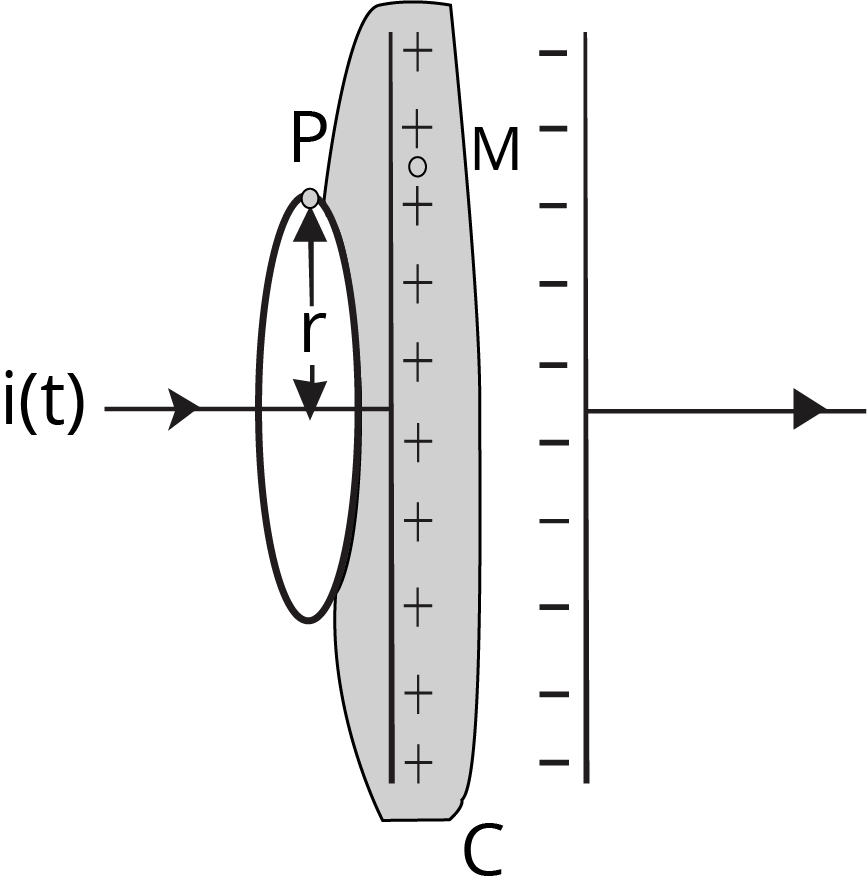
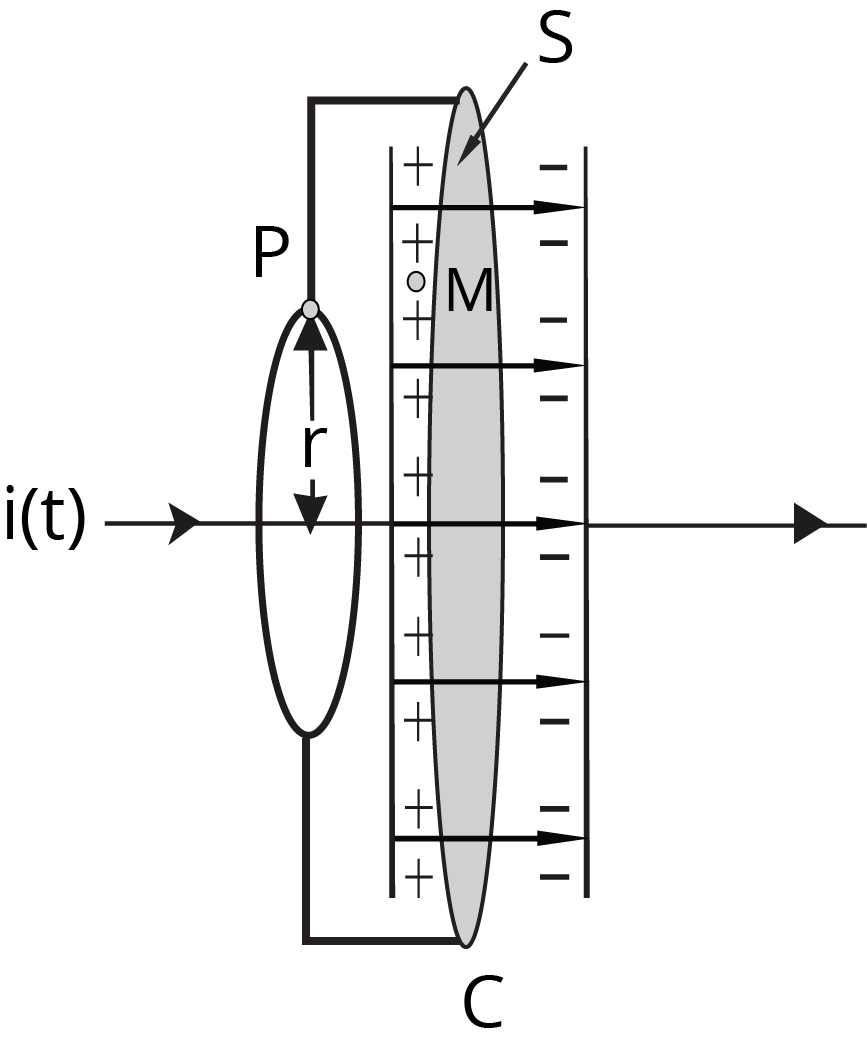
3. Why was it necessary for Maxwell to introduce the concept of 'displacement current'?
Maxwell introduced the concept of displacement current (Id) to address an inconsistency in Ampere's Circuital Law. The law failed when applied to the region between the plates of a charging capacitor, as there was no conduction current. Maxwell proposed that a time-varying electric field in this gap produces a magnetic field, just like a conduction current does. This 'displacement current' completes the circuit and makes the law universally consistent, forming the basis of the Ampere-Maxwell Law.
4. How are Maxwell's equations fundamental to the concept of electromagnetic waves?
Maxwell's four equations are fundamental because they mathematically unify electricity, magnetism, and light. They show that:
- A changing magnetic field creates an electric field (Faraday's Law of Induction).
- A changing electric field (or a conduction current) creates a magnetic field (Ampere-Maxwell Law).
5. What is the electromagnetic spectrum and how are its regions arranged?
The electromagnetic spectrum is the systematic arrangement of all electromagnetic waves in order of their wavelength or frequency. For revision, it's useful to remember the order of decreasing wavelength (and increasing frequency):
- Radio waves
- Microwaves
- Infrared
- Visible light
- Ultraviolet (UV)
- X-rays
- Gamma rays
6. How does the energy of an electromagnetic wave relate to its electric and magnetic fields?
The energy in an electromagnetic wave is stored in its oscillating electric and magnetic fields. The total energy density (energy per unit volume) is the sum of the energy densities of the electric field (UE) and the magnetic field (UB). A key concept for revision is that these two energy contributions are equal. The total energy density can be expressed solely in terms of the electric field as U = ε0E2, where E is the instantaneous electric field strength.
7. Why is it important to understand that electromagnetic waves are transverse in nature?
Understanding that EM waves are transverse is crucial because it explains phenomena like polarisation. Since the electric and magnetic field oscillations are restricted to a plane perpendicular to the wave's direction of travel, we can filter or manipulate the wave by controlling the orientation of these fields. This property distinguishes them from longitudinal waves (like sound) and is the principle behind technologies like polarised sunglasses and LCD screens.
8. How did Maxwell's equations lead to the prediction of the speed of light?
By solving his four equations for electromagnetic waves propagating in a vacuum, Maxwell derived a formula for their speed. The resulting speed was given by the expression c = 1/√(μ0ε0), where μ0 is the permeability and ε0 is the permittivity of free space. When he calculated this value using the known experimental values for μ0 and ε0, it was found to be approximately 3 x 108 m/s, which matched the experimentally measured speed of light. This was strong evidence that light itself is an electromagnetic wave.
9. When revising, how should I connect the different parts of the electromagnetic spectrum to their sources?
For effective revision, associate each type of EM wave with its typical source:
- Radio waves: Produced by accelerated motion of charges in conducting wires.
- Microwaves: Generated by special vacuum tubes like klystrons and magnetrons.
- Infrared waves: Emitted by hot bodies and molecules.
- Visible light: Produced by electrons in atoms transitioning between energy levels.
- Ultraviolet (UV) rays: Emitted by the Sun, special lamps, and very hot bodies.
- X-rays: Produced when high-energy electrons strike a metal target.
- Gamma rays: Originate from radioactive decay and nuclear reactions.