Application Of Integrals - Exercise-wise Questions and Answers For Class 12 Maths - Free PDF Download



FAQs on NCERT Solutions For Class 12 Maths Chapter 8 Application Of Integrals - 2025-26
1. What is the standard step-by-step method to solve problems in NCERT Solutions for Class 12 Maths Chapter 8, Application of Integrals?
To solve problems in this chapter as per the NCERT methodology, you should follow these steps:
- Sketch the Curve: Draw a rough sketch of the given curve(s) and lines to identify the required bounded region.
- Identify the Region: Clearly shade the area that needs to be calculated.
- Set Up the Integral: Determine whether to integrate with respect to the x-axis (using y dx) or the y-axis (using x dy).
- Determine Limits: Find the correct limits of integration (the starting and ending points) from the graph or the given equations.
- Integrate: Evaluate the definite integral to find the numerical value of the area.
2. How many exercises are in Chapter 8, Application of Integrals, according to the latest CBSE 2025-26 syllabus?
In the NCERT textbook for Class 12 Maths, Chapter 8 (Application of Integrals) contains one primary exercise (Exercise 8.1) and a Miscellaneous Exercise. Both focus on finding the area under simple curves as per the updated syllabus.
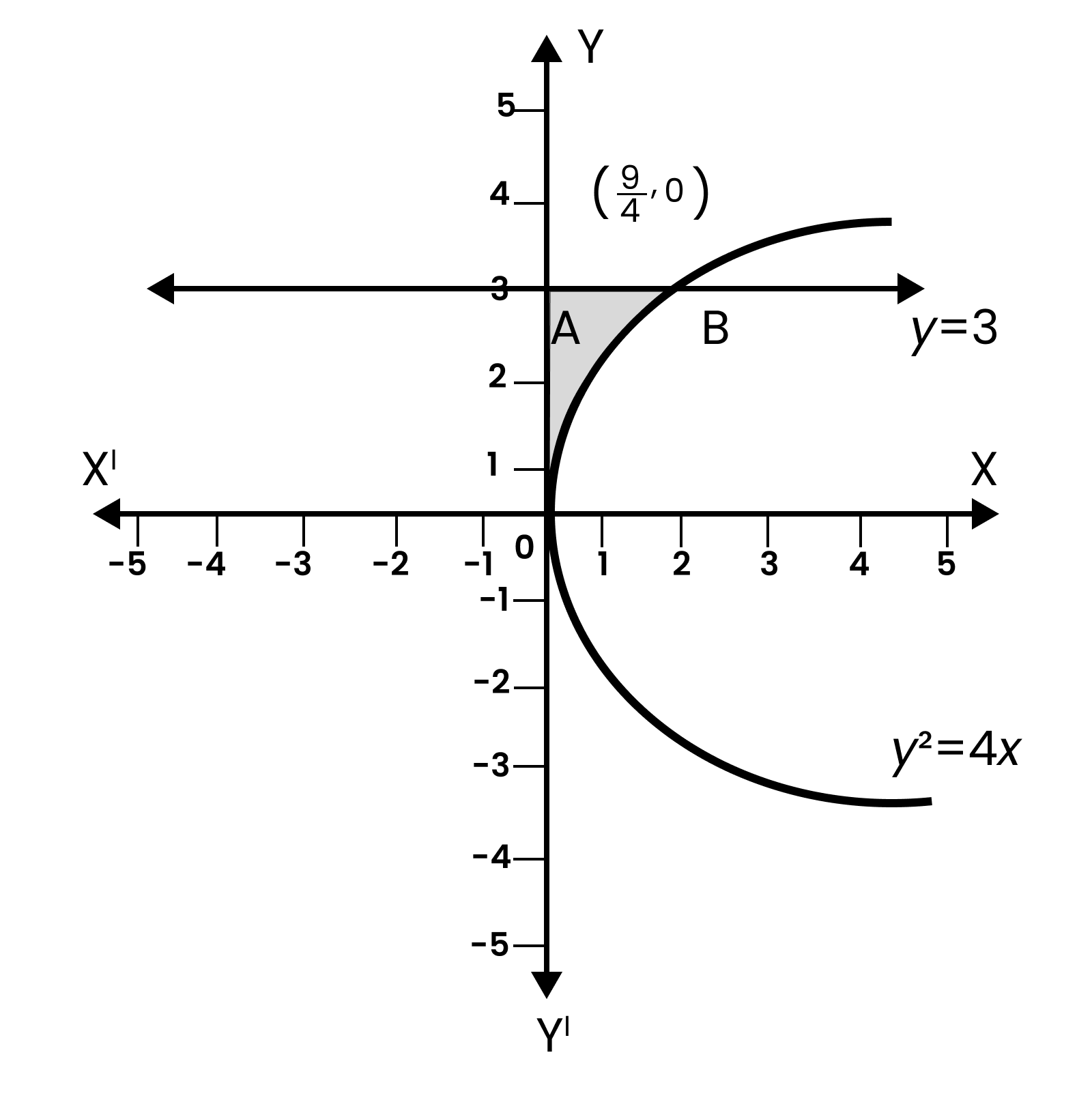
3. How do you correctly set up the definite integral to find the area bounded by a curve y = f(x), the x-axis, and the lines x = a and x = b?
The correct method is to set up the definite integral as Area = ∫ₐᵇ y dx. Here, 'y' is the function f(x), and 'a' and 'b' are the lower and upper limits (x-coordinates) of the region. This formula calculates the sum of the areas of infinite vertical strips within these boundaries.
4. When solving NCERT questions, when is it better to integrate with respect to the y-axis (using ∫ x dy)?
It is better to integrate with respect to the y-axis when the curve is expressed as x = f(y) and the region is bounded by the y-axis and horizontal lines (e.g., y = c and y = d). In such cases, the formula for the area becomes Area = ∫꜀ᵈ x dy, which simplifies the calculation.
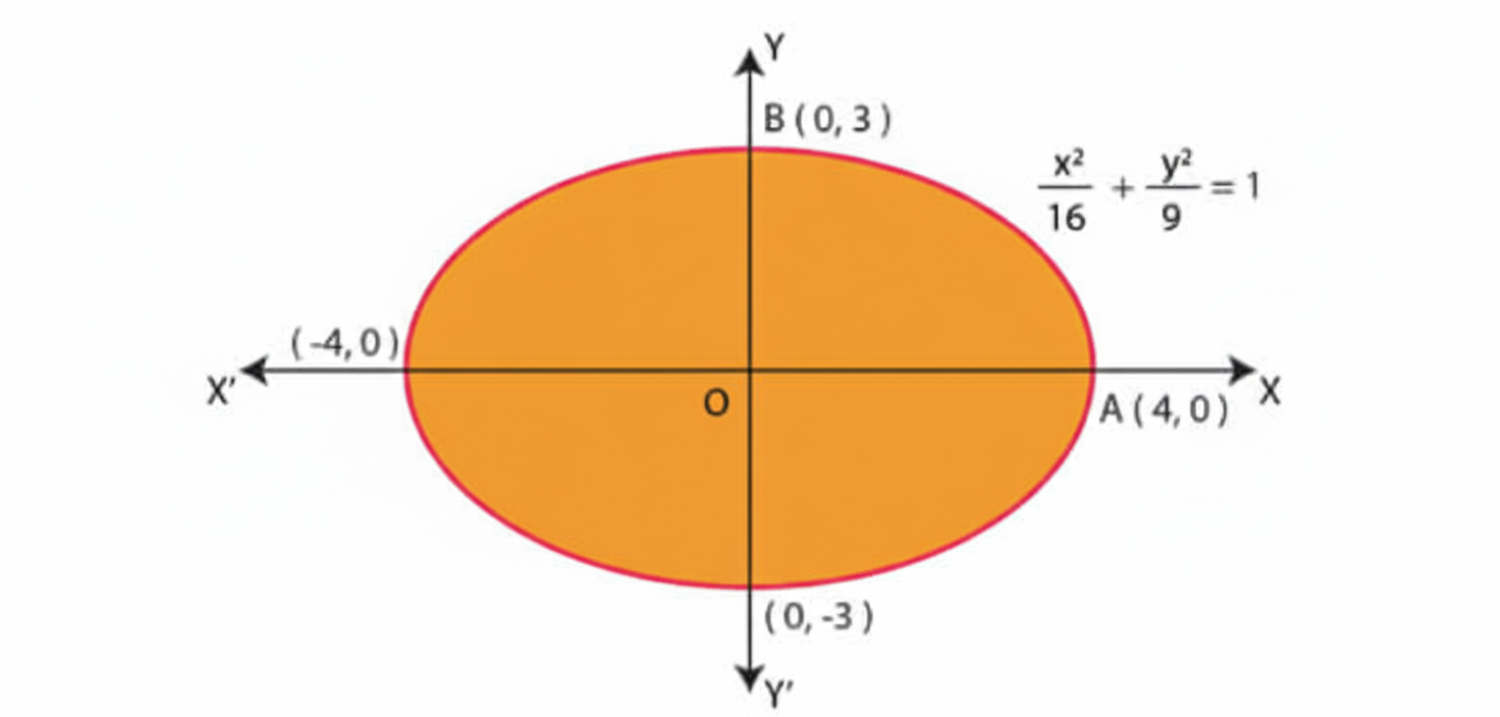
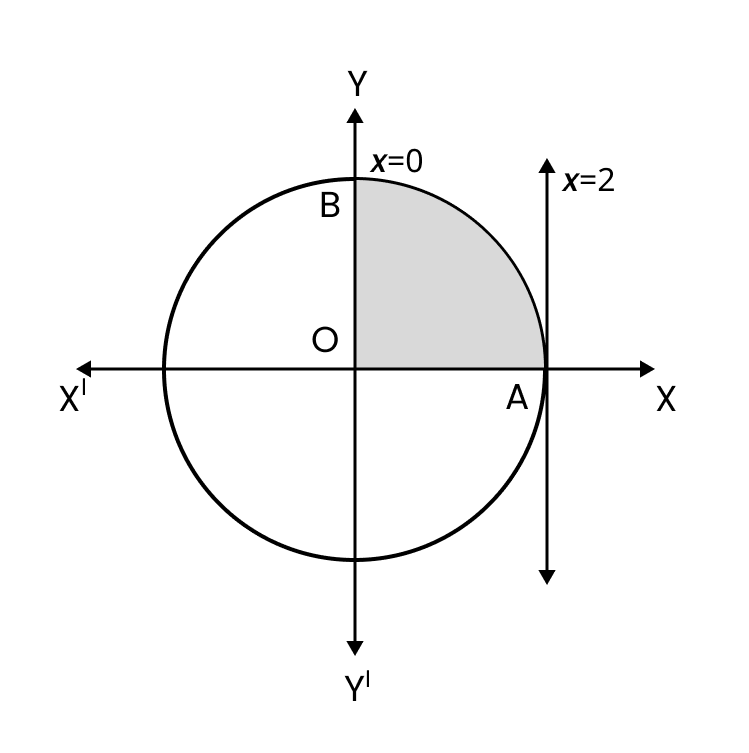
5. How are the solutions for finding the area of a standard circle (x² + y² = r²) and an ellipse (x²/a² + y²/b² = 1) structured in this chapter?
The solutions for both are structured using the concept of symmetry. The standard approach involves:
- Calculating the area in the first quadrant only.
- Setting the limits of integration from 0 to the x-intercept (e.g., 0 to 'r' for a circle, 0 to 'a' for an ellipse).
- Expressing 'y' in terms of 'x' for the first quadrant.
- Evaluating the definite integral.
- Multiplying the result by 4 to get the total area of the shape.
6. Why is sketching the curve considered a mandatory first step for solving problems on Application of Integrals?
Sketching the curve is a critical first step because it provides essential visual information. It helps to:
- Accurately identify the required bounded region.
- Determine the correct upper and lower limits for integration.
- Recognise if the area lies above or below the x-axis, which is crucial for avoiding sign errors in the final area calculation.
- Identify any symmetry that can be used to simplify the integral.
7. What is a common mistake made when finding the area for a curve that lies both above and below the x-axis, like y = sin(x) from 0 to 2π?
A common mistake is to integrate the function across the entire interval in a single step. This calculates the net displacement, where the area below the axis cancels out the area above. The correct method is to split the integral at the points where the curve crosses the x-axis. You must calculate the area of the portion below the axis, take its absolute value (magnitude), and then add it to the area of the portion above the axis to find the total area.
8. How does the concept of symmetry help simplify calculations in the NCERT Solutions for this chapter?
Symmetry is a powerful tool for simplifying problems. For curves symmetric about the x-axis, y-axis, or both (like circles, ellipses, and some parabolas), you can calculate the area of one symmetric section and multiply it by the number of such sections. This often makes the limits of integration simpler (e.g., from 0 to a instead of -a to a), which reduces the complexity of calculations.
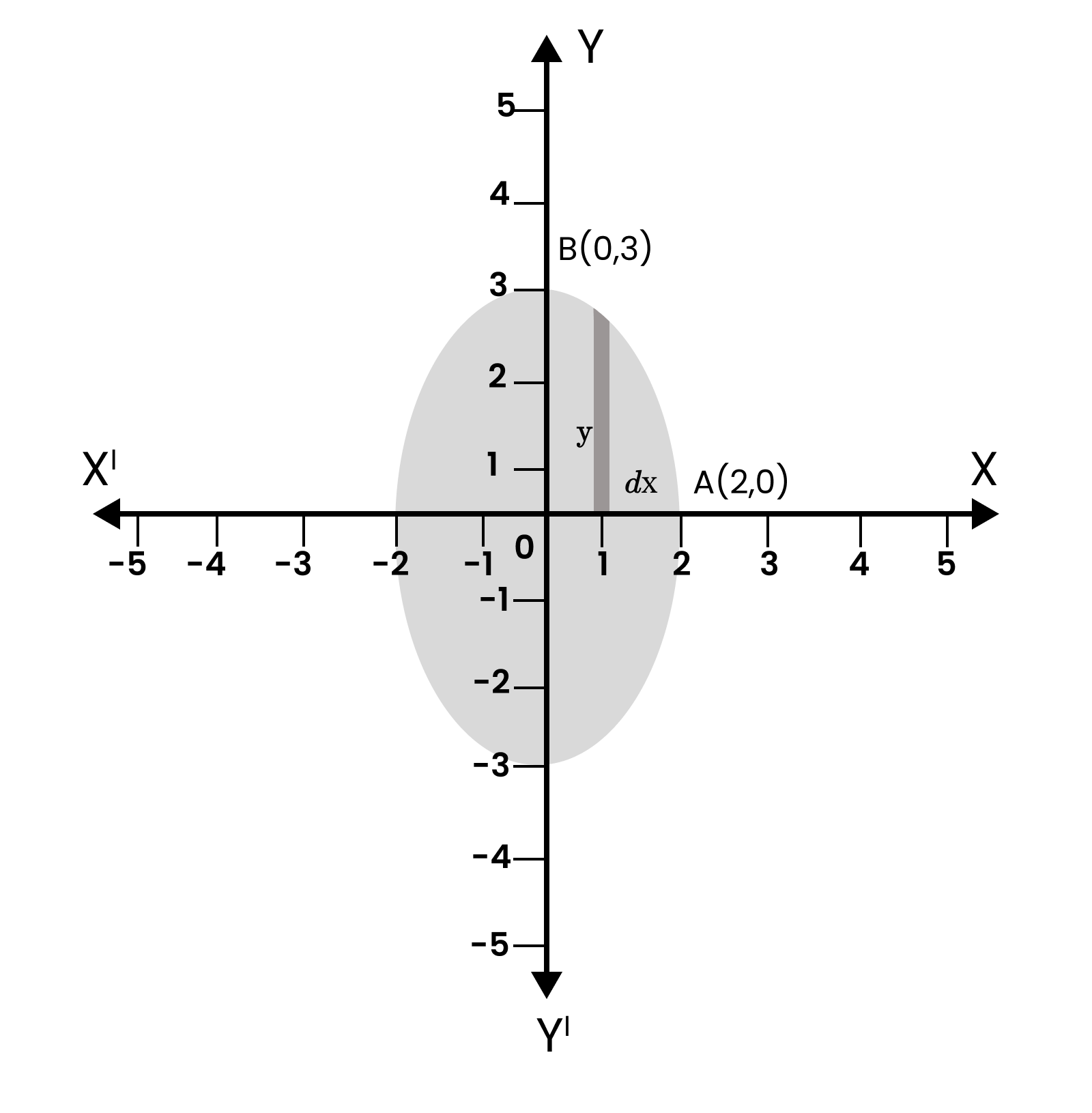
9. Geometrically, what does the element 'y dx' represent in the integral used to find the area under a curve?
The element 'y dx' represents the area of an infinitesimally thin, vertical rectangular strip. Here, 'y' is the height of the strip (the value of the function at that point) and 'dx' is its infinitesimal width. The process of integration (∫) is essentially the summation of the areas of all such an infinite number of rectangular strips across the specified interval to find the total area under the curve.
10. What is the full form of AOI in the context of Class 12 Maths?
In the context of Class 12 Maths, AOI is the common abbreviation for the chapter name Application of Integrals.