NCERT Solutions for Class 9 Maths Chapter 11 Surface Area and Volume

• Exercise 11.1: This exercise explains the surface area and volume of a cylinder. This section helps the students to understand how to find the surface area of a right circular cylinder. We need to split the cylinder into two parts: the middle part and the bottom part.

The curved surface area of cylinder= 2πrh

Total surface area of cylinder = πr2(r+h)

• Exercise 11.2: This exercise explains the surface area and volume of a cone.

This section explains about the cone which has a triangle shape and circle shape. By combining these two areas, Class 9 Surfaces Area and Volumes, the formula of the cone is derived as below,

Curved Surface Area of a Cone = ½  × l ×2πr = πrl

Total Surface Area of a Cone = πrl + πr2 = πr (l + r)

• Exercise 11.3: This exercise includes the conversion of one solid from one shape to another. This covers the volume of a cylinder. 

Volume of a Cylinder = πr2h

• Exercise 11.4: This exercise contains word problems that are based on the surface area and volume of 3D shapes. This understands the difference between cylinder and cone. From that, they derived a formula for the volume of a cone is ⅓ πr2h.

Access NCERT Solutions for Class 9 Maths Chapter 11 - Surface Areas and Volumes

Exercise (11.1)

1. Diameter of the base of a cone is $\text{10}\text{.5 cm}$ and its slant height is $\text{10 cm}$. Find its curved surface area. $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: We are given the following:

The slant height $\left( \text{l} \right)$ of the cone $\text{= 10 cm}$

The diameter of the base of cone $\text{= 10}\text{.5 cm}$

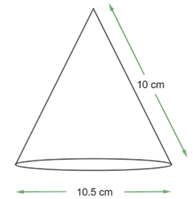
So, the radius $\left( \text{r} \right)$ of the base of cone $\text{= }\dfrac{\text{10}\text{.5}}{\text{2}}\text{ cm = 5}\text{.25 cm}$

The curved surface area of cone, $\text{A =  }\pi\text{ rl}$

$\Rightarrow \text{A = }\left( \dfrac{\text{22}}{\text{7}}\text{ }\times\text{ 5}\text{.25 }\times\text{ 10} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = }\left( \text{22 }\times\text{ 0}\text{.75 }\times\text{ 10} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 165 c}{{\text{m}}^{\text{2}}}$

Therefore, the curved surface area of the cone is $\text{165 c}{{\text{m}}^{\text{2}}}$.

2. Find the total surface area of a cone, if its slant height is $\text{21 m}$and diameter of its base is $\text{24 m}$. $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: We are given the following:

The slant height $\left( \text{l} \right)$ of the cone $\text{= 21 m}$

The diameter of the base of cone $\text{= 24 m}$

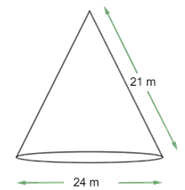
So, the radius $\left( \text{r} \right)$ of the base of cone $\text{= }\dfrac{\text{24}}{\text{2}}\text{ m = 12 m}$

The total surface area of cone, $\text{A =  }\pi\text{ r}\left( \text{l + r} \right)$

$\Rightarrow \text{A = }\left( \dfrac{\text{22}}{\text{7}}\text{  }\times\text{  12  }\times\text{  }\left( \text{21 + 12} \right) \right)\text{ }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = }\left( \dfrac{\text{22}}{\text{7}}\text{  }\times\text{  12  }\times\text{  33} \right)\text{ }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 1244}\text{.57 }{{\text{m}}^{\text{2}}}$

Therefore, the total surface area of the cone is $\text{1244}\text{.57 }{{\text{m}}^{\text{2}}}$.

3. Curved surface area of a cone is $\text{308 c}{{\text{m}}^{\text{2}}}$ and its slant height is $\text{14 cm}$. Find

(i) Radius of the base and

Ans: It is given that the slant height $\left( \text{l} \right)$ of the cone $\text{= 14 cm}$

The curved surface area of the cone $\text{= 308 c}{{\text{m}}^{\text{2}}}$

Let us assume the radius of base of the cone be $\text{r}$.

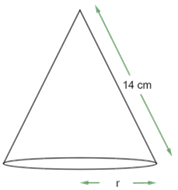
We know that curved surface area of the cone $\text{=  }\pi\text{ rl}$

$\therefore \text{ }\pi\text{ rl = 308 c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \left( \dfrac{\text{22}}{\text{7}}\text{  }\times\text{  r  }\times\text{  14} \right)\text{ cm = 308 c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{r = }\dfrac{\text{308}}{\text{44}}\text{ cm}$

$\Rightarrow \text{r = 7 cm}$

Hence, the radius of the base is $\text{7 cm}$.

(ii) Total surface area of the cone. $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: The total surface area of the cone is the sum of its curved surface area and the area of the base.

Total surface area of cone, $\text{A =  }\pi\text{ rl +  }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A = }\left[ \text{308 + }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{7} \right)}^{\text{2}}} \right]\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = }\left[ \text{308 + 154} \right]\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 462 c}{{\text{m}}^{\text{2}}}$

Hence, the total surface area of the cone is $\text{462 c}{{\text{m}}^{\text{2}}}$.

4. A conical tent is $\text{10 m}$ high and the radius of its base is $\text{24 m}$. Find

(i) slant height of the tent

Ans:

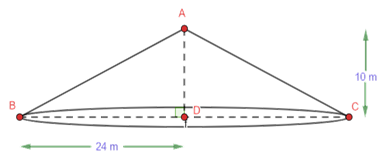
From the figure we can say that $\text{ABC}$ is a conical tent.

It is given that the height $\left( \text{h} \right)$ of conical tent $\text{= 10 m}$

The radius $\left( \text{r} \right)$ of conical tent $\text{= 24 m}$

Let us assume the slant height as $\text{l}$.

In $\text{ }\Delta\text{ ABD}$, we will use Pythagorean Theorem.

$\therefore \text{A}{{\text{B}}^{\text{2}}}\text{ = AD}{{\text{ }}^{\text{2}}}\text{ + B}{{\text{D}}^{\text{2}}}$

$\Rightarrow {{\text{l}}^{\text{2}}}\text{ = }{{\text{h}}^{\text{2}}}\text{ + }{{\text{r}}^{\text{2}}}$

\[\Rightarrow {{\text{l}}^{\text{2}}}\text{ = }{{\left( \text{10 m} \right)}^{\text{2}}}\text{ + }{{\left( \text{24 m} \right)}^{\text{2}}}\]

$\Rightarrow {{\text{l}}^{\text{2}}}\text{ = 676 }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{l = 26 m}$

The slant height of the tent is $\text{26 m}$.

(ii) cost of canvas required to make the tent, if cost of $\text{1 }{{\text{m}}^{\text{2}}}$ canvas is $\text{Rs}\text{. 70}$. $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: The curved surface area of the tent, $\text{A =  }\pi\text{ rl}$

$\Rightarrow \text{A = }\left( \dfrac{\text{22}}{\text{7}}\text{  }\times\text{  24  }\times\text{  26} \right)\text{ }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = }\left( \dfrac{13728}{7} \right)\text{ }{{\text{m}}^{\text{2}}}$

It is given that the cost of $\text{1 }{{\text{m}}^{\text{2}}}$ of canvas $\text{= Rs}\text{. 70}$

So, the cost of $\dfrac{13728}{7}\text{ }{{\text{m}}^{\text{2}}}$ canvas $\text{= Rs}\text{. }\left( \dfrac{\text{13728}}{\text{7}}\text{  }\times\text{  70} \right)\text{ = Rs}\text{. 137280}$

Hence, the cost of canvas required to make the tent is $\text{Rs}\text{. 137280}$.

5. What length of tarpaulin $\text{3 m}$ wide will be required to make conical tent of height $\text{8 m}$ and base radius $\text{6 m}$? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately $\text{20 cm}$. $\left[ \text{Use  }\pi\text{  = 3}\text{.14} \right]$

Ans: We are given the following:

The base radius $\left( \text{r} \right)$ of tent $\text{= 6 m}$

The height $\left( \text{h} \right)$ of tent $\text{= 8 m}$

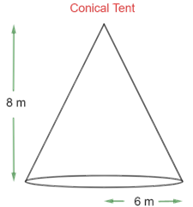
So the slant height of the tent, $\text{l = }\sqrt{{{\text{r}}^{\text{2}}}\text{ + }{{\text{h}}^{\text{2}}}}$ 

$\Rightarrow \text{l = }\left( \sqrt{{{\text{6}}^{\text{2}}}\text{ + }{{\text{8}}^{\text{2}}}} \right)\text{ m}$

$\Rightarrow \text{l = }\left( \sqrt{\text{100}} \right)\text{ m}$

$\Rightarrow \text{l = 10 m}$

The curved surface area of the tent, $\text{A =  }\pi\text{ rl}$

$\Rightarrow \text{A = }\left( \text{3}\text{.14  }\times\text{  6  }\times\text{  10} \right)\text{ }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 188}\text{.4 }{{\text{m}}^{\text{2}}}$

It is give the width of tarpaulin $\text{= 3 m}$

Let us assume the length of the tarpaulin sheet required be $\text{x}$.

It is given that there will be a wastage of $\text{20 cm}$.

So, the new length of the sheet $\text{=}\left( \text{x - 0}\text{.2} \right)\text{ m}$

We know that the area of the rectangular sheet required will be the same as curved surface area of the tent.

$\therefore \left[ \left( \text{x - 0}\text{.2} \right)\text{  }\times\text{  3} \right]\text{ m = 188}\text{.4 }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{x - 0}\text{.2 m = 62}\text{.8 m}$

$\Rightarrow \text{x = 63 m}$

The length of tarpaulin sheet required is $\text{63 m}$.

6. The slant height and base diameter of a conical tomb are $\text{25 m}$ and $\text{14 m}$ respectively. Find the cost of white-washing its curved surface at the rate of $\text{Rs}\text{. 210}$ per $\text{100 }{{\text{m}}^{\text{2}}}$. $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: We are given the following:

The base radius $\left( \text{r} \right)$ of tomb $\text{= 7 m}$

The slant height $\left( \text{l} \right)$ of tomb $\text{= 25 m}$

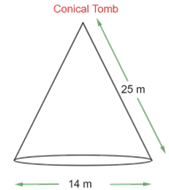
The curved surface area of the conical tomb, $\text{A =  }\pi\text{ rl}$

$\Rightarrow \text{A = }\left( \dfrac{22}{7}\text{  }\times\text{  7  }\times\text{  25} \right)\text{ }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 550 }{{\text{m}}^{\text{2}}}$

It is given that the cost of white-washing $\text{1 }{{\text{m}}^{\text{2}}}$ area $\text{= Rs}\text{. 210}$

So, the cost of white-washing $550\text{ }{{\text{m}}^{\text{2}}}$ area $\text{= Rs}\text{. }\left( \dfrac{\text{210}}{\text{100}}\text{  }\times\text{  550} \right)\text{ = Rs}\text{. 1155}$

Hence, the cost of white-washing the curved surface area of a conical tomb is $\text{Rs}\text{. 1155}$.

7. A joker’s cap is in the form of right circular cone of base radius $\text{7 cm}$ and the height $\text{24 cm}$. Find the area of sheet required to make $\text{10}$ such caps. $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: We are given the following:

The base radius $\left( \text{r} \right)$ of conical cap $\text{= 7 cm}$

The height $\left( \text{h} \right)$ of conical cap $\text{= 24 cm}$

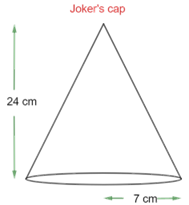
So the slant height of the tent, $\text{l = }\sqrt{{{\text{r}}^{\text{2}}}\text{ + }{{\text{h}}^{\text{2}}}}$ 

$\Rightarrow \text{l = }\left( \sqrt{{{\text{7}}^{\text{2}}}\text{ + 2}{{\text{4}}^{\text{2}}}} \right)\text{ cm}$

$\Rightarrow \text{l = }\left( \sqrt{625} \right)\text{ cm}$

$\Rightarrow \text{l = 25 cm}$

The curved surface area of one conical cap, $\text{A =  }\pi\text{ rl}$

$\Rightarrow \text{A = }\left( \dfrac{22}{7}\text{  }\times\text{  7  }\times\text{  25} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 550 c}{{\text{m}}^{\text{2}}}$

So, the curved surface area of $\text{10}$ conical caps $\text{= }\left( \text{550  }\times\text{  10} \right)\text{ c}{{\text{m}}^{\text{2}}}\text{ = 5500 c}{{\text{m}}^{\text{2}}}$

Therefore, the total area of sheet required is $\text{5500 c}{{\text{m}}^{\text{2}}}$.

8. A bus stop is barricaded from the remaining part of the road, by using $\text{50}$ hollow cones made of recycled cardboard. Each cone has a base diameter of $\text{40 cm}$ and height $\text{1 m}$. If the outer side of each of the cones is to be painted and the cost of painting is $\text{Rs}\text{. 12}$ per ${{\text{m}}^{\text{2}}}$, what will be the cost of painting all these cones? 

$\left[ \text{Use  }\pi\text{  = 3}\text{.14 and take }\sqrt{\text{1}\text{.02}}\text{=1}\text{.02} \right]$

Ans: We are given the following:

The base radius $\left( \text{r} \right)$ of cone $\text{= }\dfrac{\text{40}}{\text{2}}\text{ = 20 cm = 0}\text{.2 m}$

The height $\left( \text{h} \right)$ of cone $\text{= 1 m}$

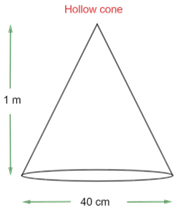
So the slant height of the cone, $\text{l = }\sqrt{{{\text{r}}^{\text{2}}}\text{ + }{{\text{h}}^{\text{2}}}}$ 

$\Rightarrow \text{l = }\left( \sqrt{{{\left( \text{0}\text{.2} \right)}^{\text{2}}}\text{ + }{{\left( \text{1} \right)}^{\text{2}}}} \right)\text{ m}$

$\Rightarrow \text{l = }\left( \sqrt{1.04} \right)\text{ m}$

$\Rightarrow \text{l = 1}\text{.02 m}$

The curved surface area of one cone, $\text{A =  }\pi\text{ rl}$

$\Rightarrow \text{A = }\left( \text{3}\text{.14  }\times\text{  0}\text{.2  }\times\text{  1}\text{.02} \right)\text{ }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 0}\text{.64056 c}{{\text{m}}^{\text{2}}}$

So, the curved surface area of $\text{50}$ cones $\text{= }\left( \text{50  }\times\text{  0}\text{.64056} \right)\text{ }{{\text{m}}^{\text{2}}}\text{ = 32}\text{.028 }{{\text{m}}^{\text{2}}}$

It is given that the cost of painting $\text{1 }{{\text{m}}^{\text{2}}}$ area $\text{= Rs}\text{. 12}$

So, the cost of painting $32.028\text{ }{{\text{m}}^{\text{2}}}$ area $\text{= Rs}\text{. }\left( \text{32}\text{.028  }\times\text{  12} \right)\text{ = Rs}\text{. 384}\text{.336}$

We can also write the cost approximately as $\text{Rs}\text{. 384}\text{.34}$.

Therefore, the cost of painting all the hollow cones is $\text{Rs}\text{. 384}\text{.34}$.

Exercise (11.2)

1. Find the surface area of a sphere of radius: $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

(i) $\text{10}\text{.5 cm}$

Ans: Given radius of the sphere $\text{r = 10}\text{.5 cm}$

The surface area of the sphere $\text{A = 4 }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A = }\left[ \text{4  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{10}\text{.5} \right)}^{\text{2}}} \right]\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = }\left( \text{88  }\times\text{  1}\text{.5  }\times\text{  1}\text{.5} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 1386 c}{{\text{m}}^{\text{2}}}$

Hence, the surface area of the sphere is $\text{1386 c}{{\text{m}}^{\text{2}}}$.

(ii) $\text{5}\text{.6 cm}$

Ans: Given radius of the sphere $\text{r = 5}\text{.6 cm}$

The surface area of the sphere $\text{A = 4 }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A = }\left[ \text{4  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{5}\text{.6} \right)}^{\text{2}}} \right]\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = }\left( \text{88  }\times\text{  0}\text{.8  }\times\text{  5}\text{.6} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 394}\text{.24 c}{{\text{m}}^{\text{2}}}$

Hence, the surface area of the sphere is $\text{394}\text{.24 c}{{\text{m}}^{\text{2}}}$.

(iii) $\text{14 cm}$ $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: Given radius of the sphere $\text{r = 14 cm}$

The surface area of the sphere $\text{A = 4 }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A = }\left[ \text{4  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{14} \right)}^{\text{2}}} \right]\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = }\left( \text{4  }\times\text{  44  }\times\text{  14} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 2464 c}{{\text{m}}^{\text{2}}}$

Hence, the surface area of the sphere is $\text{2464 c}{{\text{m}}^{\text{2}}}$.

2. Find the surface area of a sphere of diameter: $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$:

(i) $\text{14 cm}$

Ans: Given diameter of the sphere $\text{= 14 cm}$

So, the radius of the sphere $\text{r = }\dfrac{\text{14}}{\text{2}}\text{ = 7 cm}$

The surface area of the sphere $\text{A = 4 }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A = }\left[ \text{4  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{7} \right)}^{\text{2}}} \right]\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = }\left( \text{88  }\times\text{  7} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 616 c}{{\text{m}}^{\text{2}}}$

Hence, the surface area of the sphere is $\text{616 c}{{\text{m}}^{\text{2}}}$.

(ii) $\text{21 cm}$

Ans: Given diameter of the sphere $\text{= 21 cm}$

So, the radius of the sphere $\text{r = }\dfrac{\text{21}}{\text{2}}\text{ = 10}\text{.5 cm}$

The surface area of the sphere $\text{A = 4 }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A = }\left[ \text{4  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{10}\text{.5} \right)}^{\text{2}}} \right]\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 1386 c}{{\text{m}}^{\text{2}}}$

Hence, the surface area of the sphere is $\text{1386 c}{{\text{m}}^{\text{2}}}$.

(iii) $\text{3}\text{.5 m}$ $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: Given diameter of the sphere $\text{= 3}\text{.5 m}$

So, the radius of the sphere $\text{r = }\dfrac{\text{3}\text{.5}}{\text{2}}\text{ = 1}\text{.75 m}$

The surface area of the sphere $\text{A = 4 }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A = }\left[ \text{4  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{1}\text{.75} \right)}^{\text{2}}} \right]\text{ }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 38}\text{.5 }{{\text{m}}^{\text{2}}}$

Hence, the surface area of the sphere is $\text{38}\text{.5 }{{\text{m}}^{\text{2}}}$.

3. Find the total surface area of a hemisphere of radius $\text{10 cm}$. $\left[ \text{Use  }\pi\text{  = 3}\text{.14} \right]$

Ans:

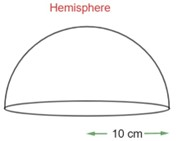
Given the radius of hemisphere $\text{r = 10 cm}$

The total surface area of the hemisphere is the sum of its curved surface area and the circular base.

Total surface area of hemisphere $\text{A = 2 }\pi\text{ }{{\text{r}}^{\text{2}}}\text{ +  }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A = 3 }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A = }\left[ \text{3  }\times\text{  3}\text{.14  }\times\text{  }{{\left( \text{10} \right)}^{\text{2}}} \right]\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 942 c}{{\text{m}}^{\text{2}}}$

Hence, the total surface area of the hemisphere is $\text{942 c}{{\text{m}}^{\text{2}}}$.

4. The radius of a spherical balloon increases from $\text{7 cm}$ to $\text{14 cm}$ as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.

Ans: Given the initial radius of the balloon ${{\text{r}}_{1}}\text{ = 10 cm}$

The final radius of the balloon ${{\text{r}}_{2}}\text{ = 14 cm}$

We have to find the ratio of surface areas of the balloon in the two cases.

The required ratio $\text{R = }\dfrac{\text{4 }\pi\text{ }{{\text{r}}_{\text{1}}}^{\text{2}}}{\text{4 }\pi\text{ }{{\text{r}}_{\text{2}}}^{\text{2}}}$

$\Rightarrow \text{R = }{{\left( \dfrac{{{\text{r}}_{\text{1}}}}{{{\text{r}}_{\text{2}}}} \right)}^{\text{2}}}$

$\Rightarrow \text{R = }{{\left( \dfrac{\text{7}}{\text{14}} \right)}^{\text{2}}}$

$\Rightarrow \text{R = }\dfrac{\text{1}}{\text{4}}$

Hence, the ratio of the surface areas of the balloon in both case is $\text{1 : 4}$.

5. A hemispherical bowl made of brass has inner diameter $\text{10}\text{.5 cm}$. Find the cost of tinplating it on the inside at the rate of $\text{Rs}\text{. 16}$ per $\text{100 c}{{\text{m}}^{\text{2}}}$. $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: Given the radius of inner hemispherical bowl $\text{r = }\dfrac{\text{10}\text{.5}}{\text{2}}\text{ = 5}\text{.25 cm}$

The surface area of the hemispherical bowl $\text{A = 2 }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A = }\left[ \text{2  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{5}\text{.25} \right)}^{\text{2}}} \right]\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 173}\text{.25 c}{{\text{m}}^{\text{2}}}$

It is given that the cost of tin-plating $\text{100 c}{{\text{m}}^{\text{2}}}$ area $\text{= Rs}\text{. 16}$

So, the cost of tin-plating $173.25\text{ c}{{\text{m}}^{\text{2}}}$ area $\text{= Rs}\text{. }\left( \dfrac{\text{16}}{\text{100}}\text{  }\times\text{  173}\text{.25} \right)\text{ = Rs}\text{. 27}\text{.72}$

Hence, the cost of tin-plating the hemispherical bowl is $\text{Rs}\text{. 27}\text{.72}$.

6. Find the radius of a sphere whose surface area is $\text{154 c}{{\text{m}}^{\text{2}}}$. $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: Let us assume the radius of sphere be $\text{r}$.

We are given the surface area of the sphere, $\text{A = 154 c}{{\text{m}}^{\text{2}}}$.

$\therefore \text{4 }\pi\text{ }{{\text{r}}^{\text{2}}}\text{ = 154 c}{{\text{m}}^{\text{2}}}$

$\Rightarrow {{\text{r}}^{\text{2}}}\text{ = }\left( \dfrac{\text{154  }\times\text{  7}}{\text{2  }\times\text{  22}} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{r = }\left( \dfrac{\text{7}}{\text{2}} \right)\text{ cm}$

$\Rightarrow \text{r = 3}\text{.5 cm}$

Therefore, the radius of the sphere is $\text{3}\text{.5 cm}$.

7. The diameter of the moon is approximately one-fourth of the diameter of the earth. Find the ratio of their surface area.

Ans: Let us assume the diameter of earth is $\text{d}$.

So, the diameter of the moon will be $\dfrac{\text{d}}{\text{4}}$.

The radius of the earth ${{\text{r}}_{\text{1}}}\text{ = }\dfrac{\text{d}}{\text{2}}$

The radius of the moon ${{\text{r}}_{\text{2}}}\text{ = }\dfrac{\text{1}}{\text{2}}\text{  }\times\text{  }\dfrac{\text{d}}{\text{2}}\text{ = }\dfrac{\text{d}}{\text{8}}$

The ratio of surface area of moon and earth $\text{R = }\dfrac{\text{4 }\pi\text{ }{{\text{r}}_{\text{2}}}^{\text{2}}}{\text{4 }\pi\text{ }{{\text{r}}_{\text{1}}}^{\text{2}}}$

$\Rightarrow \text{R = }\dfrac{\text{4 }\pi\text{ }{{\left( \dfrac{\text{d}}{\text{8}} \right)}^{\text{2}}}}{\text{4 }\pi\text{ }{{\left( \dfrac{\text{d}}{\text{2}} \right)}^{\text{2}}}}$

$\Rightarrow \text{R = }\dfrac{\text{4}}{\text{64}}$

$\Rightarrow \text{R = }\dfrac{\text{1}}{\text{16}}$

Therefore, the ratio of surface area of moon and earth is $\text{1 : 16}$.

8. A hemispherical bowl is made of steel, $\text{0}\text{.25 cm}$ thick. The inner radius of the bowl is $\text{5 cm}$. Find the outer curved surface area of the bowl. $\left[ \text{Assume }\pi=\dfrac{\text{22}}{\text{7}} \right]$

Ans: Given the inner radius $\text{= 5 cm}$

The thickness of the bowl $\text{= 0}\text{.25 cm}$

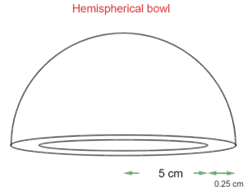
So, the outer radius of the hemispherical bowl is $\text{r = }\left( \text{5 + 0}\text{.25} \right)\text{ cm = 5}\text{.25 cm}$

The outer curved surface area of the hemispherical bowl $\text{A = 2 }\pi\text{ }{{\text{r}}^{\text{2}}}$

$\Rightarrow \text{A =}\left[ \text{ 2  }\times\text{  }\dfrac{\text{2}}{\text{7}}\text{  }\times\text{  }{{\left( \text{5}\text{.25} \right)}^{\text{2}}} \right]\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 173}\text{.25 c}{{\text{m}}^{\text{2}}}$

Therefore, the outer curved surface area of the hemispherical bowl is $\text{173}\text{.25 c}{{\text{m}}^{\text{2}}}$.

9. A right circular cylinder just encloses a sphere of radius $\text{r}$ (see figure). Find 

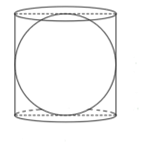
(i) surface area of the sphere, 

Ans: The surface area of the sphere is $\text{4 }\pi\text{ }{{\text{r}}^{\text{2}}}$.

(ii) curved surface area of the cylinder, 

Ans:

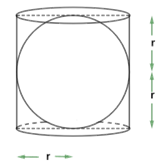
Given the radius of cylinder $\text{= r}$

The height of cylinder $\text{= r + r = 2r}$

The curved surface area of cylinder $\text{A = 2 }\pi\text{ rh}$

$\Rightarrow \text{A = 2 }\pi\text{ r }\left( \text{2r} \right)$

$\Rightarrow \text{A = 4 }\pi\text{ }{{\text{r}}^{\text{2}}}$

Therefore the curved surface area of cylinder is  $\text{4 }\pi\text{ }{{\text{r}}^{\text{2}}}$.

(iii) ratio of the areas obtained in (i) and (ii).

Ans: The ratio of surface area of the sphere and curved surface area of cylinder  $\text{R = }\dfrac{\text{4 }\pi\text{ }{{\text{r}}^{\text{2}}}}{\text{4 }\pi\text{ }{{\text{r}}^{\text{2}}}}$

$\text{R = }\dfrac{\text{1}}{\text{1}}$

Therefore, the required ratio is $\text{1 : 1}$.

Exercise (11.3)

1. Find the volume of the right circular cone with

(i) Radius $\text{6 cm}$, height $\text{7 cm}$ $\left[ \text{Assume }\pi\text{ =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: It is given the radius of cone $\text{r = 6 cm}$

The height of the cone $\text{h = 7 cm}$

The volume of the cone $\text{V = }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{6} \right)}^{\text{2}}}\text{  }\times\text{  7} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = }\left( \text{12  }\times\text{  22} \right)\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 264 c}{{\text{m}}^{\text{3}}}$

The volume of the right circular cone is $\text{264 c}{{\text{m}}^{\text{3}}}$.

(ii) Radius $\text{3}\text{.5 cm}$, height $\text{12 cm}$ $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: It is given the radius of cone $\text{r = 3}\text{.5 cm}$

The height of the cone $\text{h = 12 cm}$

The volume of the cone $\text{V = }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{3}\text{.5} \right)}^{\text{2}}}\text{  }\times\text{  12} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = }\left( \text{1}\text{.75  }\times\text{  88} \right)\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 154 c}{{\text{m}}^{\text{3}}}$

The volume of the right circular cone is $\text{154 c}{{\text{m}}^{\text{3}}}$.

2. $\left[ \text{Assume }\pi\text{ =}\dfrac{\text{22}}{\text{7}} \right]$ Find the capacity in litres of a conical vessel with

(i) Radius $\text{7 cm}$, slant height $\text{25 cm}$

Ans: It is given the radius of cone $\text{r = 7 cm}$

The slant height of the cone $\text{l = 25 cm}$

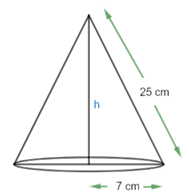
So, the height of the cone $\text{h = }\sqrt{{{\text{l}}^{\text{2}}}\text{ - }{{\text{r}}^{\text{2}}}}$

$\Rightarrow \text{h = }\sqrt{\text{2}{{\text{5}}^{\text{2}}}\text{ - }{{\text{7}}^{\text{2}}}}\text{ cm}$

$\Rightarrow \text{h = 24 cm}$

The volume of the cone $\text{V = }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{7} \right)}^{\text{2}}}\text{  }\times\text{  24} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = }\left( \text{154  }\times\text{  8} \right)\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 1232 c}{{\text{m}}^{\text{3}}}$

We know that $\text{1000 c}{{\text{m}}^{\text{3}}}\text{ = 1 litre}$

So, the capacity of the conical vessel $\text{= }\dfrac{\text{1232}}{\text{1000}}\text{ = 1}\text{.232 litres}$

Therefore, the capacity of the conical vessel is $\text{1}\text{.232 litres}$.

(ii) height $\text{12 cm}$, slant height $\text{13 cm}$ $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: It is given the height of cone $\text{h = 12 cm}$

The slant height of the cone $\text{l = 13 cm}$

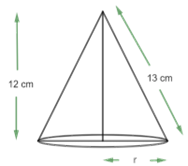
So, the radius of the cone $\text{r = }\sqrt{{{\text{l}}^{\text{2}}}\text{ - }{{\text{h}}^{\text{2}}}}$

$\Rightarrow \text{r = }\sqrt{\text{1}{{\text{3}}^{\text{2}}}\text{ - 1}{{\text{2}}^{\text{2}}}}\text{ cm}$

$\Rightarrow \text{r = 5 cm}$

The volume of the cone $\text{V = }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{5} \right)}^{\text{2}}}\text{  }\times\text{  12} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = }\left( \text{4  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  25} \right)\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = }\dfrac{2200}{7}\text{ c}{{\text{m}}^{\text{3}}}$

We know that $\text{1000 c}{{\text{m}}^{\text{3}}}\text{ = 1 litre}$

So, the capacity of the conical vessel $\text{= }\dfrac{\text{2200}}{\text{7}}\text{  }\times\text{  }\dfrac{\text{1}}{\text{1000}}\text{ = 0}\text{.314 litres}$

Therefore, the capacity of the conical vessel is $\text{0}\text{.314 litres}$.

3. The height of a cone is $\text{15 cm}$. It its volume is $\text{1570 c}{{\text{m}}^{\text{3}}}$, find the diameter of its base. $\left[ \text{Use  }\pi\text{  = 3}\text{.14} \right]$

Ans: It is given the height of cone $\text{h = 12 cm}$

Let us assume the radius of the cone be $\text{r}$.

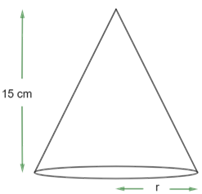
The volume of the cone is $\text{V = 1570 c}{{\text{m}}^{\text{3}}}$

We know the formula for the volume of the cone $\text{= }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\therefore \dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h = 1570 c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{r} \right)}^{\text{2}}}\text{  }\times\text{  12} \right]\text{ cm = 1570 c}{{\text{m}}^{\text{3}}}$

$\Rightarrow {{\text{r}}^{\text{2}}}\text{ = 100 c}{{\text{m}}^{\text{2}}}$

\[\Rightarrow \text{r = 10 cm}\]

Diameter of base \[\text{= 2r = 20 cm}\]

Therefore, the diameter of the cone is  \[\text{20 cm}\].

4. If the volume of right circular cone of height $\text{9 cm}$ is $\text{48 }\pi\text{  c}{{\text{m}}^{\text{3}}}$, find the diameter of its base.

Ans: It is given the height of cone $\text{h = 9 cm}$

Let us assume the radius of the cone be $\text{r}$.

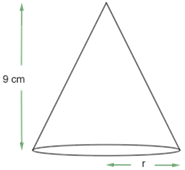
The volume of the cone is $\text{V = 48 }\pi\text{  c}{{\text{m}}^{\text{3}}}$

We know the formula for the volume of the cone $\text{= }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\therefore \dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h = 48 }\pi\text{  c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{   }\pi\text{   }\times\text{  }{{\left( \text{r} \right)}^{\text{2}}}\text{  }\times\text{  9} \right]\text{ cm = 48 }\pi\text{  c}{{\text{m}}^{\text{3}}}$

$\Rightarrow {{\text{r}}^{\text{2}}}\text{ = 16 c}{{\text{m}}^{\text{2}}}$

\[\Rightarrow \text{r = 4 cm}\]

Diameter of base \[\text{= 2r = 8 cm}\]

Therefore, the diameter of the base of the cone is \[\text{8 cm}\].

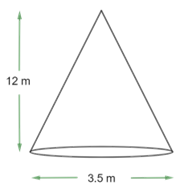
5. A conical pit of top diameter $\text{3}\text{.5 m}$ is $\text{12 m}$ deep. What is the capacity in kilolitres? $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: It is given the height of conical pit $\text{h = 12 m}$

The radius of conical pit $\text{r = }\dfrac{\text{3}\text{.5}}{\text{2}}\text{ m = 1}\text{.75 m}$

We know the volume of the conical pit $\text{V = }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{1}\text{.75} \right)}^{\text{2}}}\text{  }\times\text{  12} \right]\text{ }{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 38}\text{.5 }{{\text{m}}^{\text{3}}}$

We know that $\text{1 kilolitre = 1 }{{\text{m}}^{\text{3}}}$

So, the capacity of the pit $\text{= }\left( \text{38}\text{.5  }\times\text{  1} \right)\text{ kilolitres = 38}\text{.5 kilolitres}$

Therefore, the capacity of the conical pit is $\text{38}\text{.5 kilolitres}$.

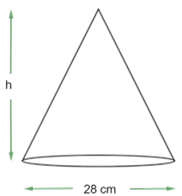
6. The volume of a right circular cone is $\text{9856 c}{{\text{m}}^{\text{3}}}$. If the diameter of the base is $\text{28 cm}$, find

(i) Height of the cone

Ans: It is given the diameter of base of cone $\text{= 28 cm}$

So, the radius $\text{r = }\dfrac{\text{28}}{\text{2}}\text{ = 14 cm}$

Let us assume the height of the cone be $\text{h}$.

The volume of the cone is $\text{V = 9856 c}{{\text{m}}^{\text{3}}}$

We know the formula for the volume of the cone $\text{= }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\therefore \dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h = 9856 c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{  }\dfrac{22}{7}\text{  }\times\text{  }{{\left( \text{14} \right)}^{\text{2}}}\text{  }\times\text{  h} \right]\text{ c}{{\text{m}}^{\text{2}}}\text{ = 9856 c}{{\text{m}}^{\text{3}}}$

\[\Rightarrow \text{h = }\left( \dfrac{\text{9856  }\times\text{  21}}{\text{22  }\times\text{  196}} \right)\text{ cm}\]

\[\Rightarrow \text{h = 48 cm}\]

Therefore, the height of the cone is \[\text{48 cm}\].

(ii) Slant height of the cone

Ans: The slant height of the cone $\text{l = }\sqrt{{{\text{h}}^{\text{2}}}\text{ + }{{\text{r}}^{\text{2}}}}$

$\Rightarrow \text{l = }\sqrt{\text{4}{{\text{8}}^{\text{2}}}\text{ + 1}{{\text{4}}^{\text{2}}}}\text{ cm}$

$\Rightarrow \text{l = }\sqrt{\text{2304 + 196}}\text{ cm}$

$\Rightarrow \text{l = 50 cm}$

Therefore, the slant height of the cone is $\text{50 cm}$.

(iii) Curved surface area of the cone. $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: The curved surface area of the cone $\text{A =  }\pi\text{ rl}$

$\Rightarrow \text{A = }\left( \dfrac{\text{22}}{\text{7}}\text{  }\times\text{  14  }\times\text{  50} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 2200 c}{{\text{m}}^{\text{2}}}$

Therefore, the curved surface area of the cone is $\text{2200 c}{{\text{m}}^{\text{2}}}$.

7. A right triangle $\text{ }\Delta\text{ ABC}$ with sides $\text{5 cm}$,$\text{12 cm}$ and \[\text{13 cm}\] is revolved about the side $\text{12 cm}$. Find the volume of the solid so obtained.

Ans: We will draw the given figure.

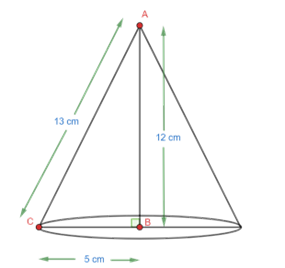
If the triangle is revolved about the side $\text{12 cm}$, we will get a cone with:

Radius $\text{r = 5 cm}$

Slant height $\text{l = 13 cm}$

Height $\text{h = 12 cm}$

We know the volume of the cone $\text{V = }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{   }\pi\text{   }\times\text{  }{{\left( \text{5} \right)}^{\text{2}}}\text{  }\times\text{  12} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 100 }\pi\text{  c}{{\text{m}}^{\text{3}}}$

Therefore, the volume of the cone will be $\text{100 }\pi\text{  c}{{\text{m}}^{\text{3}}}$.

8. If the triangle $\text{ }\Delta\text{ ABC}$ in the Question $\text{7}$ above is revolved about the side $\text{5 cm}$, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Questions $\text{7}$ and $\text{8}$.

Ans:

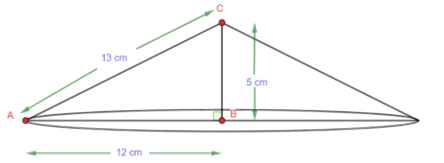
If the triangle is revolved about the side $\text{5 cm}$, we will get a cone with:

Radius $\text{r = 12 cm}$

Slant height $\text{l = 13 cm}$

Height $\text{h = 5 cm}$

We know the volume of the cone $\text{V = }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{   }\pi\text{   }\times\text{  }{{\left( \text{12} \right)}^{\text{2}}}\text{  }\times\text{  5} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 240 }\pi\text{  c}{{\text{m}}^{\text{3}}}$

Therefore, the volume of the cone will be $\text{240 }\pi\text{  c}{{\text{m}}^{\text{3}}}$.

The ratio of volume of cone from previous question an the one we obtained above $\text{= }\dfrac{\text{100 }\pi\text{ }}{\text{240 }\pi\text{ }}\text{ = }\dfrac{\text{5}}{\text{12}}\text{ = 5 : 12}$

Therefore, the required ratio is $\text{5 : 12}$.

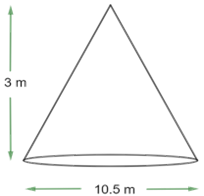
9. A heap of wheat is in the form of a cone whose diameter is $\text{10}\text{.5 m}$and height is $\text{3 m}$. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.

$\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: It is given that diameter of the heap $\text{= 10}\text{.5 m}$

So, the radius of heap $\text{r = }\dfrac{\text{10}\text{.5}}{\text{2}}\text{ = 5}\text{.25 m}$

Height of heap $\text{h = 3 m}$

We know the volume of the cone $\text{V = }\dfrac{\text{1}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{2}}}\text{h}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{1}}{\text{3}}\text{  }\times\text{  }\dfrac{22}{7}\text{  }\times\text{  }{{\left( \text{5}\text{.25} \right)}^{\text{2}}}\text{  }\times\text{  3} \right]\text{ }{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 86}\text{.625 }{{\text{m}}^{\text{3}}}$

Hence, the volume of heap is $\text{86}\text{.625 }{{\text{m}}^{\text{3}}}$.

The area of canvas required is same as curved surface area of the cone.

$\therefore \text{A =  }\pi\text{ rl}$

$\Rightarrow \text{A =  }\pi\text{ r}\sqrt{{{\text{h}}^{\text{2}}}\text{ + }{{\text{r}}^{\text{2}}}}$

$\Rightarrow \text{A = }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  5}\text{.25  }\times\text{  }\sqrt{{{\left( \text{3} \right)}^{\text{2}}}\text{ + }{{\left( \text{5}\text{.25} \right)}^{\text{2}}}}\text{ }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = }\left( \dfrac{\text{22}}{\text{7}}\text{  }\times\text{  5}\text{.25  }\times\text{  6}\text{.05} \right)\text{ }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{A = 99}\text{.825 }{{\text{m}}^{\text{2}}}$

Therefore, to protect the heap from the rain, the amount of canvas required is $\text{99}\text{.825 }{{\text{m}}^{\text{2}}}$.

Exercise (11.4)

1. $\left[ \text{Assume }\pi\text{ =}\dfrac{\text{22}}{\text{7}} \right]$ Find the volume of the sphere whose radius is

(i) $\text{7 cm}$

Ans: It is given the radius of sphere $\text{r = 7 cm}$

The volume of the sphere $\text{V = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{V =}\left[ \text{ }\dfrac{\text{4}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{7} \right)}^{\text{3}}} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = }\dfrac{\text{4312}}{\text{3}}\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 1437}\text{.33 c}{{\text{m}}^{\text{3}}}$

Therefore, the volume of the sphere is $\text{1437}\text{.33 c}{{\text{m}}^{\text{3}}}$.

(ii) $\text{0}\text{.63 m}$ $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: It is given the radius of sphere $\text{r = 0}\text{.63 m}$

The volume of the sphere $\text{V = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{V =}\left[ \text{ }\dfrac{\text{4}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{0}\text{.63} \right)}^{\text{3}}} \right]\text{ }{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 1}\text{.0478 }{{\text{m}}^{\text{3}}}$

Therefore, the volume of the sphere is $\text{1}\text{.0478 }{{\text{m}}^{\text{3}}}$.

2. $\left[ \text{Assume }\pi\text{ =}\dfrac{\text{22}}{\text{7}} \right]$ Find the amount of water displaced by a solid spherical ball of diameter

(i) $\text{28 cm}$

Ans: It is given the diameter of ball $\text{= 28 cm}$

So, the radius of ball $\text{r = }\dfrac{\text{28}}{\text{2}}\text{ = 14 cm}$

The volume of the ball $\text{V = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{V =}\left[ \text{ }\dfrac{\text{4}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{14} \right)}^{\text{3}}} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 11498 c}{{\text{m}}^{\text{3}}}$

Therefore, volume of the sphere is $\text{11498 c}{{\text{m}}^{\text{3}}}$.

(ii) $\text{0}\text{.21 m}$ $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: It is given the diameter of ball $\text{= 0}\text{.21 m}$

So, the radius of ball $\text{r = }\dfrac{\text{0}\text{.21}}{\text{2}}\text{ = 0}\text{.105 m}$

The volume of the sphere $\text{V = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{V =}\left[ \text{ }\dfrac{\text{4}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{0}\text{.105} \right)}^{\text{3}}} \right]\text{ }{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 0}\text{.004851 }{{\text{m}}^{\text{3}}}$

Therefore, the volume of the sphere is $\text{0}\text{.004851 }{{\text{m}}^{\text{3}}}$.

3. The diameter of a metallic ball is $\text{4}\text{.2 cm}$. What is the mass of the ball, if the density of the metal is $\text{8}\text{.9 g per c}{{\text{m}}^{\text{3}}}$? $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: It is given the diameter of metallic ball $\text{= 4}\text{.2 cm}$

So, the radius of ball $\text{r = }\dfrac{\text{4}\text{.2}}{\text{2}}\text{ = 2}\text{.1 cm}$

The volume of the sphere $\text{V = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{V =}\left[ \text{ }\dfrac{\text{4}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{2}\text{.1} \right)}^{\text{3}}} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 38}\text{.808 c}{{\text{m}}^{\text{3}}}$

We know that $\text{Density = }\dfrac{\text{Mass}}{\text{Volume}}$

$\Rightarrow \text{Mass = Density  }\times\text{  Volume}$

$\Rightarrow \text{Mass = }\left( \text{8}\text{.9  }\times\text{  38}\text{.808} \right)\text{ g}$

$\Rightarrow \text{Mass = 345}\text{.39 g}$

Therefore, the mass of the metallic ball is $\text{345}\text{.39 g}$.

4. The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?

Ans: Let us assume the diameter of earth be $\text{d}$.

So, the radius of earth will be $\text{R = }\dfrac{\text{d}}{\text{2}}$.

From the question, we can write the diameter of the moon as $\dfrac{\text{d}}{\text{4}}$.

So, the radius of moon will be $\text{r = }\dfrac{\text{d}}{\text{8}}$.

The volume of earth $\text{V = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{R}}^{\text{3}}}$

$\Rightarrow \text{V = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\left( \dfrac{\text{d}}{\text{2}} \right)}^{\text{3}}}$

$\Rightarrow \text{V = }\dfrac{\text{1}}{8}\text{  }\times\text{  }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{d}}^{\text{3}}}$

The volume of moon $\text{{V}' = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{{V}' = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\left( \dfrac{\text{d}}{\text{8}} \right)}^{\text{3}}}$

$\Rightarrow \text{{V}' = }\dfrac{\text{1}}{\text{512}}\text{  }\times\text{  }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{d}}^{\text{3}}}$

The ratio of volume of moon and that of earth $\text{= }\dfrac{\dfrac{\text{1}}{\text{512}}\text{  }\times\text{  }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{d}}^{\text{3}}}}{\dfrac{\text{1}}{\text{8}}\text{  }\times\text{  }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{d}}^{\text{3}}}}\text{ = }\dfrac{\text{1}}{\text{64}}$

So, $\dfrac{\text{Volume of moon}}{\text{Volume of earth}}\text{=}\dfrac{\text{1}}{\text{64}}$

$\Rightarrow \text{Volume of moon = }\left( \dfrac{\text{1}}{\text{64}} \right)\text{ Volume of earth}$

Therefore, the volume of moon is $\dfrac{\text{1}}{\text{64}}$ times the volume of earth.

5. How many litres of milk can a hemispherical bowl of diameter $\text{10}\text{.5 cm}$ can hold? $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: It is given the diameter of the hemispherical bowl $\text{= 10}\text{.5 cm}$.

So, the radius of the bowl $\text{r = }\dfrac{\text{10}\text{.5}}{\text{2}}\text{ = 5}\text{.25 cm}$.

The volume of the hemispherical bowl $\text{V = }\dfrac{\text{2}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{V =}\left[ \text{ }\dfrac{\text{2}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{5}\text{.25} \right)}^{\text{3}}} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 303}\text{.1875 c}{{\text{m}}^{\text{3}}}$

We know that $\text{1000 c}{{\text{m}}^{\text{3}}}\text{ = 1 litre}$

So, the capacity of the bowl $\text{= }\dfrac{\text{303}\text{.1875}}{\text{1000}}\text{ = 0}\text{.303 litre}$

Therefore, the volume of the hemispherical bowl is $\text{0}\text{.303 litre}$.

6. A hemispherical tank is made up of an iron sheet $\text{1 cm}$thick. If the inner radius is $\text{1 m}$, then find the volume of the iron used to make the tank. $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: The inner radius of hemispherical tank $\text{r = 1 m}$

The thickness of iron sheet $\text{= 1 cm = 0}\text{.01 m}$.

So, the outer radius of the hemispherical tank $\text{R = }\left( \text{1 + 0}\text{.01} \right)\text{ = 1}\text{.01 m}$

The volume of iron sheet required to make the tank $\text{V = }\dfrac{\text{2}}{\text{3}}\text{ }\pi\text{ }\left( {{\text{R}}^{\text{3}}}\text{ - }{{\text{r}}^{\text{3}}} \right)$

$\Rightarrow \text{V = }\dfrac{\text{2}}{\text{3}}\times \dfrac{22}{7}\times \left( {{\left( 1.01 \right)}^{\text{3}}}\text{ - }{{\left( 1 \right)}^{\text{3}}} \right)\text{ }{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = }\dfrac{\text{44}}{\text{21}}\text{  }\times\text{  }\left( \text{1}\text{.030301 - 1} \right)\text{ }{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 0}\text{.06348 }{{\text{m}}^{\text{3}}}$

Therefore, the volume of iron sheet required to make the hemispherical tank is $\text{0}\text{.06348 }{{\text{m}}^{\text{3}}}$.

7. Find the volume of a sphere whose surface area is $\text{154 c}{{\text{m}}^{\text{2}}}$. $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: Let us assume the radius of the sphere be $\text{r}$.

It is given the surface area of the sphere $\text{= 154 c}{{\text{m}}^{\text{2}}}$.

$\therefore \text{4 }\pi\text{ }{{\text{r}}^{\text{2}}}\text{ = 154 c}{{\text{m}}^{\text{2}}}$

$\Rightarrow {{\text{r}}^{\text{2}}}\text{ = }\left( \dfrac{\text{154  }\times\text{  7}}{\text{4  }\times\text{  22}} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow {{\text{r}}^{\text{2}}}\text{ = }\left( \dfrac{\text{49}}{\text{4}} \right)\text{ c}{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{r = }\left( \dfrac{\text{7}}{\text{2}} \right)\text{ cm}$

The volume of the sphere $\text{V = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{4}}{\text{3}}\text{  }\text{ }\times\text{ }\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\text{ }\times\text{ }\text{  }{{\left( \dfrac{\text{7}}{\text{2}} \right)}^{\text{3}}} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{49  }\text{ }\times\text{ }\text{  11}}{\text{3}} \right]\text{ c}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 179}\text{.67 c}{{\text{m}}^{\text{3}}}$

Therefore, the volume of the sphere is $\text{179}\text{.67 c}{{\text{m}}^{\text{3}}}$.

8. A dome of a building is in the form of a hemisphere. From inside, it was whitewashed at the cost of $\text{Rs}\text{. 498}\text{.96}$. If the cost of white-washing is $\text{Rs}\text{. 2}\text{.00}$per square meter, find the

(i) Inside surface area of the dome,

Ans: It is given that it costs $\text{Rs}\text{. 2}\text{.00}$ to whitewash an area $\text{= 1 }{{\text{m}}^{\text{2}}}$

So, it costs $\text{Rs}\text{. 498}\text{.96}$ to whitewash an area $\text{= }\dfrac{\text{498}\text{.96}}{\text{2}}\text{ }{{\text{m}}^{\text{2}}}\text{ = 249}\text{.48 }{{\text{m}}^{\text{2}}}$.

Therefore, the inner surface area of the dome is $\text{249}\text{.48 }{{\text{m}}^{\text{2}}}$.

(ii) Volume of the air inside the dome. $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: Let us assume the radius of the hemispherical dome be $\text{r}$.

We obtained the curved surface area of the inner dome $\text{= 249}\text{.48 }{{\text{m}}^{\text{2}}}$

$\therefore \text{2}{{\text{ }\pi\text{ }}^{\text{2}}}\text{ = 249}\text{.48 }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{2  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\text{r}}^{\text{2}}}\text{ = 249}\text{.48 }{{\text{m}}^{\text{2}}}$

$\Rightarrow {{\text{r}}^{\text{2}}}\text{ = }\left( \dfrac{\text{249}\text{.48  }\times\text{  7}}{\text{2  }\times\text{  22}} \right)\text{ }{{\text{m}}^{\text{2}}}$

$\Rightarrow {{\text{r}}^{\text{2}}}\text{ = 39}\text{.69 }{{\text{m}}^{\text{2}}}$

$\Rightarrow \text{r = 6}\text{.3 m}$

Volume of hemispherical dome $\text{V = }\dfrac{\text{2}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{2}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{6}\text{.3} \right)}^{\text{3}}} \right]\text{ }{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 523}\text{.908 }{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 523}\text{.9  }{{\text{m}}^{\text{3}}}\left( \text{approximately} \right)$

Therefore, the volume of air inside the hemispherical dome is $\text{523}\text{.9 }{{\text{m}}^{\text{3}}}$.

9. Twenty-seven solid iron spheres, each of radius $\text{r}$ and surface area $\text{S}$ are melted to form a sphere with surface area $\text{{S}'}$. Find the 

(i) radius $\text{{r}'}$ of the new sphere, 

Ans: It is given the radius of one iron sphere $\text{= r}$.

The volume of one iron sphere $\text{= }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

So, the volume of $\text{27}$ iron spheres $\text{= 27  }\times\text{  }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

These spheres are melted to form one big sphere.

Let us assume the radius of this new sphere be $\text{{r}'}$.

The volume of new iron sphere $\text{= }\dfrac{\text{4}}{\text{3}}\text{  }\pi\text{ }{{\text{{r}'}}^{\text{3}}}$

We can now equate the volumes.

$\Rightarrow \dfrac{\text{4}}{\text{3}}\text{  }\pi\text{ }{{\text{{r}'}}^{\text{3}}}\text{ = 27  }\times\text{  }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow {{\text{{r}'}}^{\text{3}}}\text{ = 27}{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{{r}' = 3r}$

Therefore, the radius of the new sphere is $\text{3r}$.

(ii) ratio of $\text{S}$ and $\text{{S}'}$. 

Ans: The surface area of an iron sphere of $\text{r}$is $\text{S = 4 }\pi\text{ }{{\text{r}}^{\text{2}}}$.

The surface area of an iron sphere of $\text{{r}'}$is $\text{{S}' = 4 }\pi\text{ }{{\text{{r}'}}^{\text{2}}}$.

$\Rightarrow \text{{S}' = 4 }\pi\text{ }{{\left( \text{3r} \right)}^{\text{2}}}$

$\Rightarrow \text{{S}' = 36 }\pi\text{ }{{\text{r}}^{\text{2}}}$

The ratio of $\dfrac{\text{S}}{{\text{{S}'}}}\text{ = }\dfrac{\text{4 }\pi\text{ }{{\text{r}}^{\text{2}}}}{\text{36 }\pi\text{ }{{\text{r}}^{\text{2}}}}\text{ = }\dfrac{\text{1}}{\text{9}}\text{ = 1 : 9}$

Therefore, the required ratio is $\text{1 : 9}$.

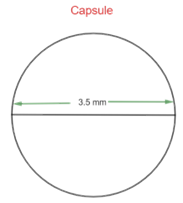
10. A capsule of medicine is in the shape of a sphere of diameter $\text{3}\text{.5 mm}$. How much medicine $\left( \text{in m}{{\text{m}}^{\text{3}}} \right)$ is needed to fill this capsule? $\left[ \text{Assume  }\pi\text{  =}\dfrac{\text{22}}{\text{7}} \right]$

Ans: It is given that the diameter of the capsule $\text{= 3}\text{.5 mm}$.

So, the radius will be $\text{r = }\left( \dfrac{\text{3}\text{.5}}{\text{2}} \right)\text{ = 1}\text{.75 mm}$.

Volume of spherical capsule $\text{V = }\dfrac{\text{4}}{\text{3}}\text{ }\pi\text{ }{{\text{r}}^{\text{3}}}$

$\Rightarrow \text{V = }\left[ \dfrac{\text{4}}{\text{3}}\text{  }\times\text{  }\dfrac{\text{22}}{\text{7}}\text{  }\times\text{  }{{\left( \text{1}\text{.75} \right)}^{\text{3}}} \right]\text{ m}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 22}\text{.458 m}{{\text{m}}^{\text{3}}}$

$\Rightarrow \text{V = 22}\text{.46 m}{{\text{m}}^{\text{3}}}\left( \text{approx} \right)$

Hence, the amount of medicine required to fill the capsule is $\text{22}\text{.46 m}{{\text{m}}^{\text{3}}}$.

Overview of Deleted Syllabus for CBSE Class 9 Maths Chapter 11

Surface Area and Volumes Class 9 NCERT Solutions

Conclusion

The NCERT Solutions for Maths class 9 Surface Area and Volume Chapter 11, provided by Vedantu, comprehensively cover Surface Area and Volume, essential for understanding 3D geometry. Focus on key concepts like the formulas for the surface area and volume of various shapes, including cylinders, cones, and spheres. Practice is crucial, so work through all exercises diligently. Vedantu highlights that previous year question papers often feature 6–8 questions from this chapter, making it a significant component for exam preparation. Mastery of these topics will aid in solving complex problems efficiently and boost overall performance in the exam.

Other Study Materials of CBSE Class 9 Maths Chapter 11

NCERT Solutions for Class 9 Maths - Chapter-wise List

Given below are the chapter-wise NCERT Solutions for Class 9 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Important Study Materials for CBSE Class 9 Maths