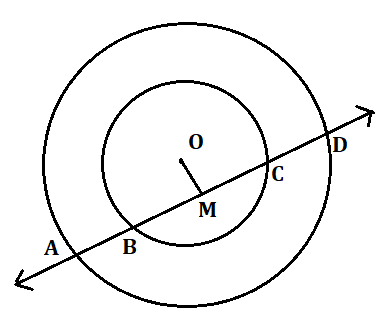
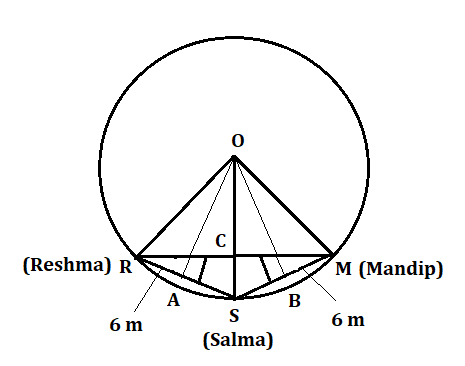
Class 9 Maths Exercise 9.2 – Circles Solutions
NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.2 Circles
FAQs on NCERT Solutions for Class 9 Maths Chapter 9 Exercise 9.2 Circles
1. What concepts are covered in NCERT Solutions for Class 9 Maths Chapter 9 Circles Exercise 9.2?
NCERT Solutions for Class 9 Maths Chapter 9 Circles Exercise 9.2 focuses on properties of circles, including equal chords, distances from the centre, properties of tangents, and application-based questions involving geometry of circles. Students learn to use theorems related to chords and their distances, apply Pythagoras’ theorem in circle geometry, and solve problems involving intersecting chords and tangents as per the CBSE 2025–26 syllabus.
2. How are equal chords and their distances from the centre of a circle explained in Exercise 9.2 Solutions?
The solutions demonstrate that equal chords of a circle are equidistant from the centre, using congruent triangles and perpendicular bisectors. This is proven step-by-step according to the CBSE Class 9 Maths pattern, following logical reasoning and geometrical construction.
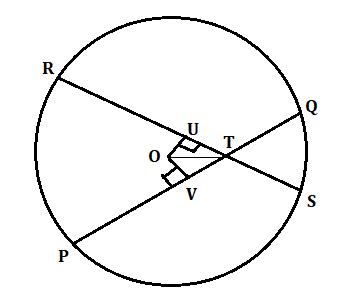
3. Why does a line joining the intersection point of two equal chords with the centre make equal angles with the chords?
The answer uses triangle congruence (RHS criteria) and properties of perpendiculars from the centre to show that the line joining the centre to the intersection point creates equal angles with both chords. This supports the concept that central symmetry leads to congruent angles, as required in NCERT Class 9 Circle problems.
4. In what ways does Exercise 9.2 develop students’ understanding of theorems in circle geometry?
Exercise 9.2 helps students master theorems such as ‘equal chords are equidistant from the centre’ and ‘chords equidistant from the centre are equal’. Each solution breaks down the proof and logic, ensuring students can apply these theorems to new problems, in line with CBSE examination standards.
5. What is the significance of the formula C = 2πr in Class 9 Maths Chapter 9?
C = 2πr gives the circumference of a circle and is fundamental for solving problems on circle perimeter, arc length, and practical geometry in Class 9 Maths Chapter 9. Understanding its derivation and application is essential for geometry questions in NCERT Solutions.
6. Do NCERT Solutions for Class 9 Maths Chapter 9 Circles Exercise 9.2 include all question types as per CBSE syllabus?
Yes, NCERT Solutions for Class 9 Maths Chapter 9 Circles Ex 9.2 include detailed solutions for all six exercise questions, matching the latest CBSE 2025–26 syllabus. Stepwise explanations support all variations of conceptual and application-based problems found in the official textbook.
7. How are real-life problems involving circles integrated in Exercise 9.2 NCERT Solutions?
Exercise 9.2 includes real-life applications such as finding distances and lengths in practical contexts (e.g., playgrounds, parks) using circle properties. Solutions show how to model such scenarios mathematically, reinforcing the importance of circle geometry for daily applications.
8. Why is it necessary to practice each question in Class 9 Maths Chapter 9 Exercise 9.2?
Practicing every question ensures students internalize circle theorems, master logical reasoning, and avoid common mistakes. Full practice is emphasized in NCERT Solutions to help students succeed in CBSE exams and build strong problem-solving foundations in geometry.
9. What should a student do if they get stuck on a proof-based problem from NCERT Class 9 Maths Circles?
- Start by carefully reading the question and drawing a labelled diagram.
- Review circle theorems related to equal chords, perpendiculars, and properties of tangents.
- Analyze known values and relationships.
- Break down the proof into logical steps, ensuring explanations for each step as shown in the official NCERT Solutions.
10. How can understanding tangents help in solving 9th class circle geometry questions?
Recognizing that a tangent touches the circle at exactly one point is critical for solving angle and length problems in circle geometry. NCERT Solutions illustrate how tangents relate to perpendicular radii and angle calculations, which often feature in CBSE board questions.
11. What is a common misconception about equal chords in circles that NCERT Solutions address?
A frequent misconception is thinking that equal chords must be diameters or that their equidistance doesn’t require perpendiculars from the centre. NCERT Solutions clarify that equality of chords relates strictly to their lengths and requires proof via perpendicular distances from the circle’s centre.
12. How does knowing the radius and diameter help in solving Exercise 9.2 questions?
In circle geometry, the radius is half the diameter. Knowledge of this relationship lets students switch between length measurements and apply formulas for circumference and area, streamlining calculations in Exercise 9.2’s NCERT Solutions.
13. Are diagrams important in writing NCERT Solutions for Class 9 Chapter 9 Circles?
Yes, diagrams are essential. They help visualize relationships, support proofs, and clarify geometric constructions. CBSE-aligned NCERT Solutions recommend stepwise diagrams for clear explanations in circle geometry problems.
14. What logical strategies are emphasized in solving NCERT Class 9 Circles Exercise 9.2 problems?
NCERT Solutions emphasize using congruency, symmetry, and construction of perpendiculars to chords when solving problems. Logical sequencing, justification of each step, and referencing circle theorems are integral strategies as per the CBSE methodology.
15. How do the theorems from Exercise 9.2 support advanced geometry in higher classes?
Mastering theorems such as equal chords and distances from the centre serves as a foundation for tackling advanced geometric proofs in higher classes. These concepts are prerequisites for coordinate geometry, locus problems, and trigonometry in Grades 10 and above.














 Watch Video
Watch Video