NCERT Solutions For Class 10 Maths Chapter 6 Triangles - 2025-26

NCERT Solutions for Class 10 Maths Chapter 6, "Triangles," is a chapter that deals with the properties and classification of triangles. The chapter contains six exercises, each covering a different aspect of the topic. Below is a brief explanation of each exercise:

Exercise 6.1: In this exercise, you will be introduced to the basic concepts of triangles, including the definition, elements, types, and angles. You will also learn about congruent triangles and the criteria for their congruence.

Exercise 6.2: This exercise focuses on the properties of triangles, such as the angle sum property, the exterior angle property, and the inequality theorem. You will also learn about the Pythagorean theorem and its applications.

Exercise 6.3: In this exercise, you will learn about the similarity of triangles, including the criteria for similarity, the theorem of basic proportionality, and the application of similarity in practical situations.

Access NCERT Solutions for Class 10 Maths Chapter 6 Triangles

Exercise 6.1

1. Fill in the Blanks Using Correct Word Given in the Brackets:

i. All circles are ______. (congruent, similar)

Ans: Similar.

ii. All squares are ______. (similar, congruent)

Ans: Similar.

iii. All ______ triangles are similar. (isosceles, equilateral)

Ans: Equilateral.

iv. Two polygons of the same number of sides are similar, if their corresponding angles are ______ (equal, proportional)

Ans: Equal

And their corresponding sides are ______. (equal, proportional)

Ans: Proportional.

2. Give Two Different Examples of Pair of -

i. Similar Figures

Ans: The two examples for similar figures are 

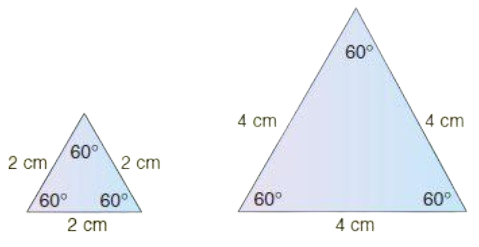
a. Two equilateral triangles having sides \[\text{2cm}\] and $\text{4cm}$.

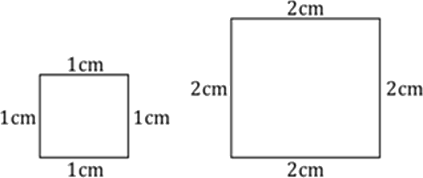
b. Two squares having sides \[\text{2cm}\] and $\text{4cm}$.

ii. Non-Similar Figures

Ans: The two examples for non - similar figures are

a. A Trapezium and Square

b. A triangle and a Paralellogram

3. State whether the following quadrilaterals are similar or not.

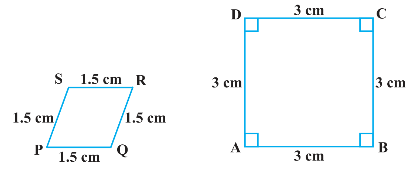
Ans: The given quadrilaterals $PQRS$ and $ABCD$ are not similar because their corresponding sides are proportional, that is, $1:2$ but their corresponding angles are not equal.

Exercise 6.2

1. (i) From the figure (i) , if \[\text{DE  }\!\!|\!\!\text{  }\!\!|\!\!\text{  BC}\]. Find \[\text{EC}\].

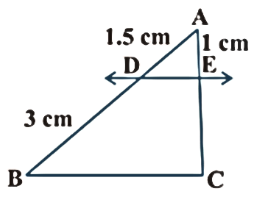
Ans: Let us assume that \[\text{EC = x cm}\]

Given that $\,\text{DE  }\!\!|\!\!\text{  }\!\!|\!\!\text{  BC}$

But from basic proportionality theorem, we know that

$\dfrac{\text{AD}}{\text{DB}}$ $=$ $\dfrac{\text{AE}}{\text{EC}}$

$\dfrac{\text{1}\text{.5}}{\text{3}}$ $=$ $\dfrac{\text{1}}{\text{x}}$

\[\text{x = }\dfrac{\text{3 x 1}}{\text{1}\text{.5}}\]

\[x\text{ }=\text{ }2\]

\[\therefore \]\[\text{EC = 2 cm}\]

(ii) From the figure (ii) , if \[\text{DE  }\!\!|\!\!\text{  }\!\!|\!\!\text{  BC}\]. \[\text{AD}\] in (ii).

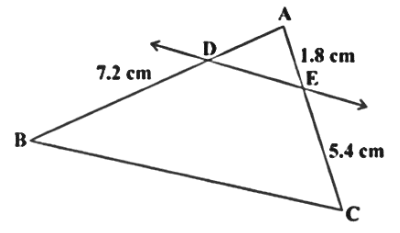
Ans: 

Let us assume that \[\text{AD = x cm}\]

Given that \[\text{DE  }\!\!|\!\!\text{  }\!\!|\!\!\text{  BC}\text{.}\]

But from basic proportionality theorem we know that

$\dfrac{\text{AD}}{\text{DB}}$ $\text{=}$ $\dfrac{\text{AE}}{\text{EC}}$

$ \dfrac{\text{x}}{\text{7}\text{.2}}\text{ = }\dfrac{\text{1}\text{.8}}{\text{5}\text{.4}} $

$ \text{x = }\dfrac{\text{1}\text{.8 x 7}\text{.2}}{\text{5}\text{.4}} $

$ \text{x = 2}\text{.4} $

\[\therefore \text{AD = 2}\text{.4}\]$\text{cm}$

2. (i) In a $\text{ }\!\!\Delta\!\!\text{ PQR,}$ \[\text{E}\] and \[\text{F}\] are any two points on the sides \[\text{PQ}\] and \[\text{PR}\] respectively. State whether \[\text{EF  }\!\!|\!\!\text{  }\!\!|\!\!\text{  QR}\] for \[\text{PE = 3}\text{.9 cm, EQ = 3 cm, PF = 3}\text{.6 cm}\] and \[\text{FR = 2}\text{.4 cm}\]

Ans:

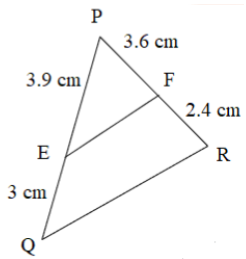
Given, \[\text{PE = 3}\text{.9 cm, EQ = 3 cm, PF = 3}\text{.6 cm}\],\[\text{FR = 2}\text{.4 cm}\]

$\dfrac{\text{PF}}{\text{EQ}}$ $\text{=}$$\dfrac{\text{3}\text{.9}}{\text{3}}$\[\text{ }\!\!~\!\!\text{ = 1}\text{.3}\]

$\dfrac{\text{PF}}{\text{FR}}$ \[\text{=}\] $\dfrac{\text{3}\text{.6}}{\text{2}\text{.4}}$ \[\text{= 1}\text{.5}\]

Hence, $\dfrac{\text{PE}}{\text{EQ}}$ \[\ne \] $\dfrac{\text{PF}}{\text{FR}}$

Therefore , \[\text{EF}\] is parallel to \[\text{QR}\].

(ii) In a $\text{ }\!\!\Delta\!\!\text{ PQR,}$ \[\text{E}\] and \[\text{F}\] are any two points on the sides \[\text{PQ}\] and \[\text{PR}\] respectively. State whether \[\text{EF  }\!\!|\!\!\text{  }\!\!|\!\!\text{  QR}\] for \[\text{PE = 4 cm, QE = 4}\text{.5 cm, PF = 8 cm}\] and \[\text{RF = 9 cm}\]

 Ans:

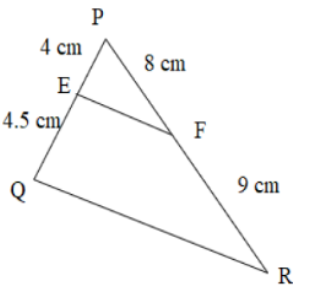
\[\text{PE = 4 cm,QE = 4}\text{.5 cm,PF = 8 cm,RF = 9 cm}\]

$\dfrac{\text{PE}}{\text{EQ}}\text{ = }\dfrac{\text{4}}{\text{4}\text{.5}}\text{ = }\dfrac{\text{8}}{\text{9}} $

$ \dfrac{\text{PF}}{\text{FR}}\text{ = }\dfrac{\text{8}}{\text{9}} $

Hence, $\dfrac{\text{PE}}{\text{EQ}}\text{ = }\dfrac{\text{PF}}{\text{FR}}$

Therefore, \[\text{EF}\] is parallel to \[\text{QR}\].

(iii) In a $\Delta PQR,$ \[\text{E}\] and \[\text{F}\] are any two points on the sides \[\text{PQ}\] and \[\text{PR}\] respectively. State whether \[\text{EF  }\!\!|\!\!\text{  }\!\!|\!\!\text{  QR}\] for \[\text{PQ = 1}\text{.28 cm, PR = 2}\text{.56 cm, PE = 0}\text{.18 cm}\] and \[\text{PF = 0}\text{.63 cm}\]

Ans:

\[\text{PQ = 1}\text{.28 cm,PR = 2}\text{.56 cm,PE = 0}\text{.18 cm,PF = 0}\text{.36 cm}\]

$\dfrac{\text{PE}}{\text{PQ}}\text{ = }\dfrac{\text{0}\text{.18}}{\text{1}\text{.28}}\text{ = }\dfrac{\text{18}}{\text{128}}\text{ = }\dfrac{\text{9}}{\text{64}} $

$\dfrac{\text{PF}}{\text{PR}}\text{ = }\dfrac{\text{0}\text{.36}}{\text{2}\text{.56}}\text{ = }\dfrac{\text{9}}{\text{64}} $

Hence, $\dfrac{\text{PE}}{\text{PQ}}\text{ = }\dfrac{\text{PF}}{\text{PR}}$

Therefore, \[\text{EF}\] is parallel to \[\text{QR}\].

3. In the figure given below, if sides \[\text{LM  }\!\!|\!\!\text{  }\!\!|\!\!\text{  CB}\] and \[\text{LN  }\!\!|\!\!\text{  }\!\!|\!\!\text{  CD,}\]Show that $\dfrac{\text{AM}}{\text{AB}}\text{ = }\dfrac{\text{AN}}{\text{AD}}$

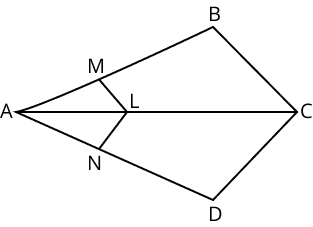
Ans:

Given that in the figure, \[\text{LM  }\!\!|\!\!\text{  }\!\!|\!\!\text{  CB}\]

But from basic proportionality theorem, we know that

$\dfrac{\text{AM}}{\text{AB}}\text{ = }\dfrac{\text{AL}}{\text{AC}}\text{ }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{ (i)}$

Also, \[\text{LN  }\!\!|\!\!\text{  }\!\!|\!\!\text{  CD}\]

$\therefore \dfrac{\text{AN}}{\text{AD}}\text{ = }\dfrac{\text{AL}}{\text{AC}}\text{ }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{ (ii)}$

From (i) and (ii), we get

$\dfrac{\text{AM}}{\text{AB}}\text{ = }\dfrac{\text{AN}}{\text{AD}}$

4. In the figure given below, if sides $\text{DE  }\!\!|\!\!\text{  }\!\!|\!\!\text{  AC}$ and $\text{DF  }\!\!|\!\!\text{  }\!\!|\!\!\text{  AE}\text{.}$Show that $\dfrac{\text{BF}}{\text{FE}}\text{ = }\dfrac{\text{BE}}{\text{EC}}$

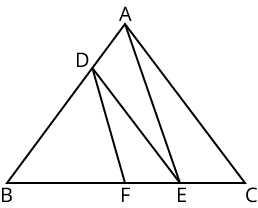
Ans:

In

$\text{ }\!\!\Delta\!\!\text{ ABC,DE  }\!\!|\!\!\text{  }\!\!|\!\!\text{  AC}$ 

$\therefore \dfrac{\text{BD}}{\text{DA}}\text{ = }\dfrac{\text{BE}}{\text{EC}} $

(By Basic proportionality theorem)

$\text{In}$ 

$\text{ }\!\!\Delta\!\!\text{ BAE,DF  }\!\!|\!\!\text{  }\!\!|\!\!\text{  AE} $

$ \therefore \dfrac{\text{BD}}{\text{DA}}\text{ = }\dfrac{\text{BE}}{\text{FE}} $

By Basic proportionality theorem

From (i) and (ii),we get

$\dfrac{\text{BE}}{\text{EC}}\text{ = }\dfrac{\text{BF}}{\text{FE}}$

5. In the figure given below, if sides $\text{DE  }\!\!|\!\!\text{  }\!\!|\!\!\text{  OQ}$ and $\text{DF  }\!\!|\!\!\text{  }\!\!|\!\!\text{  OR}$, Show that $\text{EF  }\!\!|\!\!\text{  }\!\!|\!\!\text{  QR}$

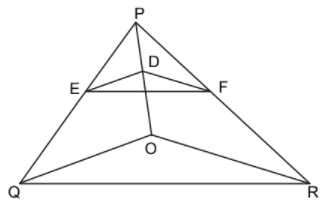
Ans:

$\text{In}$ 

$ \text{ }\!\!\Delta\!\!\text{ POQ,DE }\!\!|\!\!\text{  }\!\!|\!\!\text{ OQ} $

$ \therefore \dfrac{\text{PE}}{\text{EQ}}\text{=}\dfrac{\text{PD}}{\text{DO}} $              ……………………(i) By basic proportionality theorem$\text{In}$

$ \text{ }\!\!\Delta\!\!\text{ POR,DF  }\!\!|\!\!\text{  }\!\!|\!\!\text{  OR} $

$ \therefore \dfrac{\text{PF}}{\text{FR}}\text{=}\dfrac{\text{PD}}{\text{DO}}$

……………………(ii) By basic proportionality theorem

From (i) and (ii),we get

$\dfrac{\text{PE}}{\text{EQ}}\text{ = }\dfrac{\text{PF}}{\text{FR}} $

$ \therefore \text{EF  }\!\!|\!\!\text{  }\!\!|\!\!\text{  QR} $                             Converse of Basic proportionality theorem

6.In the figure given below, \[\text{A, Band C}\] are points on \[\text{OP, OQ and OR}\] respectively such that \[\text{AB  }\!\!|\!\!\text{  }\!\!|\!\!\text{  PQ}\] and \[\text{AC  }\!\!|\!\!\text{  }\!\!|\!\!\text{  PR}\]. Prove that \[\text{BC  }\!\!|\!\!\text{  }\!\!|\!\!\text{  QR}\].

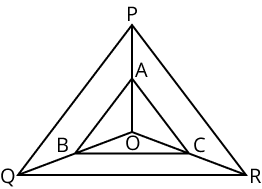
Ans:

In

$\text{ }\!\!\Delta\!\!\text{ POQ,AB  }\!\!|\!\!\text{  }\!\!|\!\!\text{  PQ} $

$\therefore \dfrac{\text{OA}}{\text{OP}}\text{ = }\dfrac{\text{OB}}{\text{PQ}} $

$……………………(i) By basic proportionality theorem

$\text{In}$ 

$\text{ }\!\!\Delta\!\!\text{ POR,AC  }\!\!|\!\!\text{  }\!\!|\!\!\text{  PR} $

\[\therefore \dfrac{\text{OA}}{\text{OP}}\text{ = }\dfrac{\text{OC}}{\text{CR}}\]  ………………(ii) By basic proportionality theorem

From (i) and (ii),we get

$\dfrac{\text{OB}}{\text{BQ}}\text{ = }\dfrac{\text{OC}}{\text{CR}} $

$ \therefore \text{BC  }\!\!|\!\!\text{  }\!\!|\!\!\text{  CR} $

Converse of Basic proportionality theorem

7. By using Basic proportionality theorem, Show that a line passing through the mid-points of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX). 

Ans:

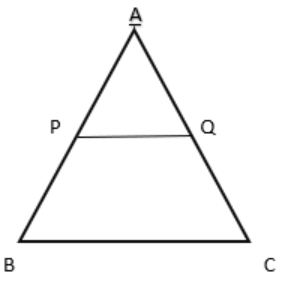
Let us assume in the given figure in which \[\text{PQ}\] is a line segment passing through the mid-point \[\text{P}\] of line \[\text{AB}\], such that \[\text{PQ  }\!\!|\!\!\text{  }\!\!|\!\!\text{  BC}\].

From basic proportionality theorem, we know that

$\dfrac{\text{AQ}}{\text{QC}}\text{ = }\dfrac{\text{AP}}{\text{PB}} $

$ \dfrac{\text{AQ}}{\text{QC}}\text{ = 1} $

As \[\text{P}\] is the midpoint of \[\text{AB}\] ,\[\text{AP  =  PB}\]

\[\Rightarrow \text{AQ = QC}\]

Or

\[\text{Q}\] is the midpoint of \[\text{AC}\]

8. By using Converse of basic proportionality theorem, Show that the line joined by the midpoints of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX). 

Ans:

Let us assume that the given figure in which \[\text{PQ}\] is a line segment joined by the mid-points \[\text{P and Q}\] of lines \[\text{AB and AC}\] respectively. 

i.e., \[\text{AP  =  PB and AQ  =  QC}\]

Also it is clear that

$\dfrac{\text{AP}}{\text{PB}}\text{ = 1}$ and

$\dfrac{\text{AQ}}{\text{QC}}\text{ = 1} $

$ \therefore \dfrac{\text{AP}}{\text{PB}}\text{ = }\dfrac{\text{AQ}}{\text{QC}} $ 

Hence, using basic proportionality theorem, we get 

\[\text{PQ  }\!\!|\!\!\text{  }\!\!|\!\!\text{  BC}\]

9. If \[\text{ABCD}\] is a trapezium where \[\text{AB  }\!\!|\!\!\text{  }\!\!|\!\!\text{  DC}\] and its diagonals intersect each other at the point \[\text{O}\]. Prove that $\dfrac{\text{AO}}{\text{BO}}\text{ = }\dfrac{\text{CO}}{\text{DO}}$

Ans:

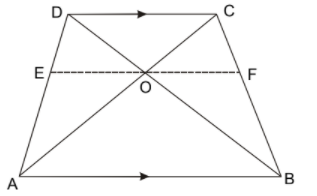
Draw a line  \[\text{EF}\] through point \[\text{O}\] , such that 

In \[\text{ }\!\!\Delta\!\!\text{ ADC}\], \[\text{EO  }\!\!|\!\!\text{  }\!\!|\!\!\text{  CD}\]

Using basic proportionality theorem, we get

$\dfrac{\text{AE}}{\text{ED}}\text{ = }\dfrac{\text{AO}}{\text{OC}}$____________________(i)

In \[\text{ }\!\!\Delta\!\!\text{ ABD}\]\[\text{, OE  }\!\!|\!\!\text{  }\!\!|\!\!\text{  AB}\] 

So, using basic proportionality theorem, we get

\[\frac{\text{AE}}{\text{ED}}\ =\ \frac{\text{BO}}{\text{DO}}\ \] ___________________(ii)

From equation (i) and (ii), we get 

$\frac{\text{AO}}{\text{CO}}\text{= }\frac{\text{BO}}{\text{DO}}$

$\therefore \ \frac{\text{AO}}{\text{BO}}\text{= }\frac{\text{CO}}{\text{DO}}$

10.  The diagonals of a quadrilateral \[\text{ABCD}\] intersect each other at the point \[\text{O}\] such that $\dfrac{\text{AO}}{\text{BO}}\text{ = }\dfrac{\text{CO}}{\text{DO}}$ Prove that \[\text{ABCD}\] is a trapezium. 

Ans: 

Let us assume the following figure for the given question.

Draw a line \[\text{OE  }\!\!|\!\!\text{  }\!\!|\!\!\text{  AB}\]

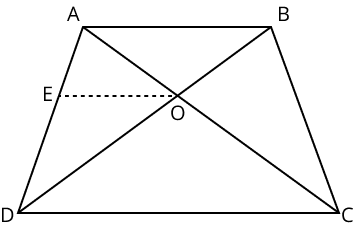
In \[\text{;ABD, OE  }\!\!|\!\!\text{  }\!\!|\!\!\text{  AB}\]

Using basic proportionality theorem, we get 

$\dfrac{\text{AE}}{\text{ED}}\text{ = }\dfrac{\text{BO}}{\text{OD}}\text{ }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{  }\!\!\_\!\!\text{ (i)}$

However, it is given that 

$\frac{\text{AO}}{\text{BO}}\text{ = }\frac{\text{CO}}{\text{DO}} $

$ \therefore \text{ }\frac{\text{AO}}{\text{CO}}\text{ = }\frac{\text{BO}}{\text{DO}}\ \text{ }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ }\!\!~\!\!\text{  }\_\text{ (ii)} $

From equations (i) and (ii), we get 

$\dfrac{\text{AE}}{\text{ED}}\text{ = }\dfrac{\text{AO}}{\text{OC}} $

$ \Rightarrow \text{EO  }\!\!|\!\!\text{  }\!\!|\!\!\text{  DC} $

By the converse of basic proportionality theorem

$\Rightarrow \text{ AB }\left| \left| \text{ OE } \right| \right|\text{ DC}  $

$\Rightarrow \text{AB  }\!\!|\!\!\text{  }\!\!|\!\!\text{  CD} $

\[\therefore \text{ ABCD}\] is a trapezium.

Exercise 6.3

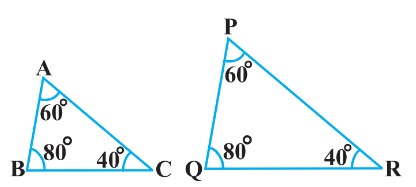
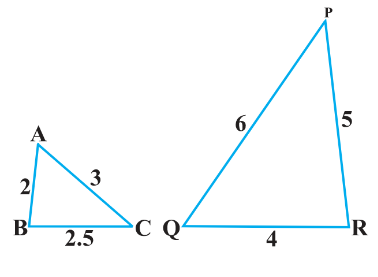
1. State which pairs of triangles in the following figure are similar? Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

(i)

(ii)

(iii)

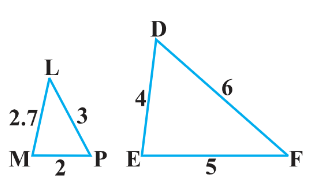
(iv)

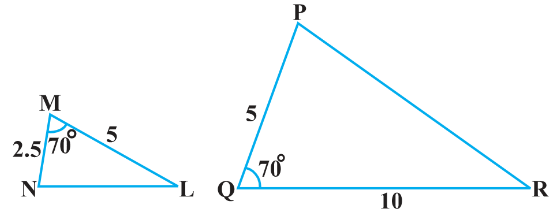
(v)

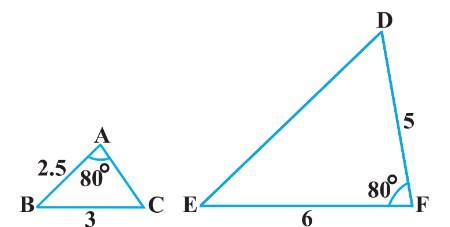
(vi)

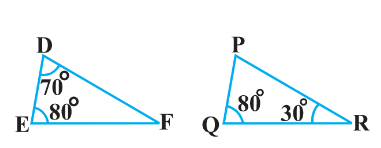
Ans: 

I. In $\triangle \mathrm{ABC}$ and $\triangle \mathrm{PQR}$

$\angle \mathrm{A}=\angle \mathrm{P}$

$\angle \mathrm{B}=\angle \mathrm{Q}$

$\angle \mathrm{C}=\angle \mathrm{R}$

$\therefore$ By AAA criterion of similarity, $\triangle \mathrm{ABC} \sim \triangle \mathrm{PQR}$

II. In $\triangle \mathrm{ABC}$ and $\triangle \mathrm{QRP}$

$\frac{\mathrm{AB}}{\mathrm{QR}}=\frac{\mathrm{BC}}{\mathrm{RP}}=\frac{\mathrm{AC}}{\mathrm{QP}}=\frac{1}{2}$

$\therefore$ By SSS criterion of similarity, $\triangle \mathrm{ABC} \sim \triangle \mathrm{QRP}$

III. In $\triangle \mathrm{LMP}$ and $\triangle \mathrm{DEF}$

$\frac{\mathrm{LM}}{\mathrm{DE}}=\frac{2.7}{4}, \frac{\mathrm{LP}}{\mathrm{DF}}=\frac{1}{2}$

The sides are not in the equal ratios, Hence the two triangles are not similar.

IV. In $\triangle \mathrm{MNL}$ and $\triangle \mathrm{QPR}$

$\angle \mathrm{M}=\angle \mathrm{Q}$

$\frac{\mathrm{MN}}{\mathrm{QP}}=\frac{\mathrm{ML}}{\mathrm{QR}}=\frac{1}{2}$

$\therefore$ By SAS criterion of similarity, $\triangle \mathrm{MNL} \sim \triangle \mathrm{QP} \mathrm{R}$

V. In $\triangle \mathrm{ABC}$ and $\triangle \mathrm{EFD}$

$\angle \mathrm{A}=\angle \mathrm{F}, $

$\frac{AB}{FD}=\frac{BC}{FD}=\frac{1}{2}$

$\therefore$ By SAS criterion of similarity, $\triangle \mathrm{ABC} \sim \triangle \mathrm{EFD}$

VI. In $\triangle \mathrm{DEF}$ and $\triangle \mathrm{PQR}$

Since, sum of angles of a triangle is $180^{\circ}$, Hence, $\angle \mathrm{F}=30^{\circ}$ and $\angle \mathrm{P}=70^{\circ}$

$\angle \mathrm{D} =\angle \mathrm{P}$

$\angle \mathrm{E} =\angle \mathrm{Q}$

$\angle \mathrm{F} =\angle \mathrm{R}$

$\therefore$ By AAA criterion of similarity, $\triangle \mathrm{DEF} \sim \triangle \mathrm{PQR}$

2. In the following figure, $\Delta \mathrm{ODC} \sim \Delta \mathrm{OBA}, \angle \mathrm{BOC}=125^{\circ}$ and $\angle \mathrm{CDO}=70^{\circ}$. Find $\angle \mathrm{DOC}, \angle \mathrm{DCO}$ and $\angle \mathrm{OAB}$

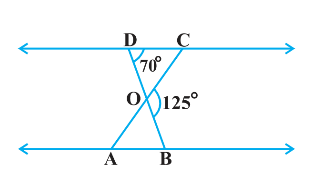
Ans: Given:

$\triangle \mathrm{ODC} \sim \triangle \mathrm{OBA}$

$\angle \mathrm{BOC}=125^{\circ}$

$\angle \mathrm{CDO}=70^{\circ}$

To find: $\angle D O C, \angle D C O$ and $\angle O A B$

Sol: Here, $B D$ is a line,

So, we can apply a linear pair on it.

$\angle B O C+\angle D O C=180^{\circ} (Linear Pair)$

$125^{\circ}+\angle D O C=180^{\circ}$

$\angle D O C=180^{\circ}-125^{\circ}$

$\angle D O C=180^{\circ}-125^{\circ}$

$\angle D O C=55^{\circ}$

Now in $\triangle \mathrm{DCO}$

$\angle C D O+\angle D C O+\angle D O C=180^{\circ}$

$70^{\circ}+\angle D C O+55^{\circ}=180^{\circ}$

$125^{\circ}+\angle D C O=180^{\circ}$

$\angle D C O=180^{\circ}-125^{\circ}$

$\angle D C O=55^{\circ}$

Now it is given that

$\triangle O D C \sim \triangle O B A$

Hence,

$\angle \mathrm{DCO}=\angle \mathrm{OAB}$

$55^{\circ}=\angle \mathrm{OAB}$

$\angle \mathrm{OAB}=55^{\circ}$

Now in $\triangle \mathrm{DCO}$

$\angle \mathrm{CDO}+\angle \mathrm{DCO}+\angle \mathrm{DOC}=180^{\circ} \quad$ (Sum of all angles of triangle is $180^0$ 

$70^{\circ}+\angle \mathrm{DCO}+55^{\circ}=180^{\circ}$ 

$125^{\circ}+\angle \mathrm{DCO}=180^{\circ}$ 

$\angle \mathrm{DCO}=180^{\circ}-125^{\circ}$ $\angle \mathrm{DCO}=55^{\circ}$

Now, it is given that

$\Delta \mathrm{ODC} \sim \triangle \mathrm{OBA}$

Hence.

$\angle D C O=\angle O A B$(Corresponding angles of a similar triangles are equal)

$55^{\circ}=\angle O A B$

3. Diagonals AC and BD of a trapezium ABCD with AB \|DC intersect each other at the point $\mathrm{O}$. Using a similarity criterion for two triangles, show that $\frac{\mathrm{AO}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}$

Ans: In $\Delta \mathrm{DOC}$ and $\triangle \mathrm{BOA}$

$\angle C D O=\angle A B O$ (Alternate interior angles as $A B \| C D)$

$\angle \mathrm{DCO}=\angle \mathrm{BAO}$ (Alternate interior angles as $\mathrm{AB} \| \mathrm{CD})$

$\angle \mathrm{DOC}=\angle \mathrm{BOA}$ (Vertically opposite angles $)$

$\therefore \Delta \mathrm{DOC} \sim \Delta \mathrm{BOA}$ (AAA similarity criterion)

$\therefore \frac{\mathrm{DO}}{\mathrm{BO}}=\frac{\mathrm{OC}}{\mathrm{OA}} \quad($ Corresponding sides are proportional)

$\Rightarrow \frac{\mathrm{OA}}{\mathrm{OC}}=\frac{\mathrm{OB}}{\mathrm{OD}}$

4.  In the figure, $\frac{\mathrm{QR}}{\mathrm{QS}}=\frac{\mathrm{QT}}{\mathrm{PR}} \text { and } \angle 1=\angle 2 \text {.Show that } \Delta \mathrm{PQS} \sim \Delta \mathrm{TQR}$

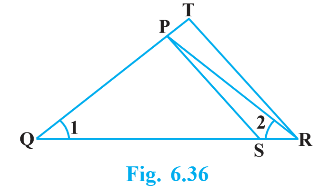
Ans: In $\delta \mathrm{PQR}, \angle \mathrm{PQR}=\angle \mathrm{PRQ}$

$\therefore \mathrm{PQ}=\mathrm{PR}(\mathrm{i})$

Given 

$\frac{\mathrm{QR}}{\mathrm{QS}}=\frac{\mathrm{QT}}{\mathrm{PR}}$

Using (i), we obtain

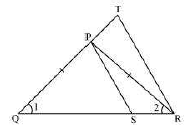
$\frac{\mathrm{QR}}{\mathrm{QS}}=\frac{\mathrm{QT}}{\mathrm{QP}}$

In $\triangle \mathrm{PQS}$ and $\triangle \mathrm{TQR}$,

$\frac{\mathrm{QR}}{\mathrm{QS}}=\frac{\mathrm{QT}}{\mathrm{QP}}[\text { [Using (ii) }]$

$\angle \mathrm{Q}=\angle \mathrm{Q}$

$\therefore \Delta \mathrm{PQS} \sim \Delta \mathrm{TQR} \quad[\text { SAS similarity criterion }]$

5. $\mathrm{S}$ and $\mathrm{T}$ are point on sides $\mathrm{PR}$ and $\mathrm{QR}$ of $\triangle \mathrm{PQR}$ such that $\angle \mathrm{P}=\angle \mathrm{RTS}$. Show that $\triangle \mathrm{RPQ} \sim \Delta \mathrm{RTS}$.

Ans: Given: $\Delta P Q R$

and the points $S$ and $T$ on sides PR and QR.

Such that $\angle P=\angle R T S$

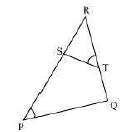
To Prove: $\triangle \mathrm{RPQ} \sim \Delta$ RTS.

Proof:

In $\triangle \mathrm{RPQ}$ and $\triangle \mathrm{RTS}$.

$\angle P=\angle R T S$

(Given)

And $\angle \mathrm{PRQ}=\angle \mathrm{TRS}=\angle \mathrm{R}$

(Common)

So, $\triangle \mathrm{RPQ} \sim \Delta \mathrm{RTS}$.

(AA similarity)

Hence proved

6. In the following figure, if $\triangle \mathrm{ABE} \cong \triangle \mathrm{ACD}$, show that $\triangle \mathrm{ADE} \sim \Delta \mathrm{ABC}$.

Ans: 

We know that the corresponding portions of two triangles that are congruent to each other are equal.

The two triangles are comparable if one of their angles is equal to one of the other triangle's angles, and the sides that include these angles are proportionate.

For two triangles, this is known as the SAS (Side - Angle - Side) similarity criteria.

In $\triangle \mathrm{ABE}$ and $\triangle \mathrm{ACD}$

$\mathrm{AD}=\mathrm{AE}(\triangle \mathrm{ABE} \cong \Delta \mathrm{ACD} \text { given }) \ldots \ldots \ldots \text { (1) }$

$\mathrm{AB}=\mathrm{AC}(\triangle \mathrm{ABE} \cong \triangle \mathrm{ACD} \text { given })$

Now Consider $\triangle A D E$ and $\triangle A B C$

and $\angle$ DAE $=\angle B A C$ (Common angle)

Thus, $\triangle$ ADE $\sim A$ ABC (SAS criterion)

7. In the following figure, altitudes $\mathrm{AD}$ and $\mathrm{CE}$ of $\Delta \mathrm{ABC}$ intersect each other at the point, P. Show, that:

I. $\triangle \mathrm{AEP} \sim \Delta \mathrm{CDP}$

Ans: When two angles from one triangle are equivalent to two angles from another triangle, the two triangles are said to be comparable.

For two triangles, this is known as the AA similarity criteria.

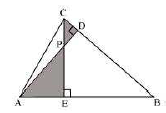
In $\triangle \mathrm{AEP}$ and $\triangle \mathrm{CDP}$

$[\because \mathrm{CE} \perp \mathrm{AB}$ and $\mathrm{AD} \perp \mathrm{BC} ;$ altitudes $]$

$\angle A P E=\angle C P D$ (Vertically opposite angles)

$\Rightarrow \triangle$ AEP $\sim \triangle$ CPD (AA criterion)

II. $\triangle \mathrm{ABD} \sim \Delta \mathrm{CBE}$

Ans: When two angles from one triangle are equivalent to two angles from another triangle, the two triangles are said to be comparable.

For two triangles, this is known as the AA similarity criteria.

In $\triangle \mathrm{ABD}$ and $\triangle \mathrm{CBE}$

$\angle \mathrm{ADB}=\angle C E B=90^{\circ}$

$\angle \mathrm{ABD}=\angle C B E \text { (Common angle) }$

$\Rightarrow \triangle \mathrm{ABD} \sim \Delta C B E \text { (AA criterion) }$

III. $\triangle \mathrm{AEP} \sim \triangle \mathrm{ADB}$

Ans: When two angles from one triangle are equivalent to two angles from another triangle, the two triangles are said to be comparable.

For two triangles, this is known as the AA similarity criteria.

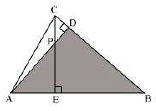
In $\triangle \mathrm{AEP}$ and $\triangle \mathrm{ADB}$

$\angle \mathrm{AEP}=\angle \mathrm{ADB}=9 \mathrm{O}^{\circ}$

$\angle \mathrm{PAE}=\angle \mathrm{BAD} \text { (Common angle) }$

$\Rightarrow \triangle \mathrm{AEP} \sim \triangle \mathrm{ADB} \text { (AA criterion) }$

IV. $\Delta \mathrm{PDC} \sim \Delta \mathrm{BEC}$

Ans: When two angles from one triangle are equivalent to two angles from another triangle, the two triangles are said to be comparable.

For two triangles, this is known as the AA similarity criteria.

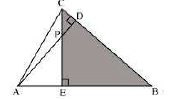
In $\triangle \mathrm{PDC}$ and $\triangle \mathrm{BEC}$

$\angle \mathrm{PDC}=\angle \mathrm{BEC}=9 \mathrm{O}^{\circ}$

$\angle \mathrm{PCD}=\angle \mathrm{BCE} \text { (Common angle) }$

$\Rightarrow \triangle \text { PDC } \sim \triangle \mathrm{BEC} \text { (AA criterion)}$

8. $\mathrm{E}$ is a point on the side AD produced of a parallelogram $\mathrm{ABCD}$ and $\mathrm{BE}$ intersects $\mathrm{CD}$ at $\mathrm{F}$. Show that $\triangle \mathrm{ABE} \sim \Delta \mathrm{CFB}$

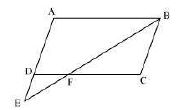
Ans:

In $\triangle \mathrm{ABE}$ and $\triangle \mathrm{CFB}$,

$\angle \mathrm{A}=\angle \mathrm{C}$ (Opposite angles of a parallelogram)

$\angle \mathrm{AEB}=\angle \mathrm{CBF}$ (Alternate interior angles as $\mathrm{AE} \| \mathrm{BC})$

$\therefore \Delta \mathrm{ABE} \sim \Delta \mathrm{CFB}$ (By AA similarity criterion)

9. In the following figure, $\mathrm{ABC}$ and AMP are two right triangles, right angled at B and M respectively, prove that:

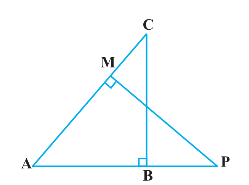
I. $\Delta \mathrm{ABC} \sim \Delta \mathrm{AMP}$

II. $\frac{\mathrm{CA}}{\mathrm{PA}}=\frac{\mathrm{BC}}{\mathrm{MP}}$

Ans: In $\triangle \mathrm{ABC}$ and $\triangle \mathrm{AMP}$

$\angle \mathrm{ABC}=\angle \mathrm{AMP}\left(\operatorname{Each} 90^{\circ}\right)$ $\angle \mathrm{A}=\angle \mathrm{A}(\mathrm{Common})$

$\therefore \Delta \mathrm{ABC} \sim \Delta \mathrm{AMP}$ (By AA similarity criterion)

$\Rightarrow \frac{\mathrm{CA}}{\mathrm{PA}}=\frac{\mathrm{BC}}{\mathrm{MP}}$ (Corresponding sides of similar triangles are proportional)

10. $\mathrm{CD}$ and $\mathrm{GH}$ are respectively the bisectors of $\angle \mathrm{ACB}$ and $\angle \mathrm{EGF}$ such that $\mathrm{D}$ and $\mathrm{H}$ lie on sides $\mathrm{AB}$ and $\mathrm{FE}$ of $\triangle \mathrm{ABC}$ and $\triangle \mathrm{EFG}$ respectively. If $\triangle \mathrm{ABC} \sim$ $\Delta \mathrm{FEG}$, Show that

(i) $\frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{AC}}{\mathrm{FG}}$

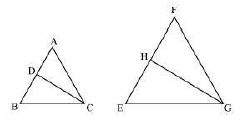
Ans: 

$\text { It is given that } \triangle \mathrm{ABC} \sim \Delta \mathrm{FEG}.$

$\therefore \angle \mathrm{A}=\angle \mathrm{F}, \angle \mathrm{B}=\angle \mathrm{E}, \text { and } \angle \mathrm{ACB}=\angle \mathrm{FGE}$

$\text { Since, } \angle \mathrm{ACB}=\angle \mathrm{FGE} $

$\therefore \angle \mathrm{ACD}=\angle \mathrm{FGH} \text { (Angle bisector) } $

$\text { And, } \angle \mathrm{DCB}=\angle \mathrm{HGE} \text { (Angle bisector) } $

$\text { In } \triangle \mathrm{ACD} \text { and } \Delta \mathrm{FGH} \text {, }$

$\angle \mathrm{A}=\angle \mathrm{F} \text { (Proved above) }$

$\angle \mathrm{ACD}=\angle \mathrm{FGH} \text { (Proved above) }$

$\therefore \Delta \mathrm{ACD} \sim \Delta \mathrm{FGH} \text { (By AA similarity criterion) }$

$\Rightarrow \frac{\mathrm{CD}}{\mathrm{GH}}=\frac{\mathrm{AC}}{\mathrm{FG}}$

(ii) $\triangle \mathrm{DCB} \sim \Delta \mathrm{HGE}$

Ans: $\text { In } \triangle \mathrm{DCB} \text { and } \triangle \mathrm{HGE} \text {, } $

$\angle \mathrm{DCB}=\angle \mathrm{HGE} \text { (Proved above) } $

$\angle \mathrm{B}=\angle \mathrm{E} \text { (Proved above) } $

$\therefore \triangle \mathrm{DCB} \sim \triangle \mathrm{HGE} \text { (By AA similarity criterion) }$

(iii) $\triangle \mathrm{DCA} \sim \Delta \mathrm{HGF}$

Ans: In $\Delta \mathrm{DCA}$ and $\Delta \mathrm{HGF}$,

$\angle \mathrm{ACD}=\angle \mathrm{FGH}$ (Proved above)

$\angle A=\angle F$ (Proved above)

$\therefore \Delta \mathrm{DCA} \sim \Delta \mathrm{HGF}$ (By AA similarity criterion)

11. In the following figure, $\mathrm{E}$ is a point on side CB produced of an isosceles triangle $\mathrm{ABC}$ with $\mathrm{AB}=\mathrm{AC}$. If $\mathrm{AD} \perp \mathrm{BC}$ and $\mathrm{EF} \perp \mathrm{AC}$, prove that $\triangle \mathrm{ABD} \sim$ $\triangle \mathrm{ECF}$

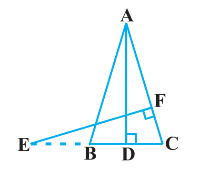
Ans: It is given that $\mathrm{ABC}$ is an isosceles triangle.

$\therefore \mathrm{AB}=\mathrm{AC}$

$\Rightarrow \angle \mathrm{ABD}=\angle \mathrm{ECF}$

In $\Delta \mathrm{ABD}$ and $\triangle \mathrm{ECF}$

$\angle \mathrm{ADB}=\angle \mathrm{EFC}\left(\operatorname{Each} 90^{\circ}\right)$

$\angle \mathrm{BAD}=\angle \mathrm{CEF}$ (Proved above)

$\therefore \Delta \mathrm{ABD} \sim \triangle \mathrm{ECF}$ (By using AA similarity criterion)

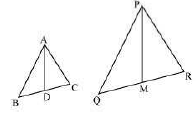
12. Sides $\mathrm{AB}$ and $\mathrm{BC}$ and median AD of a triangle $\mathrm{ABC}$ are respectively proportional to sides PQ and QR and median PM of $\triangle \mathrm{PQR}$ (see the given figure). Show that $\triangle \mathrm{ABC} \sim \triangle \mathrm{PQR}$.

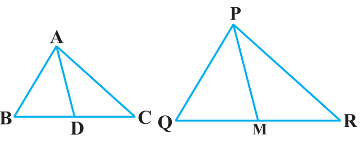
Ans: Median equally divides the opposite side.

$\therefore \mathrm{BD}=\frac{\mathrm{BC}}{2}$ and $\mathrm{QM}=\frac{\mathrm{QR}}{2}$

Given that,

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}=\frac{\mathrm{AD}}{\mathrm{PM}}$

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\frac{1}{2} \mathrm{BC}}{\frac{1}{2} \mathrm{QR}}=\frac{\mathrm{AD}}{\mathrm{PM}}$

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BD}}{\mathrm{QM}}=\frac{\mathrm{AD}}{\mathrm{PM}}$

In $\triangle \mathrm{ABD}$ and $\triangle \mathrm{PQM}$,

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BD}}{\mathrm{QM}}=\frac{\mathrm{AD}}{\mathrm{PM}} \text { (Proved above) }$

$\therefore \Delta \mathrm{ABD} \sim \Delta \mathrm{PQM}$ (By SSS similarity criterion)

$\Rightarrow \angle \mathrm{ABD}=\angle \mathrm{PQM}$ (Corresponding angles of similar triangles)

In $\triangle \mathrm{ABC}$ and $\Delta \mathrm{PQR}$,

$\angle \mathrm{ABD}=\angle \mathrm{PQM} \text { (Proved above) }$

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BC}}{\mathrm{QR}}$

$\therefore \Delta \mathrm{ABC} \sim \Delta \mathrm{PQR}$ (By SAS similarity criterion)

13. $\mathrm{D}$ is a point on the side $\mathrm{BC}$ of a triangle $\mathrm{ABC}$ such that $\angle \mathrm{ADC}=\angle \mathrm{BAC}$. Show that $\mathrm{CA}^{2}= \mathrm{CB.CD}$

Ans: $\text { In } \triangle \mathrm{ADC} \text { and } \triangle \mathrm{BAC} \text {, }$

$\angle \mathrm{ADC}=\angle \mathrm{BAC}$ (Given) $\angle \mathrm{ACD}=\angle \mathrm{BCA}$ (Common angle)

$\therefore \Delta \mathrm{ADC} \sim \triangle \mathrm{BAC}$ (By AA similarity criterion)

We know that corresponding sides of similar triangles are in proportion. $\therefore \frac{\mathrm{CA}}{\mathrm{CB}}=\frac{\mathrm{CD}}{\mathrm{CA}}$ $\Rightarrow \mathrm{CA}^{2}=\mathrm{CB} \cdot \mathrm{CD}$

14. Sides $\mathrm{AB}$ and AC and median AD of a triangle $\mathrm{ABC}$ are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that $\triangle \mathrm{ABC} \sim \Delta \mathrm{PQR}$

Ans: Given that,

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AD}}{\mathrm{PM}}$

Let us extend AD and PM up to point $E$ and $L$ respectively, such that $A D=$ DE and PM $=$ ML. 

Then, join $B$ to $E, C$ to $E, Q$ to $L$, and $R$ to $L .$

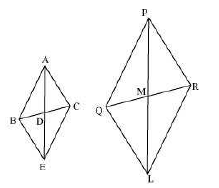
We know that medians divide opposite sides.

Therefore, $\mathrm{BD}=\mathrm{DC}$ and $\mathrm{QM}=\mathrm{MR}$

Also, $\mathrm{AD}=\mathrm{DE}$ (By construction)

And, $\mathrm{PM}=\mathrm{ML}$ (By construction)

In quadrilateral ABEC, diagonals AE and BC bisect each other at point D. Therefore, quadrilateral ABEC is a parallelogram.

$\therefore \mathrm{AC}=\mathrm{BE}$ and $\mathrm{AB}=\mathrm{EC}$ (Opposite sides of a parallelogram are equal) Similarly, we can prove that quadrilateral PQLR is a parallelogram and PR = QL, $P Q=L R$

It was given that

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{AD}}{\mathrm{PM}}$

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BE}}{\mathrm{QL}}=\frac{2 \mathrm{AD}}{2 \mathrm{PM}}$

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BE}}{\mathrm{QL}}=\frac{\mathrm{AE}}{\mathrm{PL}}$

$\therefore \triangle \mathrm{ABE} \sim \triangle \mathrm{PQL}$ (By SSS similarity criterion)

We know that corresponding angles of similar triangles are equal.

$\therefore \angle \mathrm{BAE}=\angle \mathrm{QPL} \ldots$ (1)

Similarly, it can be proved that $\triangle \mathrm{AEC} \sim \triangle \mathrm{PLR}$ and

$\angle \mathrm{CAE}=\angle \mathrm{RPL} \ldots$ (2)

Adding equation (1) and (2), we obtain

$\angle \mathrm{BAE}+\angle \mathrm{CAE}=\angle \mathrm{QPL}+\angle \mathrm{RPL}$

$\Rightarrow \angle \mathrm{CAB}=\angle \mathrm{RPQ} \ldots$ (3)

In $\triangle \mathrm{ABC}$ and $\triangle \mathrm{PQR}$,

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}$ (Given)

$\angle \mathrm{CAB}=\angle \mathrm{RPQ}[\mathrm{Using}$ equation $(3)]$

$\therefore \triangle \mathrm{ABC} \sim \triangle \mathrm{PQR}$ (By SAS similarity criterion)

15. A vertical pole of a length $6 \mathrm{~m}$ casts a shadow $4 \mathrm{~m}$ long on the ground and at the same time a tower casts a shadow $28 \mathrm{~m}$ long. Find the height of the tower.

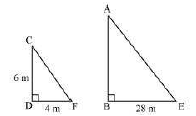
Ans: Let $\mathrm{AB}$ and $\mathrm{CD}$ be a tower and a pole respectively.

Let the shadow of $\mathrm{BE}$ and DF be the shadow of $\mathrm{AB}$ and $\mathrm{CD}$ respectively.

At the same time, the light rays from the sun will fall on the tower and the pole at the same angle.

Therefore, $\angle \mathrm{DCF}=\angle \mathrm{BAE}$

And, $\angle \mathrm{DFC}=\angle \mathrm{BEA}$

$\angle \mathrm{CDF}=\angle \mathrm{ABE}$ (Tower and pole are vertical to the ground)

$\therefore \Delta \mathrm{ABE} \sim \Delta \mathrm{CDF}$ (AAA similarity criterion)

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{CD}}=\frac{\mathrm{BE}}{\mathrm{DF}}$

$\Rightarrow \frac{\mathrm{AB}}{6 \mathrm{~cm}}=\frac{28}{4}$

$\Rightarrow \mathrm{AB}=42 \mathrm{~m}$

Therefore, the height of the tower will be 42 metres.

16. If $\mathrm{AD}$ and $\mathrm{PM}$ are medians of triangles $\mathrm{ABC}$ and $\mathrm{PQR}$, respectively where $\Delta \mathrm{ABC} \sim \Delta \mathrm{PQR}$ Prove that $\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AD}}{\mathrm{PM}}$

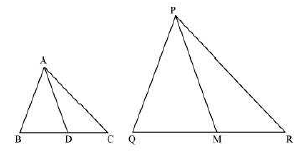
Ans: It is given that $\triangle \mathrm{ABC} \sim \Delta \mathrm{PQR}$

We know that the corresponding sides of similar triangles are in proportion. 

$\therefore \frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{AC}}{\mathrm{PR}}=\frac{\mathrm{BC}}{\mathrm{QR}} \ldots(1)$

Also, $\angle \mathrm{A}=\angle \mathrm{P}, \angle \mathrm{B}=\angle \mathrm{Q}, \angle \mathrm{C}=\angle \mathrm{R} \quad \ldots$ (2)

Since AD and PM are medians, they will divide their opposite sides. $\therefore \mathrm{BD}=\frac{\mathrm{BC}}{2}$ and $\mathrm{QM}=\frac{\mathrm{QR}}{2}$

From equations (1) and (3), we obtain

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BD}}{\mathrm{QM}}$

In $\triangle \mathrm{ABD}$ and $\triangle \mathrm{PQM}$,

$\angle B=\angle Q$ (Using equation (2))

$\frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BD}}{\mathrm{QM}}$

(Using equation (4))

$\therefore \triangle \mathrm{ABD} \sim \triangle \mathrm{PQM}$ (By SAS similarity criterion)

$\Rightarrow \frac{\mathrm{AB}}{\mathrm{PQ}}=\frac{\mathrm{BD}}{\mathrm{QM}}=\frac{\mathrm{AD}}{\mathrm{PM}}$

Overview of Deleted Syllabus for CBSE Class 10 Maths Chapter 6 Triangles

Class 10 Maths Chapter 6: Exercises Breakdown

Conclusion

NCERT Solutions for Triangle Chapter Class 10 offers a clear and comprehensive understanding of triangle concepts. It makes studying simple and interesting by simplifying difficult subjects like the Pythagorean theorem, area computation, and trigonometric ratios.  It's crucial for students to focus on understanding fundamental concepts, such as triangle properties and different theorems. Practicing with the provided solutions and solving previous year question papers is essential for exam preparation. In previous year question papers, around 4-5 questions have been typically asked Ch 6 Class 10 Maths.

Other Study Material for CBSE Class 10 Maths Chapter 6

Chapter-Specific NCERT Solutions for Class 10 Maths

Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

NCERT Study Resources for Class 10 Maths

For complete preparation of Maths for CBSE Class 10 board exams, check out the following links for different study materials available at Vedantu.