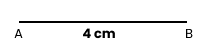
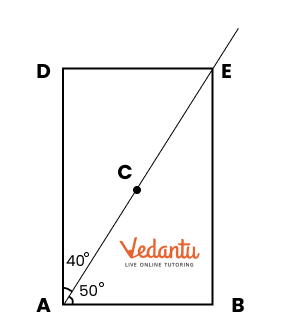
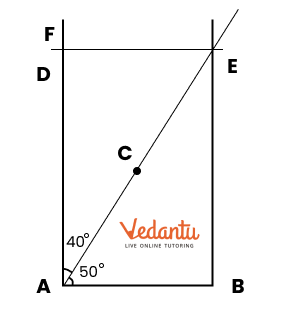
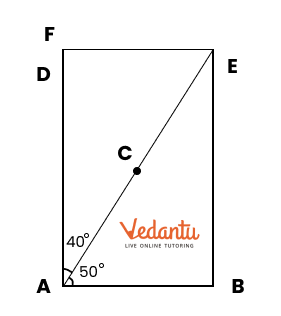
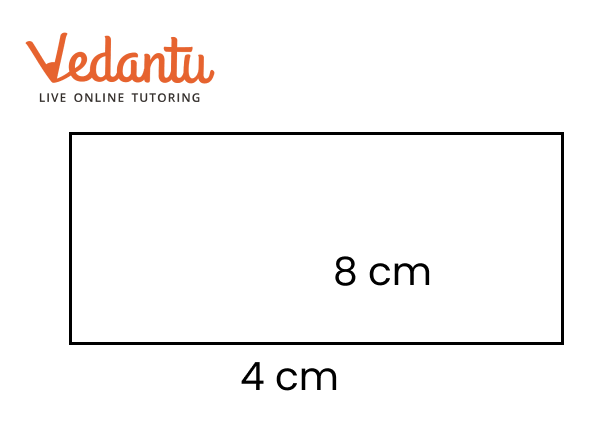
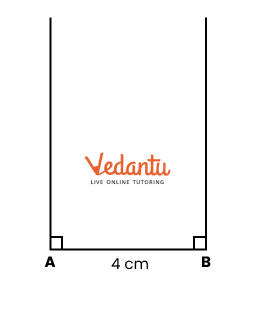
Playing With Constructions Class 6 PDF With Vedantu's Expert Guidance
FAQs on NCERT Solutions For Class 6 Maths Chapter 8 Playing With Constructions
1. What are the key steps to solve geometric construction problems in NCERT Solutions for Class 6 Maths Chapter 8?
To solve geometric construction problems in Class 6 Maths Chapter 8, students should:
- Read the problem carefully to understand which shapes and tools are required.
- Use a ruler for measuring and drawing straight lines accurately.
- Apply a compass for creating arcs and circles as instructed in each step.
- Employ a protractor to draw precise angles when specified in the question.
- Check measurements after each step to ensure correctness.
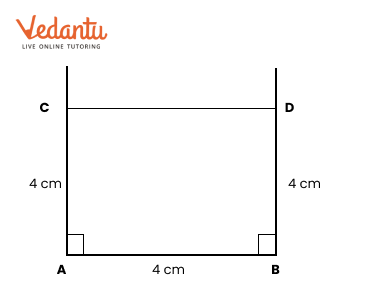
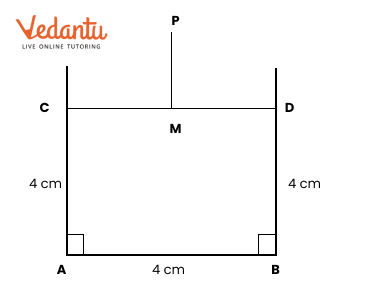
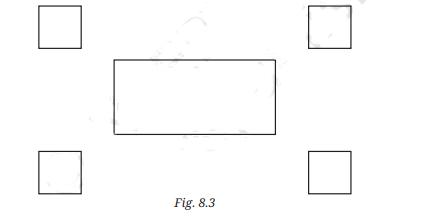
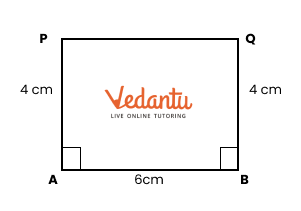
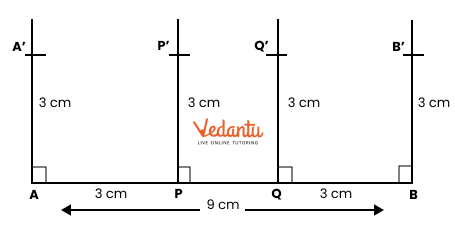
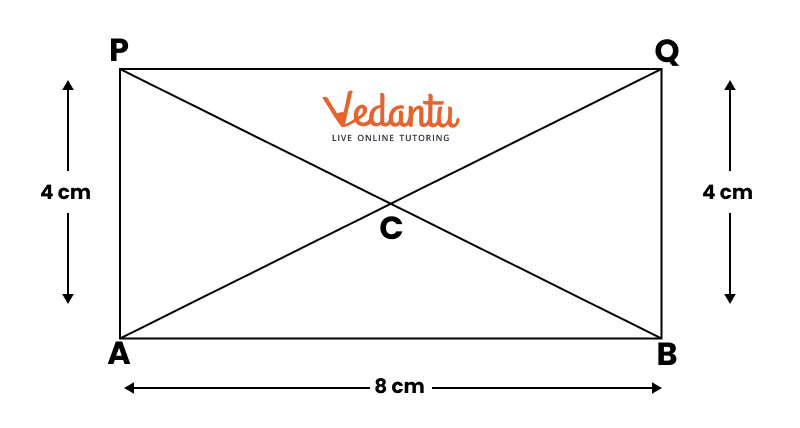
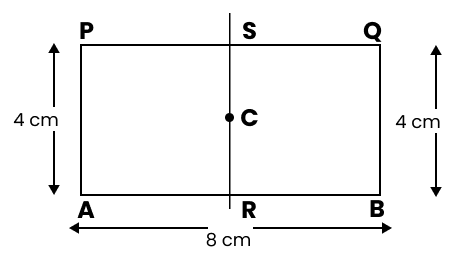
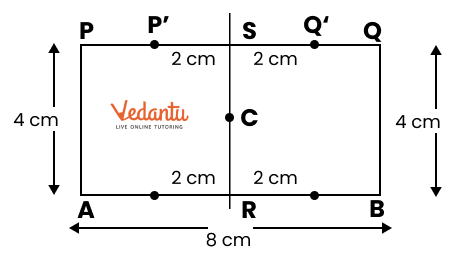
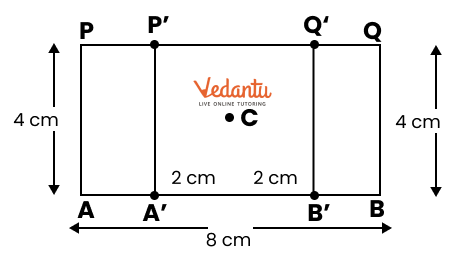
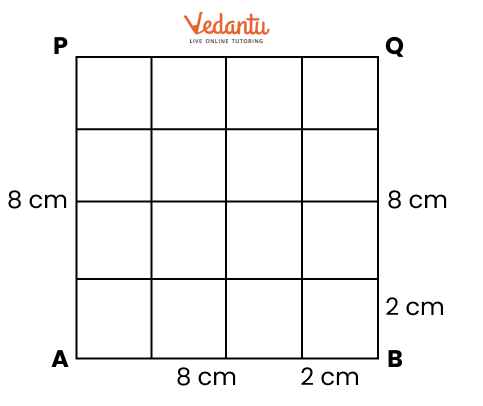
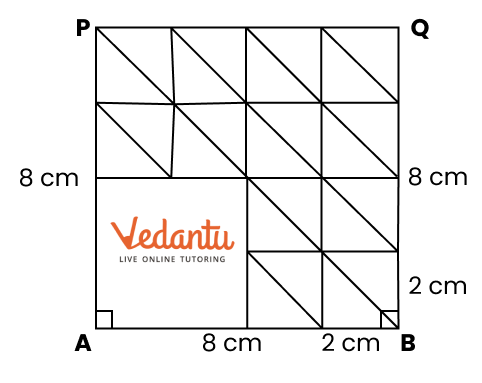
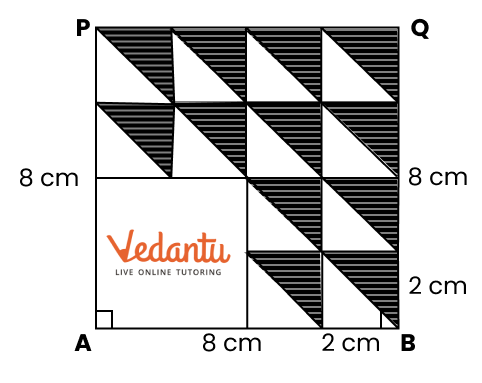
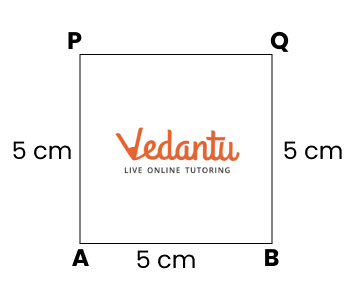
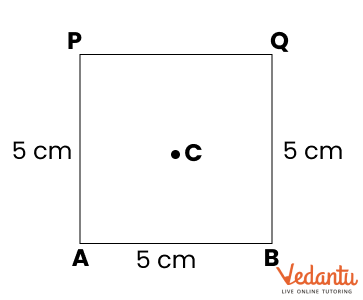
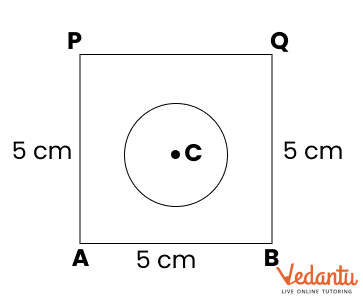
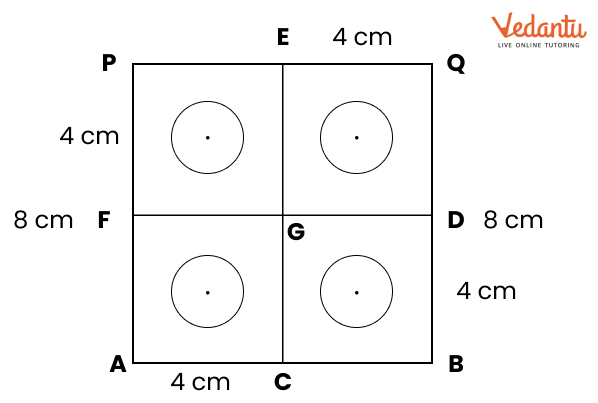
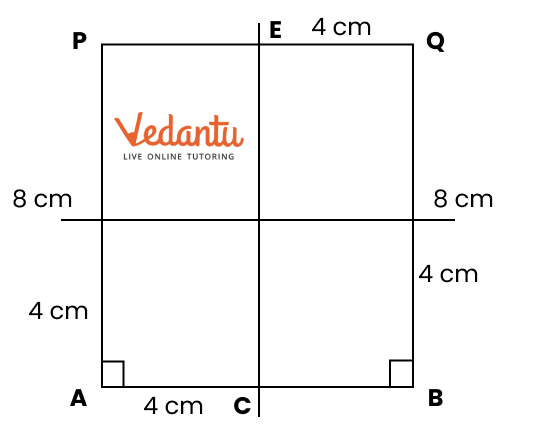
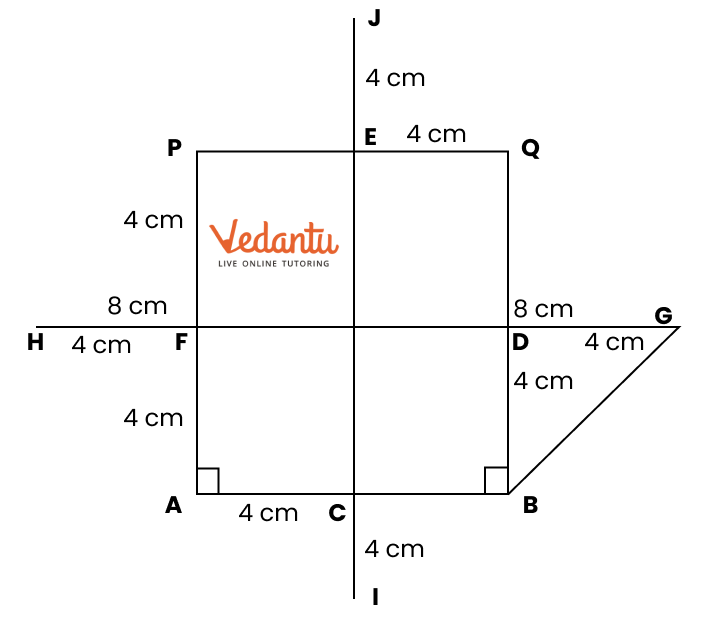
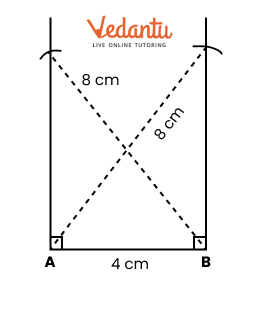
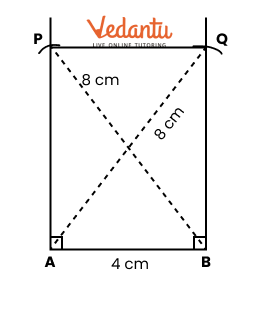
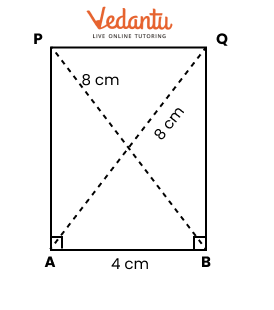
2. How do you construct a square inside a rectangle as per NCERT Solutions for Class 6 Maths Chapter 8?
To construct a square inside a rectangle, ensure the centre of the square aligns with the centre of the rectangle. Find the intersection point of the diagonals for the centre, determine the side of the inscribed square based on the rectangle’s dimensions, and use a ruler, compass, and protractor to mark and join corners, following the stepwise instructions from the official NCERT Solutions.
3. Why is a compass important in solving construction problems for Class 6 Maths Chapter 8?
A compass is essential in geometric construction because it allows students to:
- Draw precise circles and arcs required for various shapes.
- Measure and replicate lengths without needing a ruler for every step.
- Find equidistant points from given locations, which is often required in CBSE pattern construction problems.
4. What strategies can students use if they find a construction question challenging in Chapter 8?
If a construction question seems difficult, students should:
- Review the step-by-step NCERT Solutions for similar problems.
- Break the construction into smaller, manageable parts.
- Practice each construction skill separately—such as drawing perpendiculars or bisectors.
- Compare completed drawings with the official NCERT answer for accuracy.
5. What are common mistakes to avoid when solving NCERT Solutions for Class 6 Maths Chapter 8, ‘Playing with Constructions’?
Common mistakes include:
- Incorrect measurements, leading to inaccurate shapes.
- Using the wrong radius on the compass for arcs or circles.
- Not drawing perpendicular or parallel lines properly.
- Skipping steps, resulting in missing or incorrect elements in the figure.
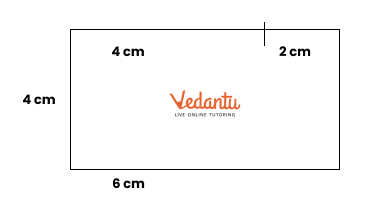
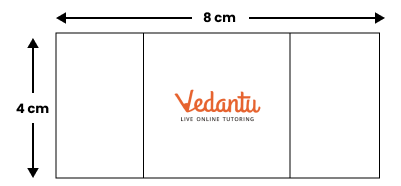
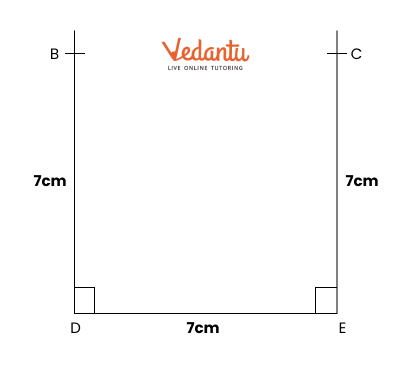
6. How does constructing rectangles and squares help understand their properties in Chapter 8?
Construction tasks allow students to physically observe the properties of rectangles and squares, such as equal sides, equal angles, and the relationship between diagonals. This hands-on approach, as promoted by NCERT Solutions, reinforces theoretical understanding through practice, which is crucial for CBSE exams.
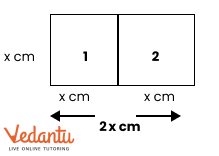
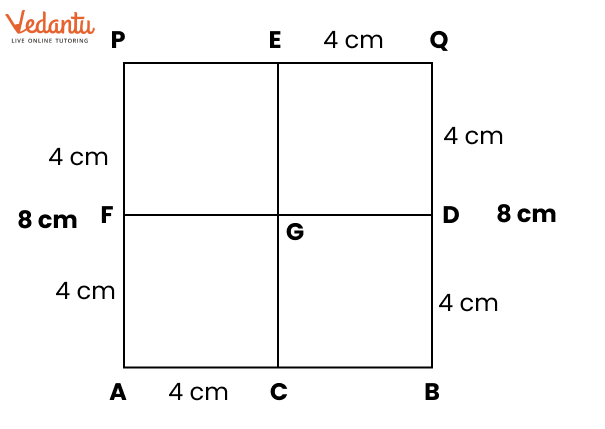
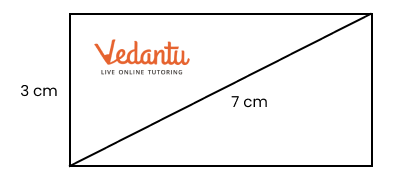
7. What if the side measurements do not allow division into identical squares—how should students answer according to the NCERT Solutions methodology?
When side measurements do not fit the criteria for dividing into identical squares, students should:
- Show calculations comparing sides with the required number of squares.
- State that division is not possible and explain with reasons based on the given dimensions.
8. Why is it important to verify right angles when drawing rectangles in NCERT Class 6 Maths Chapter 8?
Verifying right angles ensures the construction meets the defining properties of rectangles. Using a protractor guarantees each angle is exactly 90°, as required in the NCERT Solutions, which is a vital step for correctness in CBSE-formatted answers.
9. How do NCERT Solutions for Class 6 Maths Chapter 8 support learning geometry for future classes?
These solutions build foundational skills in geometric drawing, measuring, and reasoning. Consistent practice prepares students for advanced geometry topics in higher classes and ensures alignment with the CBSE syllabus progression.
10. What conceptual understanding about quadrilaterals can be gained through construction in Chapter 8 NCERT Solutions?
By constructing various quadrilaterals, students learn to distinguish between rectangles, squares, and rhombuses based on sides and angles. The exercises in Class 6 Maths Chapter 8 reinforce how properties translate into practical constructions, supporting deep conceptual mastery as expected by NCERT and CBSE.
11. Can all four-sided figures with equal sides be called squares as per Chapter 8 NCERT Solutions logic?
No, not all four-sided figures with equal sides are squares. According to NCERT Solutions, if all sides are equal but angles are not 90°, the figure is a rhombus, not a square. The construction exercises help students identify this distinction clearly.
12. How can students check the accuracy of their geometric constructions in Class 6 Maths Chapter 8?
Students can check accuracy by:
- Comparing completed diagrams with those in the NCERT Solutions
- Measuring sides and angles again using a ruler and protractor
- Ensuring the figure matches all requirements stated in the question
13. Why do NCERT Solutions for Class 6 Maths Chapter 8 use a stepwise format in construction answers?
A stepwise format ensures clarity, prevents missing details, and helps students logically sequence their actions. This aligns directly with CBSE answer expectations and aids in easy scoring for construction questions in the exam.
14. How does learning with NCERT Solutions for Chapter 8 improve spatial reasoning skills?
Practicing constructions develops the ability to visualize, analyze, and interpret geometric relationships in two dimensions. This spatial reasoning is essential for solving geometry problems not just in Class 6 but in higher maths as well.
15. What is the CBSE pattern for marking construction-based answers in Class 6 Maths Chapter 8?
CBSE typically awards marks for:
- Accurate, labelled diagrams
- Correct use of geometric tools
- Clear, logical explanation of each step
- Final figure matching question requirements