NCERT Exemplar for Class 10 Maths - Triangles - Free PDF Download
Multiple Choice Questions
Choose the correct answer from the given four options:
Sample Question 1: If in Fig, O is the point of intersection of two chords AB and CD such that OB = OD, then triangles OAC and ODB are
(A) equilateral but not similar
(B) isosceles but not similar
(C) equilateral and similar
(D) isosceles and similar
Ans: The correct option is (D) isosceles and similar
Given, O is the point of intersection of two chords AB and CD.
Also, OB = OD
We have to find the type of triangles OAC and ODB.
Chord Intersection theorem states that when two chords inside the circle intersect each other then the product of their segments are equal.
So, the product of segments,
OA × OB = OC × OD
So, OA = OC and OB = OD
In triangle OAC, the length of OA and OC are equal
So, the triangle is isosceles.
In triangle OBD, the length of OB and OD are equal
So, the triangle is isosceles.
By the property of similarity,
Similar triangles have congruent corresponding angles and the corresponding sides are in proportion.
From the given figure, Vertically opposite angles are equal.
So, ∠AOC = ∠BOD
Angles in the same segment are equal.
So,
∠OAC = ∠ODB
OA = OB = OC = OD = radius of the circle
It is clear that the corresponding sides and the corresponding angles are equal.
So, the triangles OAC and OBD are similar.
Therefore, the triangles OAC and OBD are isosceles and similar.
Sample Question 2: D and E are respectively the points on the sides AB and AC of a triangle ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE||BC. Then, length of DE (in cm) is
(A) 2.5
(B) 3
(C) 5
(D) 6
Ans: The correct option is (B) 3
Given, D and E are the points on the sides AB and AC of a triangle ABC.
The length of the segment
AD = 2 cm
BD = 3 cm
BC = 7.5 cm
Also, DE||BC
We have to find the length of DE.
Basic Proportionality Theorem (BPT) states that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
By using BPT,
$\dfrac{AE}{AC}=\dfrac{DE}{BC}=\dfrac{AD}{AB}$
So,
$\dfrac{AD}{AB}=\dfrac{DE}{BC}$
⇒AB = AD + BD = 2 + 3 = 5 cm
⇒$\dfrac{2}{5}$ = $\dfrac{DE}{7.5}$
On cross multiplication,
2(7.5) = (5)DE
⇒DE = $\dfrac{15}{5}$
⇒DE = 3 cm
Therefore, the length of DE is 3cm.
EXERCISE 6.1
Choose the correct answer from the given four options in the following questions:
1. In the given figure, if ∠BAC = 90° and AD⏊BC. Then,
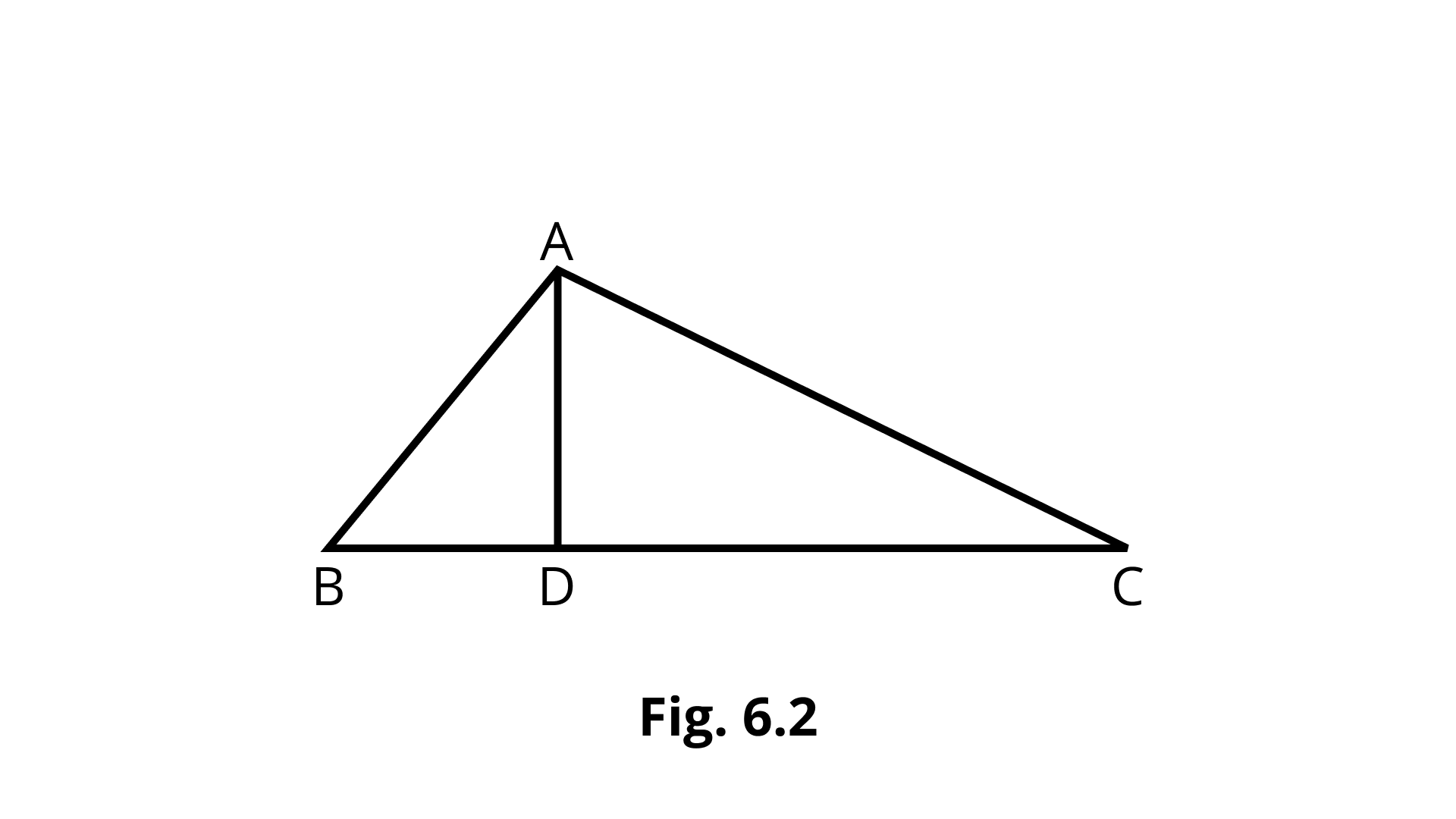
(A) BD.CD = AD2
(B) AB.AC = AD2
(C) BD.CD = AD2
(D) AB.AC = AD2
Ans: The correct option is (C): BD·CD = AD2
In ΔADB and ΔADC,
It is given that
∠BDA = ∠ADC = 90°
∠B = ∠DAC = (90°- C)
Now, by AA similarity criterion
$\triangle \mathrm{ADB} \sim \triangle \mathrm{CDA}$
$\Rightarrow \dfrac{A D}{C D}=\dfrac{A B}{C A}=\dfrac{D B}{D A}$
$\therefore \mathrm{AD}^{2}=\mathrm{BD} \cdot \mathrm{CD}$
2. The lengths of the diagonals of a rhombus are 16 cm and 12 cm. Then, the length of the side of the rhombus is
(A) 9 cm
(B) 10 cm
(C) 8 cm
(D) 20 cm
Ans: The correct option is (B) 10 cm.
Let us assume the length of the rhombus ABCD be a. Since the diagonals of rhombus bisect each other perpendicularly, so by Pythagoras theorem in ΔAOB
$a^{2}=\left(\dfrac{d_{1}}{2}\right)^{2}+\left(\dfrac{d_{2}}{2}\right)^{2}$
$=\left(\dfrac{12}{2}\right)^{2}+\left(\dfrac{16}{2}\right)^{2}$
⇒ a2 = (6)2 + (8)2
⇒ a2 = 36 + 64
⇒ a2 = 100
⇒ a = 10 cm
3. If ΔABC ~ ΔEDF and ΔABC are not similar to ΔDEF, then which of the following is not true?
(A) BC · EF = A C · FD
(B) AB · EF = AC · DE
(C) BC · DE = AB · EF
(D) BC · DE = AB · FD
Ans: The correct option is (C): BC · DE = AB · EF
It is given that,
ΔABC ~ ΔEDF
The corresponding sides in a triangle are proportional.
$\dfrac{A B}{E D}=\dfrac{A C}{E F}=\dfrac{B C}{D F}$
Hence, every statement other than (C) is correct.
4. If in two triangles ABC and PQR,
$\dfrac{A B}{Q R}=\dfrac{B C}{P R}=\dfrac{C A}{P Q}$ , then
(a) ΔCAB ~ ΔPQR
(b) ΔABC ~ ΔPQR
(c) ΔCBA ~ ΔPQR
(d) ΔBCA ~ ΔPQR
Ans: The correct option is (a) ΔCAB ~ ΔPQR
As from the given question it can be seen that vertex C is in correspondence with vertex P, vertex A is in correspondence with vertex Q and also vertex B is in correspondence with vertex R.
Therefore, it can be said that;
ΔCAB ~ ΔPQR.
Therefore, (a) is the right answer.
5. In the given figure, two line segments AC and BD intersect each other at P such that PA = 6cm, PB = 3cm, PC = 2.5 cm, PD = 5 cm, ∠APB = 50° and ∠CDP = 30°, then ∠PBA is equal to
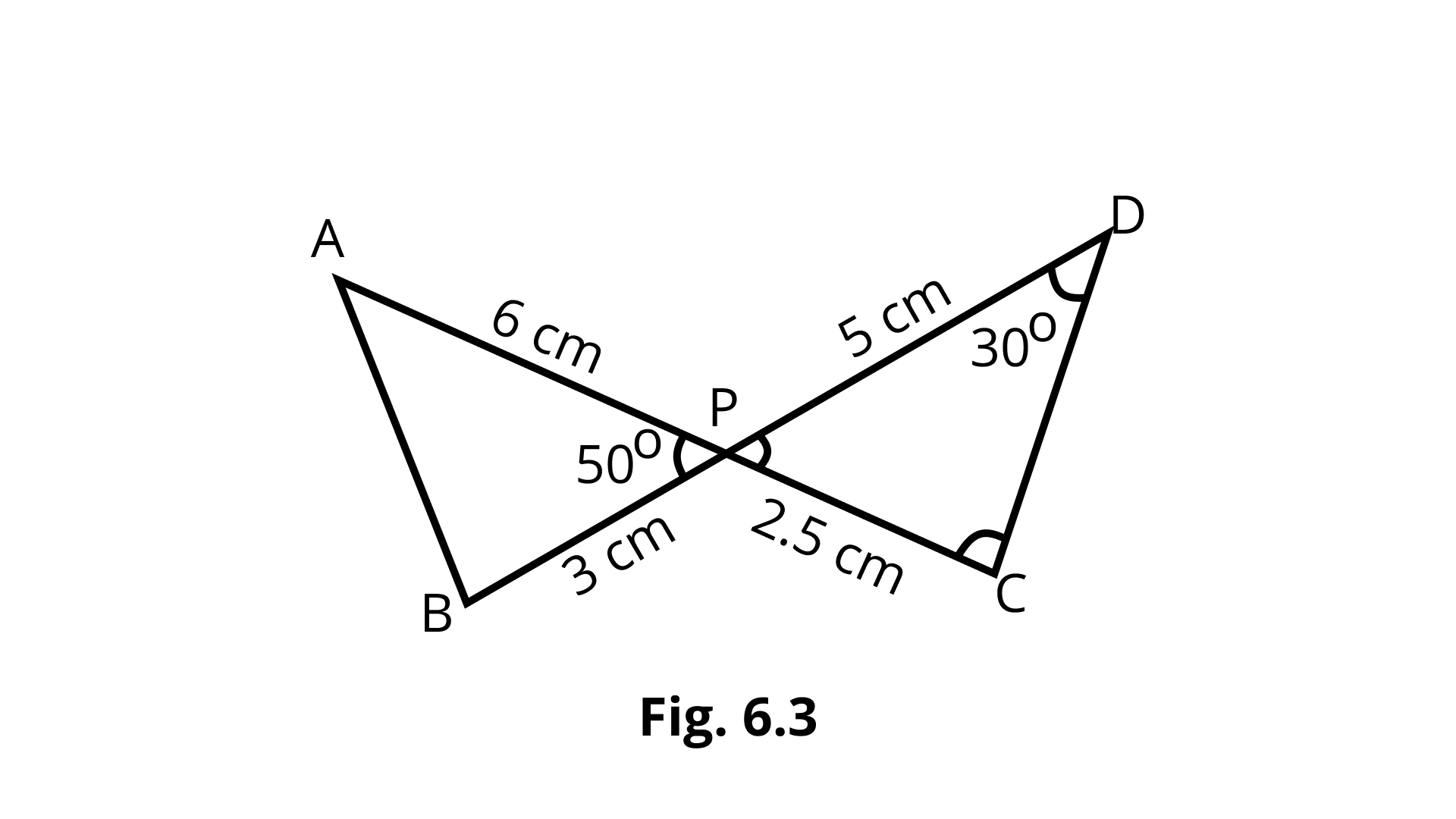
(a) 50°
(b) 30°
(c) 60°
(d) 100°
Ans: The correct option is (d): 100°
Let us consider $\triangle \mathrm{APB}$ and $\triangle \mathrm{DPC}$,
$\dfrac{P A}{P C}=\dfrac{6.0}{2.5}=\dfrac{12}{5}$
$\dfrac{P B}{P D}=\dfrac{3}{5} \neq \dfrac{P A}{P C}$
So now,
$\dfrac{P A}{P D}=\dfrac{6}{5}$
$\dfrac{P B}{P C}=\dfrac{3.0}{2.5}=\dfrac{6}{5}$
$\Rightarrow \dfrac{P A}{P D}=\dfrac{P B}{P C}$
∠APB = ∠CPD = 50° (Vertically opposite ∠s of Δs)
∴ ΔAPB ~ ΔDPC (By SAS similarity rule)
∠PBA = ∠PCD ( Since Corresponding ∠s of similar Δs are equal)
In ΔDPC, ∠DPC = ∠APB = 50° (Vertically opposite ∠s) ∠D = 30°
∴ ∠PCD = ∠C = 180° – 50° – 30° = 180 – 80° = 100°
⇒ ∠PBA = 100°
This shows that option (d) is correct.
6. If in two triangles DEF and PQR, ∠D = ∠Q and ∠R = ∠E, then which of the following is not true?
(A) $\dfrac{E F}{P R}=\dfrac{D F}{P Q}$
(B) $\dfrac{D E}{P Q}=\dfrac{E F}{R P}$
(C) $\dfrac{D E}{Q R}=\dfrac{D F}{P Q}$
(D) $\dfrac{E F}{R P}=\dfrac{D E}{Q R}$
Ans: Option B is the correct answer.
In ΔDEF and ΔPQR,
It is given that,
$\angle D =\angle Q$
$\angle E =\angle R$
$\therefore \angle F=\angle P$
$\therefore \triangle \mathrm{DEF} \sim \Delta \mathrm{QRP}$
$\therefore \dfrac{D E}{Q R}=\dfrac{D F}{Q P}=\dfrac{E F}{R P}$
Therefore, option B will not be true.
7. In ΔABC and ΔDEF, ∠B = ∠E, ∠F = ∠C and AB = 3DE. Then, the two triangles are
(a) congruent but not similar
(b) similar but not congruent
(c) neither congruent nor similar
(d) congruent as well as similar
Ans: The correct option is (b)similar but not congruent
In ΔABC and ΔDEF,
It is given that,
∠B=∠E
∠C=∠F
Therefore, by the AA similarity rule
ΔABC ~ ΔDEF
So, now AB and DE sides are corresponding sides.
But, AB = 3DE (Given)
So, ΔABC is not congruent to ΔDEF.
Hence, Δs are similar but not congruent.
8. It is given that $\triangle \mathrm{ABC} \sim \Delta \mathrm{PQR}$, with $\dfrac{B C}{Q R}=\dfrac{1}{3}$. Then $\dfrac{\operatorname{ar}(\Delta P R Q)}{\operatorname{ar}(\Delta B C A)}$ is equal to
(a) 9
(b) 3
(c) $\dfrac{1}{3}$
(d) $\dfrac{1}{9}$
Ans: The correct option is (a) 9
Since, $\triangle \mathrm{ABC} \sim \triangle \mathrm{PQR}$
$\therefore \dfrac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta P Q R)}=\dfrac{B C^{2}}{Q R^{2}}=\left(\dfrac{1}{3}\right)^{2}=\dfrac{1}{9} \quad$ (By area theorem)
Or it can be written as
$=\dfrac{\operatorname{ar}(\Delta P Q R)}{\operatorname{ar}(\Delta A B C)}=\dfrac{9}{1}$
Therefore, option A will be the correct choice.
9. It is given that ΔABC ~ ΔDFE, ∠A = 30°, ∠C = 50°, AB = 5 cm, AC = 8cm and DF = 7.5 cm, then which of the following is true?
(a) DE = 12 cm, F = 50°
(b) DE = 12 cm, F = 100°
(c) EF = 12 cm, D = 100°
(d) EF = 12, cm D = 30°
Ans: The correct option is (b): DE = 12 cm, F = 100°
Since, it is given that
ΔABC ~ ΔDFE
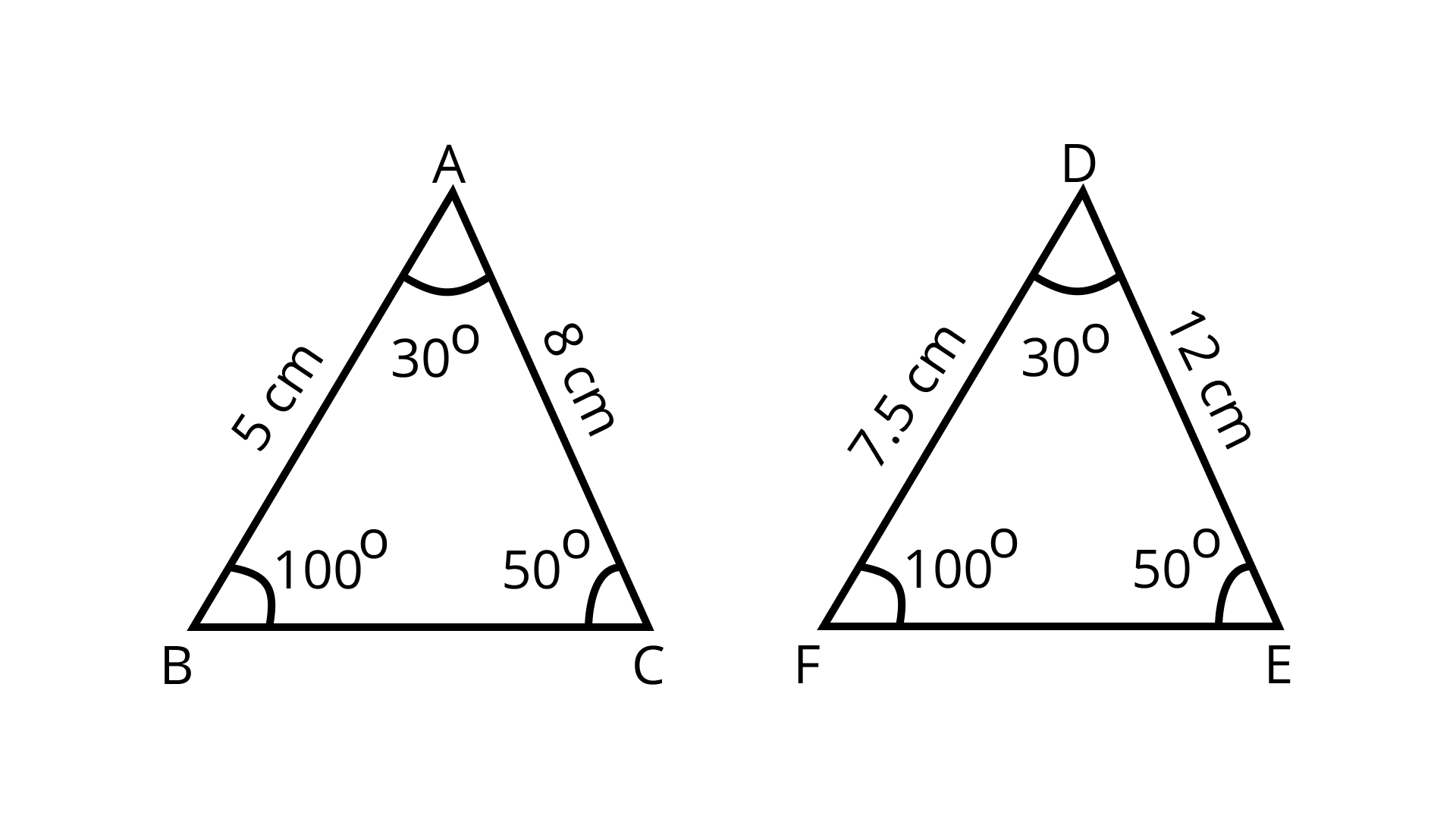
$\therefore \dfrac{A B}{D F}=\dfrac{A C}{D E}=\dfrac{B C}{F E}$
$\Rightarrow \dfrac{5}{7.5}=\dfrac{8}{D E}=\dfrac{B C}{E F}$
$\Rightarrow D E=\dfrac{8 \times 7.5}{5}=12 \mathrm{~cm}$
Now, ∠A = ∠D = 30°
∠B = ∠F = 180° – 30° – 50° = 100°
∠C = ∠E = 50°
∴ this proves that the option (b) is correct.
10. If in $\triangle \mathrm{ABC}$ and $\Delta \mathrm{DEF}, \dfrac{A B}{D E}=\dfrac{B C}{F D}$, then they will be similar, when
(a) $\angle B=\angle E$
(b) $\angle A=\angle D$
(c) $\angle B=\angle D$
(d) $\angle \mathrm{A}=\angle \mathrm{F}$
Ans: The correct option is (c) $\angle B=\angle D$
In $\triangle \mathrm{ABC}$ and $\triangle \mathrm{DEF}$,
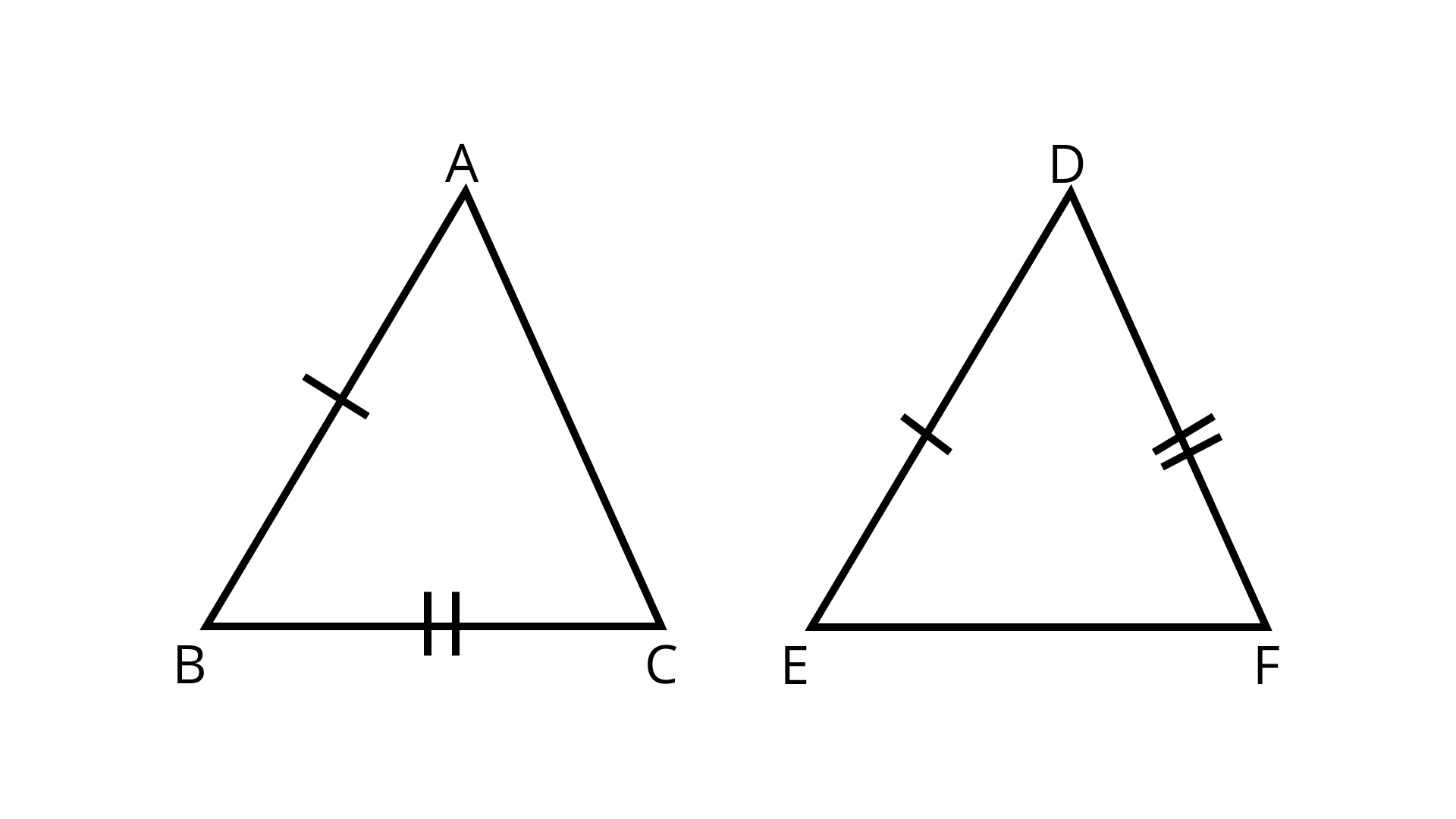
$\dfrac{A B}{D E}=\dfrac{B C}{F D}$
angle formed by $A B$ and $B C=\angle B$.
angle formed by $D E$ and $F D=\angle D$.
So, ∠B = ∠D
∴ by SAS similarity rule
ΔABC ~ ΔEDF
So, option (c) is the correct answer.
11. If $\triangle \mathrm{ABC} \sim \Delta \mathrm{QRP}, \dfrac{\operatorname{ar}(\Delta \mathrm{ABC})}{\operatorname{ar}(\Delta P Q R)}=\dfrac{9}{4}, \mathrm{AB}=18 \mathrm{~cm}$, and $\mathrm{BC}=15 \mathrm{~cm}$, then $\mathrm{PR}$ is equal to
(a) $10 \mathrm{~cm}$
(b) $12 \mathrm{~cm}$
(c) $\dfrac{20}{3} \mathrm{~cm}$
(d) $8 \mathrm{~cm}$
Ans: The correct option is (a): $10 \mathrm{~cm}$
It is given that
$\triangle \mathrm{ABC} \sim \triangle \mathrm{QRP}$ $\therefore \dfrac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta P Q R)}=\dfrac{B C^{2}}{R P^{2}}=\dfrac{A B^{2}}{Q R^{2}}$
$\dfrac{9}{4}=\dfrac{15^{2}}{R P^{2}}=\dfrac{18^{2}}{Q R^{2}}$
$\Rightarrow RP^{2}=\dfrac{15 \times 15 \times 4}{9}$
$\Rightarrow \operatorname{RP}^2=100 \Rightarrow \mathrm{RP}=10 \mathrm{~cm}$
Hence, verifies the option (a).
12. If S is a point on side PQ, of a ΔPQR such that PS = SQ = RS, then
(a) $\mathrm{PR} \cdot \mathrm{QR}=\mathrm{RS}^{2}$
(b) $Q S^{2}+R S^{2}=Q R^{2}$
(c) $\mathrm{PR}^{2}+\mathrm{QR}^{2}=\mathrm{PQ}^{2}$
(d) $\mathrm{PS}^{2}+\mathrm{RS}^{2}=\mathrm{PR}^{2}$
Ans: The correct option is (c).
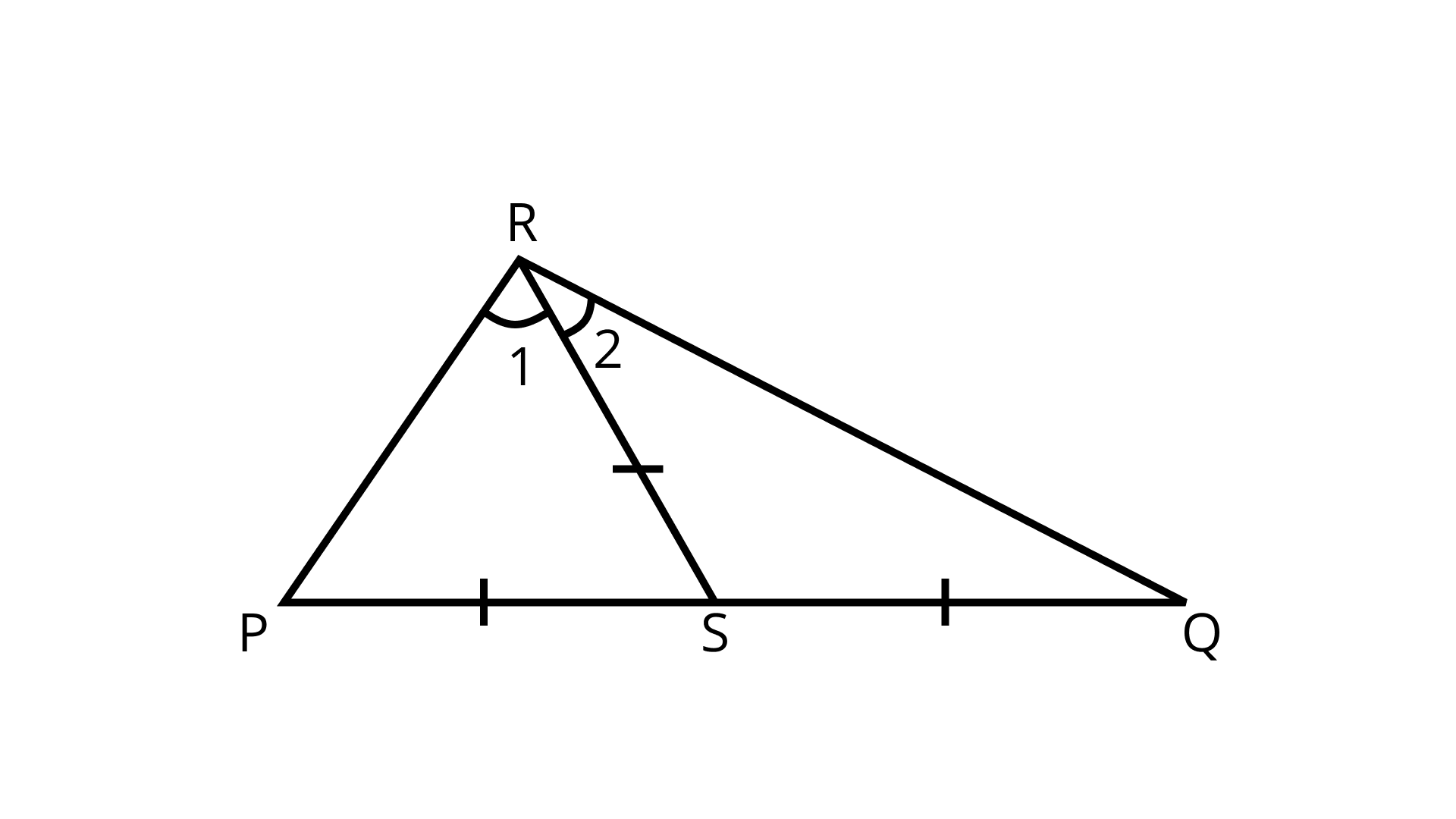
In ΔPQR,
PS = SQ = RS ( given )
Now, in ΔPSR,
PS = SR ( given )
∴ ∠1 = ∠P (Angles opposite to equal sides in a triangle are equal)
Similarly, in ∠SRQ,
RS = SQ (given)
∠Q = ∠2
Now, in ΔPQR,
∠P + ∠Q + ∠PRQ = 180° (By Angle sum property of a triangle)
⇒ ∠1 + ∠2 + (∠1 + ∠2) = 180°
⇒ 2(∠1 + ∠2) = 180°
⇒ ∠1 + ∠2 = 90°
⇒ ∠PRQ = 90°
By Pythagoras theorem,
we have PQ2 = PR2 + RQ2
This proves that the option (c) is correct.
(C) Short Answer Questions with Reasoning
Sample Question 1: In ABC, AB = 24 cm, BC = 10 cm and AC = 26 cm. Is this triangle a right triangle? Give reasons for your answer.
Ans: Here AB2 = 576, BC2= 100 and AC2= 676.
Therefore, AC2=AB2+BC2
So, the given triangle is a right triangle.
Sample Question 2: P and Q are the points on the sides DE and DF of a triangle DEF such that DP = 5 cm, DE = 15 cm, DQ= 6 cm and QF = 18 cm. Is PQ∥EF? Give reasons for your answer.
Ans: Here,
$\dfrac{DP}{PE}=\dfrac{5}{15-5}=\dfrac{1}{2}$ and $\dfrac{DQ}{QF}=\dfrac{6}{18}=\dfrac{1}{3}$
As we can see that
$\dfrac{DP}{PE} \ne \dfrac{DQ}{QF}$
Therefore, PQ is not parallel to EF.
Sample Question 3: It is given that FED ∽ STU . Is it true to say that $\dfrac{DE}{ST}=\dfrac{EF}{TU}$? Why?
Ans:
No, as the correct correspondence is F↔S, E↔T, D↔U. With this correspondence,
$\dfrac{EF}{ST}=\dfrac{DE}{TU}$
EXERCISE 6.2
1. Is the triangle with sides 25 cm, 5 cm, and 24 cm a right triangle? Give reasons for your answer.
Ans: False.
Reason:- Square of longest side = (25)2 = 625..........(i)
Now, the sum of the squares of other two sides = (5)2 + (24)2 = 25 + 576 = 601.............(ii)
From (i) and (ii) we see that
(25)2 ≠ (5)2 + (24)2
By converse of Pythagoras theorem,
this Δ will be right angle triangle if
(25)2 = (5)2 + (24)2
So, the given triangle is not right angled.
2. It is given that ΔDEF ~ ΔRPQ. Is it true to say that ∠D = ∠R and ∠F = ∠P? Why?
Ans: False.
When ΔDEF ~ ΔRPQ,
Since each angle of a triangle is equal to the corresponding angle of a similar triangle so
∠D = ∠R
∠E = ∠P
∠F = ∠Q
So, ∠D = ∠R is true
but ∠F ≠ ∠P.
Hence, it is not true that ∠F = ∠P.
3. A and B are respectively the points on the sides PQ and PR of a ΔPQR such that PQ = 12.5 cm, PA = 5 cm, BR = 6 cm, and PB = 4 cm. Is AB || QR? Give reasons for your answer.
Ans: True.
By converse of BPT, AB will be parallel to QR if AB, divides PQ and PR in the same ratio i.e.,
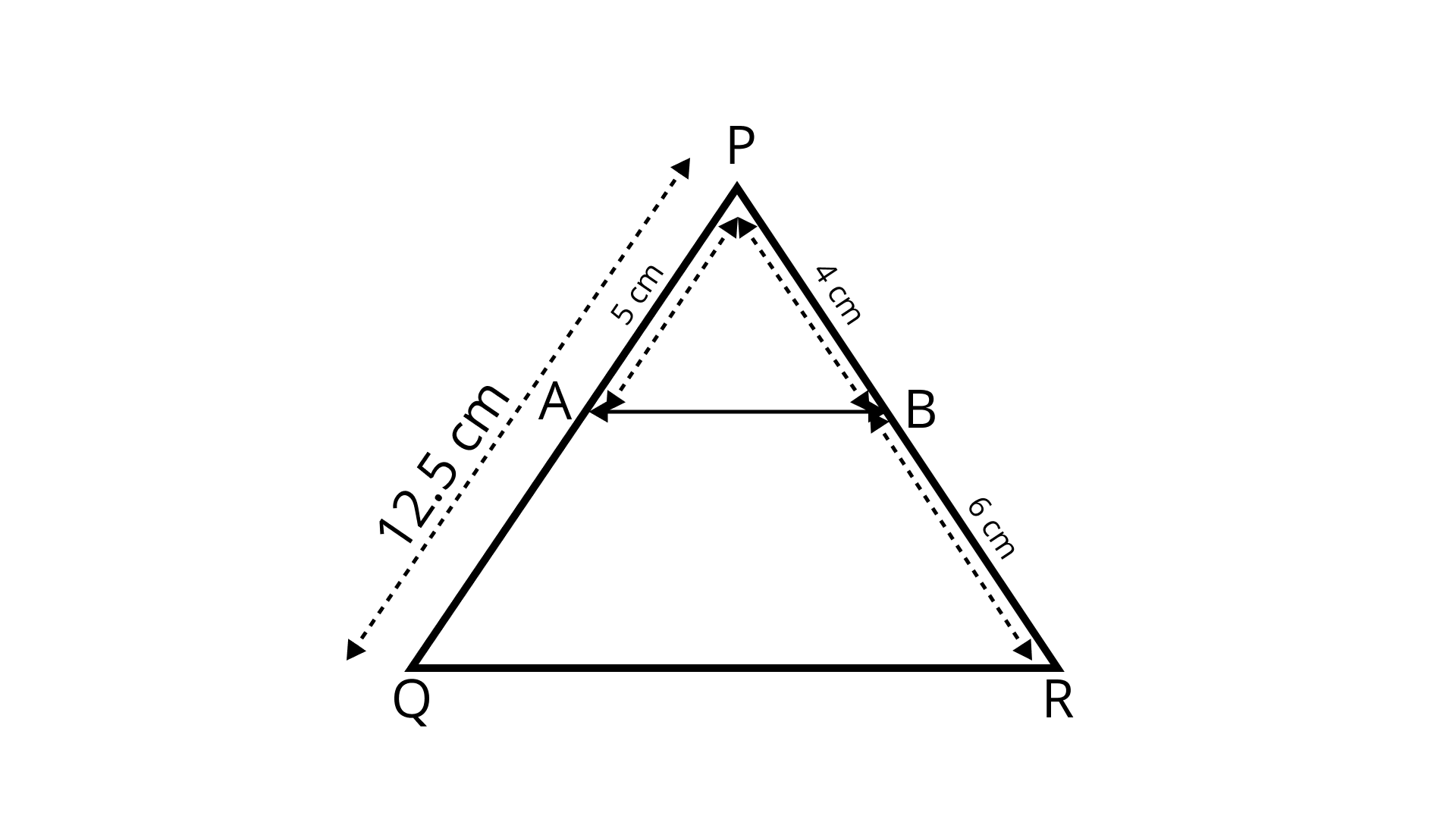
$\dfrac{A P}{A Q}=\dfrac{P B}{B R}$
$\Rightarrow \dfrac{5}{12.5-5}=\dfrac{4}{6}$
$\Rightarrow \dfrac{5.0}{7.5}=\dfrac{2}{3}$
$\text { or } \dfrac{2}{3}=\dfrac{2}{3}$
So, AB is parallel to QR. Hence, the given statement AB || QR is true.
4. In the given figure, BD and CE intersect each other at P. Is ΔPBC ~ ΔPDE? Why?
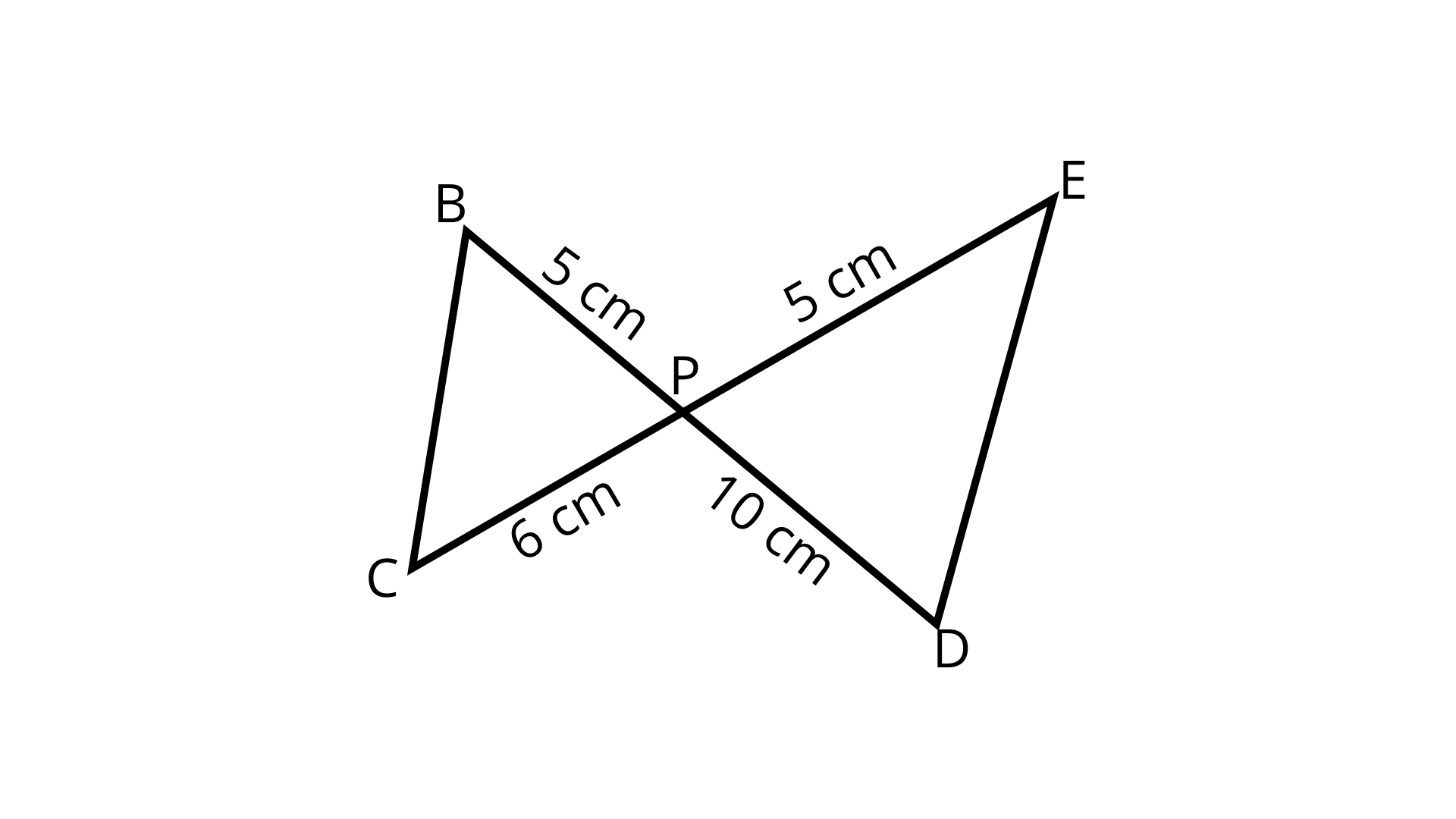
Ans: True.
In ΔPBC and ΔPDE, we have
∠BPC = ∠DPE (Vertically opposite angles)
$\dfrac{B P}{P D}=\dfrac{5}{10}=\dfrac{1}{2}$
$\dfrac{P C}{P E}=\dfrac{6}{12}=\dfrac{1}{2}$
$\therefore \dfrac{B P}{P D}=\dfrac{P C}{P E}$, (By SAS similarity criterion)
$\triangle \mathrm{BPC} \sim \triangle \mathrm{DPE}$
Hence, the given statement is CORRECT.
5. In ΔPQR and ΔMST, ∠P = 55°, ∠Q = 25°, ∠M = 100°, ∠S = 25°. Is ΔQPR ~ ΔTSM? Why?
Ans: False
ΔQPR and ΔTSM will be similar only if the corresponding angles of the triangles are equal.
∠Q = 25°
∠P = 55°
⇒ ∠R = 180° – (25° + 55°) =180° – 80°
⇒ ∠R = 100° ∠S = 25° ∠M = 100°
⇒ ∠T = 180° – (100° + 25°) = 55°
∴ ∠Q ≠ ∠T
∠P ≠ ∠S Since corresponding angles are not equal.
So, ΔQPR is not similar to ΔTSM.
Hence, the given statement ΔQPR ~ ΔTSM is FALSE.
6. Is the following statement true? Why? “Why quadrilaterals are similar if their corresponding angles are equal”.
Ans: False: Two quadrilaterals will be similar if their corresponding angles, as well as the ratio of sides, are also equal. So, the given statements are false.
For example, rectangles and squares.
7. Two sides and the perimeter of one triangle are respectively three times the corresponding sides and the perimeter of the other triangle. Are the two triangles similar? Why?
Ans: True
Let the two sides of ΔABC be
AB = 3cm
AC = 4 cm
Perimeter(AB + BC + AC) = 13 cm
Then,
BC = 13 – 7 = 6 cm.
Now according to the question,
the sides of another ΔDEF are
DE = 3 × 3 = 9
DF = 3 × 4 = 12, and
DE + DF + EF = 3 × 13 = 39
So, EF = 39 – 12 – 9 = 18
$\therefore \dfrac{D E}{A B}=\dfrac{9}{3}=\dfrac{3}{1}$
$\dfrac{D F}{A C}=\dfrac{12}{4}=\dfrac{3}{1}$
$\dfrac{E F}{B C}=\dfrac{18}{6}=\dfrac{3}{1}$
$\therefore \dfrac{D E}{A B}=\dfrac{D F}{A C}=\dfrac{E F}{B C}=\dfrac{3}{1}$
As the ratio of corresponding sides in two Δs are same
then by SSS similarity rule
ΔDEF ~ ΔABC
Hence, the triangles are similar and the given statement is correct.
8. If in two right triangles, one of the acute angles of one triangle is equal to an acute angle of the other triangle, can you say that two triangles will be similar? Why?
Ans: True
In ΔABC and ΔPQR,
∠B = ∠Q = 90° (Given)
∠C = ∠R (Given)
∴ ΔABC ~ ΔPQR (By AA similarity criterion)
Hence, the statement that two triangles are similar is true.
9. The ratio of the corresponding altitudes of two similar triangles is $\dfrac{3}{5}$. Is it correct to say that the ratio of their areas is $\dfrac{6}{5}$? Why?
Ans: False.
If two triangles are similar, then the ratio of areas of two triangles will be equal to the square of the ratio of their corresponding sides or altitudes or angle bisectors.
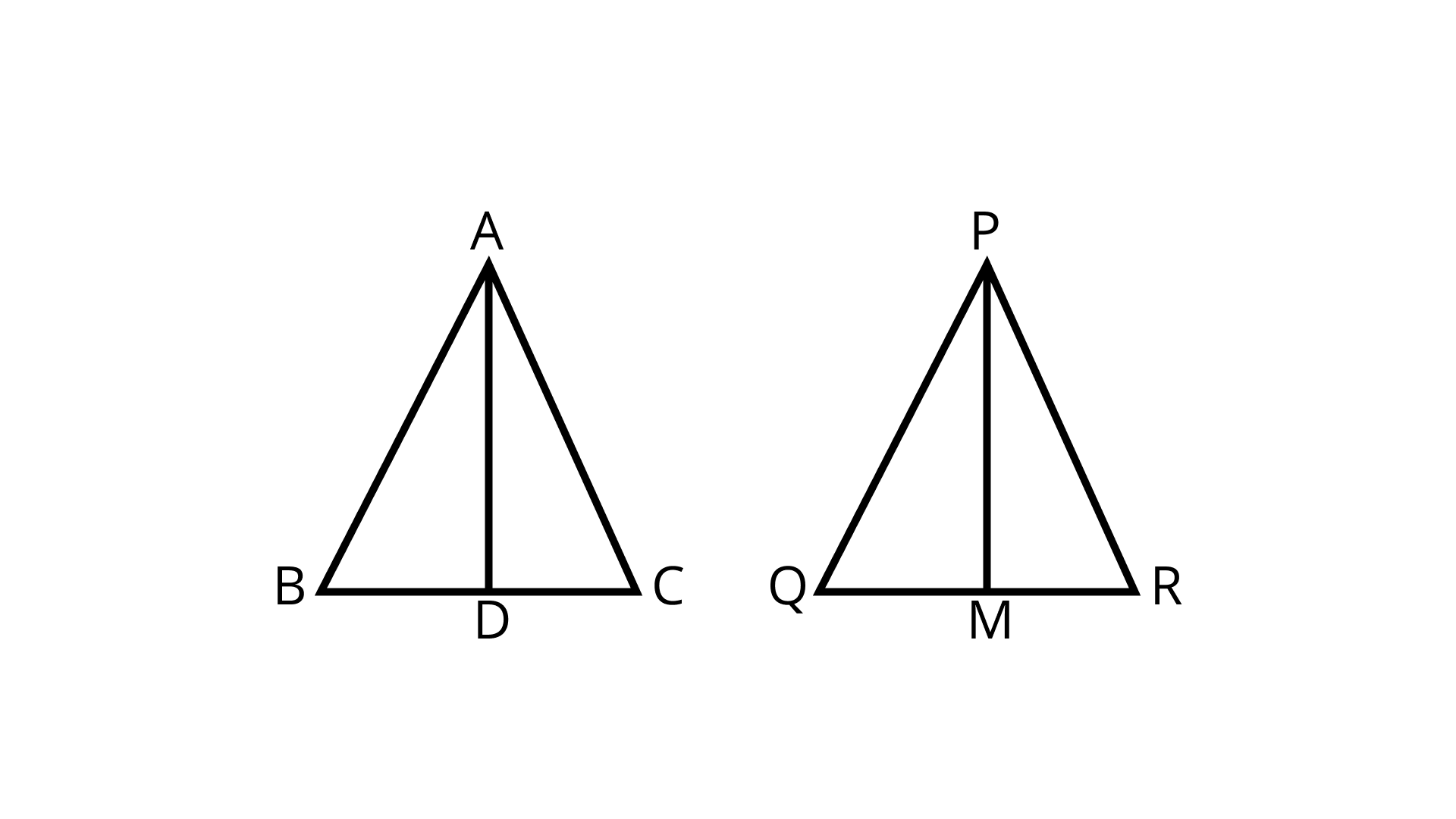
So, If ΔABC ~ ΔPQR,
Then, by area theorem
$\dfrac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta P Q R)}=\left(\dfrac{A D}{P M}\right)^{2}$
$\dfrac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta P Q R)}=\left(\dfrac{3}{5}\right)^{2}$
$\Rightarrow \dfrac{9}{25} \neq \dfrac{6}{5}$
So, the given statement is false.
10. D is the point on side QR of ΔPQR such that PD丄QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
Ans: False
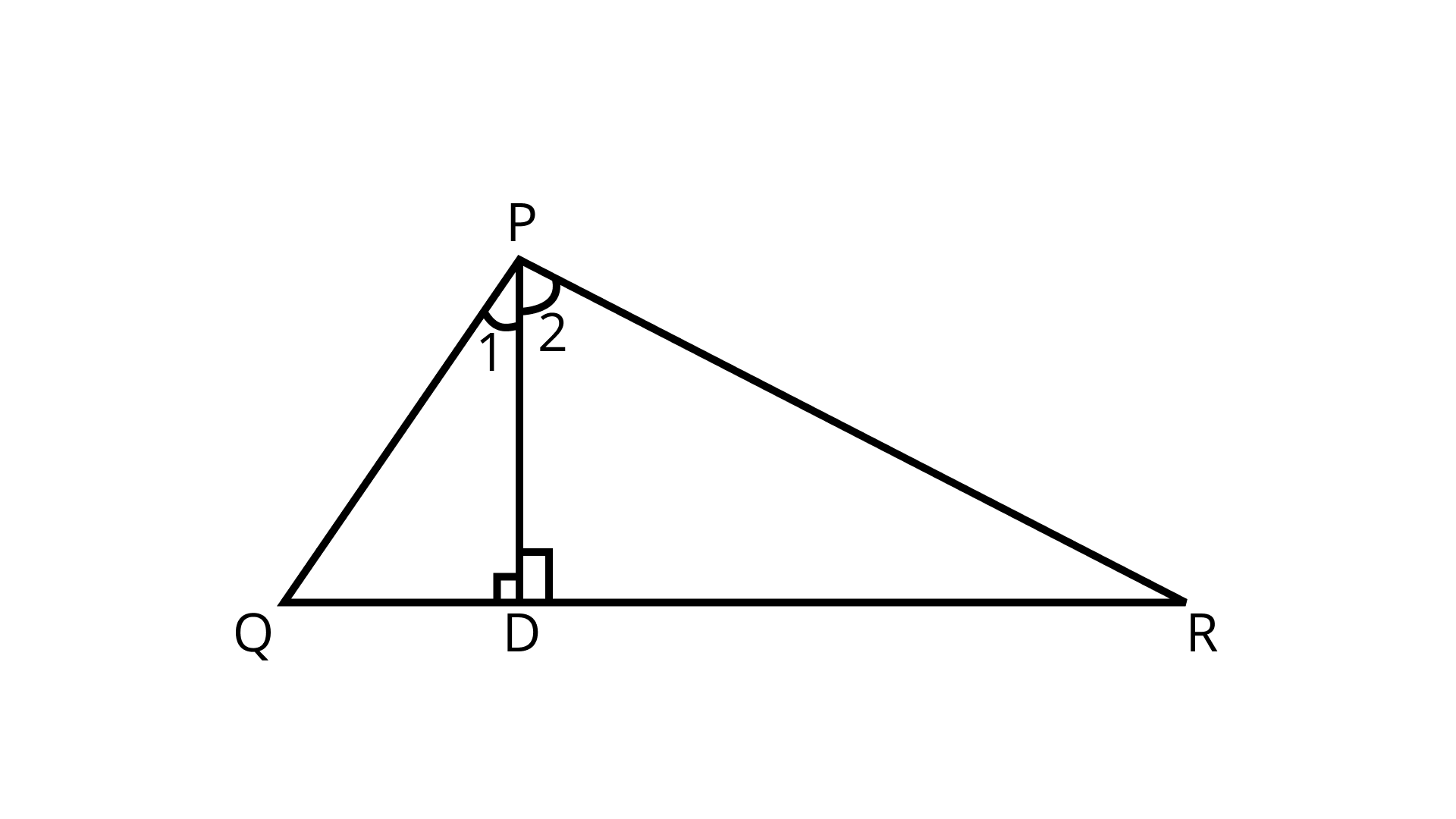
In ΔPDQ and ΔPDR
PD⊥QR (Given)
∴ ∠PDQ = ∠PDR = 90°
PD does not bisect ∠P.
∴ ∠1 ≠ ∠2
∠1 ≠ ∠R
∠Q ≠ ∠2
∠Q ≠ ∠R (PQ ≠ PR) Any ratio of sides is also not equal.
So, ΔPQD is not similar to ΔRPD. Hence, the given statement is false.
11. In the given figure, ∠D = ∠C, then is it true that ΔADE ~ ΔACB? Why?
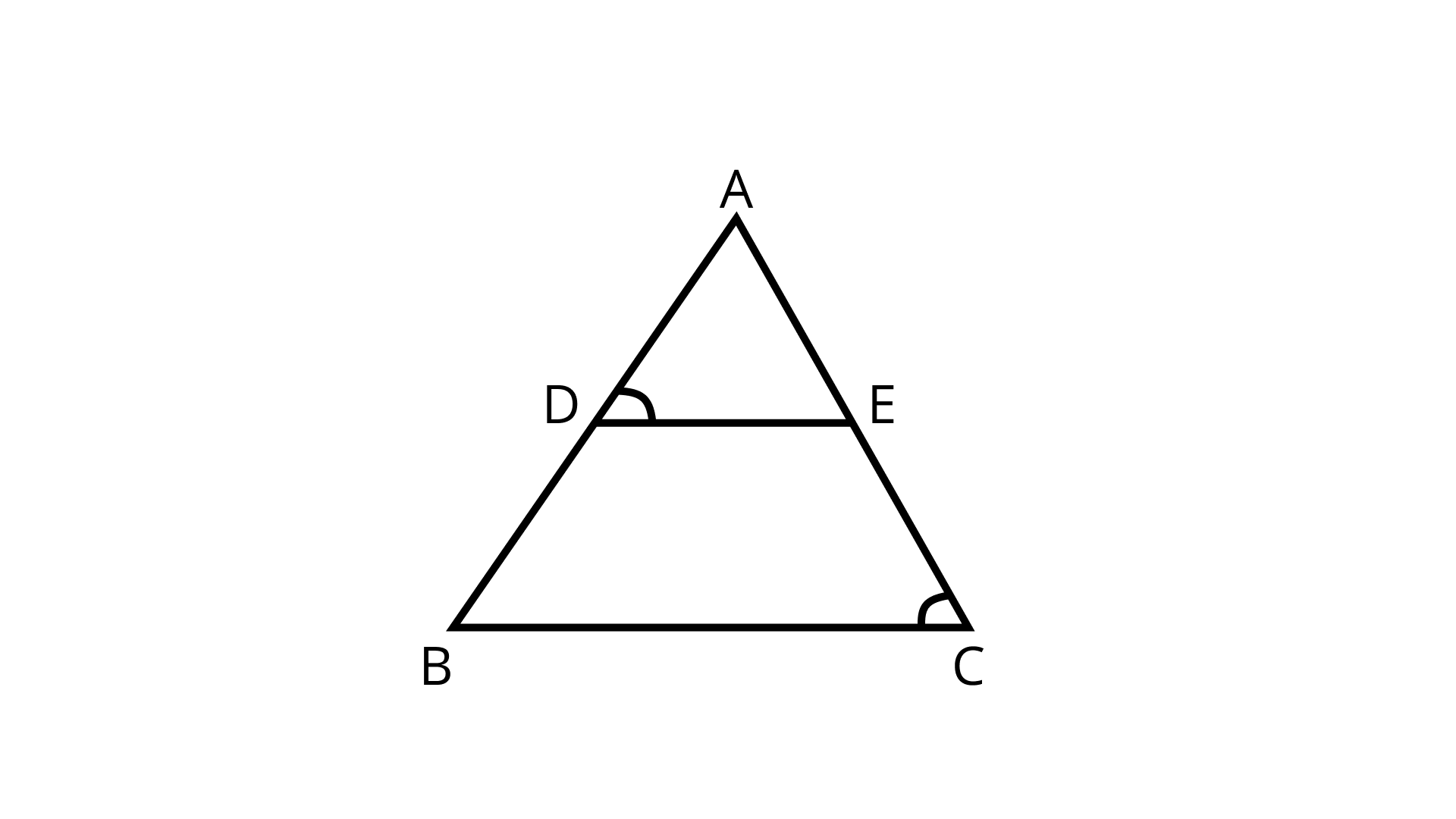
Ans: True.
In ΔADE and ΔABC,
∠D = ∠C (Given)
∠A = ∠A (Common)
∴ ΔADE ~ ΔACB (By AA similarity criterion)
12. Is it true to say that if in two triangles, an angle of one triangle is equal to an angle of another triangle and two sides of one triangle are proportional to the two sides of the other triangle, then triangles are similar? Give reasons for your answer.
Ans: False.
Reason: Here, an angle of one triangle is equal to an angle of another triangle and, two sides of one triangle are proportional to the two sides of the other triangle, even then the triangles are not similar because the sides include these angles must be proportional. So, triangles are not similar. Hence, the given statement is false.
(D) Short Answer Questions
Sample Question 1: Legs (sides other than the hypotenuse) of a right triangle are of lengths 16cm and 8 cm. Find the length of the side of the largest square that can be inscribed in the triangle.
Ans: Let ABC be a right triangle right angled at B with AB = 16 cm and BC = 8 cm. Then, the largest square BRSP which can be inscribed in this triangle will be as shown in the fig.
Let PB=x cm.
So, AP=(16−x)cm.
Now, in △APS and △ABC,
∠APS=∠ABC (Each 90°❳
△APS ∽ △ABC (by AA similarity rule)
Therefore,
$\dfrac{AP}{AB}=\dfrac{PS}{BC}$
$\Rightarrow \dfrac{16-x}{16}=\dfrac{x}{8}$
$\Rightarrow 128-8x=16x$
$\Rightarrow x=\dfrac{128}{24}=\dfrac{16}{3}$
Thus, the length of the required square is of $\dfrac{16}{3}$ cm.
Sample Question 2: Hypotenuse of a right triangle is 25 cm and out of the remaining two sides, one is longer than the other by 5 cm. Find the lengths of the other two sides.
Ans: Let one side be x cm. Then the other side will be (x + 5) cm.
Therefore, by Pythagoras Theorem
${x}^{2}+{(x+5)}^{2}={25}^{2}$
$\Rightarrow {x}^{2}+5{x}-300=0$
$\Rightarrow {x}^{2}+20{x}-15{x}-300=0$
$\Rightarrow x(x+20)-15(x+20)=0$
$\Rightarrow (x+20)(x-15)=0$
$\Rightarrow x=15$ or $x=-20$
Rejecting x = – 20,
we have length of one side = 15 cm
and length of the other side = (15 + 5) cm = 20 cm
Sample Question 3: In the fig. ∠D = ∠E and $\dfrac{AD}{DB}=\dfrac{AE}{EC}$. Prove that BAC is an isosceles triangle.
Ans: Given: $\dfrac{AD}{DB}=\dfrac{AE}{EC}$
Therefore, DE∥BC (Converse of Basic Proportionality Theorem)
So, ∠D = ∠B and ∠E = ∠C (Corresponding angles)......(1)
But, it is given that
∠D = ∠E
Therefore, ∠B = ∠C ……[ From (1)]
So, AB = AC (Sides opposite to equal angles)
i.e., BAC is an isosceles triangle.
EXERCISE 6.3
1. In a ΔPQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM⊥PR. Prove that QM2 = PM × MR.
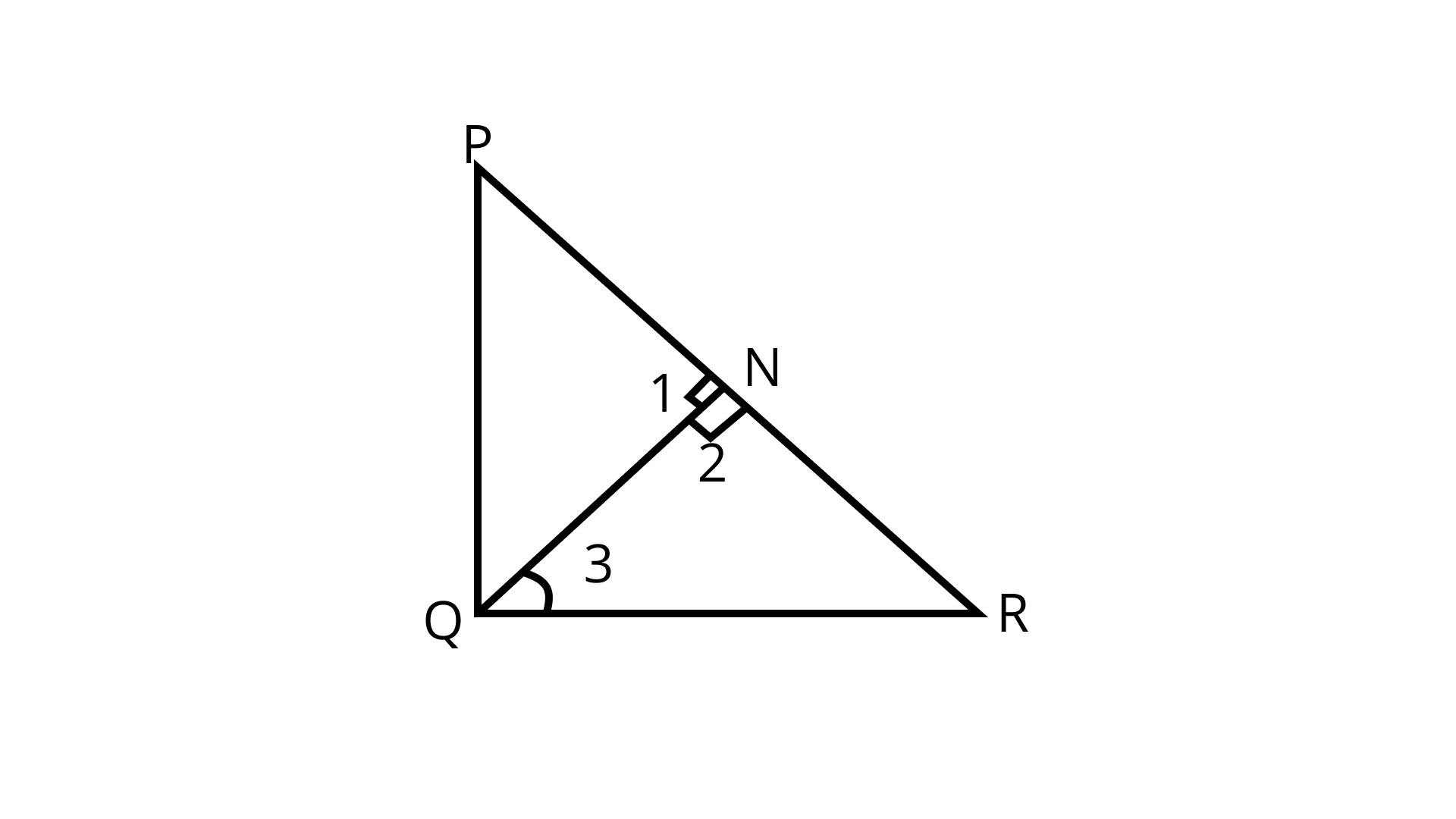
Ans: It is given that
In ΔPQR, PR2 – PQ2 = QR2 and QM⊥PR
Prove that MQ2 = MP × MR
Proof:
In ΔPQR,
PR2 – PQ2 = QR2 (Given)
⇒ PR2 = PQ2 + QR2
∴ ∠PQR = 90° (By conv. of Pythagoras theorem)
Now,
In ΔQMP and ΔQMR,
∠1 = ∠2 = 90° (QM⊥PR)
∠P = 90° – ∠R
∠3 = 90° – ∠R
⇒ ∠P = ∠3
$\therefore \triangle \mathrm{QMP} \sim \triangle \mathrm{RMQ}$ (By AA similarity criterion)
$\Rightarrow \dfrac{P Q}{Q R}=\dfrac{P M}{Q M}=\dfrac{Q M}{R M}$
$\Rightarrow \mathrm{QM}^{2}=\mathrm{PM} \times \mathrm{RM}$
Hence proved.
2. Find the value of x for which DE || AB in the given figure.
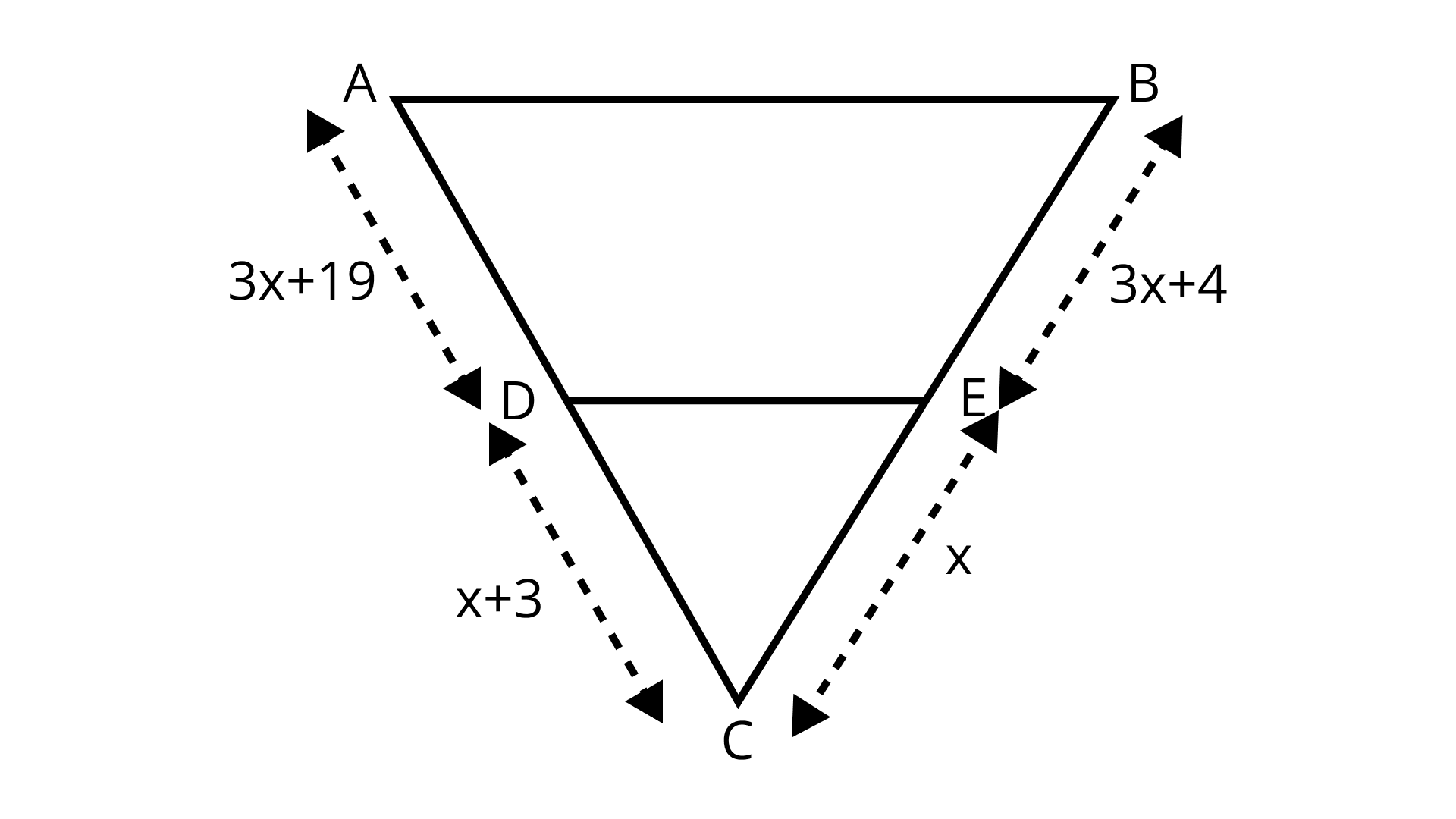
Ans: In ΔABC,
DE || AB
$\Rightarrow \dfrac{A D}{D C}=\dfrac{B E}{E C} \text { (By Basic Proportionality Theorem) }$
$\Rightarrow \dfrac{3 x+19}{x+3}=\dfrac{3 x+4}{x}$
$\Rightarrow x(3 x+19)=(x+3)(3 x+4)$
$\Rightarrow 3 \mathrm{x}^{2}+19 \mathrm{x}=3 \mathrm{x}^{2}+4 x+9 x+12$
$\Rightarrow 3 \mathrm{x}^{2}-3 \mathrm{x}^{2}+19 x-13 x=12$
$\Rightarrow 6 x=12$
$\Rightarrow x=2$
Hence, the value of x = 2.
3. In the given figure, if ∠1 = ∠2 and ΔNSQ ≅ ΔMTR. Prove that ΔPTS ~ ΔPRQ.
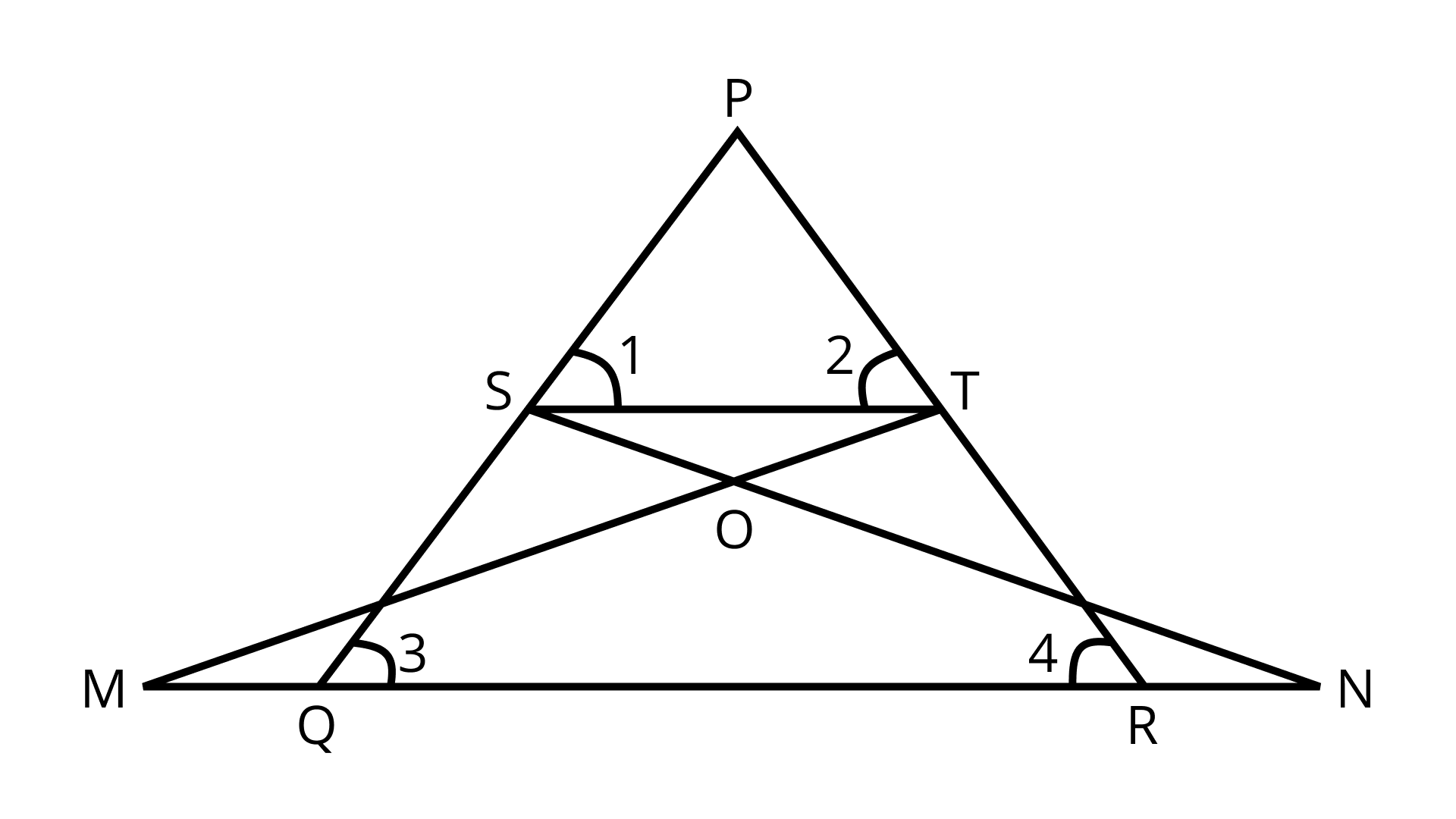
Ans: Given: In ΔPQR,
∠1 = ∠2 and ΔNSQ ≅ ΔMTR
To Prove: ΔPTS ~ ΔPRQ
Proof:
ΔNSQ ≅ ΔMTR (Given)
∴ SQ = TR (CPCT)……. (I)
∠1 = ∠2 (Given)
∴ PT = PS (Sides opposite to equal angles in ΔPTS)
or PS = PT ......(II)
now, by dividing eq. (I) and eq. (II)
$\dfrac{P T}{T R}=\dfrac{P S}{S Q}$
∴ ST || QR (By converse of BPT)
Now, in ΔPTS and ΔPRQ,
we have Proved above that
ST || QR
∠1 = ∠3 (Corresponding angles are equal)
Similarly,
∠2 = ∠4 (Corresponding angles)
By AA similarity criterion
∴ ΔPTS ~ ΔPRQ
Hence proved.
4. Diagonals of a trapezium PQRS intersect each other at the point O, PQ || RS and PQ = 3 RS. Find the ratio of the areas of triangles ΔPOQ and ΔROS.
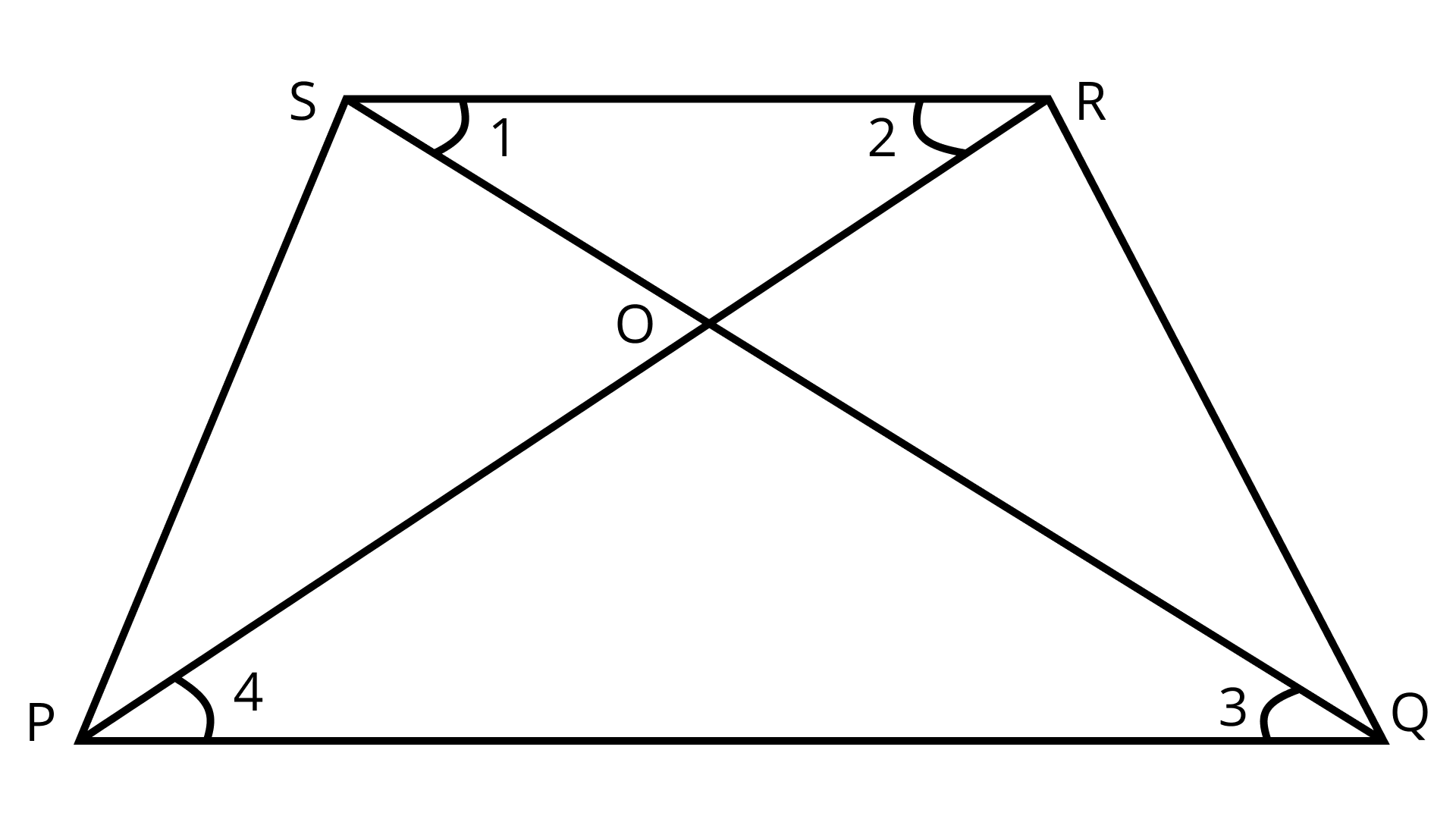
Ans: Given: $P Q R S$ is a trapezium with $P Q|| R S$ and $P Q=3 R S$
To find: $\dfrac{\operatorname{ar}(\Delta P O Q)}{\operatorname{ar}(\Delta R O S)}$
Sol: In $\triangle \mathrm{POQ}$ and $\triangle \mathrm{ROS}$,
It is given that
$\mathrm{PQ} \| \mathrm{RS}$
$\therefore \angle 3=\angle 1$ (Alternate interior angles)
Similarly,
$\angle 4=\angle 2$ (Alternate interior angles)
Therefore, by AA similarity criterion
$\triangle \mathrm{POQ} \sim \triangle \mathrm{ROS}$
So, by area theorem
$\dfrac{\operatorname{ar}(\Delta P O Q)}{\operatorname{ar}(\Delta R O S)}=\left(\dfrac{P Q}{R S}\right)^{2}$
But it is given that
$P Q=3 R S$
$\Rightarrow \dfrac{\operatorname{ar}(\Delta P O Q)}{\operatorname{ar}(\Delta R O S)}=\left(\dfrac{3 R S}{R S}\right)^{2}=\dfrac{9}{1}$
Hence, the required ratio is $9: 1$.
5. In the given figure, if AB || DC, and AC and PQ intersect each other at the point O, prove that OA. CQ = OC · AP.
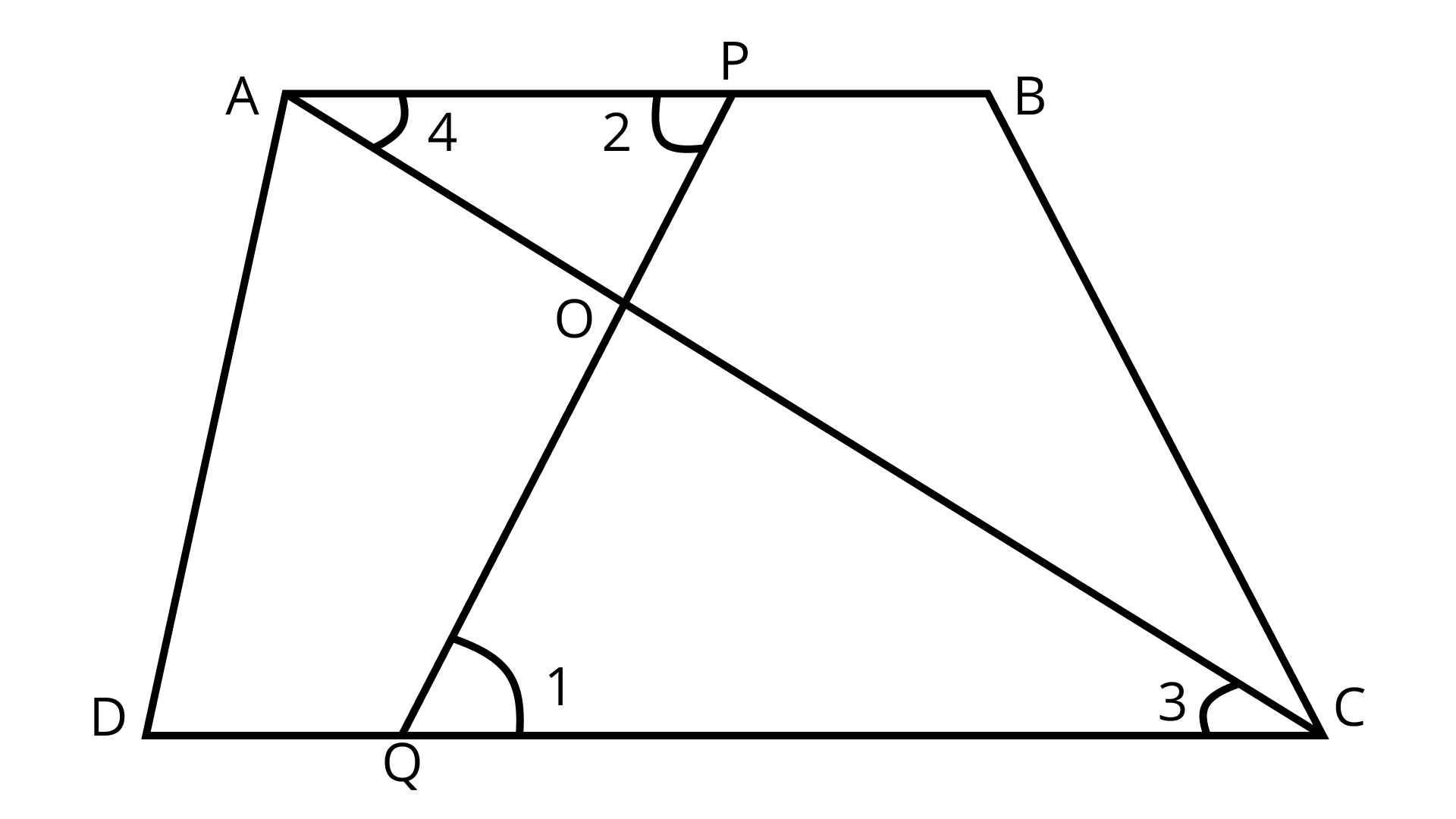
Ans: Given: In ABCD, AB || DC, PQ intersect AC at O (as shown in figure)
To Prove: OA · CQ = OC · AP
Proof:
In ΔOQC and ΔOPA,
∠1 = ∠2 (Alternate interior angles)
Similarly,
∠3 = ∠4 (Alternate interior angles)
∴ ΔOQC ~ ΔOPA (By AA similarity criterion)
Since, Corresponding sides of two similar triangles are proportional
$\dfrac{O Q}{O P}=\dfrac{O C}{O A}=\dfrac{Q C}{P A}$
$\Rightarrow \mathrm{OA} \cdot \mathrm{CQ}=\mathrm{OC} \cdot \mathrm{PA}$
Hence, proved.
6. Find the altitude of an equilateral triangle of side $8 \mathrm{~cm}$.
Ans: Given: $\triangle \mathrm{ABC}$ is an equilateral triangle.
$\mathrm{AD} \perp \mathrm{BC}$ (Given)
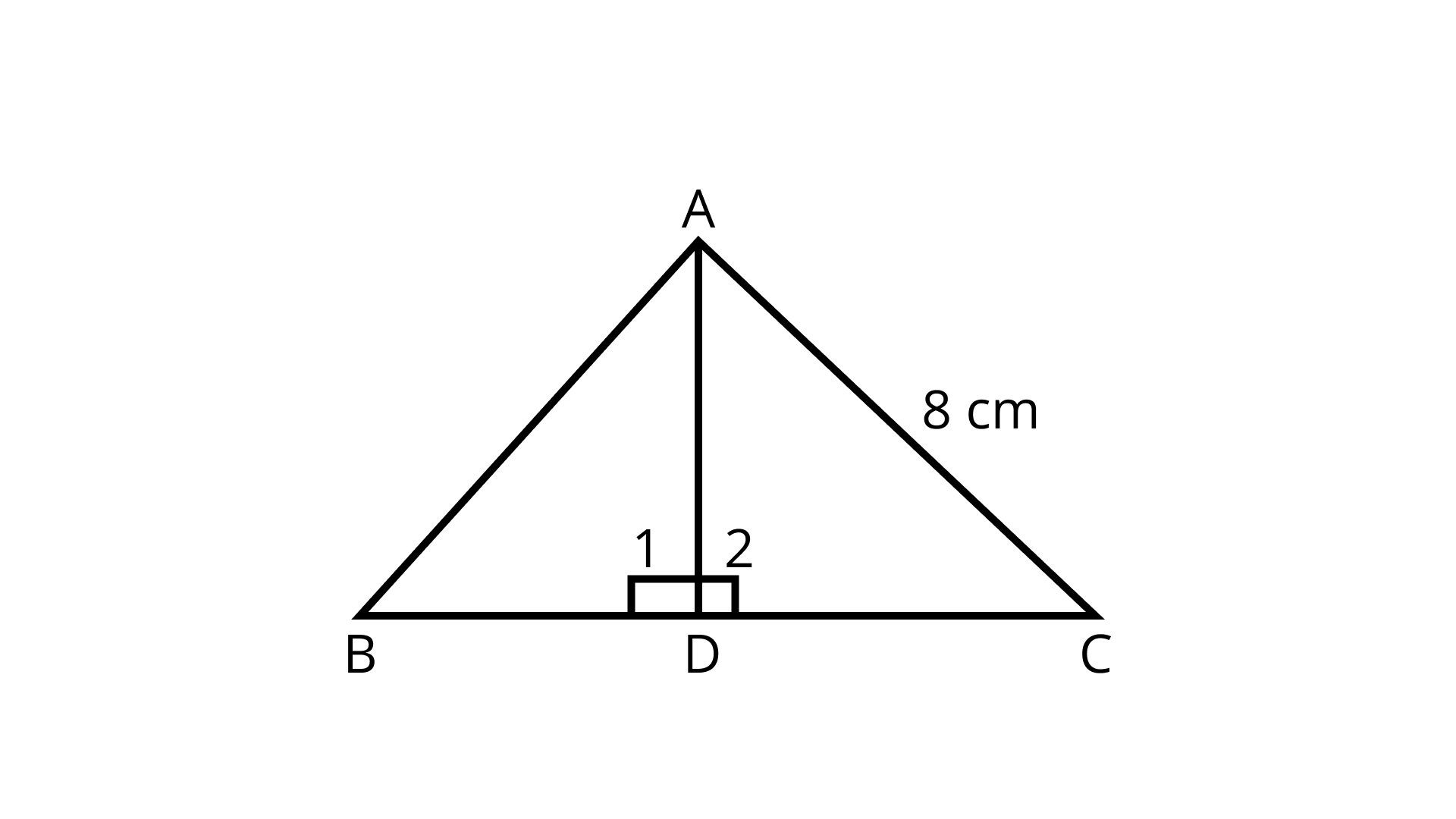
Now In $\triangle \mathrm{ADB}$ and $\triangle \mathrm{ADC}$,
$\mathrm{AB}=\mathrm{AC}$ $[\text { Sides of an equilateral } \triangle]$
$\angle 1=\angle 2=90^{\circ}$
$\mathrm{AD}=\mathrm{AD}$ $[\text { Common }]$
$\therefore \triangle \mathrm{ADB} \cong \triangle \mathrm{ADC}$ $[\mathrm{By} \mathrm{RHS} \text { congruence rule }]$
$\Rightarrow \mathrm{BD}=\mathrm{DC}[\mathrm{CPTC}]$
$\therefore \mathrm{BD}=\mathrm{DC}=\dfrac{B C}{2}=\dfrac{8}{2}=4 \mathrm{~cm}$
Therefore, by Pythagoras theorem,
In right angled triangle $A D B$,
we have $A D^{2}+B D^{2}=A B^{2}$
⇒ AD2 + (4)2 = (8)2
⇒ AD2= 64 – 16
⇒ AD2= 48
⇒ AD = $4\sqrt{3}cm$
7. If ΔABC ~ ΔDEF, AB = 4 cm, DE = 6 cm, EF = 9 cm and FD = 12 cm, find the perimeter of ΔABC.
Ans: Given: In ΔABC and ΔDEF,
AB = 4 cm, DE = 6 cm EF = 9 cm, FD = 12 cm
Find: Perimeter of ΔABC
So, now it is given that ΔABC ~ ΔDEF
$\therefore \dfrac{A B}{D E}=\dfrac{A C}{D F}=\dfrac{B C}{E F}$
$\Rightarrow \dfrac{4}{6}=\dfrac{A C}{12}=\dfrac{B C}{9}$
$\Rightarrow A C=\dfrac{4}{6} \times 12=8 \mathrm{~cm}$
$\text { and } B C=\dfrac{4}{6} \times 9=6 \mathrm{~cm}$
∴ The perimeter of ΔABC = AB + BC + AC = 4cm + 6cm + 8 cm = 18 cm
8. In the given figure, if DE || BC, find the ratio of ar(ΔADE) and ar(DECB).
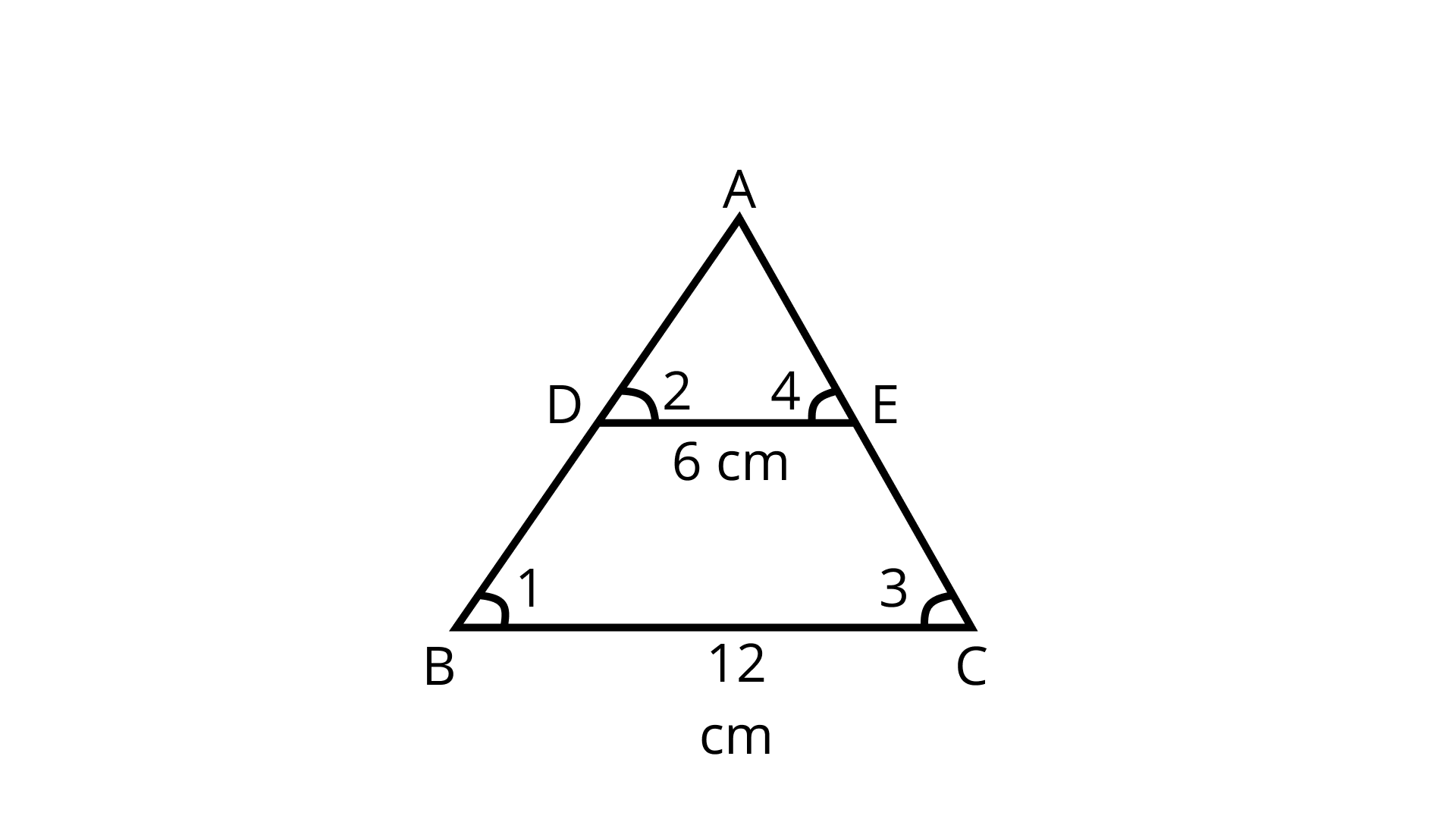
Ans:
$\mathrm{DE} \| \mathrm{BC}$ and $\mathrm{DE}=6 \mathrm{~cm}$ and $\mathrm{BC}=12 \mathrm{~cm}$
To find: $\dfrac{\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\square D E C B)}$
Now, it is given that in $\triangle A B C$ and $\triangle A D E$,
DE || BC
$\angle 1=\angle 2$ (corresponding angles)
Similarly,
$\angle 3=\angle 4$ (corresponding angles)
Therefore, by AA similarity criterion
$\therefore \triangle \mathrm{ABC} \sim \triangle \mathrm{ADE}$
Now,
$\dfrac{\operatorname{ar}(\Delta ABC)}{\operatorname{ar}(\Delta A D E)}=\left(\dfrac{B C}{D E}\right)^{2}$
Since, the ratio of the areas of two similar triangles is equal to the squares of the ratio of their corresponding sides.
$\Rightarrow \dfrac{\operatorname{ar}(\square D E C B)+\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\Delta A D E)}=\left(\dfrac{12}{6}\right)^{2}$
$\Rightarrow \dfrac{\operatorname{ar}(\square D E C B)}{\operatorname{ar}(\Delta A D E)}+\dfrac{\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\Delta A D E)}=(2)^{2}$
$\Rightarrow \dfrac{\operatorname{ar}(\square D E C B)}{\operatorname{ar}(\Delta A D E)}+1=4$
$\Rightarrow \dfrac{\operatorname{ar}(\square D E C B)}{\operatorname{ar}(\Delta A D E)}=4-1=3$
$\Rightarrow \dfrac{\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\square D E C B)}=\dfrac{1}{3}$
Hence, the required ratio is $1: 3$.
9. ABCD is a trapezium in which AB || DC and P and Q are points on AD and BC, respectively such that PQ || DC. If PD = 18 cm, BQ = 35 cm and QC = 15 cm, find AD.
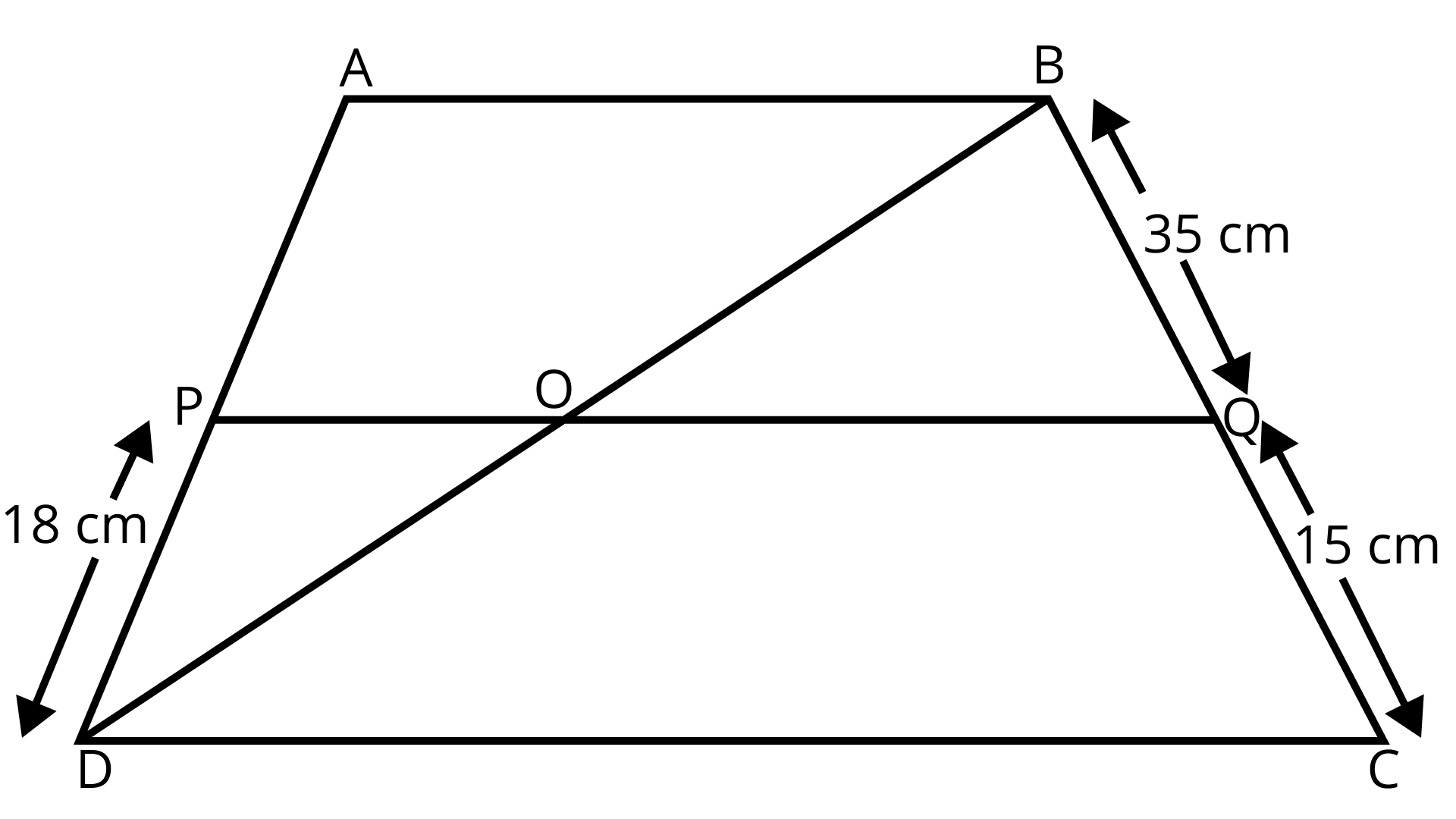
Ans: Given: ABCD is a trapezium in which AB || CD and PQ || DC (follow figure)
Also, PD = 18 cm, BQ = 35 cm and QC = 15 cm
Find: AD
In trapezium ABCD
AB || CD (Given)
PQ || DC (Given)
∴ AB || CD || PQ ...............(I)
In $\triangle \mathrm{BCD}, \mathrm{OQ}|| \mathrm{CD}$ (From (I))
$\therefore \dfrac{B O}{O D}=\dfrac{B Q}{Q C} \ldots \ldots$ ……………(II) (By BPT)
Similarly, in $\triangle \mathrm{DAB}$,
$\mathrm{PO} \| \mathrm{AB}$ (From eq.(I))
$\therefore \dfrac{B O}{O D}=\dfrac{A P}{P D}$.............(III) (By BPT)
$\dfrac{A P}{P D}=\dfrac{B Q}{Q C}$
$\Rightarrow \dfrac{A P}{18}=\dfrac{35}{15}$
$\Rightarrow A P=\dfrac{35}{15} \times 18=7 \times 6$
$\Rightarrow \mathrm{AP}=42 \mathrm{~cm}$
$\therefore \mathrm{AD}=\mathrm{AP}+\mathrm{PD}=42 \mathrm{~cm}+18 \mathrm{~cm}=60 \mathrm{~cm}$
10. Corresponding sides of two similar triangles are in the ratio of 2:3. If the area of the smaller triangle is 48 cm2, find the area of the larger triangle.
Ans: If ΔABC ~ ΔDEF,
Then by area theorem,
$\dfrac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta D E F)}=\left(\dfrac{A B}{D E}\right)^{2}$
But, $A B: D E=2: 3$ (Given)
and $\operatorname{ar}(\Delta \mathrm{ABC})=48 \mathrm{~cm}^{2}$
$\therefore \dfrac{48}{\operatorname{ar}(\Delta D E F)}=\left(\dfrac{2}{3}\right)^{2}$ $\Rightarrow \operatorname{ar}(\Delta \mathrm{DEF})=\dfrac{48 \times 9}{4}=108 \mathrm{~cm}^{2}$
11. In a triangle ΔPQR, N is a point on PR such that QN⊥PR. If PN × NR = QN2 , then prove that ∠PQR = 90°.
Ans: Given: ΔPQR in which QN⊥PR and PN × NR = QN2
To Prove: ∠PQR = 90°
Proof:
In ΔQNP and ΔQNR, QN⊥PR (Given)
∴ ∠1 = ∠2 = 90°
QN2 = NR × NP (Given)
QN x QN = NR x NP
$\dfrac{Q N}{N R}=\dfrac{N P}{Q N}$
∴ ΔPNQ ~ ΔQNR (By SAS similarity criterion)
∠P = ∠RQN = x ……..(I)
∠PQN = ∠R = y ……..(II)
In ΔPQR, we have
∠P + ∠PQR + ∠R = 180° (Angle sum property of a triangle)
⇒ x + x + y + y = 180° (Using (I) and (II))
⇒ 2x + 2y = 180°
⇒ x + y = 90°
⇒ ∠PQR = 90°
Hence, proved.
12. Areas of two similar triangles are 36 cm2 and 100 cm2. If the length of a side of the larger triangle is 20 cm, find the length of the corresponding side of the smaller triangle.
Ans: Here, $\operatorname{ar}(\triangle \mathrm{ABC})=36 \mathrm{~cm}^{2}, \operatorname{ar}(\triangle \mathrm{DEF})=100 \mathrm{~cm}^{2}, \mathrm{DE}=20 \mathrm{~cm}, \mathrm{AB}=?$ If $\triangle \mathrm{ABC} \sim \triangle \mathrm{DEF}$, then by area theorem $\dfrac{\operatorname{ar}(\Delta A B C)}{\operatorname{ar}(\Delta D E F)}=\left(\dfrac{A B}{D E}\right)^{2}$
$\Rightarrow \dfrac{36}{100}=\left(\dfrac{A B}{D E}\right)^{2}$
$\Rightarrow \dfrac{6}{10}=\left(\dfrac{A B}{D E}\right)$
$\Rightarrow \dfrac{6}{10}=\left(\dfrac{A B}{20}\right)$
$\Rightarrow A B=\dfrac{6 \times 20}{10}=12 \mathrm{~cm}$
13. In the given figure, if ∠ACB = ∠CDA, AC = 8 cm and AD = 3 cm, find BD.
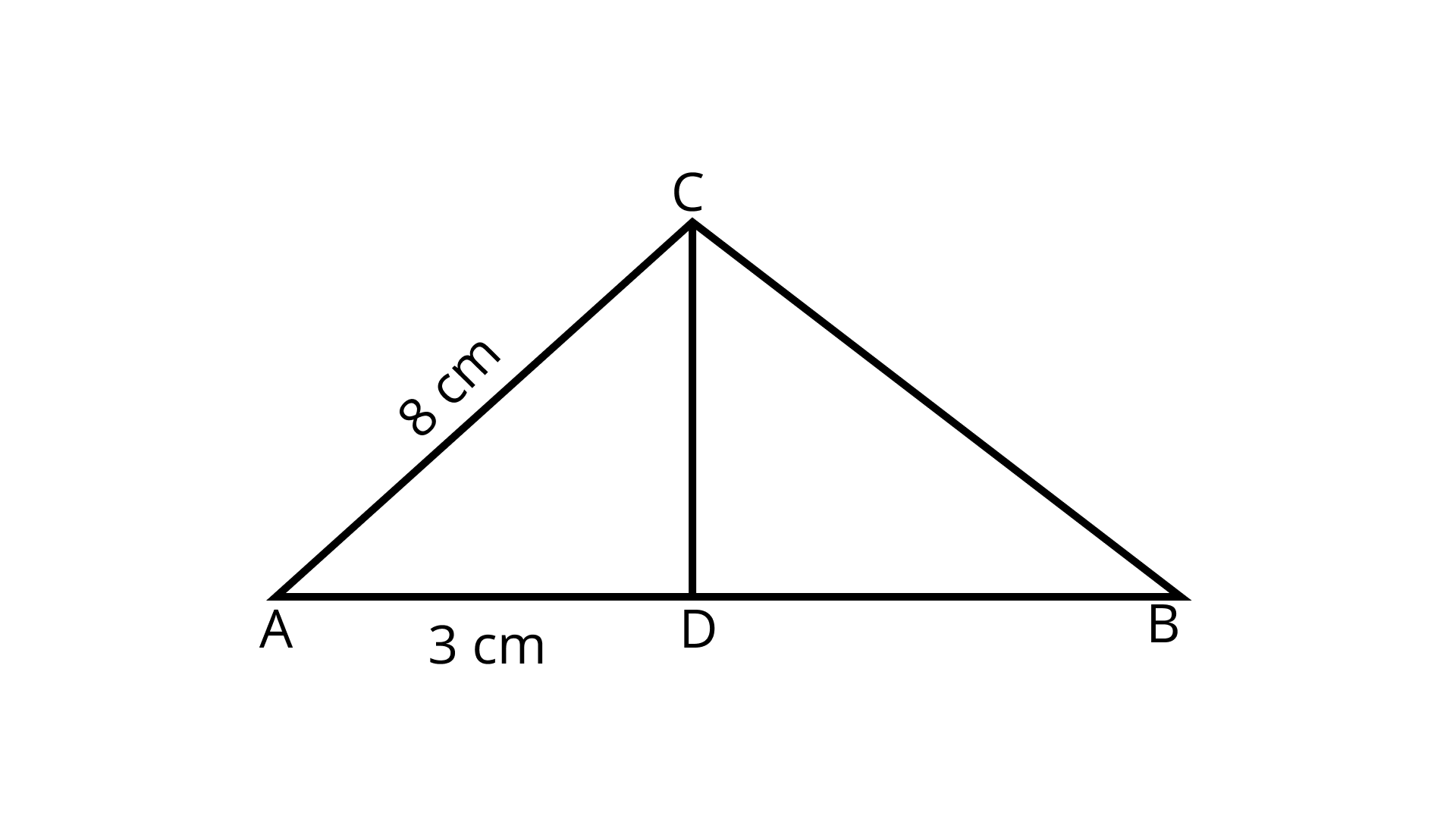
Ans: In ΔACD and ΔACB,
we have ∠CDA = ∠ACB (Given)
∠A = ∠A (Common)
∴ ΔACD ~ ΔABC (BY AA similarity criterion)
$\dfrac{A C}{A B}=\dfrac{D C}{B C}=\dfrac{A D}{A C}$
$\Rightarrow \dfrac{8}{A B}=\dfrac{D C}{B C}=\dfrac{3}{8}$
Now,
$\dfrac{8}{A B}=\dfrac{3}{8}$
$\Rightarrow A B=\dfrac{8 \times 8}{3}=\dfrac{64}{3}$
$B D=AB-AD=\dfrac{64}{3}-3=\dfrac{64-9}{3}$
$=\dfrac{55}{3} c m$
Hence, BD = 18.3 cm.
14. A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
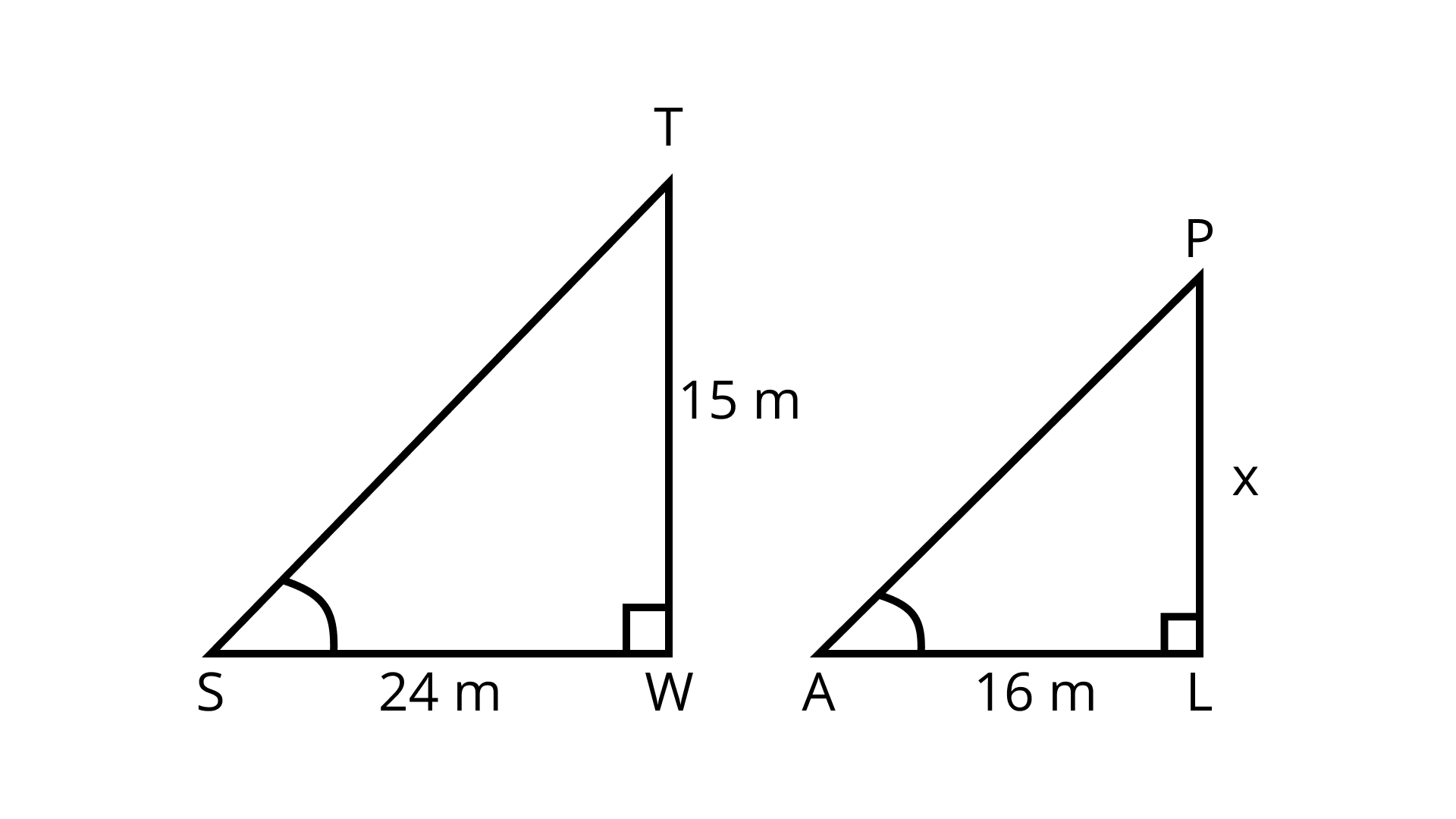
Ans: Let us assume that TW = 15m be the height of the tower and SW = 24m be the shadow's length.
Also, let PL = x be the height of the telephone pole and AL = 16m be the shadow's length.
In ΔTWS and ΔPLA,
∠W = ∠L = 90°
∠S = ∠A (Since both the figures occur at the same therefore angles of elevation will be equal]
∴ ΔTWS ~ ΔPLA (By AA similarity criterion)
$\Rightarrow \dfrac{T W}{P L}=\dfrac{T S}{P A}=\dfrac{W S}{L A}$(Corresponding sides of two similar triangles are proportional)
$\Rightarrow \dfrac{15}{x}=\dfrac{24}{16}$
$\Rightarrow \mathrm{x}=\dfrac{15 \times 16}{24}=5 \times 2$
$\Rightarrow \mathrm{x}=10 \mathrm{~m}$
Hence, the height of the telephone pole is 10 m.
15. Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
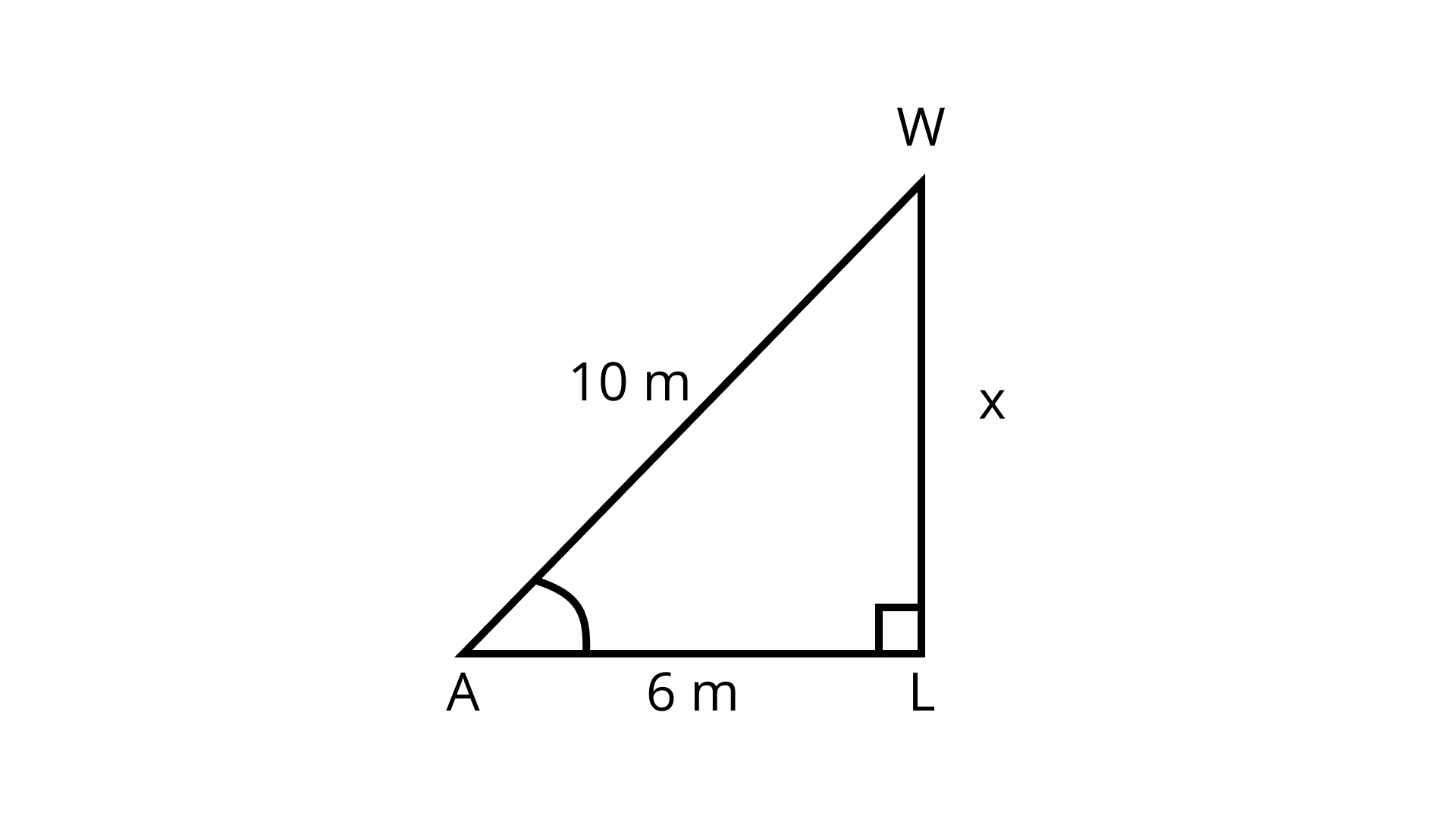
Ans: Let WA = 10 m be the length of the ladder and WL = x m be the height of the wall.
As wall WL = x is vertically up
so, by Pythagoras theorem,
In right angled triangle WLA
WL2 + AL2 = WA2
⇒ x2 + 62 = 102
⇒ x2 = 102 – 62 = 100 – 36
⇒ x2 = 64
⇒ x = 8
Hence, the height of the point on the wall where the top of the ladder reaches is 8 m.
(E) Long Answer Questions
Sample Question 1: In Fig 6.13, OB is the perpendicular bisector of the line segment DE, FA ⊥ OB and F E intersects OB at the point C.
Prove that $\dfrac{1}{OA}+\dfrac{1}{OB}=\dfrac{2}{OC}$
Ans:
OB is ⊥ bisector of line segment DE,FA ⊥ to OB and FE intersects OB at the point C as shown in figure
Now △OAF and △ODB
∠OAF=∠OBD=90° (because OB ⊥er bisector of DE,So OB⊥AF and OB⊥DE)
∠FOA=∠DOB (common angle)
From A−A,
△OAF≌△ODB
Similarly,
△AFC and △BEC
∠FCA=∠BCE
∠FAC=∠CBE=90°
from A−A,
△AFC≅△BEC
So, $\dfrac{AF}{BE}=\dfrac{AC}{CB}=\dfrac{FC}{CE}$
We know that DE=BE (⊥ er bisector of DE is OB)
$\dfrac{AF}{DB}=\dfrac{AC}{CB}=\dfrac{FC}{CE}$
As we have
$\dfrac{OA}{OB}=\dfrac{AF}{DB}=\dfrac{OF}{OD}$
$\Rightarrow \dfrac{OA}{OB}=\dfrac{AC}{CB}=\dfrac{OC-OA}{OB-OC}$
$\Rightarrow \dfrac{OA}{OB}=\dfrac{OC-OA}{OB-OC}$
⇒OA(OB−OC)=(OC−OA)OB
⇒OA.OB−OA.OC=OB.OC−OA.OB
⇒2.OA.OB=OB.OC+OA.OC
Divide by OA.OB.OC
$\Rightarrow\dfrac{2OA.OB}{OA.OB.OC}=\dfrac{OB.OC}{OA.OB.OC}=\dfrac{OA.OC}{OA.OB.OC}$
$\Rightarrow \dfrac{1}{OA}+\dfrac{1}{OB}=\dfrac{2}{OC}$
Hence proved.
Sample Question 2: Prove that if in a triangle square on one side is equal to the sum of the squares on the other two sides, then the angle opposite the first side is a right angle.
Ans:
Given:- ABC is a triangle, AC2 = AB2+BC2
To prove:- ∠B=90°
Construction:- Construct a triangle PQR right angled at Q such that, PQ=AB and QR=BC
Proof:-
In △PQR
PR2 =PQ2 +QR2 (By pythagoras theorem)
⇒PR2 = PQ2 +QR2 .....(1)
(∵AB=PQ and QR=BC)
AC2=AB2+BC2 .....(2)(Given)
From equation (1)&(2), we have
AC2= PR2
⇒AC=PR.....(3)
Now,
In △ABC and △PQR
AB=PQ
BC=QR
AC=PR(From (3))
∴△ABC≅△PQR (By SSS congruency)
Therefore, by C.P.C.T.,
∠B=∠Q
∵∠Q=90°
∴∠B=90°
Hence proved.
Sample Question 3: An aeroplane leaves an Airport and flies due North at 300 km/h. At the same time, another aeroplane leaves the same Airport and flies due West at 400 km/h. How far apart the two aeroplanes would be after 112hours?
Ans: Given, an aeroplane leaves an airport and flies due North at 300km/h
Another aeroplane leaves the same airport at the same time and flies due West at 400km/hr.
We have to find the distance between two aeroplanes after 1½ hours.
We know that, Distance = Speed × Time
Distance traveled by aeroplane which flies due North in 1½ hours,
Time = (2 + 1)/2 = $\dfrac{3}{2}$ hours
Distance = 300 × $\dfrac{3}{2}$ = 150 × 3 = 450 km
Distance traveled by aeroplane which flies due West in 1½ hours,
Distance = 400 × $\dfrac{3}{2}$ = 200 × 3 = 600 km
From the above figure, OA is the distance traveled by the plane flying due North
OB is the distance traveled by the plane flying due West
The triangle OAB represents a right triangle with O at the right triangle.
Applying Pythagoras theorem,
AB2=OA2+OB2
⇒AB2=(450)2+(600)2
⇒AB2=202500+360000=562600
⇒AB=750
AB=750km
Therefore, the two aeroplanes are 750 km apart in 1½ hours.
Sample Question 4: In Fig. 6.15, if ∆ ABC ~ ∆ DEF and their sides are of lengths (in cm) as marked along them, then find the lengths of the sides of each triangle.
Ans: Given, the triangles ABC and DEF are similar.
The length of the sides are marked in the given figure.
We have to find the length of the sides of each triangle.
Similar triangles have congruent corresponding angles and the corresponding sides are in proportion.
Similar triangles have the same shape, but not the same size.
From the figure,
AB=2x-1
BC=2x+2
AC=3x
DF=6x
EF=3x+9
DE=18
By the property of similarity,
The corresponding sides are in proportion.
So,
$\dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}$
Now,
$\dfrac{2x-1}{18}=\dfrac{2x+2}{3x+9}=\dfrac{3x}{6x}$
Taking $\dfrac{2x-1}{18}=\dfrac{3x}{6x}$
$\dfrac{2x-1}{18}=\dfrac{1}{2}$
On cross multiplication,
⇒2(2x-1)=18
⇒4x-2=18
⇒4x=20
⇒x=5
Substitute the value of x to find the length of sides of the triangle.
Now,
AB = 2(5) - 1 = 10 - 1 = 9
BC = 2(5) + 2 = 10 + 2 = 12
AC = 3x = 3(5) = 15
DF = 6(5) = 30
EF = 3(5) + 9 = 15 + 9 = 24
Therefore, the length of the sides of the triangle are
AB = 9 cm, BC = 12 cm, AC = 15 cm, DE = 18 cm, EF = 24 cm, and DF = 30 cm.
EXERCISE 6.4
1. In the given figure, if ∠A = ∠C, AB = 6cm, BP = 15 cm, AP = 12cm and CP = 4, then find the lengths of PD and CD.
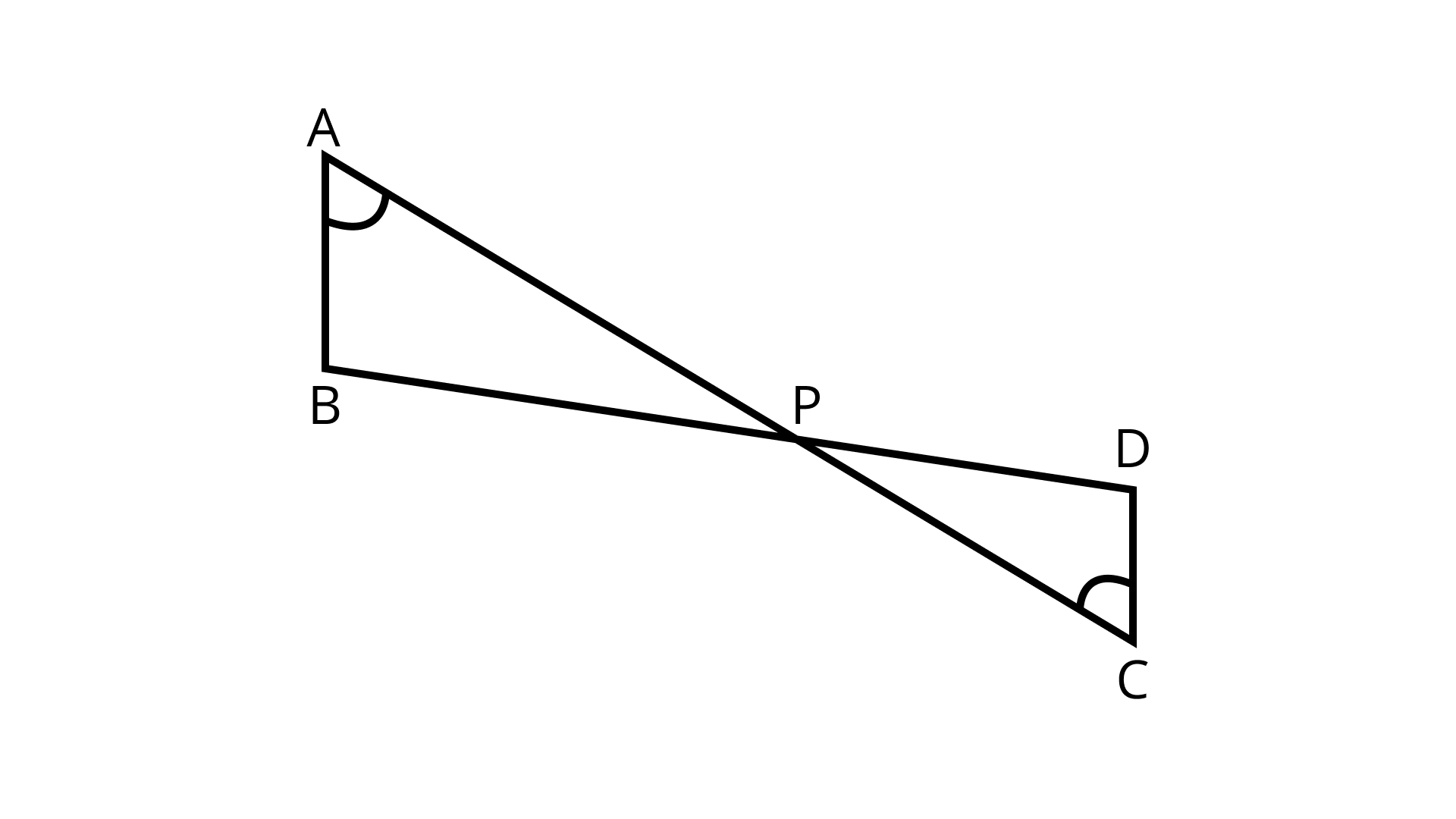
Ans: Given. ∠A = ∠C, AB = 6cm, BP = 15 cm, AP = 12cm and CP = 4,
Find: lengths of PD and CD
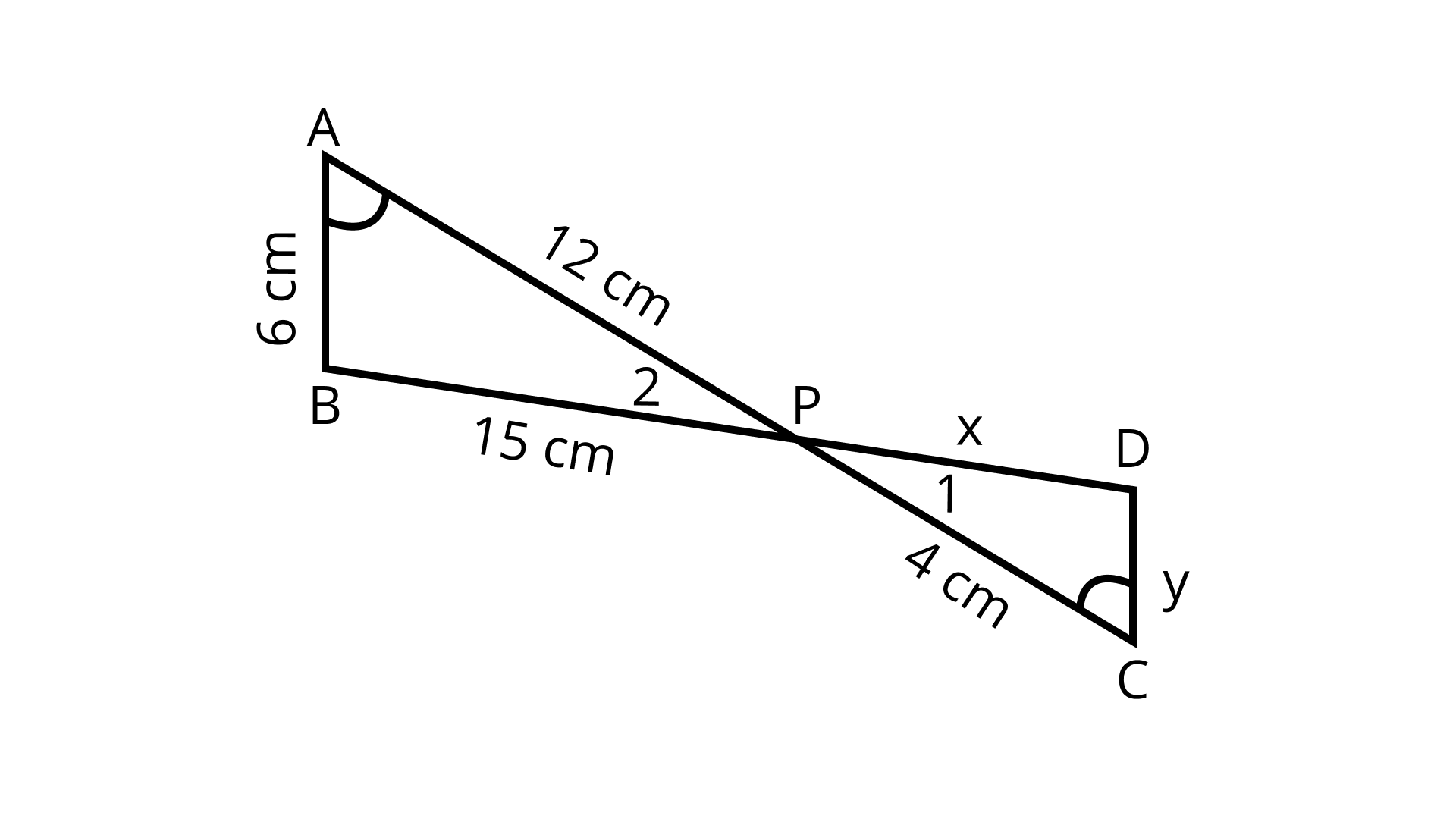
In ΔABP and ΔCDP,
∠A = ∠C (Given)
∠2 = ∠1 (Vertically opposite angles)
∴ ΔABP ~ ΔCDP (By AA similarity criterion)
Since corresponding sides of two similar triangles are proportional
$\Rightarrow \dfrac{A B}{C D}=\dfrac{A P}{C P}=\dfrac{B P}{D P}$
$\Rightarrow \dfrac{6}{y}=\dfrac{12}{4}=\dfrac{15}{x}$
$\Rightarrow \dfrac{6}{y}=\dfrac{12}{4}$
$\Rightarrow y=\dfrac{6 \times 4}{12}=2 \mathrm{~cm}$
$\Rightarrow \dfrac{15}{x}=\dfrac{12}{4}$
$\Rightarrow \dfrac{15}{x}=3$
$\Rightarrow x=5 \mathrm{~cm}$
$\therefore P D=5 \mathrm{~cm} \text { and } \mathrm{CD}=2 \mathrm{~cm}$
2. It is given that $\triangle A B C \sim \triangle E D F$ such that $A B=5 \mathrm{~cm}, A C=7 \mathrm{~cm}, D F=15 \mathrm{~cm}$ and $D E=12$ $\mathrm{cm}$. Find the lengths of the remaining sides of the triangles.
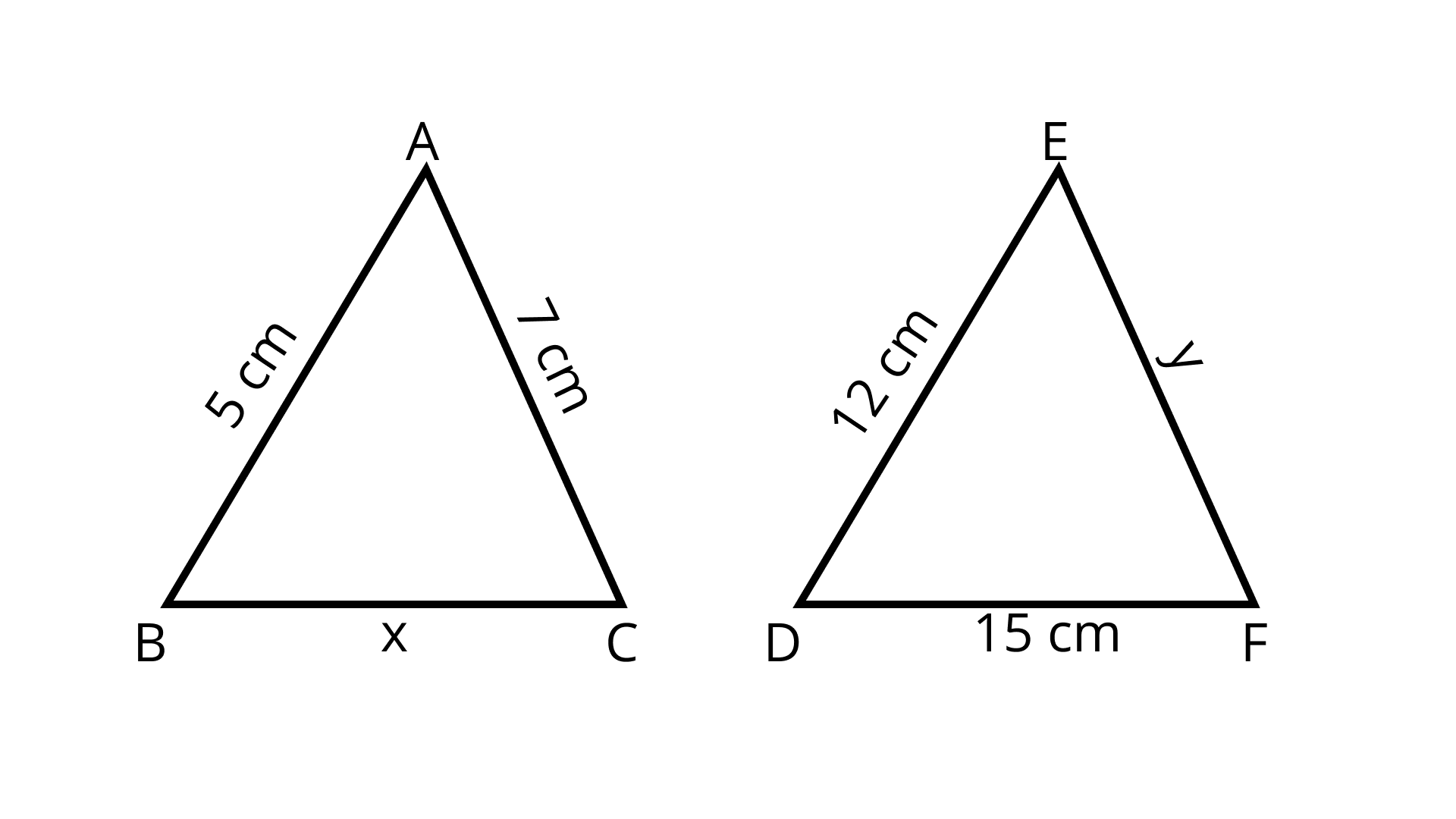
Ans: $\triangle \mathrm{ABC} \sim \triangle \mathrm{EDF}[$ Given $]$
$\therefore \dfrac{A B}{E D}=\dfrac{A C}{E F}=\dfrac{B C}{D F}$
$\Rightarrow \dfrac{5}{12}=\dfrac{7}{y}=\dfrac{x}{15}$
$\Rightarrow \dfrac{5}{12}=\dfrac{7}{y}$
$\Rightarrow y=\dfrac{7 \times 12}{5}=\dfrac{84}{5}=16.8 \mathrm{~cm}$
and
$x=\dfrac{5 \times 15}{12}=\dfrac{25}{4}=6.25 \mathrm{~cm}$
3. Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides, then the two sides are divided in the same ratio.
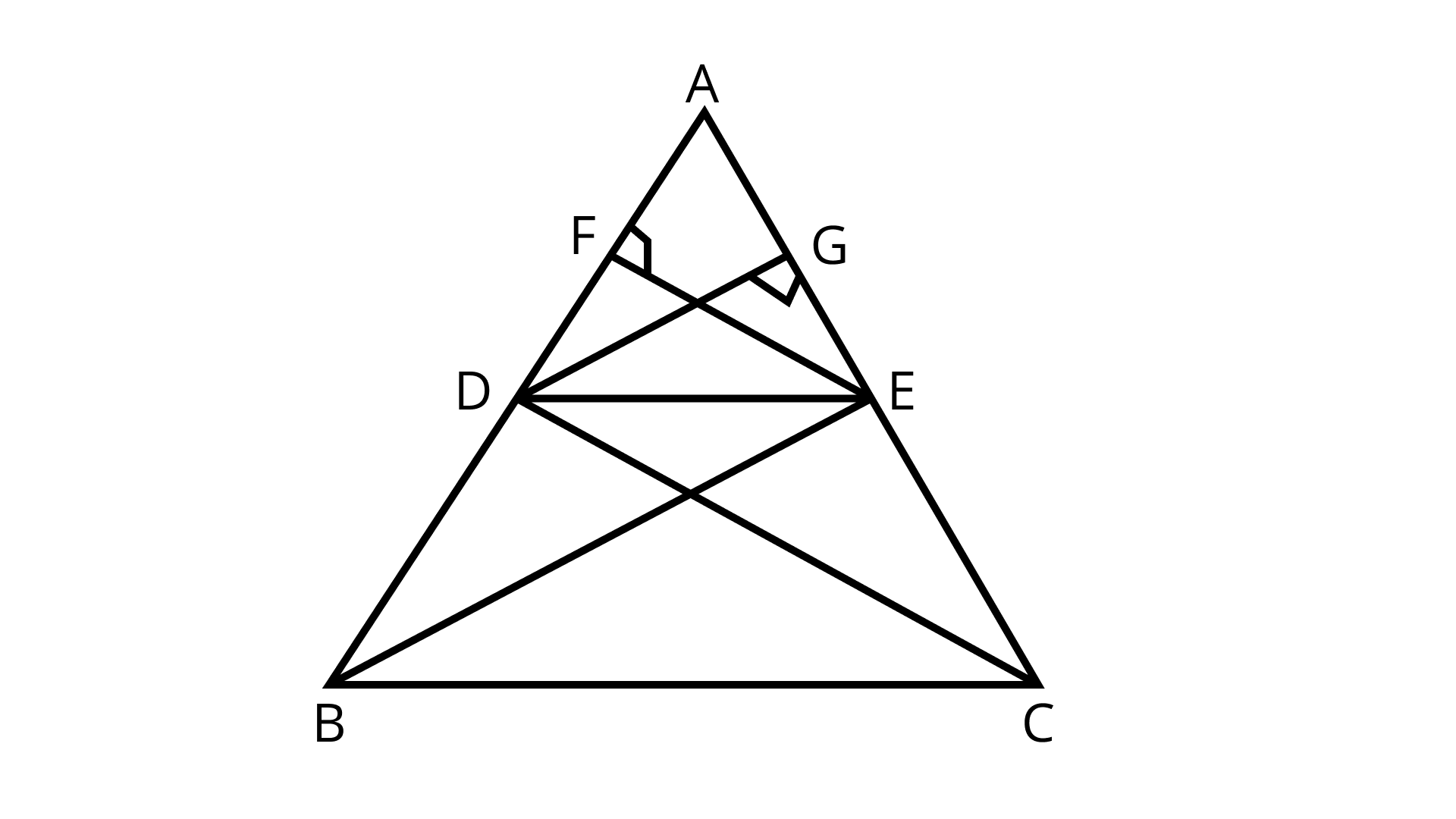
Ans: Given: In ΔABC, DE || BC
To prove: $\dfrac{A D}{D B}=\dfrac{A E}{E C}$
Construction: Draw EF⊥AB and DG⊥AC. Join DC and BE
Proof:
$\dfrac{\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\triangle D B E)}=\dfrac{\dfrac{1}{2} A D \times E F}{\dfrac{1}{2} D B \times E F}=\dfrac{A D}{D B}$
And
$\dfrac{\operatorname{ar}(\Delta A E D)}{\operatorname{ar}(\Delta E C D)}=\dfrac{\dfrac{1}{2} A E \times D G}{\dfrac{1}{2} E C \times D G}=\dfrac{A E}{E C}$
Note that $\triangle D B E$ and $\triangle E C D$ are on same base $D E$ and between same parallel lines $D E$ and $B C .$
$\therefore \operatorname{ar}(\Delta \mathrm{DBE})=\operatorname{ar}(\Delta \mathrm{ECD}) \ldots \ldots \ldots . .(\mathrm{III})$
So from equations (II) and (III), we have
$\dfrac{\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\triangle D B E)}=\dfrac{A E}{E C}$
from equations (I) and (IV), we have
$\dfrac{A D}{D B}=\dfrac{A E}{E C}$
Hence, proved.
4. In the given figure, if PQRS is a parallelogram and AB || PS, then prove that OC || SR.
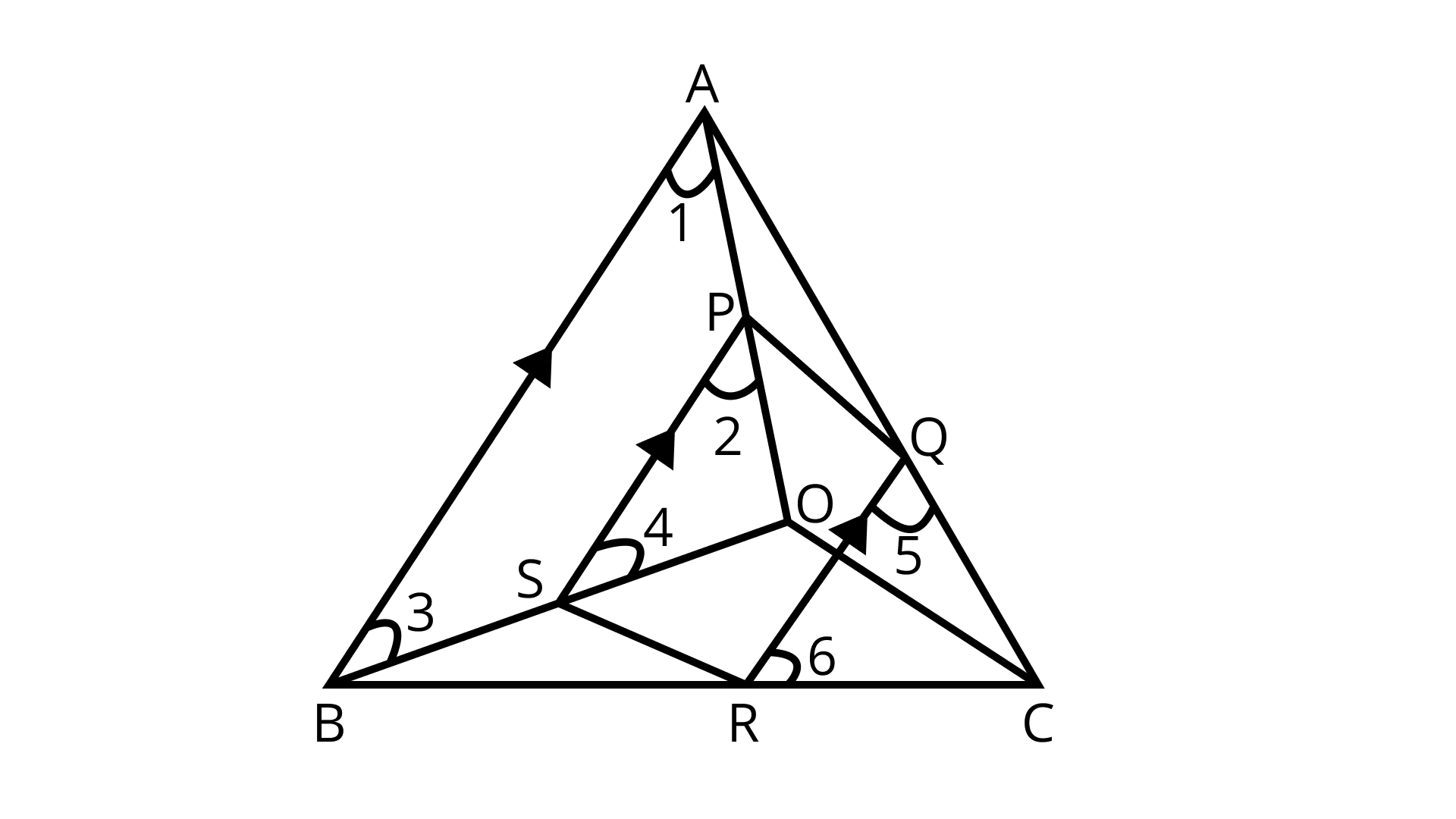
Ans: Given: In ΔABC, PQRS is a parallelogram and PS || AB.
To Prove: OC || SR
Proof: In ΔOAB and ΔOPS
PS || AB (Given)......(I)
∴ ∠1 = ∠2 (corresponding angles)
Similarly,
∠3 = ∠4 (corresponding angles)
∴ ΔOPS ~ ΔOAB (By AA similarity criterion)
$\Rightarrow \dfrac{O P}{O A}=\dfrac{O S}{O B}=\dfrac{P S}{A B}$……..(II)
PQRS is a parallelogram so PS || QR….. (III)
⇒ QR || AB………. (IV) (From (I), (III))
In ΔCQR and ΔCAB,
QR || AB ( From (IV) )
∴ ∠5 = ∠CAB (corresponding angles)
Similarly,
∠6 = ∠CBA (corresponding angles)
∴ ΔCQR ~ ΔCAB (By AA similarity criterion)
$\Rightarrow \dfrac{C Q}{C A}=\dfrac{C R}{C B}=\dfrac{Q R}{A B}$
$\mathrm{PQRS}$ is a parallelogram.
$\therefore \mathrm{PS}=\mathrm{QR}$
$\therefore \dfrac{P S}{A B}=\dfrac{C R}{C B}=\dfrac{C Q}{C A} \ldots \ldots . .(\mathrm{V})$
$\Rightarrow \dfrac{C R}{C B}=\dfrac{O S}{O B} \quad[\text { from eq.(II)and eq.(V)] }$
These are the ratios of two sides of ΔBOC and are equal so by converse of BPT,
SR || OC.
Hence, proved.
5. A 5m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4m high. If the foot of the ladder is moved 1.6m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
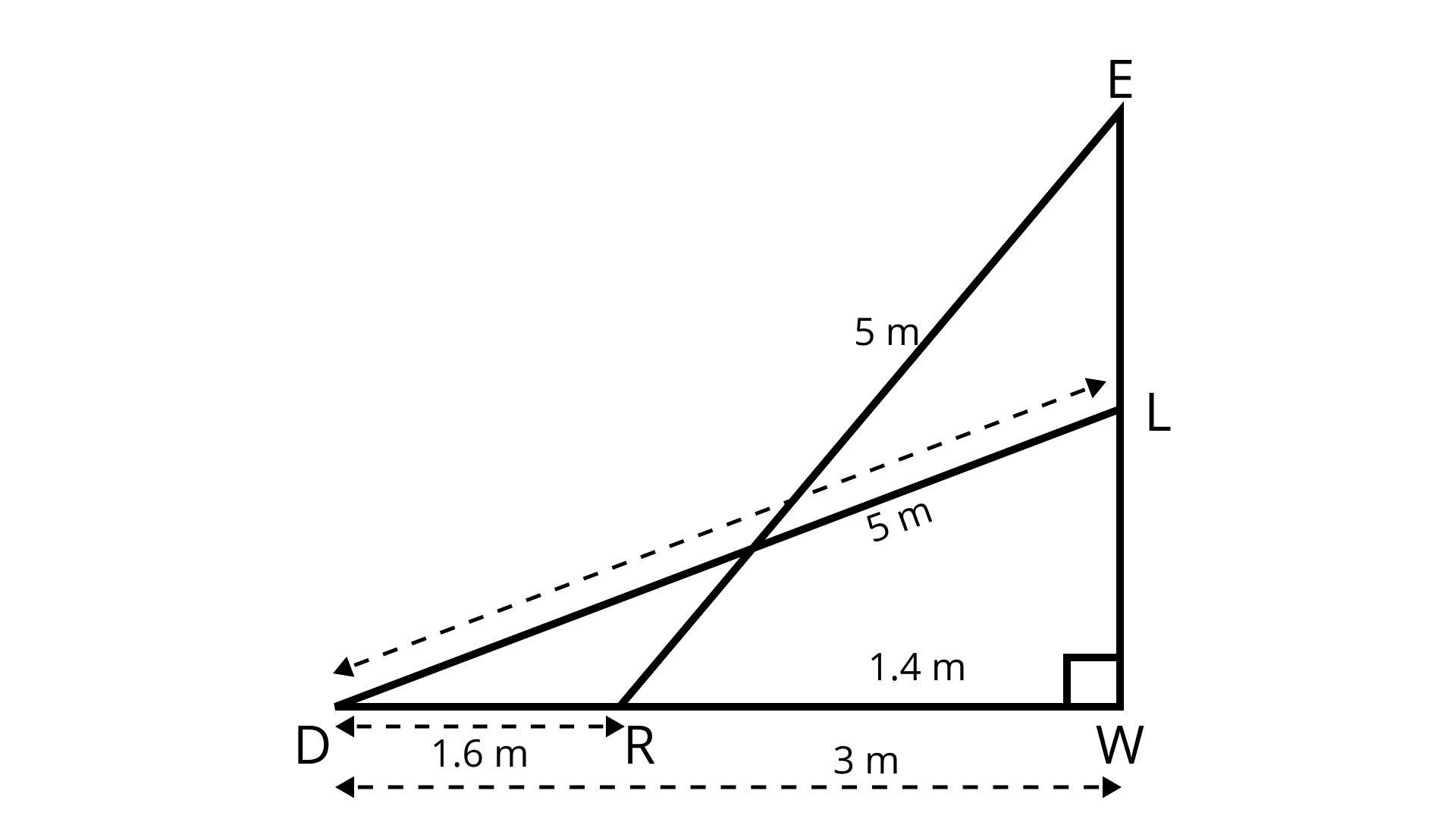
Ans: In the figure, ELW is a wall.
DL and RE are two positions of the ladder of length 5 m.
In right angled ΔLWD,
DW2 + LW2 = DL2 (By Pythagoras)
DW2 = DL2 – LW2
$\Rightarrow$ DW2 = 52 – 42 = 25 – 16 = 9
$\Rightarrow$ DW = 3m
Now,
RW = DW – DR = 3 – 1.6 = 1.4 m
In right angled triangle RWE,
$\Rightarrow$EW2 + RW2 = RE2 (By Pythagoras Theorem)
$\Rightarrow$ EW2 = RE2 – RW2
$\Rightarrow$EW2 = 52 – 1.42
$\Rightarrow$ EW2 = 25 – 1.96
$\Rightarrow$ EW2 = 23.04
$\Rightarrow$ EW = $\sqrt{23.04}$ = 4.8 m.
∴ The distance by which the ladder shifted upward = EL = 4.8 m – 4 m = 0.8m
Hence, the ladder would slide upwards on the wall by 0.8 m.
6. For going to a city B from city A, there is a route via city C, such that AC⊥CB, AC = 2x km and CB = 2 (x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
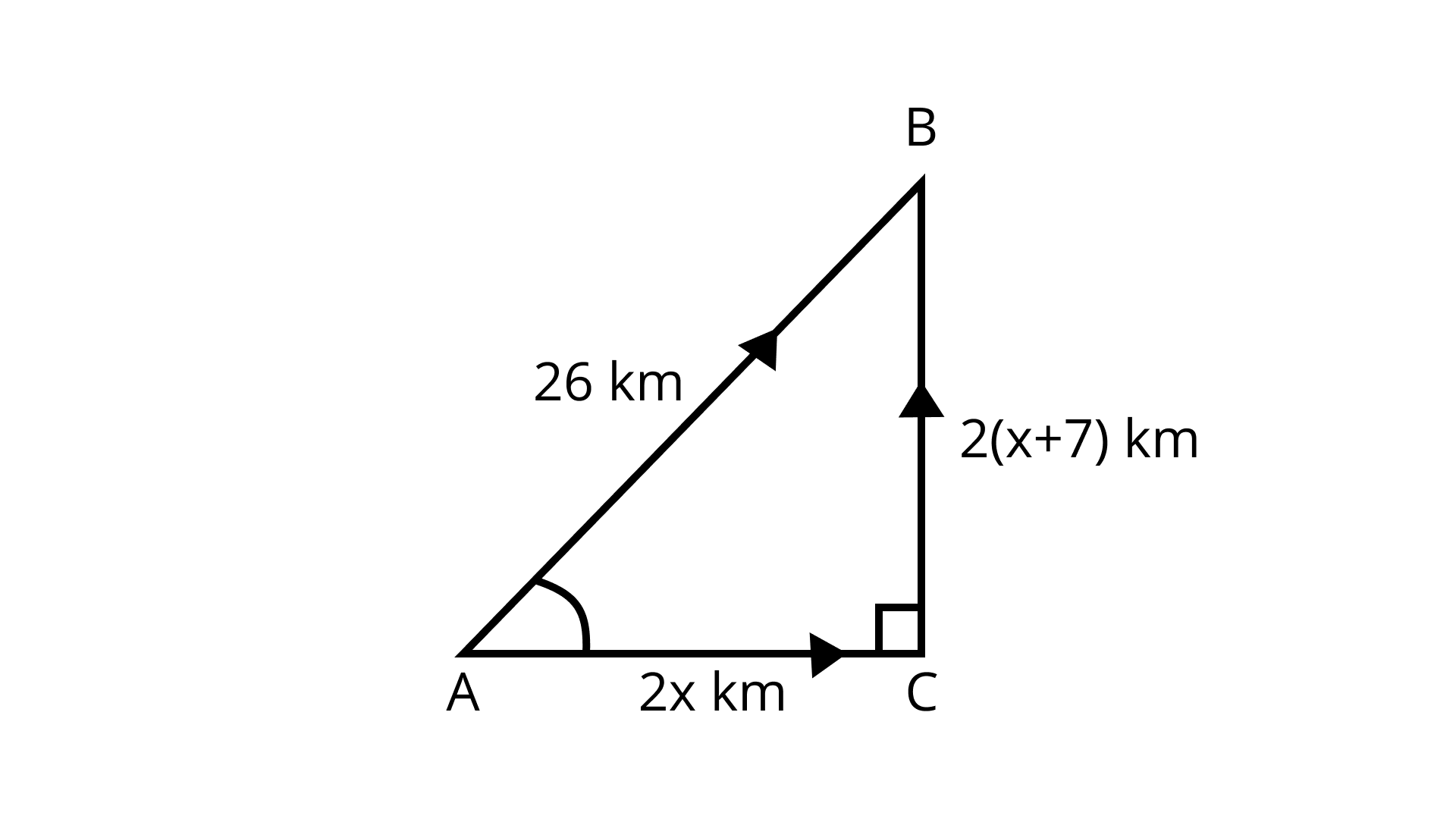
Ans: Distance saved due to direct highway = (AC + BC) – AB
So, by Pythagoras theorem
AC2 + BC2 = AB2
⇒ (2x)2 + [2(x + 7)]2 = 262
⇒ (2x)2 + 22(x + 7)2 = 676
⇒ 4x2 + 4(x2 + 49 + 14x) = 676
⇒ 4[x2 + x2 + 49 + 14x] = 676
⇒ 2x2 + 14x + 49 = $\dfrac{676}{4}$
⇒ 2x2 + 14x + 49 = 169
⇒ 2x2 + 14x + 49 – 169 = 0
⇒ 2x2 + 14x – 120 = 0
⇒ x2 + 7x – 60 = 0
⇒ x2 + 12x – 5x – 60 = 0
⇒ x(x + 12) – 5 (x + 12) = 0
⇒ (x + 12) (x – 5) = 0
⇒ x + 12 = 0 or x – 5 = 0
⇒ x = –12(rejected) or x = 5
∴ The required distance = AC + BC – AB
= 2x + 2x + 14 – 26
= 4x – 12
= 4 × 5 – 12
= 20 – 12 (∵ x = 5)
= 8km
Hence, the distance saved by highway is 8 km.
7. A flag pole 18 m high casts a shadow 9.6 m long. Find the distance of the top of the pole from the far end of the shadow.
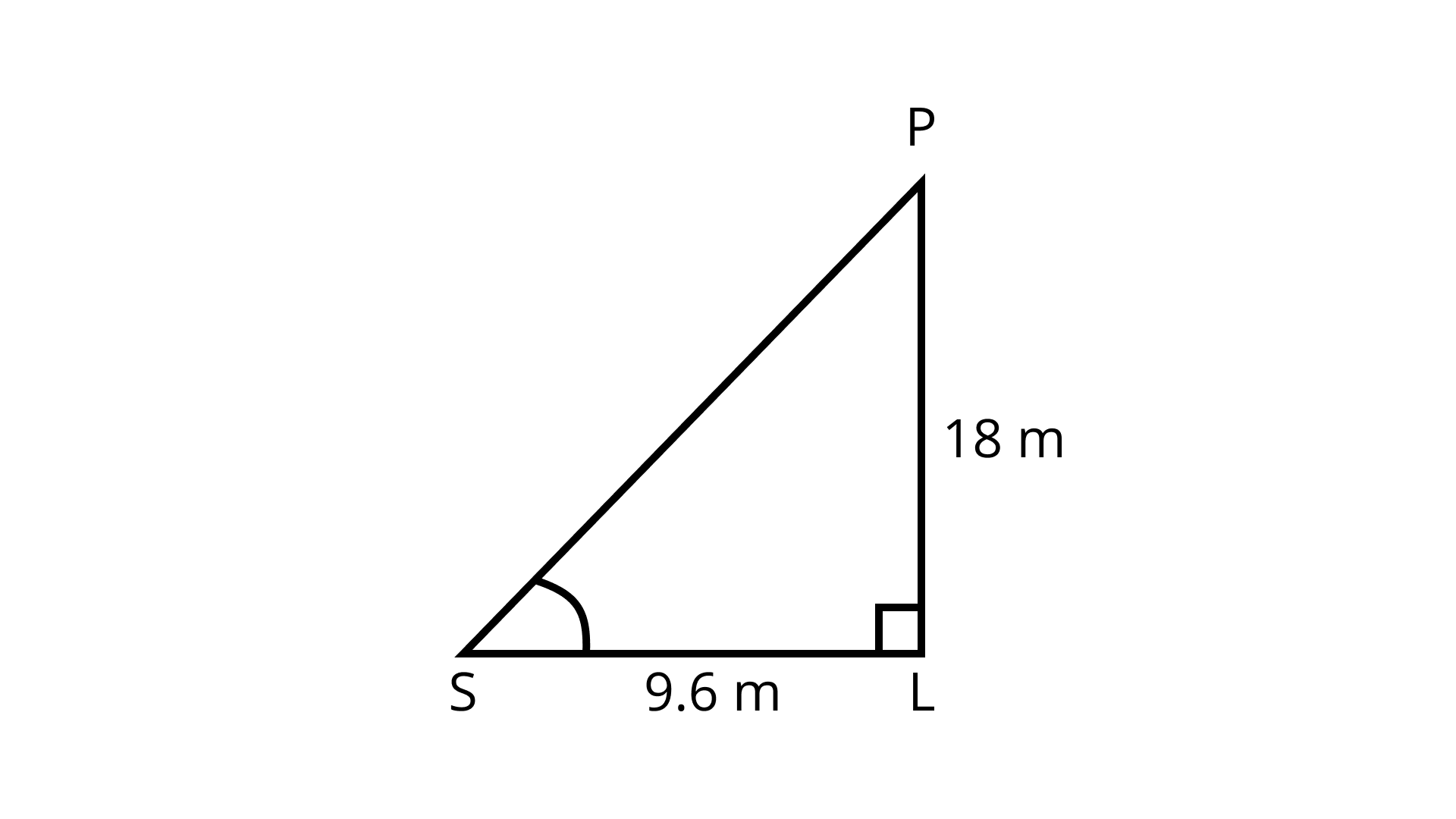
Ans: Pole PL = 18 m casts shadow LS = 9.6 m
The required distance between the top of the pole and the far end of shadow is equal to PS as the pole is vertical so ∠L = 90°.
∴ By Pythagoras theorem,
PS2 = PL2 + SL2
PS2 = 182 + 9.62
⇒ PS2 = 324 + 92.16 = 416.16
⇒ PS = $\sqrt{416.16}$
⇒ PS = 20.4m
Hence, the required distance = 20.4 m
8. A street light bulb is fixed on a pole 6 m above the level of the street. If a woman of height 1.5 m casts a shadow of 3m, find how far she is away from the base of the pole.
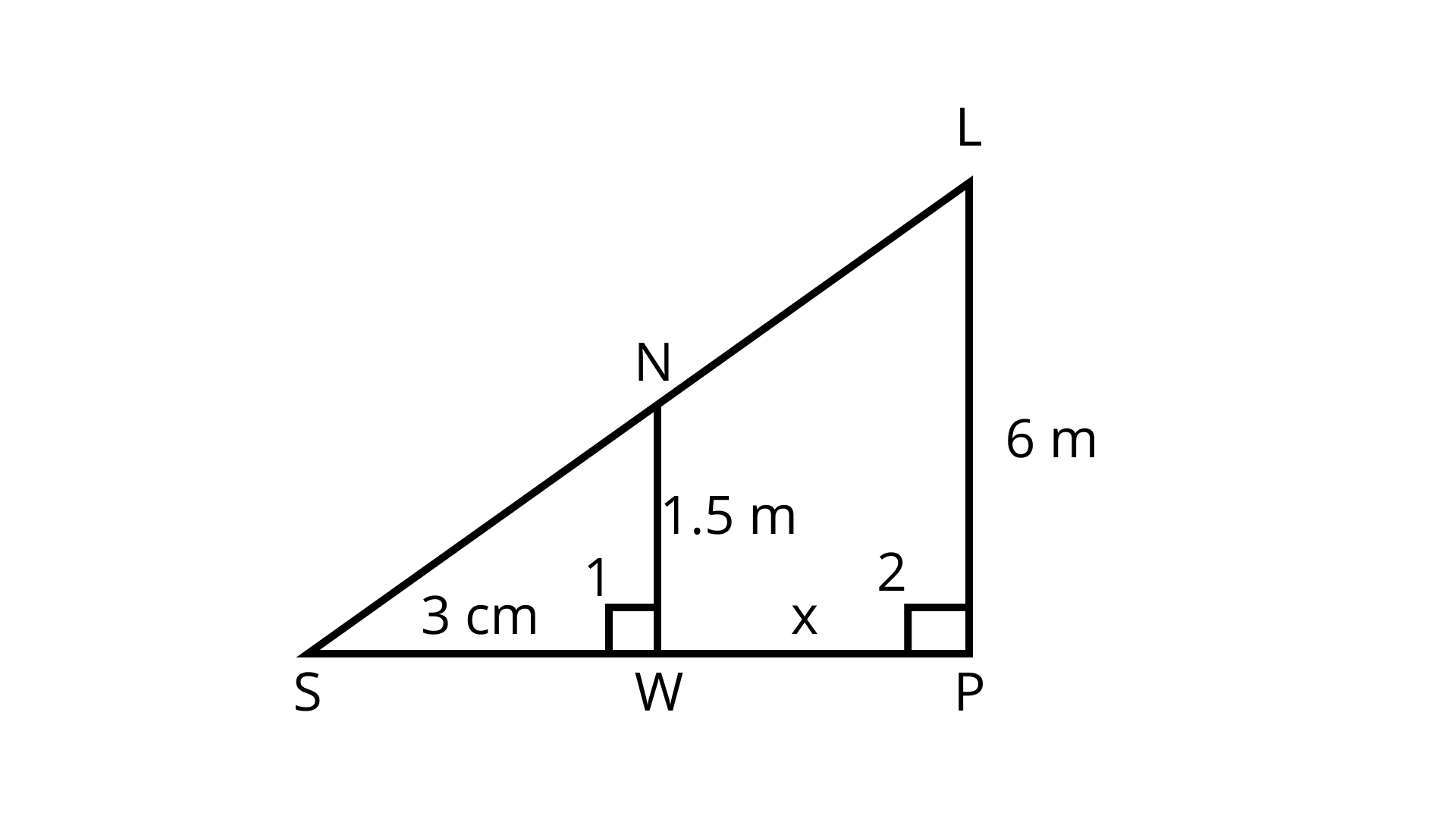
Ans: In ΔLPS and ΔNWS,
Bulb L is fixed at a height of 6m above the road SP.
Woman and pole are vertical.
∴ ∠2 = ∠1 = 90°
∠S = ∠S (Common)
∴ ΔLPS ~ ΔNWS (By AA similarity criterion)
$\Rightarrow \dfrac{L P}{N W}=\dfrac{L S}{N S}=\dfrac{P S}{W S}$
$\Rightarrow \dfrac{6 m}{1.5 m}=\dfrac{L S}{N S}=\dfrac{3+x}{3}$
$\Rightarrow \dfrac{6 m}{1.5 m}=\dfrac{3+x}{3}$
$\Rightarrow 4.5+1.5 x=18$
$\Rightarrow 1.5 x=18-4.5$
$\Rightarrow x=\dfrac{13.5}{1.5}=9 m$
Hence, the woman is 9m away from the pole.
9. In the given figure, ABC is a triangle right angled at B and BD⊥AC. If AD = 4 cm, and CD = 5 cm then find BD and AB.
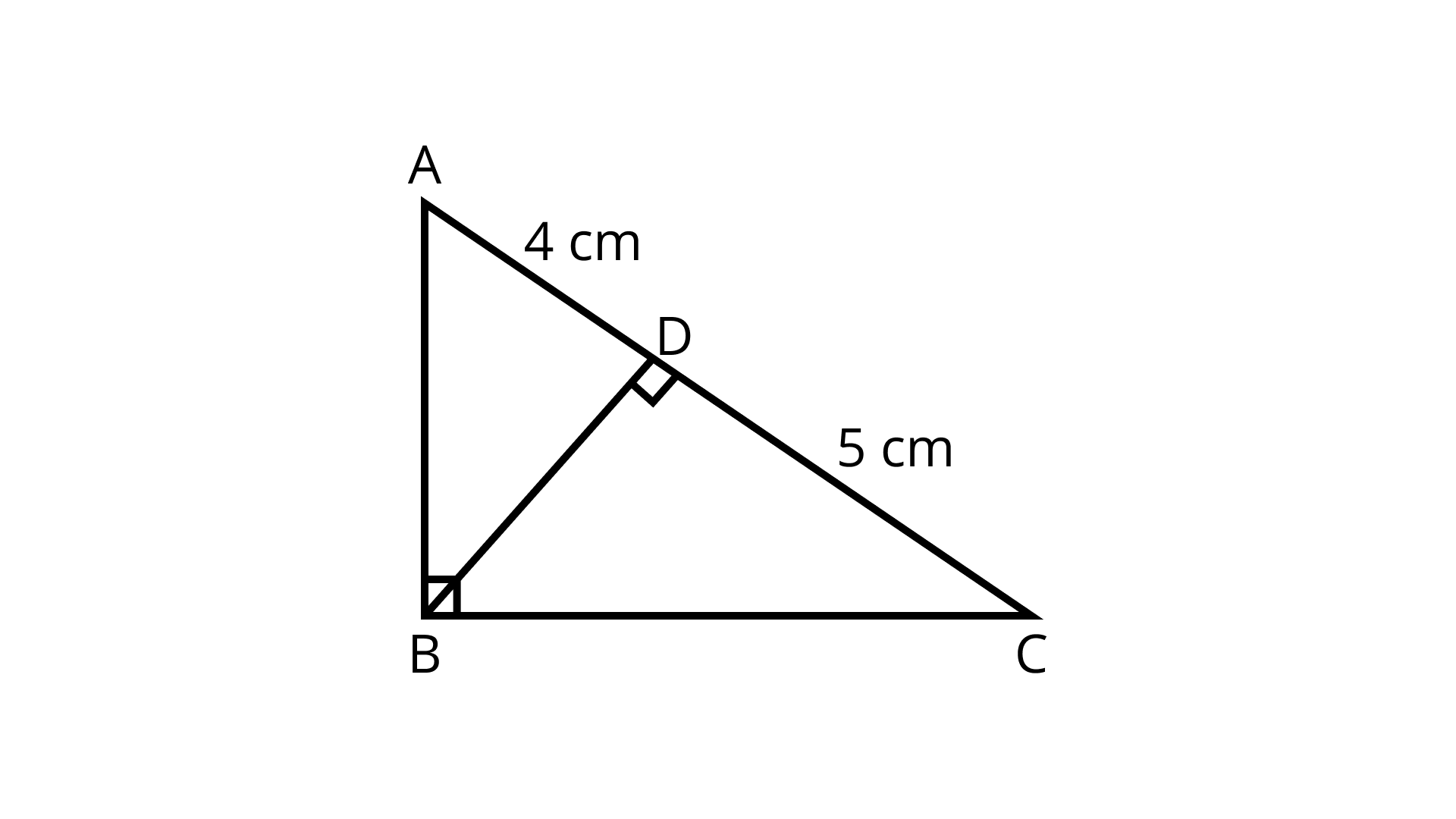
Ans: In ΔABC,
∠ABC = 90° (Given)
BD⊥AC (From vertex B to hypotenuse AC)
∴ BD2 = DA × DC (By theorem)
⇒ BD2 = 4 × 5
$\Rightarrow B D=2 \sqrt{5} \mathrm{~cm}$
In right angled $\triangle B D A$, BD⊥AC $[$ Given $]$
$\therefore \angle B D A=90^{\circ}$
$\Rightarrow A B^{2}=A D^{2}+B D^{2}[$ By Pythagoras theorem $]$
$=4^{2}+(2 \sqrt{5})^{2}$
$=16+20=36$
$\Rightarrow AB=6 \mathrm{~cm}$
10. In the given figure, $P Q R$ is a right triangle right angled at $Q$ and $Q S \perp P R$. If $P Q=6 \mathrm{~cm}$ and $P S=4 \mathrm{~cm}$, find $Q S, R S$ and $Q R$.
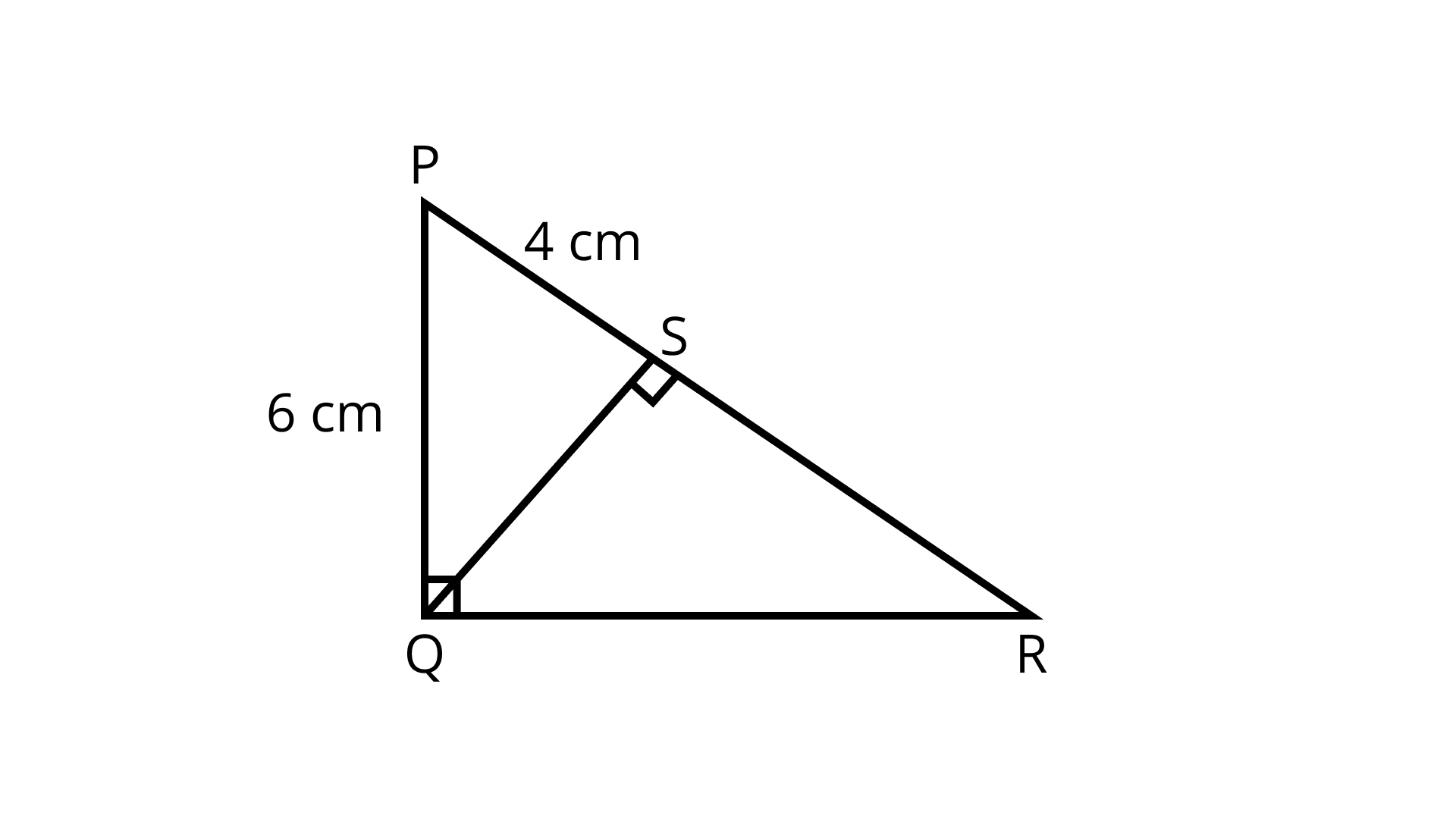
Ans: In $\triangle P Q R$
$\angle \mathrm{PQR}=90^{\circ}[$ Given $]$
$Q S \perp P R$ (From vertex Q to hypotenuse PR)
$\therefore \mathrm{QS}^{2}=\mathrm{PS} \times \mathrm{SR} .$.....(I) (By theorem)
Now, in $\triangle \mathrm{PSQ}$ we have
$\mathrm{QS}^{2}=\mathrm{PQ}^{2}-\mathrm{PS}^{2}$ (By Pythagoras theorem )
$\Rightarrow Q S^{2}=6^2-4^2$
$\Rightarrow \mathrm{QS}^{2}=36-16$
$\Rightarrow \mathrm{QS}^{2}=20$
$\Rightarrow Q S=2 \sqrt{5} \mathrm{~cm}$
$\mathrm{QS}^{2}=\mathrm{PS} \times \mathrm{SR}........(\mathrm{I})$
$\Rightarrow(2 \sqrt{5})^{2}=4 \times \mathrm{SR}$
$\Rightarrow \dfrac{20}{4}=\mathrm{SR}$
$\Rightarrow \mathrm{SR}=5 \mathrm{~cm}$
Now, $Q S \perp P R$
$\therefore \angle Q S R=90^{\circ}$
$\Rightarrow Q R^{2}=Q S^{2}+S R^{2}[\text { By Pythagoras theorem }]$
$\Rightarrow Q R^{2}=20+25$
$\Rightarrow Q R^{2}=45$
$\Rightarrow Q R=3 \sqrt{5} \mathrm{~cm}$
Hence, $Q S=2 \sqrt{5} \mathrm{~cm}, R S=5 \mathrm{~cm}$ and $Q R=3 \sqrt{5} \mathrm{~cm}$.
11. In ΔPQR, $PD \perp QR$ such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b) (a – b) = (c + d) (c – d).
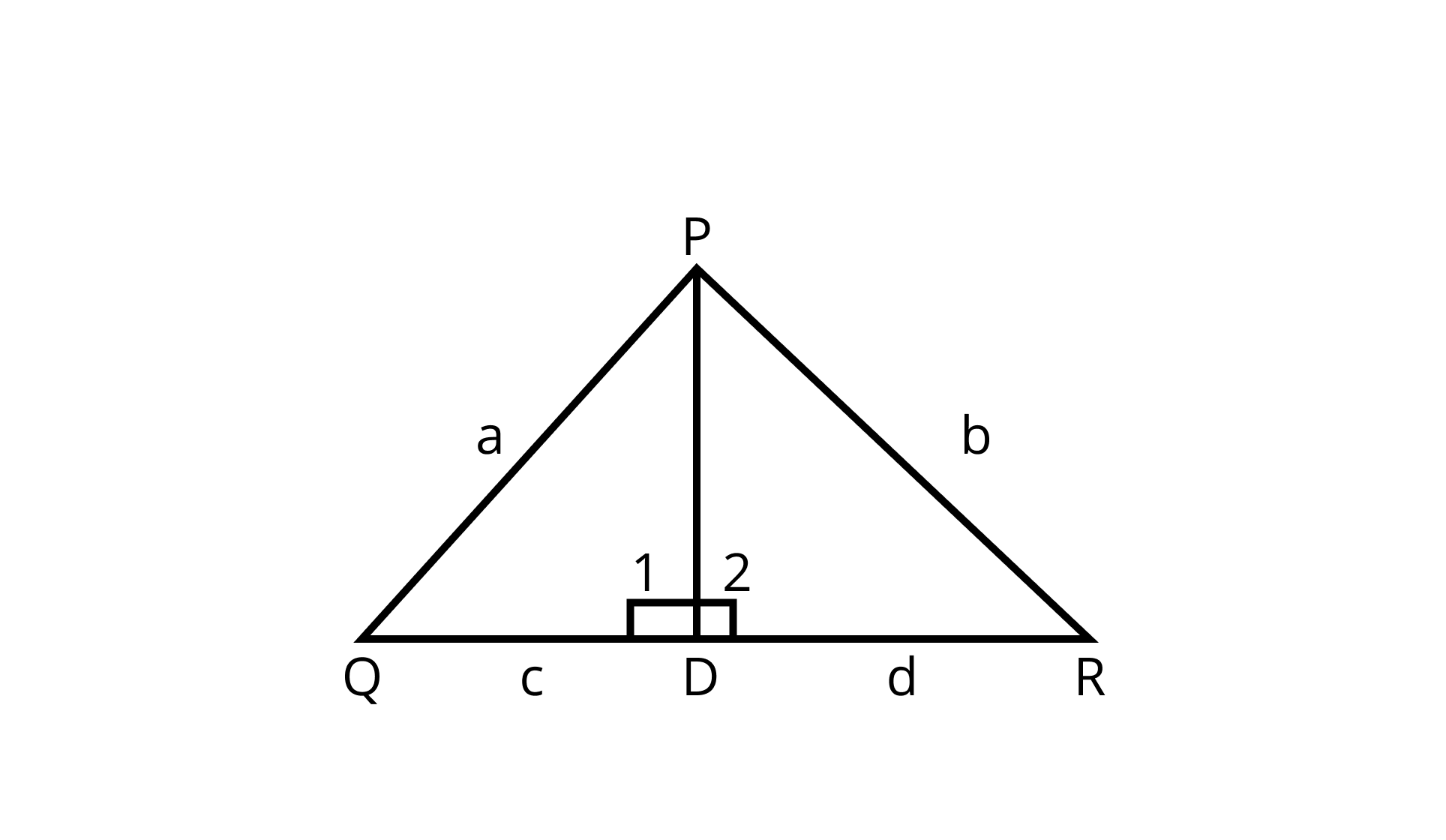
Ans: Given: In ΔPQR,
$PD \perp QR$
so ∠1 = ∠2
PQ = a, PR = b, QD = c and DR = d.
To Prove: (a + b)(a – b) = (c + d)(c – d)
Proof: In right angled ΔPDQ,
PD2 = PQ2 – QD2 (By Pythagoras theorem)
⇒ PD2 = a2 – c2 --------------------(I)
Similarly, in right angled ΔPDR,
PD2 = PR2 – DR2 (By Pythagoras theorem)
⇒ PD2 = b2 – d2 ------------------(II)
From (I) and (II), we have
a2 – c2 = b2 – d2
⇒ a2 – b2 = c2 – d2
⇒ (a – b)(a + b) = (c – d)(c + d)
Hence proved.
12. In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2 (Hint: Produce AB and DC to meet at E.)
Ans: Given: A quadrilateral ABCD in which ∠A + ∠D = 90°
To Prove: AC2 + BD2 = AD2 + BC2
Construction: Produce AB and DC to meet at E.
Proof: In ΔADE,
∠BAD + ∠CDA = 90° (Given)
∴ ∠E = 90° (Int. angles of a Δ)
By Pythagoras theorem in ΔADE and ΔBCE,
AD2 = AE2 + DE2 ……(I)
BC2 = BE2 + EC2 …..(II)
Adding (I) and (II), we get
AD2 + BC2 = AE2 + EC2 + DE2 + BE2 ……(III)
By Pythagoras theorem in ΔECA and ΔEBD,
AC2 = AE2 + CE2 ……………………(IV)
BD2 = BE2 + DE2 ……………………(V)
⇒ AC2 + BD2 = AE2 + BE2 + CE2 + DE2 ………………..(VI) (Adding (IV) and (V))
⇒ AC2 + BD2 = AD2 + BC2 (From (III) and (VI) )
Hence, proved
13. In the given figure, $l \| m$ and line segments $A B, C D$ and $E F$ are concurrent at point Prove that: $\dfrac{A E}{B F}=\dfrac{A C}{B D}=\dfrac{C E}{F D}$
Ans: Given: $l \| m$
Line segments $A B, C D$ and $E F$ are concurrent at $P$.
Points A, $E$ and $C$ are on line l.
Points $D, F$ and $B$ are on line $m$.
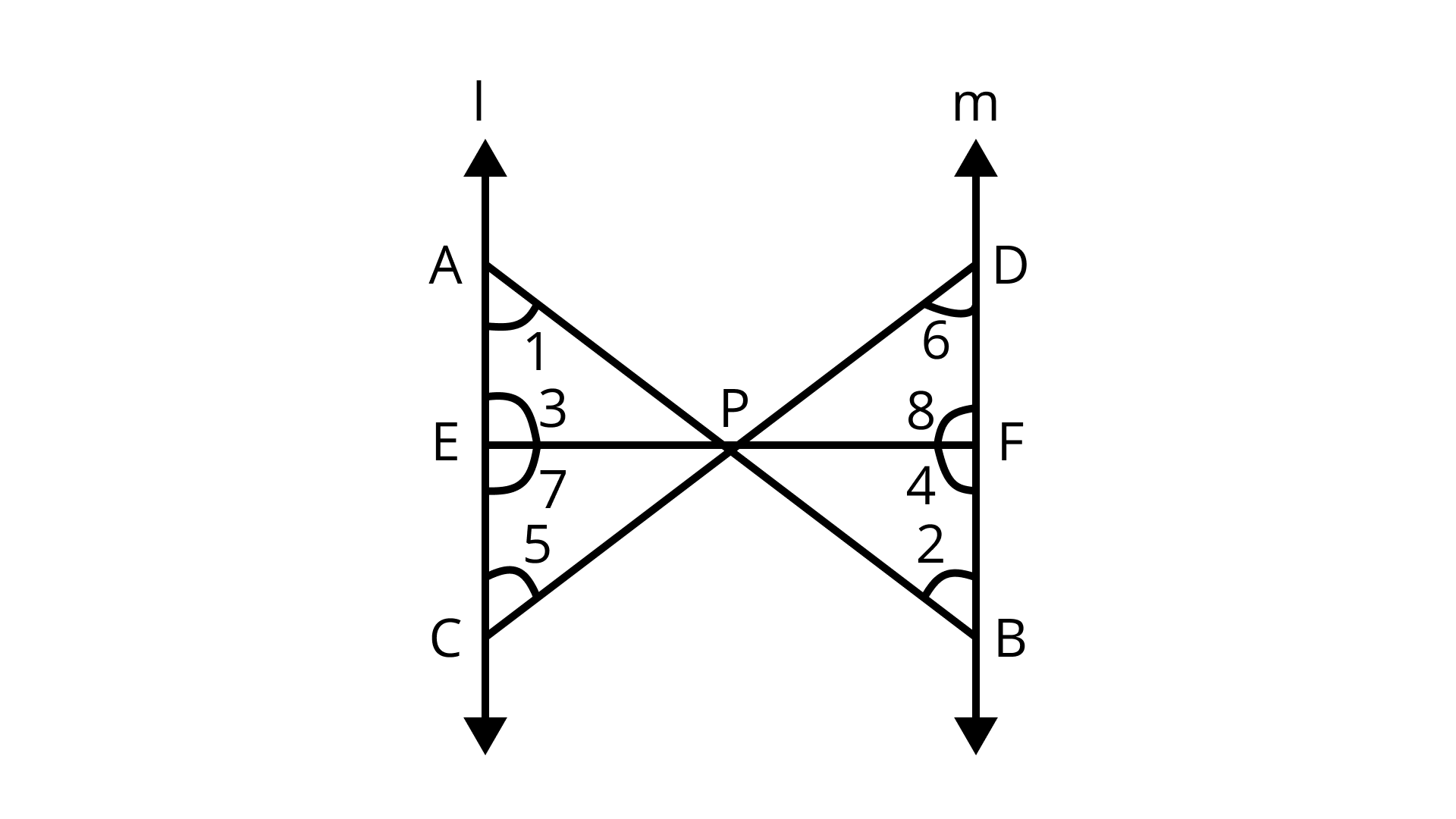
To Prove: $\dfrac{A E}{B F}=\dfrac{A C}{B D}=\dfrac{C E}{F D}$
Proof: In $\triangle A E P$ and $\triangle B F P$,
It is given that $l \| m$
$\angle 1=\angle 2$ (alternate interior angles)
Similarly, $\angle 3=\angle 4$ (alternate interior angles)
$\therefore$ by AA similarity criterion
$\Rightarrow \dfrac{A E}{B F}=\dfrac{A P}{B P}=\dfrac{E P}{F P}$
$\triangle A E P \sim \triangle B F P$
It is given that $l \| m$ $\angle 7=\angle 8$ (alternate interior angles)
Similarly,
∠5 = ∠6 (alternate interior angles)
∴ ΔACP ~ ΔBDP (By AA similarity criterion)
$\Rightarrow \dfrac{A C}{B D}=\dfrac{A P}{B P}=\dfrac{C P}{D P} \ldots \ldots \ldots . . .(I I I)$
$\Rightarrow \dfrac{A P}{B P}=\dfrac{A C}{B D}=\dfrac{C P}{D P}=\dfrac{C E}{D F}=\dfrac{E P}{E F}=\dfrac{A E}{B F}$
$\Rightarrow \dfrac{A C}{B D}=\dfrac{A E}{B F}=\dfrac{C E}{D F}$
Hence, proved.
14. In the given figure, PA, QB, RC and SD are all perpendiculars to a line ‘l’, AB = 6 cm, BC = 9 cm, CD = 12 cm and SP = 36 cm. Find PQ, QR and RS.
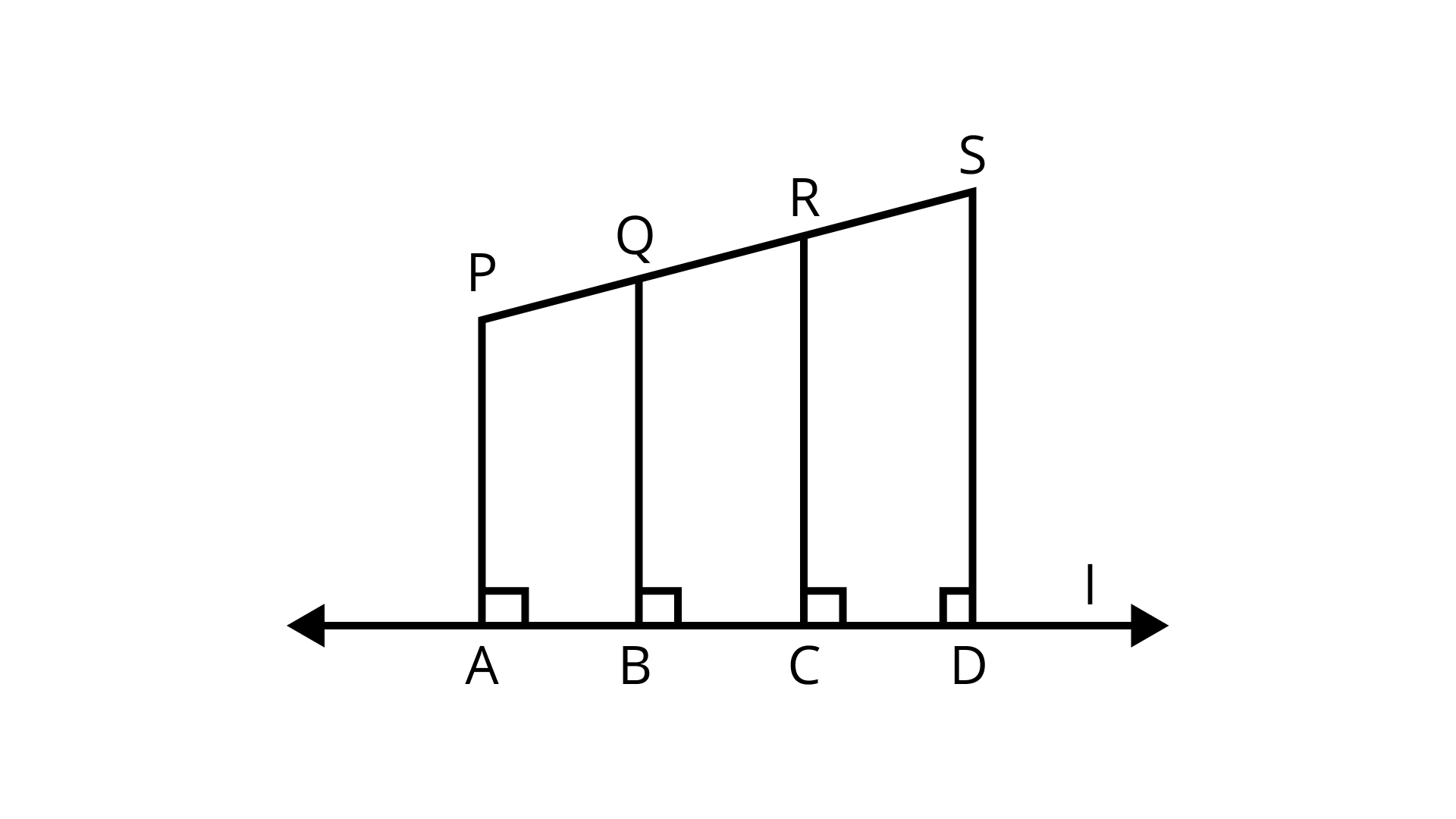
Ans: Given: PA, QB, RC and SD are perpendicular on line l.
AB = 6 cm, BC = 9 cm, CD = 12 cm
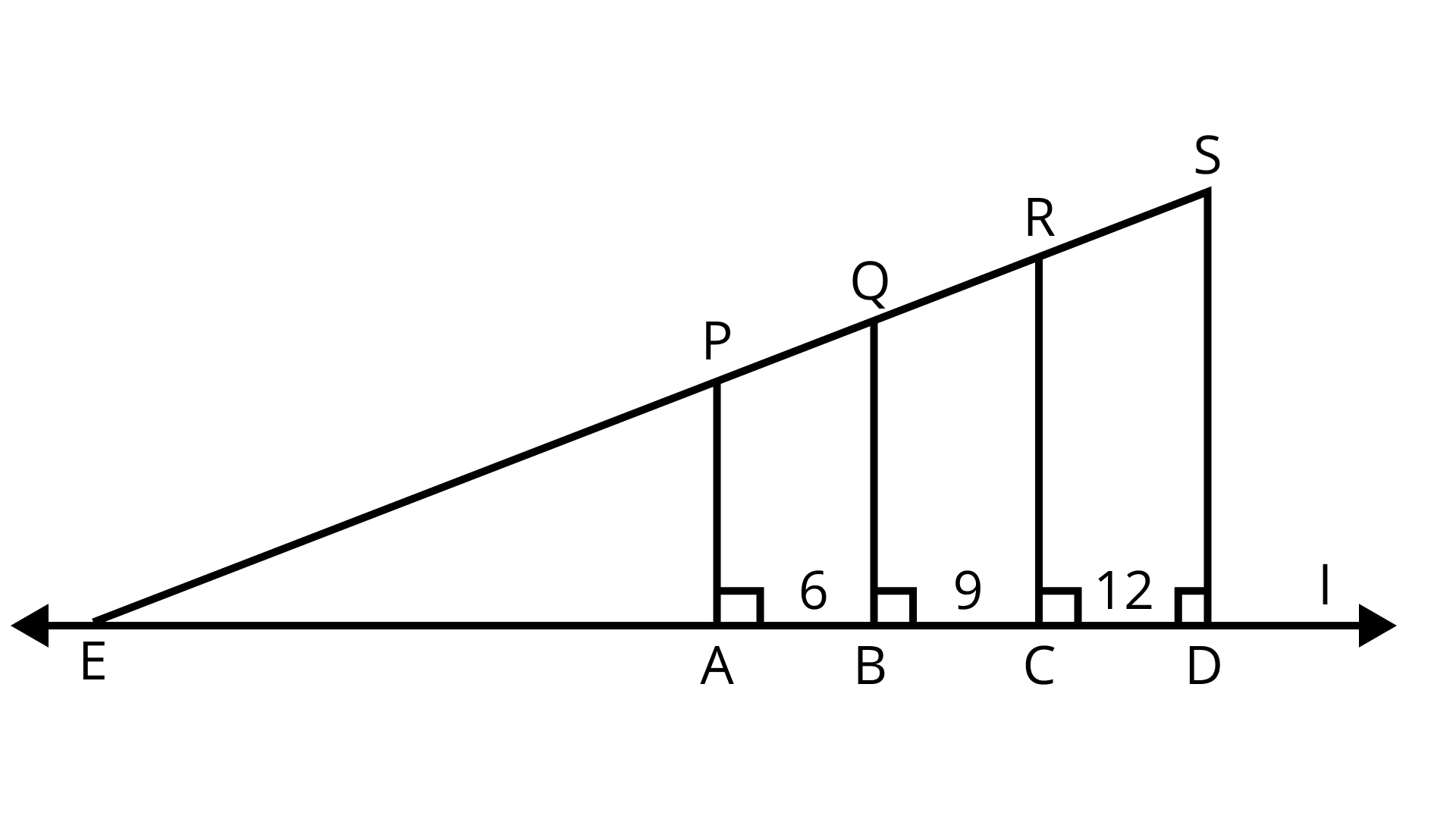
To find: PQ, QR and RS
Construction: Produce SP and l to meet each other at E.
Proof: In ΔEDS,
AP || BQ || DS || CR (Given)
∴ PQ : QR : RS = AB : BC : CD
PQ : QR : RS = 6 : 9 : 12
Let PQ = 6x
then QR = 9x
and RS = 12x
∴ PQ + QR + RS = 36 cm
⇒ 6x + 9x + 12x = 36
⇒ 27x = 36
$\Rightarrow x=\dfrac{36}{27}=\dfrac{4}{3}$
$\therefore \mathrm{PQ}=6 \times \dfrac{4}{3}=8 \mathrm{~cm}$
$\mathrm{QR}=9 \times \dfrac{4}{3}=12 \mathrm{~cm}$
15. ‘O’ is the point of intersection of the diagonals AC and BD of a trapezium ABCD with AB || DC. Through ‘O’, a line segment PQ is drawn parallel to AB meeting AD in P and BC in Q. Prove that PO = QO.
Ans: To Prove: PO = QO
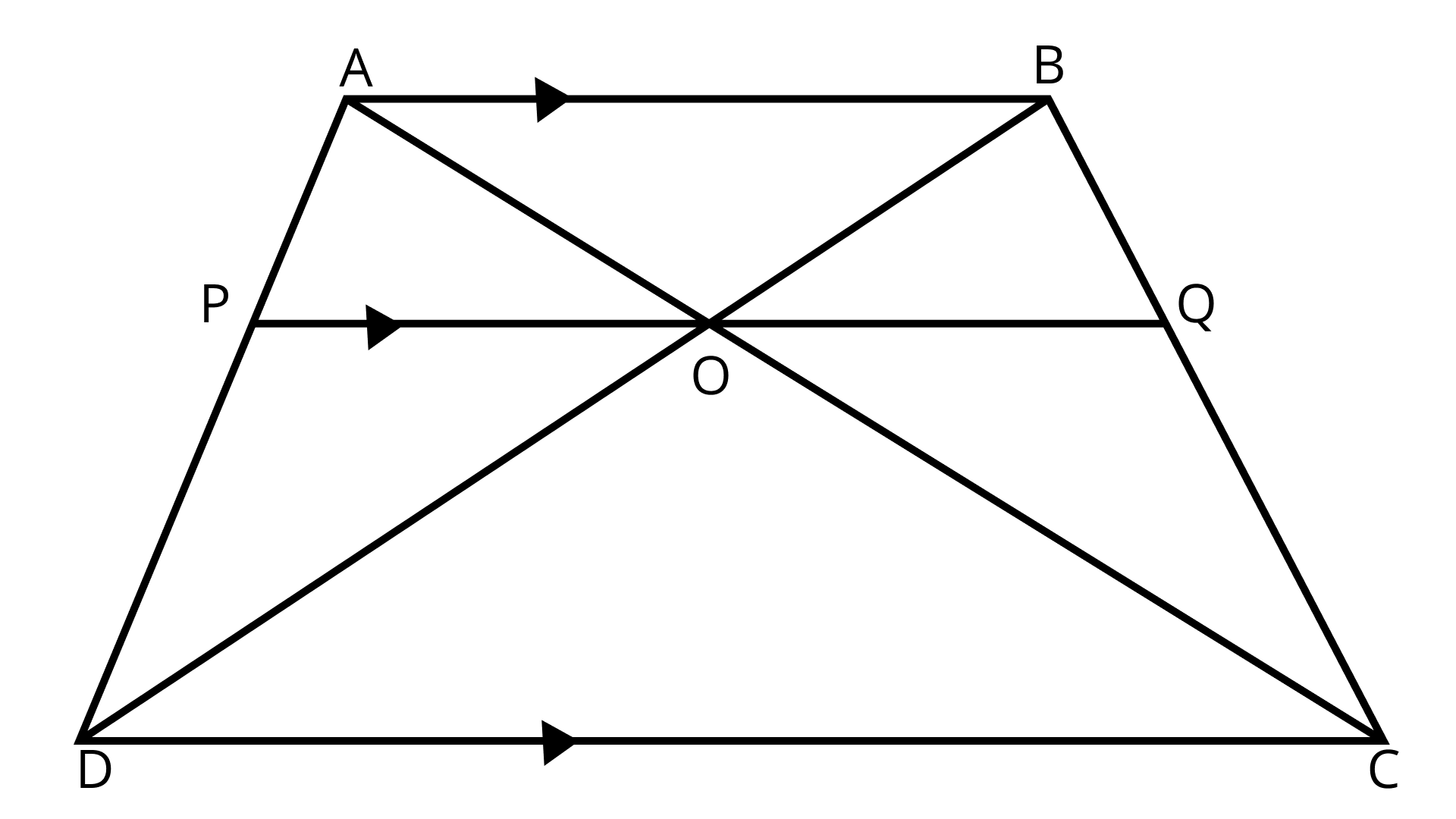
Proof: In ΔABD,
PO || AB (Given)
$\therefore \dfrac{A P}{P D}=\dfrac{B O}{O D}$ ……….(I) ( By BPT )
Similarly, in ΔBDC,
OQ || DC
$\therefore \dfrac{B O}{O D}=\dfrac{B Q}{Q C} \ldots \ldots . .(II)$
From (I) and (II), we have
$\Rightarrow \dfrac{A P}{P D}=\dfrac{B Q}{Q C}$
$\Rightarrow \dfrac{A P}{P D}+1=\dfrac{B Q}{Q C}+1$
Adding 1 both the sides
$\Rightarrow \dfrac{A P+P D}{P D}=\dfrac{B Q+Q C}{Q C}$
$\Rightarrow \dfrac{A D}{P D}=\dfrac{B Q}{Q C} \text { or } \dfrac{P D}{A D}=\dfrac{Q C}{B C} \ldots \ldots \ldots . .(I I I)$
In $\triangle D O P \text { and } \triangle D B A$,
AB|| PO
Given $\angle D P O=\angle D A B$ Corresponding angles
Similarly,
$\angle D O P=\angle D B A[\text{Corresponding angles }]$
$\therefore \Delta D O P \sim \triangle D B A$ (B y A A similarity criterion
$\Rightarrow \dfrac{P O}{A B}=\dfrac{D P}{D A} \ldots \ldots \ldots .(I V)$
$\text { Similarly, }$
$\triangle C O Q \sim \triangle C A B$ By AA similarity criterion
$\therefore \dfrac{O Q}{A B}=\dfrac{Q C}{B C} \ldots \ldots .(V)$
From (III), (IV) and (V), we have
$\therefore \dfrac{O Q}{A B}=\dfrac{Q C}{B C}$
$\Rightarrow \mathrm{PO}=\mathrm{OQ}$
Hence, proved.
16. In the given figure, line segment DF intersect the side AC of a triangle ΔABC at the point E such that E is the mid–point of CA and ∠AEF = ∠AFE. Prove that: $\dfrac{B D}{C B}=\dfrac{B F}{C E}$.
(Hint: Take point G on AB such that CG || DF.)
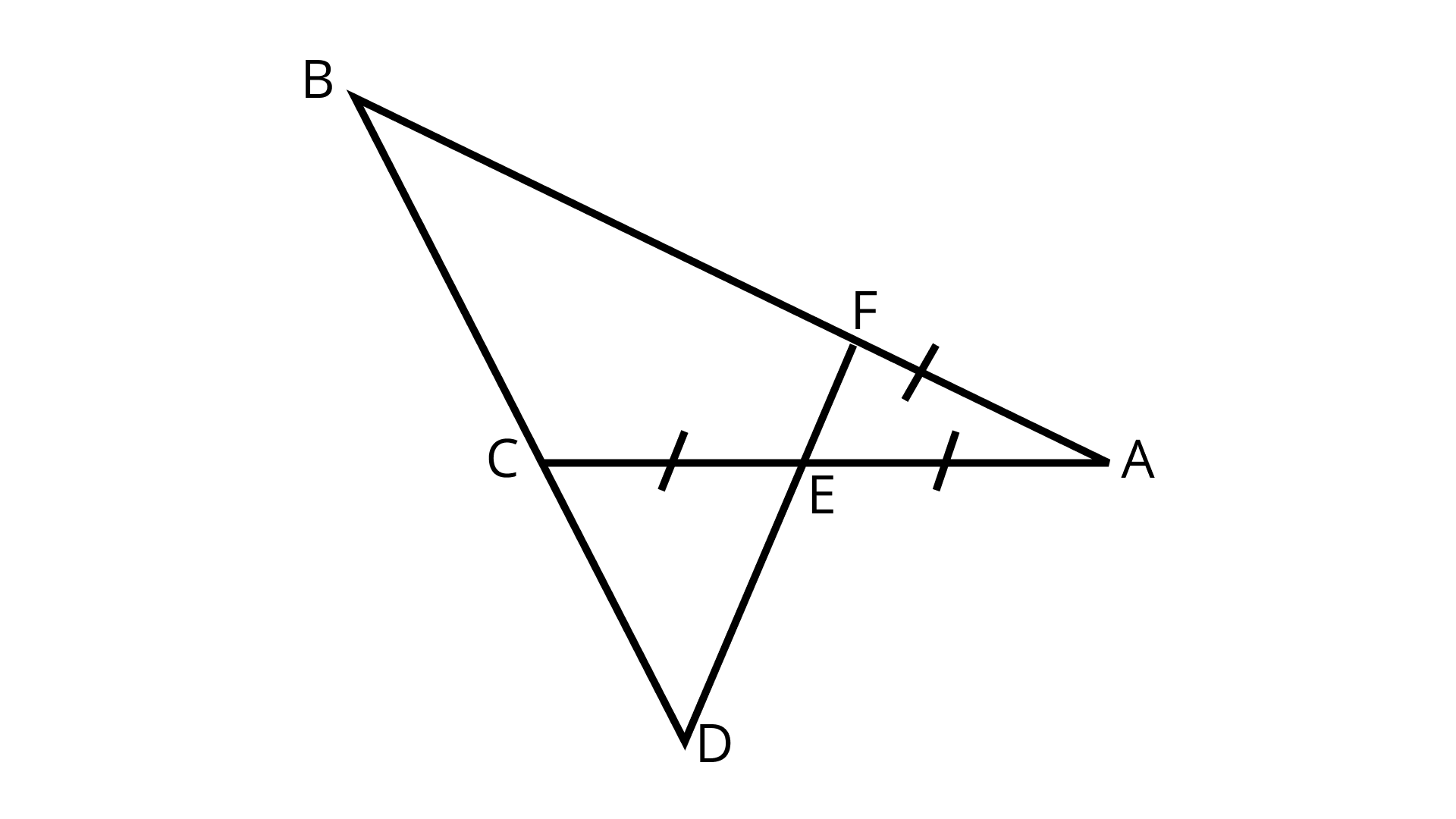
Ans: In the given figure of ΔABC,
EA = EC and ∠AEF = ∠AFE
To Prove: Construction: Draw CG || EF.
Proof: In ΔACG,
CG || EF.
E is the mid point of AC
F will be the midpoint of AG.
⇒ FG = FA But,
EC = EA = AF (Given)
∴ FG = FA = EA = EC (I)
In ΔBCG and BDF,
CG || EF (By construction)
$\therefore \dfrac{B C}{C D}=\dfrac{B G}{G F}[\mathrm{By} \mathrm{BPT}]$
$\Rightarrow\dfrac{B C}{C D}+1=\dfrac{B G}{G F}+1$
$\Rightarrow \dfrac{B C+C D}{C D}=\dfrac{B G+G F}{G F}$ $\Rightarrow \dfrac{B D}{C D}=\dfrac{B F}{G F}$
But FG=CE .....From(I)
$\Rightarrow \dfrac{B D}{C D}=\dfrac{B F}{C E}$
$\Rightarrow \dfrac{B D}{C D}=\dfrac{B F}{C E}$
Hence, proved.
17. Prove that the area of the semicircle drawn on the hypotenuse of a right-angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
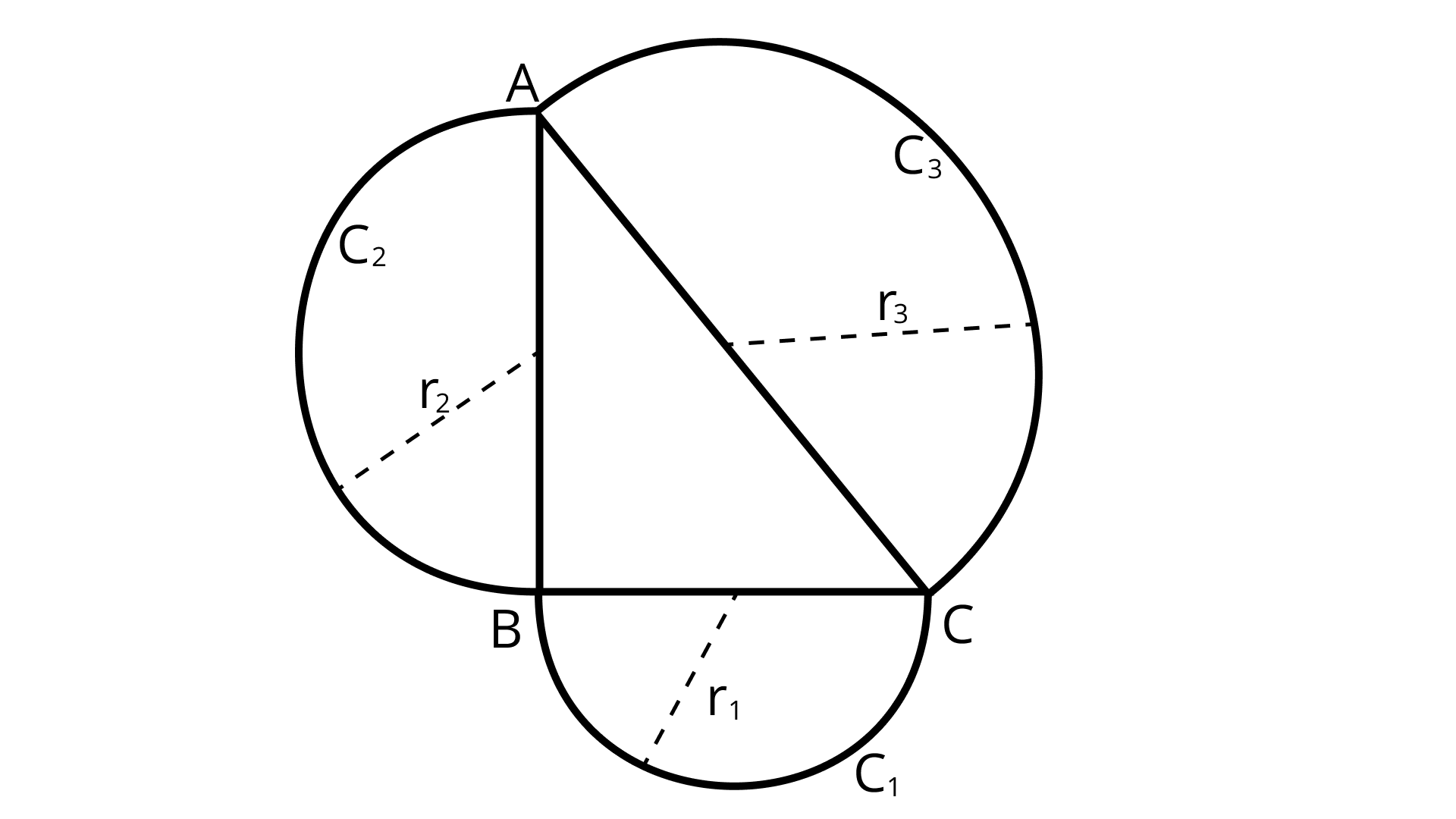
Ans: Given: In figure,
ΔABC is right at B.
Three semi–circles C1, C2, and C3 are drawn taking the sides BC, AB and AC of the triangle ABC as diameters.
To Prove: Area of semicircles (C1 + C2) = Area of semicircle C3
Proof: In ΔABC,
∠B = 90°
∴ BC2 + AB2 = AC2 (By Pythagoras theorem)
⇒ (2r1 )2 + (2r2 )2 = (2r3)2 (From figure as BC, AB and AC are diameters)
$\Rightarrow 4\left(r_{1}{ }^{2}+r_{2}{ }^{2}\right)=4 r_{3}{ }^{2}$
$\Rightarrow r_{1}{ }^{2}+r_{2}{ }^{2}=r_{3}{ }^{2}$
$\Rightarrow \dfrac{1}{2} \pi r_{1}{ }^{2}+\dfrac{1}{2} \pi r_{2}{ }^{2}=\dfrac{1}{2} \pi r_{3}{ }^{2}$
(Multiplying both sides by $\dfrac{1}{2} \pi$ )
ar(semi–circle C1) + ar(semi–circle C2 ) = ar(semi–circle C3)
Hence, proved.
18. Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
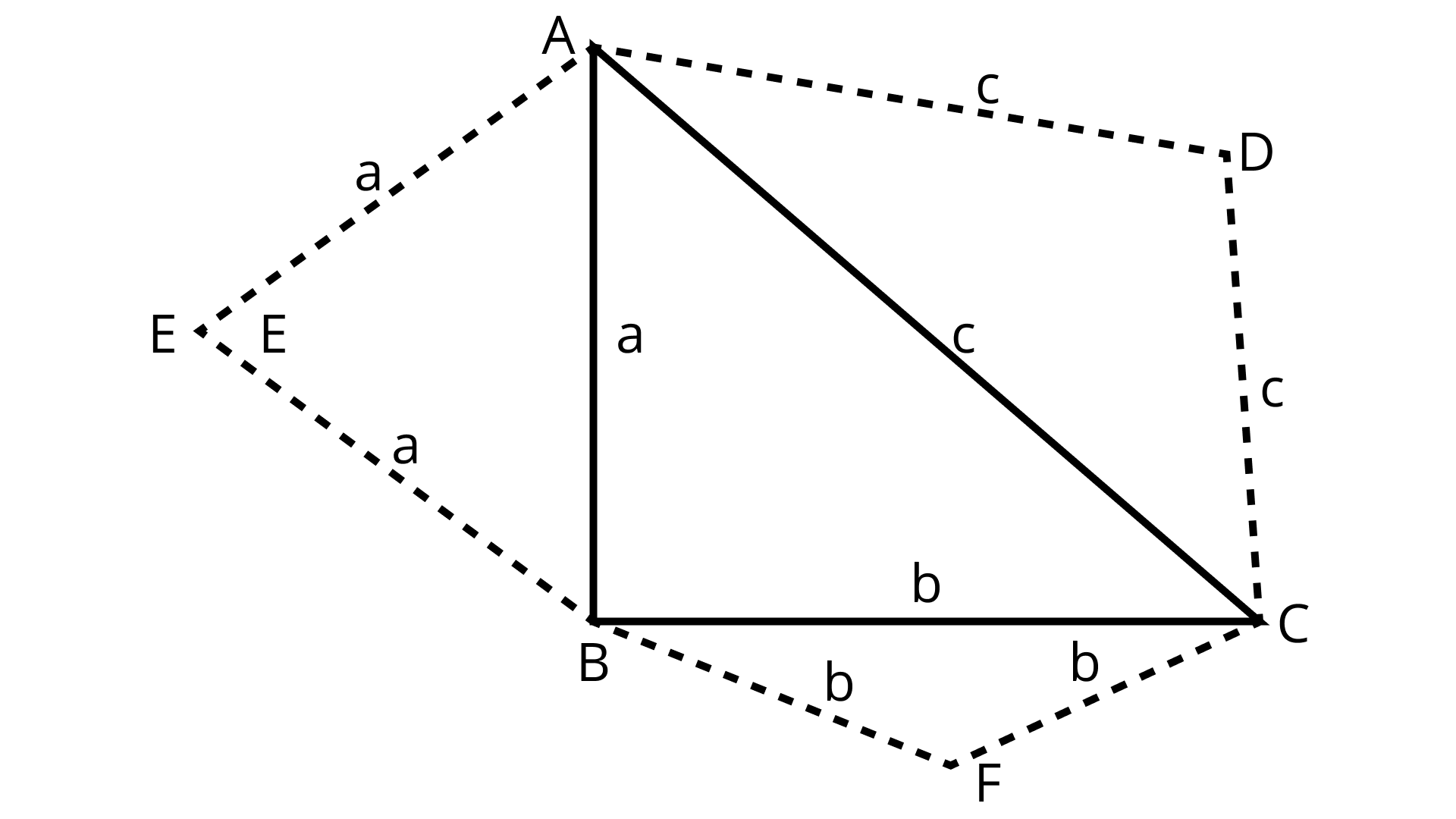
Ans: Given: A right triangle ABC.
Let $A B=a, B C=b, A C=c$ and $B=\angle 90^{\circ}$.
Equilateral triangles with sides $A B=a, B C=b$ and $A C=c$ are drawn respectively.
To Prove: Area of equilateral triangle with side hypotenuse (c) is equal to the sum of the areas of equilateral triangles with side $a$ and $b$.
or $\dfrac{\sqrt{3}}{4} c^{2}=\dfrac{\sqrt{3}}{4} a^{2}+\dfrac{\sqrt{3}}{4} b^{2}$
Proof: In $\triangle \mathrm{ABC}$,
$\angle \mathrm{ABC}=90^{\circ}$ (Given)
$\therefore A C^{2}=A B^{2}+B C^{2}[$ By Pythagoras theorem $]$
$\Rightarrow c^{2}=a^{2}+b^{2}$
$\Rightarrow \dfrac{\sqrt{3}}{4} c^{2}=\dfrac{\sqrt{3}}{4} a^{2}+\dfrac{\sqrt{3}}{4} b^{2}$ (Multiplying by $\dfrac{\sqrt{3}}{4}$ to both sides)
$\Rightarrow($ Area of equilateral $\Delta$ with side $c)=($ Area of equilateral $\Delta$ with side a) $+($ Area of equilateral $\Delta$ with side b)
Hence, the area of equilateral $\Delta$ with hypotenuse is equal to the sum of areas of equilateral triangles on the other two sides. Hence, proved.
