Master Class 10 Maths Chapter 6 Exercise 6.3 With Vedantu's Expert Guidance
NCERT Solutions For Class 10 Maths Chapter 6 Triangles
FAQs on NCERT Solutions For Class 10 Maths Chapter 6 Triangles
1. What is the main concept tested in NCERT Solutions for Class 10 Maths Chapter 6 Exercise 6.3?
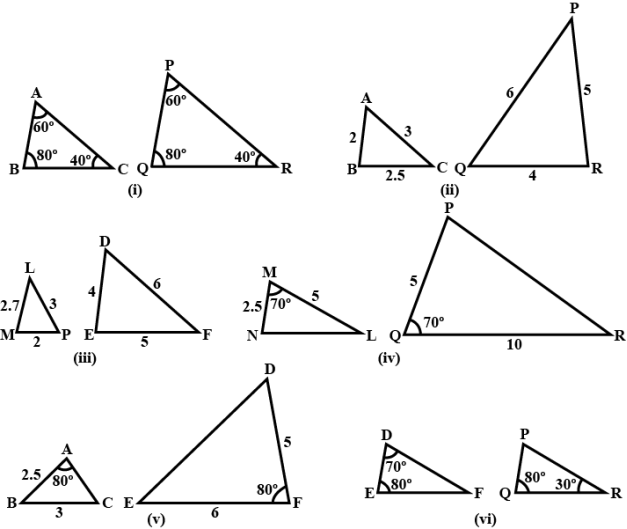
Exercise 6.3 in NCERT Solutions for Class 10 Maths Chapter 6 focuses on the similarity of triangles. The exercise examines various criteria for triangle similarity such as AAA (Angle-Angle-Angle), SSS (Side-Side-Side), and SAS (Side-Angle-Side), and tests students through proof-based and application questions aligned with CBSE guidelines for 2025–26.
2. How do you determine if two triangles are similar as per the CBSE Class 10 Maths syllabus?
To determine similarity of two triangles using NCERT Solutions for Class 10 Maths Chapter 6:
- Check if any similarity criterion holds: AAA, SSS, or SAS.
- AAA: All corresponding angles are equal.
- SSS: All sides are proportional.
- SAS: Two sides are in proportion and the included angles are equal.
3. Why is the SAS criterion important for solving triangles in Exercise 6.3 NCERT Solutions?
The SAS (Side-Angle-Side) criterion allows students to establish similarity even when one angle and its adjacent sides are known to be in correct proportion. This criterion is essential because it enables the solving of problems where all three sides or all the angles may not be directly given, reflecting frequent CBSE exam application-based questions.
4. What are common student mistakes when answering similarity of triangles questions in Exercise 6.3?
Students often:
- Mistake congruence for similarity (congruence requires equal sides and angles, while similarity only needs proportional sides and equal angles).
- Mix up the criteria (AAA/SSS/SAS) and use an incorrect theorem.
- Forget to check all necessary correspondence between sides and angles.
5. Can you explain with proof how the properties of similar triangles are used to solve application problems in Class 10 Maths NCERT Solutions?
In application questions, such as those involving heights and distances, the properties of similar triangles (corresponding sides in equal ratios and equal corresponding angles) help set up proportional equations. For example, relating the height of a pole and its shadow to an unknown height uses the AA similarity criterion, a frequently tested scenario in CBSE board exams.
6. How should one write stepwise solutions for similarity questions to align with NCERT Solutions for Class 10 Maths Chapter 6?
For full marks in CBSE, each step should state:
- The given information and the required proof/result.
- The similarity criterion applied (AAA, SSS, SAS) with clear matching of corresponding sides/angles.
- The proportionality or equality setup, justified with correct theorem names.
7. When applying the SSS criterion in Exercise 6.3, what must you check before concluding triangles are similar?
For the SSS (Side-Side-Side) criterion, confirm that:
- All three corresponding sides of the two triangles are proportional (i.e., AB/PQ = BC/QR = AC/PR).
8. What if a triangle question in Exercise 6.3 presents only angle information—how can similarity be established?
If only angles are given, use the AAA criterion. If all three corresponding angles in two triangles are equal, the triangles are similar, no matter the side lengths.
9. How does the NCERT Solutions approach help in mastering CBSE-style similarity proofs?
NCERT Solutions provide stepwise answers modeled after CBSE exam requirements:
- List all given facts.
- Identify and cite the criterion (AAA, SSS, SAS) relevant to the problem.
- Justify every proportionality or equality used.
10. What is a real-life application of the similarity of triangles concept studied in Chapter 6?
One practical use is measuring inaccessible heights (like towers or trees) using proportions created by their shadows and that of a smaller measurable object, applying the similarity of triangles (typically by AA/AAA criteria).
11. In Class 10 Maths Chapter 6, why are medians and altitudes commonly used in NCERT Solutions for similarity questions?
Medians and altitudes often create triangles within triangles, offering required geometric elements (equal sides, right angles, or known ratios) that facilitate the use of similarity criteria. These constructs align with CBSE's focus on multidimensional triangle problems.
12. Which similarity criteria are most likely to appear in CBSE 2025–26 board exams, based on current NCERT Solutions patterns?
The AAA, SSS, and SAS similarity criteria are most frequently tested, especially in multi-step or proof-based questions drawing directly from NCERT Solutions for Class 10 Maths Chapter 6 Triangles.
13. How can similarity of triangles help in solving coordinate geometry questions in later chapters?
By establishing similar triangles within coordinate axes setups, you can:
- Find unknown lengths by proportionality.
- Prove collinearity or equal slopes.
- Simplify area or ratio-based questions—techniques that build upon similarity methods outlined in Chapter 6.
14. What if two triangles share a side and have two pairs of equal angles as per Class 10 NCERT Solutions?
If two triangles share a side and have two corresponding angles equal, the AA criterion confirms similarity irrespective of side length. This scenario often arises in proofs with shared vertices/segments.
15. How do you choose the right similarity criterion in a mixed-question in Exercise 6.3?
Read the problem and:
- Identify what is given (sides or angles).
- If all angles—apply AAA; all sides—apply SSS; two sides and included angle—apply SAS.




















 Watch Video
Watch Video