Courses

Courses for Kids

Free study material

Store

Talk to our experts

1800-120-456-456

NCERT Solutions

Class 10

Maths

Chapter 8 Introduction To Trigonometry

NCERT Solutions for Class 10 Maths Chapter 8 Introduction To Trigonometry

NCERT Solutions for Maths Chapter 8 Class 10 Introduction to Trigonometry - Free PDF Download

NCERT Solutions for Class 10 Maths Chapter 8 - Introduction to Trigonometry. Trigonometry, a fundamental branch of mathematics, explores the relationships between angles and sides of triangles. In this chapter, students delve into the basic concepts of trigonometry, such as trigonometric ratios, complementary angles, trigonometric identities, and their applications in solving problems related to heights and distances. These solutions are meticulously crafted by Vedantu’s subject expert with a clear understanding of the concepts, aiding students in mastering the fundamentals of trigonometry and preparing them for more advanced topics in mathematics.

Table of Content

Glance of NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry | Vedantu

Trigonometry comes from Greek words meaning "three sides" and "measure."
The article covers the basics of Trigonometry and Trigonometric Ratios.
This chapter focuses on trigonometric ratios for acute angles (less than 90 degrees).
You will learn how to calculate these ratios for specific angles.
A table for the values of angles (0 Degree, 30 Degree, 45 Degree, 60 Degree, 90 Degree) with their corresponding trigonometric functions(sin, cos, tan, cot, sec, cosec) is provided.
There are relationships between these ratios, which you will explore (trigonometric identities).

Also, This article contains chapter notes, formulas, exercises links, and important questions for chapter 8 -Introduction to Trigonometry.
There are four exercises (27 fully solved questions) in class 10th maths chapter 8 Introduction to Trigonometry.

Access Exercise Wise NCERT Solutions for Chapter 8 Maths Class 10

S. No	Current Syllabus Exercises of Class 10 Maths Chapter 8
1	NCERT Solutions of Class 10 Maths Introduction to Trigonometry Exercise 8.1
2	NCERT Solutions of Class 10 Maths Introduction to Trigonometry Exercise 8.2
3	NCERT Solutions of Class 10 Maths Introduction to Trigonometry Exercise 8.3

Courses

Watch videos on

NCERT Solutions for Class 10 Maths Chapter 8 Introduction To Trigonometry

Vedantu 9&10

Download Notes

TRIGONOMETRY Class 10 in One Shot (Complete Chapter) | CBSE 10 Math Chapter 8 [Term 1 Exam] Vedantu

7.2K likes

155.6K Views

3 years ago

Vedantu 9&10

Download Notes

TRIGONOMETRY L-2 (Trigonometric Identities) CBSE Class 10 Maths Chapter 8 | Term 1 Exam | Vedantu

7.9K likes

142.8K Views

3 years ago

More Free Study Material for Introduction to Trigonometry

Revision notes

857.1k views • 14k downloads

Important questions

766.8k views • 15k downloads

Ncert books

783.3k views • 14k downloads

Exercises Under NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Exercise 8.1 - In this exercise, students are introduced to the basic trigonometric ratios - sine, cosine, and tangent, and their reciprocal functions. They learn how to find the values of these ratios for acute angles in a right triangle. The exercise also covers the concept of trigonometric identities, which are fundamental relationships between trigonometric functions.

Exercise 8.2 - This exercise deals with the application of trigonometric ratios to solve real-life problems. Students learn how to use trigonometric ratios to find the height and distance of an object, as well as the angle of elevation and depression. They also learn how to use the Pythagorean theorem to solve problems involving right triangles.

Exercise 8.3 - The final exercise covers the concept of trigonometric equations. Students learn how to solve trigonometric equations using the identities and ratios learned in the previous exercises. They also learn how to find the general solution of a trigonometric equation, which involves finding all the possible solutions. Finally, the exercise covers the concept of the period of a trigonometric function and how to find it for different functions.

Access NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry

Exercise 8.1

1. In $Δ A B C$ right angled at $B$ , $A B = 24 cm$ , $B C = 7 cm$ . Determine

(i) $\sin A, \cos A$

Ans: Given that in the right angle triangle $Δ A B C$ , $A B = 24 cm$ , $B C = 7 cm$ .

Let us draw a right triangle $Δ A B C$ , also $A B = 24 cm$ , $B C = 7 cm$ . We get

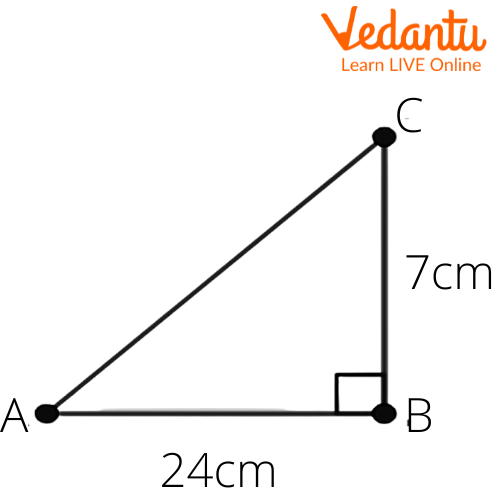
We have to find $\sin A, \cos A$ .

We know that for right triangle

$\sin θ = \frac{opposite side}{hypotenuse}$ and

$\cos θ = \frac{adjacent side}{hypotenuse}$

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $Δ A B C$ , by Pythagoras theorem ,

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

Here, $A B = 24 cm$ , $B C = 7 cm$

We get

$\Rightarrow {(AC)}^{2} = {(A B)}^{2} + {(B C)}^{2}$

$\Rightarrow {(AC)}^{2} = {(24)}^{2} + {(7)}^{2}$

$\Rightarrow {(AC)}^{2} = 576 + 49$

$\Rightarrow {(AC)}^{2} = 625 c m^{2}$

$\Rightarrow A C = 25 cm$

Now,

$\sin θ = \frac{opposite side}{hypotenuse}$

$\Rightarrow \sin A = \frac{B C}{A C}$

$∴ \sin A = \frac{7}{25}$

$\cos θ = \frac{adjacent side}{hypotenuse}$

$\Rightarrow \cos A = \frac{A B}{A C}$

$∴ \cos A = \frac{24}{25}$

(ii) $\sin C, \cos C$

Ans: Given that in the right angle triangle $Δ A B C$ , $A B = 24 cm$ , $B C = 7 cm$ .

Let us draw a right triangle $Δ A B C$ , also $A B = 24 cm$ , $B C = 7 cm$ . We get

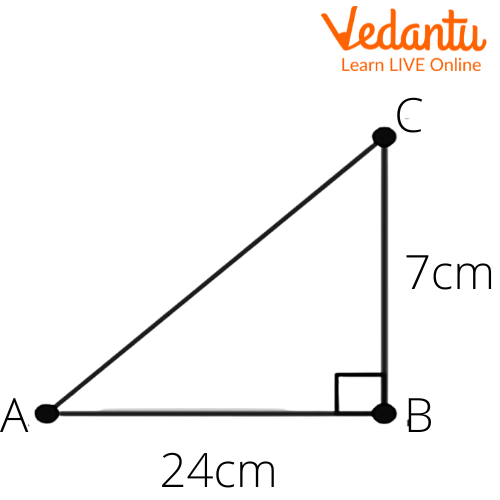
We have to find $\sin C, \cos C$ .

We know that for right triangle

$\sin θ = \frac{opposite side}{hypotenuse}$ and

$\cos θ = \frac{adjacent side}{hypotenuse}$

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $Δ A B C$ , by Pythagoras theorem ,

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

Here, $A B = 24 cm$ , $B C = 7 cm$

We get

$\Rightarrow {(AC)}^{2} = {(A B)}^{2} + {(B C)}^{2}$

$\Rightarrow {(AC)}^{2} = {(24)}^{2} + {(7)}^{2}$

$\Rightarrow {(AC)}^{2} = 576 + 49$

$\Rightarrow {(AC)}^{2} = 625 c m^{2}$

$\Rightarrow A C = 25 cm$

Now,

$\sin θ = \frac{opposite side}{hypotenuse}$

$\Rightarrow \sin C = \frac{A B}{A C}$

$∴ \sin C = \frac{24}{25}$

$\cos θ = \frac{adjacent side}{hypotenuse}$

$\Rightarrow \cos C = \frac{B C}{A C}$

$∴ \cos A = \frac{7}{25}$

3. In the given figure find $\tan P - \cot R$ .

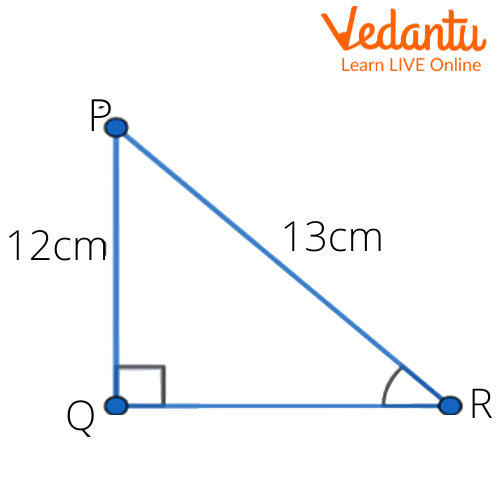
Ans: Given in the figure,

$P Q = 12 cm$

$P Q = 13 cm$

We know that for right triangle

$\tan θ = \frac{opposite side}{adjacent side}$ and

$\cot θ = \frac{adjacent side}{opposite side}$

Now, we need to apply the Pythagoras theorem to find the measure of adjacent side/base.

In $Δ P Q R$ , by Pythagoras theorem ,

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

We get

$\Rightarrow {(P R)}^{2} = {(P Q)}^{2} + {(Q R)}^{2}$

$\Rightarrow {(13)}^{2} = {(12)}^{2} + {(Q R)}^{2}$

$\Rightarrow 169 = 144 + {(Q R)}^{2}$

$\Rightarrow {(Q R)}^{2} = 169 - 144$

$\Rightarrow {(Q R)}^{2} = 25 c m^{2}$

$\Rightarrow Q R = 5 cm$

Now,

$\tan P = \frac{opposite side}{adjacent side}$

$\Rightarrow \tan P = \frac{Q R}{P Q}$

$∴ \tan P = \frac{5}{12}$

$\cot R = \frac{adjacent side}{opposite side}$

$\Rightarrow \cot R = \frac{Q R}{P Q}$

$∴ \cot R = \frac{5}{12}$

$\Rightarrow \tan P - \cot R = \frac{5}{12} - \frac{5}{12}$

$∴ \tan P - \cot R = 0$

3. If $\sin A = \frac{3}{4}$ , calculate $\cos A$ and $\tan A$ .

Ans: Let us consider a right angled triangle $Δ A B C$ . We get

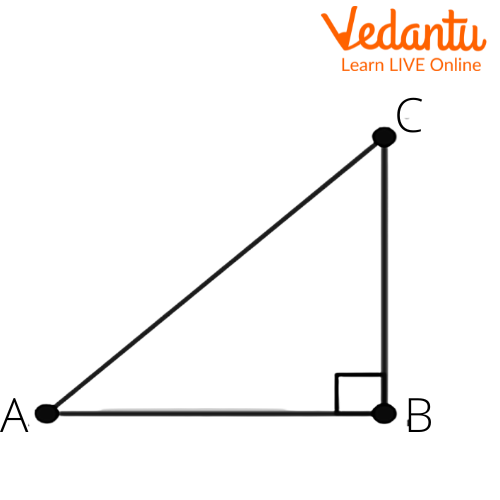
Given that $\sin A = \frac{3}{4}$ .

We know that $\sin θ = \frac{opposite side}{hypotenuse}$ .

From the above figure, we get

$\sin A = \frac{B C}{A C}$

Therefore, we get

$\Rightarrow B C = 3$ and

$\Rightarrow A C = 4$

Now, we have to find the values of $\cos A$ and $\tan A$ .

We know that $\cos θ = \frac{adjacent side}{hypotenuse}$ and $\tan θ = \frac{opposite side}{adjacent side}$ .

Now, we need to apply the Pythagoras theorem to find the measure of adjacent side/base.

In $Δ A B C$ , by Pythagoras theorem ,

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

Here, $A C = 4 cm$ , $B C = 3 cm$

We get

$\Rightarrow {(AC)}^{2} = {(A B)}^{2} + {(B C)}^{2}$

$\Rightarrow 4^{2} = A B^{2} + 3^{2}$

$\Rightarrow 16 = A B^{2} + 9$

$\Rightarrow A B^{2} = 16 - 9$

$\Rightarrow A B^{2} = 7$

$\Rightarrow A B = \sqrt{7} cm$

Now, we get

$\cos A = \frac{A B}{A C}$

$∴ \cos A = \frac{\sqrt{7}}{4}$

And $\tan A = \frac{B C}{A B}$

$∴ \tan A = \frac{3}{\sqrt{7}}$

4. Given $15 \cot A = 8$ . Find $\sin A$ and $\sec A$ .

Ans: Let us consider a right angled triangle $Δ A B C$ . We get

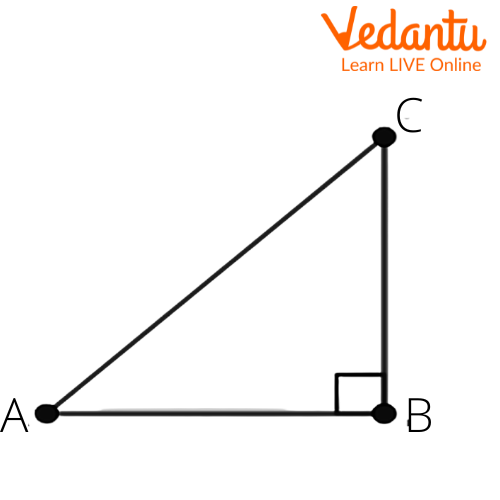
Given that $15 \cot A = 8$ .

We get $\cot A = \frac{8}{15}$ .

We know that $\cot θ = \frac{adjacent side}{opposite side}$ .

From the above figure, we get

$\cot A = \frac{A B}{B C}$

Therefore, we get

$\Rightarrow B C = 15$ and

$\Rightarrow A B = 8$

Now, we have to find the values of $\sin A$ and $\sec A$ .

We know that $\sin θ = \frac{opposite side}{hypotenuse}$ and $\sec θ = \frac{hypotenuse}{adjacent side}$ .

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $Δ A B C$ , by Pythagoras theorem ,

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

We get

$\Rightarrow {(AC)}^{2} = {(A B)}^{2} + {(B C)}^{2}$

$\Rightarrow A C^{2} = 8^{2} + 15^{2}$

$\Rightarrow A C^{2} = 64 + 225$

$\Rightarrow A C^{2} = 289$

$\Rightarrow A C = 17 cm$

Now, we get

$\sin A = \frac{B C}{A C}$

$∴ \sin A = \frac{15}{17}$

And $\sec A = \frac{A C}{A B}$

$∴ \sec A = \frac{17}{8}$

5. Given $\sec θ = \frac{13}{12}$ , calculate all other trigonometric ratios.

Ans: Let us consider a right angled triangle $Δ A B C$ . We get

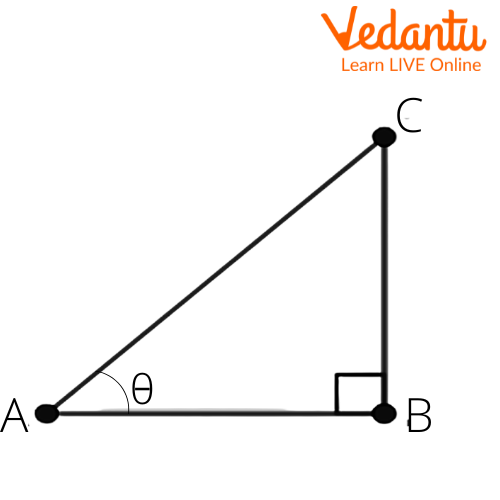
Given that $\sec θ = \frac{13}{12}$ .

We know that $\sec θ = \frac{hypotenuse}{adjacent side}$ .

From the above figure, we get

$\sec θ = \frac{A C}{A B}$

Therefore, we get

$\Rightarrow A C = 13$ and

$\Rightarrow A B = 12$

Now, we need to apply the Pythagoras theorem to find the measure of the perpendicular/opposite side.

In $Δ A B C$ , by Pythagoras theorem ,

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

We get

$\Rightarrow {(AC)}^{2} = {(A B)}^{2} + {(B C)}^{2}$

$\Rightarrow 13^{2} = 12^{2} + B C^{2}$

$\Rightarrow 169 = 144 + B C^{2}$

$\Rightarrow B C^{2} = 25$

$\Rightarrow B C = 5 cm$

Now, we know that

$\sin θ = \frac{opposite side}{hypotenuse}$

Here, $\sin θ = \frac{B C}{A C}$

$∴ \sin θ = \frac{5}{13}$

We know that $\cos θ = \frac{adjacent side}{hypotenuse}$

Here, $\cos θ = \frac{A B}{A C}$

$∴ \cos θ = \frac{12}{13}$

We know that $\tan θ = \frac{opposite side}{adjacent side}$

Here, $\tan θ = \frac{B C}{A B}$

$∴ \tan θ = \frac{5}{12}$

We know that $cosec θ = \frac{hypotenuse}{opposite side}$

Here, $cosec θ = \frac{A C}{B C}$

$∴ cosec θ = \frac{13}{5}$

We know that $\cot θ = \frac{adjacent side}{opposite side}$

Here, $\cot θ = \frac{AB}{B C}$

$∴ \cot θ = \frac{12}{5}$ .

6. If $∠ A$ and $∠ B$ are acute angles such that $\cos A = \cos B$ , then show that $∠ A = ∠ B$ .

Ans: Let us consider a right angled triangle $Δ A B C$ . We get

Given that $\cos A = \cos B$ .

In a right triangle $Δ A B C$ , we know that

$\cos θ = \frac{adjacent side}{hypotenuse}$

Here,

$\cos A = \frac{A C}{A B}$

And $\cos B = \frac{B C}{A B}$

As given $\cos A = \cos B$ , we get

$\Rightarrow \frac{A C}{A B} = \frac{B C}{A B}$

$\Rightarrow A C = A B$

Now, we know that angles opposite to the equal sides are also equal in measure.

Then, we get

$∠ A = ∠ B$

Hence proved.

7. Evaluate the following if $\cot θ = \frac{7}{8}$

(i) $\frac{(1 + \sin θ) (1 - \sin θ)}{(1 + \cos θ) (1 - \cos θ)}$

Ans: Let us consider a right angled triangle $Δ A B C$ . We get

Now, in a right triangle we know that $\cot θ = \frac{adjacent side}{opposite side}$ .

Here, from the figure $\cot θ = \frac{B C}{A B}$ .

We get

$A B = 8$ and

$B C = 7$

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $Δ A B C$ , by Pythagoras theorem ,

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

We get

$\Rightarrow {(AC)}^{2} = {(A B)}^{2} + {(B C)}^{2}$

$\Rightarrow {(AC)}^{2} = 8^{2} + 7^{2}$

$\Rightarrow {(AC)}^{2} = 64 + 49$

$\Rightarrow {(AC)}^{2} = 113$

$\Rightarrow A C = \sqrt{113}$

Now, we know that

$\sin θ = \frac{opposite side}{hypotenuse}$

Here, we get

$\sin θ = \frac{A B}{A C} = \frac{8}{\sqrt{113}}$ and

$\cos θ = \frac{adjacent side}{hypotenuse}$

Here, we get

$\cos θ = \frac{B C}{A C} = \frac{7}{\sqrt{113}}$

Now, we have to evaluate

$\frac{(1 + \sin θ) (1 - \sin θ)}{(1 + \cos θ) (1 - \cos θ)}$

Applying the identity $(a + b) (a - b) = a^{2} - b^{2}$ , we get

$\Rightarrow \frac{(1 + \sin θ) (1 - \sin θ)}{(1 + \cos θ) (1 - \cos θ)} = \frac{1 - \sin^{2} θ}{1 - \cos^{2} θ}$

Substituting the values, we get

$\Rightarrow \frac{(1 + \sin θ) (1 - \sin θ)}{(1 + \cos θ) (1 - \cos θ)} = \frac{1 - {(\frac{8}{\sqrt{113}})}^{2}}{1 - {(\frac{7}{\sqrt{113}})}^{2}}$

$\Rightarrow \frac{(1 + \sin θ) (1 - \sin θ)}{(1 + \cos θ) (1 - \cos θ)} = \frac{1 - \frac{64}{113}}{1 - \frac{49}{113}}$

$\Rightarrow \frac{(1 + \sin θ) (1 - \sin θ)}{(1 + \cos θ) (1 - \cos θ)} = \frac{\frac{113 - 64}{113}}{\frac{113 - 49}{113}}$

$\Rightarrow \frac{(1 + \sin θ) (1 - \sin θ)}{(1 + \cos θ) (1 - \cos θ)} = \frac{\frac{49}{113}}{\frac{64}{113}}$

$∴ \frac{(1 + \sin θ) (1 - \sin θ)}{(1 + \cos θ) (1 - \cos θ)} = \frac{49}{64}$

(ii) $\cot^{2} θ$

Ans: Given that $\cot θ = \frac{7}{8}$ .

Now, $\cot^{2} θ = {(\frac{7}{8})}^{2}$

$∴ \cot^{2} θ = \frac{49}{64}$

8. If $3 \cot A = 4$ , check whether $\frac{1 - \tan^{2} A}{1 + \tan^{2} A} = \cos^{2} A - \sin^{2} A$ or not.

Ans: Let us consider a right angled triangle $Δ A B C$ . We get

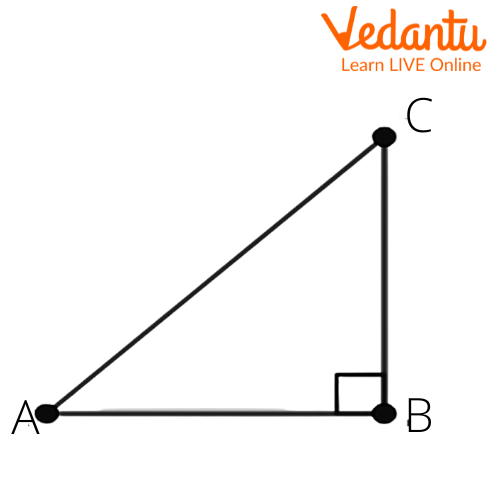
Given that $3 \cot A = 4$ .

We get $\cot A = \frac{4}{3}$ .

We know that $\cot θ = \frac{adjacent side}{opposite side}$ .

From the above figure, we get

$\cot A = \frac{A B}{B C}$

Therefore, we get

$\Rightarrow B C = 3$ and

$\Rightarrow A B = 4$

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $Δ A B C$ , by Pythagoras theorem ,

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

We get

$\Rightarrow {(AC)}^{2} = {(A B)}^{2} + {(B C)}^{2}$

$\Rightarrow A C^{2} = 4^{2} + 3^{2}$

$\Rightarrow A C^{2} = 16 + 9$

$\Rightarrow A C^{2} = 25$

$\Rightarrow A C = 5$

Now, let us consider LHS of the expression $\frac{1 - \tan^{2} A}{1 + \tan^{2} A} = \cos^{2} A - \sin^{2} A$ , we get

$L H S = \frac{1 - \tan^{2} A}{1 + \tan^{2} A}$

Now, we know that $\tan θ = \frac{opposite side}{adjacent side}$

Here, we get

$\tan A = \frac{B C}{A B} = \frac{3}{4}$

Substitute the value, we get

$\Rightarrow \frac{1 - \tan^{2} A}{1 + \tan^{2} A} = \frac{1 - {(\frac{3}{4})}^{2}}{1 + {(\frac{3}{4})}^{2}}$

$\Rightarrow \frac{1 - \tan^{2} A}{1 + \tan^{2} A} = \frac{1 - \frac{9}{16}}{1 + \frac{9}{16}}$

$\Rightarrow \frac{1 - \tan^{2} A}{1 + \tan^{2} A} = \frac{\frac{16 - 9}{16}}{\frac{16 + 9}{16}}$

$\Rightarrow \frac{1 - \tan^{2} A}{1 + \tan^{2} A} = \frac{\frac{7}{16}}{\frac{25}{16}}$

$\Rightarrow \frac{1 - \tan^{2} A}{1 + \tan^{2} A} = \frac{7}{25}$

Now, let us consider RHS of the expression $\frac{1 - \tan^{2} A}{1 + \tan^{2} A} = \cos^{2} A - \sin^{2} A$ , we get

$R H S = \cos^{2} A - \sin^{2} A$

We know that $\sin θ = \frac{opposite side}{hypotenuse}$ and $\cos θ = \frac{adjacent side}{hypotenuse}$ .

Here, we get

$\sin A = \frac{B C}{A C} = \frac{3}{5}$

And $\cos A = \frac{A B}{A C} = \frac{4}{5}$

Substitute the values, we get

$\Rightarrow \cos^{2} A - \sin^{2} A = {(\frac{4}{5})}^{2} - {(\frac{3}{5})}^{2}$

$\Rightarrow \cos^{2} A - \sin^{2} A = \frac{16}{25} - \frac{9}{25}$

$\Rightarrow \cos^{2} A - \sin^{2} A = \frac{7}{25}$

Hence, we get LHS=RHS

$∴ \frac{1 - \tan^{2} A}{1 + \tan^{2} A} = \cos^{2} A - \sin^{2} A$ .

9. In $A B C$ , right angled at $B$ . If $\tan A = \frac{1}{\sqrt{3}}$ , find the value of

(i) $\sin A \cos C + \cos A \sin C$

Ans: Let us consider a right angled triangle $Δ A B C$ . We get

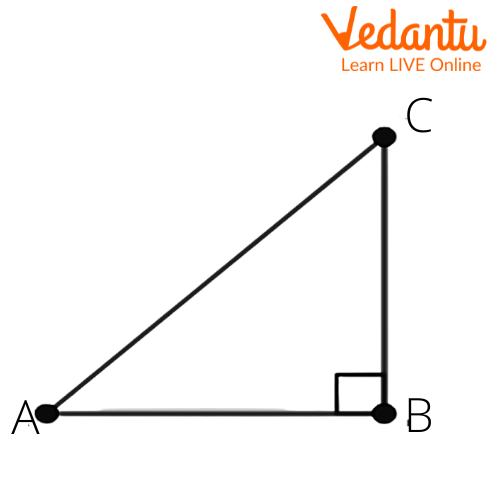
Let us consider a right angled triangle Delta ABC

Given that $\tan A = \frac{1}{\sqrt{3}}$ .

In a right triangle, we know that $\tan θ = \frac{opposite side}{adjacent side}$

Here, from the figure we get

$\tan A = \frac{B C}{A B} = \frac{1}{\sqrt{3}}$

We get $B C = 1$ and $A B = \sqrt{3}$ .

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $Δ A B C$ , by Pythagoras theorem ,

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

We get

$\Rightarrow {(AC)}^{2} = {(A B)}^{2} + {(B C)}^{2}$

$\Rightarrow A C^{2} = {(\sqrt{3})}^{2} + 1^{2}$

$\Rightarrow A C^{2} = 3 + 1$

$\Rightarrow A C^{2} = 4$

$\Rightarrow A C = 2$

We know that $\sin θ = \frac{opposite side}{hypotenuse}$ and $\cos θ = \frac{adjacent side}{hypotenuse}$ .

Here, we get

$\sin A = \frac{B C}{A C} = \frac{1}{2}$ and $\sin C = \frac{A B}{A C} = \frac{\sqrt{3}}{2}$

And $\cos A = \frac{A B}{A C} = \frac{\sqrt{3}}{2}$ and $\cos C = \frac{B C}{A C} = \frac{1}{2}$

Now, we have to find the value of the expression $\sin A \cos C + \cos A \sin C$ .

Substituting the values we get

$\Rightarrow \sin A \cos C + \cos A \sin C = \frac{1}{2} \times \frac{1}{2} + \frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}$

$\Rightarrow \sin A \cos C + \cos A \sin C = \frac{1}{4} + \frac{3}{4}$

$\Rightarrow \sin A \cos C + \cos A \sin C = \frac{4}{4}$

$∴ \sin A \cos C + \cos A \sin C = 1$

(ii) $\cos A \cos C - \sin A \sin C$

Ans: Let us consider a right angled triangle $Δ A B C$ . We get

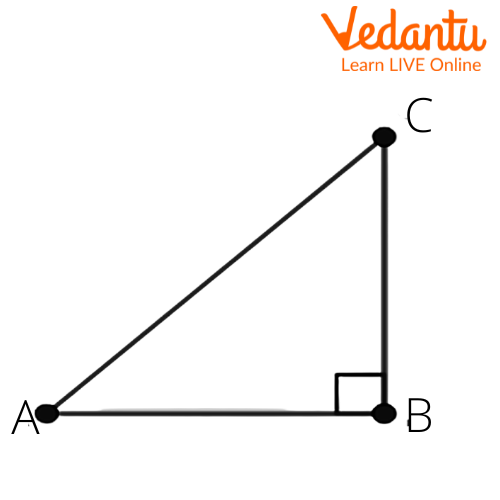
Given that $\tan A = \frac{1}{\sqrt{3}}$ .

In a right triangle, we know that $\tan θ = \frac{opposite side}{adjacent side}$

Here, from the figure we get

$\tan A = \frac{B C}{A B} = \frac{1}{\sqrt{3}}$

We get $B C = 1$ and $A B = \sqrt{3}$ .

Now, we need to apply the Pythagoras theorem to find the measure of hypotenuse.

In $Δ A B C$ , by Pythagoras theorem ,

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

We get

$\Rightarrow {(AC)}^{2} = {(A B)}^{2} + {(B C)}^{2}$

$\Rightarrow A C^{2} = {(\sqrt{3})}^{2} + 1^{2}$

$\Rightarrow A C^{2} = 3 + 1$

$\Rightarrow A C^{2} = 4$

$\Rightarrow A C = 2$

We know that $\sin θ = \frac{opposite side}{hypotenuse}$ and $\cos θ = \frac{adjacent side}{hypotenuse}$ .

Here, we get

$\sin A = \frac{B C}{A C} = \frac{1}{2}$ and $\sin C = \frac{A B}{A C} = \frac{\sqrt{3}}{2}$

And $\cos A = \frac{A B}{A C} = \frac{\sqrt{3}}{2}$ and $\cos C = \frac{B C}{A C} = \frac{1}{2}$

Now, we have to find the value of the expression $\cos A \cos C - \sin A \sin C$ .

Substituting the values we get

$\Rightarrow \cos A \cos C - \sin A \sin C = \frac{\sqrt{3}}{2} \times \frac{1}{2} - \frac{1}{2} \times \frac{\sqrt{3}}{2}$

$\Rightarrow \cos A \cos C - \sin A \sin C = \frac{\sqrt{3}}{4} - \frac{\sqrt{3}}{4}$

$∴\Rightarrow \cos A \cos C - \sin A \sin C = 0$

10. In $Δ P Q R$ , right angled at $Q$ , $P R + Q R = 25 cm$ and $P Q = 5 cm$ . Determine the values of $\sin P, \cos P$ and $\tan P$ .

Ans: Let us consider a right angled triangle $Δ P Q R$ , we get

Let us consider a right angled triangle with delta

Given that $P R + Q R = 25 cm$ and $P Q = 5 cm$ .

Let $Q R = 25 - P R$

Now, applying the Pythagoras theorem in $Δ P Q R$ , we get

${(hypotenuse)}^{2} = {(b a s e)}^{2} + {(p e r p e n d i c u l a r)}^{2}$

We get

$\Rightarrow {(P R)}^{2} = {(P Q)}^{2} + {(Q R)}^{2}$

$\Rightarrow P R^{2} = 5^{2} + {(25 - P R)}^{2}$

$\Rightarrow P R^{2} = 25 + 25^{2} + P R^{2} - 50 P R$

$\Rightarrow P R^{2} = P R^{2} + 25 + 625 - 50 P R$

$\Rightarrow 50 P R = 650$

$\Rightarrow P R = 13 cm$

Therefore,

$Q R = 25 - 13$

$\Rightarrow Q R = 12 cm$

Now, we know that in right triangle,

$\sin θ = \frac{opposite side}{hypotenuse}$ , $\cos θ = \frac{adjacent side}{hypotenuse}$ and $\tan θ = \frac{opposite side}{adjacent side}$ .

Here, we get

$\sin P = \frac{Q R}{P R}$

$∴ \sin P = \frac{12}{13}$

$\cos P = \frac{P Q}{P R}$

$∴ \cos P = \frac{5}{13}$

$\tan P = \frac{Q R}{P Q}$

$∴ \tan P = \frac{12}{5}$

11. State whether the following are true or false. Justify your answer.

(i) The value of $\tan A$ is always less than $1$ .

Ans: The given statement is false. The value of $\tan A$ depends on the length of sides of a right triangle and sides of a triangle may have any measure.

(ii) For some value of angle $A$ , $\sec A = \frac{12}{5}$ .

Ans: We know that in the right triangle $\sec A = \frac{hypotenuse}{adjacent side of ∠ A}$ .

We know that in the right triangle the hypotenuse is the largest side.

Therefore, the value of $\sec A$ must be greater than $1$ .

In the given statement $\sec A = \frac{12}{5}$ , which is greater than $1$ .

Therefore, the given statement is true.

(iii) $\cos A$ is the abbreviation used for the cosecant of angle $A$ .

Ans: The given statement is false because $\cos A$ is the abbreviation used for the cosine of angle $A$ . Abbreviation used for the cosecant of angle $A$ is $cosec A$ .

(iv) $\cot A$ is the product of $\cot$ and $A$ .

Ans: $\cot A$ is the abbreviation used for the cotangent of angle $A$ . Hence the given statement is false.

(v) For some angle $θ$ , $\sin θ = \frac{4}{3}$ .

Ans: We know that in the right triangle $\sin θ = \frac{opposite side}{hypotenuse}$ .

We know that in the right triangle the hypotenuse is the largest side.

Therefore, the value of $\sin θ$ must be less than $1$ .

In the given statement $\sin θ = \frac{4}{3}$ , which is greater than $1$ .

Therefore, the given statement is false.

Exercise 8.2

1. Evaluate the following:

(i) $\sin 60^{\circ} \cos 30^{\circ} + \sin 30^{\circ} \cos 60^{\circ}$

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

Exact Values of Trigonometric Functions
Angle $θ$		$\sin θ$	$\cos θ$	$\tan θ$
Degrees	Radians	$\sin θ$	$\cos θ$	$\tan θ$
$0^{\circ}$	$0$	$0$	$1$	$0$
$30^{\circ}$	$\frac{π}{6}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{3}}$
$45^{\circ}$	$\frac{π}{4}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$	$1$
$60^{\circ}$	$\frac{π}{3}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$
$90^{\circ}$	$\frac{π}{2}$	$1$	$0$	Not defined

We have to evaluate $\sin 60^{\circ} \cos 30^{\circ} + \sin 30^{\circ} \cos 60^{\circ}$ .

Substitute the values from the above table, we get

$\Rightarrow \frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2} + \frac{1}{2} \times \frac{1}{2}$

$\Rightarrow \frac{3}{4} + \frac{1}{4}$

$\Rightarrow \frac{4}{4}$

$∴ \sin 60^{\circ} \cos 30^{\circ} + \sin 30^{\circ} \cos 60^{\circ} = 1$ .

(ii) $2 \tan^{2} 45^{\circ} + \cos^{2} 30^{\circ} - \sin^{2} 60^{\circ}$

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

Exact Values of Trigonometric Functions
Angle $θ$		$\sin θ$	$\cos θ$	$\tan θ$
Degrees	Radians	$\sin θ$	$\cos θ$	$\tan θ$
$0^{\circ}$	$0$	$0$	$1$	$0$
$30^{\circ}$	$\frac{π}{6}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{3}}$
$45^{\circ}$	$\frac{π}{4}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$	$1$
$60^{\circ}$	$\frac{π}{3}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$
$90^{\circ}$	$\frac{π}{2}$	$1$	$0$	Not defined

We have to evaluate $2 \tan^{2} 45^{\circ} + \cos^{2} 30^{\circ} - \sin^{2} 60^{\circ}$ .

Substitute the values from the above table, we get

$\Rightarrow 2 {(1)}^{2} + {(\frac{\sqrt{3}}{2})}^{2} - {(\frac{\sqrt{3}}{2})}^{2}$

$\Rightarrow 2 + \frac{3}{4} - \frac{3}{4}$

$\Rightarrow 2$

$∴ 2 \tan^{2} 45^{\circ} + \cos^{2} 30^{\circ} - \sin^{2} 60^{\circ} = 2$ .

(iii) $\frac{\cos 45^{\circ}}{\sec 30^{\circ} + cosec 30^{\circ}}$

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

Exact Values of Trigonometric Functions
Angle $θ$		$\sin θ$	$\cos θ$	$\tan θ$
Degrees	Radians	$\sin θ$	$\cos θ$	$\tan θ$
$0^{\circ}$	$0$	$0$	$1$	$0$
$30^{\circ}$	$\frac{π}{6}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{3}}$
$45^{\circ}$	$\frac{π}{4}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$	$1$
$60^{\circ}$	$\frac{π}{3}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$
$90^{\circ}$	$\frac{π}{2}$	$1$	$0$	Not defined

We have to evaluate $\frac{\cos 45^{\circ}}{\sec 30^{\circ} + cosec 30^{\circ}}$ .

Substitute the values from the above table, we get

$\Rightarrow \frac{\frac{1}{\sqrt{2}}}{\frac{2}{\sqrt{3}} + 2}$

$\Rightarrow \frac{\frac{1}{\sqrt{2}}}{\frac{2 + 2 \sqrt{3}}{\sqrt{3}}}$

$\Rightarrow \frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2 + 2 \sqrt{3}}$

Multiplying and dividing by $\sqrt{3} - 1$ , we get

$\Rightarrow \frac{1}{\sqrt{2}} \times \frac{\sqrt{3}}{2 + 2 \sqrt{3}} \times \frac{\sqrt{3} - 1}{\sqrt{3} - 1}$

$\Rightarrow \frac{\sqrt{3} (\sqrt{3} - 1)}{\sqrt{2} (2 + 2 \sqrt{3}) (\sqrt{3} - 1)}$

$\Rightarrow \frac{\sqrt{3} (\sqrt{3} - 1)}{2 \sqrt{2} (\sqrt{3} + 1) (\sqrt{3} - 1)}$

$\Rightarrow \frac{3 - \sqrt{3}}{2 \sqrt{2} ({(\sqrt{3})}^{2} - 1^{2})}$

$\Rightarrow \frac{3 - \sqrt{3}}{2 \sqrt{2} (3 - 1)}$

$\Rightarrow \frac{3 - \sqrt{3}}{4 \sqrt{2}}$

$∴ \frac{\cos 45^{\circ}}{\sec 30^{\circ} + cosec 30^{\circ}} = \frac{3 - \sqrt{3}}{4 \sqrt{2}}$

(iv) $\frac{\sin 30^{\circ} + \tan 45^{\circ} - cosec 60^{\circ}}{\sec 30^{\circ} + \cos 60^{\circ} - \cot 45^{\circ}}$

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

Exact Values of Trigonometric Functions
Angle $θ$		$\sin θ$	$\cos θ$	$\tan θ$
Degrees	Radians	$\sin θ$	$\cos θ$	$\tan θ$
$0^{\circ}$	$0$	$0$	$1$	$0$
$30^{\circ}$	$\frac{π}{6}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{3}}$
$45^{\circ}$	$\frac{π}{4}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$	$1$
$60^{\circ}$	$\frac{π}{3}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$
$90^{\circ}$	$\frac{π}{2}$	$1$	$0$	Not defined

We have to evaluate $\frac{\sin 30^{\circ} + \tan 45^{\circ} - cosec 60^{\circ}}{\sec 30^{\circ} + \cos 60^{\circ} - \cot 45^{\circ}}$ .

Substitute the values from the above table, we get

$\Rightarrow \frac{\frac{1}{2} + 1 - \frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}} + \frac{1}{2} + 1}$

$\Rightarrow \frac{\frac{3}{2} - \frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}} + \frac{3}{2}}$

$\Rightarrow \frac{\frac{3 \sqrt{3} - 4}{2 \sqrt{3}}}{\frac{3 \sqrt{3} + 4}{2 \sqrt{3}}}$

$\Rightarrow \frac{3 \sqrt{3} - 4}{3 \sqrt{3} + 4}$

Multiplying and dividing by $3 \sqrt{3} - 4$ , we get

$\Rightarrow \frac{3 \sqrt{3} - 4}{3 \sqrt{3} + 4} \times \frac{3 \sqrt{3} - 4}{3 \sqrt{3} - 4}$

Now, applying the identity $(a + b) (a - b) = a^{2} - b^{2}$ , we get

$\Rightarrow \frac{{(3 \sqrt{3} - 4)}^{2}}{{(3 \sqrt{3})}^{2} - 4^{2}}$

$\Rightarrow \frac{27 + 16 - 24 \sqrt{3}}{27 - 16}$

$\Rightarrow \frac{43 - 24 \sqrt{3}}{11}$

$∴ \frac{\sin 30^{\circ} + \tan 45^{\circ} - cosec 60^{\circ}}{\sec 30^{\circ} + \cos 60^{\circ} - \cot 45^{\circ}} = \frac{43 - 24 \sqrt{3}}{11}$

(v) $\frac{5 \cos^{2} 60^{\circ} + 4 \sec^{2} 30^{\circ} - \tan^{2} 45^{\circ}}{\sec^{2} 30^{\circ} + \cos^{2} 30^{\circ}}$

Ans: With the help of trigonometric ratio tables we can find the values of standard trigonometric angles. The trigonometric ratio table is as follows:

Exact Values of Trigonometric Functions
Angle $θ$		$\sin θ$	$\cos θ$	$\tan θ$
Degrees	Radians	$\sin θ$	$\cos θ$	$\tan θ$
$0^{\circ}$	$0$	$0$	$1$	$0$
$30^{\circ}$	$\frac{π}{6}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{3}}$
$45^{\circ}$	$\frac{π}{4}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$	$1$
$60^{\circ}$	$\frac{π}{3}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$
$90^{\circ}$	$\frac{π}{2}$	$1$	$0$	Not defined

We have to evaluate $\frac{5 \cos^{2} 60^{\circ} + 4 \sec^{2} 30^{\circ} - \tan^{2} 45^{\circ}}{\sec^{2} 30^{\circ} + \cos^{2} 30^{\circ}}$ .

Substitute the values from the above table, we get

$\Rightarrow \frac{5 {(\frac{1}{2})}^{2} + 4 {(\frac{2}{\sqrt{3}})}^{2} - 1^{2}}{{(\frac{1}{2})}^{2} + {(\frac{\sqrt{3}}{2})}^{2}}$

$\Rightarrow \frac{5 (\frac{1}{4}) + 4 (\frac{4}{3}) - 1}{(\frac{1}{4}) + (\frac{3}{4})}$

$\Rightarrow \frac{\frac{15 + 64 - 12}{12}}{\frac{1 + 3}{4}}$

$\Rightarrow \frac{\frac{15 + 64 - 12}{12}}{\frac{4}{4}}$

$\Rightarrow \frac{\frac{67}{12}}{1}$

$∴ \frac{5 \cos^{2} 60^{\circ} + 4 \sec^{2} 30^{\circ} - \tan^{2} 45^{\circ}}{\sec^{2} 30^{\circ} + \cos^{2} 30^{\circ}} = \frac{67}{12}$ .

2. Choose the correct option and justify your choice.

(i) $\frac{2 \tan 30^{\circ}}{1 + \tan^{2} 30^{\circ}} =$ ………

(a) $\sin 60^{\circ}$

(b) $\cos 60^{\circ}$

(d) $\sin 30^{\circ}$

Ans: The given expression is $\frac{2 \tan 30^{\circ}}{1 + \tan^{2} 30^{\circ}}$ .

We know that from the trigonometric ratio table we have $\tan 30^{\circ} = \frac{1}{\sqrt{3}}$ .

Substitute the value in the given expression we get

$\frac{2 \tan 30^{\circ}}{1 + \tan^{2} 30^{\circ}} = \frac{2 (\frac{1}{\sqrt{3}})}{1 + {(\frac{1}{\sqrt{3}})}^{2}}$

$\Rightarrow \frac{2 \tan 30^{\circ}}{1 + \tan^{2} 30^{\circ}} = \frac{\frac{2}{\sqrt{3}}}{1 + \frac{1}{3}}$

$\Rightarrow \frac{2 \tan 30^{\circ}}{1 + \tan^{2} 30^{\circ}} = \frac{\frac{2}{\sqrt{3}}}{\frac{4}{3}}$

$\Rightarrow \frac{2 \tan 30^{\circ}}{1 + \tan^{2} 30^{\circ}} = \frac{\sqrt{3}}{2}$

From the trigonometric table we know that

$\sin 60^{\circ} = \frac{\sqrt{3}}{2}$

$\cos 60^{\circ} = \frac{1}{2}$

$\tan 60^{\circ} = \sqrt{3}$

$\sin 30^{\circ} = \frac{1}{2}$

Hence, $\frac{2 \tan 30^{\circ}}{1 + \tan^{2} 30^{\circ}} = \sin 60^{\circ}$ .

Therefore, option (A) is the correct answer.

(ii) $\frac{1 - \tan^{2} 45^{\circ}}{1 + \tan^{2} 45^{\circ}} =$ ………

(a) $\tan 90^{\circ}$

(b) $1$

(d) $0$

Ans: The given expression is $\frac{1 - \tan^{2} 45^{\circ}}{1 + \tan^{2} 45^{\circ}}$ .

We know that from the trigonometric ratio table we have $\tan 45^{\circ} = 1$ .

Substitute the value in the given expression we get

$\frac{1 - \tan^{2} 45^{\circ}}{1 + \tan^{2} 45^{\circ}} = \frac{1 - 1^{2}}{1 + 1^{2}}$

$\Rightarrow \frac{1 - \tan^{2} 45^{\circ}}{1 + \tan^{2} 45^{\circ}} = \frac{1 - 1}{1 + 1}$

$\Rightarrow\Rightarrow \frac{1 - \tan^{2} 45^{\circ}}{1 + \tan^{2} 45^{\circ}} = \frac{0}{2}$

$∴ \frac{1 - \tan^{2} 45^{\circ}}{1 + \tan^{2} 45^{\circ}} = 0$

Therefore, option (D) is the correct answer.

(iii) $\sin 2 A = 2 \sin A$ is true when $A =$ ……..

(a) $0^{\circ}$

(b) $30^{\circ}$

(d) $60^{\circ}$

Ans: The given expression is $\sin 2 A = 2 \sin A$ .

We know that from the trigonometric ratio table we have

$\sin 0^{\circ} = 0$

$\sin 30^{\circ} = \frac{1}{2}$

$\sin 45^{\circ} = \frac{1}{\sqrt{2}}$

$\sin 60^{\circ} = \frac{\sqrt{3}}{2}$

$\sin 90^{\circ} = 1$

The given statement is true when $A = 0^{\circ}$ .

Substitute the value in the given expression we get

$\Rightarrow \sin 2 A = 2 \sin A$

$\Rightarrow \sin 2 \times 0^{\circ} = 2 \sin 0^{\circ}$

$0 = 0$

Therefore, option (A) is the correct answer.

(iv) $\frac{2 \tan 30^{\circ}}{1 - \tan^{2} 30^{\circ}} =$ ………

(a) $\sin 60^{\circ}$

(b) $\cos 60^{\circ}$

(d) $\sin 30^{\circ}$

Ans: The given expression is $\frac{2 \tan 30^{\circ}}{1 - \tan^{2} 30^{\circ}}$ .

We know that from the trigonometric ratio table we have $\tan 30^{\circ} = \frac{1}{\sqrt{3}}$ .

Substitute the value in the given expression we get

$\frac{2 \tan 30^{\circ}}{1 - \tan^{2} 30^{\circ}} = \frac{2 (\frac{1}{\sqrt{3}})}{1 - {(\frac{1}{\sqrt{3}})}^{2}}$

$\Rightarrow \frac{2 \tan 30^{\circ}}{1 - \tan^{2} 30^{\circ}} = \frac{\frac{2}{\sqrt{3}}}{1 - \frac{1}{3}}$

$\Rightarrow \frac{2 \tan 30^{\circ}}{1 - \tan^{2} 30^{\circ}} = \frac{\frac{2}{\sqrt{3}}}{\frac{2}{3}}$

$\Rightarrow \frac{2 \tan 30^{\circ}}{1 - \tan^{2} 30^{\circ}} = \sqrt{3}$

From the trigonometric table we know that

$\sin 60^{\circ} = \frac{\sqrt{3}}{2}$

$\cos 60^{\circ} = \frac{1}{2}$

$\tan 60^{\circ} = \sqrt{3}$

$\sin 30^{\circ} = \frac{1}{2}$

Hence, $\frac{2 \tan 30^{\circ}}{1 - \tan^{2} 30^{\circ}} = \tan 60^{\circ}$ .

Therefore, option (C) is the correct answer.

3. If $\tan (A + B) = \sqrt{3}$ and $\tan (A - B) = \frac{1}{\sqrt{3}}$ , $0^{\circ} < A + B \leq 90^{\circ}$ . Find $A$ and $B$ .

Ans: Given that $\tan \left( A+ dB \right)=\sqrt{3} $a n d$ \tan \left( A-B \right)=\dfrac{1}{\sqrt{3}}$.

From the trigonometric ratio table we know that $\tan 60^{\circ} = \sqrt{3}$ and $\tan 30^{\circ} = \frac{1}{\sqrt{3}}$ .

Then we get

$\tan (A + B) = \sqrt{3}$

$\Rightarrow \tan (A + B) = \tan 60^{\circ}$

$\Rightarrow A + B = 60^{\circ}$ ……….(1)

Also, $\tan (A - B) = \frac{1}{\sqrt{3}}$

$\Rightarrow \tan (A - B) = \tan 30^{\circ}$

$\Rightarrow A - B = 30^{\circ}$ ……….(2)

Adding eq. (1) and (2), we get

$2 A = 90^{\circ}$

$∴ A = 45^{\circ}$

Substitute the obtained value in eq. (1), we get

$45^{\circ} + B = 60^{\circ}$

$\Rightarrow B = 60^{\circ} - 45^{\circ}$

$∴ B = 15^{\circ}$

Therefore, the values of $A$ and $B$ is $45^{\circ}$ and $15^{\circ}$ respectively.

4. State whether the following are true or false. Justify your answer.

(i) $\sin (A + B) = \sin A + \sin B$ .

Ans: Let us assume $A = 30^{\circ}$ and $B = 60^{\circ}$ .

Now, let us consider LHS of the given expression, we get

$\sin (A + B)$

Substitute the assumed values in the LHS, we get

$\sin (A + B) = \sin (30^{\circ} + 60^{\circ})$

$\Rightarrow \sin (A + B) = \sin (90^{\circ})$

From the trigonometric ratio table we know that $\sin 90^{\circ} = 1$ , we get

$\Rightarrow \sin (A + B) = 1$

Now, let us consider the RHS of the given expression and substitute the values, we get

$\sin A + \sin B = \sin 30^{\circ} + \sin 60^{\circ}$

From the trigonometric ratio table we know that $\sin 30^{\circ} = \frac{1}{2}$ and $\sin 60^{\circ} = \frac{\sqrt{3}}{2}$ , we get

$\Rightarrow \sin A + \sin B = \frac{1}{2} + \frac{\sqrt{3}}{2}$

$\Rightarrow \sin A + \sin B = \frac{1 + \sqrt{3}}{2}$

Thus, $L H S \neq R H S$ .

Therefore, the given statement is false.

(ii) The value of $\sin θ$ increases as $θ$ increases.

Ans: The value of sine from the trigonometric ratio table is as follows:

$\sin 0^{\circ} = 0$

$\sin 30^{\circ} = \frac{1}{2} = 0.5$

$\sin 45^{\circ} = \frac{1}{\sqrt{2}} = 0.707$

$\sin 60^{\circ} = \frac{\sqrt{3}}{2} = 0.866$

$\sin 90^{\circ} = 1$

Therefore, we can conclude that the value of $\sin θ$ increases as $θ$ increases.

Therefore, the given statement is true.

(iii) The value of $\cos θ$ increases as $θ$ increases.

Ans: The value of cosine from the trigonometric ratio table is as follows:

$\cos 0^{\circ} = 1$

$\cos 30^{\circ} = \frac{\sqrt{3}}{2} = 0.866$

$\cos 45^{\circ} = \frac{1}{\sqrt{2}} = 0.707$

$\cos 60^{\circ} = \frac{1}{2} = 0.5$

$\cos 90^{\circ} = 0$

Therefore, we can conclude that the value of $\cos θ$ decreases as $θ$ increases.

Therefore, the given statement is false.

(iv) $\sin θ = \cos θ$ for all values of $θ$ .

Ans: The trigonometric ratio table is given as follows:

Exact Values of Trigonometric Functions
Angle $θ$		$\sin θ$	$\cos θ$	$\tan θ$
Degrees	Radians	$\sin θ$	$\cos θ$	$\tan θ$
$0^{\circ}$	$0$	$0$	$1$	$0$
$30^{\circ}$	$\frac{π}{6}$	$\frac{1}{2}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{\sqrt{3}}$
$45^{\circ}$	$\frac{π}{4}$	$\frac{1}{\sqrt{2}}$	$\frac{1}{\sqrt{2}}$	$1$
$60^{\circ}$	$\frac{π}{3}$	$\frac{\sqrt{3}}{2}$	$\frac{1}{2}$	$\sqrt{3}$
$90^{\circ}$	$\frac{π}{2}$	$1$	$0$	Not defined

From the above table we can conclude that $\sin θ = \cos θ$ is true only for $θ = 45^{\circ}$ .

$\sin θ = \cos θ$ is not true for all values of $θ$ .

Therefore, the given statement is false.

(v) $\cot A$ is not defined for $A = 0^{\circ}$ .

Ans: We know that $\cot A = \frac{\cos A}{\sin A}$ .

If $A = 0^{\circ}$ , then $\cot 0^{\circ} = \frac{\cos 0^{\circ}}{\sin 0^{\circ}}$

From trigonometric ratio table we get

$\sin 0^{\circ} = 0$ and $\cos 0^{\circ} = 1$

We get

$\cot 0^{\circ} = \frac{1}{0}$ , which is undefined.

Therefore, the given statement is true.

Exercise 8.3

1. Express the trigonometric ratios $\sin A, \sec A$ and $\tan A$ in terms of $\cot A$ .

Ans: For a right triangle we have an identity ${cosec}^{2} A = 1 + \cot^{2} A$ .

Let us consider the above identity, we get

${cosec}^{2} A = 1 + \cot^{2} A$

Now, reciprocating both sides we get

$\Rightarrow \frac{1}{{cosec}^{2} A} = \frac{1}{1 + \cot^{2} A}$

Now, we know that $\frac{1}{{cosec}^{2} A} = \sin^{2} A$ , we get

$\Rightarrow \sin^{2} A = \frac{1}{1 + \cot^{2} A}$

$\Rightarrow \sin A = \pm \frac{1}{\sqrt{1 + \cot^{2} A}}$

Now, we know that sine value will be negative for angles greater than $180^{\circ}$ , for a triangle sine value is always positive with respect to an angle. Then we will consider only positive values.

$∴ \sin A = \frac{1}{\sqrt{1 + \cot^{2} A}}$

We know that $\tan A = \frac{1}{\cot A}$

Also, we will use the identity $\sec^{2} A = 1 + \tan^{2} A$ , we get

$\sec^{2} A = 1 + \tan^{2} A$

$\Rightarrow \sec^{2} A = 1 + \frac{1}{\cot^{2} A}$

$\Rightarrow \sec^{2} A = \frac{\cot^{2} A + 1}{\cot^{2} A}$

$\Rightarrow \sec A = \frac{\sqrt{\cot^{2} A + 1}}{\sqrt{\cot^{2} A}}$

$∴ \sec A = \frac{\sqrt{\cot^{2} A + 1}}{\cot A}$

2. Write all the other trigonometric ratios of $∠ A$ in terms of $\sec A$ .

Ans:

We know that $\cos A = \frac{1}{\sec A}$ .

$∴ \cos A = \frac{1}{\sec A}$

For a right triangle we have an identity $\sin^{2} A + \cos^{2} A = 1$ .

Let us consider the above identity, we get

$\sin^{2} A + \cos^{2} A = 1$

Now, we know that $\cos A = \frac{1}{\sec A}$ , we get

$\Rightarrow \sin^{2} A = 1 - \cos^{2} A$

$\Rightarrow \sin^{2} A = 1 - \frac{1}{\sec^{2} A}$

$\Rightarrow \sin A = \sqrt{1 - {(\frac{1}{\sec A})}^{2}}$

$∴ \sin A = \frac{\sqrt{\sec^{2} A - 1}}{\sec A}$

Also, we will use the identity $\sec^{2} A = 1 + \tan^{2} A$ , we get

$\tan^{2} A = \sec^{2} A - 1$

$∴ \tan A = \sqrt{\sec^{2} A - 1}$

Now, we know that $\cot A = \frac{\cos A}{\sin A}$ , we get

$\Rightarrow \cot A = \frac{\frac{1}{\sec A}}{\frac{\sqrt{\sec^{2} A - 1}}{\sec A}}$

$∴ \cot A = \frac{1}{\sqrt{\sec^{2} A - 1}}$

We know that $c o s e c A = \frac{1}{\sin A}$ , we get

$∴ c o s e c A = \frac{\sec A}{\sqrt{\sec^{2} A - 1}}$

3. Evaluate the following:

(i) $\frac{\sin^{2} 63^{\circ} + \sin^{2} 27^{\circ}}{\cos^{2} 17^{\circ} + \cos^{2} 73^{\circ}}$

Ans: The given expression is $\frac{\sin^{2} 63^{\circ} + \sin^{2} 27^{\circ}}{\cos^{2} 17^{\circ} + \cos^{2} 73^{\circ}}$ .

The above expression can be written as

$\frac{\sin^{2} 63^{\circ} + \sin^{2} 27^{\circ}}{\cos^{2} 17^{\circ} + \cos^{2} 73^{\circ}} = \frac{{[\sin (90^{\circ} - 27^{\circ})]}^{2} + \sin^{2} 27^{\circ}}{{[\cos (90^{\circ} - 73^{\circ})]}^{2} + \cos^{2} 73^{\circ}}$

Now, we can apply the identity $\cos (90^{\circ} - θ) = \sin θ$ and $\sin (90^{\circ} - θ) = \cos θ$ , we get

$\Rightarrow \frac{\sin^{2} 63^{\circ} + \sin^{2} 27^{\circ}}{\cos^{2} 17^{\circ} + \cos^{2} 73^{\circ}} = \frac{\cos^{2} 27^{\circ} + \sin^{2} 27^{\circ}}{\sin^{2} 73^{\circ} + \cos^{2} 73^{\circ}}$

Now, by applying the trigonometric identity $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow \frac{\sin^{2} 63^{\circ} + \sin^{2} 27^{\circ}}{\cos^{2} 17^{\circ} + \cos^{2} 73^{\circ}} = \frac{1}{1}$

$∴ \frac{\sin^{2} 63^{\circ} + \sin^{2} 27^{\circ}}{\cos^{2} 17^{\circ} + \cos^{2} 73^{\circ}} = 1$

(ii) $\sin 25^{\circ} \cos 65^{\circ} + \cos 25^{\circ} \sin 65^{\circ}$

Ans: The given expression is $\sin 25^{\circ} \cos 65^{\circ} + \cos 25^{\circ} \sin 65^{\circ}$ .

The above expression can be written as

$\sin 25^{\circ} \cos 65^{\circ} + \cos 25^{\circ} \sin 65^{\circ} = \sin 25^{\circ} \cos (90^{\circ} - 25^{\circ}) + \cos 25^{\circ} \sin (90^{\circ} - 25^{\circ})$

Now, we can apply the identity $\cos (90^{\circ} - θ) = \sin θ$ and $\sin (90^{\circ} - θ) = \cos θ$ , we get

$\Rightarrow \sin 25^{\circ} \cos 65^{\circ} + \cos 25^{\circ} \sin 65^{\circ} = \sin 25^{\circ} \sin 25^{\circ} + \cos 25^{\circ} \cos 25^{\circ}$

$\Rightarrow \sin 25^{\circ} \cos 65^{\circ} + \cos 25^{\circ} \sin 65^{\circ} = \sin^{2} 25^{\circ} + \cos^{2} 25^{\circ}$

Now, by applying the trigonometric identity $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow \sin 25^{\circ} \cos 65^{\circ} + \cos 25^{\circ} \sin 65^{\circ} = 1$

$∴ \sin 25^{\circ} \cos 65^{\circ} + \cos 25^{\circ} \sin 65^{\circ} = 1$

4. Choose the correct option and justify your choice:

(i) $9 \sec^{2} A - 9 \tan^{2} A =$ …….

(a) $1$

(b) $9$

(d) $0$

Ans: The given expression is $9 \sec^{2} A - 9 \tan^{2} A$ .

The given expression can be written as

$\Rightarrow 9 \sec^{2} A - 9 \tan^{2} A = 9 (\sec^{2} A - \tan^{2} A)$

Now, we will use the identity $\sec^{2} A = 1 + \tan^{2} A$ , we get

$\sec^{2} A - \tan^{2} A = 1$

$\Rightarrow 9 \sec^{2} A - 9 \tan^{2} A = 9 (1)$

$∴ 9 \sec^{2} A - 9 \tan^{2} A = 9$

Therefore, option (B) is the correct answer.

(ii) $(1 + \tan θ + \sec θ) (1 + \cot θ - cosec θ)$

(a) $0$

(b) $1$

(d) $- 1$

Ans: The given expression is $(1 + \tan θ + \sec θ) (1 + \cot θ - cosec θ)$ .

We know that the trigonometric functions have values as:

$\tan θ = \frac{\sin θ}{\cos θ}$ , $\cot θ = \frac{\cos θ}{\sin θ} = \frac{1}{\tan θ}$ , $c o s e c θ = \frac{1}{\sin θ}$ and $s e c θ = \frac{1}{\cos θ}$

Substituting these values in the given expression, we get

$\Rightarrow (1 + \tan θ + \sec θ) (1 + \cot θ - cosec θ) = (1 + \frac{\sin θ}{\cos θ} + \frac{1}{\cos θ}) (1 + \frac{\cos θ}{\sin θ} - \frac{1}{\sin θ})$

$\Rightarrow (1 + \tan θ + \sec θ) (1 + \cot θ - cosec θ) = (\frac{\cos θ + \sin θ + 1}{\cos θ}) (\frac{\sin θ + \cos θ - 1}{\sin θ})$

Now, by applying the identity $(a + b) (a - b) = a^{2} - b^{2}$ , we get

$\Rightarrow (1 + \tan θ + \sec θ) (1 + \cot θ - cosec θ) = \frac{{(\sin θ + \cos θ)}^{2} - 1^{2}}{\sin θ \cos θ}$

$\Rightarrow (1 + \tan θ + \sec θ) (1 + \cot θ - cosec θ) = \frac{\sin^{2} θ + \cos^{2} θ + 2 \sin θ \cos θ - 1}{\sin θ \cos θ}$

Now, by applying the trigonometric identity $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow (1 + \tan θ + \sec θ) (1 + \cot θ - cosec θ) = \frac{1 + 2 \sin θ \cos θ - 1}{\sin θ \cos θ}$

$\Rightarrow (1 + \tan θ + \sec θ) (1 + \cot θ - cosec θ) = \frac{2 \sin θ \cos θ}{\sin θ \cos θ}$

$∴ (1 + \tan θ + \sec θ) (1 + \cot θ - cosec θ) = 2$

Therefore, option (C) is the correct answer.

(iii) $(\sec A + \tan A) (1 - \sin A) =$ ………

(a) $\sec A$

(b) $\sin A$

(d) $\cos A$

Ans: Given expression is $(\sec A + \tan A) (1 - \sin A)$ .

We know that $\tan θ = \frac{\sin θ}{\cos θ}$ and $s e c θ = \frac{1}{\cos θ}$

Substituting these values in the given expression, we get

$(\sec A + \tan A) (1 - \sin A) = (\frac{1}{\cos A} + \frac{\sin A}{\cos A}) (1 - \sin A)$

$\Rightarrow (\sec A + \tan A) (1 - \sin A) = (\frac{1 + \sin A}{\cos A}) (1 - \sin A)$

$\Rightarrow (\sec A + \tan A) (1 - \sin A) = (\frac{(1 + \sin A) (1 - \sin A)}{\cos A})$

Now, by applying the identity $(a + b) (a - b) = a^{2} - b^{2}$ , we get

$\Rightarrow (\sec A + \tan A) (1 - \sin A) = (\frac{1^{2} - \sin^{2} A}{\cos A})$

Now, we know that $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow (\sec A + \tan A) (1 - \sin A) = (\frac{\cos^{2} A}{\cos A})$

$∴ (\sec A + \tan A) (1 - \sin A) = \cos A$

Therefore, option (D) is the correct answer.

(iv) $\frac{1 + \tan^{2} A}{1 + \cot^{2} A}$

(a) $\sec^{2} A$

(b) $- 1$

(d) $\tan^{2} A$

Ans: Given expression is $\frac{1 + \tan^{2} A}{1 + \cot^{2} A}$ .

We know that the trigonometric functions have values as:

$\tan θ = \frac{\sin θ}{\cos θ}$ and $\cot θ = \frac{\cos θ}{\sin θ} = \frac{1}{\tan θ}$ .

Substituting these values in the given expression, we get

$\frac{1 + \tan^{2} A}{1 + \cot^{2} A} = \frac{1 + \frac{\sin^{2} A}{\cos^{2} A}}{1 + \frac{\cos^{2} A}{\sin^{2} A}}$

$\Rightarrow \frac{1 + \tan^{2} A}{1 + \cot^{2} A} = \frac{\frac{\cos^{2} A + \sin^{2} A}{\cos^{2} A}}{\frac{\sin^{2} A + \cos^{2} A}{\sin^{2} A}}$

Now, we know that $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow \frac{1 + \tan^{2} A}{1 + \cot^{2} A} = \frac{\frac{1}{\cos^{2} A}}{\frac{1}{\sin^{2} A}}$

$\Rightarrow \frac{1 + \tan^{2} A}{1 + \cot^{2} A} = \frac{\sin^{2} A}{\cos^{2} A}$

$\Rightarrow \frac{1 + \tan^{2} A}{1 + \cot^{2} A} = \tan^{2} A$

Therefore, option (D) is the correct answer.

5. Prove the following identities, where the angles involved are acute angles for which the expressions are defined.

(i) ${(c o s e c θ - c o t θ)}^{2} = \frac{1 - \cos θ}{1 + \cos θ}$

Ans: Given expression is ${(c o s e c θ - \cot θ)}^{2} = \frac{1 - \cos θ}{1 + \cos θ}$ .

Let us consider the LHS of the given expression, we get

$L H S = {(c o s e c θ - \cot θ)}^{2}$

Now, we know that $\cot θ = \frac{\cos θ}{\sin θ} = \frac{1}{\tan θ}$ and $c o s e c θ = \frac{1}{\sin θ}$ .

By substituting the values, we get

$\Rightarrow {(c o s e c θ - \cot θ)}^{2} = {(\frac{1}{\sin θ} - \frac{\cos θ}{\sin θ})}^{2}$

$\Rightarrow {(c o s e c θ - \cot θ)}^{2} = {(\frac{1 - \cos θ}{\sin θ})}^{2}$

$\Rightarrow {(c o s e c θ - \cot θ)}^{2} = \frac{{(1 - \cos θ)}^{2}}{\sin^{2} θ}$

Now, we know that $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow {(c o s e c θ - \cot θ)}^{2} = \frac{{(1 - \cos θ)}^{2}}{1 - \cos^{2} θ}$

Now, by applying the identity $(a + b) (a - b) = a^{2} - b^{2}$ , we get

$\Rightarrow {(c o s e c θ - \cot θ)}^{2} = \frac{{(1 - \cos θ)}^{2}}{(1 - \cos θ) (1 + \cos θ)}$

$\Rightarrow {(c o s e c θ - \cot θ)}^{2} = \frac{(1 - \cos θ)}{(1 + \cos θ)}$

$\Rightarrow {(c o s e c θ - \cot θ)}^{2} = R H S$

$∴ {(c o s e c θ - \cot θ)}^{2} = \frac{1 - \cos θ}{1 + \cos θ}$

Hence proved

(ii) $\frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = 2 \sec A$

Ans: Given expression is $\frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = 2 \sec A$ .

Let us consider the LHS of the given expression, we get

$L H S = \frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A}$

Now, taking LCM, we get

$\Rightarrow \frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = \frac{\cos^{2} A + (1 + \sin A) (1 + \sin A)}{(1 + \sin A) \cos A}$

$\Rightarrow \frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = \frac{\cos^{2} A + \sin^{2} A + 2 \sin A + 1}{(1 + \sin A) \cos A}$

Now, we know that $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow \frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = \frac{1 + 2 \sin A + 1}{(1 + \sin A) \cos A}$

$\Rightarrow \frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = \frac{2 + 2 \sin A}{(1 + \sin A) \cos A}$

$\Rightarrow \frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = \frac{2 (1 + \sin A)}{(1 + \sin A) \cos A}$

$\Rightarrow \frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = \frac{2}{\cos A}$

We know that $s e c θ = \frac{1}{\cos θ}$ , we get

$\Rightarrow \frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = 2 \sec A$

$\Rightarrow \frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = R H S$

$∴ \frac{\cos A}{1 + \sin A} + \frac{1 + \sin A}{\cos A} = 2 \sec A$

Hence proved

(iii) $\frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = 1 + \sec θ c o s e c θ$

Ans: Given expression is $\frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = 1 + \sec θ cosec θ$ .

Let us consider the LHS of the given expression, we get

$L H S = \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ}$

Now, we know that $\tan θ = \frac{\sin θ}{\cos θ}$ and $\cot θ = \frac{\cos θ}{\sin θ} = \frac{1}{\tan θ}$ .

By substituting the values, we get

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = (\frac{\frac{\sin θ}{\cos θ}}{1 - \frac{\cos θ}{\sin θ}} + \frac{\frac{\cos θ}{\sin θ}}{1 - \frac{\sin θ}{\cos θ}})$

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = (\frac{\frac{\sin θ}{\cos θ}}{\frac{\sin θ - \cos θ}{\sin θ}} + \frac{\frac{\cos θ}{\sin θ}}{\frac{\cos θ - \sin θ}{\cos θ}})$

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = (\frac{\sin^{2} θ}{\cos θ (\sin θ - \cos θ)} + \frac{\cos^{2} θ}{\sin θ (\sin θ - \cos θ)})$

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = \frac{1}{(\sin θ - \cos θ)} (\frac{\sin^{2} θ}{\cos θ} + \frac{\cos^{2} θ}{\sin θ})$

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = \frac{1}{(\sin θ - \cos θ)} (\frac{\sin^{3} θ - \cos^{3} θ}{\sin θ \cos θ})$

Now, by applying the identity $a^{3} - b^{3} = (a - b) (a^{2} + a b + b^{2})$ , we get

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = \frac{1}{(\sin θ - \cos θ)} [\frac{(\sin θ - \cos θ) (\sin^{2} θ + \cos^{2} θ + \sin θ \cos θ)}{\sin θ \cos θ}]$

Now, we know that $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = \frac{1}{(\sin θ - \cos θ)} [\frac{(\sin θ - \cos θ) (1 + \sin θ \cos θ)}{\sin θ \cos θ}]$

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = \frac{(1 + \sin θ \cos θ)}{\sin θ \cos θ}$

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = \frac{1}{\sin θ \cos θ} + \frac{\sin θ \cos θ}{\sin θ \cos θ}$

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = \frac{1}{\sin θ \cos θ} + 1$

We know that $c o s e c θ = \frac{1}{\sin θ}$ and $s e c θ = \frac{1}{\cos θ}$ , we get

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = \sec θ c o s e c θ + 1$

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = 1 + \sec θ c o s e c θ$

$\Rightarrow \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = R H S$

$∴ \frac{\tan θ}{1 - \cot θ} + \frac{\cot θ}{1 - \tan θ} = 1 + \sec θ c o s e c θ$

Hence proved

(iv) $\frac{1 + \sec A}{\sec A} = \frac{\sin^{2} A}{1 - \cos A}$

Ans: Given expression is $\frac{1 + \sec A}{\sec A} = \frac{\sin^{2} A}{1 - \cos A}$ .

Let us consider the LHS of the given expression, we get

$L H S = \frac{1 + \sec A}{\sec A}$

Now, we know that $\sec θ = \frac{1}{\cos θ}$ .

By substituting the value, we get

$\Rightarrow \frac{1 + \sec A}{\sec A} = \frac{1 + \frac{1}{\cos A}}{\frac{1}{\cos A}}$

$\Rightarrow \frac{1 + \sec A}{\sec A} = \frac{\frac{\cos A + 1}{\cos A}}{\frac{1}{\cos A}}$

$\Rightarrow \frac{1 + \sec A}{\sec A} = \cos A + 1$

Multiply and divide by $(1 - \cos A)$ , we get

$\Rightarrow \frac{1 + \sec A}{\sec A} = \frac{(1 + \cos A) (1 - \cos A)}{(1 - \cos A)}$

Now, by applying the identity $(a + b) (a - b) = a^{2} - b^{2}$ , we get

$\Rightarrow \frac{1 + \sec A}{\sec A} = \frac{1 - \cos^{2} A}{(1 - \cos A)}$

Now, we know that $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow \frac{1 + \sec A}{\sec A} = \frac{\sin^{2} A}{(1 - \cos A)}$

$\Rightarrow \frac{1 + \sec A}{\sec A} = R H S$

$∴ \frac{1 + \sec A}{\sec A} = \frac{\sin^{2} A}{1 - \cos A}$

Hence proved

(v) $\frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = c o s e c A + \cot A$

Ans: Given expression is $\frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = c o s e c A + \cot A$ .

Now, let us consider the LHS of the given expression, we get

$L H S = \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1}$

Dividing numerator and denominator by $\sin A$ , we get

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = \frac{\frac{\cos A}{\sin A} - \frac{\sin A}{\sin A} + \frac{1}{\sin A}}{\frac{\cos A}{\sin A} + \frac{\sin A}{\sin A} - \frac{1}{\sin A}}$

Now, we know that $\cot θ = \frac{\cos θ}{\sin θ} = \frac{1}{\tan θ}$ and $c o s e c θ = \frac{1}{\sin θ}$ , we get

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = \frac{\cot A - 1 + cosec A}{\cot A + 1 - cosec A}$

Now, by applying the identity ${cosec}^{2} A = 1 + \cot^{2} A$ , substitute $1 = \cot^{2} A - {cosec}^{2} A$ , we get

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = \frac{\cot A - (\cot^{2} A - {cosec}^{2} A) + cosec A}{\cot A + \cot^{2} A - {cosec}^{2} A - cosec A}$

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = \frac{\cot A - \cot^{2} A + {cosec}^{2} A + cosec A}{\cot A + \cot^{2} A - {cosec}^{2} A - cosec A}$

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = \frac{{(\cot A - 1 + cosec A)}^{2}}{\cot^{2} A - 1 + {cosec}^{2} A + 2 cosec A}$

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = \frac{2 {cosec}^{2} A + 2 \cot A cosec A - 2 \cot A - 2 cosec A}{\cot^{2} A - 1 + {cosec}^{2} A + 2 cosec A}$

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = \frac{2 cosec A (\cot A - cosec A) - 2 (\cot A - cosec A)}{\cot^{2} A - 1 + {cosec}^{2} A + 2 cosec A}$

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = \frac{(2 cosec A - 2) (\cot A - cosec A)}{1 - 1 + 2 cosec A}$

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = \frac{(2 cosec A - 2) (\cot A - cosec A)}{2 cosec A}$

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = cosec A + \cot A$

$\Rightarrow \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = R H S$

$∴ \frac{\cos A - \sin A + 1}{\cos A + \sin A - 1} = cosec A + \cot A$

Hence proved

(vi) $\sqrt{\frac{1 + \sin A}{1 - \sin A}} = \sec A + \tan A$

Ans: Given expression is $\sqrt{\frac{1 + \sin A}{1 - \sin A}} = \sec A + \tan A$ .

Let us consider the LHS of the given expression, we get

$L H S = \sqrt{\frac{1 + \sin A}{1 - \sin A}}$

Now, multiply and divide the expression by $\sqrt{1 + \sin A}$ , we get

$\Rightarrow \sqrt{\frac{1 + \sin A}{1 - \sin A}} = \sqrt{\frac{(1 + \sin A) (1 + \sin A)}{(1 - \sin A) (1 + \sin A)}}$

Now, by applying the identity $(a + b) (a - b) = a^{2} - b^{2}$ , we get

$\Rightarrow \sqrt{\frac{1 + \sin A}{1 - \sin A}} = \sqrt{\frac{{(1 + \sin A)}^{2}}{1 - \sin^{2} A}}$

Now, we know that $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow \sqrt{\frac{1 + \sin A}{1 - \sin A}} = \frac{1 + \sin A}{\sqrt{\cos^{2} A}}$

$\Rightarrow \sqrt{\frac{1 + \sin A}{1 - \sin A}} = \frac{1 + \sin A}{\cos A}$

$\Rightarrow \sqrt{\frac{1 + \sin A}{1 - \sin A}} = \frac{1}{\cos A} + \frac{\sin A}{\cos A}$

$\Rightarrow \sqrt{\frac{1 + \sin A}{1 - \sin A}} = \sec A + \tan A$

$\Rightarrow \sqrt{\frac{1 + \sin A}{1 - \sin A}} = R H S$

$∴ \sqrt{\frac{1 + \sin A}{1 - \sin A}} = \sec A + \tan A$

Hence proved

(vii) $\frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ} = \tan θ$

Ans: Given expression is $\frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ} = \tan θ$ .

Let us consider the LHS of the given expression, we get

$L H S = \frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ}$

Taking common terms out, we get

$\Rightarrow \frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ} = \frac{\sin θ (1 - 2 \sin^{2} θ)}{\cos θ (2 \cos^{2} θ - 1)}$

Now, we know that $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow \frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ} = \frac{\sin θ (1 - 2 \sin^{2} θ)}{\cos θ (2 (1 - 2 \sin^{2} θ) - 1)}$

$\Rightarrow \frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ} = \frac{\sin θ (1 - 2 \sin^{2} θ)}{\cos θ (2 - 2 \sin^{2} θ - 1)}$

$\Rightarrow \frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ} = \frac{\sin θ (1 - 2 \sin^{2} θ)}{\cos θ (1 - 2 \sin^{2} θ)}$

$\Rightarrow \frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ} = \frac{\sin θ}{\cos θ}$

$\Rightarrow \frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ} = \tan θ$

$\Rightarrow \frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ} = R H S$

$∴ \frac{\sin θ - 2 \sin^{3} θ}{2 \cos θ - \cos θ} = \tan θ$

Hence proved

(viii) ${(\sin A + c o s e c A)}^{2} + {(\cos A + s e c A)}^{2} = 7 + \tan^{2} A + \cot^{2} A$

Ans: Given expression is ${(\sin A + c o s e c A)}^{2} + {(\cos A + \sec A)}^{2} = 7 + \tan^{2} A + \cot^{2} A$ .

Let us consider the LHS of the given expression, we get

$L H S = {(\sin A + c o s e c A)}^{2} + {(\cos A + \sec A)}^{2}$

Now, by applying the identity ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ , we get

$\Rightarrow {(\sin A + c o s e c A)}^{2} + {(\cos A + \sec A)}^{2} = \sin^{2} A + c o s e c A^{2} + 2 \sin A c o s e c A + \cos^{2} A + \sec^{2} A + 2 \cos A \sec A$ $\Rightarrow {(\sin A + c o s e c A)}^{2} + {(\cos A + \sec A)}^{2} = \sin^{2} A + \cos^{2} A + c o s e c A^{2} + \sec^{2} A + 2 \sin A c o s e c A + 2 \cos A \sec A$ We know that $\sin^{2} θ + \cos^{2} θ = 1$ , $c o s e c θ = \frac{1}{\sin θ}$ and $s e c θ = \frac{1}{\cos θ}$ , we get

$\Rightarrow {(\sin A + c o s e c A)}^{2} + {(\cos A + \sec A)}^{2} = 1 + c o s e c^{2} θ + \sec^{2} θ + 2 \sin A \frac{1}{\sin A} + 2 \cos A \frac{1}{\cos A}$

$\Rightarrow {(\sin A + c o s e c A)}^{2} + {(\cos A + \sec A)}^{2} = 1 + (1 + \cot^{2} A + 1 + \tan^{2} A) + 2 + 2$

$\Rightarrow {(\sin A + c o s e c A)}^{2} + {(\cos A + \sec A)}^{2} = 7 + \tan^{2} A + \cot^{2} A$

$\Rightarrow {(\sin A + c o s e c A)}^{2} + {(\cos A + \sec A)}^{2} = R H S$

$∴ {(\sin A + c o s e c A)}^{2} + {(\cos A + \sec A)}^{2} = 7 + \tan^{2} A + \cot^{2} A$

Hence proved

(ix) $(c o s e c A - \sin A) (\sec A - \cos A) = \frac{1}{\tan A + \cot A}$

Ans: Given expression is $(c o s e c A - \sin A) (\sec A - \cos A) = \frac{1}{\tan A + \cot A}$ .

Let us consider the LHS of the given expression, we get

$L H S = (c o s e c A - \sin A) (\sec A - \cos A)$

We know that $c o s e c θ = \frac{1}{\sin θ}$ and $s e c θ = \frac{1}{\cos θ}$ , we get

$\Rightarrow (c o s e c A - \sin A) (\sec A - \cos A) = (\frac{1}{\sin A} - \sin A) (\frac{1}{\cos A} - \cos A)$

$\Rightarrow (c o s e c A - \sin A) (\sec A - \cos A) = (\frac{1 - \sin^{2} A}{\sin A}) (\frac{1 - \cos^{2} A}{\cos A})$

Now, we know that $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow (c o s e c A - \sin A) (\sec A - \cos A) = (\frac{\cos^{2} A}{\sin A}) (\frac{\sin^{2} A}{\cos A})$

$\Rightarrow (c o s e c A - \sin A) (\sec A - \cos A) = \sin A \cos A$

Now, consider the RHS of the given expression, we get

$R H S = \frac{1}{\tan A + \cot A}$

Now, we know that $\tan θ = \frac{\sin θ}{\cos θ}$ and $\cot θ = \frac{\cos θ}{\sin θ} = \frac{1}{\tan θ}$ .

$\Rightarrow \frac{1}{\tan A + \cot A} = \frac{1}{\frac{\sin A}{\cos A} + \frac{\cos A}{\sin A}}$

$\Rightarrow \frac{1}{\tan A + \cot A} = \frac{1}{\frac{\sin^{2} A + \cos^{2} A}{\sin A \cos A}}$

$\Rightarrow \frac{1}{\tan A + \cot A} = \frac{\sin A \cos A}{\sin^{2} A + \cos^{2} A}$

Now, we know that $\sin^{2} θ + \cos^{2} θ = 1$ , we get

$\Rightarrow \frac{1}{\tan A + \cot A} = \sin A \cos A$

Here, we get LHS=RHS

$∴ (c o s e c A - \sin A) (\sec A - \cos A) = \frac{1}{\tan A + \cot A}$

Hence proved

(x) $(\frac{1 + \tan^{2} A}{1 + \cot^{2} A}) = {(\frac{1 - \tan A}{1 - \cot A})}^{2}$

Ans: Given expression is $\frac{1 + \tan^{2} A}{1 + \cot^{2} A} = {(\frac{1 - \tan A}{1 - \cot A})}^{2}$ .

Let us consider the LHS of the given expression, we get

$L H S = \frac{1 + \tan^{2} A}{1 + \cot^{2} A}$

By applying the identities $\sec^{2} A = 1 + \tan^{2} A$ and ${cosec}^{2} A = 1 + \cot^{2} A$ , we get

$\Rightarrow \frac{1 + \tan^{2} A}{1 + \cot^{2} A} = \frac{s e c^{2} A}{{cosec}^{2} A}$

We know that $c o s e c θ = \frac{1}{\sin θ}$ and $s e c θ = \frac{1}{\cos θ}$ , we get

$\Rightarrow \frac{1 + \tan^{2} A}{1 + \cot^{2} A} = \frac{\frac{1}{\cos^{2} A}}{\frac{1}{\sin^{2} A}}$

$\Rightarrow \frac{1 + \tan^{2} A}{1 + \cot^{2} A} = \frac{\sin^{2} A}{\cos^{2} A}$

$\Rightarrow \frac{1 + \tan^{2} A}{1 + \cot^{2} A} = \tan^{2} A$

Now, consider the RHS of the given expression, we get

$R H S = {(\frac{1 - \tan A}{1 - \cot A})}^{2}$

Now, we know that $\cot θ = \frac{1}{\tan θ}$ , we get

$\Rightarrow {(\frac{1 - \tan A}{1 - \cot A})}^{2} = {(\frac{1 - \tan A}{1 - \frac{1}{\tan A}})}^{2}$

$\Rightarrow {(\frac{1 - \tan A}{1 - \cot A})}^{2} = {(\frac{1 - \tan A}{\frac{\tan A - 1}{\tan A}})}^{2}$

$\Rightarrow {(\frac{1 - \tan A}{1 - \cot A})}^{2} = {(- \tan A)}^{2}$

$\Rightarrow {(\frac{1 - \tan A}{1 - \cot A})}^{2} = \tan^{2} A$

Here, we get LHS=RHS

$∴ \frac{1 + \tan^{2} A}{1 + \cot^{2} A} = {(\frac{1 - \tan A}{1 - \cot A})}^{2}$

Hence proved

NCERT Solutions for Class 10 Maths Chapter 8 - Summary

Introduction to Trigonometry

Trigonometry is all about triangles. It is all about right-angled triangles, triangles with one angle equal to 90 degrees, to be more precise. It's a method that helps us find a triangle's missing angles and missing sides. The ‘trigono’ word means triangle and the ‘metry’ word means to measure.

Trigonometric Ratios

In ΔABC, right-angled at ∠B, the trigonometric ratios of the ∠A are as follows:

sin A=opposite side/hypotenuse=BC/AC
cos A=adjacent side/hypotenuse=AB/AC
tan A=opposite side/adjacent side=BC/AB
cosec A=hypotenuse/opposite side=AC/BC
sec A=hypotenuse/adjacent side=AC/AB
cot A=adjacent side/opposite side=AB/BC

Standard Values of Trigonometric Ratios:

∠A	0 Degrees	30 Degrees	45 Degrees	60 Degrees	90 Degrees
sin A	0	1/2	1/√2	√3/2	1
cos A	1	√3/2	1/√2	1/2	0
tan A	0	1/√3	1	√3	not defined
cosec A	not defined	2	√2	2/√3	1
sec A	1	2/√3	√2	2	not defined
cot A	not defined	√3	1	1/√3	0

Trigonometric Identities: Trigonometric identities are essential tools in trigonometry for simplifying expressions, solving equations, and proving other mathematical statements.There are three Pythagorean trigonometric identities in trigonometry that are based on the right-triangle theorem or Pythagoras theorem.

$\sin^{2} (x) + \cos^{2} (x) = 1$
$1 + \tan^{2} (x) = \sec^{2} (x)$
${cosec}^{2} (x) = 1 + \cot^{2} (x)$

Overview of Deleted Syllabus for CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry

Chapter	Dropped Topics
Introduction to Trigonometry	Trigonometric Ratios of Complementary Angles

Class 10 Maths Chapter 8: Exercise Breakdown

Exercise	Number of Questions
Exercise 8.1	11 Questions & Solutions
Exercise 8.2	4 Questions & Solutions
Exercise 8.3	7 Questions & Solutions

Conclusion

NCERT Solutions for Class 10 Maths Introduction to Trigonometry, provided by Vedantu, offer a comprehensive understanding of this foundational topic. By focusing on key concepts like trigonometric ratios, Pythagorean identities, and solving triangles, students can develop a strong foundation in trigonometry. Pay attention to the step-by-step solutions provided in the NCERT Solutions, as they help clarify concepts and reinforce problem-solving techniques. Understanding trigonometry is crucial as it forms the basis for more advanced topics in mathematics and has practical applications in fields like engineering, physics, and navigation. In previous years question papers, around 5-6 questions have been typically asked from this chapter.

Other Study Materials of CBSE Class 10 Maths Chapter 8

S.No.	Important links for Chapter 8 Introduction to Trigonometry
1	Introduction to Trigonometry Revision Notes
2	Introduction to Trigonometry Important Questions
3	Introduction to Trigonometry Important Formulas
4	Introduction to Trigonometry NCERT Exemplar Solution

Chapter-Specific NCERT Solutions for Class 10 Maths

Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

S.No.	NCERT Solutions Class 10 Chapter-wise Maths PDF
1	Chapter 1 - Real Numbers Solutions
2	Chapter 2 - Polynomials Solutions
3	Chapter 3 - Pair Of Linear Equations In Two Variables Solutions
4	Chapter 4 - Quadratic Equations Solutions
5	Chapter 5 - Arithmetic Progressions Solutions
6	Chapter 6 - Triangles Solutions
7	Chapter 7 - Coordinate Geometry Solutions
8	Chapter 9 - Some Applications of Trigonometry Solutions
9	Chapter 10 - Circles Solutions
10	Chapter 11 - Areas Related to Circles Solutions
11	Chapter 12 - Surface Area and Volume Solutions
12	Chapter 13 - Statistics Solutions
13	Chapter 14 - Probability Solutions

Study Resources for Class 10 Maths

For complete preparation of Maths for CBSE Class 10 board exams, check out the following links for different study materials available at Vedantu.

S.No.	NCERT Study Resources for Class 10 Maths
1	CBSE Class 10 Maths Syllabus
2	CBSE Class 10 Maths Previous Year Question Paper
3	CBSE Class 10 Maths Sample Paper
4	CBSE Class 10 Maths Revision Notes
5	CBSE Class 10 Maths Important Questions
6	CBSE Class 10 Maths Formulas

Best Seller - Grade 10

Vedantu CBSE Class 10 Quick Revision Cards | Maths, Science & SST | Smart Study Companion for Exams

₹1799.00Sale

₹1554.00

Vedantu Tatva Pro Question Bank Book CBSE Class 10 Mathematics Chapterwise - Topicwise Theory and Previous Year Questions | Free CBSE Class 10 Year Long Recorded Course

₹1000.00Sale

₹700.00

Vedantu Tatva Pro Question Bank Book CBSE Class 10 Set of 3 Books |Physics, Chemistry, Biology | Chapterwise - Topicwise Theory and Previous Year Questions | Free CBSE Class 10 Year Long Recorded Course

₹2000.00Sale

₹1100.00

FAQs on NCERT Solutions for Class 10 Maths Chapter 8 Introduction To Trigonometry

1. Can I completely rely on NCERT solutions on Vedantu for exam preparation?

Yes, you may focus entirely on the NCERT Solutions provided on Vedantu for exam preparation. Many students face difficulties when searching for a reliable study-guide for several subjects. The subject-experts at Vedantu have prepared these NCERT Solutions in a simple language. You can also download the same from our app from the play store and view all the solutions in one place at any time. All solutions are developed with utmost care to ease the examination preparation. So download the NCERT solutions now and start preparing efficiently for the exams.

2. Can I find solutions for all the subjects of Class 10 on Vedantu?

You can find all the solution for all Class 10 subjects provided by Vedantu for the preparation of the exam. Many students face difficulties in finding a reliable study guide for a range of subjects. These NCERT Solutions have been prepared in a clear language by the subject experts at Vedantu. You can also download our Play Store app and view all the solutions in one location at any time. All answers are developed with the utmost care to facilitate the preparation of the examination.

3. What do you learn about trigonometry in Class 10 Maths Chapter 8?

Chapter 8 of Class 10 Maths is basically about trigonometry which is a very important topic for Class 10. It covers the introduction to the ratios and identities, trigonometric ratios of some specific angles, ratios of some complementary angles, and trigonometric identities to solve equations. Visit Vedantu’s website(vedantu.com) to take a look at the solutions for all the exercises. You can refer to Vedantu’s NCERT Solutions for Chapter 8 of Class 10 Maths Trigonometry to understand the concepts better and score high marks in exams. These solutions are available at free of cost on Vedantu website and mobile app.

4. What is the objective of Chapter 8 in Class 10 Maths Trigonometry?

The main objective of Chapter 8 of Class 10 Maths is to introduce a very important concept to students. Trigonometry is a key concept which will play a role in higher studies and also be a part of Physics numerical problems. Students should make sure that the basics of this chapter are understood well. To get an in-depth understanding of the concepts, refer to NCERT solutions, revision notes and important questions offered by Vedantu. These are available free of cost.

5. What does Exercise 8.4 of Chapter 8 Trigonometry of Class 10 Maths deal with?

Exercise 8.4 of Chapter 8 Trigonometry of Class 10 Maths deals with trigonometric ratios of complementary angles. Complementary angles are those angles whose sum adds up to a total of 90 degrees. There are some standard formulae which are important to be memorised. Students are advised to solve every single question from this exercise and refer to Vedantu’s solutions for further answers.

6. What is important in trigonometry class 10?

The three fundamental functions of trigonometry are sine, cosine, and tangent and all other essential trigonometric functions can be built using these three basic ratios or functions: cotangent, secant, and cosecant.

7. Which is the hardest question in trigonometry class 10?

Here are some specific examples of potentially challenging questions:

Prove that (cos^2 A + sin^2 A) + (1 + tan^2 A) = sec^2 A.

In a right triangle ABC where angle B = 30° and AB = 2a, find AC without using trigonometric tables.

Prove that sin 2A ≤ 2 sin A cos A for all angles A in the interval (0°, 180°).

8. Is class 10 trigonometry hard?

Class 10 trigonometry might seem challenging at first, but with practice and understanding, it becomes manageable. It's a new concept for many students, so it's natural to find it a bit difficult initially. However, with clear explanations, practice exercises, and guidance from teachers or resources like NCERT Solutions, it becomes easier to grasp. Trigonometry involves learning new terms, formulas, and solving problems using trigonometric ratios. By breaking down the concepts into smaller steps and practicing regularly, students can overcome any difficulties and feel more confident in their abilities. Remember, persistence and patience are key to mastering trigonometry, and seeking help when needed can make the learning process smoother.

9. How many trigonometric identities are there in class 10?

There are three basic Trigonometric Identities. They are

For Pythagorean Identities

sin^2 (x) + cos^2 (x) = 1.
1+tan^2 (x) = sec^2 (x).

For Reciprocal Identities

csx(x) = 1/sin(x)
sec(x) = 1/cos(x)
cot(x) = 1/tan(x)

For Quotient Identities

tan(x) = sin(x)/cos(x)
cot(x) = cos(x)/sin(x)
sec(x) = 1/os(x)

10. How many marks is trigonometry class 10?

Trigonometry questions generally carry a moderate weightage, often ranging from 10% to 20% of the total marks allocated for the mathematics paper.

11. What is the easiest way to learn trigonometry class 10?

The easiest way to learn trigonometry in Class 10 is through a combination of clear explanations, practice, and real-life applications.

12. How to be perfect in trigonometry class 10?

Becoming proficient in trigonometry in Class 10 requires dedication, practice, and a systematic approach.

NCERT Solutions for Class 10 Maths Chapter 8 Introduction To Trigonometry

NCERT Solutions for Maths Chapter 8 Class 10 Introduction to Trigonometry - Free PDF Download

Glance of NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry | Vedantu

Access Exercise Wise NCERT Solutions for Chapter 8 Maths Class 10

Exercises Under NCERT Solutions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Access NCERT Solutions for Class 10 Maths Chapter 8 – Introduction to Trigonometry

Exercise 8.1

Exercise 8.2

Exercise 8.3

NCERT Solutions for Class 10 Maths Chapter 8 - Summary

Introduction to Trigonometry

Trigonometric Ratios

Standard Values of Trigonometric Ratios:

Overview of Deleted Syllabus for CBSE Class 10 Maths Chapter 8 Introduction to Trigonometry

Class 10 Maths Chapter 8: Exercise Breakdown

Conclusion

Other Study Materials of CBSE Class 10 Maths Chapter 8

Chapter-Specific NCERT Solutions for Class 10 Maths

Study Resources for Class 10 Maths

Vedantu CBSE Class 10 Quick Revision Cards | Maths, Science & SST | Smart Study Companion for Exams

Vedantu Tatva Pro Question Bank Book CBSE Class 10 Mathematics Chapterwise - Topicwise Theory and Previous Year Questions | Free CBSE Class 10 Year Long Recorded Course

Vedantu Tatva Pro Question Bank Book CBSE Class 10 Set of 3 Books |Physics, Chemistry, Biology | Chapterwise - Topicwise Theory and Previous Year Questions | Free CBSE Class 10 Year Long Recorded Course

Vedantu Tatva Pro CBSE Class 10 book set- 4 subjects

Vedantu's Instasolve - 1 Month - 24 hours Unlimited Instant Doubt Solving

Vedantu's Instasolve - 12 Months - 24 hours Unlimited Instant Doubt Solving

Vedantu's Instasolve - 3 Months - 24 hours Unlimited Instant Doubt Solving

Biology - Vedantu - Round Neck T-Shirt

Doctor in the House - Women's Round Neck T-Shirt

Doctor in the House - Men's Round Neck T-Shirt

Dream Hustle Achieve - Men's Hooded Sweatshirt

Vedantu - (Bag + Bottle + Coffee Mug) & (Set of 6 Notebooks, Highlighter Set, Set of 4 Pens)

FAQs on NCERT Solutions for Class 10 Maths Chapter 8 Introduction To Trigonometry