Find All Circles Class 10 Questions and Answers With Detailed Solutions Here
NCERT Solutions for Class 10 Maths Chapter 10 Circles



FAQs on NCERT Solutions for Class 10 Maths Chapter 10 Circles
1. What are NCERT Solutions for Class 10 Maths Chapter 10 Circles?
NCERT Solutions for Class 10 Maths Chapter 10 Circles are step-by-step explanations and answers to all textbook questions in this chapter, helping students understand circle theorems, tangents, and related problems as per CBSE 2025–26 guidelines.
2. How should students approach solving Class 10 Circles problems using NCERT Solutions?
Students should:
- Carefully read and understand each theorem or formula related to circles.
- Draw diagrams to visualize the geometry problem.
- Follow the structured, stepwise method shown in NCERT solutions.
- Use correct terminology like tangent, secant, and radius as per CBSE patterns.
3. What are the key concepts covered in NCERT Solutions for Circles Class 10?
The key concepts include:
- Tangent and secant definitions
- Properties and theorems of tangents
- Number of tangents from an external point
- Proving geometric properties using theorems about circles
- Applications of tangents and chords
4. Why is it important to follow CBSE marking schemes when using NCERT Solutions for Class 10 Maths Chapter 10?
Adhering to CBSE marking schemes ensures students write answers in the expected format, include all necessary steps, and secure step marks in the exams for each part of the solution, which is crucial for scoring full marks.
5. How many exercises are there in Class 10 Maths Chapter 10 Circles, and what do they focus on?
Chapter 10 contains two exercises (Ex 10.1 and Ex 10.2) that focus on properties of tangents, circle theorems, construction, and application of tangent theorems to geometric problems.
6. Can a circle have more than two parallel tangents? Why/why not? (FUQ)
No, a circle can have only two parallel tangents at most, because parallel tangents must touch on opposite sides, and only two unique tangents can fulfill this condition according to the geometry of circles.
7. What common mistakes should be avoided when applying theorems from NCERT Solutions for Circles?
Students often make these errors:
- Forgetting that a tangent is always perpendicular to the radius at the point of contact
- Mixing up secant and tangent definitions
- Not writing all stepwise reasoning or skipping construction steps
- Incorrect or missing diagrams
8. How do NCERT Solutions for Class 10 Circles develop problem-solving abilities for board exams? (FUQ)
They teach students to:
- Break down complex geometry questions into logical steps
- Apply relevant theorems methodically
- Visualize with labelled diagrams
- Write clear justifications for each step, mirroring CBSE requirements
9. What types of questions are typically asked from Class 10 Maths Chapter 10 Circles in board exams?
Board exams often feature:
- Proofs of properties and theorems involving tangents
- Constructions and diagram-based questions
- Numerical application of tangent theorems using Pythagoras
- Short-answer conceptual questions on definitions
10. What is the most important theorem in Class 10 Circles and how is it used? (FUQ)
The tangent–radius theorem (The tangent to a circle is perpendicular to the radius at the point of contact) is foundational. It's used to prove relationships in problems, deduce lengths via the Pythagoras theorem, and establish the properties of tangents from external points.
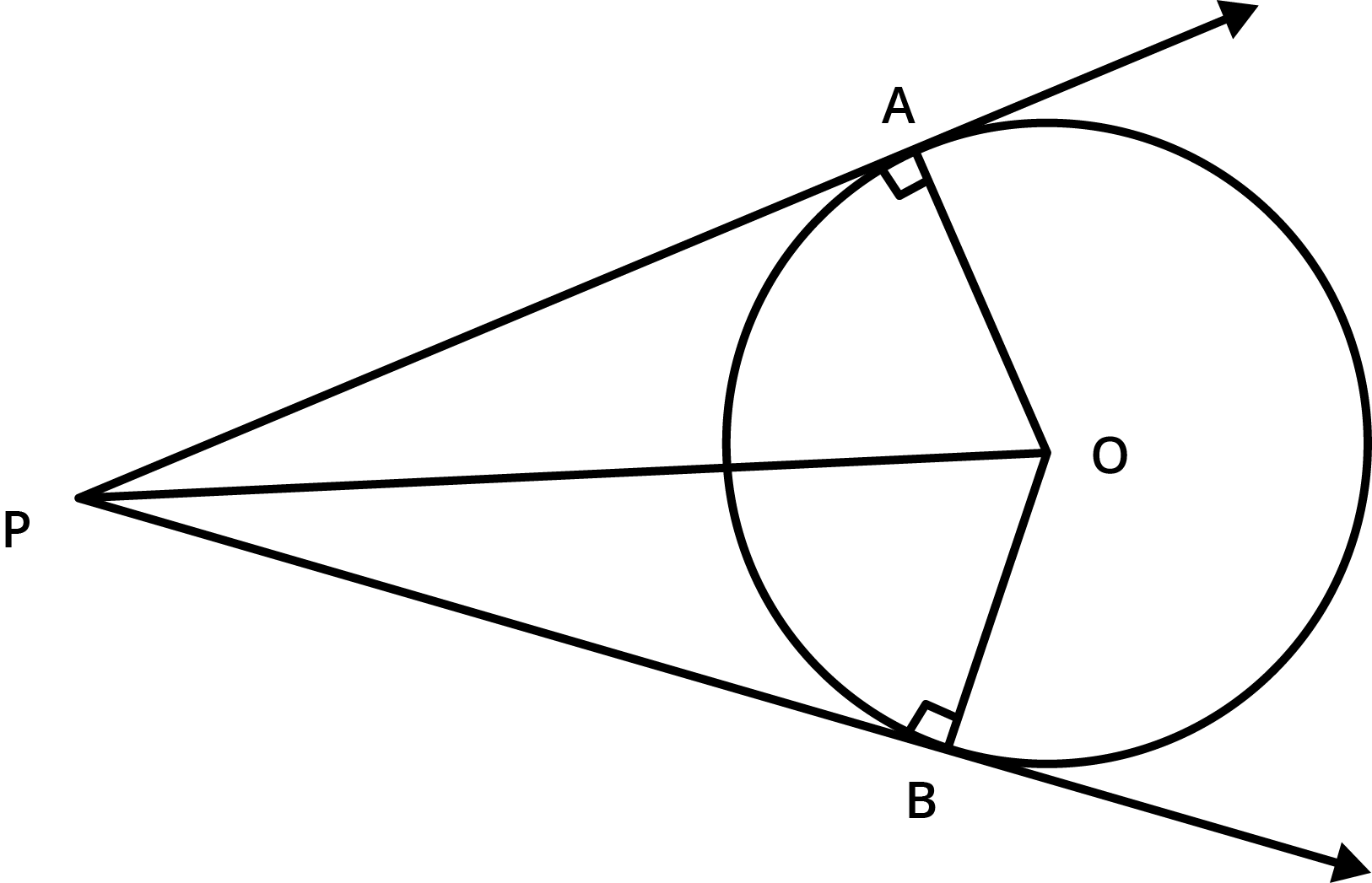
11. How do you prove that two tangents drawn from an external point to a circle are equal in length using NCERT Solutions? (FUQ)
By connecting the external point to the points of contact, both tangents are shown to form two congruent triangles with the circle's center. Using the tangent–radius theorem and congruence criteria, it's proved that the lengths are equal—a standard stepwise proof in NCERT Solutions.
12. What is a secant, and how does it differ from a tangent in Class 10 Circles?
A secant is a line that intersects a circle at exactly two points, whereas a tangent touches the circle at only one point. This distinction is critical in solving and classifying circle problems.
13. Why are diagrams essential in solving NCERT Solutions questions for Circles Class 10? (FUQ)
Diagrams help:
- Visualize relationships among points, tangents, and radii
- Identify where theorems apply
- Communicate steps to the examiner, often earning diagram marks per the CBSE marking scheme
14. What is the application of the Pythagoras theorem in Class 10 Circles problems?
The Pythagoras theorem is applied in right triangles formed by the center, the point of tangency, and an external point/tangent, allowing calculation of lengths of tangents, radii, or distances between known points as required by NCERT Solutions.
15. How do NCERT Solutions for Circles help in preparation for higher-level concepts in mathematics? (FUQ)
They lay the foundation for understanding advanced geometry, proofs, and logical reasoning needed for competitive exams (JEE, Olympiads), and deepen conceptual clarity for topics like loci, coordinate geometry, and conic sections studied in higher classes.




















 Watch Video
Watch Video






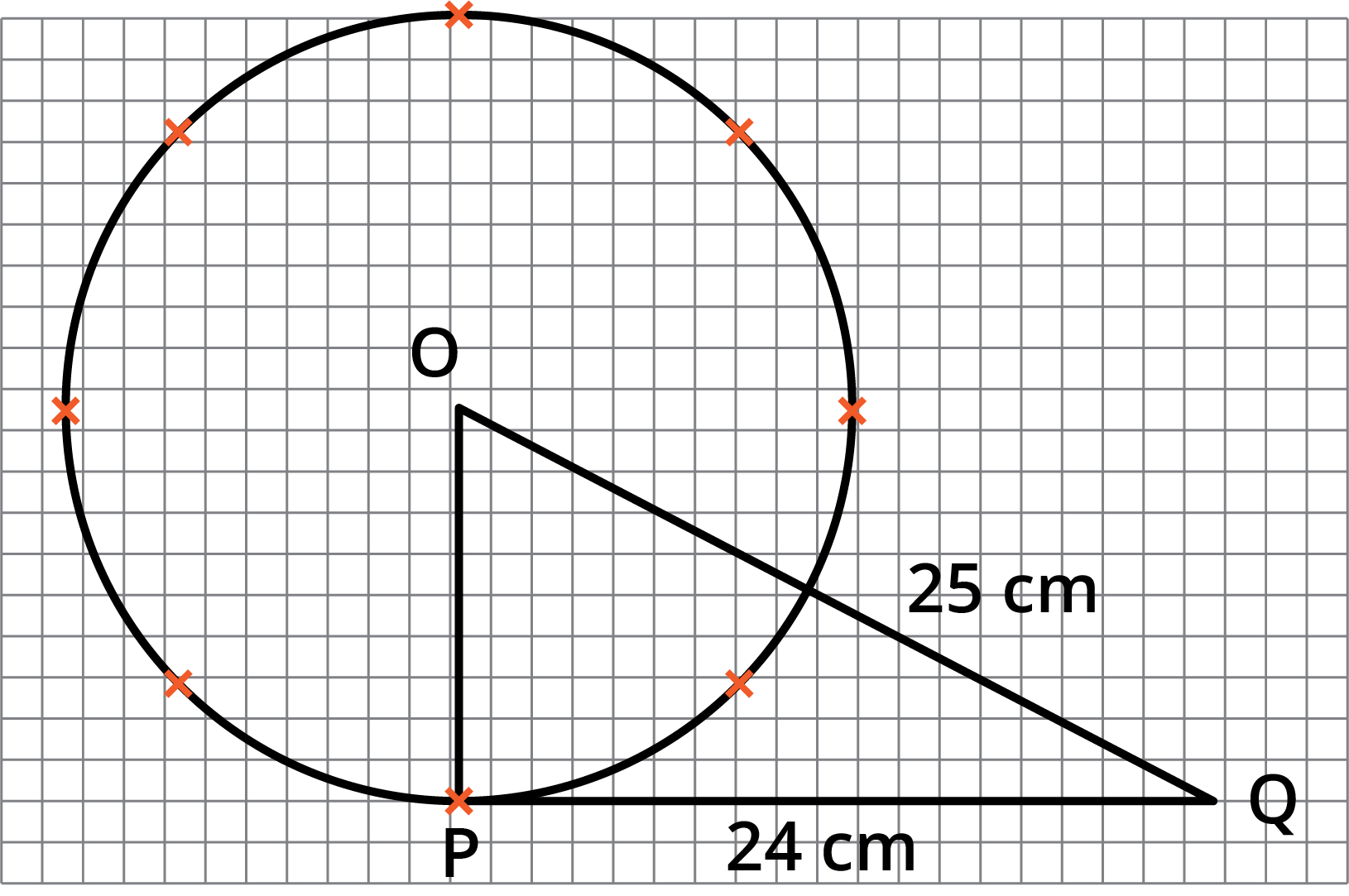
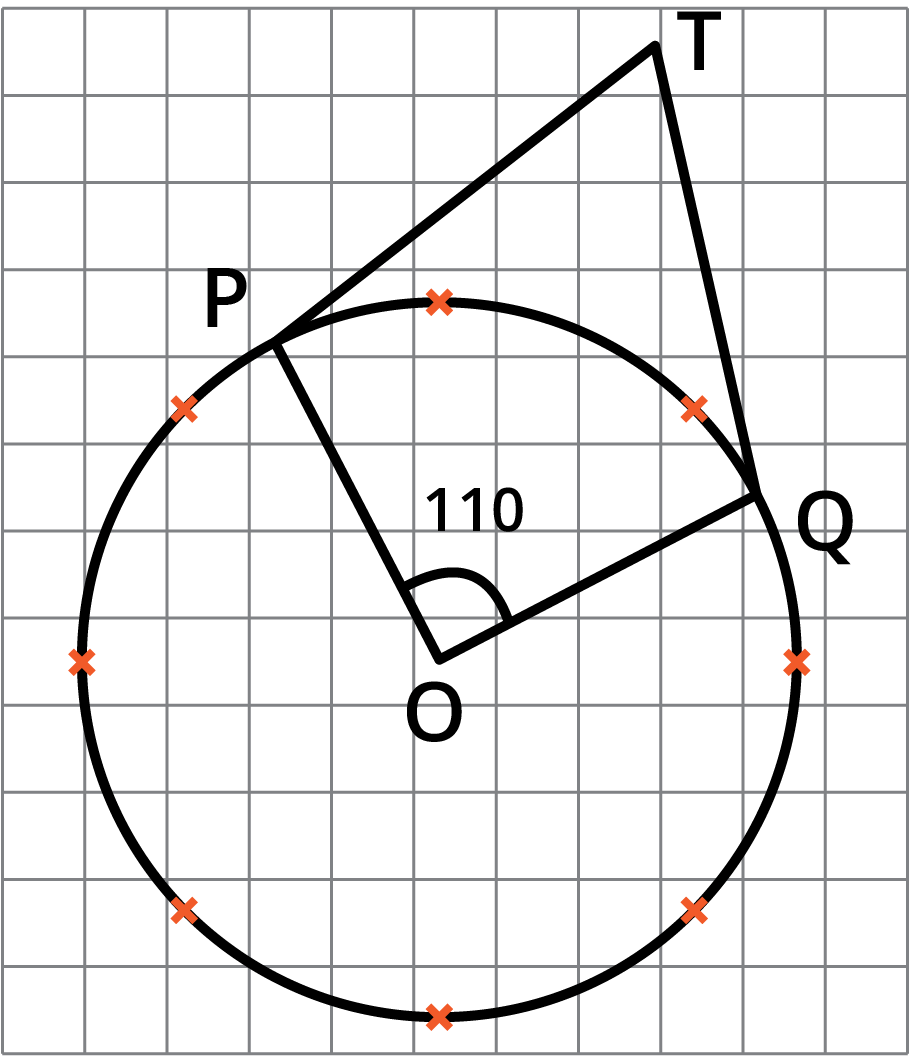


![The length of a tangent from a point \[A\] at distance \[5\ \text{cm}\] from the centre of the circle is \[4\ \text{cm}\].](https://www.vedantu.com/seo/content-images/eb745167-72ab-43c5-afd0-b50d06bbb585.png)
![Two concentric circles are of radii \[5\ \text{cm}\] and \[3\ \text{cm}\]](https://www.vedantu.com/seo/content-images/4ae23b52-8e21-42f2-9dbd-61c1e56c4022.png)
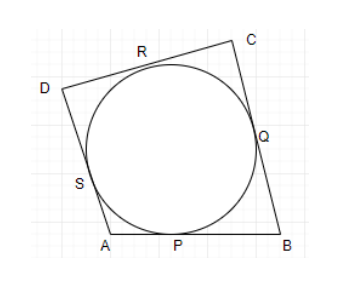
![\[XY\] and \[X'Y'\] are two parallel tangents to a circle with centre \[O\] and another tangent \[AB\] with point of contact \[C\] intersecting \[XY\] at \[A\] and \[X'Y'\] at \[B\]](https://www.vedantu.com/seo/content-images/d7c1ab06-ceb6-4ab7-bc2c-70e44f7d3ca9.png)
![A triangle \[ABC\] is drawn to circumscribe a circle of radius \[4\ \text{cm}\] such that the Segments \[BD\] and \[DC\] into which \[BC\] is divided by the point of contact \[D\] are of lengths \[8\ \text{cm}\] and \[6\ \text{cm}\] respectively](https://www.vedantu.com/seo/content-images/5ad089ce-f737-4b35-a21d-6c10294c57f1.png)