NCERT Solutions for Class 10 Maths Chapter 5 Arithmetic Progressions

Exercise 5.1 - This exercise contains four problems, each with multiple parts. These problems aim to introduce students to the fundamental formulas of Arithmetic Progressions. These formulas include those for finding the first and last terms, calculating the sum of an A.P., and finding an unknown term of an A.P. using the common difference, among others.

Exercise 5.2 - This is the second exercise contains 20 problems. This exercise covers several problems that involve finding the terms of an A.P. by using formulas and substituting known values of the A.P. The exercise also includes numerous word problems to help students understand how to apply A.P. formulas.

Exercise 5.3 - It contains 20 problems related to arithmetic progressions. The problems in this exercise range from very easy to difficult word problems. To solve these problems, students are advised to have a thorough understanding of all the A.P. formulas provided in the chapter.

Exercise 5.4 - It is the final exercise and contains five problems. The first two problems require students to find the first negative term of a given A.P. or the first term of a given A.P. from the sum and product of two other known terms of the same A.P. The remaining problems are word problems that involve basic applications of volume, length, and other physical measurements.

Access NCERT Solutions for Maths  Chapter 5 – Arithmetic Progression

Exercise 5.1

1. In Which of the Following Situations, Does the List of Numbers Involved Make As Arithmetic Progression and Why?

(i). The Taxi Fare After Each Km When the Fare is Rs $15$ for the First Km and Rs $8$ for Each Additional Km.

Ans: Given the fare of first km is Rs.$15$ and the fare for each additional km is Rs. $8$. Hence, 

Taxi fare for ${{1}^{st}}$ km is Rs. $15$.  

Taxi fare for ${{2}^{nd}}$ km is Rs. $15+8=23$.  

Taxi fare for ${{3}^{rd}}$ km is Rs. \[23+8=31\].  

Similarly, Taxi fare for ${{n}^{th}}$ km is Rs. \[15+\left( n-1 \right)8\]. 

Therefore, we can conclude that the above list forms an A.P with common difference of $8$.

(ii). The Amount of Air Present in a Cylinder When a Vacuum Pump Removes a Quarter of the Air Remaining in the Cylinder at a Time.

Ans: Let the initial volume of air in a cylinder be $V$ liter. In each stroke, the vacuum pump removes $\dfrac{1}{4}$ of air remaining in the cylinder at a time. Hence, 

Volume after ${{1}^{st}}$ stroke is $\dfrac{3V}{4}$.   

Volume after ${{2}^{nd}}$ stroke is $\dfrac{3}{4}\left( \dfrac{3V}{4} \right)$.   

Volume after ${{3}^{rd}}$ stroke is ${{\left( \dfrac{3}{4} \right)}^{2}}\left( \dfrac{3V}{4} \right)$.   

Similarly, Volume after ${{n}^{th}}$ stroke is ${{\left( \dfrac{3}{4} \right)}^{n}}V$.   

We can observe that the subsequent terms are not added with a constant digit but are being multiplied by $\dfrac{3}{4}$. Therefore, we can conclude that the above list does not forms an A.P.

(iii). The cost of digging a well after every meter of digging, when it costs Rs $150$ for the first meter and rises by Rs $50$ for each subsequent meter.

Ans: Given the cost of digging for the first meter is Rs.$150$ and the cost for each additional meter is Rs. $50$. Hence, 

Cost of digging for ${{1}^{st}}$ meter is Rs. $150$.  

Cost of digging for ${{2}^{nd}}$ meter is Rs. $150+50=200$.  

Cost of digging for ${{3}^{rd}}$ meter is Rs. \[200+50=250\].  

Similarly, Cost of digging for ${{n}^{th}}$ meter is Rs. \[150+\left( n-1 \right)50\]. 

Therefore, we can conclude that the above list forms an A.P with common difference of $50$.

(iv). The amount of money in the account every year, when Rs \[\mathbf{10000}\] is deposited at compound interest at \[\mathbf{8}\%\] per annum.

Ans: Given the principal amount is Rs.\[\mathbf{10000}\] and the compound interest is \[\mathbf{8}\%\] per annum. Hence, 

Amount after ${{1}^{st}}$ year is Rs. $10000\left( 1+\dfrac{8}{100} \right)$.  

Amount after ${{2}^{nd}}$ year is Rs. $10000{{\left( 1+\dfrac{8}{100} \right)}^{2}}$.  

Amount after ${{3}^{rd}}$ year is Rs. $10000{{\left( 1+\dfrac{8}{100} \right)}^{3}}$.  

Similarly, Amount after ${{n}^{th}}$ year is Rs. $10000{{\left( 1+\dfrac{8}{100} \right)}^{n}}$.

We can observe that the subsequent terms are not added with a constant digit but are being multiplied by \[\left( 1+\dfrac{8}{100} \right)\]. Therefore, we can conclude that the above list does not forms an A.P.

2. Write first four terms of the A.P. when the first term $a$ and the common difference $d$ are given as follows:

1. \[a=10,d=10\]

Ans: We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(1)

Substituting \[a=10,d=10\] in (1) we get, ${{a}_{n}}=10+10\left( n-1 \right)=10n$ …..(2)

Therefore, from (2)

${{a}_{1}}=10$, ${{a}_{2}}=20$, ${{a}_{3}}=30$ and ${{a}_{4}}=40$.

2. \[a=-2,d=0\]

Ans: We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(1)

Substituting \[a=-2,d=0\] in (1) we get, ${{a}_{n}}=-2+0\left( n-1 \right)=-2$ …..(2)

Therefore, from (2)

${{a}_{1}}=-2$, ${{a}_{2}}=-2$, ${{a}_{3}}=-2$ and ${{a}_{4}}=-2$.

3. \[a=4,d=-3\]

Ans: We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(1)

Substituting \[a=4,d=-3\] in (1) we get, ${{a}_{n}}=4-3\left( n-1 \right)=7-3n$ …..(2)

Therefore, from (2)

${{a}_{1}}=4$, ${{a}_{2}}=1$, ${{a}_{3}}=-2$ and ${{a}_{4}}=-5$.

4. \[a=-1\text{,}d=1/2\]

Ans: We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(1)

Substituting \[a=-1\text{,}d=1/2\] in (1) we get, ${{a}_{n}}=-1+\dfrac{1}{2}\left( n-1 \right)=\dfrac{n-3}{2}$ …..(2)

Therefore, from (2)

${{a}_{1}}=-1$, ${{a}_{2}}=-\dfrac{1}{2}$, ${{a}_{3}}=0$ and ${{a}_{4}}=\dfrac{1}{2}$.

5. \[a=-1.25,d=-0.25\]

Ans: We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(1)

Substituting \[a=-1.25,d=-0.25\] in (1) we get, ${{a}_{n}}=-1.25-0.25\left( n-1 \right)=-1-0.25n$ …..(2)

Therefore, from (2)

${{a}_{1}}=-1.25$, ${{a}_{2}}=-1.5$, ${{a}_{3}}=-1.75$ and ${{a}_{4}}=-2$.

3. For the following A.P.s, write the first term and the common difference.

1. \[\mathbf{3},\mathbf{1},-\mathbf{1},-\mathbf{3},...\]

Ans: From the given AP, we can see that the first term is $3$.

The common difference is the difference between any two consecutive numbers of the A.P.

Common difference $=$ ${{2}^{nd}}\text{ }term-{{1}^{st}}\ term$

$\therefore $ Common difference $=$ $1-3=-2$.

2. \[-5,-1,3,7,...\]

Ans: From the given AP, we can see that the first term is $-5$.

The common difference is the difference between any two consecutive numbers of the A.P. 

Common difference $=$ ${{2}^{nd}}\text{ }term-{{1}^{st}}\ term$

$\therefore $ Common difference $=$ $-1-\left( -5 \right)=4$.

3. \[\dfrac{1}{3}\text{,}\dfrac{5}{3}\text{,}\dfrac{9}{3}\text{,}\dfrac{13}{3},...\]

Ans: From the given AP, we can see that the first term is $\dfrac{1}{3}$.

The common difference is the difference between any two consecutive numbers of the A.P. 

Common difference $=$ ${{2}^{nd}}\text{ }term-{{1}^{st}}\ term$

$\therefore $ Common difference $=$ $\dfrac{5}{3}-\dfrac{1}{3}=\dfrac{4}{3}$.

4. \[0.6,1.7,2.8,3.9,...\]

Ans: From the given AP, we can see that the first term is $0.6$.

The common difference is the difference between any two consecutive numbers of the A.P. 

Common difference $=$ ${{2}^{nd}}\text{ }term-{{1}^{st}}\ term$

$\therefore $ Common difference $=$ $1.7-0.6=1.1$.

4. Which of the following are AP’s? If they form an AP, find the common difference $d$ and write three more terms.

1. \[\text{2,4,8,16}...\]

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${{a}_{2}}-{{a}_{1}}=4-2=2$              …..(1)

${{a}_{3}}-{{a}_{2}}=8-4=4$              …..(2)

${{a}_{4}}-{{a}_{3}}=16-8=8$              …..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is not equal.

Therefore, the given series does not form an A.P.

2. \[\text{2,}\dfrac{5}{2}\text{,3,}\dfrac{7}{2}\text{,}...\]

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${{a}_{2}}-{{a}_{1}}=\dfrac{5}{2}-2=\dfrac{1}{2}$              …..(1)

${{a}_{3}}-{{a}_{2}}=3-\dfrac{5}{2}=\dfrac{1}{2}$              …..(2)

${{a}_{4}}-{{a}_{3}}=\dfrac{7}{2}-3=\dfrac{1}{2}$              …..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is equal.

Therefore, the given series form an A.P. with first term $2$ and common difference $\dfrac{1}{2}$.

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(4)

Substituting \[a=2,d=\dfrac{1}{2}\] in (1) we get, ${{a}_{n}}=2+\dfrac{1}{2}\left( n-1 \right)=\dfrac{n+3}{2}$ …..(5)

Therefore, from (5)

${{a}_{5}}=4$, ${{a}_{6}}=\dfrac{9}{2}$ and ${{a}_{7}}=5$.

3. \[1.2,3.2,5.2,7.2...\]

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${{a}_{2}}-{{a}_{1}}=3.2-1.2=2$              …..(1)

${{a}_{3}}-{{a}_{2}}=5.2-3.2=2$              …..(2)

${{a}_{4}}-{{a}_{3}}=7.2-5.2=2$              …..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is equal.

Therefore, the given series form an A.P. with first term $1.2$ and common difference $2$.

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(4)

Substituting \[a=1.2,d=2\] in (1) we get, ${{a}_{n}}=1.2+2\left( n-1 \right)=2n-0.8$ …..(5)

Therefore, from (5)

${{a}_{5}}=9.2$, ${{a}_{6}}=11.2$ and \[{{a}_{7}}=13.2\].

4. $-10,-6,-2,2,...$

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${{a}_{2}}-{{a}_{1}}=-6-\left( -10 \right)=4$              …..(1)

${{a}_{3}}-{{a}_{2}}=-2-\left( -6 \right)=4$              …..(2)

${{a}_{4}}-{{a}_{3}}=2-\left( -2 \right)=4$              …..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is equal.

Therefore, the given series form an A.P. with first term $-10$ and common difference $4$.

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(4)

Substituting \[a=-10,d=4\] in (1) we get, ${{a}_{n}}=-10+4\left( n-1 \right)=4n-14$ …..(5)

Therefore, from (5)

${{a}_{5}}=6$, ${{a}_{6}}=10$ and \[{{a}_{7}}=14\].

5. \[3,3+\sqrt{2},3+2\sqrt{2},3+3\sqrt{2},...\]

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

\[{{a}_{2}}-{{a}_{1}}=\left( 3+\sqrt{2} \right)-\left( 3 \right)=\sqrt{2}\]              …..(1)

${{a}_{3}}-{{a}_{2}}=\left( 3+2\sqrt{2} \right)-\left( 3+\sqrt{2} \right)=\sqrt{2}$              …..(2)

${{a}_{4}}-{{a}_{3}}=\left( 3+3\sqrt{2} \right)-\left( 3+2\sqrt{2} \right)=\sqrt{2}$              …..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is equal.

Therefore, the given series form an A.P. with first term $3$ and common difference \[\sqrt{2}\]. 

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(4)

Substituting \[a=3,d=\sqrt{2}\] in (1) we get, ${{a}_{n}}=3+\left( n-1 \right)\sqrt{2}$   …..(5)

Therefore, from (5)

${{a}_{5}}=3+4\sqrt{2}$, ${{a}_{6}}=3+5\sqrt{2}$ and \[{{a}_{7}}=3+6\sqrt{2}\].

6. \[\text{0}\text{.2,0}\text{.22,0}\text{.222,0}\text{.2222}.....\]

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${{a}_{2}}-{{a}_{1}}=0.22-0.2=0.02$              …..(1)

${{a}_{3}}-{{a}_{2}}=0.222-0.22=0.002$              …..(2)

${{a}_{4}}-{{a}_{3}}=0.2222-0.222=0.0002$              …..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is not equal.

Therefore, the given series does not form an A.P.

7. \[0,-4,-8,-12....\]

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${{a}_{2}}-{{a}_{1}}=-4-0=-4$              …..(1)

${{a}_{3}}-{{a}_{2}}=-8-\left( -4 \right)=-4$              …..(2)

${{a}_{4}}-{{a}_{3}}=-12-\left( -8 \right)=-4$              …..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is equal.

Therefore, the given series form an A.P. with first term $0$ and common difference $-4$. 

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(4)

Substituting \[a=0,d=-4\] in (1) we get, ${{a}_{n}}=0-4\left( n-1 \right)=4-4n$ …..(5)

Therefore, from (5)

${{a}_{5}}=-16$, ${{a}_{6}}=-20$ and \[{{a}_{7}}=-24\].

8. $-\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{1}{2},-\dfrac{1}{2}....$

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${{a}_{2}}-{{a}_{1}}=\left( -\dfrac{1}{2} \right)-\left( -\dfrac{1}{2} \right)=0$              …..(1)

${{a}_{3}}-{{a}_{2}}=\left( -\dfrac{1}{2} \right)-\left( -\dfrac{1}{2} \right)=0$              …..(2)

${{a}_{4}}-{{a}_{3}}=\left( -\dfrac{1}{2} \right)-\left( -\dfrac{1}{2} \right)=0$              …..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is equal.

Therefore, the given series form an A.P. with first term $-\dfrac{1}{2}$ and common difference $0$. 

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$       …..(4)

Substituting \[a=-\dfrac{1}{2},d=0\] in (1) we get, ${{a}_{n}}=-\dfrac{1}{2}+0\left( n-1 \right)=-\dfrac{1}{2}$ …..(5)

Therefore, from (5)

${{a}_{5}}=-\dfrac{1}{2}$, ${{a}_{6}}=-\dfrac{1}{2}$ and \[{{a}_{7}}=-\dfrac{1}{2}\].

9. $1,3,9,27, \ldots $

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${a_2} - {a_1} = 3 - 1 = 2$         …..(1)

${a_3} - {a_2} = 9 - 3 = 6$           …..(2)

${a_4} - {a_3} = 27 - 9 = 18$           …..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is not equal.

10. $a,2a,3a,4a, \ldots $

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${a_2} - {a_1} = 2a - a = a$              …..(1)

${a_3} - {a_2} = 3a - 2a = a$              …..(2)

${a_4} - {a_3} = 4a - 3a = a$              …..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is equal.

Therefore, the given series form an A.P. with first term $a$ and common difference $a$. 

We know that the ${n^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${a_n} = a + \left( {n - 1} \right)d$       …..(4)

Substituting, $a = a,d = a$in (4)

we get, ${a_n} = a + \left( {n - 1} \right)d$....(5)

${a_5} = a + (5 - 1)a = 5a$

${a_6} = a + (6 - 1)a = 6a$

${a_7} = a + (7 - 1)a = 7a$

11. $a,{a^2},{a^3},{a^4}, \ldots $

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.${a_2} - {a_1} = {a^2} - a = a\left( {a - 1} \right)$              …..(1)

${a_3} - {a_2} = {a^3} - {a^2} = {a^2}\left( {a - 1} \right)$         …..(2)

${a_4} - {a_3} = {a^4} - {a^3} = {a^3}\left( {a - 1} \right)$  ……..(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is not equal.

Therefore, the given series does not form an A.P.

12. $\sqrt 2 ,\sqrt 8 ,\sqrt {18} ,\sqrt {32} , \ldots $

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${a_2} - {a_1} = \sqrt 8  - \sqrt 2  = 2\sqrt 2  - \sqrt 2  = \sqrt 2 $     ……(1)

${a_3} - {a_2} = \sqrt {18}  - \sqrt 8  = 3\sqrt 2  - 2\sqrt 2  = \sqrt 2 $   ………(2)

${a_4} - {a_3} = \sqrt {32}  - \sqrt {18}  = 4\sqrt 2  - 3\sqrt 2  = \sqrt 2 $.......(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is equal.

Therefore, the given series form an A.P. with first term $a$ and common difference is given by${a_n} = a + (n - 1)d$      …..(4)

Substituting, a = $\sqrt 2 $d = $\sqrt 2 $ in (4)

we get, 

${a_5} = \sqrt 2  + \left( {5 - 1} \right)\sqrt 2  = \sqrt 2  + 4\sqrt 2  = 5\sqrt 2  = \sqrt {50} $

${a_6} = \sqrt 2  + \left( {6 - 1} \right)\sqrt 2  = \sqrt 2  + 5\sqrt 2  = 6\sqrt 2  = \sqrt {72} $

${a_7} = \sqrt 2  + \left( {7 - 1} \right)\sqrt 2  = \sqrt 2  + 6\sqrt 2  = 7\sqrt 2  = \sqrt {98} $

13. $\sqrt 3 ,\sqrt 6 ,\sqrt 9 ,\sqrt {12} , \ldots $

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${a_2} - {a_1} = \sqrt 6  - \sqrt 3  = \sqrt 3  \times \sqrt 2  - \sqrt 3  = \sqrt 3 \left( {\sqrt 2  - 1} \right)$     ……(1)

${a_3} - {a_2} = \sqrt 9  - \sqrt 6  = 3 - \sqrt 6  = \sqrt 3 \left( {\sqrt 3  - \sqrt 2 } \right)$   ………(2)

${a_4} - {a_3} = \sqrt {12}  - \sqrt 9  = 2\sqrt 3  - 3 = \sqrt 3 \left( {2 - \sqrt 3 } \right)$……….(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is not equal.

Therefore, the given series does not form an A.P.

14. \[{1^2},{3^2},{5^2},{7^2}, \ldots \]

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${a_2} - {a_1} = {3^2} - {1^2} = 8$     ……(1)

${a_3} - {a_2} = {5^2} - {3^2} = 16$  ………(2)

${a_4} - {a_3} = {7^2} - {5^2} = 24$……….(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is not equal.

Therefore, the given series does not form an A.P.

15.\[{1^2},{5^2},{7^2},73,...\]

Ans: For the given series, let us check the difference between all consecutive terms and find if they are equal or not.

${a_2} - {a_1} = {5^2} - {1^2} = 24$ ……(1)

${a_3} - {a_2} = {7^2} - {5^2} = 24$………(2)

${a_4} - {a_3} = 73 - {7^2} = 24$  ……….(3)

From (1), (2), and (3) we can see that the difference between all consecutive terms is equal.

Therefore, the given series form an A.P. with first term a and common difference is given by${a_n} = a + (n - 1)d$      …..(4)

Substituting a = ${1^2}$, d=24 in (4)

we get, 

${a_5} = {1^2} + \left( {5 - 1} \right)24 = 1 + \left( 4 \right)24 = 97$

${a_6} = {1^2} + \left( {6 - 1} \right)24 = 1 + \left( 5 \right)24 = 121$

${a_7} = {1^2} + \left( {7 - 1} \right)24 = 1 + \left( 6 \right)24 = 145$

Exercise 5.2

1. Fill in the blanks in the following table, given that $a$ is the first term, $d$ the common difference and \[{{a}_{n}}\] the \[{{n}^{th}}\] term of the A.P.

(i). Ans: Given, the first Term, $a=7$  ….. (1)

Given, the common Difference, \[d=3\] …..(2)

Given, the number of Terms, \[n=8\]  …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get,

${{a}_{n}}=7+\left( 8-1 \right)3$

$\Rightarrow {{a}_{n}}=7+21$

$\therefore {{a}_{n}}=28$

(ii). Ans: Given, the first Term, $a=-18$  ….. (1)

Given, the ${{n}^{th}}$ term, \[{{a}_{n}}=0\] …..(2)

Given, the number of Terms, \[n=10\]  …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get,

$0=-18+\left( 10-1 \right)d$

$\Rightarrow 18=9d$

$\therefore d=2$

(iii). Ans: Given, the ${{n}^{th}}$ term, \[{{a}_{n}}=-5\] ….. (1)

Given, the common Difference, \[d=-3\] …..(2)

Given, the number of Terms, \[n=18\]  …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get,

$-5=a+\left( 18-1 \right)\left( -3 \right)$

$\Rightarrow -5=a-51$

$\therefore {{a}_{n}}=46$

(iv) Ans: Given, the first Term, $a=-18.9$  ….. (1)

Given, the common Difference, \[d=2.5\] …..(2)

Given, the ${{n}^{th}}$ term, \[{{a}_{n}}=3.6\] …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get,

$3.6=-18.9+\left( n-1 \right)\left( 2.5 \right)$

$\Rightarrow 22.5=\left( n-1 \right)\left( 2.5 \right)$

$\Rightarrow 9=\left( n-1 \right)$

$\therefore {{a}_{n}}=10$

(v). Ans: Given, the first Term, $a=3.5$  ….. (1)

Given, the common Difference, \[d=0\] …..(2)

Given, the number of Terms, \[n=105\]  …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get,

${{a}_{n}}=3.5+\left( 105-1 \right)\left( 0 \right)$

$\therefore {{a}_{n}}=3.5$

2. Choose the correct choice in the following and justify

(i). \[{{30}^{th}}\] term of the A.P \[10,7,4,...,\] is

1. \[97\]

2. \[77\]

3. \[77\]

4. \[87\]

Ans: C. $-77$ 

Given, the first Term, $a=10$  ….. (1)

Given, the common Difference, \[d=7-10=-3\] …..(2)

Given, the number of Terms, \[n=30\]  …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get, ${{a}_{n}}=10+\left( 30-1 \right)\left( -3 \right)$

$\Rightarrow {{a}_{n}}=10-87$

$\therefore {{a}_{n}}=-77$

(ii). \[{{11}^{th}}\] term of the A.P \[-3,-\dfrac{1}{2},2,...,\] is

1. \[28\]

2. \[22\] 

3. \[38\]

4. \[48\dfrac{1}{2}\]

Ans: B. $22$ 

Given, the first Term, $a=-3$  ….. (1)

Given, the common Difference, \[d=-\dfrac{1}{2}-\left( -3 \right)=\dfrac{5}{2}\] …..(2)

Given, the number of Terms, \[n=11\]  …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get, ${{a}_{n}}=-3+\dfrac{5}{2}\left( 11-1 \right)$

$\Rightarrow {{a}_{n}}=-3+25$

$\therefore {{a}_{n}}=22$

3. In the following APs find the missing term in the blanks

(i). \[2,\_\_,26\] 

Ans: Given, first term $a=2$ …..(1)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     

Substituting the values from (1) we get, ${{a}_{n}}=2+\left( n-1 \right)d$  …..(2)

Given, third term ${{a}_{3}}=26$. From (2) we get, 

$26=2+\left( 3-1 \right)d$

$\Rightarrow 26=2+2d$ 

$\therefore d=12$  ….(3)

From (1), (2) and (3) we get for $n=2$ 

${{a}_{2}}=2+\left( 2-1 \right)\left( 12 \right)$

$\therefore {{a}_{2}}=14$

$\therefore $ The sequence is \[2,14,26\].

(ii). \[\_\_,13,\_\_,3\]

Ans: Given, second term ${{a}_{2}}=13$ …..(1)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$ …..(2)

Substituting the values from (1) for $n=2$ we get, $13=a+d$  …..(3)

Given, fourth term ${{a}_{4}}=3$. From (2) we get, 

$3=a+3d$  …..(4)

Solving (3) and (4) by subtracting (3) from (4) we get,

$3-13=\left( a+3d \right)-\left( a+d \right)$

$\Rightarrow -10=2d$ 

$\therefore d=-5$  ….(5)

From (3) and (5) we get 

$13=a-5$

$\Rightarrow a=18$ ……(6)

Substituting the values from (5) and (6) in (2) we get,

${{a}_{n}}=18-5\left( n-1 \right)$   …..(7)

First term, $a=18$ and third term ${{a}_{3}}=8$

$\therefore $ The sequence is \[18,13,8,3\].

(iii). $5,\_\_,\_\_,9\dfrac{1}{2}$

Ans: Given, first term $a=5$ …..(1)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$ …..(2)

Substituting the values from (1) in (2) we get, ${{a}_{n}}=5+\left( n-1 \right)d$  …..(3)

Given, fourth term ${{a}_{4}}=9\dfrac{1}{2}$. From (3) we get, 

$9\dfrac{1}{2}=5+\left( 4-1 \right)d$ 

$\Rightarrow 9\dfrac{1}{2}=5+3d$ 

$\therefore d=\dfrac{3}{2}$  ….(4)

From (3) and (4) we get 

${{a}_{n}}=5+\dfrac{3}{2}\left( n-1 \right)$ ……(5)

Second term, ${{a}_{2}}=\dfrac{13}{2}$ and third term ${{a}_{3}}=8$

$\therefore $ The sequence is $5,\dfrac{13}{2},8,9\dfrac{1}{2}$.

(iv). $-4,\_\_,\_\_,\_\_,\_\_,6$

Ans: Given, first term $a=-4$ …..(1)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$ …..(2)

Substituting the values from (1) in (2) we get, ${{a}_{n}}=-4+\left( n-1 \right)d$  …..(3)

Given, sixth term ${{a}_{6}}=6$. From (3) we get, 

$6=-4+\left( 6-1 \right)d$ 

$\Rightarrow 6=-4+5d$ 

$\therefore d=2$  ….(4)

From (3) and (4) we get 

${{a}_{n}}=-4+2\left( n-1 \right)$ ……(5)

Second term ${{a}_{2}}=-2$, third term ${{a}_{3}}=0$, fourth term ${{a}_{4}}=2$ and fifth term ${{a}_{5}}=4$.

$\therefore $ The sequence is $-4,-2,0,2,4,6$

(v). $\_\_,38,\_\_,\_\_,\_\_,-22$

Ans: Given, second term ${{a}_{2}}=38$ …..(1)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$ …..(2)

Substituting the values from (1) for $n=2$ we get, $38=a+d$  …..(3)

Given, sixth term ${{a}_{6}}=-22$. From (2) we get, 

$-22=a+5d$  …..(4)

Solving (3) and (4) by subtracting (3) from (4) we get,

$-22-38=\left( a+5d \right)-\left( a+d \right)$

$\Rightarrow -60=4d$ 

$\therefore d=-15$  ….(5)

From (3) and (5) we get 

$38=a-15$

$\Rightarrow a=53$ ……(6)

Substituting the values from (5) and (6) in (2) we get,

${{a}_{n}}=53-15\left( n-1 \right)$   …..(7)

First term, $a=53$, second term ${{a}_{3}}=23$, third term ${{a}_{3}}=8$ and fourth term ${{a}_{4}}=-7$

$\therefore $ The sequence is \[53,38,23,8,-7,-22\].

4. Which term of the A.P. \[3,8,13,18,...\] is \[78\]?

Ans: Given, the first Term, $a=3$  ….. (1)

Given, the common Difference, \[d=8-3=5\] …..(2)

Given, the ${{n}^{th}}$ term, \[{{a}_{n}}=78\] …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get,

$78=3+5\left( n-1 \right)$

$\Rightarrow 75=5\left( n-1 \right)$

$\Rightarrow 15=\left( n-1 \right)$

$\therefore n=16$ 

Therefore, \[{{16}^{th}}\] term of this A.P. is \[78\].

5. Find the number of terms in each of the following A.P.

(i). \[\text{7,13,19,}...\text{,205}\]

Ans: Given, the first Term, $a=7$  ….. (1)

Given, the common Difference, \[d=13-7=6\] …..(2)

Given, the ${{n}^{th}}$ term, \[{{a}_{n}}=205\] …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get,

$205=7+6\left( n-1 \right)$

$\Rightarrow 198=6\left( n-1 \right)$

$\Rightarrow 33=\left( n-1 \right)$

$\therefore n=34$ 

Therefore, given A.P. series has \[34\] terms.

(ii). \[18,15\dfrac{1}{2},13,....,-47\] 

Ans: Given, the first Term, $a=18$  ….. (1)

Given, the common Difference, \[d=15\dfrac{1}{2}-18=-\dfrac{5}{2}\] …..(2)

Given, the ${{n}^{th}}$ term, \[{{a}_{n}}=-47\] …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get,

$-47=18-\dfrac{5}{2}\left( n-1 \right)$

$\Rightarrow -65=-\dfrac{5}{2}\left( n-1 \right)$

$\Rightarrow 26=\left( n-1 \right)$

$\therefore n=27$ 

Therefore, given A.P. series has \[27\] terms.

6. Check whether \[-150\] is a term of the A.P. \[11,8,5,2,...\]

Ans: Given, the first Term, $a=11$  ….. (1)

Given, the common Difference, \[d=8-11=-3\] …..(2)

Given, the ${{n}^{th}}$ term, \[{{a}_{n}}=-150\] …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get,

$-150=11-3\left( n-1 \right)$

$\Rightarrow -161=-3\left( n-1 \right)$

$\Rightarrow \dfrac{161}{3}=\left( n-1 \right)$

$\therefore n=\dfrac{164}{3}$ 

Since $n$ is nor a natural number. Therefore, $-150$ is not a term of the given A.P. series.

7. Find the \[{{31}^{st}}\] term of an A.P. whose \[{{11}^{th}}\] term is \[38\] and the \[{{16}^{th}}\] term is \[73\].

Ans: Given, the \[{{11}^{th}}\] Term, ${{a}_{11}}=38$  ….. (1)

Given, the \[{{16}^{th}}\] Term, ${{a}_{16}}=73$  …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(3)

Substituting the values from (1) in (3) we get,

$38=a+\left( 11-1 \right)d$

$\Rightarrow 38=a+10d$      …..(4)

Substituting the values from (2) in (3) we get,

$73=a+\left( 16-1 \right)d$

$\Rightarrow 73=a+15d$      …..(5)

Solving equations (4) and (5) by subtracting (4) from (5) we get,

$\Rightarrow 73-38=\left( a+15d \right)-\left( a+10d \right)$

$\Rightarrow 5=35d$

$\therefore d=7$   …..(6)

Substituting value from (6) in (4) we get,

$\Rightarrow 38=a+70$

$\therefore a=-32$   …..(7)

Again, substituting the values from (6) and (7) in (3) we get,

${{a}_{n}}=-32+7\left( n-1 \right)$  …..(8)

To find the ${{31}^{st}}$ term substitute $n=31$ in (8) we get, 

${{a}_{31}}=-32+7\left( 31-1 \right)$

$\Rightarrow {{a}_{31}}=-32+210$

$\therefore {{a}_{31}}=178$

Therefore, the \[{{31}^{st}}\] term of an A.P. whose \[{{11}^{th}}\] term is \[38\] and the \[{{16}^{th}}\] term is \[73\] is $178$.

8. An A.P. consists of \[50\] terms of which \[{{3}^{rd}}\] term is \[12\] and the last term is \[106\]. Find the \[{{29}^{th}}\] term.

Ans: Given, the \[{{3}^{rd}}\] Term, ${{a}_{3}}=12$  ….. (1)

Given, the \[{{50}^{th}}\] Term, ${{a}_{50}}=106$  …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(3)

Substituting the values from (1) in (3) we get,

$12=a+\left( 3-1 \right)d$

$\Rightarrow 12=a+2d$      …..(4)

Substituting the values from (2) in (3) we get,

$106=a+\left( 50-1 \right)d$

$\Rightarrow 106=a+49d$      …..(5)

Solving equations (4) and (5) by subtracting (4) from (5) we get,

$\Rightarrow 106-12=\left( a+49d \right)-\left( a+2d \right)$

$\Rightarrow 94=47d$

$\therefore d=2$   …..(6)

Substituting value from (6) in (4) we get,

$\Rightarrow 12=a+4$

$\therefore a=8$   …..(7)

Again, substituting the values from (6) and (7) in (3) we get,

${{a}_{n}}=8+2\left( n-1 \right)$  …..(8)

To find the ${{29}^{th}}$ term substitute $n=29$ in (8) we get, 

${{a}_{29}}=8+2\left( 29-1 \right)$

$\Rightarrow {{a}_{29}}=8+56$

$\therefore {{a}_{29}}=64$

Therefore, the ${{29}^{th}}$ term of the A.P. is $64$.

9. If the \[{{3}^{rd}}\] and the \[{{9}^{th}}\] terms of an A.P. are $4$ and \[8\] respectively. Which term of this A.P. is zero.

Ans: Given, the \[{{3}^{rd}}\] Term, ${{a}_{3}}=4$  ….. (1)

Given, the \[{{9}^{th}}\] Term, ${{a}_{9}}=-8$  …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     …..(3)

Substituting the values from (1) in (3) we get,

$4=a+\left( 3-1 \right)d$

$\Rightarrow 4=a+2d$      …..(4)

Substituting the values from (2) in (3) we get,

$-8=a+\left( 9-1 \right)d$

$\Rightarrow -8=a+8d$      …..(5)

Solving equations (4) and (5) by subtracting (4) from (5) we get,

$\Rightarrow -8-4=\left( a+8d \right)-\left( a+2d \right)$

$\Rightarrow -12=6d$

$\therefore d=-2$   …..(6)

Substituting value from (6) in (4) we get,

$\Rightarrow 4=a-4$

$\therefore a=8$   …..(7)

Again, substituting the values from (6) and (7) in (3) we get,

${{a}_{n}}=8-2\left( n-1 \right)$  …..(8)

T find the term which is zero, substitute ${{a}_{n}}=0$ in (8)

$0=8-2\left( n-1 \right)$

$\Rightarrow 8=2\left( n-1 \right)$

$\Rightarrow 4=\left( n-1 \right)$

$\therefore n=5$

Therefore, given A.P. series has \[{{5}^{th}}\] term as zero.

10. If \[{{17}^{th}}\] term of an A.P. exceeds its \[{{10}^{th}}\] term by \[7\]. Find the common difference.

Ans: Given that the \[{{17}^{th}}\] term of an A.P. exceeds its \[{{10}^{th}}\] term by \[7\] i.e., 

${{a}_{17}}={{a}_{10}}+7$ …..(1)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     ….. (2)

For \[{{17}^{th}}\] term substitute $n=17$ in (2) i.e., ${{a}_{17}}=a+16d$  ….. (3)

For \[{{10}^{th}}\] term substitute $n=10$ in (2) i.e., ${{a}_{10}}=a+9d$  ….. (4)

Therefore, from (1), (3) and (4) we get, 

$a+16d=a+9d+7$

$\Rightarrow 7d=7$

$\therefore d=1$ 

Therefore, the common difference is $1$.

11. Which term of the A.P. \[3,15,27,39,...\] will be \[132\] more than its \[{{54}^{th}}\] term?

Ans: Let ${{n}^{th}}$ term of A.P. be \[132\] more than its \[{{54}^{th}}\] term i.e.,

${{a}_{n}}={{a}_{54}}+132$ …..(1)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     ….. (2)

For \[{{54}^{th}}\] term substitute $n=54$ in (2) i.e., ${{a}_{54}}=a+53d$  ….. (3)

Therefore, from (1), (2) and (3) we get, 

$a+\left( n-1 \right)d=a+53d+132$

$\Rightarrow \left( n-1 \right)d-53d=132$

$\therefore d=\dfrac{132}{n-54}$  ….. (4)

Now, given A.P. \[3,15,27,39,...\] 

Common difference $d=15-3=12$  ….. (5)

Hence, from (4) and (5) we get $12=\dfrac{132}{n-54}$

$\Rightarrow n-54=11$ 

$\therefore n=65$ 

Therefore, ${{65}^{th}}$ term of the given A.P. will be \[132\] more than its \[{{54}^{th}}\] term.

12. Two APs have the same common difference. The difference between their \[{{100}^{th}}\] term is \[100\], what is the difference between their \[{{1000}^{th}}\] terms?

Ans: Let $2$ A.P.’s be 

$a,a+d,a+2d,a+3d,....$   …..(1)

$b,b+d,b+2d,b+3d,....$    …..(2)

(Since common difference is same)

Given that the difference between their \[{{100}^{th}}\] term is \[100\] i.e., 

${{a}_{100}}-{{b}_{100}}=100$ …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     ….. (4)

Therefore, from (3) and (4) we get, 

$a+\left( 100-1 \right)d-\left( b+\left( 100-1 \right)d \right)=100$

$\Rightarrow a-b=100$  ….. (5)

Similarly, the difference between their \[{{1000}^{th}}\] terms is, 

${{a}_{1000}}-{{b}_{1000}}=\left[ a+\left( 1000-a \right)d \right]-\left[ b+\left( 1000-a \right)d \right]$

$\Rightarrow {{a}_{1000}}-{{b}_{1000}}=a-b$

$\therefore {{a}_{1000}}-{{b}_{1000}}=100$ 

Therefore, the difference between their \[{{1000}^{th}}\] terms is $100$.

13. How many three-digit numbers are divisible by $7$?

Ans: First three-digit number that is divisible by $7$ is \[105\] then the next number will be \[105+7=112\]. 

Therefore, the series becomes \[105,112,119,....\] 

This is an A.P. having first term as \[105\] and common difference as \[7\].

Now, the largest $3$ digit number is $999$.

Leu us divide it by \[7\] , to get the remainder.

$999=142\times 7+5$ 

Therefore, \[999-5=994\] is the maximum possible three-digit number that is divisible by $7$.

Also, this will be the last term of the A.P. series.

Hence the final series is as follows: \[105,112,119,...,994\] 

Let 994 be the \[{{n}^{th}}\] term of this A.P.

Then, \[{{a}_{n}}=105+7\left( n-1 \right)\] 

\[\Rightarrow 994=105+7\left( n-1 \right)\]

\[\Rightarrow 889=7\left( n-1 \right)\]

\[\Rightarrow 127=\left( n-1 \right)\]

$\therefore n=128$ 

Therefore, $128$ three-digit numbers are divisible by $7$.

14. How many multiples of $4$ lie between $10$ and $250$?

Ans: First number that is divisible by $4$ and lie between $10$ and $250$ is $12$. The next number will be \[12+4=16\]. 

Therefore, the series becomes \[12,16,20,....\] 

This is an A.P. having first term as \[12\] and common difference as \[4\].

Now, the largest number in range is $250$.

Leu us divide it by \[4\] to get the remainder.

$250=62\times 4+2$ 

Therefore, \[250-2=248\] is the last term of the A.P. series.

Hence the final series is as follows: \[12,16,20,....,248\] 

Let $248$ be the \[{{n}^{th}}\] term of this A.P.

Then, \[{{a}_{n}}=12+4\left( n-1 \right)\] 

\[\Rightarrow 248=12+4\left( n-1 \right)\]

\[\Rightarrow 236=4\left( n-1 \right)\]

\[\Rightarrow 59=\left( n-1 \right)\]

$\therefore n=60$ 

Therefore, $60$ multiples of $4$ lie between $10$ and $250$.

15. For what value of $n$, are the ${{n}^{th}}$ terms of two APs \[63,65,67,....\] and \[3,10,17,....\] equal

Ans: Given $2$ A.P.’s are

\[63,65,67,....\]   …..(1)

Its first term is $63$ and common difference is $65-63=2$ 

\[3,10,17,....\]    …..(2)

Its first term is $3$ and common difference is $10-3=7$ 

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     ….. (3)

Therefore, from (1) and (3) we get the ${{n}^{th}}$ term of the first A.P. is

${{a}_{n}}=63+2\left( n-1 \right)$

$\Rightarrow {{a}_{n}}=61+2n$  ….. (4)

And from (2) and (3) we get the ${{n}^{th}}$ term of the second A.P. is

${{b}_{n}}=3+7\left( n-1 \right)$

$\Rightarrow {{b}_{n}}=-4+7n$  ….. (5)

If the ${{n}^{th}}$ terms of two APs \[63,65,67,....\] and \[3,10,17,....\] are equal the from (4) and (5),

\[{{a}_{n}}={{b}_{n}}\]

$\Rightarrow 61+2n=-4+7n$

$\Rightarrow 65=5n$

$\therefore n=13$ 

Therefore, the ${{13}^{th}}$ term of both the A.P.’s are equal.

16. Determine the A.P. whose third term is \[16\] and the \[{{7}^{th}}\] term exceeds the \[{{5}^{th}}\] term by $12$.

Ans: Given the ${{7}^{th}}$ term of A.P. is \[12\] more than its \[{{5}^{th}}\] term i.e.,

${{a}_{7}}={{a}_{5}}+12$ …..(1)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     ….. (2)

For \[{{5}^{th}}\] term substitute $n=5$ in (2) i.e., ${{a}_{5}}=a+4d$  ….. (3)

For \[{{7}^{th}}\] term substitute $n=7$ in (2) i.e., ${{a}_{7}}=a+6d$  ….. (4)

Therefore, from (1), (3) and (4) we get, 

$a+6d=a+4d+12$

$\Rightarrow 2d=12$

$\therefore d=6$   ….. (5)

Substituting (5) in (2) we get, ${{a}_{n}}=a+6\left( n-1 \right)$ ……(6)

Given the third term of the A.P. is \[16\]. Hence from (6),

$16=a+6\left( 3-1 \right)$

$\Rightarrow 16=a+12$

$\therefore a=4$   ….. (7)

Hence from (6), ${{a}_{n}}=4+6\left( n-1 \right)$

Therefore, the A.P. will be \[4,10,16,22,....\].

17. Find the \[{{20}^{th}}\] term from the last term of the A.P. \[3,8,13,...,253\] 

Ans: Given A.P. \[3,8,13,...,253\]. To find the \[{{20}^{th}}\] term from the last write the given A.P. in reverse order and then find its \[{{20}^{th}}\] term.

Required A.P. is $253,...,13,8,3$  ….. (1) 

Its first A.P. is $253$ and common difference is $8-13=-5$.  …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     ….. (3)

Hence from (2) and (3) we get, ${{a}_{n}}=253-5\left( n-1 \right)$   …..(4)

Substitute $n=20$ in (4) we get, 

${{a}_{20}}=253-5\left( 20-1 \right)$

$\Rightarrow {{a}_{20}}=158$.

Therefore, ${{20}^{th}}$ term from the last is $158$.

18. The sum of \[{{4}^{th}}\] and \[{{8}^{th}}\] terms of an A.P. is \[24\] and the sum of the \[{{6}^{th}}\] and \[{{10}^{th}}\] terms is \[44\]. Find the first three terms of the A.P.

Ans: Given the sum of \[{{4}^{th}}\] and \[{{8}^{th}}\] terms of an A.P. is \[24\] i.e.,

${{a}_{4}}+{{a}_{8}}=24$ …..(1)

Given the sum of \[{{6}^{th}}\] and \[{{10}^{th}}\] terms is \[44\] i.e.,

${{a}_{6}}+{{a}_{10}}=44$ …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$     ….. (3)

For \[{{4}^{th}}\] term substitute $n=4$ in (3) i.e., ${{a}_{4}}=a+3d$  ….. (4)

For \[{{6}^{th}}\] term substitute $n=6$ in (3) i.e., ${{a}_{6}}=a+5d$  ….. (5)

For \[{{8}^{th}}\] term substitute $n=8$ in (3) i.e., ${{a}_{8}}=a+7d$  ….. (6)

For \[{{10}^{th}}\] term substitute $n=10$ in (3) i.e., ${{a}_{10}}=a+9d$  ….. (7)

Therefore, from (1), (6) and (4) we get, 

$\left( a+3d \right)+\left( a+7d \right)=24$

$\Rightarrow 2a+10d=24$

$\Rightarrow a+5d=12$   ….. (8)

From (2), (5) and (7) we get, 

$\left( a+5d \right)+\left( a+9d \right)=44$

$\Rightarrow 2a+14d=44$

$\Rightarrow a+7d=22$   ….. (9)

Subtracting (8) from (9) we get,  

$\Rightarrow \left( a+7d \right)-\left( a+5d \right)=22-12$

$\Rightarrow 2d=10$

$\therefore d=5$ ….. (10)

Substituting this value from (10) in (9) we get,

$a+35=22$

$\therefore a=-13$ ….. (11)

Therefore from (10) and (11), the first three terms of the A.P. are $-13,-8,-3$.

19. Subba Rao started work in \[1995\] at an annual salary of Rs \[5000\] and received an increment of Rs \[~200\] each year. In which year did his income reach Rs \[7000\]?

Ans: Given in the first year, annual salary is Rs $5000$.  

In the second year, annual salary is Rs $5000+200=5200$.  

In the third year, annual salary is Rs $5200+200=5400$. 

This series will form an A.P. with first term $5000$ and common difference $200$.  

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$  

Therefore, In the ${{n}^{th}}$ year, annual salary is ${{a}_{n}}=5000+200\left( n-1 \right)$

$\Rightarrow {{a}_{n}}=4800+200n$ …. (1)

To find the year in which his annual income reaches Rs \[7000\], substitute ${{a}_{n}}=7000$ in (1) and find the value of $n$i.e., 

$7000=4800+200n$

$\Rightarrow 2200+200n$

$\therefore n=11$ 

Therefore, in ${{11}^{th}}$ year i.e., in $2005$ his salary will be Rs $7000$.

20. Ramkali saved Rs \[5\] in the first week of a year and then increased her weekly saving by Rs \[1.75\]. If in the ${{n}^{th}}$ week, her weekly savings become Rs \[20.75\], find $n$.

Ans: Given in the first week the savings is Rs $5$.  

In the second week the savings is Rs $5+1.75=6.75$.  

In the third week the savings is Rs $6.75+1.75=8.5$. 

This series will form an A.P. with first term $5$ and common difference $1.75$.  

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$  

Therefore, In the ${{n}^{th}}$ week the savings is ${{a}_{n}}=5+1.75\left( n-1 \right)$

$\Rightarrow {{a}_{n}}=3.25+1.75n$ …. (1)

To find the week in which her savings reaches Rs \[20.75\], substitute ${{a}_{n}}=20.75$ in (1) and find the value of $n$i.e., 

$20.75=3.25+1.75n$

$\Rightarrow 17.5=1.75n$

$\therefore n=10$ 

Therefore, in ${{10}^{th}}$ week her savings will be Rs $20.75$.

Exercise 5.3

1. Find the sum of the following APs.

(i). \[\mathbf{2},\mathbf{7},\mathbf{12},....\] to \[\mathbf{10}\] terms.

Ans: Given, the first Term, $a=2$  ….. (1)

Given, the common Difference, \[d=7-2=5\] …..(2)

Given, the number of Terms, \[n=10\]  …..(3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get, ${{S}_{n}}=\dfrac{10}{2}\left[ 2\left( 2 \right)+\left( 10-1 \right)\left( 5 \right) \right]$

$\Rightarrow {{S}_{n}}=5\left[ 4+45 \right]$

$\therefore {{S}_{n}}=245$

(ii). \[-\mathbf{37},-\mathbf{33},-\mathbf{29},...\] to \[\mathbf{12}\] terms

Ans: Given, the first Term, $a=-37$  ….. (1)

Given, the common Difference, \[d=-33-\left( -37 \right)=4\] …..(2)

Given, the number of Terms, \[n=12\]  …..(3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get, ${{S}_{n}}=\dfrac{12}{2}\left[ 2\left( -37 \right)+\left( 12-1 \right)\left( 4 \right) \right]$

$\Rightarrow {{S}_{n}}=6\left[ -74+44 \right]$

$\therefore {{S}_{n}}=-180$

(iii).\[\mathbf{0}.\mathbf{6},\mathbf{1}.\mathbf{7},\mathbf{2}.\mathbf{8},.....\] to \[\mathbf{100}\] terms

Ans: Given, the first Term, $a=0.6$  ….. (1)

Given, the common Difference, \[d=1.7-0.6=1.1\] …..(2)

Given, the number of Terms, \[n=100\]  …..(3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get, ${{S}_{n}}=\dfrac{100}{2}\left[ 2\left( 0.6 \right)+\left( 100-1 \right)\left( 1.1 \right) \right]$

$\Rightarrow {{S}_{n}}=50\left[ 1.2+108.9 \right]$

$\therefore {{S}_{n}}=5505$

(iv). $\dfrac{1}{15},\dfrac{1}{12},\dfrac{1}{10},.....$ to 11 terms

Ans: Given, the first Term, $a=\dfrac{1}{15}$  ….. (1)

Given, the common Difference, \[d=\dfrac{1}{12}-\dfrac{1}{15}=\dfrac{1}{60}\] …..(2)

Given, the number of Terms, \[n=11\]  …..(3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(4)

Substituting the values from (1), (2) and (3) in (4) we get, ${{S}_{n}}=\dfrac{11}{2}\left[ 2\left( \dfrac{1}{15} \right)+\left( 11-1 \right)\left( \dfrac{1}{60} \right) \right]$

$\Rightarrow {{S}_{n}}=\dfrac{11}{2}\left[ \dfrac{4+5}{30} \right]$

\[\therefore {{S}_{n}}=\dfrac{33}{20}\]

2. Find the sums given below

(i). $7+10\dfrac{1}{2}+14+.....+84$

Ans: Given, the first Term, $a=7$  ….. (1)

Given, the common Difference, \[d=10\dfrac{1}{2}-7=\dfrac{7}{2}\] …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (3)

Substituting the values from (1) and (2) in (3) we get, 

${{a}_{n}}=7+\dfrac{7}{2}\left( n-1 \right)=\dfrac{7}{2}\left( n+1 \right)$  ….. (4)

Given, last term of the series, \[{{a}_{n}}=84\]  …..(5)

Substituting (5) in (4) we get, $84=\dfrac{7}{2}\left( n+1 \right)$

$\Rightarrow 24=\left( n+1 \right)$ 

\[\therefore n=23\]  ……(6)

We know that the sum of $n$ terms of the A.P. with first term $a$ and last term $l$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ a+l \right]$     …..(7)

Substituting the values from (1), (5) and (6) in (7) we get, ${{S}_{n}}=\dfrac{23}{2}\left[ 7+84 \right]$

$\Rightarrow {{S}_{n}}=\dfrac{23}{2}\left( 91 \right)$

\[\therefore {{S}_{n}}=1046\dfrac{1}{2}\]

(ii). \[\mathbf{34}+\mathbf{32}+\mathbf{30}+.....+\mathbf{10}\] 

Ans: Given, the first Term, $a=34$  ….. (1)

Given, the common Difference, \[d=32-34=-2\] …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (3)

Substituting the values from (1) and (2) in (3) we get, 

${{a}_{n}}=34-2\left( n-1 \right)=36-2n$  ….. (4)

Given, last term of the series, \[{{a}_{n}}=10\]  …..(5)

Substituting (5) in (4) we get, $10=36-2n$

$\Rightarrow 2n=26$ 

\[\therefore n=13\]  ……(6)

We know that the sum of $n$ terms of the A.P. with first term $a$ and last term $l$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ a+l \right]$     …..(7)

Substituting the values from (1), (5) and (6) in (7) we get, ${{S}_{n}}=\dfrac{13}{2}\left[ 34+10 \right]$

$\Rightarrow {{S}_{n}}=\dfrac{13}{2}\left( 44 \right)$

\[\therefore {{S}_{n}}=286\]

(iii). \[-5+\left( -8 \right)+\left( -11 \right)+.....+\left( -230 \right)\] 

Ans: Given, the first Term, $a=-5$  ….. (1)

Given, the common Difference, \[d=-8-\left( -5 \right)=-3\] …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (3)

Substituting the values from (1) and (2) in (3) we get, 

${{a}_{n}}=-5-3\left( n-1 \right)=-2-3n$  ….. (4)

Given, last term of the series, \[{{a}_{n}}=-230\]  …..(5)

Substituting (5) in (4) we get, $-230=-2-3n$

$\Rightarrow -228=-3n$ 

\[\therefore n=76\]  ……(6)

We know that the sum of $n$ terms of the A.P. with first term $a$ and last term $l$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ a+l \right]$     …..(7)

Substituting the values from (1), (5) and (6) in (7) we get, ${{S}_{n}}=\dfrac{76}{2}\left[ -5+\left( -230 \right) \right]$

$\Rightarrow {{S}_{n}}=\dfrac{76}{2}\left( -235 \right)$

\[\therefore {{S}_{n}}=-8930\]

3. In an AP

(i). Given \[a=5\], \[d=3\], \[{{\mathbf{a}}_{\mathbf{n}}}=\mathbf{50}\], find \[\mathbf{n}\] and \[{{\mathbf{S}}_{\mathbf{n}}}\].

Ans: Given, the first Term, $a=5$  ….. (1)

Given, the common Difference, \[d=3\] …..(2)

Given, ${{n}^{th}}$ term of the A.P., \[{{\mathbf{a}}_{\mathbf{n}}}=\mathbf{50}\]  …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (4)

Substituting the values from (1), (2) and (3) in (4) we get, 

$50=5+3\left( n-1 \right)=2+3n$ 

Simplifying it further we get, 

$n=\dfrac{50-2}{3}$ 

$\therefore n=16$   …..(5)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(6)

Substituting the values from (1), (2) and (5) in (6) we get, ${{S}_{n}}=\dfrac{16}{2}\left[ 2\left( 5 \right)+\left( 16-1 \right)\left( 3 \right) \right]$

$\Rightarrow {{S}_{n}}=8\left[ 10+45 \right]$

\[\therefore {{S}_{n}}=440\]

(ii). Given \[a=7\], \[{{a}_{13}}=35\], find \[d\] and \[{{\mathbf{S}}_{13}}\].

Ans: Given, the first Term, $a=7$  ….. (1)

Given, ${{13}^{th}}$ term of the A.P., \[{{a}_{13}}=35\]  …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (3)

Substituting the values from (1), (2) in (3) we get, 

$35=7+\left( 13-1 \right)d=7+12d$ 

Simplifying it further we get, 

$d=\dfrac{28}{12}$ 

\[\therefore d=\dfrac{7}{3}\]   …..(4)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(5)

Substituting the values from (1) and (4) in (5) we get, ${{S}_{13}}=\dfrac{13}{2}\left[ 2\left( 7 \right)+\left( 13-1 \right)\left( \dfrac{7}{3} \right) \right]$

$\Rightarrow {{S}_{13}}=\dfrac{13}{2}\left[ 14+28 \right]$

\[\therefore {{S}_{13}}=273\]

(iii). Given \[d=3\], \[{{\mathbf{a}}_{12}}=37\], find \[a\] and \[{{\mathbf{S}}_{12}}\].

Ans: Given, the common difference, $d=3$  ….. (1)

Given, ${{12}^{th}}$ term of the A.P., \[{{\mathbf{a}}_{12}}=37\]  …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (3)

Substituting the values from (1), (2) in (3) we get, 

$37=a+3\left( 12-1 \right)=a+33$ 

Simplifying it further we get,  

\[\therefore a=4\]   …..(4)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(5)

Substituting the values from (1) and (4) in (5) we get, ${{S}_{12}}=\dfrac{12}{2}\left[ 2\left( 4 \right)+\left( 12-1 \right)\left( 3 \right) \right]$

$\Rightarrow {{S}_{12}}=6\left[ 8+33 \right]$

\[\therefore {{S}_{12}}=246\]

(iv). Given \[{{\mathbf{a}}_{3}}=1\mathbf{5}\], \[{{\mathbf{S}}_{10}}=125\] find \[{{a}_{10}}\] and \[d\].

Ans: Given, ${{3}^{rd}}$ term of the A.P., \[{{\mathbf{a}}_{3}}=1\mathbf{5}\]  …..(1)

Given, the sum of terms, \[{{\mathbf{S}}_{10}}=125\]  ….. (2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (3)

Substituting the values from (1) in (3) we get, 

$15=a+\left( 3-1 \right)d=a+2d$  …..(4)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(5)

Substituting the values from (1) in (5) we get, $125=\dfrac{10}{2}\left[ 2a+\left( 10-1 \right)d \right]$

$\Rightarrow 125=5\left[ 2a+9d \right]$

\[\therefore 25=2a+9d\]  …..(5)

Let us solve equations (4) and (5) by subtracting twice of (4) from (5) we get,

\[25-30=\left( 2a+9d \right)-\left( 2a+4d \right)\]

$\Rightarrow -5=5d$ 

$\therefore d=-1$    …..(6)

From (4) and (6) we get, $a=17$   …..(7)

From (3), (6) and (7) for $n=10$ we get,

${{a}_{10}}=17-\left( 10-1 \right)$

$\therefore {{a}_{10}}=8$

(v). Given \[{{\mathbf{S}}_{9}}=75\], \[d=5\] find \[a\] and \[{{a}_{9}}\].

Ans: Given, common difference, \[d=5\]  …..(1)

Given, the sum of terms, \[{{\mathbf{S}}_{9}}=75\]  ….. (2)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(3)

Substituting the values from (1), (2) in (3) we get, $75=\dfrac{9}{2}\left[ 2a+5\left( 9-1 \right) \right]$

$\Rightarrow 25=3\left[ a+20 \right]$

$\Rightarrow 3a=-35$

\[\therefore a=-\dfrac{35}{3}\]  …..(4)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (5)

Substituting the values from (1), (4) in (5) we get, 

${{a}_{9}}=-\dfrac{35}{3}+5\left( 9-1 \right)$ 

$\Rightarrow {{a}_{9}}=-\dfrac{35}{3}+40$ 

$\therefore {{a}_{9}}=\dfrac{85}{3}$

(vi) Given \[a=2\], \[d=8\], \[{{S}_{\mathbf{n}}}=9\mathbf{0}\], find \[\mathbf{n}\] and \[{{a}_{\mathbf{n}}}\].

Ans: Given, common difference, \[d=8\]  …..(1)

Given, first term, \[a=2\]  …..(2)

Given, the sum of terms, \[{{S}_{\mathbf{n}}}=9\mathbf{0}\]  ….. (3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(3)

Substituting the values from (1), (2), (3) in (4) we get, $90=\dfrac{n}{2}\left[ 2\left( 2 \right)+8\left( n-1 \right) \right]$

$\Rightarrow 45=n\left[ 2n-1 \right]$

$\Rightarrow 2{{n}^{2}}-n-45=0$

$\Rightarrow 2{{n}^{2}}-10n+9n-45=0$

$\Rightarrow 2n\left( n-5 \right)+9\left( n-5 \right)=0$

$\Rightarrow \left( n-5 \right)\left( 2n+9 \right)=0$

\[\therefore n=5\]  …..(4)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (5)

Substituting the values from (1), (2), (4) in (5) we get, 

${{a}_{5}}=2+8\left( 5-1 \right)$ 

$\Rightarrow {{a}_{5}}=2+32$ 

$\therefore {{a}_{5}}=34$

(vii). Given \[a=8\], \[{{S}_{\mathbf{n}}}=21\mathbf{0}\], \[{{\mathbf{a}}_{\mathbf{n}}}=62\], find \[\mathbf{n}\] and \[d\].

Ans: Given, first term, \[a=8\]  …..(1)

Given, the sum of terms, \[{{S}_{\mathbf{n}}}=21\mathbf{0}\]  ….. (2)

Given, the ${{n}^{th}}$ term, \[{{\mathbf{a}}_{\mathbf{n}}}=62\] …..(3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(4)

Substituting the values from (1), (2) in (4) we get, $210=\dfrac{n}{2}\left[ 2\left( 8 \right)+d\left( n-1 \right) \right]$

$\Rightarrow 420=n\left[ 16+\left( n-1 \right)d \right]$  …..(4)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (5)

Substituting the values from (1), (3) in (5) we get, 

$62=8+\left( n-1 \right)d$   …..(6) 

Let us solve equations (4) and (6) by subtracting $n$ times of (6) from (4) we get,

$420-62n=\left( 16n+n\left( n-1 \right)d \right)-\left( 8n+n\left( n-1 \right)d \right)$

$\Rightarrow 420-62n=8n$ 

$\Rightarrow 420=70n$

$\therefore n=6$  ……(7)

Substituting the values from (7) in (6) we get, 

$62=8+\left( 6-1 \right)d$

$\Rightarrow 54=5d$ 

$\therefore d=\dfrac{54}{5}$

(viii). Given \[{{S}_{\mathbf{n}}}=-14\], \[d=2\], \[{{\mathbf{a}}_{\mathbf{n}}}=4\], find \[\mathbf{n}\] and \[a\].

Ans: Given, common difference, \[d=2\]  …..(1)

Given, the sum of terms, \[{{S}_{\mathbf{n}}}=-14\]  ….. (2)

Given, the ${{n}^{th}}$ term, \[{{\mathbf{a}}_{\mathbf{n}}}=4\] …..(3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(4)

Substituting the values from (1), (2) in (4) we get, $-14=\dfrac{n}{2}\left[ 2a+2\left( n-1 \right) \right]$

$\Rightarrow -14=n\left[ a+n-1 \right]$  …..(5)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (6)

Substituting the values from (1), (3) in (6) we get, 

$4=a+2\left( n-1 \right)$   …..(7) 

Let us solve equations (5) and (7) by substituting the value of $a$ from (7) in (5) we get,

$-14=n\left[ \left( 4-2\left( n-1 \right) \right)+n-1 \right]$

\[\Rightarrow -14=n\left[ 5-n \right]\]

$\Rightarrow {{n}^{2}}-5n-14=0$ 

$\Rightarrow {{n}^{2}}-7n+2n-14=0$

$\Rightarrow \left( n-7 \right)\left( n+2 \right)=0$

$\therefore n=7$ (Since $n$ cannot be negative)  ……(8)

Substituting the values from (8) in (7) we get, 

$4=a+2\left( 7-1 \right)$

$\Rightarrow 4=a+12$ 

$\therefore a=-8$

(ix). Given \[a=3\], \[n=8\], \[S=192\], find \[d\].

Ans: Given, first term, \[a=3\]  …..(1)

Given, the sum of terms, \[{{S}_{\mathbf{n}}}=192\]  ….. (2)

Given, the number of terms, \[n=8\] …..(3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(4)

Substituting the values from (1), (2) in (4) we get, $192=\dfrac{8}{2}\left[ 2\left( 3 \right)+d\left( 8-1 \right) \right]$

$\Rightarrow 192=4\left[ 6+7d \right]$

$\Rightarrow 48=6+7d$

$\Rightarrow 42=7d$

$\therefore d=6$

(x). Given \[l=28\], \[S=144\] and there are total $9$ terms. Find \[a\].

Ans: Given, last term, \[l=28\]  …..(1)

Given, the sum of terms, \[{{S}_{\mathbf{n}}}=144\]  ….. (2)

Given, the number of terms, \[n=9\] …..(3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and last term $l$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ a+l \right]$     …..(4)

Substituting the values from (1), (2) in (4) we get, $144=\dfrac{9}{2}\left[ a+28 \right]$

$\Rightarrow 32=a+28$

$\therefore a=4$

4. How many terms of the A.P. \[9,17,25...\] must be taken to give a sum of \[\mathbf{636}\]?

Ans: Given, common difference, \[d=17-9=8\]  …..(1)

Given, first term, \[a=9\]  …..(2)

Given, the sum of terms, \[{{S}_{\mathbf{n}}}=636\]  ….. (3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(3)

Substituting the values from (1), (2), (3) in (4) we get, $636=\dfrac{n}{2}\left[ 2\left( 9 \right)+8\left( n-1 \right) \right]$

$\Rightarrow 636=n\left( 5+4n \right)$

$\Rightarrow 4{{n}^{2}}+5n-636=0$

$\Rightarrow 4{{n}^{2}}+53n-48n-636=0$

$\Rightarrow n\left( 4n+53 \right)-12\left( 4n+53 \right)=0$

$\Rightarrow \left( n-12 \right)\left( 4n+53 \right)=0$

$\Rightarrow n=12\text{ }or\text{ }-\dfrac{53}{4}$

Since $n$ can only be a natural number \[\therefore n=12\]

5. The first term of an AP is $5$, the last term is $45$ and the sum is $400$. Find the number of terms and the common difference.

Ans: Given, first term, \[a=5\]  …..(1)

Given, the sum of terms, \[{{S}_{\mathbf{n}}}=400\]  ….. (2)

Given, the ${{n}^{th}}$ term, \[{{\mathbf{a}}_{\mathbf{n}}}=45\] …..(3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and last term $l$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ a+l \right]$     …..(4)

Substituting the values from (1), (2), (3) in (4) we get, $400=\dfrac{n}{2}\left[ 5+45 \right]$

$\Rightarrow 400=25n$ 

$\therefore n=16$ 

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (5)

Substituting the values from (1), (3) in (5) we get, 

$45=5+\left( 16-1 \right)d$   

$\Rightarrow 40=15d$ 

$\therefore d=\dfrac{8}{3}$

6. The first and the last term of an AP are $17$ and $350$ respectively. If the common difference is $9$, how many terms are there and what is their sum?

Ans: Given, first term, \[a=17\]  …..(1)

Given, the common difference, \[d=9\]  ….. (2)

Given, the ${{n}^{th}}$ term, \[{{\mathbf{a}}_{\mathbf{n}}}=350\] …..(3)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (4)

Substituting the values from (1), (2), (3) in (4) we get, 

$350=17+9\left( n-1 \right)$   

$\Rightarrow 333=9\left( n-1 \right)$ 

$\Rightarrow 37=\left( n-1 \right)$

$\therefore n=38$ ……(5)

We know that the sum of $n$ terms of the A.P. with first term $a$ and last term $l$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ a+l \right]$     …..(6)

Substituting the values from (1), (5), (3) in (6) we get, ${{S}_{38}}=\dfrac{38}{2}\left[ 17+350 \right]$

$\Rightarrow {{S}_{38}}=19\left( 367 \right)$ 

$\therefore {{S}_{38}}=6973$

7. Find the sum of first \[22\] terms of an AP in which \[d=7\] and \[{{22}^{nd}}\] term is \[149\].

Ans: Given, the common difference, \[d=7\]  ….. (1)

Given, the ${{22}^{nd}}$ term, \[{{\mathbf{a}}_{22}}=149\] …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (3)

Substituting the values from (1), (2) in (3) we get, 

$149=a+7\left( 22-1 \right)$   

$\Rightarrow 149=a+147$ 

$\therefore a=2$  ……(4)

We know that the sum of $n$ terms of the A.P. with first term $a$ and last term $l$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ a+l \right]$     …..(5)

Substituting the values from (1), (2), (4) in (5) we get, ${{S}_{22}}=\dfrac{22}{2}\left[ 2+149 \right]$

$\Rightarrow {{S}_{22}}=11\left( 151 \right)$ 

$\therefore {{S}_{22}}=1661$

8. Find the sum of first \[51\] terms of an AP whose second and third terms are \[14\] and \[18\] respectively.

Ans: Given, the ${{2}^{nd}}$ term, \[{{\mathbf{a}}_{2}}=14\]  ….. (1)

Given, the ${{3}^{rd}}$ term, \[{{\mathbf{a}}_{3}}=18\] …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$   ….. (3)

Substituting the values from (1) in (3) we get, 

$14=a+d$   …..(4)

Substituting the values from (2) in (3) we get, 

$18=a+2d$   …..(5)

Solving equations (4) and (5) by subtracting (4) from (5) we get,

$18-14=\left( a+2d \right)-\left( a+d \right)$ 

$\therefore d=4$  ……(6)

Substituting the value from (6) in (4) we get $a=10$.   …..(7) 

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     …..(8)

Substituting the values from (7), (6) in (8) we get for $n=51$ ,

 ${{S}_{51}}=\dfrac{51}{2}\left[ 2\left( 10 \right)+4\left( 51-1 \right) \right]$

$\Rightarrow {{S}_{51}}=\dfrac{51}{2}\left[ 20+200 \right]$ 

$\therefore {{S}_{51}}=5610$

9. If the sum of first \[7\] terms of an AP is \[49\] and that of \[17\] terms is \[289\], find the sum of first \[n\] terms.

Ans: Given, the sum of first $7$ terms, \[{{S}_{7}}=49\]  ….. (1)

Given, the sum of first $17$ terms, \[{{S}_{17}}=289\]   …..(2)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     ….. (3)

Substituting the values from (1) in (3) we get, 

\[49=\dfrac{7}{2}\left[ 2a+\left( 7-1 \right)d \right]\]

\[\Rightarrow 7=a+3d\]   …..(4)

Substituting the values from (2) in (3) we get, 

\[289=\dfrac{17}{2}\left[ 2a+\left( 17-1 \right)d \right]\]

\[\Rightarrow 17=a+8d\]   …..(5)

Solving equations (4) and (5) by subtracting (4) from (5) we get,

$17-7=\left( a+8d \right)-\left( a+3d \right)$ 

$\Rightarrow 10=5d$ 

$\therefore d=2$  ……(6)

Substituting the value from (6) in (4) we get $a=1$.   …..(7) 

Substituting the values from (7), (6) in (3) we get,

 ${{S}_{n}}=\dfrac{n}{2}\left[ 2+2\left( n-1 \right) \right]$

$\therefore {{S}_{n}}={{n}^{2}}$

10. Show that \[{{a}_{1}},{{a}_{2}}...,{{a}_{n}},...\] form an AP where ${{a}_{n}}$ is defined as below. Also find the sum of the first $15$ terms in each case. 

(i). \[{{a}_{n}}=3+4n\] 

Ans:  Consider two consecutive terms of the given sequence. Say ${{a}_{n}},{{a}_{n+1}}$. Difference between these terms will be 

${{a}_{n+1}}-{{a}_{n}}=\left[ 3+4\left( n+1 \right) \right]-\left[ 3+4n \right]$ 

$\Rightarrow {{a}_{n+1}}-{{a}_{n}}=4\left( n+1 \right)-4n$ 

$\Rightarrow {{a}_{n+1}}-{{a}_{n}}=4$

Which is a constant $\forall n\in \mathbb{N}$. 

For $n=1$, ${{a}_{1}}=3+4=7$ 

Therefore, it is an A.P. with first term $7$ and common difference $4$. 

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     

Therefore, ${{S}_{15}}=\dfrac{15}{2}\left[ 2\left( 7 \right)+4\left( 15-1 \right) \right]$

$\Rightarrow {{S}_{15}}=\dfrac{15}{2}\left[ 14\left( 5 \right) \right]$ 

$\therefore {{S}_{15}}=525$

(ii). \[{{a}_{n}}=9-5n\] 

Ans:  Consider two consecutive terms of the given sequence. Say ${{a}_{n}},{{a}_{n+1}}$. Difference between these terms will be 

${{a}_{n+1}}-{{a}_{n}}=\left[ 9-5\left( n+1 \right) \right]-\left[ 9-5n \right]$ 

$\Rightarrow {{a}_{n+1}}-{{a}_{n}}=-5\left( n+1 \right)+5n$ 

$\Rightarrow {{a}_{n+1}}-{{a}_{n}}=-5$

Which is a constant $\forall n\in \mathbb{N}$. 

For $n=1$, ${{a}_{1}}=9-5=4$ 

Therefore, it is an A.P. with first term $4$ and common difference $-5$. 

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     

Therefore, ${{S}_{15}}=\dfrac{15}{2}\left[ 2\left( 4 \right)-5\left( 15-1 \right) \right]$

\[\Rightarrow {{S}_{15}}=15\left[ -31 \right]\] 

$\therefore {{S}_{15}}=-465$

11. If the sum of the first $n$ terms of an AP is \[4n-{{n}^{2}}\], what is the first term (that is ${{S}_{1}}$)? What is the sum of first two terms? What is the second term? Similarly find the \[{{3}^{rd}}\], the \[{{10}^{th}}\] and the \[{{n}^{th}}\] terms. 

Ans:  Given, the sum of the first $n$ terms of an A.P. is \[4n-{{n}^{2}}\].

First term $={{S}_{1}}=4-1=3$. …..(1)

Sum of first two terms $={{S}_{2}}=8-{{\left( 2 \right)}^{2}}=4$  …..(2) 

From (1) and (2), ${{2}^{nd}}$ term $={{S}_{2}}-{{S}_{1}}=4-3=1$. 

Sum of first three terms $={{S}_{3}}=12-{{\left( 3 \right)}^{2}}=3$  …..(3) 

From (3) and (2), ${{3}^{rd}}$ term $={{S}_{3}}-{{S}_{2}}=3-4=-1$. 

Similarly, 

Sum of first $n$ terms $={{S}_{n}}=4n-{{n}^{2}}$  …..(4) 

Sum of first $n-1$ terms $={{S}_{n-1}}=4\left( n-1 \right)-{{\left( n-1 \right)}^{2}}=-{{n}^{2}}+6n-5$  …..(5) 

From (4) and (5), ${{n}^{th}}$ term $={{S}_{n}}-{{S}_{n-1}}=\left( 4n-{{n}^{2}} \right)-\left( -{{n}^{2}}+6n-5 \right)=5-2n$  …..(6)

From (6), ${{10}^{th}}$ term is $5-2\left( 10 \right)=-15$.

12. Find the sum of first $40$ positive integers divisible by $6$. 

Ans:  First positive integer that is divisible by $6$ is $6$ itself. 

Second positive integer that is divisible by $6$ is \[6+6=12\].

Third positive integer that is divisible by $6$ is \[12+6=18\].  

Hence, it is an A.P. with first term and common difference both as $6$.  

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     

Therefore, for $n=40$,

${{S}_{40}}=\dfrac{40}{2}\left[ 2\left( 6 \right)+6\left( 40-1 \right) \right]$

\[\Rightarrow {{S}_{40}}=120\left[ 41 \right]\] 

$\therefore {{S}_{40}}=4920$

13. Find the sum of first $15$ multiples of $8$.

Ans:  First positive integer that is divisible by $8$ is $8$ itself. 

Second positive integer that is divisible by $8$ is \[8+8=16\].

Third positive integer that is divisible by $8$ is \[16+8=24\].  

Hence, it is an A.P. with first term and common difference both as $8$.  

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$     

Therefore, for $n=15$,

${{S}_{15}}=\dfrac{15}{2}\left[ 2\left( 8 \right)+8\left( 15-1 \right) \right]$

\[\Rightarrow {{S}_{15}}=60\left[ 16 \right]\]

$\therefore {{S}_{15}}=960$

14. Find the sum of the odd numbers between $0$ and $50$.

Ans: The odd numbers between $0$ and $50$ are $1,3,5,...,49$. 

It is an A.P. with first term $1$ and common difference $2$.  ….(1)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$  … (2)

Substitute ${{a}_{n}}=49$ and values from (1) into (2)

$49=1+2\left( n-1 \right)$

$\Rightarrow 24=\left( n-1 \right)$ 

$\therefore n=25$  ……(3)

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$  …..(4)

Substituting values from (1), (3) in (4) we get,

${{S}_{25}}=\dfrac{25}{2}\left[ 2+2\left( 25-1 \right) \right]$

\[\Rightarrow {{S}_{25}}=25\left[ 25 \right]\] 

$\therefore {{S}_{25}}=625$

15. A contract on construction job specifies a penalty for delay of completion beyond a certain date as follows: Rs. \[\mathbf{200}\] for the first day, Rs. \[\mathbf{250}\] for the second day, Rs. \[\mathbf{300}\] for the third day, etc., the penalty for each succeeding day being Rs. \[\mathbf{50}\] more than for the preceding day. How much money the contractor has to pay as penalty, if he has delayed the work by \[\mathbf{30}\] days.

Ans: Penalty of delay for first day is Rs. $200$.

Penalty of delay for second day is Rs. $250$.

Penalty of delay for third day is Rs. $300$.

Hence it is an A.P. with first term $200$ and common difference $50$.

Money the contractor has to pay as penalty, if he has delayed the work by \[\mathbf{30}\] days is the sum of first $30$ terms of the A.P.

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$. Therefore,

${{S}_{30}}=\dfrac{30}{2}\left[ 2\left( 200 \right)+50\left( 30-1 \right) \right]$

\[\Rightarrow {{S}_{30}}=15\left[ 400+50\left( 29 \right) \right]\]

$\therefore {{S}_{30}}=27750$

Therefore, the contractor has to pay Rs \[27750\] as penalty.

16. A sum of Rs \[700\] is to be used to give seven cash prizes to students of a school for their overall academic performance. If each prize is Rs $20$ less than its preceding prize, find the value of each of the prizes.

Ans: Let the first prize be of Rs. $a$ then the second prize will be of Rs. $a-20$, the third prize will be of Rs. $a-40$.

Therefore, it is an A.P. with first term $a$ and common difference $-20$.

Given, ${{S}_{7}}=700$

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$. Therefore,

${{S}_{7}}=\dfrac{7}{2}\left[ 2a-20\left( 7-1 \right) \right]$

\[\Rightarrow 700=7\left[ a-60 \right]\]

\[\Rightarrow 100=a-60\]

$\therefore a=160$

Therefore, the value of each of the prizes was \[Rs\text{ }160,\text{ }Rs\text{ }140,\text{ }Rs\text{ }120,Rs\text{ }100,\text{ }Rs\text{ }80,\text{ }Rs\text{ }60,\text{ }and\text{ }Rs\text{ }40.\]

17. In a school, students thought of planting trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be the same as the class, in which they are studying, e.g., a section of class I will plant \[\mathbf{1}\] tree, a section of class II will plant \[\mathbf{2}\] trees and so on till class XII. There are three sections of each class. How many trees will be planted by the students?

Ans: Each section of class I will plant $1$ tree each. Therefore, total trees planted by class I are $3$.

Each section of class II will plant $2$ trees each. Therefore, total trees planted by class II are $3\times 2=6$.

Each section of class III will plant $3$ trees each. Therefore, total trees planted by class III are $3\times 3=9$.

Therefore, it is an A.P series with first term and common difference both as $3$.

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$. Therefore,

${{S}_{12}}=\dfrac{12}{2}\left[ 2\left( 3 \right)-3\left( 12-1 \right) \right]$

\[\Rightarrow {{S}_{12}}=6\left[ 39 \right]\]

$\therefore {{S}_{12}}=234$

Therefore, $234$ trees will be planted by the students.

18. A spiral is made up of successive semicircles, with centers alternately at A and B, starting with center at A of radii \[\mathbf{0}.\mathbf{5}\], \[\mathbf{1}.\mathbf{0}\] cm, \[\mathbf{1}.\mathbf{5}\] cm, \[\mathbf{2}.\mathbf{0}\] cm, ......... as shown in figure. What is the total length of such a spiral made up of thirteen consecutive semicircles?

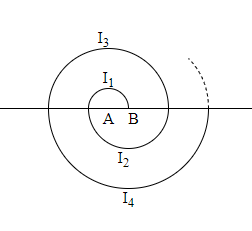
Ans: Length of first semi-circle ${{I}_{1}}=\pi \left( 0.5 \right)$ cm. 

Length of second semi-circle ${{I}_{2}}=\pi \left( 1 \right)$ cm.

Length of third semi-circle ${{I}_{3}}=\pi \left( 1.5 \right)$ cm.

Therefore, it is an A.P series with first term and common difference both as $\pi \left( 0.5 \right)$. 

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$. Therefore,

${{S}_{13}}=\dfrac{13}{2}\left[ 2\left( 0.5\pi  \right)+\left( 0.5\pi  \right)\left( 13-1 \right) \right]$

\[\Rightarrow {{S}_{13}}=7\times 13\times \left( 0.5\pi  \right)\]

\[\Rightarrow {{S}_{13}}=7\times 13\times \dfrac{1}{2}\times \dfrac{22}{7}\] 

$\therefore {{S}_{13}}=143$

Therefore, the length of such spiral of thirteen consecutive semi-circles

will be \[143\] cm.

19. The \[200\] logs are stacked in the following manner: \[20\] logs in the bottom row, \[19\] in the next row, \[18\] in the row next to it and so on. In how many rows are the \[200\] logs placed and how many logs are in the top row?

Ans: Total logs in first row are $20$.  

Total logs in second row are $19$.

Total logs in third row are $18$.

Therefore, it is an A.P series with first term $20$ and common difference $-1$. 

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$. Therefore,

$200=\dfrac{n}{2}\left[ 2\left( 20 \right)-\left( n-1 \right) \right]$

\[\Rightarrow 400=n\left[ 41-n \right]\]

\[\Rightarrow {{n}^{2}}-41n+400=0\]

\[\Rightarrow {{n}^{2}}-16n-25n+400=0\]

\[\Rightarrow n\left( n-16 \right)-25\left( n-16 \right)=0\]

\[\Rightarrow \left( n-16 \right)\left( n-25 \right)=0\] 

For $n=25$, after ${{20}^{th}}$ term, all terms are negative, which is illogical as terms are representing the number of logs and number of logs being negative is illogical.

$\therefore n=16$ 

Total logs in ${{16}^{th}}$ row $=20-\left( 16-1 \right)=5$ 

Therefore, $200$ logs will be placed in $16$ rows and the total logs in ${{16}^{th}}$ row will be $5$.

20. In a potato race, a bucket is placed at the starting point, which is $5$m from the first potato and other potatoes are placed $3$m apart in a straight line. There are ten potatoes in the line. 

A competitor starts from the bucket, picks up the nearest potato, runs back with it, drops it in the bucket, runs back to pick up the next potato, runs to the bucket to drop it in, and she continues in the same way until all the potatoes are in the bucket. What is the total distance the competitor has to run?

(Hint: to pick up the first potato and the second potato, the total

distance (in metres) run by a competitor is \[\mathbf{2}\times \mathbf{5}+\mathbf{2}\times \left( \mathbf{5}+\mathbf{3} \right)\])

Ans: Total distance run by competitor to collect and drop first potato $=2\times 5=10$m.

Total distance run by competitor to collect and drop second potato $=2\times \left( 5+3 \right)=16$m. 

Total distance run by competitor to collect and drop third potato $=2\times \left( 5+3+3 \right)=22$m. 

Therefore, it is an A.P series with first term $10$ and common difference $6$. 

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$. Therefore, to collect and drop $10$ potatoes total distance covered is

${{S}_{10}}=\dfrac{10}{2}\left[ 2\left( 10 \right)+6\left( 10-1 \right) \right]$

\[\Rightarrow {{S}_{10}}=5\left[ 74 \right]\]

$\therefore {{S}_{13}}=370$

Therefore, the competitor will run a total distance of \[370\]m.

Exercise 5.4

1. Which term of the A.P. \[\mathbf{121},\mathbf{117},\mathbf{113},...\] is its first negative term?

(Hint: Find $n$ for ${{a}_{n}}  <0$)

Ans: Given A.P. \[\mathbf{121},\mathbf{117},\mathbf{113},...\] 

Its first term is $121$ and common difference is $117-121=-4$. 

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$.

Therefore the ${{n}^{th}}$ term of the given A.P. is ${{a}_{n}}=121-4\left( n-1 \right)$   ….. (1)

To find negative term, find $n$ such that ${{a}_{n}} <0$  

Hence from (1),

$121-4\left( n-1 \right) <0$

$\Rightarrow 121 <4\left( n-1 \right)$ 

\[\Rightarrow \dfrac{121}{4}+1 < n\]

$\Rightarrow n >\dfrac{125}{4}$ 

$\therefore n >31.25$ 

Therefore, the ${{32}^{nd}}$ term of the given A.P. will be its first negative term.

2. The sum of the third and the seventh terms of an A.P is \[6\] and their product is \[8\]. Find the sum of first sixteen terms of the A.P.

Ans: Given the sum of third and seventh term of A.P., ${{a}_{3}}+{{a}_{7}}=6$  …..(1)

Given the sum of third and seventh term of A.P., ${{a}_{3}}\cdot {{a}_{7}}=8$  …..(2)

We know that the ${{n}^{th}}$ term of the A.P. with first term $a$ and common difference $d$ is given by ${{a}_{n}}=a+\left( n-1 \right)d$. Therefore, 

For $n=3,{{a}_{3}}=a+2d$ 

For $n=7,{{a}_{7}}=a+6d$ 

From (1), ${{a}_{3}}+{{a}_{7}}=\left( a+2d \right)+\left( a+6d \right)$ 

$\Rightarrow 2a+8d=6$ 

$\therefore a+4d=3$   ….. (3)

From (2), ${{a}_{3}}\cdot {{a}_{7}}=\left( a+2d \right)\cdot \left( a+6d \right)$ 

$\therefore {{a}^{2}}+8ad+12{{d}^{2}}=8$   …..(4)

Let us now solve equations (3) and (4) by substituting the value of $a$ from (3) into (4).

${{\left( 3-4d \right)}^{2}}+8d\left( 3-4d \right)+12{{d}^{2}}=8$

$\Rightarrow 9-24d+16{{d}^{2}}+24d-32{{d}^{2}}+12{{d}^{2}}=8$ 

$\Rightarrow -4{{d}^{2}}+1=0$

$\Rightarrow {{d}^{2}}=\dfrac{1}{4}$

$\therefore d=\dfrac{1}{2},-\dfrac{1}{2}$ …..(5)

CASE 1: For $d=\dfrac{1}{2}$ 

Substitute $d=\dfrac{1}{2}$ in (6) we get, $a=1$ …..(6)

Therefore, it is an A.P series with first term $1$ and common difference $\dfrac{1}{2}$. 

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$. Therefore, 

${{S}_{16}}=\dfrac{16}{2}\left[ 2+\dfrac{1}{2}\left( 16-1 \right) \right]$

$\Rightarrow {{S}_{16}}=4\left[ 19 \right]$ 

$\therefore {{S}_{16}}=76$ 

CASE 2: For $d=-\dfrac{1}{2}$ 

Substitute $d=-\dfrac{1}{2}$ in (6) we get, $a=5$ …..(7)

Therefore, it is an A.P series with first term $5$ and common difference $-\dfrac{1}{2}$ and hence, 

${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$

$\Rightarrow {{S}_{16}}=\dfrac{16}{2}\left[ 2\left( 5 \right)-\dfrac{1}{2}\left( 16-1 \right) \right]$

$\Rightarrow {{S}_{16}}=4\left[ 5 \right]$ 

$\therefore {{S}_{16}}=20$

3. A ladder has rungs \[\mathbf{25}\] cm apart. (See figure). The rungs decrease uniformly in length from \[\mathbf{45}\] cm at the bottom to \[\mathbf{25}\] cm at the top. If the top and bottom rungs are $2\dfrac{1}{2}$ m apart, what is the length of the wood required for the rungs? 

(Hint: number of rungs $=\dfrac{250}{25}$ )

Ans: Distance between first and last rungs is $2\dfrac{1}{2}m=\dfrac{5}{2}m=250cm$.

Distance between two consecutive rungs is $25cm$.

Therefore, total number of rungs are $\dfrac{250}{25}+1=11$.

Also, we can observe that the length of each rung is decreasing in a uniform order. So, we can conclude that the length of rungs is in A.P. with first term $45$, common difference $-25$ and number of terms $11$.

We know that the sum of $n$ terms of the A.P. with first term $a$ and last term $l$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ a+l \right]$. Therefore, 

${{S}_{11}}=\dfrac{11}{2}\left[ 45+25 \right]$

$\Rightarrow {{S}_{11}}=11\left[ 35 \right]$ 

$\therefore {{S}_{11}}=385$

Therefore, the length of the wood required for the rungs is \[385\]cm.

4. The houses of a row are number consecutively from \[1\] to \[49\]. Show that there is a value of \[x\] such that the sum of numbers of the houses preceding the house numbered \[x\] is equal to the sum of the number of houses following it.

Find this value of \[x\].

(Hint:\[{{S}_{x-1}}={{S}_{49}}-{{S}_{x}}\])

Ans: Given houses are numbered $1,2,3,4,....$

Clearly, they are numbered in A.P. series with both first term and common difference as $1$.

Now, there is house numbered $x$ such that the sum of numbers of the houses preceding the house numbered \[x\] is equal to the sum of the number of houses following it i.e., \[{{S}_{x-1}}={{S}_{49}}-{{S}_{x}}\]

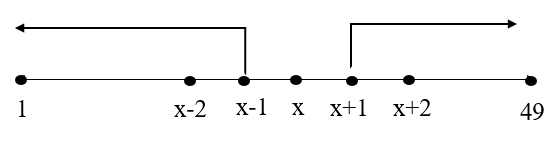
We know that the sum of $n$ terms of the A.P. with first term $a$ and last term $l$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ a+l \right]$. Therefore, 

\[{{S}_{x-1}}={{S}_{49}}-{{S}_{x}}\]

$\Rightarrow \left\{ \dfrac{\left( x-1 \right)}{2}\left[ 1+\left( x-1 \right) \right] \right\}=\left\{ \dfrac{49}{2}\left[ 1+49 \right] \right\}-\left\{ \dfrac{x}{2}\left[ 1+x \right] \right\}$

$\Rightarrow \dfrac{x\left( x-1 \right)}{2}=49\left[ 25 \right]-\dfrac{x\left( x+1 \right)}{2}$ 

$\Rightarrow x\left( x-1 \right)=2450-x\left( x+1 \right)$

$\Rightarrow 2{{x}^{2}}=2450$

$\therefore x=35$   (Since house number cannot be negative)

Therefore, house number \[35\] is such that the sum of the numbers of houses preceding the house numbered \[35\] is equal to the sum of the numbers of the houses following it.

5. A small terrace at a football ground comprises of \[15\] steps each of which is \[50\] m long and built of solid concrete. Each step has a rise of $\dfrac{1}{4}$m and a tread of $\dfrac{1}{2}$m (See figure) calculate the total volume of concrete required to build the terrace.

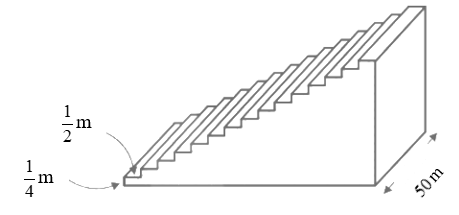
Ans: Given that a football ground comprises of \[15\] steps each of which is \[50\] m long and built of solid concrete. Each step has a rise of $\dfrac{1}{4}$m and a tread of $\dfrac{1}{2}$m. An easy illustration of the problem is depicted below.

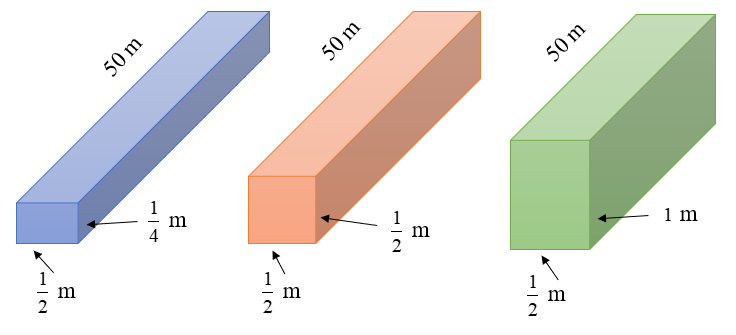
Here blue step is the lowermost step. Let it be known as step $1$. The volume of step $1$ is $\dfrac{1}{2}\times \dfrac{1}{4}\times 50\text{ }{{m}^{3}}$.

The red step is the second lowermost step. Let it be known as step $2$. The volume of step $2$ is $\dfrac{1}{2}\times \dfrac{1}{2}\times 50\text{ }{{m}^{3}}$.

The green step is the third lower step. Let it be known as step $3$. The volume of step $3$ is $\dfrac{1}{2}\times 1\times 50\text{ }{{m}^{3}}$.

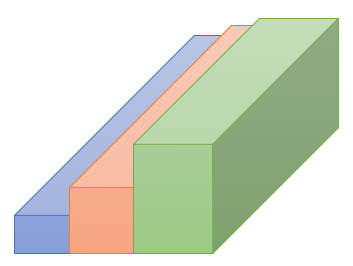
We can see that the height is increasing with each increasing step by a factor of $\dfrac{1}{4}$, length and width being constant. Hence the volume of each step is increasing by $\dfrac{1}{2}\times \dfrac{1}{4}\times 50\text{ }{{m}^{3}}$.

Therefore, we can conclude that the volume of steps is in A.P. with first term and common difference both as $\dfrac{1}{2}\times \dfrac{1}{4}\times 50=\dfrac{25}{4}\text{ }{{m}^{3}}$.

We know that the sum of $n$ terms of the A.P. with first term $a$ and common difference $d$ is given by ${{S}_{n}}=\dfrac{n}{2}\left[ 2a+\left( n-1 \right)d \right]$. Therefore, 

${{S}_{15}}=\dfrac{15}{2}\left[ 2\left( \dfrac{25}{4} \right)+\left( \dfrac{25}{4} \right)\left( 15-1 \right) \right]$

$\Rightarrow {{S}_{15}}=\dfrac{15}{2}\left( \dfrac{25}{4} \right)\left[ 16 \right]$ 

$\Rightarrow {{S}_{15}}=15\cdot 25\cdot 2$

$\therefore {{S}_{15}}=750$

Therefore, volume of concrete required to build the terrace is $750\text{ }{{m}^{3}}$.

NCERT Solutions for Class 10 Maths Chapter 5 solutions PDF download

5.1 Introduction: In this chapter, we'll understand the unique number patterns and will learn how to identify them, finding specific numbers in the given sequence and also how to find the sum of all numbers in a given sequence of numbers.

5.2 Arithmetic Progression: In simple terms, Arithmetic Progression or AP can be defined as a sequence of numbers. This sequence exists in an order in which the difference between any two consecutive numbers would be constant.

For Example: if 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 is a series of natural numbers. It can be said that this series is also an arithmetic progression between the difference between every two successive terms is 1. If we have a similar series of odd and even numbers, still, the difference between two successive terms will be two. This means that the odd and even number series will also be arithmetic progressions.

There are three different types of progressions. These different types of progressions that are mentioned in Chapter 5 Class 10 Maths NCERT book are:

• Arithmetic Progression (AP)

• Geometric Progression (GP)

• Harmonic Progression (HP)

There are also three other definitions of arithmetic progression that students should remember for writing Arithmetic Progression Class 10 NCERT Solutions. These definitions are:

Definition One: Arithmetic progression is a mathematical sequence in which the difference between any two consecutive terms is always a constant. It can also be abbreviated as AP

Definition Two: It is also mentioned in NCERT Solutions Class 10 Maths Chapter 5 that arithmetic progression or sequence is the sequence of numbers. In this sequence of consecutive numbers, it is possible to find the next number by adding a fixed number to the previous number in the chain

Definition Three: In Arithmetic Progression Class 10 Solutions, the common difference of the AP is the fixed number that one should add to any term of the arithmetic progression. For example, in the arithmetic progression 1, 4, 7, 10, 13, 16, 19, 22, the value of the common difference is 3

In Class 10 Maths Chapter 5 Solutions, there are three main terms. These terms are:

• The common difference (d)

• nth Term (an)

• The num of the first n terms (Sn)

• These three terms are used to represent the property of arithmetic progression. In the next section, we will look at these three properties in more detail.

The Common Difference in Arithmetic Progression

For any given series of arithmetic progression, the terms that are used are the first term, the common difference between any two terms, and the nth term. Let’s assume that a1, a2, a3, a4, …, an is an arithmetic progression.

This means that the value of the common difference ‘d’ is:

$D = a_2 - a_1 = a_3 - a_2 = … = a_1 - a_{n-1}$

Here, d is the value of the common difference. The value of d can be positive, negative, or zero.

The First Term of Arithmetic Progression

If an individual wants to write the arithmetic progression in terms of its common difference for solving, then it can be written as:

A, a + d, a + 2d, a + 3d, a + 4d, a + 5d, …, a + (n - 1) d

In this sequence, a is the first term of the progression.

The General Form of an Arithmetic Progression

In this section, students will be able to do just that. Before we proceed, a student should begin with an assumption that the arithmetic progression for class 10 maths chapter 5 solutions is $a_1, a_2, a_3, …, a_n$

5.3 The nth Term of Arithmetic Progression (AP)

This formula can be used for finding the class 10 maths chapter 5 NCERT solutions in which one needs to get the value of the nth term of an arithmetic progression. The formula can be written as:

$A_n = a + (n - 1) d$

Here, a is the first term, d is the value of the common difference, n is the number of terms, and an is the nth term.

Let’s take an example. Try to find out the nth term of the following arithmetic progression 1, 2, 3, 4, 5, …, an. The total number of terms is 15.

We know that n = 15. This means that according to the formula, we can say that:

$A_n = a + (n - 1) d$

Since, a = 1, and the common difference or d = 2 - 1 = 1

Then, $a_n = 1 + (15 - 1) 1 = 1 + 14 = 15$.

The behaviour of the entire sequence will also depend on the values of the common difference. This means that if the value of the common difference is positive, then the member terms will grow towards positive infinity. And if the value of the common difference is negative, then the member terms will move towards negative infinity.

5.4 The Sum of the First n Terms of an Arithmetic Progression(AP)

One can easily calculate the sum of n terms of any known progression. For an arithmetic progression, it is possible to calculate the sum of the first n terms if the value of the first term and the total terms are known. The formula is mentioned below.

$S = \dfrac{n}{2}$

$2a+(n-1) \times d$

But what if the value of the last term of the arithmetic progression is given? In that case, students should use the formula that is mentioned below.

S = $\dfrac{n}{2}$(first term + last term)

For ease of revision, we have also summarized all the major formulas of this chapter in a table. That table is mentioned below.

Class 10 Maths Chapter 5: Exercises Breakdown

Conclusion

NCERT Solutions for Class 10 Maths Chapter on Arithmetic Progressions provided by Vedantu offer a comprehensive understanding of this fundamental concept.Students can gain a solid understanding of arithmetic progressions by concentrating on important concepts such as calculating the sum of terms, nth term, and common difference. It's important to pay close attention to the step-by-step solutions provided in the NCERT Solutions, as they help clarify concepts and reinforce problem-solving techniques.Arithmetic progressions are fundamental to more advanced mathematical ideas, hence it's important to understand them. This chapter has usually been the subject of five or six questions on previous year's exam papers. Therefore, practicing a variety of problems from NCERT Solutions and previous year papers can enhance preparation and confidence for exams.

Other Related Links for CBSE Class 10 Maths Chapter 5

Chapter-Specific NCERT Solutions for Class 10 Maths

Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

NCERT Study Resources for Class 10 Maths

For complete preparation of Maths for CBSE Class 10 board exams, check out the following links for different study materials available at Vedantu.