NCERT Solutions for Class 12 Physics Chapter 8 - Electromagnetic Waves

EXERCISE

1. Figure Drawn below Shows a Capacitor Made of Two Circular Plates Each of Radius \[{\mathbf{12}}{\text{ }}{\mathbf{cm}}\], and Separated by \[{\mathbf{5}}.{\mathbf{0}}{\text{ }}{\mathbf{cm}}\]. The capacitor is being Charged by an External Source (not Shown in the Figure). The Charging Current is Constant and Equal to \[{\mathbf{0}}.{\mathbf{15}}{\text{ }}{\mathbf{A}}\].

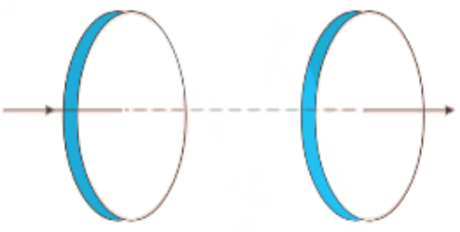
1. Calculate the Capacitance and the Rate of Change of the Potential Difference Between the Plates.

Ans: Radius of each circular plates, \[r = 12{\text{ cm}} = 0.12{\text{ m}}\]

Distance between the given plates, \[d = 5{\text{ }}cm = 0.05{\text{ }}m\]

Charging current, $I = 0.15A$

The permittivity of free space, ${\varepsilon _0} = 8.85 \times {10^{ - 12}}{C^2}{N^{ - 1}}{m^{ - 2}}$

Capacitance between the two plates can be given as: 

$C = \frac{{{\varepsilon _0}A}}{d}$

Where, 

$A = \pi {r^2}$. 

Hence,

$C = \frac{{{\varepsilon _0}\pi {r^2}}}{d}$

$C = \frac{{8.85 \times {{10}^{ - 12}} \times {{(0.12)}^2}}}{{0.05}}$

$C = 8.0032 \times {10^{ - 12}}F$   

$C = 80.032pF$

Charge on each plate is given as, \[q = CV\], where,

V = Potential difference across the plates

Differentiating both sides with respect to time (t), we get:

$\frac{{dq}}{{dt}} = C\frac{{dV}}{{dt}}$

As, $\frac{{dq}}{{dt}} = I$, so, the rate of change of potential difference between the plates can be given as:

$\frac{{dV}}{{dt}} = \frac{I}{C} = \frac{{0.15}}{{80.032 \times {{10}^{ - 12}}}}$

$\therefore \frac{{dV}}{{dt}} = 1.87 \times {10^9}{\kern 1pt} V/s$

2. Obtain the Displacement Current Across the Plates.

Ans: The displacement current across the plates would be the same as the conduction current. Hence, the displacement current, ${I_d}$ would be \[0.15{\text{ }}A\].

3. Is Kirchhoff’s First Rule (junction Rule) Valid at Each Plate of the Capacitor? Explain.

Ans: Yes, Kirchhoff’s first rule would be valid at each plate of the capacitor, provided that sum of conduction and displacement currents, i.e., $I = {I_c} + {I_d}$ (junction rule of Kirchhoff’s law).

2) A Parallel Plate Capacitor (figure) Made of Circular Plates Each of Radius \[R = 6.0{\text{ }}cm\] has a capacitance \[C = 100{\text{ }}pF\]. The Capacitor is Connected to a \[{\mathbf{230}}{\text{ }}{\mathbf{V}}\] ac supply with a (angular) frequency of \[300{\kern 1pt} {\kern 1pt} rad{\kern 1pt} {\kern 1pt} {s^{ - 1}}\].

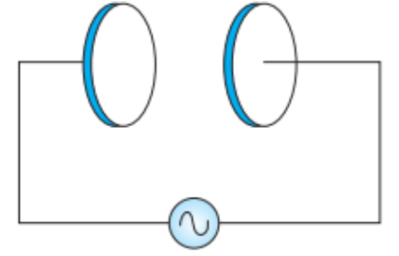
1. What is the RMS Value of the Conduction Current?

Ans: Radius of each circular plate, \[R = 6.0{\text{ }}cm = 0.06{\text{ }}m\]

Capacitance of a parallel plate capacitor, \[C = 100{\text{ }}pF = 100 \times {10^{ - 12}}F\]

Supply voltage, \[V = 230{\text{ }}V\]

Angular frequency, $\omega  = 300{\kern 1pt} {\kern 1pt} rad{\kern 1pt} {\kern 1pt} {s^{ - 1}}$

Rms value of conduction current can be given as: $I = \frac{V}{{{X_C}}}$.

Where, ${X_C}$ = capacitive currant $ = \frac{1}{{\omega C}}$

$\therefore I = V \times \omega C$    

$I = 230 \times 300 \times 100 \times {10^{ - 12}}$  

$I = 6.9 \times {10^{ - 6}}$    

$I = 6.9\mu A$

Therefore, the RMS value of conduction current will be $6.9\mu A$.

2. Is the Conduction Current Equal to the Displacement Current?

Ans: Yes, the conduction current will be the same as the displacement current. i.e., the conduction current is equal to the displacement current.

3. Determine the Amplitude of ${\overrightarrow B}$ at a point \[{\mathbf{3}}.{\mathbf{0}}{\text{ }}{\mathbf{cm}}\] from the Axis Between the Plates.

Ans: Magnetic field is given as: $\overrightarrow B = \frac{{{\mu _0}r}}{{2\pi {R^2}}}{I_0}$

Where,

${\mu _0}$= Free space permeability $ = 4\pi  \times {10^{ - 7}}N{A^{ - 2}}$

${I_0}$ = Maximum value of current = $\sqrt 2 I$

$r$= Distance between the plates from the axis = $3.0cm = 0.03cm$.

$\therefore {\overrightarrow B} = \frac{{4\pi  \times {{10}^{ - 7}} \times 0.03 \times \sqrt 2  \times 6.9 \times {{10}^{ - 6}}}}{{2\pi  \times {{(0.06)}^2}}}$      

${\overrightarrow B} = 1.63 \times {10^{ - 11}}T$

Therefore, the magnetic field at that point will be $1.63 \times {10^{ - 11}}T$.

3. What Physical Quantity is the Same for X-Rays of Wavelength \[{\mathbf{1}}{{\mathbf{0}}^{ - {\mathbf{10}}}}{\mathbf{m}}\], red light of wavelength \[6800{\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop A\limits^ \circ  \] and radio waves of wavelength \[{\mathbf{500}}{\text{ }}{\mathbf{m}}\]?

Ans: The speed of light (\[3 \times {10^8}m/s\]) is independent of the wavelength in the vacuum. Hence, it is the same for all wavelengths in a vacuum.

4. A Plane Electromagnetic Wave Travels in Vacuum Along Z-Direction. What Can You Say About the Directions of Its Electric and Magnetic Field Vectors? If the Frequency of the Wave is \[{\mathbf{30MHz}}\], what is its wavelength?

Ans: The electromagnetic wave is travelling along the z-direction, in a vacuum. The electric field (E) and the magnetic field (H) will lie in the x-y plane and they will be mutually perpendicular.

Frequency of the wave, \[\nu  = 30{\text{ }}MHz = 30 \times {10^6}{s^{ - 1}}\]

Speed of light in a vacuum, \[c = 3 \times {10^8}m/s\]

Wavelength, $\lambda $ of the wave can be given as: $\lambda  = \frac{c}{\nu }$

$\therefore \lambda  = \frac{{3 \times {{10}^8}}}{{30 \times {{10}^6}}} = 10m$

5. A Radio Can Tune in to Any Station in the \[{\mathbf{7}}.{\mathbf{5}}{\text{ }}{\mathbf{MHz}}\]  to \[{\mathbf{12}}{\text{ }}{\mathbf{MHz}}\] Band. What is the corresponding Wavelength Band?

Ans: A radio can tune to minimum frequency, \[{\nu _1} = 7.5{\text{ }}MHz = 7.5 \times {10^6}{\kern 1pt} {\kern 1pt} Hz\]

Maximum frequency, \[{\nu _2} = 12{\text{ }}MHz = 12 \times {10^6}Hz\]

Speed of light, \[c = 3 \times {10^8}m/s\]

Wavelength for frequency, ${\nu _1}$ can be calculated as: 

${\lambda _1} = \frac{c}{{{\nu _1}}}$    

${\lambda _1}= \frac{{3 \times {{10}^8}}}{{7.5 \times {{10}^6}}}$    

${\lambda _1} = 40m$

Wavelength for frequency, ${\nu _2}$ can be calculated as: 

${\lambda _2} = \frac{c}{{{\nu _2}}}$

${\lambda _2} = \frac{{3 \times {{10}^8}}}{{12 \times {{10}^6}}}$      

$ {\lambda _2} = 25m$

Therefore, the corresponding wavelength band would be between $40m$ to $25m$.

6. A Charged Particle Oscillates About Its Mean Equilibrium Position With a Frequency of ${10^9}Hz$. What is the Frequency of the Electromagnetic Waves Produced by the Oscillator?

Ans: The frequency of an electromagnetic wave produced by the oscillator will be equal to the frequency of charged particle oscillating about its mean position i.e., \[{10^9}Hz\].

7. The Amplitude of the Magnetic Field Part of a Harmonic Electromagnetic Wave in Vacuum is B0 = 510nT. What is the Amplitude of the Electric Field Part of the Wave?

Ans: Amplitude of magnetic field of an electromagnetic wave in a vacuum, is:

${B_0} = 510nT = 510 \times {10^{ - 9}}T$

Speed of light in a vacuum, $c = 3 \times {10^8}m/s$

Amplitude of electric field of the electromagnetic wave can be given as:

$E = cB = 3 \times {10^8} \times 510 \times {10^{ - 9}} = 153N/C$.

8. Suppose that the electric field amplitude of an electromagnetic wave is E0 = 120N/C and that its frequency is \[\nu  = 50.0{\text{ }}MHz\].

1. Determine, ${B_0}$, $\omega $, $k$, and $\lambda $.

Ans: Electric field amplitude, ${E_0} = 120N/C$

Frequency of source, \[\nu  = 50.0MHz = 50 \times {10^6}Hz\]

Speed of light, \[c = 3 \times {10^8}m/s\]

Magnetic field strength can be given as:

${B_0} = \frac{{{E_0}}}{c}$     

${B_0} = \frac{{120}}{{3 \times {{10}^8}}}$

${B_0} = 4 \times {10^{ - 7}}T$

${B_0} = 400nT$

Angular Frequency of Source Can be Given As:

$\omega  = 2\pi \nu$    

$\omega = 2\pi (50 \times {10^6})$    

$\omega = 3.14 \times {10^8}{\kern 1pt} {\kern 1pt} rad/s$

Propagation Constant Can be Given As:

$k = \frac{\omega }{c}$

$k = \frac{{3.14 \times {{10}^8}}}{{3 \times {{10}^8}}}$

$k = 1.05{\kern 1pt} {\kern 1pt} rad/m$

Wavelength of Wave Can be Given As:

$\lambda  = \frac{c}{\nu }$   

$\lambda = \frac{{3 \times {{10}^8}}}{{50 \times {{10}^6}}}$

$\lambda = 6.0{\kern 1pt} {\kern 1pt} m$

2. Find Expressions for E and B.

Ans: If the wave propagates in the positive x-direction. Then, the electric field vector would be in the positive y-direction and the magnetic field vector will lie in the positive z-direction. This is because all three vectors are mutually perpendicular.

Equation of electric field vector can be given as:

\[\overrightarrow E  = \;{E_0}sin(kx - \omega t)\hat j\]

$\overrightarrow E  = 120\sin \left[ {1.05x - 3.14 \times {{10}^8}t} \right]\hat j$

And, magnetic field vector can be given as:

\[\overrightarrow B  = \;{B_0}sin(kx - \omega t)\hat k\]

$\overrightarrow B = (4 \times {10^{ - 7}})\sin \left[ {1.05x - 3.14 \times {{10}^8}t} \right]\hat k$

9. The Terminology of Different Parts of the Electromagnetic Spectrum Is Given in the Text. Use the Formula E = hv (for Energy of a Quantum of Radiation: Photon) and Obtain the Photon Energy in Units of ev for Different Parts of the Electromagnetic Spectrum. in What Way are the Different Scales of Photon Energies That You Obtain Related to the Sources of Electromagnetic Radiation?

Ans: The energy of photon can be given as:

$E = h\nu  = \frac{{hc}}{\lambda }$

Where,

$h$ = Planck’s constant $ = 6.6 \times {10^{ - 34}}Js$

$c$ = speed of light $ = 3 \times {10^8}m/s$

$\lambda $ = wavelength of radiation

$\therefore E = \frac{{6.6 \times {{10}^{ - 34}} \times 3 \times {{10}^8}}}{\lambda }J$

$E = \frac{{19.8 \times {{10}^{ - 26}}}}{\lambda }J$

$E = \frac{{19.8 \times {{10}^{ - 26}}}}{{\lambda  \times 1.6 \times {{10}^{ - 19}}}}{\kern 1pt} {\kern 1pt} eV$

$E = \frac{{12.375 \times {{10}^{ - 7}}}}{\lambda }{\kern 1pt} {\kern 1pt} eV$

For Different Values of in an Electromagnetic Spectrum, Photon Energies 

are Listed in Below Table:

10. In a Plane Electromagnetic Wave, the Electric Field Oscillates Sinusoidally at a Frequency of $2 \times {10^{10}} Hz$ and amplitude 48Vm- 1

1. What is the Wavelength of the Wave?

Ans: Frequency of the electromagnetic wave, \[\nu  = 2.0 \times {10^{10}}Hz\]

Electric field amplitude, \[{E_0} = 48{\text{ }}V{m^{ - 1}}\]

Speed of light, \[c = 3 \times {10^8}m/s\]

Wavelength of wave can be given as:

$\lambda  = \frac{c}{\nu }$

$\lambda = \frac{{3 \times {{10}^8}}}{{2 \times {{10}^{10}}}}$

$\lambda = 0.015m$

2. What is the Amplitude of the Oscillating Magnetic Field?

Ans: Magnetic field strength can be given as:

${B_0} = \frac{{{E_0}}}{c}$

      $ = \frac{{48}}{{3 \times {{10}^8}}}$

      $ = 1.6 \times {10^{ - 7}}T$

3. Show That the Average Energy Density of the E Field Equals the Average Energy Density of the B field. C = 3 x 108m/s

Ans: Energy density of the electric field is given as:

${U_E} = \frac{1}{2}{ \in _0}{E^2}$

Energy density of the magnetic field can be given as:

${U_B} = \frac{1}{{2{\mu _0}}}{B^2}$

Where,

${ \in _0}$ = Permittivity of free space

${\mu _0}$ = Permeability of free space

The relation between E and B can be given as:

$E = cB$  ….(1)

Where,

$c = \frac{1}{{\sqrt {{ \in _0}{\mu _0}} }}$   ….(2)

Substituting equation (2) in equation (1), we get:

$E = \frac{1}{{\sqrt {{ \in _0}{\mu _0}} }}B$

Squaring both the sides, we get:

${E^2} = \frac{1}{{{ \in _0}{\mu _0}}}{B^2}$

${E^2}{ \in _0} = \frac{{{B^2}}}{{{\mu _0}}}$

$\frac{1}{2}{E^2}{ \in _0} = \frac{1}{2}\frac{{{B^2}}}{{{\mu _0}}}$

$ \Rightarrow {U_E} = {U_B}$.

11. Suppose That the Electric Field Part of an Electromagnetic Wave in Vacuum is \[\overrightarrow E  = \;\{ (3.1N/C)\;\left. {cos\;\left[ {(1.8rad/m)\;y\; + (5.4 \times {{10}^6}\;rad/s)t} \right]\;} \right\}\hat i\].

1. What is the Direction of Propagation?

Ans: From the given electric field vector, we can say that the electric field will be directed along the negative x direction. Hence, the direction of motion will be along the negative y direction i.e., $ - j$.

2. What is the Wavelength $\lambda $?

Ans: The general equation for electric field in the positive x direction is given as: \[\overrightarrow E  = {E_0}sin(kx - \omega t)\hat i\]. By comparing the given equation, \[\overrightarrow E  = \;\{ (3.1N/C)\;\left. {cos\;\left[ {(1.8rad/m)\;y\; + (5.4 \times {{10}^6}\;rad/s)t} \right]\;} \right\}\hat i\] with general equation, we get:

Electric field amplitude, ${E_0} = 3.1N/C$

Wave number, $k = 1.8{\kern 1pt} {\kern 1pt} rad/m$

Angular frequency, $\omega  = 5.4 \times {10^6}\;rad/s$

Wavelength, $\lambda  = \frac{{2\pi }}{k} = \frac{{2\pi }}{{1.8}} = 3.490m$.

3. What is the Frequency $\nu $?

Ans: The frequency, $\nu $ of the wave can be given as: $\nu  = \frac{\omega }{{2\pi }}$

$ = \frac{{5.4 \times {{10}^8}}}{{2\pi }} = 8.6 \times {10^7}Hz$.

4. What is the Amplitude of the Magnetic Field Part of the Wave?

Ans: Magnetic field strength can be given as:

${B_0} = \frac{{{E_0}}}{c}$

$\therefore {B_0} = \frac{{3.1}}{{3 \times {{10}^8}}} = 1.03 \times {10^{ - 7}}T$.

5. Write an Expression for the Magnetic Field Part of the Wave.

Ans: We can observe that the magnetic field vector will be directed along the negative z direction. Hence, the general equation for the magnetic field vector is written as: \[\overrightarrow B  = \;{B_0}\cos (ky + \omega t)\hat k\], hence, \[\overrightarrow B  = \;\{ (1.03 \times {10^{ - 7}}T)\;\left. {cos\;\left[ {(1.8rad/m)\;y\; + (5.4 \times {{10}^6}\;rad/s)t} \right]\;} \right\}\hat k\].

12. About \[{\mathbf{5}}\% \] of the power of a \[{\mathbf{100}}{\text{ }}{\mathbf{W}}\] light bulb is converted to visible radiation. What is the average intensity of visible radiation

1. At a Distance of \[{\mathbf{1}}{\text{ }}{\mathbf{m}}\] from the bulb? Assume That the Radiation Is Emitted Isotropically and Neglect Reflection.

Ans: Power rating of bulb, \[P = 100{\text{ }}W\]

About \[5\% \] of its power has been converted into visible radiation.

Therefore, power of visible radiation is given as:

${{p}^{'}} = \frac{5}{{100}} \times 100 = 5W$

Average intensity at distance, $d = 1m$ can be given as:

$I = \frac{{{P}^{'}}}{A} = \frac{{{{p}^{'}}}}{{4\pi {d^2}}}$  

$I = \frac{5}{{4 \times 3.14 \times {{(1)}^2}}} = 0.398{\kern 1pt} W/{m^2}$

2. At a Distance of 10m? Assume That the Radiation is Emitted Isotropically and Neglect Reflection.

Ans: Power of visible radiation can be given as:

${{p}^{'}} = \frac{5}{{100}} \times 100 = 5W$.

Average intensity at distance, $d = 10m$ can be given as:

$I = \frac{{{{p}^{'}}}}{A} = \frac{{{{p}^{'}}}}{{4\pi {d^2}}}$ 

$I = \frac{5}{{4 \times 3.14 \times {{(10)}^2}}} = 0.00398{\kern 1pt} W/{m^2}$

13. Use the Formula ${\lambda _m} = \frac{{0.29}}{T}{\kern 1pt} {\kern 1pt} cm{\kern 1pt} {\kern 1pt} K$ to Obtain the Characteristic Temperature Ranges for Different Parts of the Electromagnetic Spectrum. What Do the Numbers That You Obtain Tell You?

Ans: At a particular temperature, a body produces a continuous spectrum of wavelengths. In case of a black body, the wavelength corresponding to maximum intensity of radiation is given by Planck’s law. It can be represented as:

${\lambda _m} = \frac{{0.29}}{T}{\kern 1pt} {\kern 1pt} cm{\kern 1pt} {\kern 1pt} K$.

Where,

${\lambda _m}$ = maximum wavelength

$T$ = temperature

Therefore, the temperature for different wavelengths can be given as:

For, ${\lambda _m} = {10^{ - 4}}cm$, $T = \frac{{0.29}}{{{{10}^{ - 4}}}} = 2900{}^ \circ K$

For, ${\lambda _m} = 5 \times {10^{ - 5}}cm$, $T = \frac{{0.29}}{{5 \times {{10}^{ - 5}}}} = 5800{}^ \circ K$

For, ${\lambda _m} = {10^{ - 6}}cm$, $T = \frac{{0.29}}{{{{10}^{ - 6}}}} = 290000{}^ \circ K$

We can see that, as the maximum wavelength decreases, the corresponding temperature increases. At lower temperature, wavelength produced will not have maximum intensity.

14. Given Below Are Some Famous Numbers Associated With Electromagnetic Radiations in Different Contexts in Physics. State the Part of the Electromagnetic Spectrum to Which Each Belongs.

1. \[21{\text{ }}cm\] (Wavelength Emitted by Atomic Hydrogen in Interstellar Space).

Ans: Wavelength of \[21{\text{ }}cm\] belongs to a short radio wave,

which is present at the end of the electromagnetic spectrum.

2. \[1057{\kern 1pt} {\kern 1pt} MHz\] (Frequency of Radiation Arising from Two Close Energy Levels in Hydrogen; Known as Lamb Shift).

Ans: Frequency of \[1057{\kern 1pt} {\kern 1pt} MHz\] belongs to radio waves. As, radio waves generally belong to the frequency range of $500kHz$ to \[1000MHz\]. The range of wavelength for radio waves is, $ > 0.1m$.

3. \[2.7K\] [Temperature Associated With the Isotropic Radiation Filling All Space-Thought to Be a Relic of the ‘Big-Bang’ Origin of the Universe].

Ans: Given, temperature,  \[T = 2.7K\].

According to Planck's law, \[\lambda  = 0.29\left( {cm} \right){\kern 1pt} {\kern 1pt} T\left( K \right)\]

Substituting the value of temperature, we get: $\lambda  = \frac{{0.29}}{{2.7}} = 0.11cm$.

Now, \[\lambda  = 0.11cm\] belongs to the Microwave region of electromagnetic spectrum.

4. $5890\mathop A\limits^ \circ   - 5896\mathop A\limits^ \circ  $ [double lines of sodium]

Ans: This wavelength belongs to yellow light of visible spectrum.

5. \[{\mathbf{14}}.{\mathbf{4}}{\text{ }}{\mathbf{keV}}\] [energy of a particular transition in \[^{{\mathbf{57}}}{\mathbf{Fe}}\] nucleus Associated With a Famous High Resolution Spectroscopic Method (Mossbauer Spectroscopy)].

Ans: Given: $14.4keV$

The transition energy can be given as: $E = h\nu $.

Where,

$h$ is Planck's constant ,

$\nu $ is frequency of radiation.

Substituting the values, we get:

$\nu  = \frac{E}{h} = \frac{{14.4 \times {{10}^3} \times 1.6 \times {{10}^{ - 19}}}}{{6.6 \times {{10}^{ - 34}}}} = 3.4 \times {10^{18}}Hz$.

Now, $3.4 \times {10^{18}}Hz$ belongs to range of X-ray frequencies. As, range of frequency for X-rays lies between \[1016Hz - 1020Hz\].

15. Answer the Following Questions:

1. Long-Distance Radio Broadcasts Use Short-Wave Bands. Why?

Ans: Short wave bands are used for long distance broadcasting because, after getting reflected from ionosphere present in our environment, these waves can reach to longer distances.

2. It Is Necessary to Use Satellites for Long Distance Tv Transmission. Why?

Ans: Yes, for long-distance TV transmission, it is compulsory to use satellites, because TV signal contains very high frequency of range \[54MHz - 890MHz\], and this much high frequency does not get reflected by ionosphere, and communication does not get stablished. Hence, we need to use satellites for TV transmission, over long distance.

3. Optical and Radio Telescopes Are Built on the Ground but X-Ray Astronomy Is Possible Only from Satellites Orbiting the Earth. Why?

Ans: Light and radio waves used in optical and radio telescopes respectively, penetrate through the atmosphere but X-rays used in X-ray astronomy, are absorbed by the atmosphere. Hence, optical and radio telescopes are built on earth's surface and for X-ray astronomy, satellites orbiting the earth are necessary.

4. The Small Ozone Layer on Top of the Stratosphere is Crucial for Human Survival. Why?

Ans: The ozone layer, present on the top of the stratosphere layer is essential for human survival because it prevents the harmful radiations, (like, ultraviolet rays, $\gamma $ rays, cosmic rays) coming from the sun to earth's atmosphere, which can cause many diseases like cancer and genetic damage in cells and plants. The ozone layer also traps the infrared radiations and maintains earth's warmth.

5. If the Earth Did Not Have an Atmosphere, Would Its Average Surface Temperature Be Higher or Lower Than What it Is Now?

Ans: If the earth would not have any atmosphere, then there will not

be any greenhouse effect. And if the greenhouse effect would not be present, then infrared radiations and $C{O_2}$would not retain in the atmosphere. The infrared radiations and $C{O_2}$ gets reflected from  the atmosphere and keep the earth's surface warm. But in the absence 

of an atmosphere, this would not be possible and the average surface 

temperature of the earth would become lower.

6. Some Scientists Have Predicted That a Global Nuclear War on the Earth Would Be Followed by a Severe ‘nuclear Winter’ With a Devastating Effect on Life on Earth. What Might Be the Basis of This Prediction?

Ans: A global nuclear war on the earth would be followed by a severe ‘nuclear winter’, as the nuclear weapons would create clouds of smoke and dust, which would stop the solar light to reach the earth's surface and would stop the greenhouse effect. This would cause extreme winter conditions.

NCERT Solutions for Class 12 Physics – Free PDF Download

An Overview of Class 12 Physics Chapter 8: Electromagnetic Waves

Chapter 8 Electromagnetic Waves Class 12th Physics deals with various types of radiations sustaining in the environment. It helps us to categorize various waves based on their frequency, wavelength, uses, and origin.

Each electromagnetic wave has its characteristic properties and features. The chapter also explains the difference between electromagnetic and magnetic waves. It exposes some instruments and their working for detecting these radiations. 

It deals with the electromagnetic spectrum and many types of radiation such as infrared, radio, gamma, UV, visible, microwaves, and many more. It also explains the basic properties of waves categorized as electromagnetic waves that each of them possesses and the sources which deflect them or absorb them.

The chapter might be short but has many concepts and important points to learn. Every year a portion of the questions is fixed from the chapter, and if you get it in hand, it’s very easy to solve its numerical too.

Related Study Materials for Class 12 Physics Chapter 8 Electromagnetic Waves

Vedantu provides several important study materials for Class 12 Physics Chapter 8. After covering the NCERT Solutions, students can revise the chapter thoroughly by referring to the NCERT Exemplar Book Solutions, Important Questions, Short keynotes, etc. They can also solve and practice the CBSE Class 12 Physics sample papers and previous years’ question papers from Vedantu for free. The below-given links are for the related study materials of Class 12 Physics Chapter 8 Electromagnetic Waves.

• Important Questions for CBSE Class 12 Physics Chapter 8 - Electromagnetic Waves

• Class 12 Physics Revision Notes for Chapter 8 - Electromagnetic Waves

• NCERT Exemplar for Class 12 Physics Chapter-8 (Book Solutions)

• CBSE Sample Papers 2024-25 for Class 12 Physics

• Previous Year Question Paper for CBSE Class 12 Physics (2023-2013)
  

Benefits of NCERT Solutions for Class 12 Physics

NCERT Solutions are very beneficial, especially in the board exams. The examiner sets the paper criteria based on all examples, exercises, and other questions of NCERT. Physics NCERT Solutions are tricky, and you need a simplified version of thinking to solve these questions. There are many benefits of NCERT Solutions Class 12 Physics, such as:

• Solving NCERT questions also gives an idea to you about the pattern of questions coming in the exam.

• NCERT Solutions are explained in detail with every justified logic.

• These NCERT Solutions are specified as marks-oriented maths important questions simultaneously.

• NCERT Solutions will surely help you boost your performance and improve in solving problems.

CBSE Class 12 Physics Chapter-8 Important Questions - Extra Questions For Practice 

1. A wave of frequency 5 x 1019 Hz belongs to which part of the electromagnetic spectrum?

2. Mention the conditions that will promote an electron's undeflected movement when magnetic fields and crossed eclectic.

3. Welders and electricians wear goggles and face masks while working with glass windows to save their eyes from electromagnetic radiation. What is the name of this electromagnetic radiation, and what is its frequency? 

4. Which electromagnetic waves keep the earth warm?

5. What are the uses of infrared rays?

6. How are infrared rays created?

7. What are the two uses of X-rays?

8. Which electromagnetic waves are used in the navigation of aircraft?

9. Which wave has the shortest wavelength?

10. Specify the part of the electromagnetic spectrum that has the strongest penetrating power.

How does Vedantu Study Material Help Students?

Vedantu’s study material is created from tip to toe by one of the best teachers across the country. Their experience and way of teaching make the study material very useful in improving performance.

The study material aims to create meaningful content in an easy language using simple, less time-consuming, and precise methods.

Hence, accuracy, speed, and reliability go hand-in-hand. These solutions are timely updated and strictly bound to the latest CBSE guidelines and curriculum. For quick revisions, Vedantu has brought many practice question sets, mock test series, previous year solved questions, questions based on various categories, quizzes, and much more.

Thus, Vedantu brings out the best of you by exposing a new world of concepts, their applications, and their implementation.

Conclusion

Electromagnetic waves are generated when an electric field is in contact with a magnetic field. Hence electromagnetic waves are said to be composed of oscillating magnetic and electric fields. CBSE Class 12 Physics Chapter 8 Electromagnetic Waves covers the definition and explanation of electromagnetic waves, their transverse nature and characteristics, complex concepts of the electromagnetic spectrum, and their uses. Students can comprehensively understand the topics and subtopics covered in this chapter by referring to the NCERT Solutions. 

They can revise the chapter effectively with the help of the important questions, revision notes, and other related study materials on Electromagnetic Waves. All study materials are free for download on the Vedantu mobile app and its official website.

Other Study Material for CBSE Class 12 Physics Chapter 8

Chapter-Specific NCERT Solutions for Class 12 Physics

Given below are the chapter-wise NCERT Solutions for Class 12 Physics. You can use it as your 12th Physics guide. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Related Links for NCERT Class 12 Physics in Hindi

Discover relevant links for NCERT Class 12 Physics in Hindi, offering comprehensive study materials, solutions, and resources to enhance understanding and aid in exam preparation.

Chapter-Specific NCERT Solutions for Class 12 Physics

Given below are the chapter-wise NCERT Solutions for Class 12 Physics. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.