Complete Step by step Question answers for Class 9 Maths Exercise 7.1 with FREE PDF download
NCERT Solutions for Class 9 Maths Chapter 7 Triangles Exercise 7.1|Vedantu
FAQs on NCERT Solutions for Class 9 Maths Chapter 7 Triangles Exercise 7.1|Vedantu
1. What core concepts are covered in NCERT Solutions for Class 9 Maths Chapter 7 – Triangles?
NCERT Solutions for Class 9 Maths Chapter 7 – Triangles focus on fundamental concepts including the congruence of triangles, congruence criteria (SAS, ASA, SSS, RHS), basic properties of triangles, and inequalities in triangles. These concepts are essential for understanding proofs and solving geometry questions as per the CBSE 2025–26 syllabus.
2. How should students approach proving congruence in triangle-based questions in Exercise 7.1?
To solve congruence proofs in Exercise 7.1 of Class 9 Maths Chapter 7, students should:
- Identify given congruent sides or angles.
- Select the correct congruence criterion (SAS, ASA, SSS, or RHS) as per the question statement.
- State each step with a valid reason (e.g., ‘Given’, ‘By CPCT’, ‘By definition’).
- Ensure that no steps or reasons are skipped, as CBSE marks for stepwise accuracy.
3. Which criteria are most commonly applied for triangle congruence, as per CBSE Class 9 Maths Chapter 7 NCERT Solutions?
The most frequently used triangle congruence criteria in NCERT Solutions for Class 9 Maths Chapter 7 include:
- SAS (Side-Angle-Side)
- ASA (Angle-Side-Angle)
- SSS (Side-Side-Side)
- RHS (Right angle–Hypotenuse–Side) (special for right-angled triangles)
4. What are the basic properties of triangles highlighted in the Class 9 Maths Chapter 7 NCERT Solutions?
Key properties of triangles emphasized in NCERT Solutions for Chapter 7 are:
- The sum of all angles in a triangle is 180°.
- The sum of the lengths of any two sides is greater than the third side.
- The side opposite the greater angle is longest.
- The exterior angle equals the sum of the two interior opposite angles.
5. How can students avoid common mistakes when writing proofs using CPCT in Chapter 7 Triangles?
To avoid errors with CPCT (Corresponding Parts of Congruent Triangles):
- Use CPCT only after formally proving congruence.
- State the congruence criterion and result before applying CPCT.
- Explicitly mention which sides or angles correspond.
- Never use CPCT as a reason without a prior congruence statement.
6. Why is learning the congruence of triangles important for other mathematical applications as per CBSE standards?
Congruence of triangles forms the basis for advanced geometry, constructions, and trigonometry. It helps in real-world applications such as architecture and engineering where identical measurements or structures are required for stability and accuracy. Mastery of these criteria also builds logical reasoning skills valued in higher-level mathematics as per the CBSE curriculum.
7. What are the different types of triangles according to Class 9 Chapter 7, and how does this classification help in solving questions?
In Class 9 Maths Chapter 7, triangles are classified as:
- Scalene: All sides and angles are unequal.
- Isosceles: Two sides and corresponding angles are equal.
- Equilateral: All sides and angles are equal (each angle = 60°).
- Right-angled, Acute-angled, Obtuse-angled: Based on largest angle (90°, <90°, >90°).
8. How do Class 9 Maths Chapter 7 NCERT Solutions handle ‘what if’ scenarios, such as missing information in triangle proofs?
If a triangle problem appears to have missing information (like a side or angle not labeled), NCERT Solutions recommend:
- Checking if the property of triangles can deduce the missing value (using angle sum, exterior angle property, etc.).
- Looking for congruent or shared parts in diagrams.
- Applying geometric logic such as parallel lines or mid-point theorems as per the context.
9. What kinds of real-life applications can be found for congruent triangles as discussed in Class 9 NCERT Solutions Chapter 7?
Congruence principles are applied in construction projects for creating stable structures, designing identical supports, and ensuring uniformity in bridges or trusses. In art and architecture, congruence ensures visual symmetry and balance, which are essential for both aesthetics and functional strength.
10. What is the significance of the RHS congruence rule, and when should it be applied according to the NCERT Solutions for Class 9 Maths Chapter 7?
The RHS (Right angle–Hypotenuse–Side) congruence rule is significant for proving congruence specifically in right-angled triangles. It applies when two right triangles have equal hypotenuses and one other side equal; only then can congruence be claimed using this rule, as per CBSE 2025–26 guidelines.
11. How does understanding congruence criteria help you solve advanced geometry problems in later grades?
Building a strong foundation in congruence criteria in Class 9 makes it easier to tackle proofs, circle theorems, and property-based questions in higher classes. It also lays the groundwork for coordinate geometry and trigonometry where congruent triangles routinely establish relationships and aid in complex constructions.
12. What is the best strategy for writing stepwise solutions for Class 9 Maths Chapter 7 NCERT problems to maximize CBSE marks?
For full marks in CBSE exams, students should:
- Begin with a clear given statement.
- Identify what needs to be proved.
- Cite the congruence criterion and state triangles being compared.
- Support every step with proper reasons (e.g., by property, by construction, by definition).
- Conclude with the justification for each deduction, especially when using CPCT.
13. Which question in Exercise 7.1 of Chapter 7 is seen as most challenging, and what key concepts does it test?
Question 8 is often considered the most challenging in Exercise 7.1, Chapter 7. It incorporates multiple concepts including SAS congruence, CPCT application, vertically opposite angles, and properties of co-interior angles. Its solution tests a student’s conceptual clarity and ability to sequence reasoning as per CBSE requirements.
14. What is the typical difficulty level of Exercise 7.1 in Class 9 Maths NCERT, and how should students prepare?
Exercise 7.1 of Chapter 7 is generally considered moderate. It includes both short and long-answer proofs. Students can best prepare by practicing each criterion, writing complete stepwise solutions, and reviewing solved examples from NCERT Solutions to master the solution technique required by CBSE.
15. How do NCERT Solutions for Class 9 Maths Chapter 7 ensure alignment with the official CBSE 2025–26 syllabus?
All Chapter 7 NCERT Solutions are curated to match the latest CBSE 2025–26 syllabus, including updated exercise patterns and marking schemes. Topics and criteria reflect current exam expectations, and solutions model the precise step-by-step working required for CBSE assessments.














 Watch Video
Watch Video





![In quadrilateral ACBD, AC = AD and AB bisects \[\angle A\]](https://www.vedantu.com/seo/content-images/022ae806-c622-436d-8fb9-de1994dcc4cd.png)
![ABCD is a quadrilateral in which AD = BC and \[\angle DAB{\text{ }} = \angle CBA\]](https://www.vedantu.com/seo/content-images/49493929-facc-409e-b432-ac77b407d608.png)

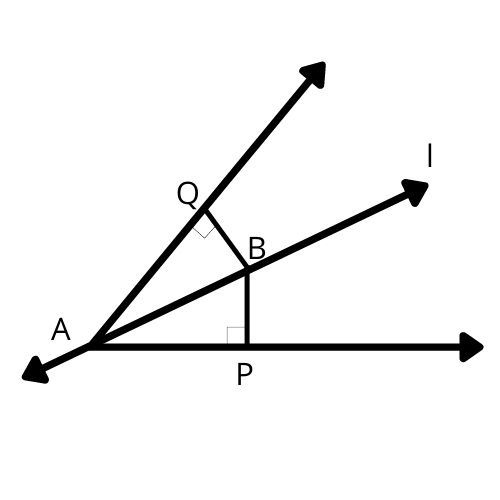
![\[AC{\text{ }} = {\text{ }}AE,{\text{ }}AB{\text{ }} = {\text{ }}AD\] and \[\angle BAD{\text{ }} = \angle EAC\]](https://www.vedantu.com/seo/content-images/08a10653-36c1-44ce-a830-9587a4b21c90.png)