CBSE Class 9 Maths Revision Notes For Chapter 7- Triangles

• Introduction:

Congruent geometrical figures are those that have the same shape and dimension. To test if two plane figures are congruent, lay one atop the other (superimpose) and compare the results.

Some examples of congruent figures are:

• Drag the shaded portion of each figure over the unshaded portion of the figure. That pair of figures is said to be congruent if the shaded portion matches (coincides) with the corresponding unshaded component.

• Recall the axiom on real numbers “if a and b are two real numbers, then they must follow one of the three relations, \[\text{a = b}\] or \[\text{a  b}\] or \[\text{a  b}\].

Equality relation: \[\text{a = b}\]

• In the below figure, the two magnitude of the two line segments is the same, hence they are congruent)

They are denoted as $\text{AB }\cong \text{ CD}$.

• Angles having equal magnitude are called congruent angles. 

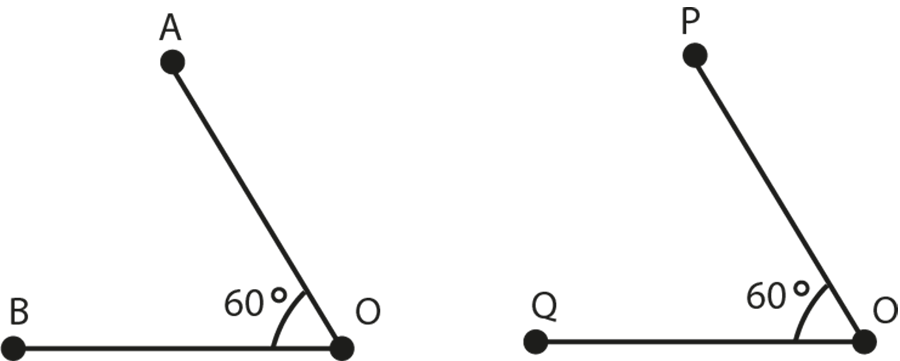
(i)

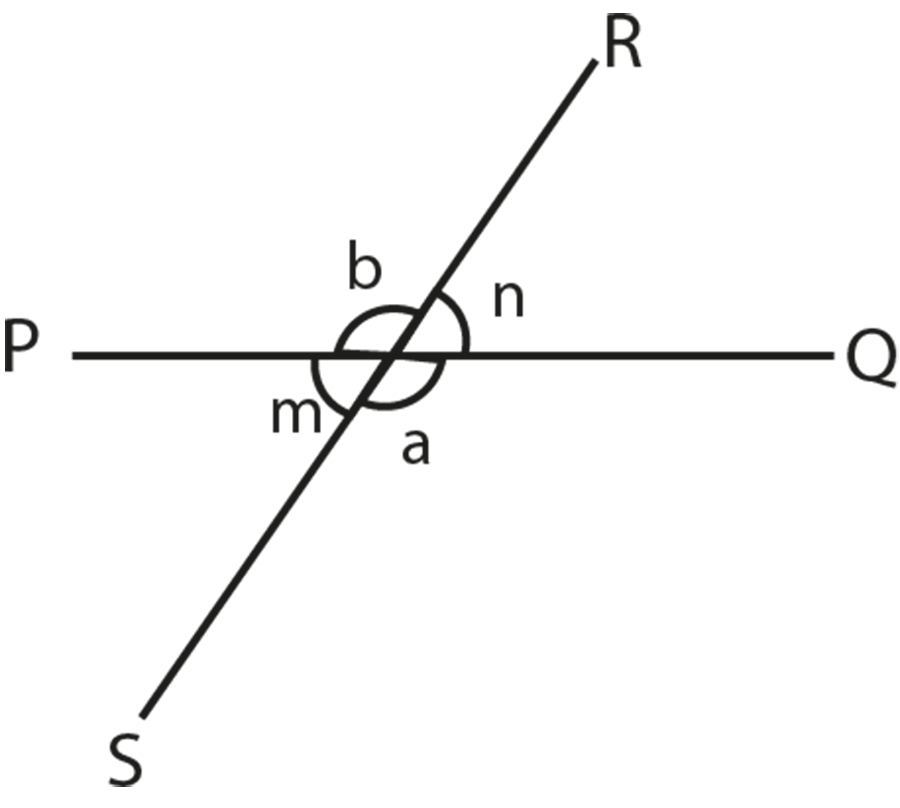
(ii)

Here, in figure (i), $\angle \text{AOB }\cong \text{ }\angle \text{POQ}$, as they are of the same magnitude and for figure (ii), $\angle \text{a = }\angle \text{b}$ and $\angle \text{m = }\angle \text{n}$ as they are vertically opposite angles.

• Congruent Circles:

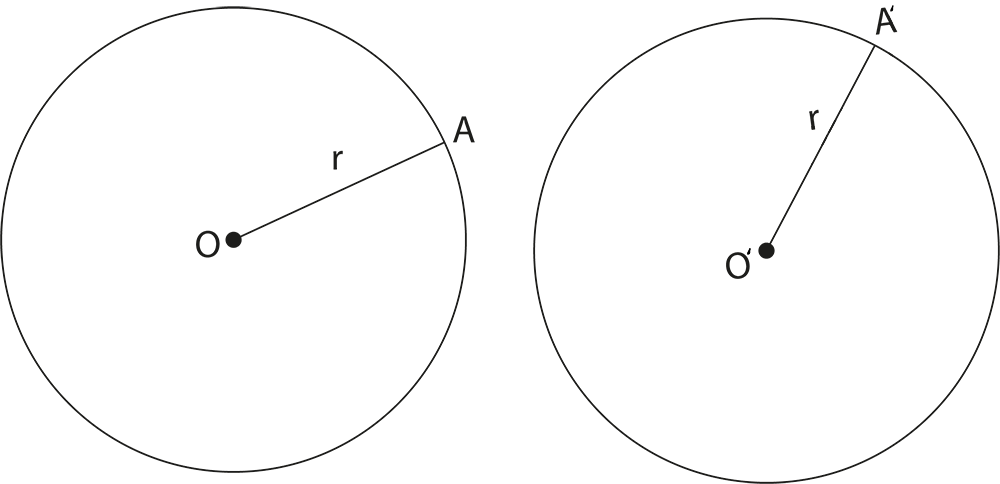
Two circles are said to be congruent if they have the same radius.

In the above figure, both the circles have the same radius\[\text{OA = O }\!\!'\!\!\text{ A }\!\!'\!\!\text{  = r}\].

• Congruent Triangles:

Triangles with the same shape and size are called congruent triangles. The three angles of a triangle determine the shape of the triangle, while the three sides determine its size.

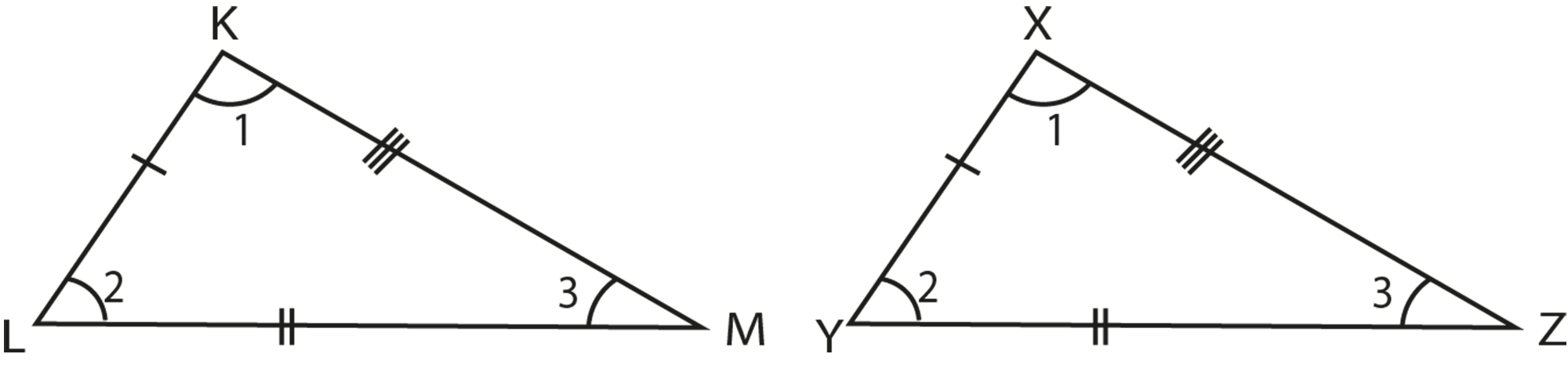
As a result, the congruency of triangles is determined by angles and sides.

Observe \[\Delta \text{KLM}\] and \[\Delta \text{XYZ}\]. If you superimpose one on top of the other, they will match, hence we can say that they are congruent. You'll notice in both the triangles, the three angles are congruent and the three sides, $\text{KL }\cong \text{ XY}$, $\text{LM }\cong \text{ YZ}$ and $\text{KM }\cong \text{ XZ}$.

For the two triangles to be congruent, all six elements (3 angles and 3 sides) of one must be congruent with the corresponding six elements of the other.

• Triangles' Postulates of Congruency:

The following definition for congruency of two triangles is based on the preceding observation.

Definition: 

"Two triangles are congruent if and only if all of one's sides and angles are equal to the corresponding sides and angles of the other," says the definition.

• Sufficient Condition for Two Triangles to Be Congruent:

We can see from the definition of congruence of two triangles that there are six conditions that must be met for two triangles to be congruent (3 sides and 3 angles). However, we shall discover through activities that if three of the six prerequisites are met, the remaining three are met automatically.

• Activity

In the two triangles, $\Delta \text{ABC}$ and $\Delta \text{DEF}$, $\text{AB = DE = 4 cm}$

$\text{AC = DF = 4}\text{.5 cm}$ and $\angle \text{BAC = }\angle \text{EDF = 95}{}^\circ $

Here, we can see that the two sides and their included angle of $\Delta \text{ABC}$ is equal in magnitude with the corresponding sides and angle of $\Delta \text{DEF}$.

By dragging $\Delta \text{ABC}$ on $\Delta \text{DEF}$, we can confirm that they match completely.

Therefore, $\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$.

The activity is known as the SAS congruency postulate, where SAS stands for Side-Angle-Side.

• SAS Congruency Condition:

"Two triangles are congruent if two sides and the included angle of one are equal to the corresponding sides and the included angle of the other."

• Theorem 9:

"Two triangles are congruent if any two sides and the included angle of one triangle are equal to the corresponding sides and the included angle of the other triangle".

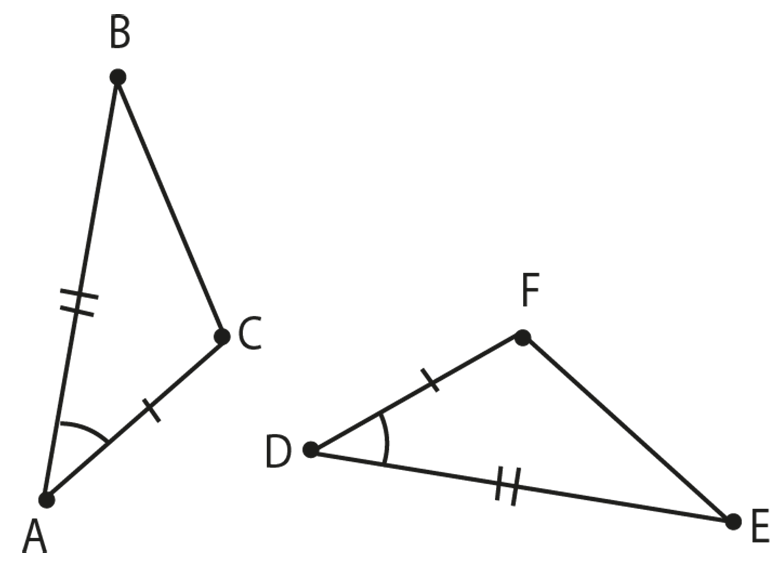
In the two given triangles, $\Delta \text{ABC}$ and $\Delta \text{DEF}$, $\text{AB = DE }$

$\text{AC = DF}$ and

$\angle \text{BAC = }\angle \text{EDF }$.

To prove: $\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$

Proof:

If we rotate and drag $\Delta \text{ABC}$ on $\Delta \text{DEF}$, such the vertices B falls on the vertex of the other triangle E and place BC along EF, we will find that, since $\text{AB = DE }$, C falls on F.

Also, $\angle \text{B = }\angle \text{E}$.

AB falls on DE, A will coincide with the vertex D and C with F.

So, AC coincides with DF.

$\therefore \Delta \text{ABC}$ coincides with $\Delta \text{DEF}$.

$\therefore \Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$

• Application of SAS Congruency:

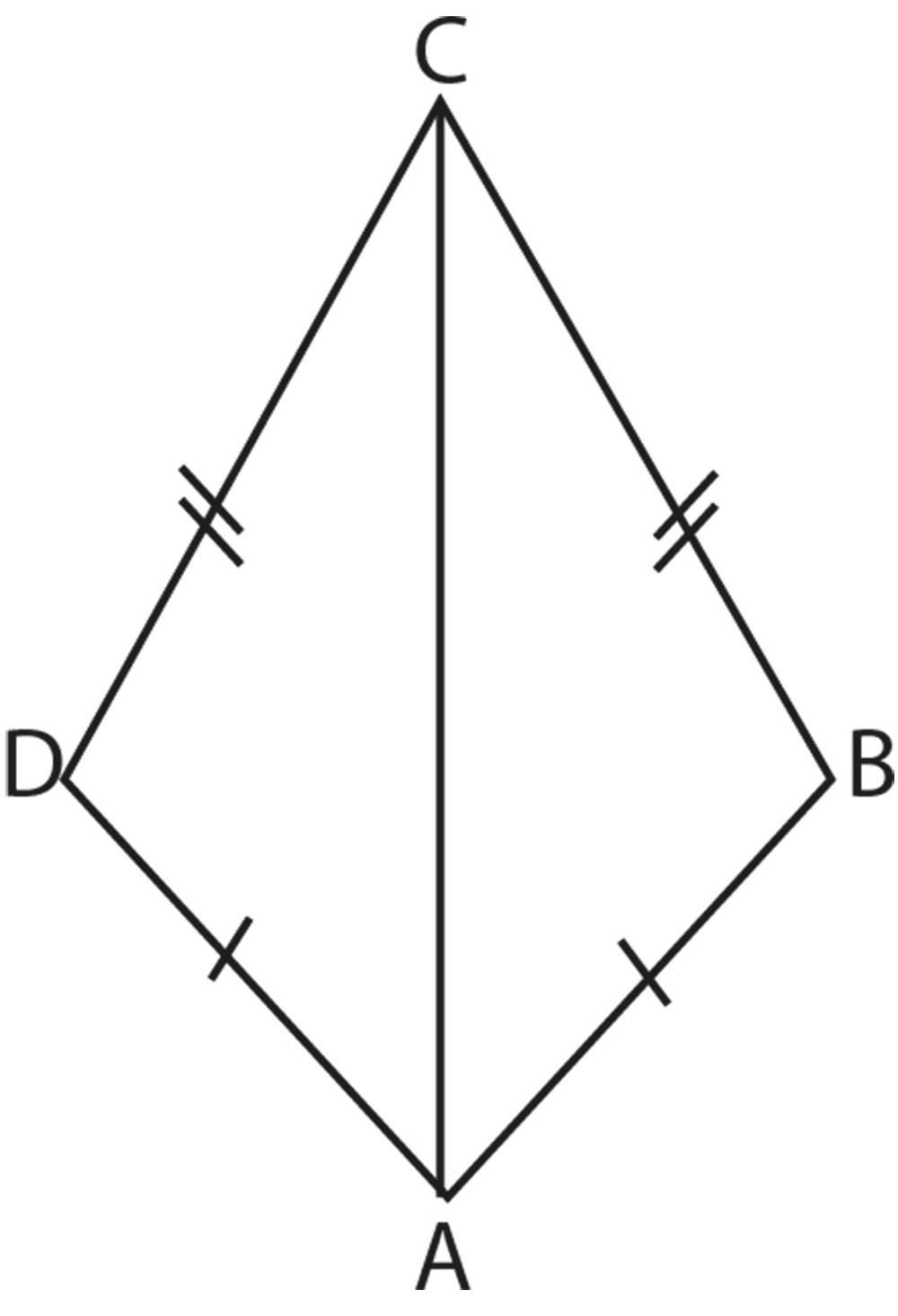
In this figure we cannot apply SAS as the given data is not sufficient. On the basis of angles and sides, the SAS congruency criterion defines the relationship between two triangles. As a result, here we cannot say if AC is the angle bisector of $\angle \text{A}$,  hence we cannot determine if the two triangles that may be shown are congruent.

• Theorem 10

"Angles opposite to equal sides are equal".

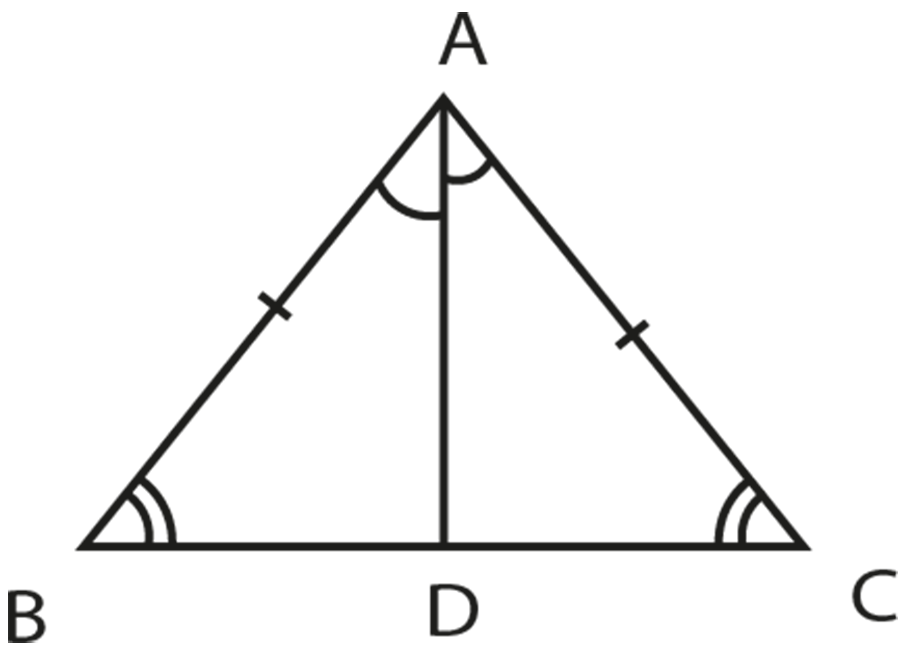
In $\Delta \text{ABC}$, $\text{AB = AC}$

To prove:

$\angle \text{ABC = }\angle \text{ACB}$

Construction: Draw the angle bisector of A, AD.

Proof:

Comparing both the triangles, 

Given that $\text{AB = AC}$

AD is the common side.

$\angle \text{BAD = }\angle \text{DAC}$ (as AD is the angle bisector)

$\therefore \Delta \text{BAD = }\Delta \text{DAC}$ (by SAS congruency rule)

$\therefore \angle \text{ABD = }\angle \text{ACD}$ (by CPCT)

$\therefore \angle \text{B = }\angle \text{C}$

Hence, proved.

• ASA Congruence Condition:

“Two triangles are congruent if two angles and the included side of one triangle are equal to the corresponding two angles and the included side of the other triangle”. 

• Theorem 11:

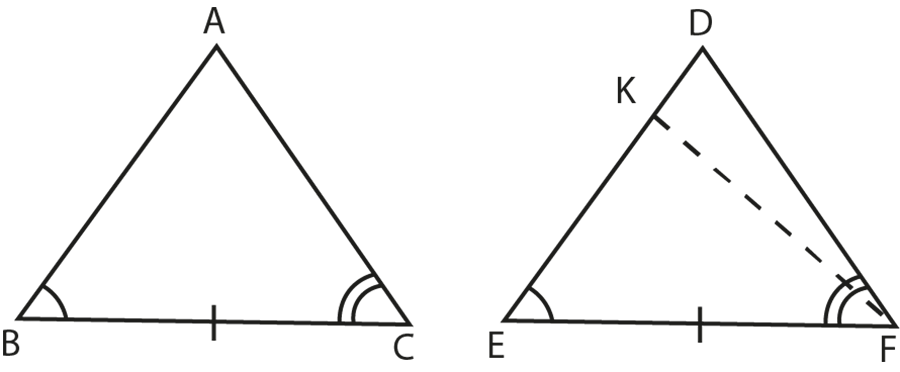
Given:

In $\Delta \text{ABC}$ and $\Delta \text{DEF}$,

$\angle \text{B = }\angle \text{E}$ and $\angle \text{C = }\angle \text{F}$

$\text{BC = EF}$.

To prove:

$\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$

Proof:

There are three possibilities

Case I: \[\text{AB = DE}\]

Case II: \[\text{AB  DE}\]

Case III: \[\text{AB  DE}\]

Case I: In addition to data, if \[\text{AB = DE}\] then 

$\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$  (by SAS congruence postulate)

Case II: If \[\text{AB  DE}\] and let K is any point on DE such that \[\text{EK = AB}\].

Join KF.

Now compare triangles ABC and KCF.

\[\text{BC = EF}\] (given)

$\angle \text{B = }\angle \text{E}$(given)

Let \[\text{AB = EK}\]

\[\Delta \text{ABC }\cong \text{ }\Delta \text{KEF}\] (SAS criterion)

Hence, \[\angle \text{ABC = }\angle \text{KEF}\]

But, \[\angle \text{ABC = }\angle \text{DEF}\]  (given)

Hence, K coincides with D.

Therefore, AB must be equal to DE.

Case III: If \[\text{AB  DE}\], then a similar argument applies. 

AB must be equal to DE.

Hence the only possibility is that AB must be equal to DE and from SAS congruence condition

$\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$

Hence the theorem is proved.

•  Theorem 12:

"In a triangle the sides opposite to equal angles are equal". 

This theorem can also be stated as 

"The sides opposite to equal angles of a triangle are equal".

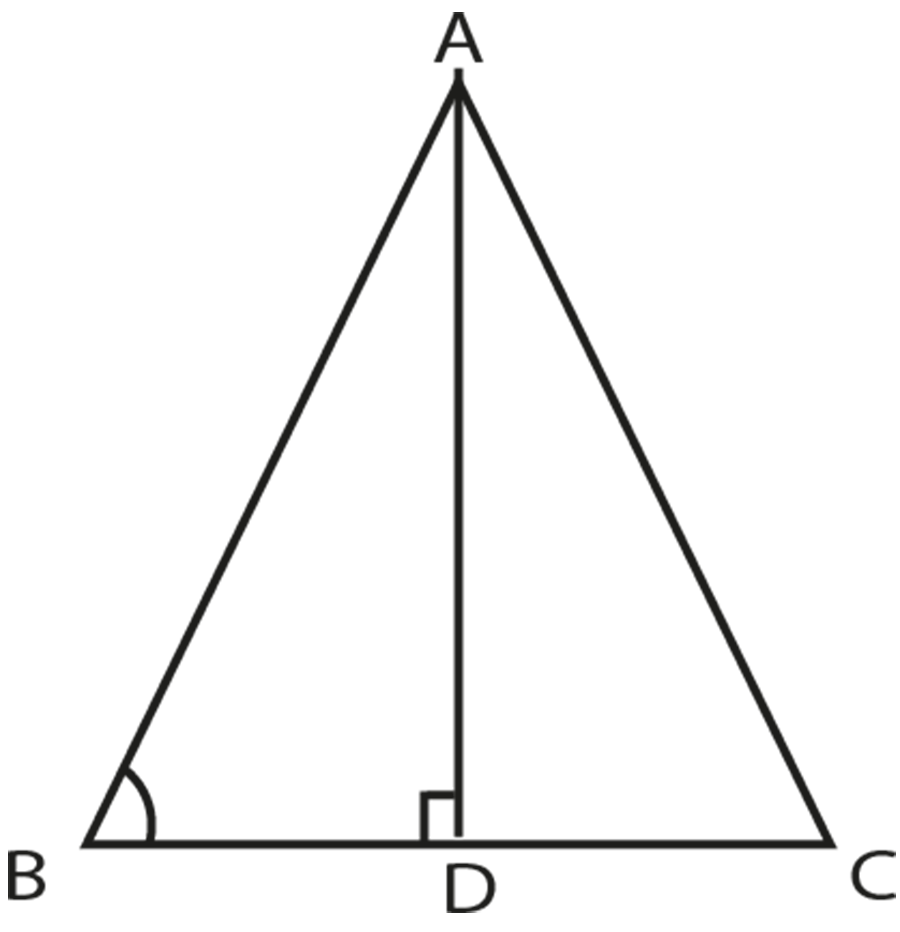
Given:

In \[\Delta \text{ABC},\text{ }\angle \text{B = }\angle \text{C}\]

To prove: 

$\overline{\text{AB}}\text{ = }\overline{\text{AC}}$

Construction:

Draw $\overline{\text{AD}}\text{ }\bot \text{ }\overline{\text{BC}}$

Proof:

Construct two right angle triangles, ADB and ADC, right angled at D.

Here, \[\Delta \text{ABC},\text{ }\angle \text{B = }\angle \text{C}\]

$\angle \text{ADB = }\angle \text{ADC = 90}{}^\circ $ (from the construction)

$\overline{\text{AD}}$ is common for both the triangles.

$\therefore \Delta \text{ADB }\cong \text{ }\Delta \text{ADC }$   (by ASA postulate)

$\overline{\text{AB}}\text{ = }\overline{\text{AC}}$   (corresponding sides)

• AAS Congruence Condition:

The two triangles are congruent if instead of two angles and an included side, two angles and a non-included side of one triangle are equal to the corresponding angles and side of another triangle.

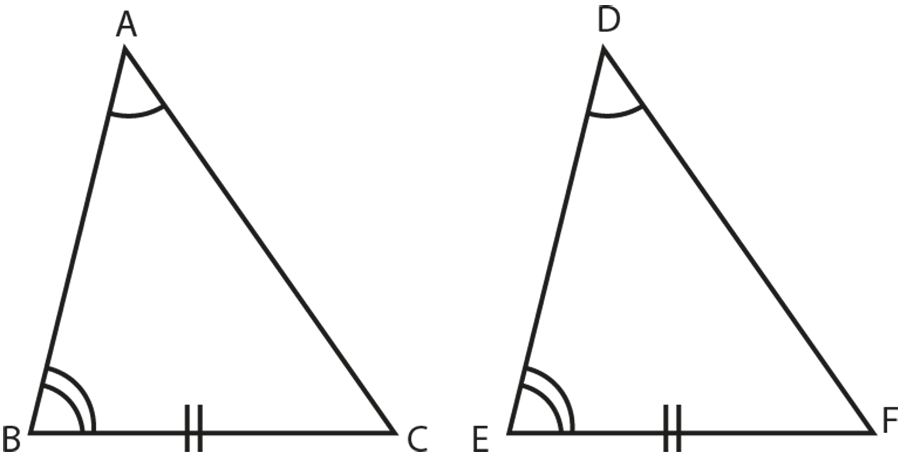
Given: 

In triangles ABC and DEF,

\[\text{BC = EF}\] (non-included sides)

\[\angle \text{B = }\angle \text{E}\]

\[\angle \text{A = }\angle \text{D}\]

To prove:

$\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$

Proof:

\[\angle \text{B = }\angle \text{E}\]  (given)

\[\angle \text{A = }\angle \text{D}\]  (given)

Now, adding both, \[\angle \text{A +}\angle \text{B = }\angle \text{E +}\angle \text{D}\]…(1)

Since, \[\angle \text{A +}\angle \text{B +}\angle \text{C = }\angle \text{E +}\angle \text{D+}\angle \text{F = 180}{}^\circ \], considering (1) we can say that,

\[\angle \text{C = }\angle \text{F}\]…(2)

Now in triangle ABC and DEF, 

\[\angle \text{B = }\angle \text{E}\]  (given)

\[\angle \text{C = }\angle \text{F}\] (proved in (2))

$\text{BC = EF}$ (given)

$\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$   (by SAS congruency)

• SSS Congruence Condition:

"Two triangles are congruent if the three sides of one triangle are equal to the corresponding three sides of the other triangle".

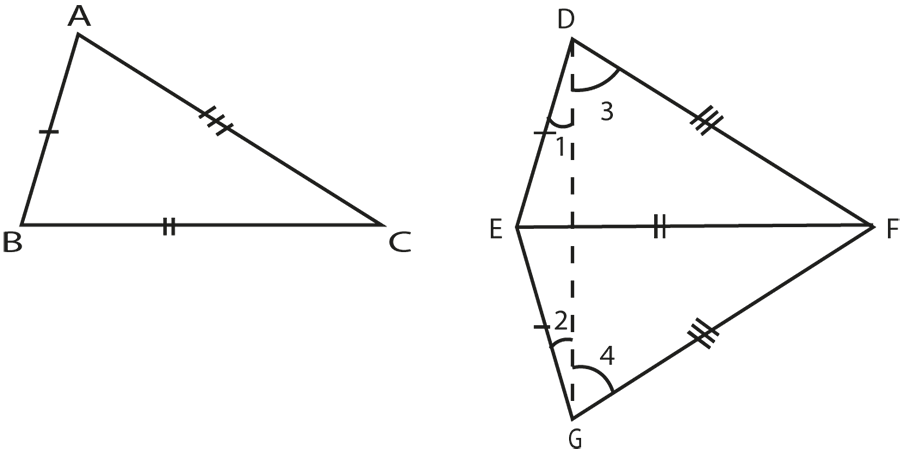
Given: 

In triangles ABC and DEF,

\[\text{AB = DE}\]

\[\text{BC = EF}\]

\[\text{AC = DF}\]

Note:

Let BC and EF be the longest sides of triangles ABC and DEF respectively.

To prove:

$\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$

Construction: If BC is the longest side, draw EG such that $\text{EG = AB}$ and $\angle \text{GEF = }\angle \text{ABC}$.

Join GF and DG.

Proof:

In triangles ABC and GEF,

\[\text{AB = GE}\] (by construction)

\[\text{BC = EF}\] (given)

$\angle \text{ABC = }\angle \text{GEF}$ (by construction)

$\therefore \Delta \text{ABC = }\Delta \text{GEF}$  (SAS congruence condition)

$\angle \text{BAC = }\angle \text{EGF}$ (by CPCT) 

and $\text{AC = GF}$ (by construction)

But $\text{AB = DE}$ (given)

$\therefore \text{DE = GE}$

Similarly, $\text{DF = GF}$

In $\Delta \text{EDG}$,

$\text{DE = GE}$ (Proved)

$\therefore \angle 1=\angle 2$…(1) (angles opposite equal sides)

In $\Delta \text{EGF}$,

$\text{DF = GF}$ (Proved)

$\therefore \angle 3=\angle 4$…(2) (angles opposite equal sides)

By adding (1) and (2), we get, 

$\therefore \angle 1+\angle 3=\angle 4+\angle 2$

$\angle \text{EDF = }\angle \text{EGF}$ but we have proved that $\angle \text{BAC = }\angle \text{EGF}$

Therefore, $\angle \text{EDF = }\angle \text{BAC }$

Now in triangles ABC and DEF,

\[\text{AB = DE}\] (given)

\[\text{AC = DF}\] (given)

$\angle \text{EDF = }\angle \text{BAC }$ (proved)

$\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$ (by SAS congruency)

• Theorem of RHS (Right Angle Hypotenuse Side) Congruence

If the hypotenuse and one side of one triangle are equal to the hypotenuse and corresponding side of the other triangle, the two triangles are congruent.

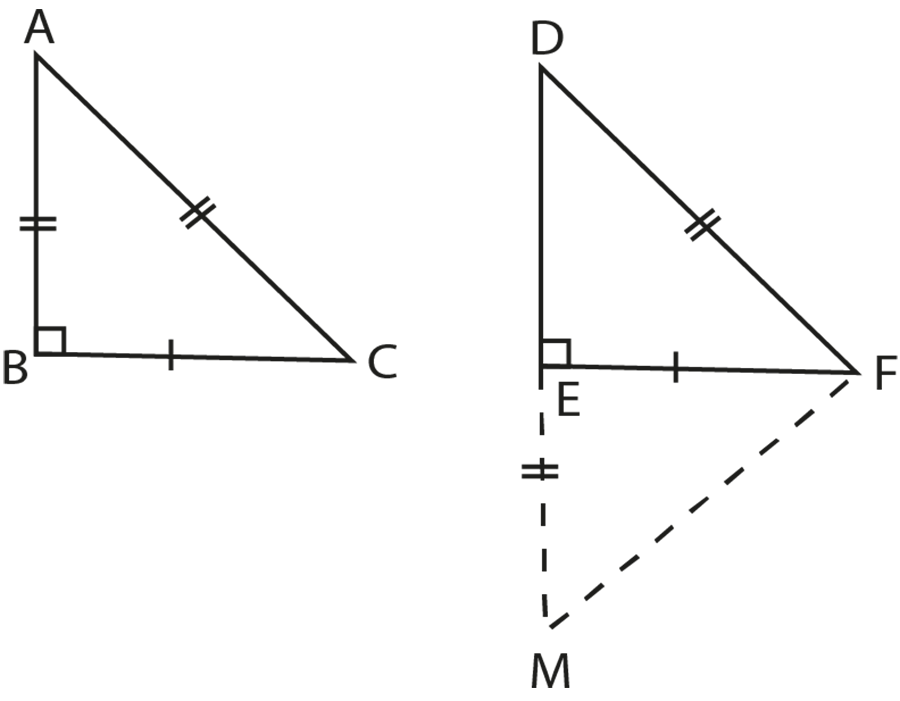
Given: 

ABC and DEF are two right-angled triangles such that

1. $\angle \text{B = }\angle \text{E = 90}{}^\circ $

2. Hypotenuse $\overline{\text{AC }}\text{ =}$ Hypotenuse $\overline{\text{DF}}$ and 

3. Side $\overline{\text{BC }}=$ Side $\overline{\text{EF}}$

To prove:

$\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$

Construction

Produce DE to M so that \[\text{EM = AB}\]. Join MF.

Proof: 

In triangles ABC and MEF,

\[\text{EM = AB}\]  (construction)

\[\text{BC = EF}\] (given)
$\angle \text{ABC = }\angle \text{MEF = 90}{}^\circ $

Therefore, $\Delta \text{ABC }\cong \text{ }\Delta \text{MEF}$ (SAS congruency)

Hence, $\angle \text{A = }\angle \text{M}$…(1) (by CPCT)

$\overline{\text{AC}}=\overline{\text{MF}}$…(2) (by CPCT)

Also, $\text{AC = DF}$ … (3) (given)

From (1) and (3), $\text{DF = MF}$

Therefore, $\angle \text{D = }\angle \text{M}$...(4) (Angles opposite to equal sides of \[\Delta \text{DFM}\])

From (2) and (4),

$\angle \text{A = }\angle \text{D}$…(5)

Now compare triangles ABC and DEF,

$\angle \text{A = }\angle \text{D}$ (from 5)

$\angle \text{B = }\angle \text{E = 90}{}^\circ $ (given)

$\therefore \angle \text{C=}\angle \text{F}$…(6)

Compare triangles ABC and DEF,

$\overline{\text{BC}}=\overline{\text{EF}}$  (given)

$\overline{\text{AC}}=\overline{\text{DF}}$  (given)

$\angle \text{C=}\angle \text{F}$  (from 6)

Therefore, $\Delta \text{ABC }\cong \text{ }\Delta \text{DEF}$ (by SAS congruency)

• Inequality of Angles:

Here we can see that, both these angles are not equal, as $135{}^\circ <160{}^\circ $

• Inequality in a Triangle:

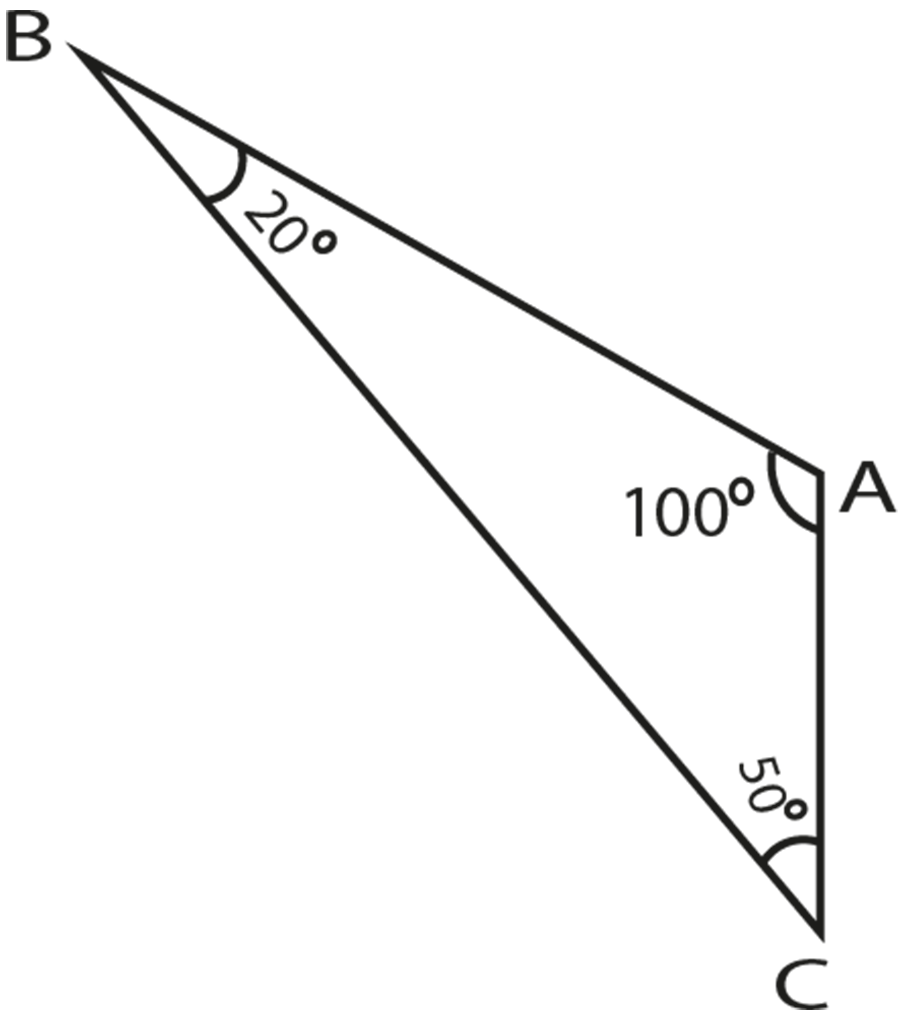
Construct a triangle ABC as shown in the figure.

Observe that in triangle ABC,
$\overline{\text{AC}}$ is the smallest side (2 cm)

B is the angle opposite to $\overline{\text{AC}}$ and $\angle \text{B = 20}{}^\circ $

$\overline{\text{BC}}$ is the greatest side (6 cm)

A is the angle opposite to $\overline{\text{BC}}$ and $\angle \text{A = 100}{}^\circ $

From the measurements made above of side and angle opposite to it, we can write the relation in the form of a statement.

"If two sides of a triangle are unequal then the longer side has the greater angle opposite to it”.

• Theorem on Inequalities:

Theorem 1:

If two sides of a triangle are unequal, the longer side has the greater angle opposite to it.

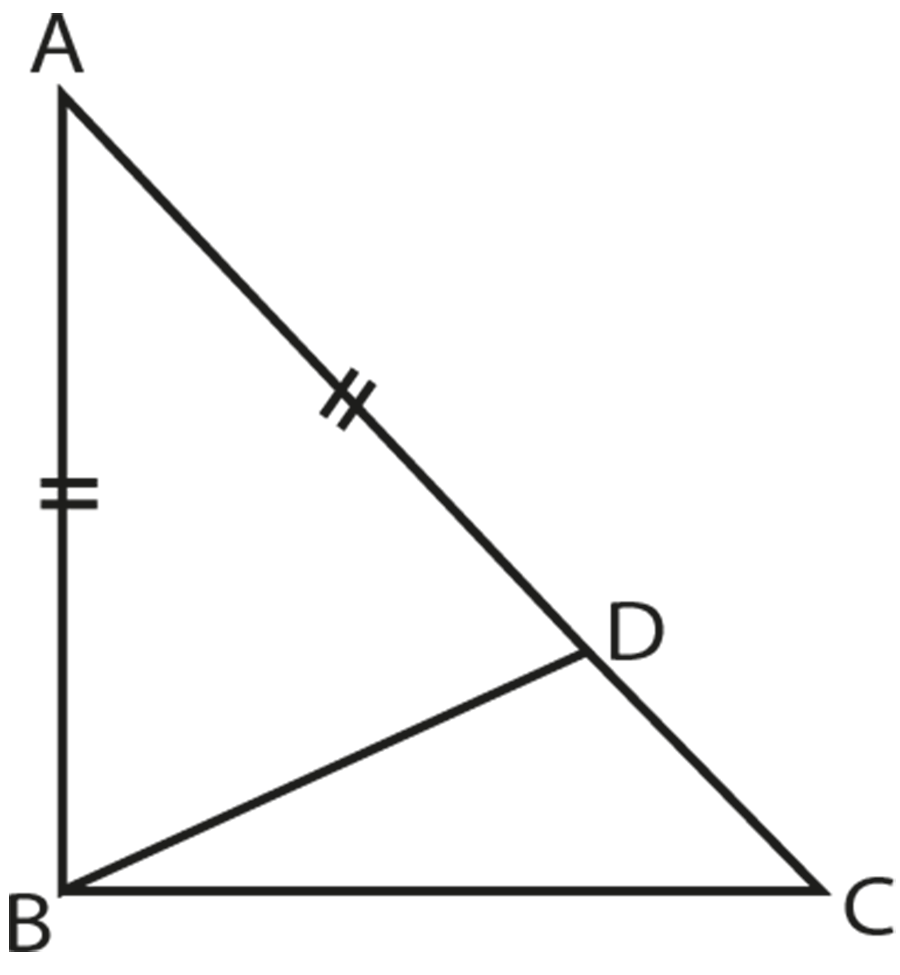
Read the statement and draw a triangle as per data. 

Draw \[\Delta \text{ABC}\], such that \[\text{AC  AB}\].

Data:

\[\text{AC  AB}\]

To Prove:

$\angle \text{ABC = }\angle \text{ACB}$

Construction:

Take a point D on $\overline{\text{AC}}$ such that $\overline{\text{AB}}\text{ = }\overline{\text{AD}}$. Join B to D.

Proof: 

In $\Delta \text{ABC}$, $\overline{\text{AB}}\text{ = }\overline{\text{AD}}$   (by construction)

$\therefore \angle \text{ABD = }\angle \text{ADB}$…(1)

but $\angle \text{ADB}$ is the exterior angle with reference to $\Delta \text{DBC}$. 

$\angle \text{ADB  }\angle \text{DCB}$ … (2)

From relation (1) and (2) we can write $\angle \text{ABD  }\angle \text{DCB}$

But $\angle \text{ABD}$ is a part of $\angle \text{ACB}$.

$\therefore \angle \text{ACB  }\angle \text{DCB}$ or $\therefore \angle \text{ABC  }\angle \text{ACB}$

Hence, proved.

• Angle Side Relation

Theorem 2:

In a triangle, if two angles are unequal, the side opposite to greater angle is longer than the side opposite to the smaller angle.

• Theorem 3

In a triangle, the greater angle has the longer side opposite to it.

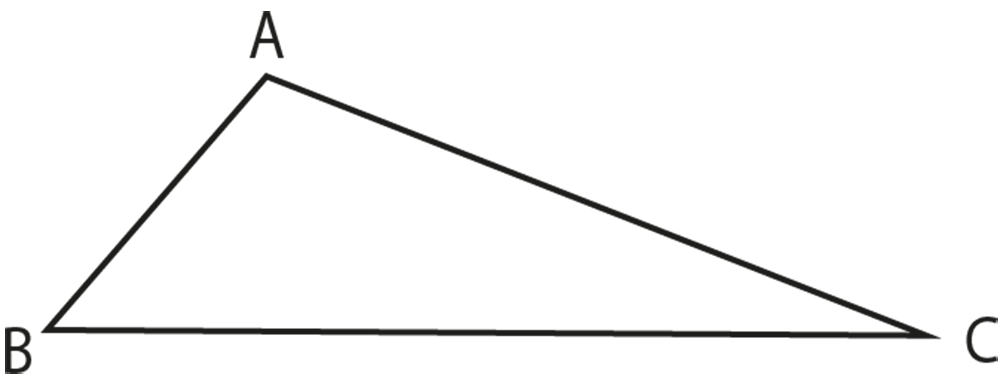
Given:

In $\Delta \text{ABC}$, $\angle \text{ABC  }\angle \text{ACB}$

To prove: 

\[\text{AC  AB}\]

Proof: 

In \[\Delta \text{ABC}\], AB and AC are two line segments. So the following are the three possibilities of which 

exactly one must be true.

1. either \[\text{AB = AC}\], then $\angle \text{B = }\angle \text{C}$ which is contrary to the hypothesis.

\[\therefore \text{AB }\ne \text{ AC}\]

2. \[\text{AB  AC}\], then $\angle \text{B  }\angle \text{C}$ which is contrary to the hypothesis.

3. \[\text{AB  AC}\], this is the only condition we are left with, so \[\text{AB  AC}\] must be true.

Hence, proved.

• Theorem 4

Prove that in any triangle the sum of the lengths of any two sides of a triangle is greater than the length of its third side.
Draw $\text{ }\!\!\Delta\!\!\text{ ABC}$.

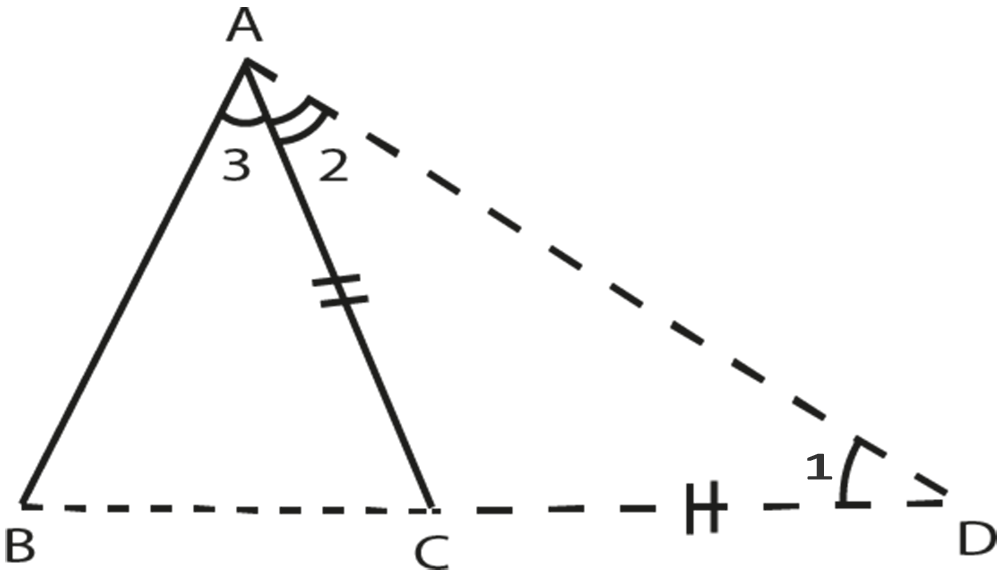
Data:

ABC is a triangle.

To prove: 

$\overline{\text{AB}}+\overline{\text{AC}}>\overline{\text{BC}}$

$\overline{\text{AB}}+\overline{\text{BC}}>\overline{\text{AC}}$

$\overline{\text{AC}}+\overline{\text{BC}}>\overline{\text{BA}}$

Construction:

Produce $\overline{\text{BC}}$ to D such that \[\overline{\text{AC}}\text{ = }\overline{\text{CD}}\]. Join A to D.

Proof: 

\[\overline{\text{AC}}\text{ = }\overline{\text{CD}}\]  (by construction)

$\angle 1=\angle 2$…(1)

From the figure, 

$\angle \text{BAD = }\angle \text{2+}\angle \text{3}$ …(2)

$\angle \text{BAD  }\angle \text{2}$

$\therefore \angle \text{BAD  }\angle 1$   (proved from 1)

$\overline{\text{AB}}$ is opposite to $\angle 1$ and $\overline{\text{BD}}$ is opposite to $\angle \text{BAD }$.

In $\Delta \text{BAD }$, $\angle \text{1  }\angle \text{2+}\angle \text{3}$

\[\text{BD  AB }\](side opposite to greater angle is greater)

From figure \[\text{BD = BC + CD}\]

\[\therefore \text{BC + CDAB}\]

\[\therefore \text{BC + ACAB}\]

Since, $\text{CD = AC}$, hence, sum of two sides of a triangle is greater than the third side.

Similarly, $\overline{\text{AB}}+\overline{\text{BC}}>\overline{\text{AC}}$ and $\overline{\text{AC}}+\overline{\text{BC}}>\overline{\text{BA}}$.

Hence, proved.

• Theorem 5:

Of all the line segments that can be drawn to a given line, from a point not lying on it, the perpendicular line segment is the shortest.

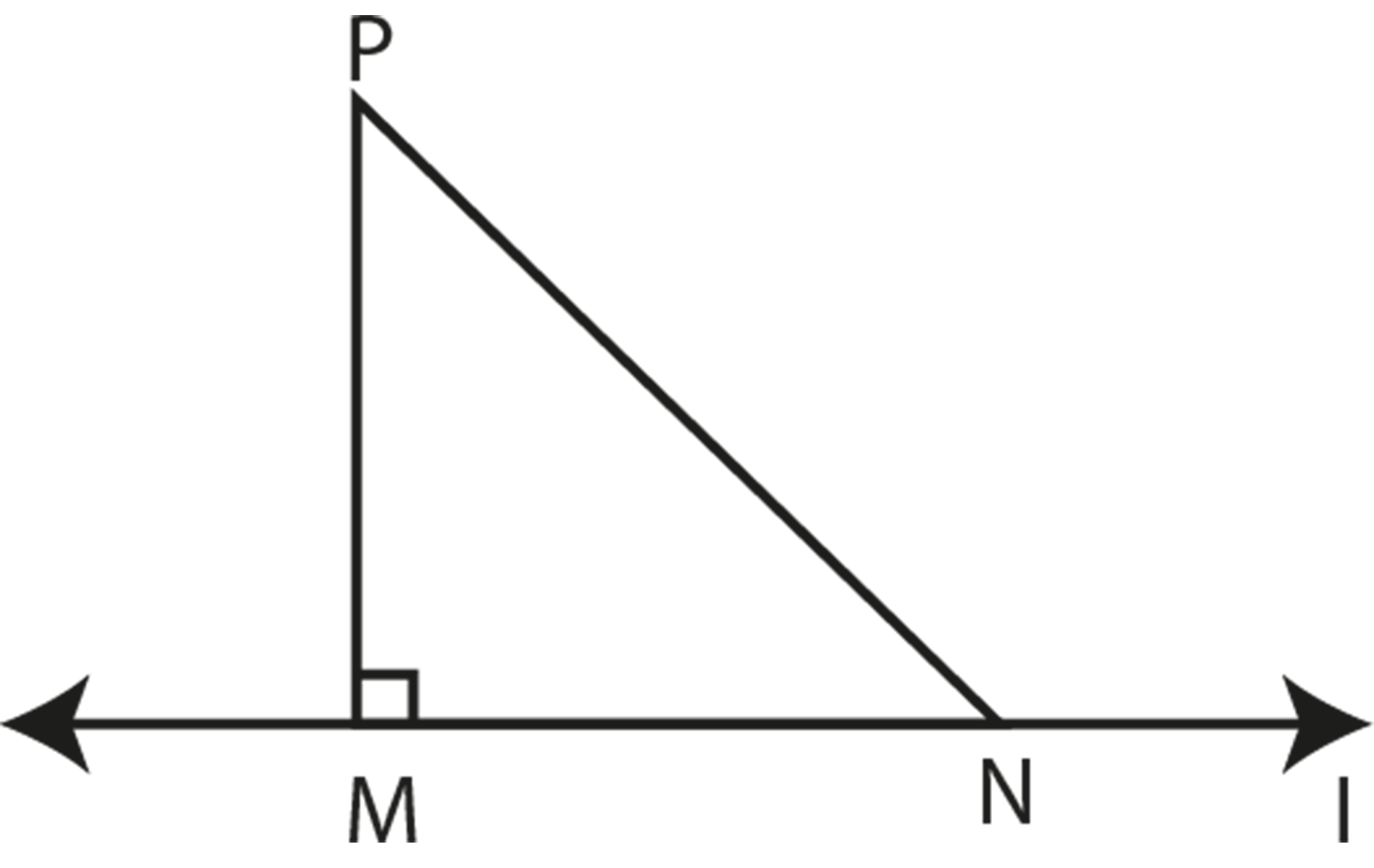
Given:

$l$ is a line and P is a point not lying on it. \[\text{PM}\bot l\]. N is any point on l other than M.

To prove: 

\[\text{PM  PN}\]

Proof:

In $\text{ }\!\!\Delta\!\!\text{ PMN}$, $\angle \text{M}$ is the right angle.

$\therefore \angle \text{N}$ is an acute angle, from angle sum property.

$\because \angle \text{M  }\angle \text{N}$

$\text{PN  PM}$ (side opposite to greater angle)

$\therefore \text{PMPN}$.

Class 9 Maths Revision Notes for Triangles of Chapter 7 - Free PDF Download

Properties of Triangles

Triangles are closed three-sided figures. The triangles are of the following forms depending on the measurement of the sides and angles:

• Equilateral Triangles: The equilateral triangle has all sides and angles of equal measure. This type of triangle is often called an acute triangle, as all its angles measure 60°.

• Isosceles Triangle: The isosceles triangle is one in which there are two equal sides and two equal angles.

• Scalene Triangle: No sides and angles are equal to each other in the scalene triangle.

The triangles are of the following forms, depending on the angle:

• Acute Triangle: triangles, where all sides are acute-angled to one another, are called acute triangles. The simplest example of this triangle is the equilateral triangle.

• Obtuse Triangle: The obtuse-angled triangle is the one with an obtuse-angled side. Isosceles triangles and scale triangles fall under this group of triangles.

• Right Angled Triangle: a triangle with an angle equal to 90° is considered a right-angled triangle.

Congruent Triangles

Two triangles are said to be congruent if all three sides and three angles are equal. But all six dimensions need to be found. The congruence of triangles can therefore be calculated by knowing just three values out of six. The congruent meaning in Maths is that two figures are identical to each other on the basis of their shape and size.

Δ XYZ ≅ Δ LMN.

Each congruent object seems like the same figure when positioned over its other counterpart. Likewise, congruent triangles are those triangles that are the exact replica of each other in terms of the measurement of the sides and angles.

Similarity of Triangles

Two triangles are said to be identical if the corresponding angles are equal and the corresponding sides are proportional. Similar triangles, in other words, have almost the same shape, but not necessarily the same size. 

Inequalities of Triangles

The theorem of triangle inequality defines the relationship between a triangle's three sides. According to this theorem, the number of two-side lengths is always greater than the third side for any triangle. In other words, this theorem states that a straight line is always the shortest path between two different points.

The triangle inequality theorem states that:

a < b + c,

b < a + c,

c < a + b

Pythagoras Theorem and its Applications

In the right-angled triangle, the hypotenuse square is equal to the sum of the squares of the other two sides.

(AC)²=(AB)²+(BC)²

AC is the hypotenuse.

AB is perpendicular.

BC is the base.

Basic Proportionality Theorem and Equal Intercept Theorem

If a line is parallel to the side of a triangle that divides the other sides into two different points, then those sides are proportionally divided by the line. Thales, a Greek mathematician, first stated the basic proportionality theorem. It is, therefore, also known as the Thales Theorem.

DE is parallel to BC

Then, according to the theorem,

AD/BD=AE/CE

Fun Facts about the Basic Proportionality Theorem

Did you know that the basic proportionality theorem has two properties? These two properties are:

• Property of an angle bisector.

• Property of Intercepts made by three parallel lines on a transversal.

Benefits of Downloading Triangle Class 9 Maths Revision Notes from Vedantu