NCERT Exemplar for Class 9 Maths Chapter 7 - Triangles - Free PDF Download

Sample Question 1: If \[\Delta ABC \cong \Delta PQR\] and \[\Delta ABC\] is not congruent to \[\Delta RPQ\], then which of the following is not true: 

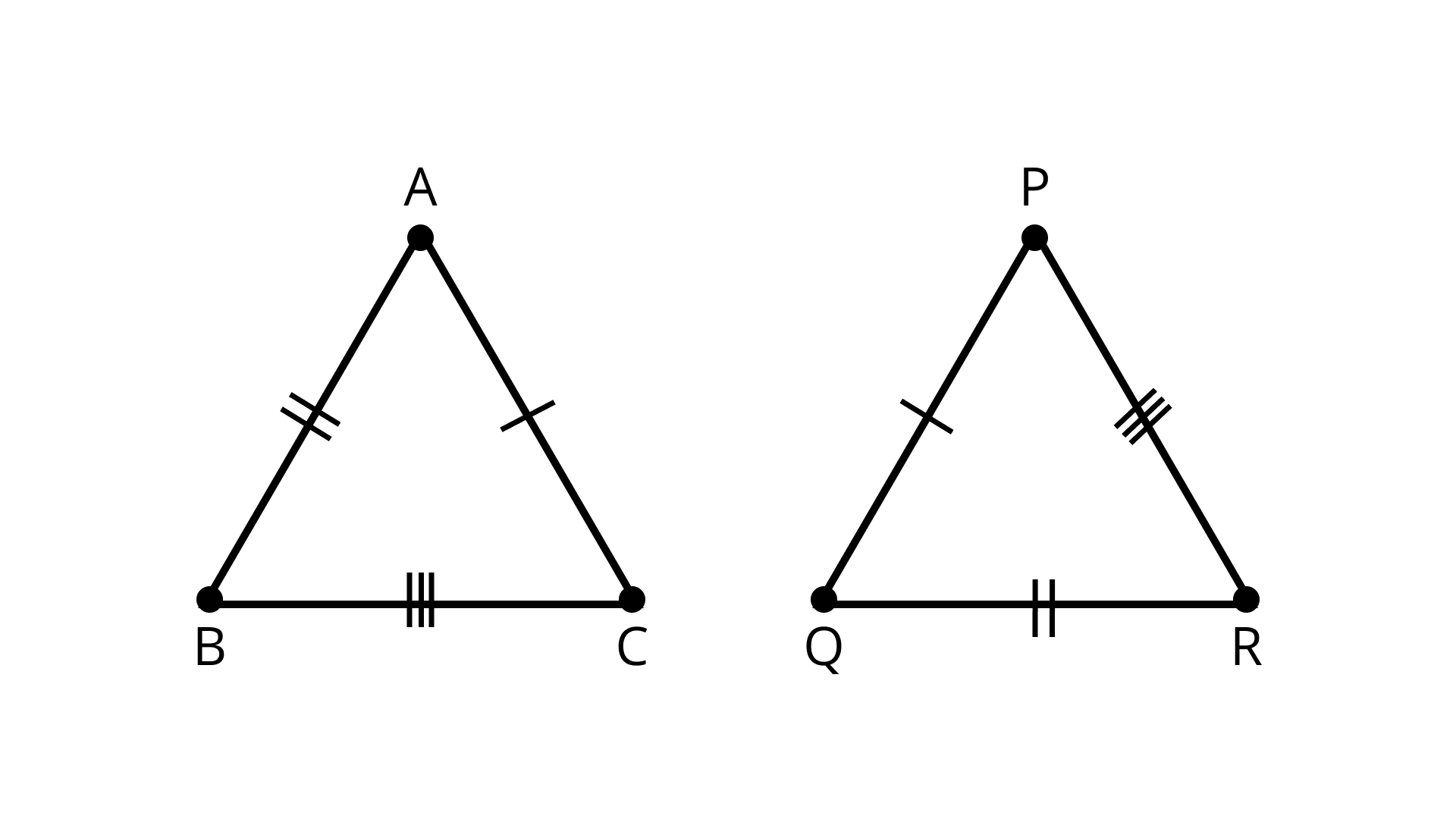
(A) \[BC  =  PQ\]

(B) \[AC  =  PR\]

(C) \[QR  =  BC\]

(D) \[AB  =  PQ\]

Ans: Correct option - A

Given, \[ABC \cong PQR\]

We know that:

Two triangles are said to be congruent if pairs of their corresponding sides and their corresponding angles are equal. 

Hence,

  ${\text{AC}}{\text{ = }}{\text{PR}}$

  ${\text{AB}}{\text{ = }}{\text{PQ}}$

  ${\text{QR}}{\text{ = }}{\text{BC}}$ 

Therefore, \[{\text{BC}}{\text{ = }}{\text{PQ}}\] is not true for triangles.

EXERCISE 7.1

1. Which of the following is not a criterion for congruence of triangles?

A. SAS

B. ASA

C. SSA

D. SSS

Ans: Correct option - C

A. SAS: If two pairs of corresponding sides of two triangles are equal in length, and the corresponding included angles are equal in measurement, then the triangles are congruent.

B. ASA: If two pairs of corresponding angles of two triangles are equal in measurement, and the corresponding included sides are equal in length, then the triangles are congruent.

C. SSA: The SSA condition (Side-Side-Angle) which specifies two sides and a non-included angle (also known as ASS, or Angle-Side-Side) do not by itself prove congruence.

D. SSS: If three pairs of corresponding sides of two triangles are equal in length, then the triangles are congruent.

2. If \[AB = QR, BC = PR\] and \[CA = PQ\], then

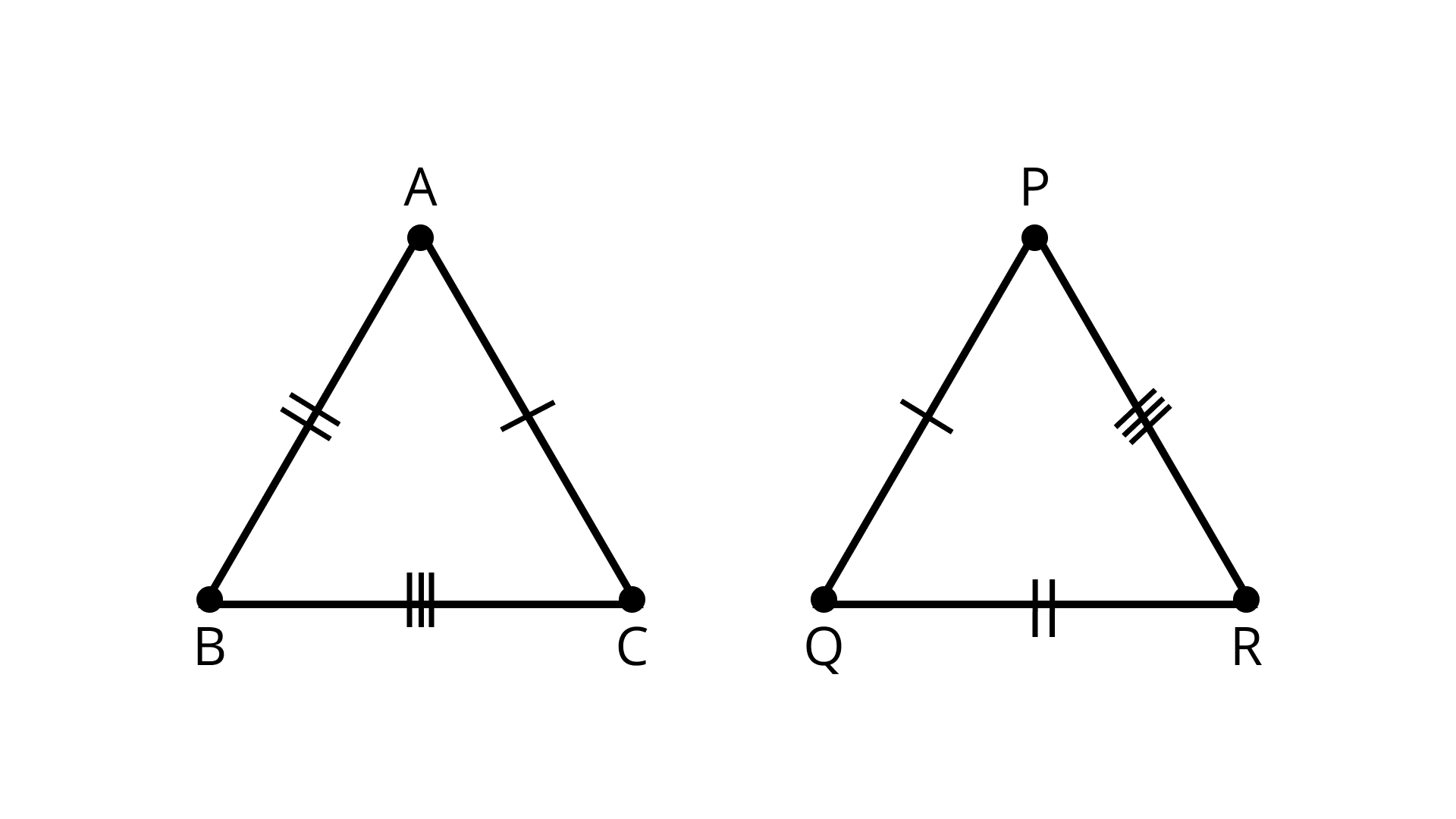
A. \[\Delta ABC \cong \Delta PQR\]

B. \[\Delta CBA \cong \Delta PRQ\]

C. \[\Delta BAC \cong \Delta RPQ\] 

D. \[\Delta PQR \cong \Delta BCA\]

Ans: Correct option - B

Given: \[{\text{AB}}{\text{ = }}{\text{QR, BC}}{\text{ = }}{\text{PR and CA}}{\text{ = }}{\text{PQ}}\]

\[{\text{AB}}{\text{ = }}{\text{QR, BC}}{\text{ = }}{\text{PR and CA}}{\text{ = }}{\text{PQ}}\]

Here, the three pairs of corresponding sides of two triangles are equal in length.

Apply the SSS rule of congruence, we have:

\[\Delta CBA \cong \Delta PQR\]  

3. In \[\Delta ABC,{\text{ }}AB = AC{\text{ and }}\angle B = 50^\circ \]. Then \[\angle C\] is equal to

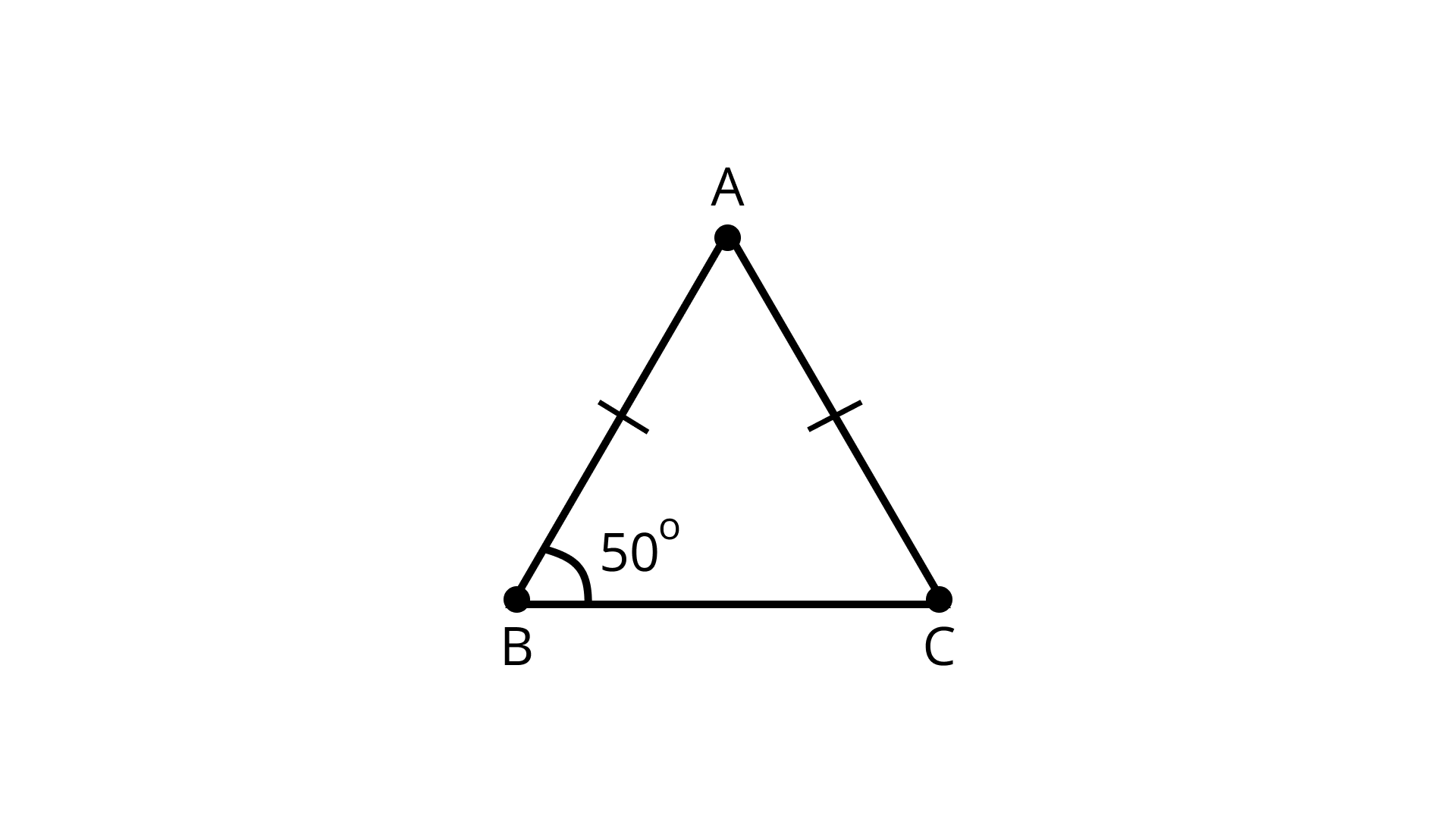
A. $4{0^\circ }$

B. $5{0^\circ }$

C. $8{0^\circ }$  

D. $13{0^\circ }$

Ans: Correct option - B

Given: \[\Delta ABC,{\text{ }}AB = AC{\text{ and }}\angle B = 50^\circ \]

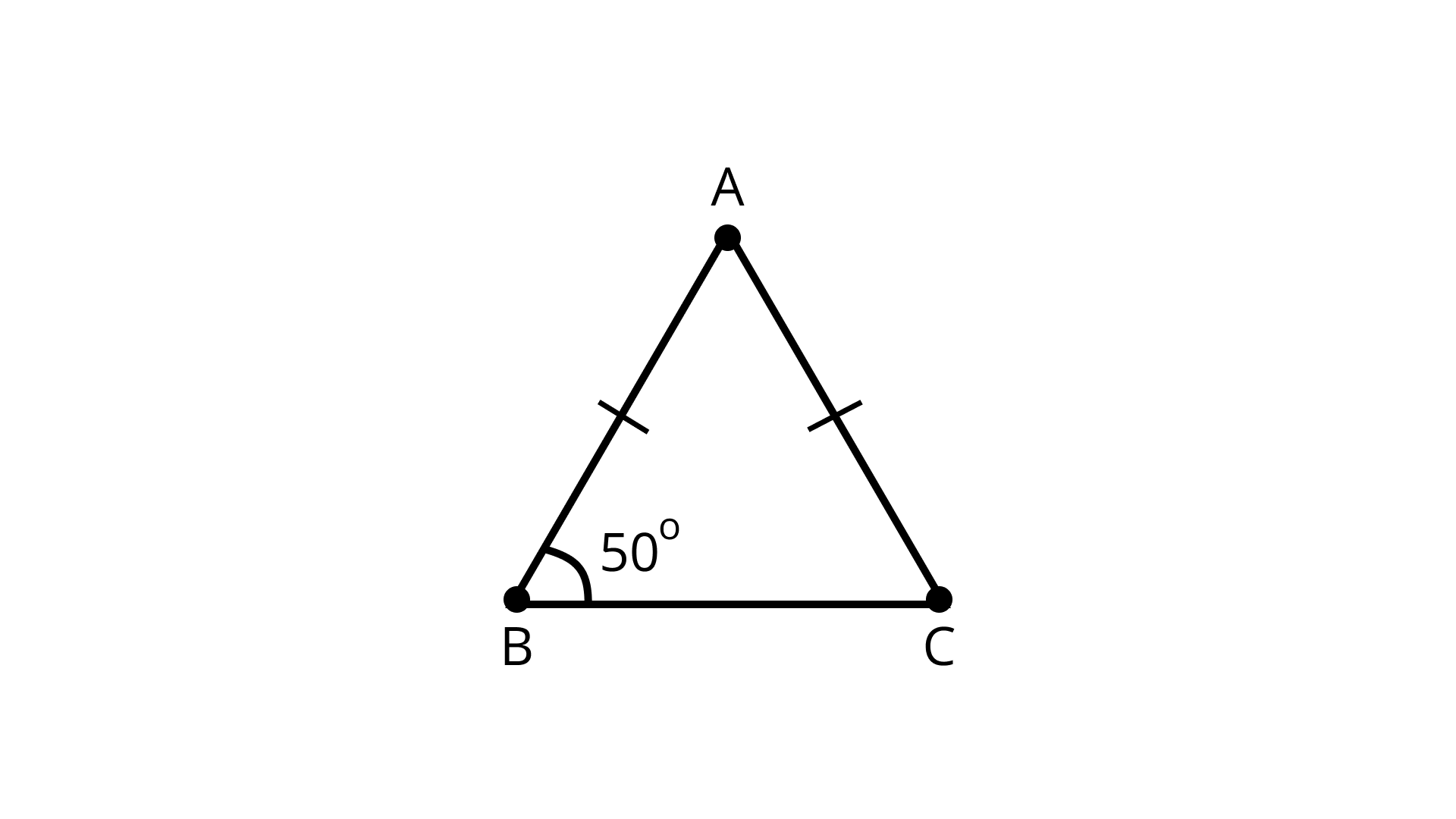
Since, \[AB = AC{\text{ and }}\angle B = 50^\circ \]
\[\angle B = \angle C = 50^\circ \]          (Angles opposite to equal sides are equal)

4. In \[\Delta ABC, BC = AB\] and \[\angle B = 80^\circ .\] Then \[\angle A\] is equal to

A. $8{0^\circ }$  

B. $4{0^\circ }$

C. $5{0^\circ }$ 

D. $10{0^\circ }$

Ans: Correct option - C

The angles opposite to the equal side are equal.

\[BC = AB{\text{ and }}\angle B = 80^\circ \]

let \[\angle A\] = \[x\]

\[\angle A = \angle C = x\]                             (As angles opposite to equal side are equal)

Now by angle sum property, we have:

 $\angle A + \angle B + \angle C = 180^\circ$

  $\Rightarrow x + 80^\circ  + x = 180^\circ$

  $\Rightarrow 2x + 80^\circ  = 180^\circ$

  $\Rightarrow 2x = 180^\circ$

  $\Rightarrow x = \dfrac{{100^\circ }}{2} = 50^\circ$ 

Therefore, \[x = 50^\circ \]

5. In \[\Delta PQR,\angle R = \angle P\] and QR = 4cm and PR = 5cm. 

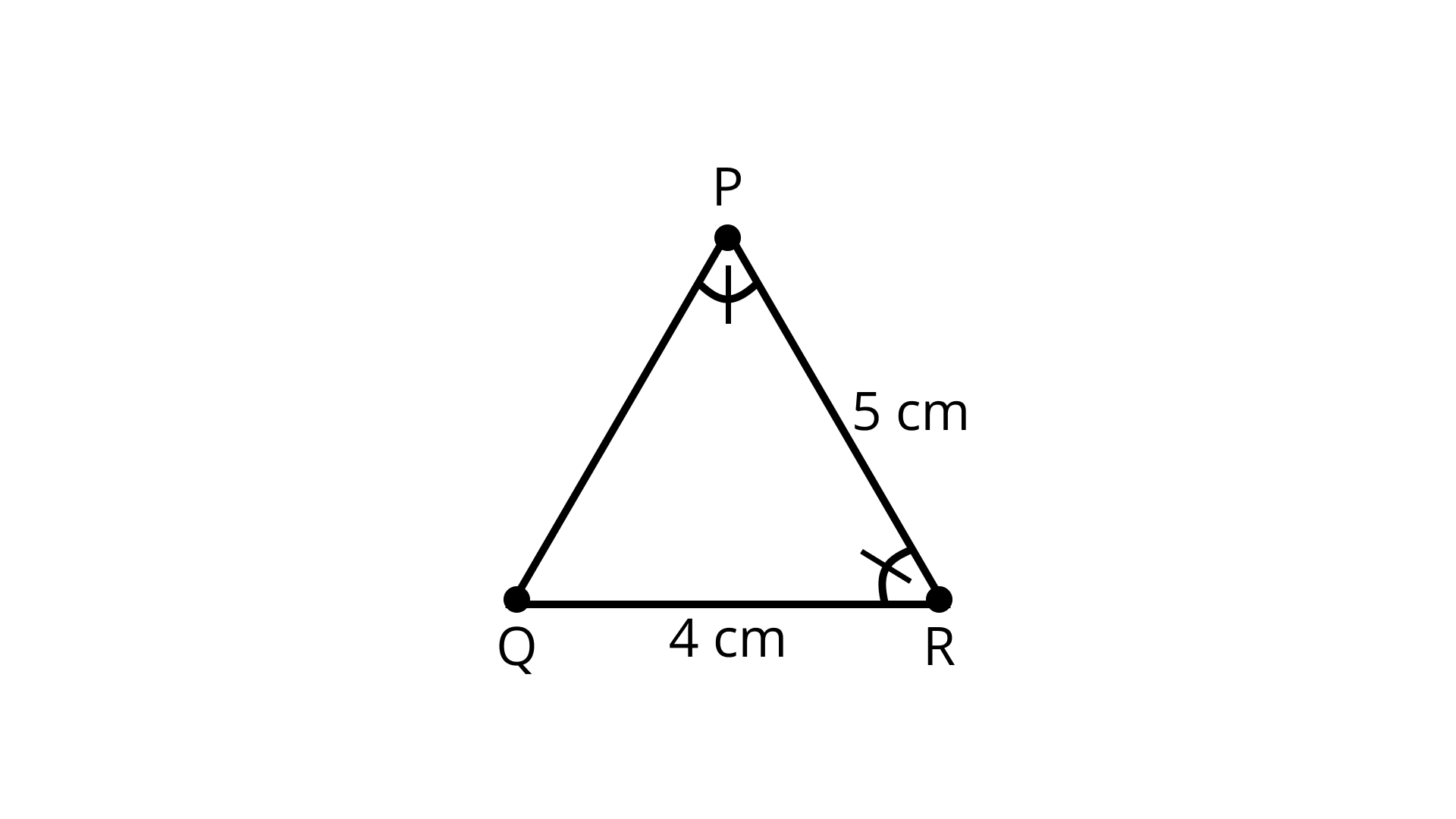
Then the length of \[{\text{PQ}}\] is

A. 4cm

B. 5cm

C. 2cm

D. 2.5cm 

Ans: Correct option - A

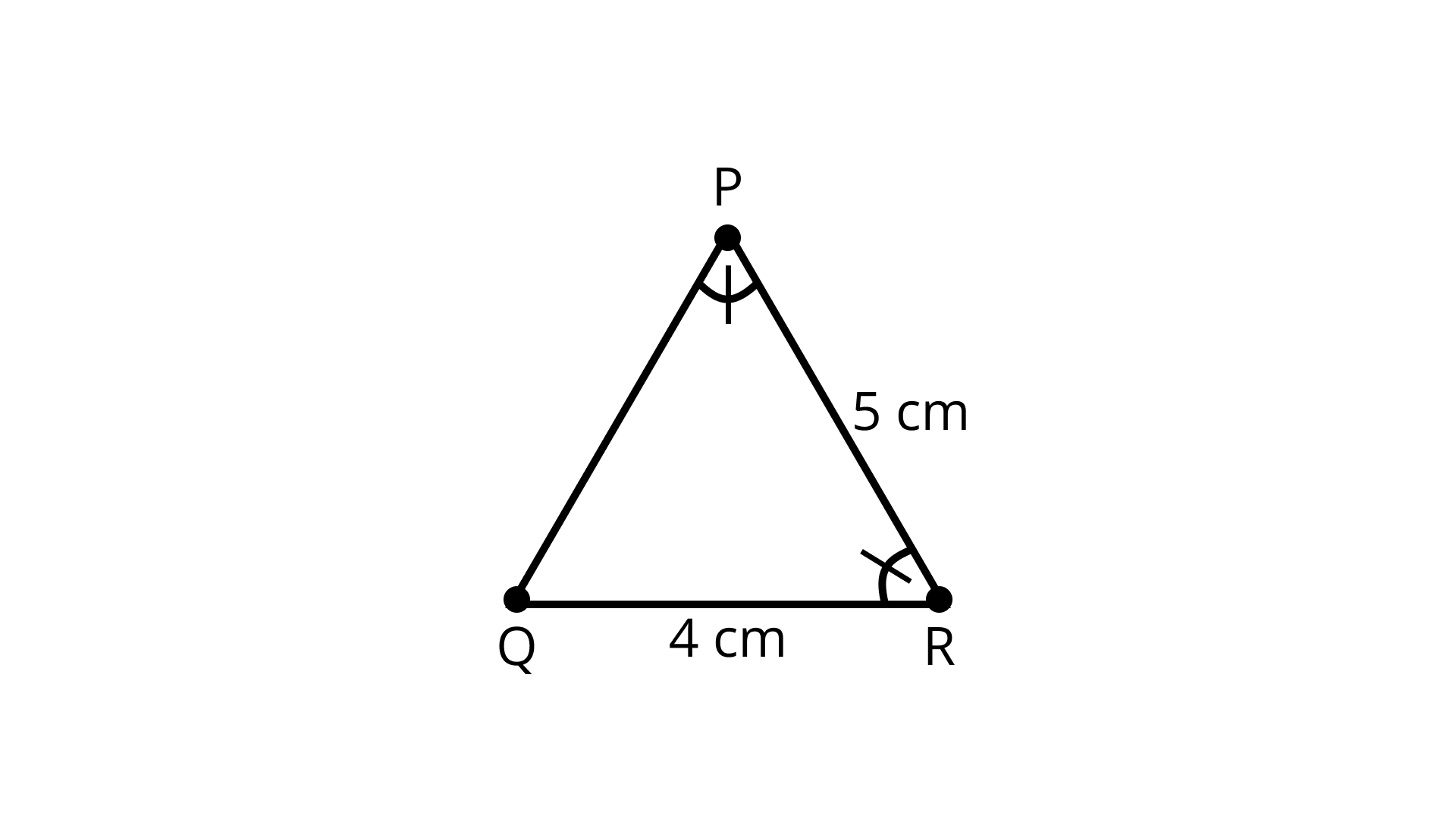
\[\angle R{\text{ }} = \angle P{\text{ and }}QR{\text{ }} = 4{\text{ cm and }}PR{\text{ }} = {\text{ }}5{\text{ cm}}\]

Since, \[\angle R = \angle P\]

\[PQ = QR = 4{\text{cm}}\](Sides opposite to equal angles are equal)

6. \[D\] is a point on the side \[BC\] of a \[{\Delta }ABC\] such that \[AD\] bisects \[\angle BAC\]. 

Then,

A. BD  =  CD

B. BA  >  BD

C. BD  >  BA

D. CD  >  CA 

Ans: Correct option - B

Given, ${\Delta ABC}$ such that ${\text{AD}}$ bisects \[\angle BAC\]

The bisector divides a given angle into two angles with equal measures.

$\therefore \angle BAD = \angle CAD...\left( i \right)$

In $\Delta ACD,\angle BDA$ is an exterior angle.

$\therefore \angle BDA > \angle CAD...\left( {ii} \right)$            $[\because $ Exterior angle > interior opposite angle]

$\Rightarrow \angle BDA > \angle BAD$           {from Eq. (i)}

$\Rightarrow BA > BD\left[ {{\text{side opposite to greater angle is greater}}} \right]$

7. It is given that \[\Delta ABC \cong \Delta FDE\] and AB = 5cm,\[\angle B = 40^\circ {\text{ and }}\angle A = 80^\circ .\] 

Then which of the following is true?

A. $DF = 5 cm,{\text{ }}\angle F = 60^\circ  $

B. $DF = 5 cm,{\text{ }}\angle E = 60^\circ {\text{ }}$

C. $DE = 5 cm,{\text{ }}\angle E = 60^\circ {\text{ }}$

D. $DE = 5 cm,{\text{ }}\angle D = 40^\circ$ 

Ans: Correct option - B

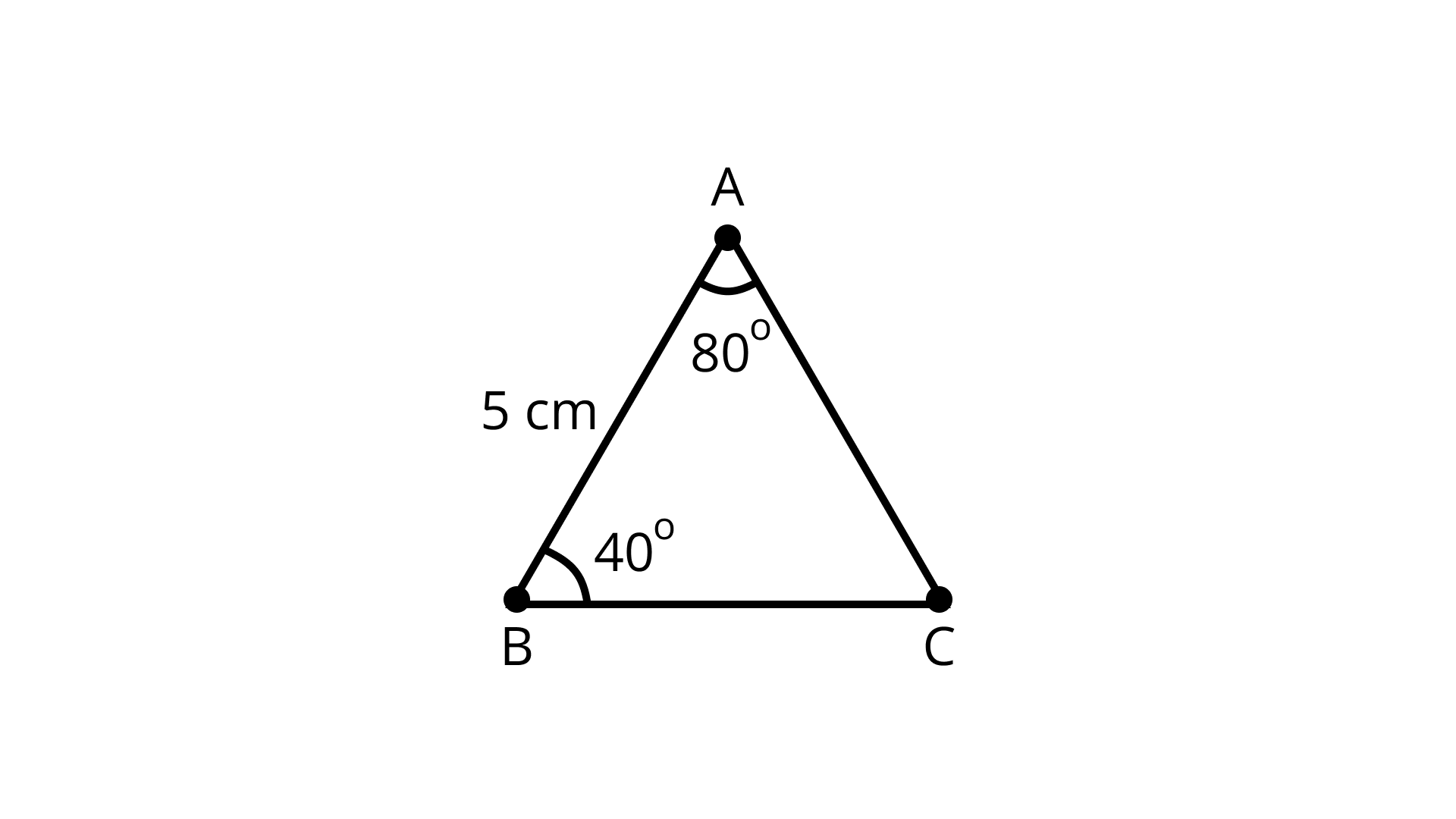
It is given that \[\Delta ABC \cong \Delta FDE{\text{ and }}AB = 5{\text{cm}},\angle B = 40^\circ {\text{ and}}\angle A = 80^\circ .\]

Two triangles are congruent if their corresponding sides are equal in length and their corresponding angles are equal in size.

In the first option, \[DF = 5{\text{cm}}\] but \[\angle F\] is not equal to \[60^\circ .\]

In the second option, \[DF = 5{\text{cm}}\] and \[\angle E = 60^\circ \] is satisfied. 

In the third and the fourth options, the length of \[DE \ne 5{\text{cm}}\], since it is not defined.

8. Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be

A. 3.6 cm

B. 4.1 cm 

C. 3.8 cm 

D. 3.4 cm 

Ans: Correct option - D

Two sides of a triangle are of lengths 5 cm and 1.5 cm.

In a triangle, the difference between two sides should be less than the third side.

In a triangle, the difference between two sides should be less than the third side.

Hence, option D is correct \[3.4{\text{ cm}}\]

9. In \[\Delta PQR\], if \[\angle R > \angle Q\], then

A. QR  >  PR 

B. PQ  >  PR 

C. PQ  <  PR 

D. QR  <  PR 

Ans: Correct option - B

We have:

In \[\Delta PQR\], \[\angle R > \angle Q\]

We know that: 

The sides opposite greater angles are greater.

Hence, 

\[PQ > PR\]

10. In triangles \[ABC\] and \[PQR, AB = AC,\angle C = \angle P\] and \[\angle B  = \angle Q\]. The two triangles are

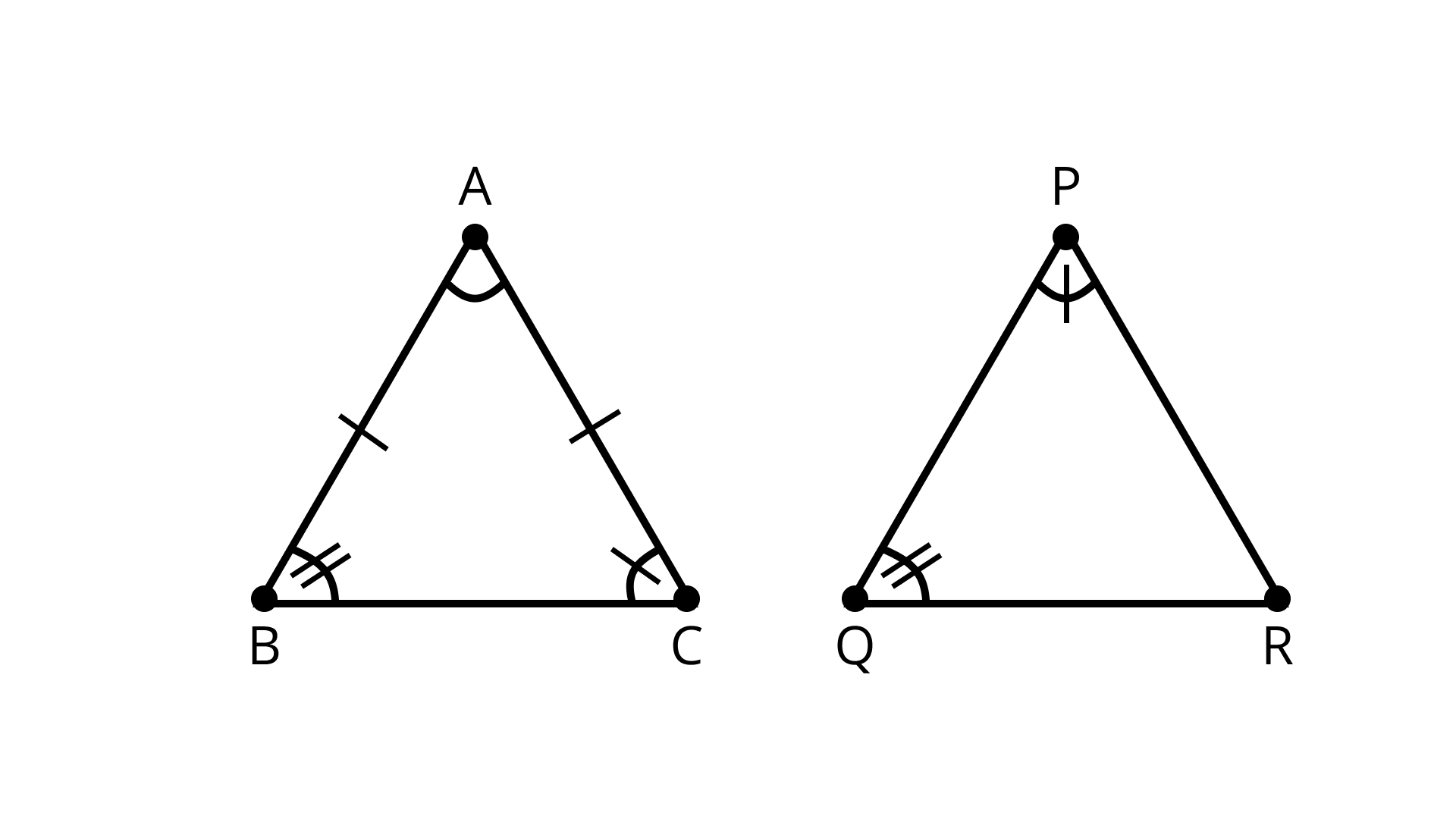
A. isosceles but not congruent 

B. isosceles and congruent 

C. congruent but not isosceles 

D. neither congruent nor isosceles

Ans: Correct option - A

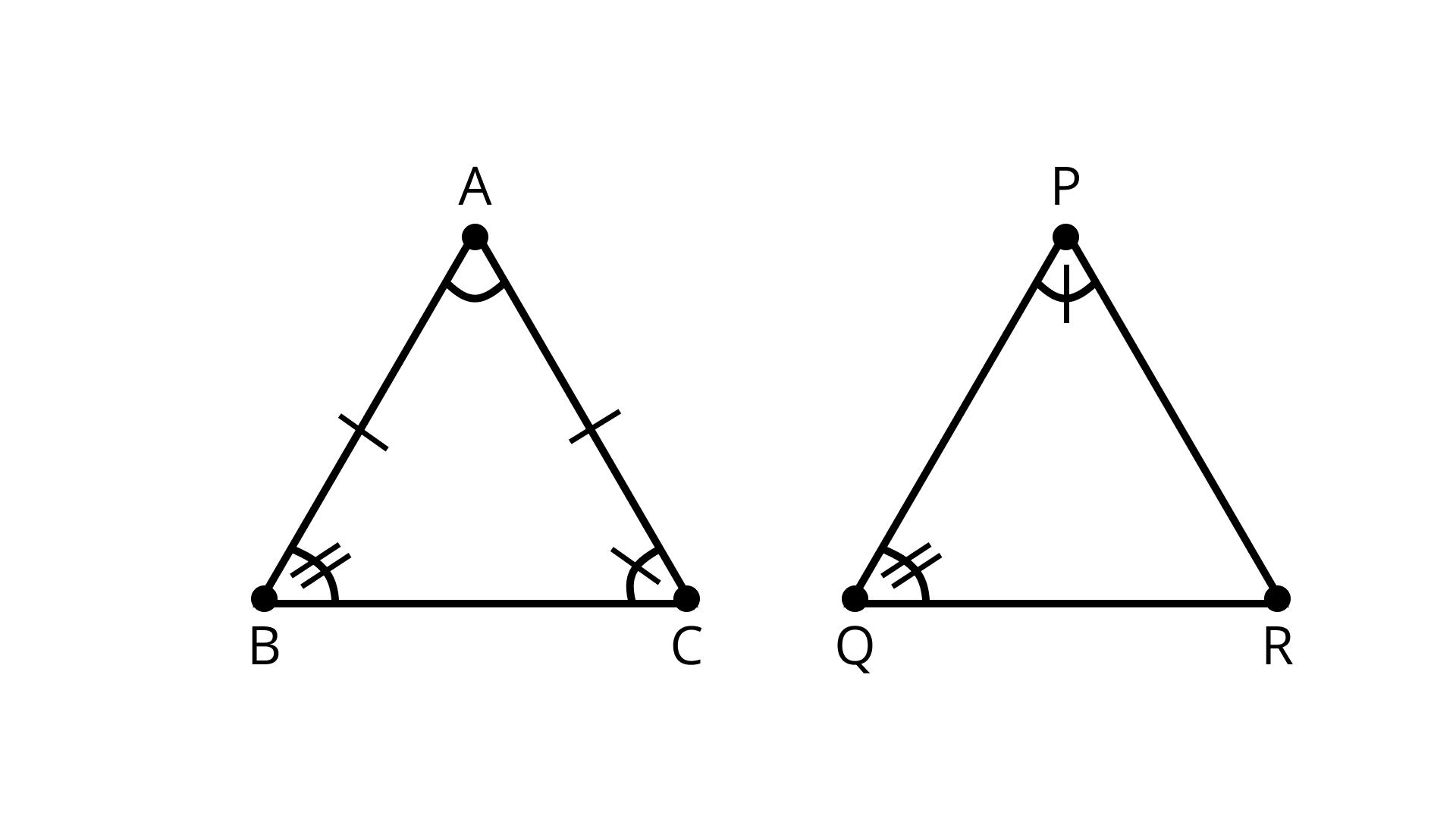
In \[\Delta ABC{\text{ and}}\Delta PQR\]

\[\angle C = \angle P\](Given)

\[\angle B = \angle Q\](Given)

\[\angle A = \angle R\](Third angle of the triangle)

Also, given, \[AB = AC\]

Thus, \[\angle B = \angle C\](Isosceles triangle Property)

But,\[\angle B = \angle Q\]and \[\angle C = \angle P\]

Hence, \[\angle Q = \angle P\]

\[PR = QR\]      (sides opposite equal angles are equal)

Thus, both the triangles are isosceles but not congruent.

11. In triangles \[ABC\] and \[DEF, AB = FD\] and \[\angle A = \angle D.\] The two triangles will be congruent by SAS axiom if

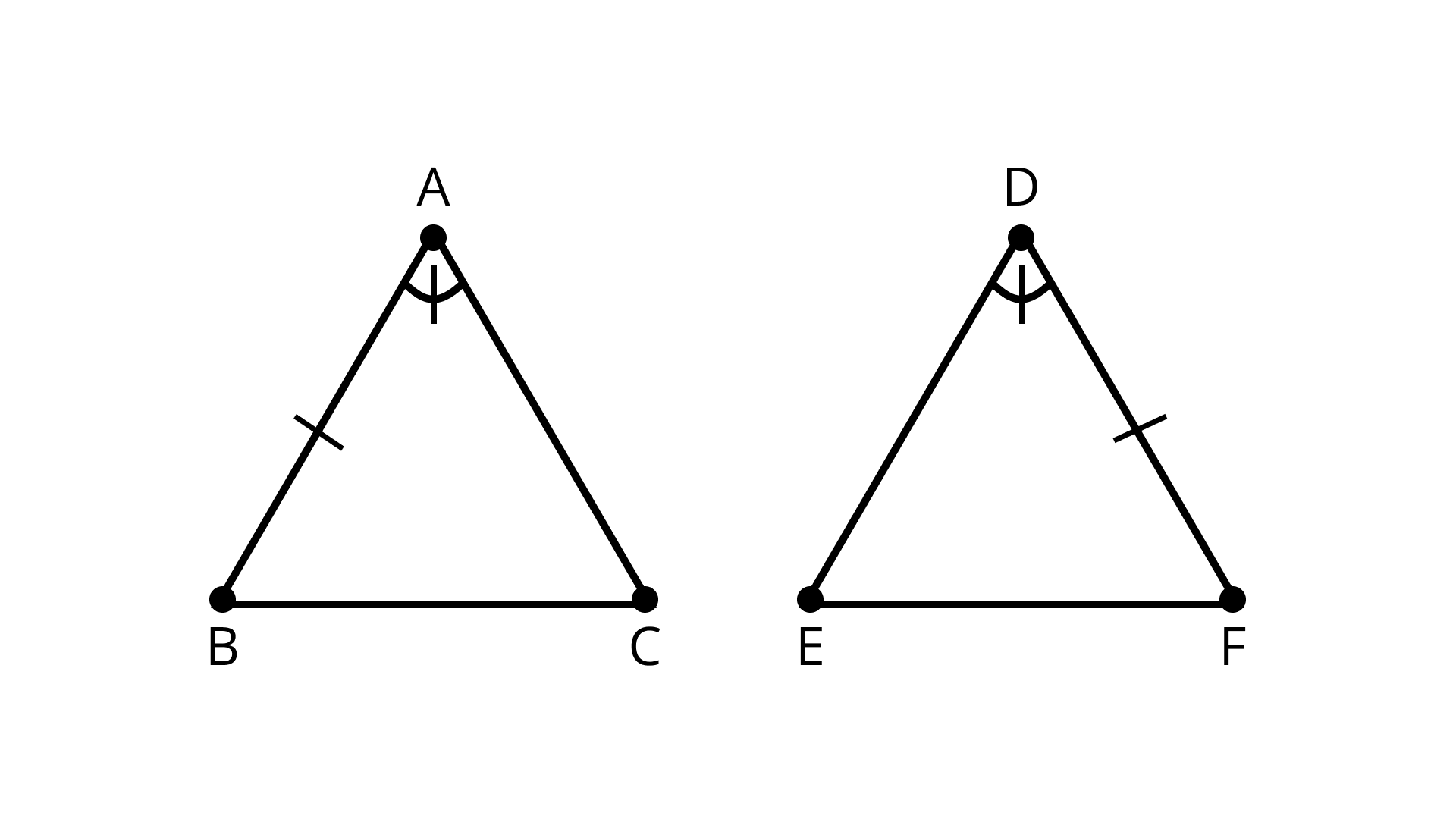
A. BC = EF 

B. AC = DE 

C. AC = EF 

D. BC = DE 

Ans: Correct option - B

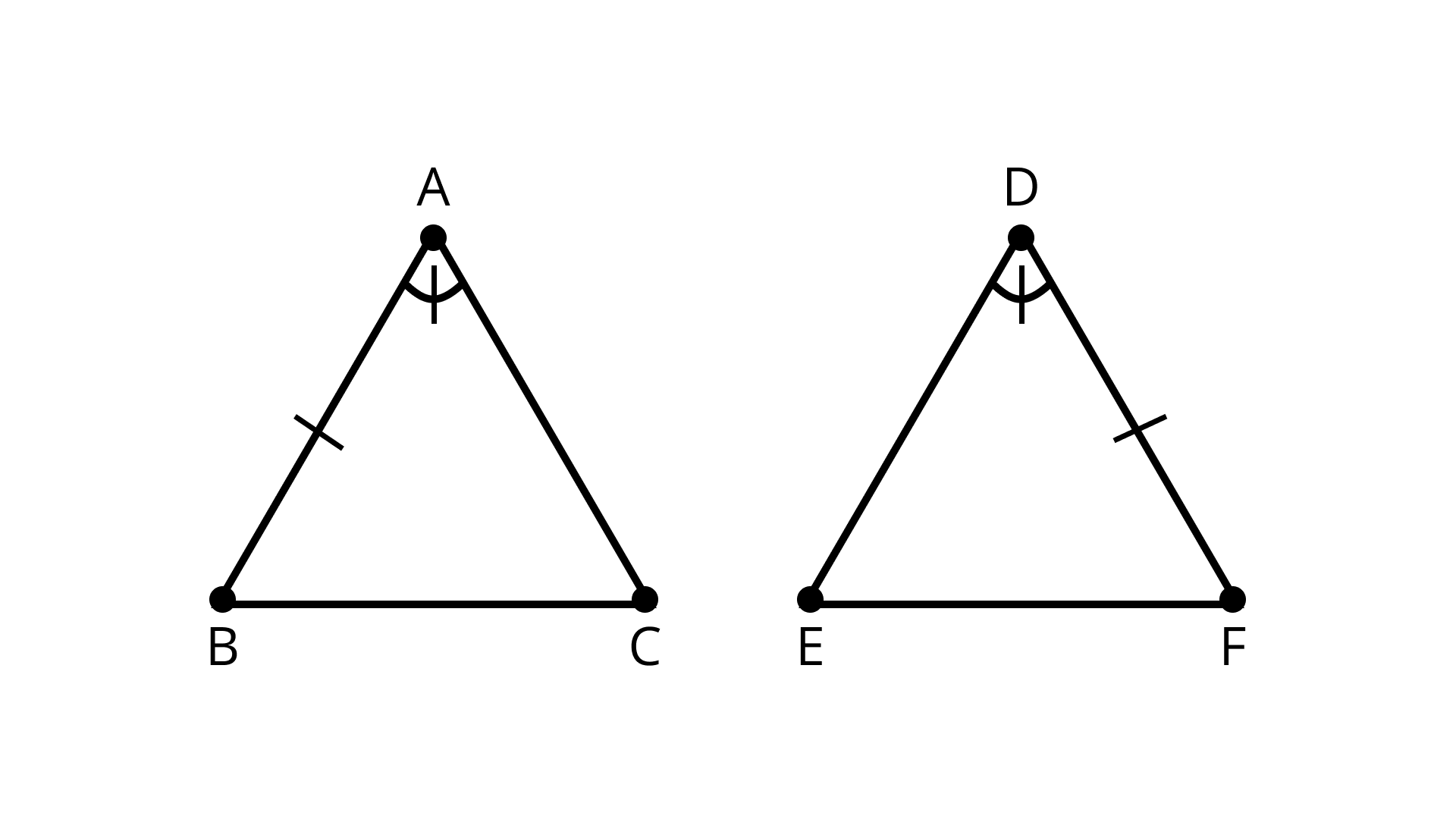
In triangles \[ABC{\text{ and }}DEF,{\text{ }}AB = FD{\text{ and}}\angle A = \angle D.\]

SAS axiom:

If one angle between two adjacent sides of a triangle is similar to angle between two sides of another triangle then two triangles are congruent.

The two triangles \[ABC{\text{ and }}DEF\] will be congruent by SAS axiom if \[AC = DE{\text{ }}\]

Sample Question 1: In the two triangles \[ABC\] and \[DEF, AB = DE\] and \[AC = EF\]. Name two angles from the two triangles that must be equal so that the two triangles are congruent. Give reason for your answer. 

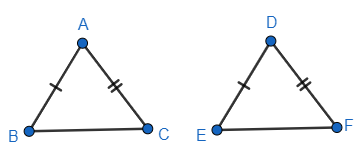
Ans: In the two triangles\[{\text{ABC}}\]\[{\text{ and DEF}},{\text{ AB}}{\text{ = }}{\text{DE and AC}}{\text{ = }}{\text{EF}}\].

By SAS criterion of congruence, we have:

If one angle between two adjacent sides of a triangle is similar to angle between two sides of another triangle then two triangles are congruent. 

\[{\text{ }}\Delta ABC \cong \Delta EDF{\text{ if}}\angle A = \angle E\]

The required two angles are \[\angle A{\text{ and}}\angle E.{\text{ }}\]

Sample Question 2: In triangles ABC and DEF\[,\angle A = \angle D,\angle B = \angle E{\text{ and }}AB = EF\]. Will the two triangles be congruent? Give reasons for your answer. 

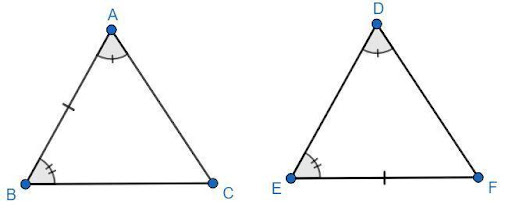
Ans: In triangles ABC and DEF\[,\angle A = \angle D,\angle B = \angle E{\text{ and AB}}{\text{ = }}{\text{EF}}\].

Here, \[{\text{AB and EF}}\] are not corresponding sides that touch the same two angle pairs in the two triangles.

Hence, the two triangles ABC and DEF will not be congruent.

EXERCISE 7.2

1. In triangles \[ABC\] and \[PQR,\angle A = \angle Q\] and \[\angle B = \angle R\]. Which side of ${\Delta }PQR$ should be equal to side $AB$ of ${\Delta }ABC$ so that the two triangles are congruent? Give reason for your answer.

Ans: In triangles \[{\text{ABC and PQR}},\angle A = \angle Q{\text{ and}}\angle B = \angle R\].

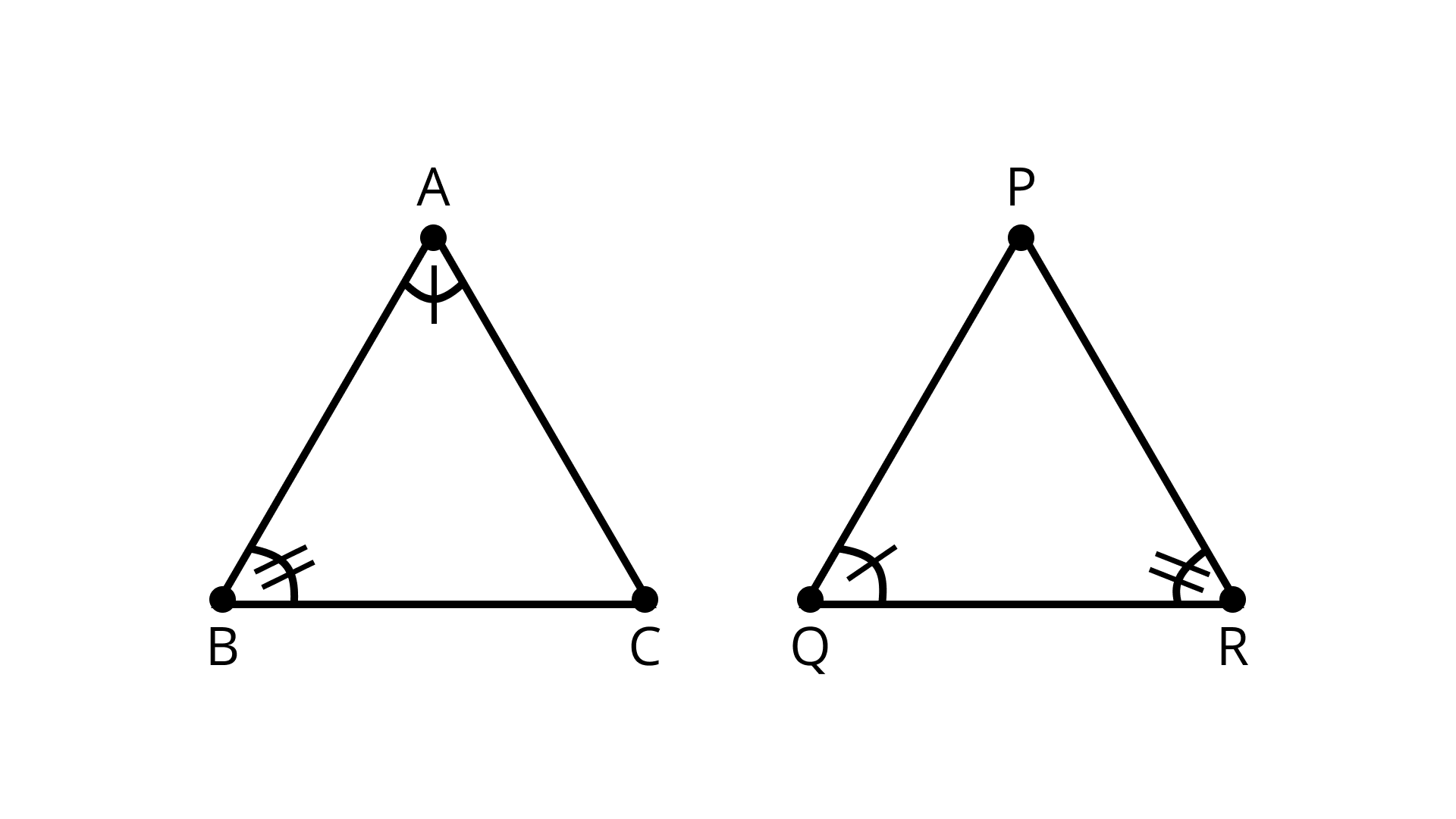
The corresponding sides needs to be equal for the triangles to be congruent.

\[\therefore {\text{AB}}{\text{ = }}{\text{PQ}}\]

Therefore,\[\Delta ABC \cong \Delta PQR\left( {{\text{SAS axiom of congruency}}} \right)\]

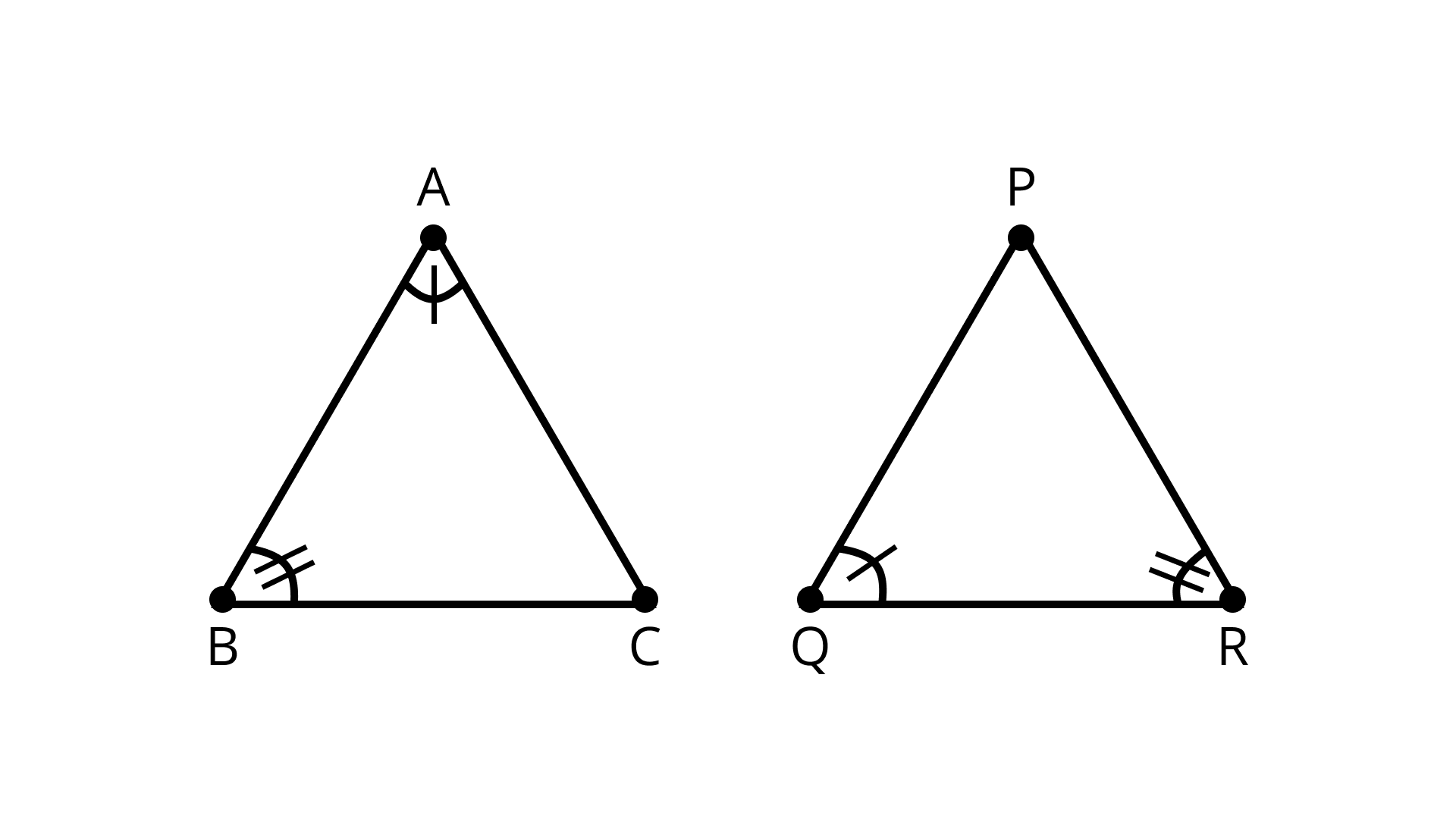
2. In triangles \[ABC\] and \[PQR,\angle A = \angle Q\] and\[\angle B = \angle R.\] Which side of \[{\Delta }PQR\] should be equal to side BC of \[{ \Delta }ABC\] so that the two triangles are congruent? Give reason for your answer.

Ans: In triangles \[{\text{ABC and PQR}},\angle A = \angle Q{\text{ and}}\angle B = \angle R.\]

We know that:

The two triangles are congruent if the corresponding side that touches the same two angle pairs is equal in the given pair of triangles.

Here,\[{\text{BC}}{\text{ = }}{\text{RP}}\]                          (Corresponding side.)

Therefore, \[\Delta ABC \cong \Delta PQR\left( {{\text{SAS axiom of congruency}}} \right)\]

3. “If two sides and an angle of one triangle are equal to two sides and an angle of Another triangle, then the two triangles must be congruent.” Is the statement true? Why?

Ans: The given statement is “If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.”

We know that:

If two sides and the included angle of one triangle is equal to corresponding two sides and the included angle of another triangle then the two triangles must be congruent.

Hence, the given statement is false.

4. “If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?

Ans: The statement is “If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.”

We know that:

If two angles and the corresponding side of one triangle are equal to the two included angles and the corresponding side of another triangle then the two triangles must be congruent. 

The given statement is false.

5. Is it possible to construct a triangle with lengths of its sides as \[4 cm, 3 cm\] and \[7 cm\]? Give reason for your answer.

Ans: Given 3 sides are \[4{\text{ cm}},{\text{ }}3{\text{ cm and }}7{\text{ cm}}\].

To construct the triangle of given sides, we need to check property of triangle “The sum of any two sides of a triangle is always greater than the third side" is satisfied by the lengths of all the three sides.

Here, $4 + 3\not  > 7$

Hence, it is not possible to construct a triangle with the given lengths \[4{\text{ cm}},{\text{ }}3{\text{ cm and }}7{\text{ cm}}\].

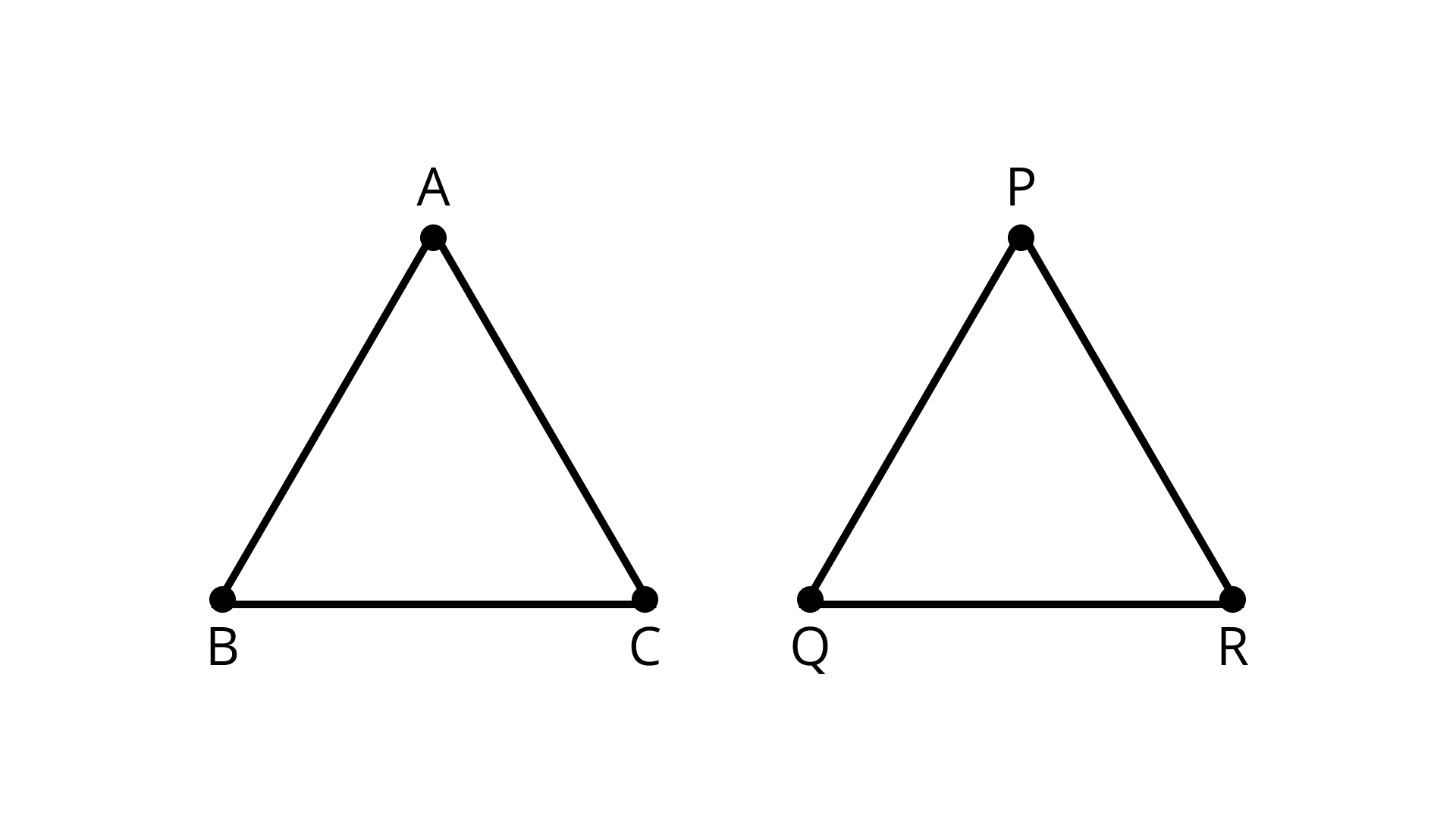
6. It is given that \[\Delta ABC \cong \Delta RPQ\]. Is it true to say that \[{\text{BC}}{\text{ = }}{\text{QR}}\]? Why?

Ans: It is given that \[\Delta ABC \cong \Delta RPQ\].

We know that:

The two triangles are congruent, if the sides and angles of one triangle are equal to the corresponding side and angles of other triangle.
For \[\Delta ABC \cong \Delta RPQ\].
We have,  \[AB = RP, BC = PQ\] and \[AC = RQ\], 

Hence, it is not true to say that \[BC = QR\].

7. If \[\Delta PQR \cong \Delta EDF\], then is it true to say that \[PR = EF\]? Give reason for your Answer.

Ans: \[\Delta PQR \cong \Delta EDF\]

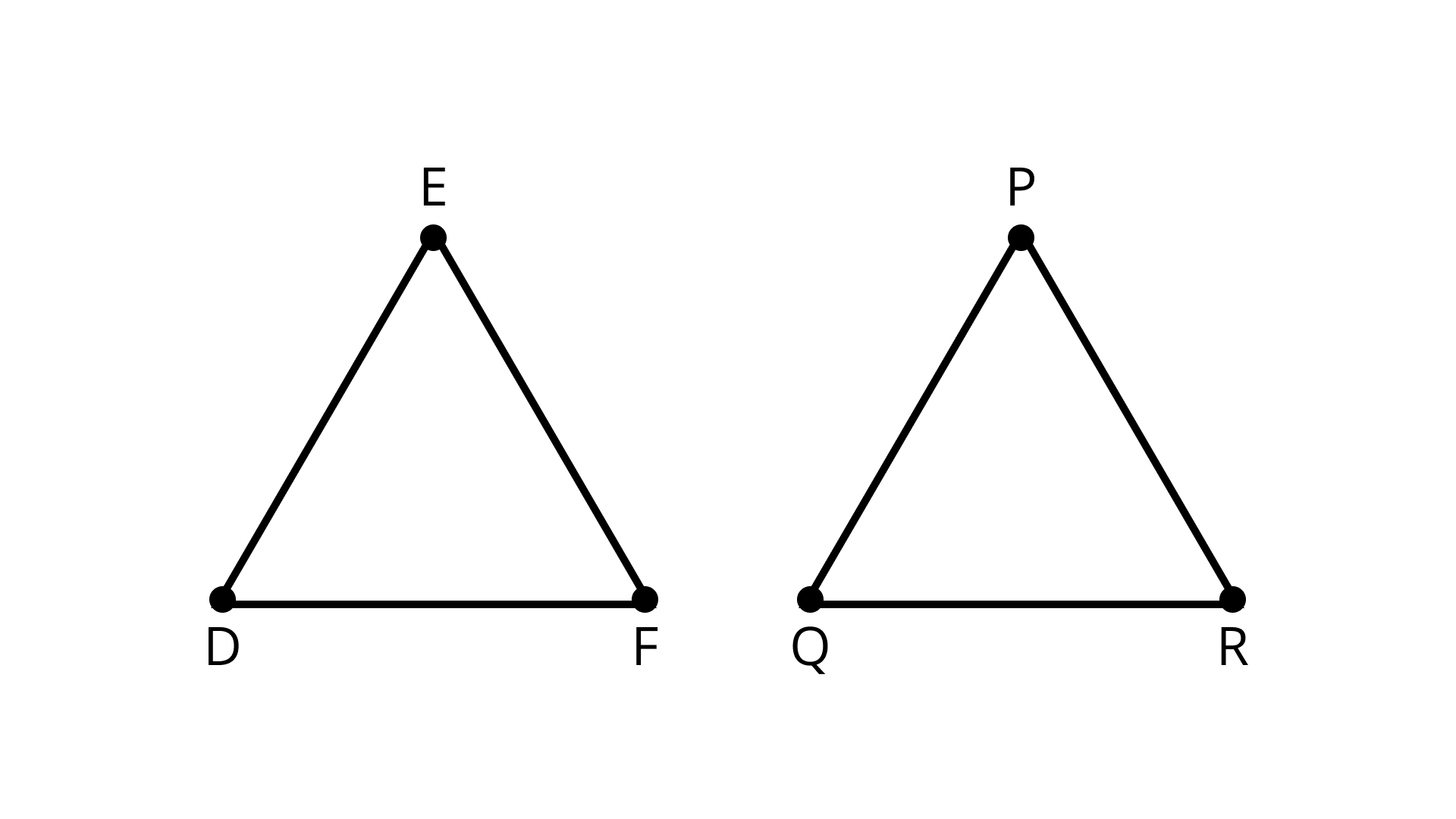
\[{\text{For }}\Delta PQR \cong \Delta EDF\], we have

 \[{\text{PR}}{\text{ = }}{\text{EF}}\]           (Corresponding sides)

8. In \[{\Delta }PQR\], \[\angle P = 70^\circ\] and \[\angle R = 30^\circ \]. Which side of this triangle is the longest? Give Reason for your answer.

Ans: In \[{{\Delta PQR}}\], \[\angle P = 70^\circ ,\angle R= 30^\circ \]

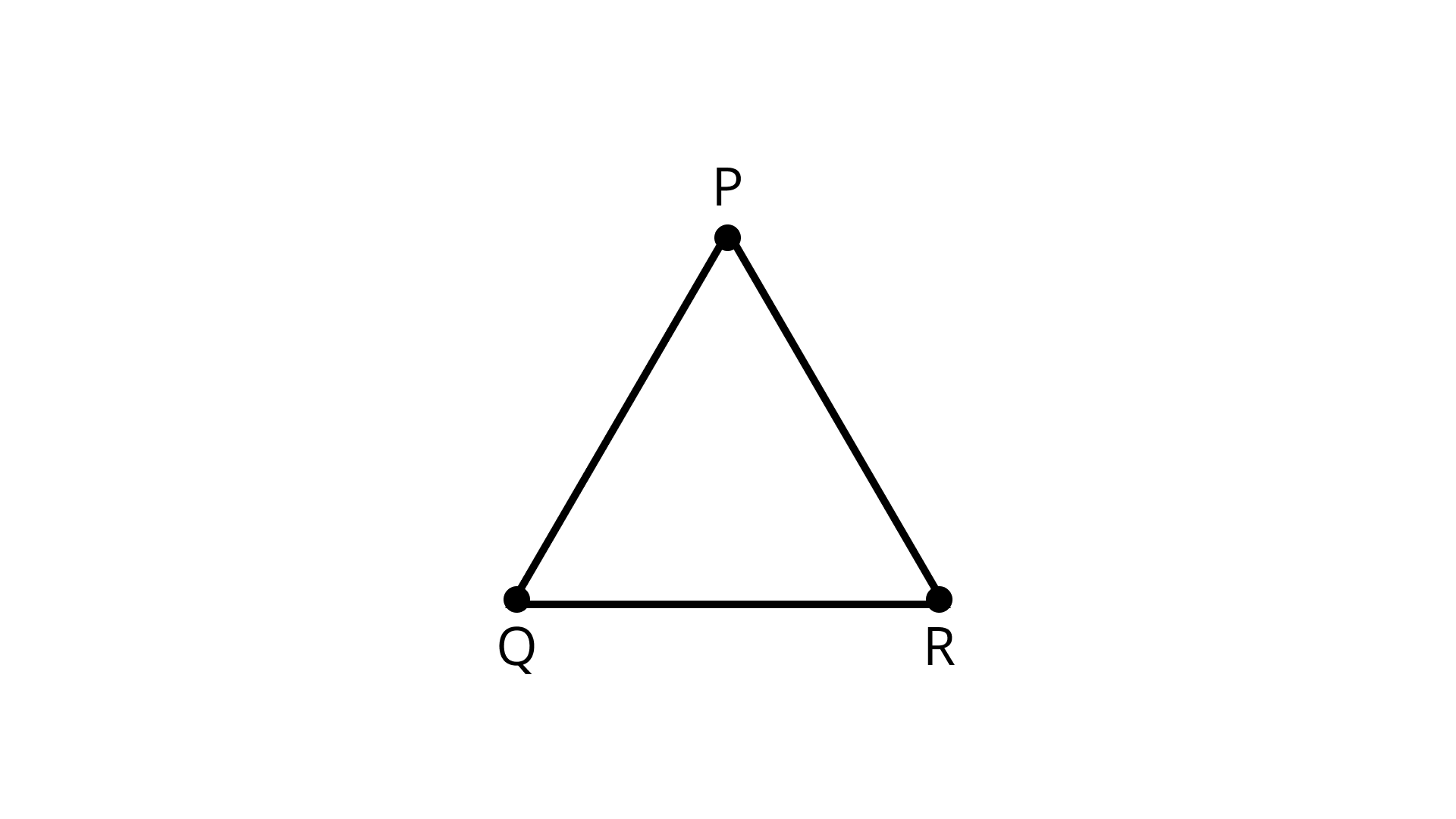
By Angle sum property of triangle, we have:

\[\angle P + \angle Q + \angle R = 180^\circ \]     (sum of angles in a triangle is \[180^\circ \])

\[100^\circ  + \angle Q = 180^\circ \]

\[\angle Q = 180^\circ  - 100^\circ  = 80^\circ \]

\[\angle Q = 80^\circ \] the greatest angle.   

Its opposite side \[{\text{PR}}\]

  We know that, the side opposite greatest angle is longest.

The side \[{\text{PR}}\] is the longest side.

9.\[{\text{}}AD\] is a median of the triangle\[{\text{ABC}}\]. Is it true that\[AB  +  BC  +  CA  >  2 AD\]? Give Reason for your answer.

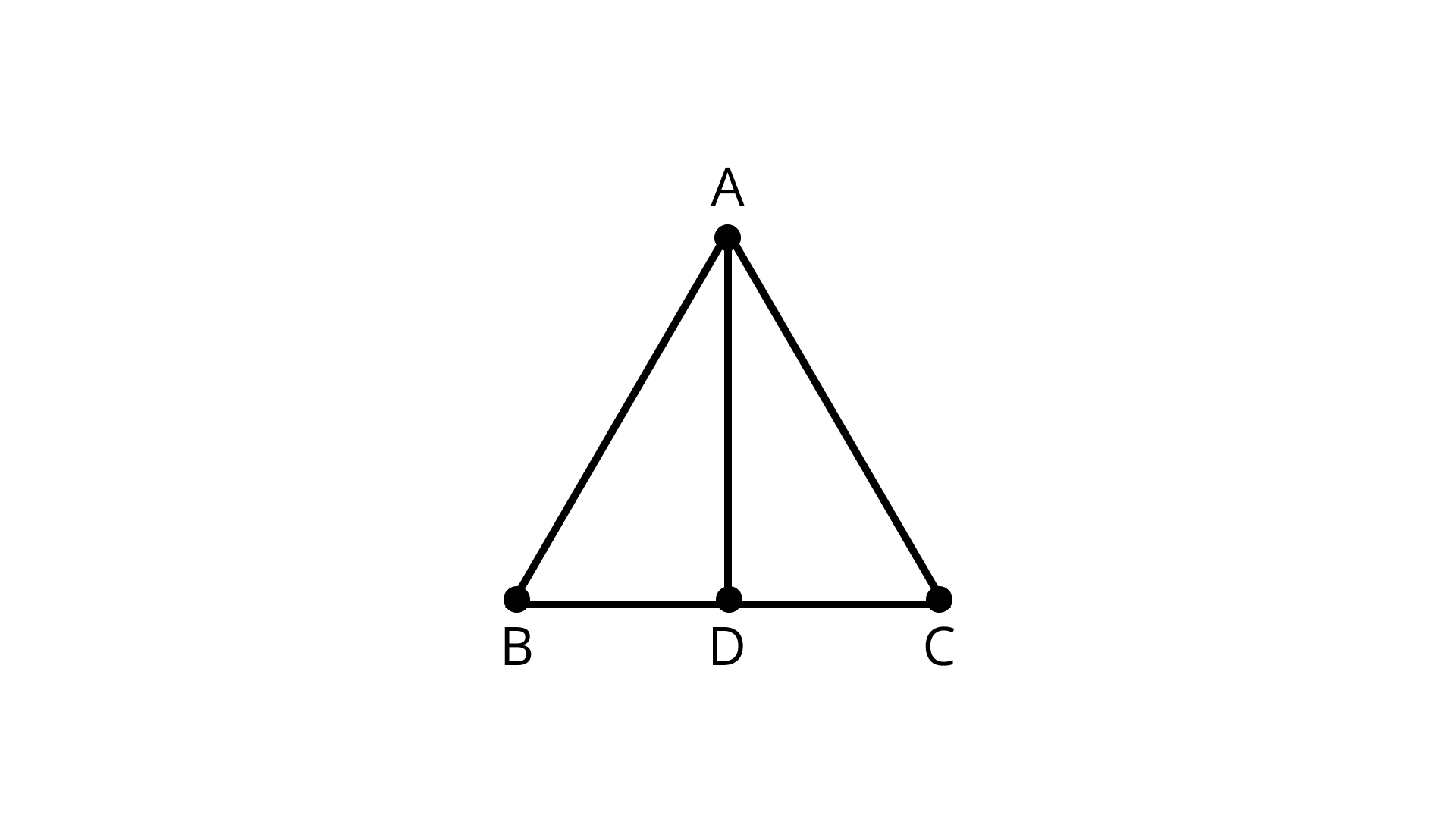
Ans: \[{\text{AD}}\] is a median of the triangle \[{\text{ABC}}\].

The median AD of a triangle \[{\text{ABC}}\]divides it into two triangles of equal areas \[{{\Delta ABD}}\] and \[{{\Delta ACD}}\].

 In \[{{\Delta ABD}}\],

\[{\text{AB}}{\text{ + }}{\text{BD}}{\text{ > }}{\text{AD}}\]                          (Sum of two sides of triangle is greater than the third side)

 In \[{{\Delta ACD}}\],

\[{\text{AC}}{\text{ + }}{\text{CD}}{\text{ > }}{\text{AD}}\]                                    (Sum of two sides of triangle is greater than the third side)

On adding above inequalities,

\[{\text{AB}}{\text{ + }}{\text{BD}}{\text{ + }}{\text{AC}}{\text{ + }}{\text{CD}}{\text{ > }}{\text{2AD}}\]

\[{\text{AB}}{\text{ + }}{\text{AC}}{\text{ + }}{\text{BC}}{\text{ > }}{\text{2AD}}\]

Hence, the statement “\[{\text{AB  +  BC  +  CA  >  2 AD}}\]” is true.

10. \[M\] is a point on side \[BC\] of a triangle \[ABC\] such that \[AM\] is the bisector of \[\angle BAC\]. Is it true to say that perimeter of the triangle is greater than \[2AM\]? Give reason for your answer.

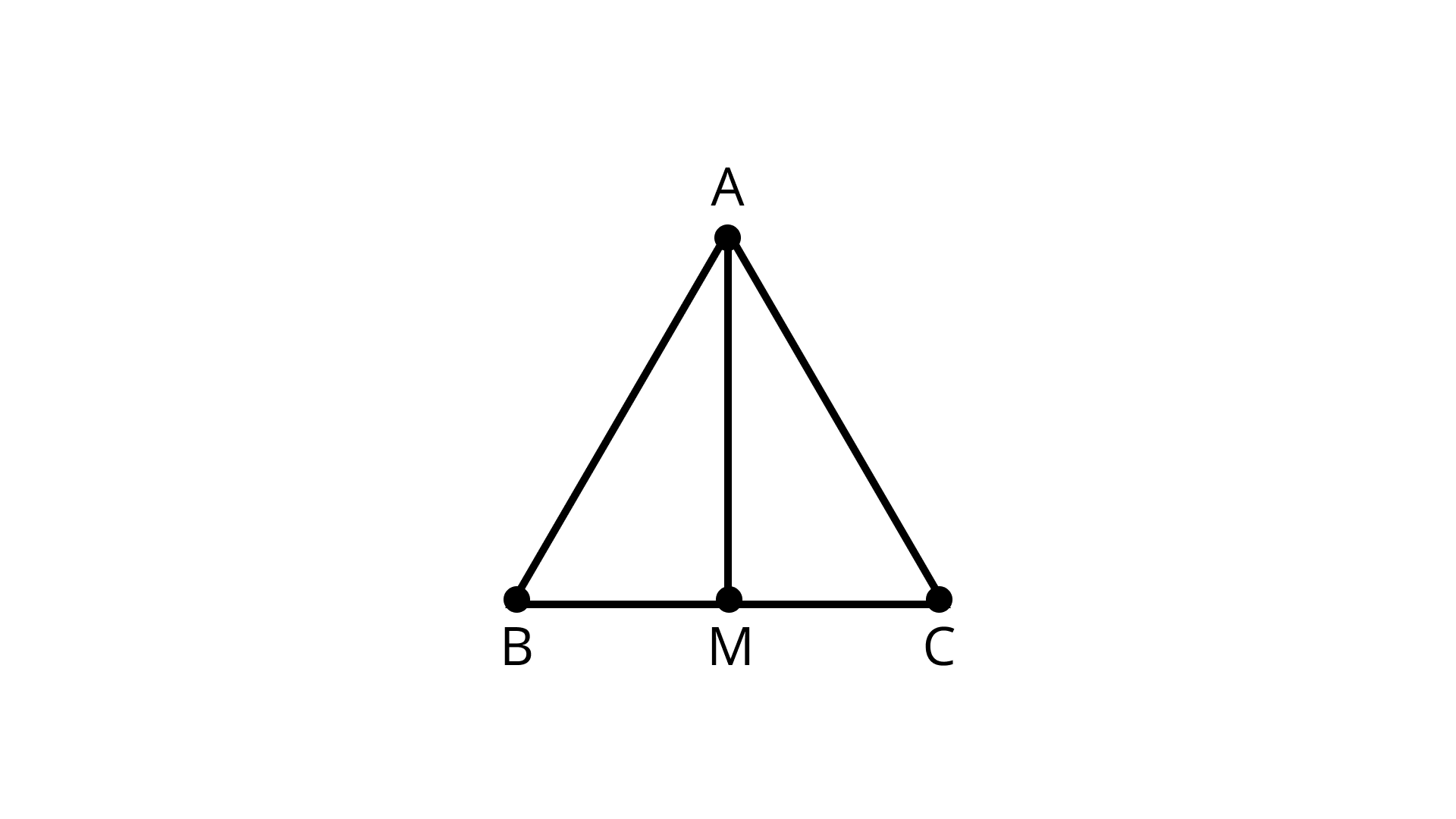
Ans: \[{\text{M}}\] is a point on side \[{\text{BC}}\] of a triangle \[{\text{ABC}}\] such that \[{\text{AM}}\] is the bisector of \[\angle BAC\]. The triangle \[{\text{ABC}}\]divides it into two triangles \[{{\Delta ABM}}\] and \[{{\Delta ACM}}\].

In \[{{\Delta ABM}}\]

The sum of the two sides of a triangle is always greater that the third side.

\[{\text{AB}}{\text{ + }}{\text{BM}}{\text{ > }}{\text{AM}}\]                             …... (1)

In \[{{\Delta ACM}}\],

The sum of the two sides of a triangle is always greater that the third side.

\[{\text{AC}}{\text{ + }}{\text{CM}}{\text{ > }}{\text{AM}}\] ......(2)

Now, adding equation (1) and (2),

\[{\text{AB}}{\text{ + }}{\text{BM}}{\text{ + }}{\text{AC}}{\text{ + }}{\text{CM}}{\text{ > }}{\text{AM}}{\text{ + }}{\text{AM}}\]

\[{\text{AB}}{\text{ + }}{\text{AC}}{\text{ + }}{\text{BC}}{\text{ > }}{\text{2AM}}\]

Hence, the perimeter of \[{{\Delta ABC}}\] is greater than\[{\text{2AM}}\].

11. Is it possible to construct a triangle with lengths of its sides as \[9{\text{ cm}},7{\text{ cm and }}17{\text{ cm}}\]? Give reason for your answer.

Ans: Given sides, \[9{\text{ cm}},7{\text{ cm and }}17{\text{ cm}}\]

To construct the triangle of given sides, we need to check property of triangle “The sum of any two sides of a triangle is always greater than the third side" is satisfied by the lengths of all the three sides.

Here, \[{\text{9}}{\text{ + }}{\text{7}}{\text{ = }}{\text{16}}{\text{ < }}{\text{17}}\]

The sum of two sides is less than the third side. Hence, it is not possible to construct a triangle with lengths of its sides as \[9{\text{ cm}},7{\text{ cm and }}17{\text{ cm}}\].

12. Is it possible to construct a triangle with lengths of its sides as \[{\text{8 cm}},7{\text{ cm and 4 cm}}\]? Give reason for your answer.

Ans: Given sides, \[{\text{8 cm}},7{\text{ cm and 4 cm}}\]

To construct the triangle of given sides, we need to check property of triangle “The sum of any two sides of a triangle is always greater than the third side" is satisfied by the lengths of all the three sides.

Here, 

\[8 + 7 = 15 > 4\]

\[8 + 4 = 12 > 7\]

\[7 + 4 = 11 > 8\]

The sum of two sides is less than the third side. 

Hence, it is possible to construct a triangle with lengths of its sides as \[{\text{8 cm}},7{\text{ cm and 4 cm}}\]

Sample Question 1: In Fig\[,PQ = PR\] and \[\angle Q = \angle R.\]

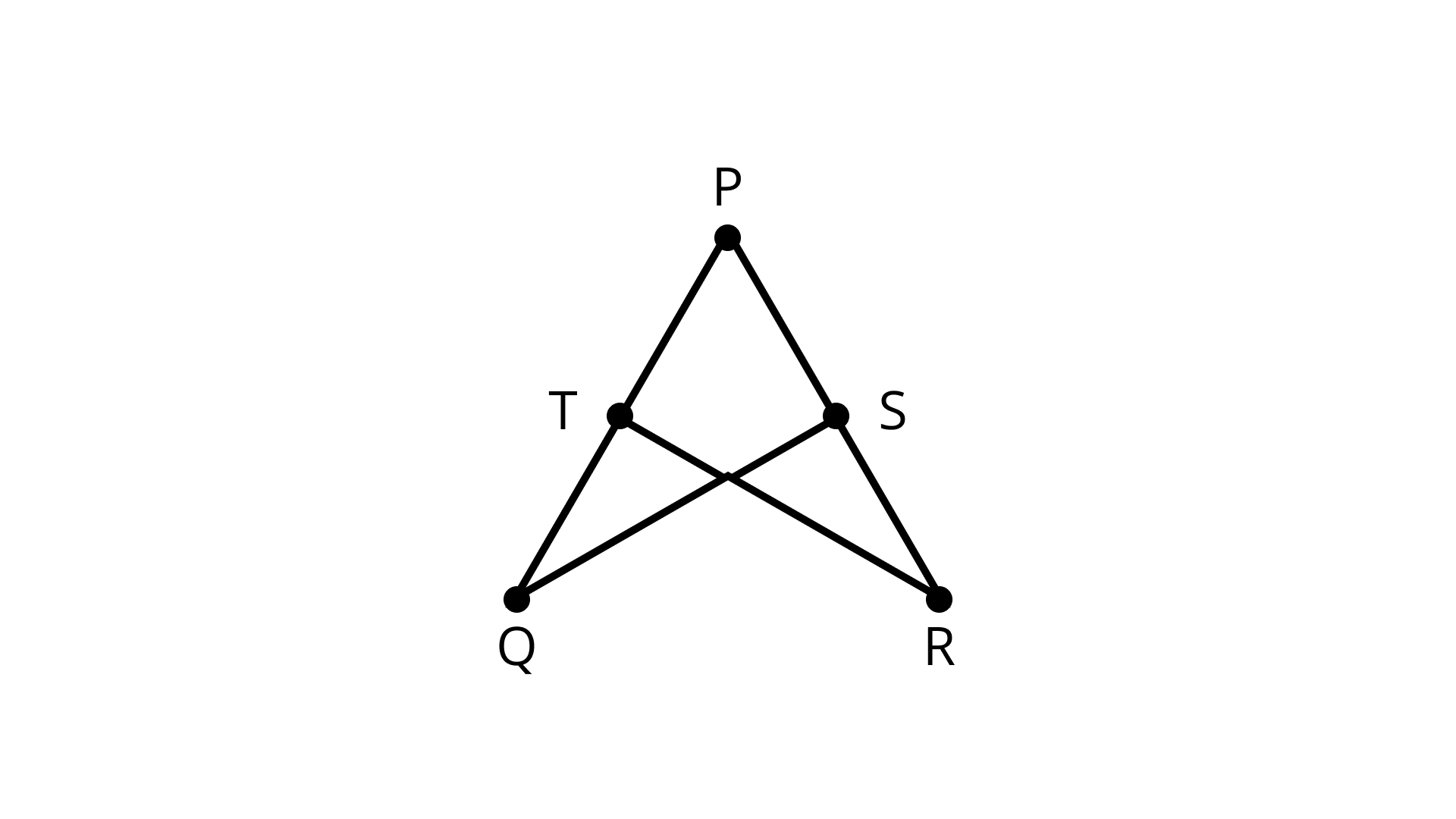
Prove that \[\Delta PQS \cong \Delta PRT\]

Ans: In \[{\Delta PQS} and {\Delta PRT}\],

  ${{\text{PQ}}{\text{ =  PR }}\left( {{\text{Given}}} \right)}$

  ${\angle Q = \angle R{\text{ }}\left( {{\text{Given}}} \right)}$ 

and  \[\angle QPS{\text{ }} = \angle RPT\] (same angle) 

Therefore\[,{\text{ }}\Delta PQS \cong \Delta PRT\] (ASA criterion of congruence.)

Sample Question 2: In Fig., two lines \[{\text{AB}}\] and \[{\text{CD}}\] intersect each other at the point ${\text{O}}$ such that ${\text{BC}}{\text{|}}{\text{|}}{\text{AD}}$ and \[{\text{BC  =  DA}}\]. Show that ${\text{O}}$ is the midpoint of both the line-segments \[{\text{AB}}\] and \[{\text{CD}}\].

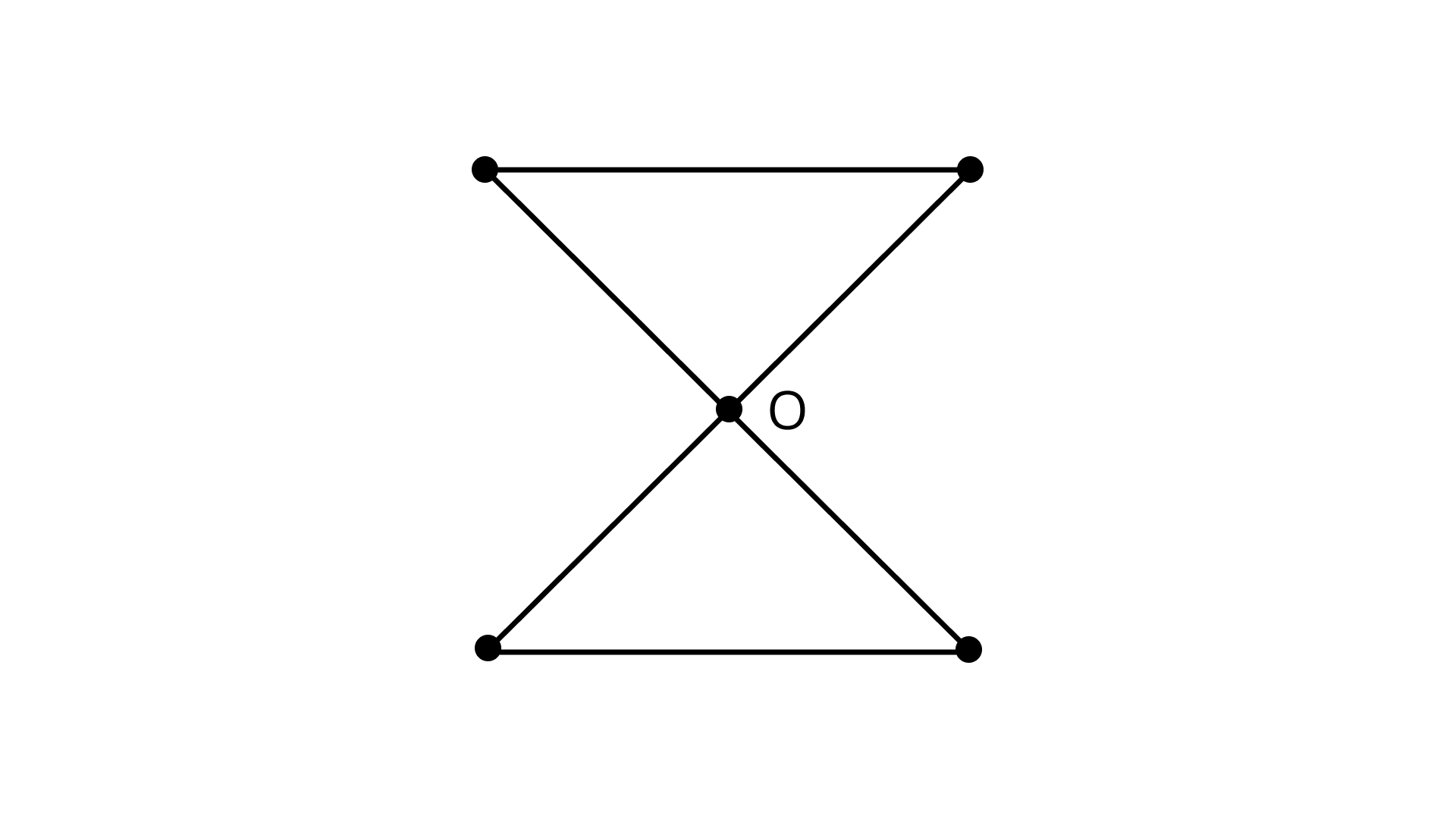
Ans: The two lines \[{\text{AB}}\]and \[{\text{CD}}\]intersect each other at the point ${\text{O}}$ such that ${\text{BC}}{\text{|}}{\text{|}}{\text{AD}}$ 

\[{\text{BC||AD}}\]     (Given) 

We know that:

If a transversal intersects two parallel lines, then alternate interior angles are equal and conversely.

Therefore, \[\angle CBO = \angle DAO\] (Alternate interior angles)

and \[\angle BCO{\text{ }} = \angle ADO\] (Alternate interior angles)

Also, \[{\text{BC  =  DA}}\]           (Given)

 So, \[\Delta BOC \cong \Delta AOD\] (ASA)

 Therefore, \[{\text{OB}}{\text{ = }}{\text{OA}}\] and \[{\text{OC}}{\text{ = }}{\text{OD}}\], i.e., \[{\text{O}}\] is the mid-point of both \[{\text{AB and CD}}\].

Sample Question 3: In Fig, \[PQ  >  PR\] and QS and RS are the bisectors of \[\angle Q\]  and \[\angle R,\] respectively. Show that \[SQ  >  SR.\]

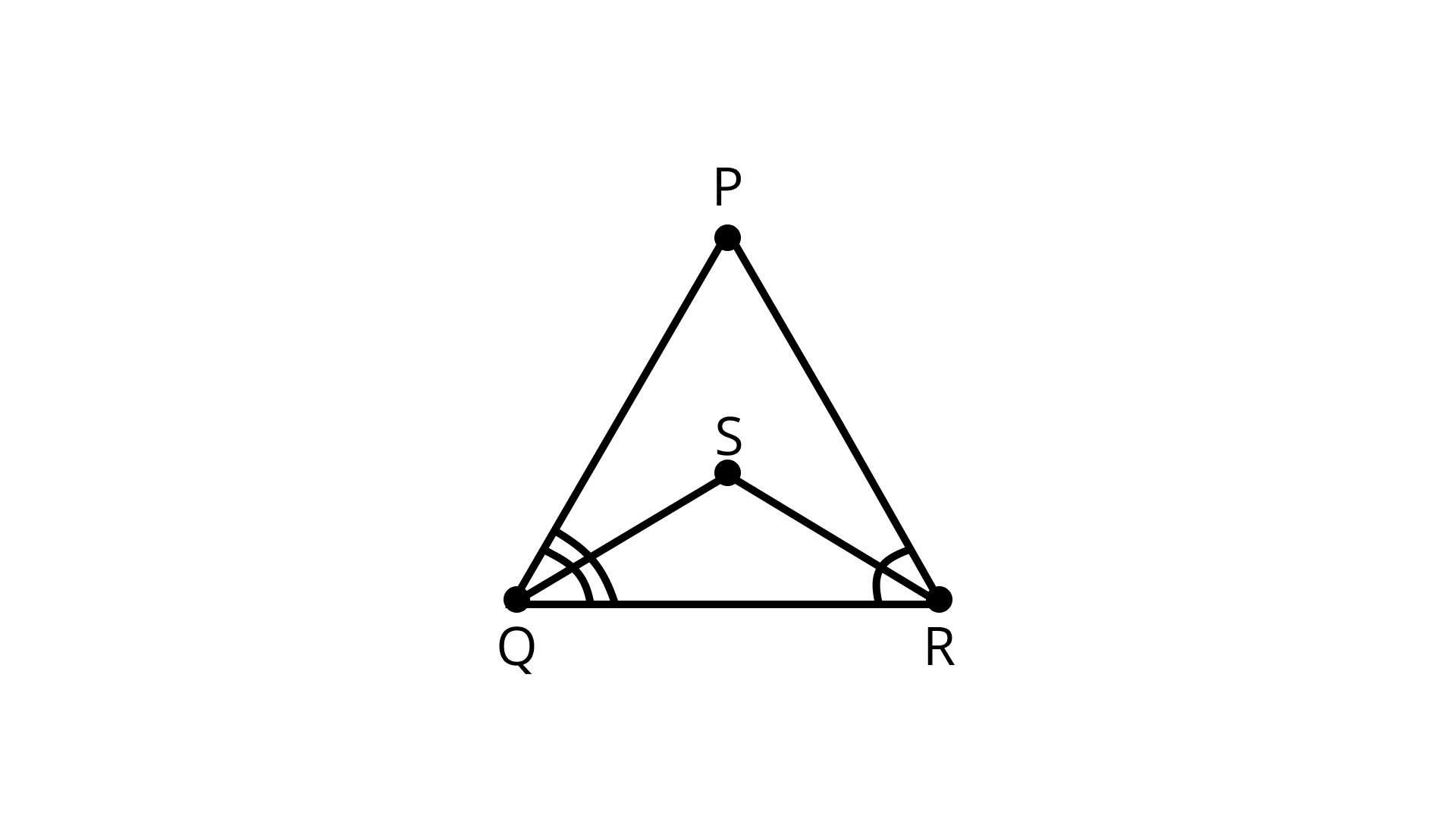
Ans: \[{\text{PQ  >  PR}}\]            (Given) 

Therefore\[,\angle R{\text{ }} > \angle Q\]           (Angles opposite to the longer side is greater) 

\[\dfrac{1}{2}\angle R{\text{ }} > \dfrac{1}{2}\angle Q\]           (multiply$\dfrac{1}{2}$ on both sides)

\[\angle SRQ{\text{ }} > \angle SQR\]      \[\left( {{\text{as SQ and SR are the angle bisectors}}} \right)\]

Therefore\[,{\text{ }}SQ{\text{ }} > {\text{ }}SR\]            (Side opposite the greater angle will be longer)

EXERCISE 7.3

1. ABC is an isosceles triangle with AB  =  AC and BD and CE are its two medians. Show that \[BD  =  CE\]

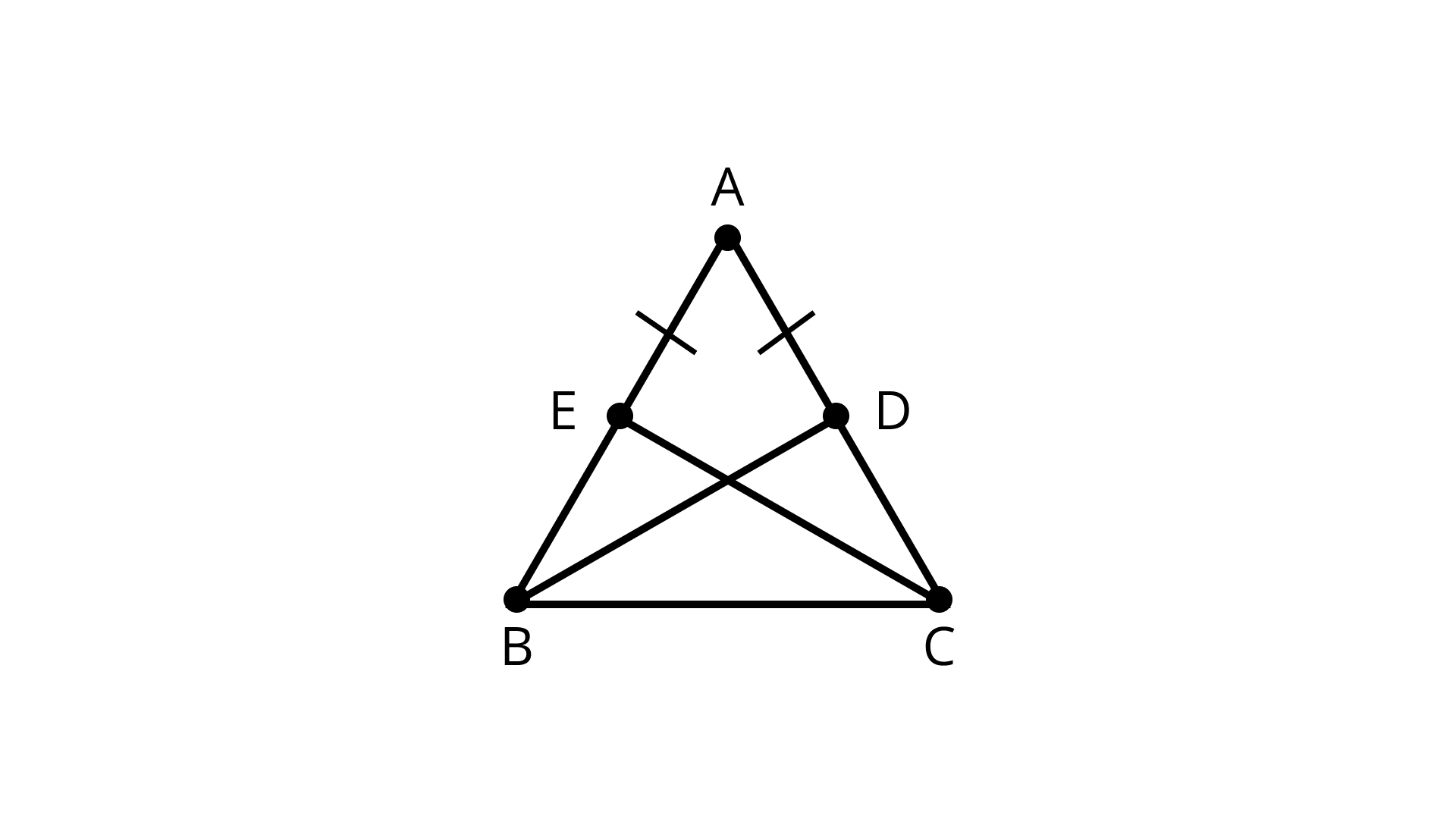
Ans: Given:

\[{\text{AB  =  AC}}\]

Also, \[{\text{BD and CE}}\] are two medians.

Hence, ${\text{E}}$ is the midpoint of \[{\text{AB}}\] and ${\text{D}}$ is the midpoint of \[{\text{CE}}\]

\[\dfrac{1}{2}AB{\text{ }} = {\text{ }}\dfrac{1}{2}AC\]

\[{\text{BE  =  CD}}\]

  In \[{\Delta BEC}\] and \[{{\Delta CDB}}\],

\[{\text{BE  =  CD}}\]                   (Given)

\[\angle EBC = \angle DCB\]                               (Angles opposite to equal sides \[{\text{AB}}\]and\[{\text{AC}}\])

\[{\text{BC  =  CB}}\]                                     ( Common )

By SAS axiom, we have:

 \[\Delta BEC \cong \Delta CDB\]                               

 \[{\text{BD  =  CE}}\]                                         (by cpct)

2. In Fig.7.4, D and E are points on side \[BC\] of a \[{\Delta }ABC\] such that BD  =  CE and AD  =  AE. Show that \[\Delta ABD \cong \Delta  ACE\].

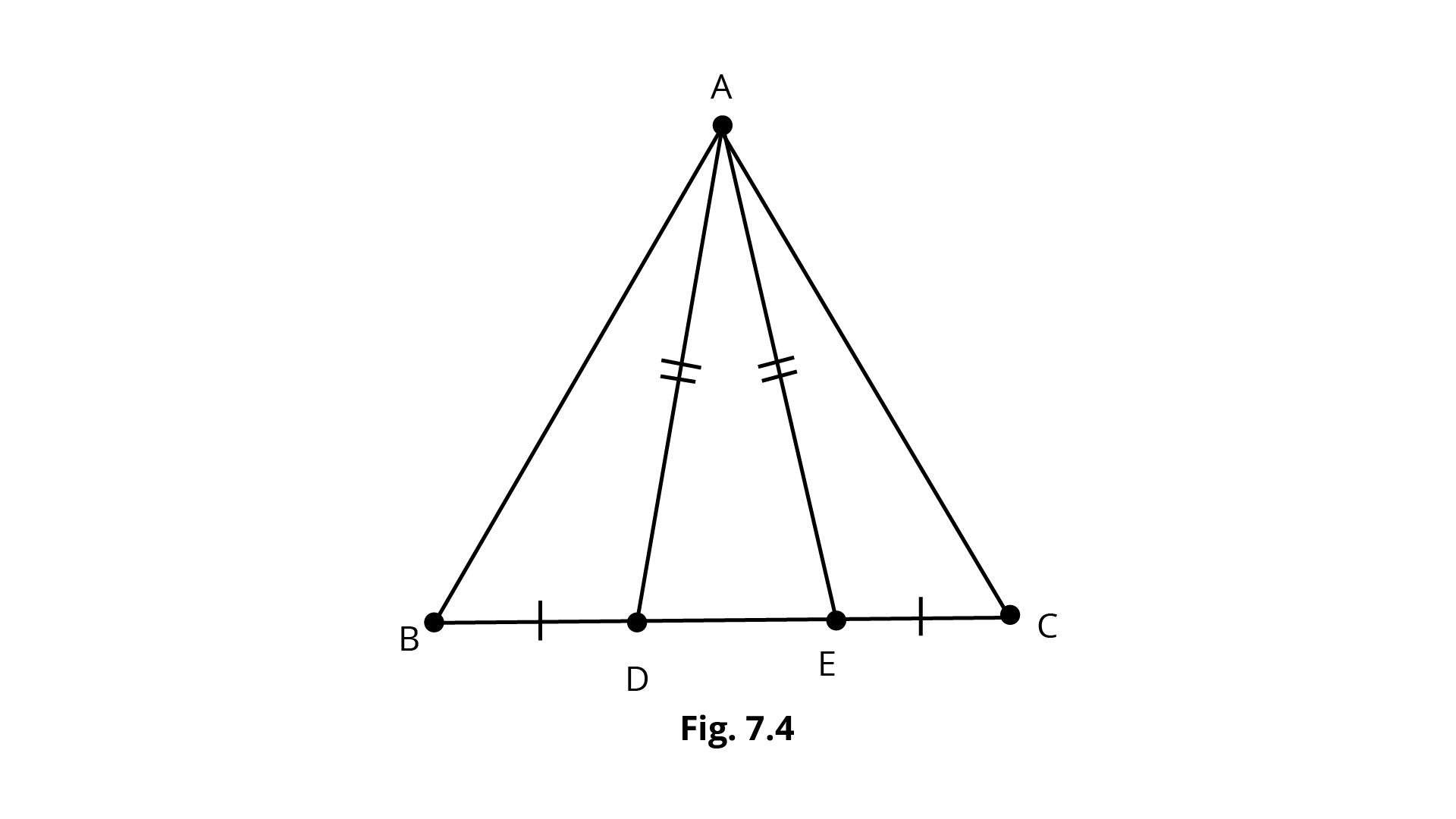
Ans: According to the question,

In\[{{\Delta ABC}}\],

\[{\text{BD  =  CE}}{\text{and AD  =  AE}}\].

In\[{{\Delta ADE}}\],

\[{\text{AD  =  AE}}\]

Since opposite angles to equal sides are equal,

We have,

\[\angle ADE = \angle AED...{\text{ }}\left( 1 \right)\]

Now, \[\angle ADE + \angle ADB = 180^\circ \](linear pair)

\[\angle ADB = 180^\circ  - \angle ADE\]\[...{\text{ }}\left( 2 \right)\]

Also, \[\angle AED + \angle AEC = 180^\circ \](linear pair)

\[\angle AEC = {\text{1}}80^\circ  - \angle AED\]

\[{\text{Since}},\angle ADE = \angle AED\]

\[\angle AEC = 180^\circ {\text{ }} - \angle ADE...{\text{ }}\left( 3 \right)\]

From equation (2) and (3)

\[\angle ADB{\text{ }} = {\text{ }}\angle AEC...{\text{ }}\left( 4 \right)\]

Now, In  \[{{\Delta ADB}}\] and \[{{\Delta AEC}}\],

\[{\text{AD  =  AE}}\]      (given)

\[{\text{BD  =  EC}}\]       (given)

\[\angle ADB = \angle AEC\]( from (4))

Hence, \[\Delta ABD \cong \Delta ACE\](by SAS)

3. \[CDE\] is an equilateral triangle formed on a side \[CD\] of a square \[ABCD\] (Fig.7.5). Show that \[\Delta ADE \cong \Delta BCE\].

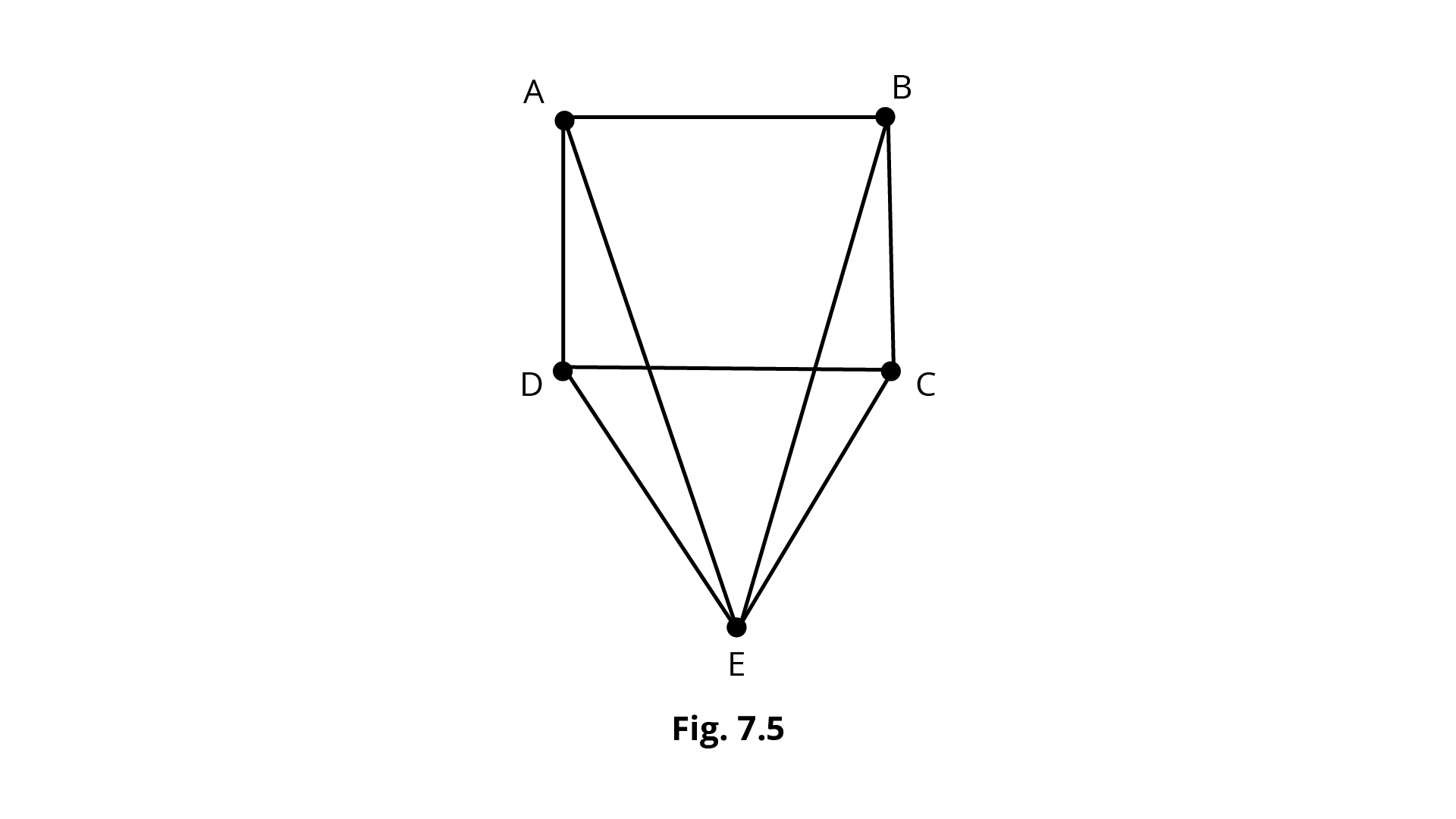
Ans: Given \[{\text{ABCD}}\] is a square

So \[{\text{AB  =  BC  =  CD  =  AD}}\]

Now in \[{{\Delta EDC}}\] is an equilateral triangle.

So \[{\text{DE  =  EC  =  CB}}\]

In \[{{\Delta AED}}\] and \[{{\Delta CEB}}\]

\[{\text{AD  =  BC}}\]          (Side of triangle)

\[{\text{DE  =  CE}}\]           (Side of equilateral triangle)

\[\angle ADE = \angle ADC + \angle CDE\]

  ${ = {{90}^\circ } + {{60}^\circ }}$

  ${ = {{150}^\circ }}$ 

And,

\[\angle BCE = \angle BCD{\text{ }} + {\text{ }}\angle DCE\]

  ${ = {{90}^\circ } + {{60}^\circ }}$ 

  ${ = {{150}^\circ }}$ 

\[\Rightarrow \angle ACE = \angle BCDE\]

Hence from SAS criterion of congruence \[\Delta ADE \cong \Delta BCE\].

4. In Fig.7.6, \[BA \bot AC,{\text{ }}DE \bot DF\] such that BA  =  DE and BF  =  EC. Show that \[\Delta ABC \cong \Delta DEF.\]

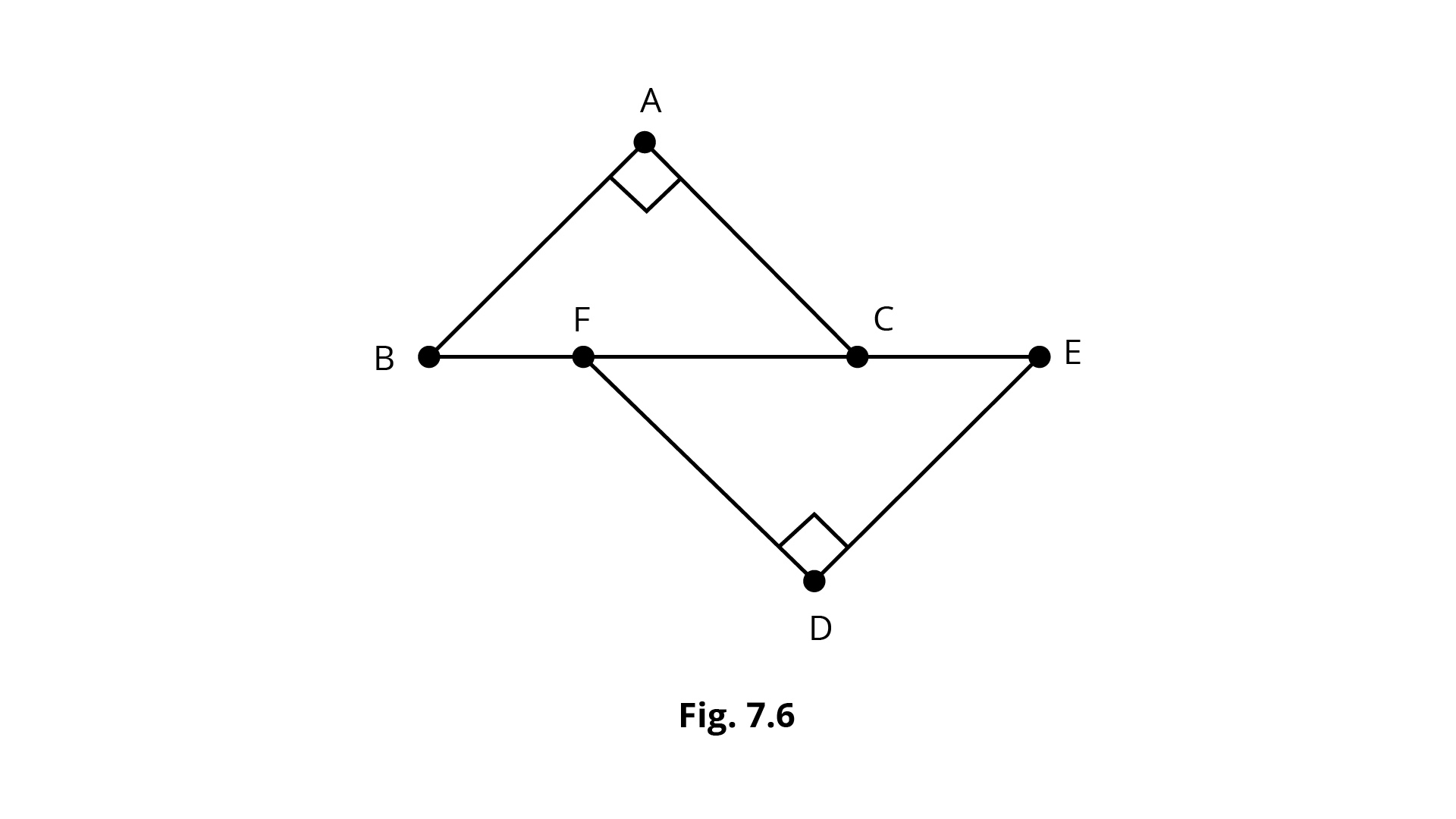
Ans: According to the question,

\[BA \bot AC,DE \bot DF\] such that \[{\text{BA  =  DE and }}{\text{BF  =  EC}}\].

In \[{{\Delta ABC}}\] and \[{{\Delta DEF}}\]

\[{\text{BA  =  DE}}\] (given)

\[{\text{BF  =  EC}}\] (given)

\[\angle A = \angle D\left( {{\text{both }}90^\circ } \right)\]

\[BC = BF + FC\]

\[EF = EC + FC = BF + FC\left( {\because EC{\text{ = }}BF} \right)\]

\[\Rightarrow EF = BC\]

By SSS axiom, we have:

\[\Delta ABC \cong \Delta DEF\]

5.\[Q\] is a point on the side \[SR\] of a \[{\Delta }PSR\] such that \[PQ  =  PR\]. Prove that \[PS  >  PQ\].

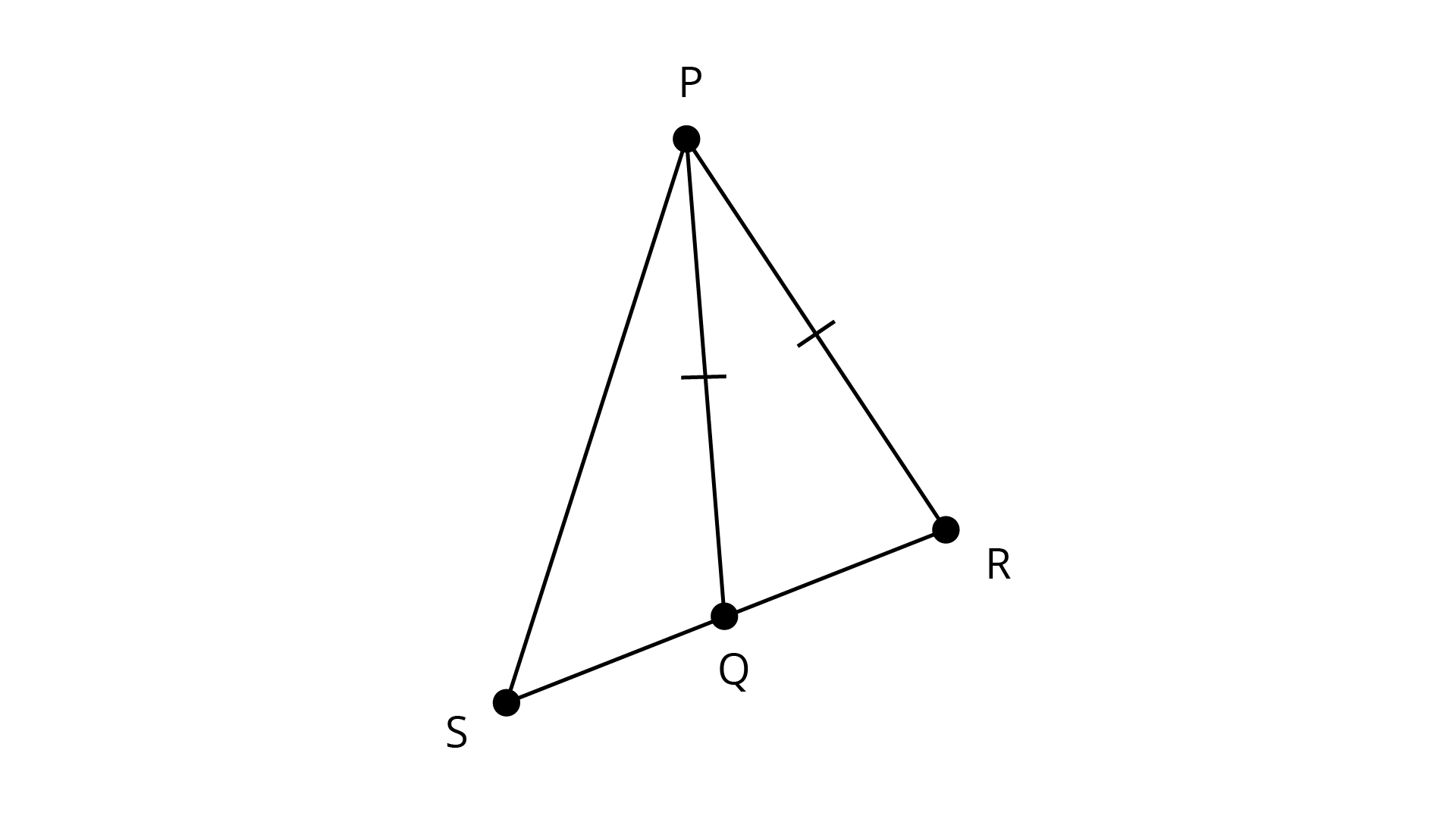
Ans: Given: ${\text{Q}}$ is a point on side \[{\text{SR in \Delta PSR}}\]such that \[{\text{PQ  =  PR}}\]

\[\Rightarrow PS > PR \ldots  \ldots \left( 1 \right)\]

In \[{{\Delta PQR}}\],

\[PQ = PR\]

\[\Rightarrow \angle PQR = \angle PRQ\] (angle opposite to equal sides are equal) 

 Now, from \[\left( 1 \right)\]

\[\angle PRQ > \angle PSQ{\text{ or }}\angle PRS > \angle PSR\]

Now, in \[{{\Delta PSR}}\],

\[\angle PRS > \angle PSR\]

\[\Rightarrow PS > PR\]                 (Side opposite greater angle is greater)

\[\Rightarrow PS > PQ\]

Hence, proved.

6. $S$ is any point on the side \[QR\] of a ${\Delta }PQR$. Show that: \[PQ  +  QR  +  RP > 2 PS\]

Ans: ${\text{S}}$ is any point on the side \[{\text{QR}}\]of a ${{\Delta PQR}}$.

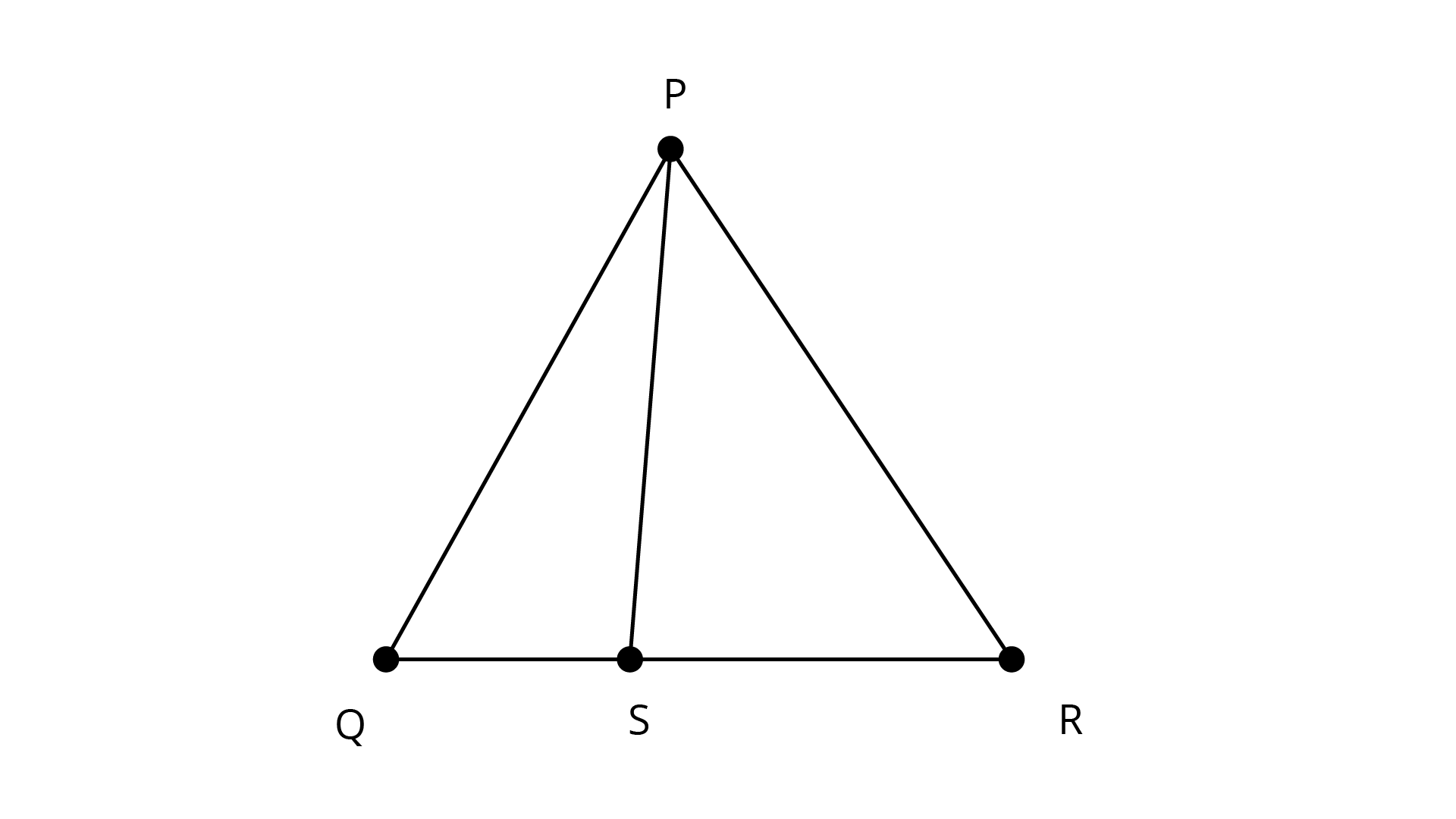
Join the points \[{\text{P}}\] and \[{\text{S}}\].

We know that:

The sum of the length of any two sides is greater than the third side.

In \[{{\Delta PQS}}\], \[PQ + QS > PS...........{\text{ }}\left( 1 \right)\]

In \[{{\Delta PSR}}\],\[PR + SR > PS...........{\text{ }}\left( 2 \right)\]

\[{\text{on adding equation }}\left( 1 \right){\text{ and }}\left( 2 \right)\],

\[PQ + QS + SR + PR > PS + PS\]

\[PQ + \left( {QS + SR} \right) + PR > 2PS\]

\[PQ + QR + PR > 2PS\]

7. D is any point on the side \[AC\] of a \[\Delta ABC\] with AB  =  AC. Show that \[CD  <  BD\].

Ans: D is any point on side \[{\text{AC}}\] of a \[{{\Delta ABC}}\] with AB  =  AC.

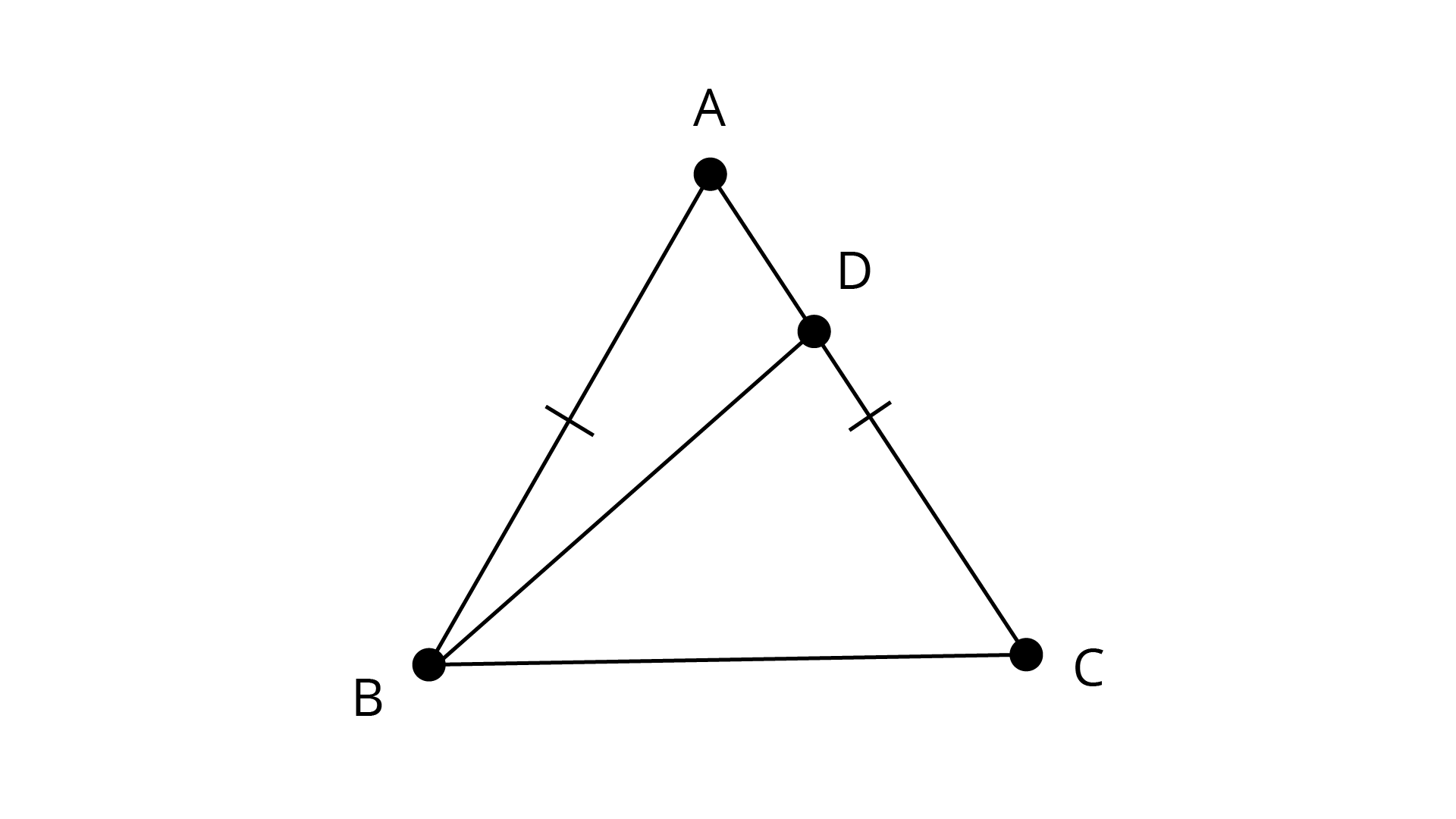
We know that:

Opposite angles to equal sides are equal.

\[\angle ABC{\text{ }} = \angle ACB{\text{ }}......{\text{ }}\left( 1 \right)\]

From the figure, we have: 

\[\angle ABC > \angle DBC\]

From equation \[(1)\], we have:

\[\angle ACB > \angle DBC\]

i.e.\[\angle DCB{\text{ }} > \angle DBC\]

It means that

\[BD > CD\]………………{Opposite side}

So we get

\[CD < BD\]

Therefore, it is proved that \[CD < BD\].

8. In Fig. 7.7, \[l||m\] and M is the midpoint of a line segment \[AB\]. Show that $M$ is also the mid-point of any line segment \[CD\], having its end points on $l$ and$m$, respectively.

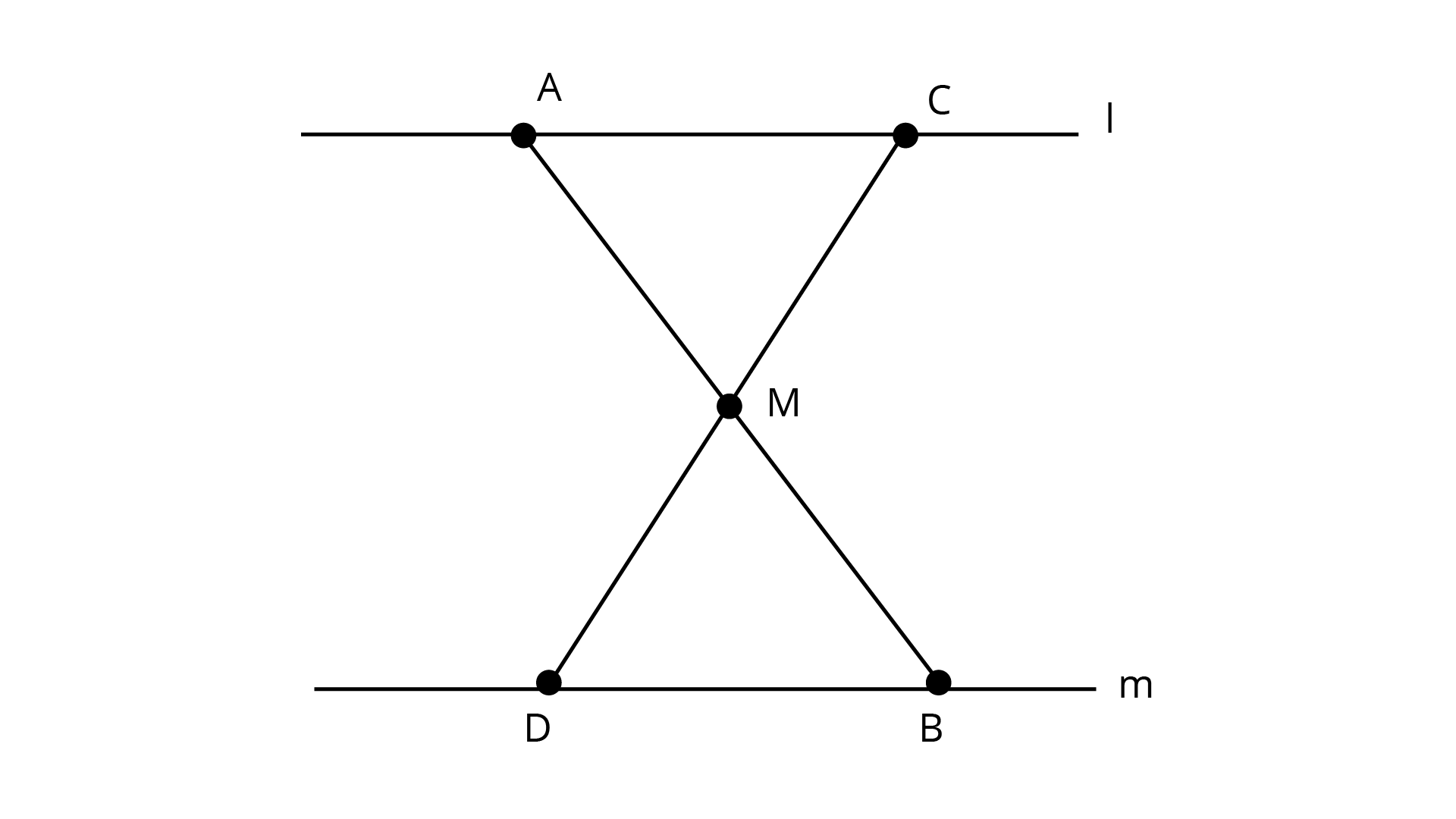
Ans: \[{\text{AM  =  MB}}\]                 (Given) 

\[\angle DMB = \angle AMC\]             (Vertically Opposite Angle)

\[\angle ACD = \angle CDB\]                (Alternating Angle)

Hence, According to ASA Congruence Criterion

\[\Delta AMC \cong \Delta DMB\]

Hence, \[{\text{DM  =  MC}}\]

So, Point ${\text{M}}$ is mid-point of ${\text{CD}}$.

9. Bisectors of the angles $B$ and $C$ of an isosceles triangle with \[AB  =  AC\] intersect each other at \[O\]. \[BO\] is produced to a point \[M\]. Prove that \[\angle MOC = \angle ABC\]

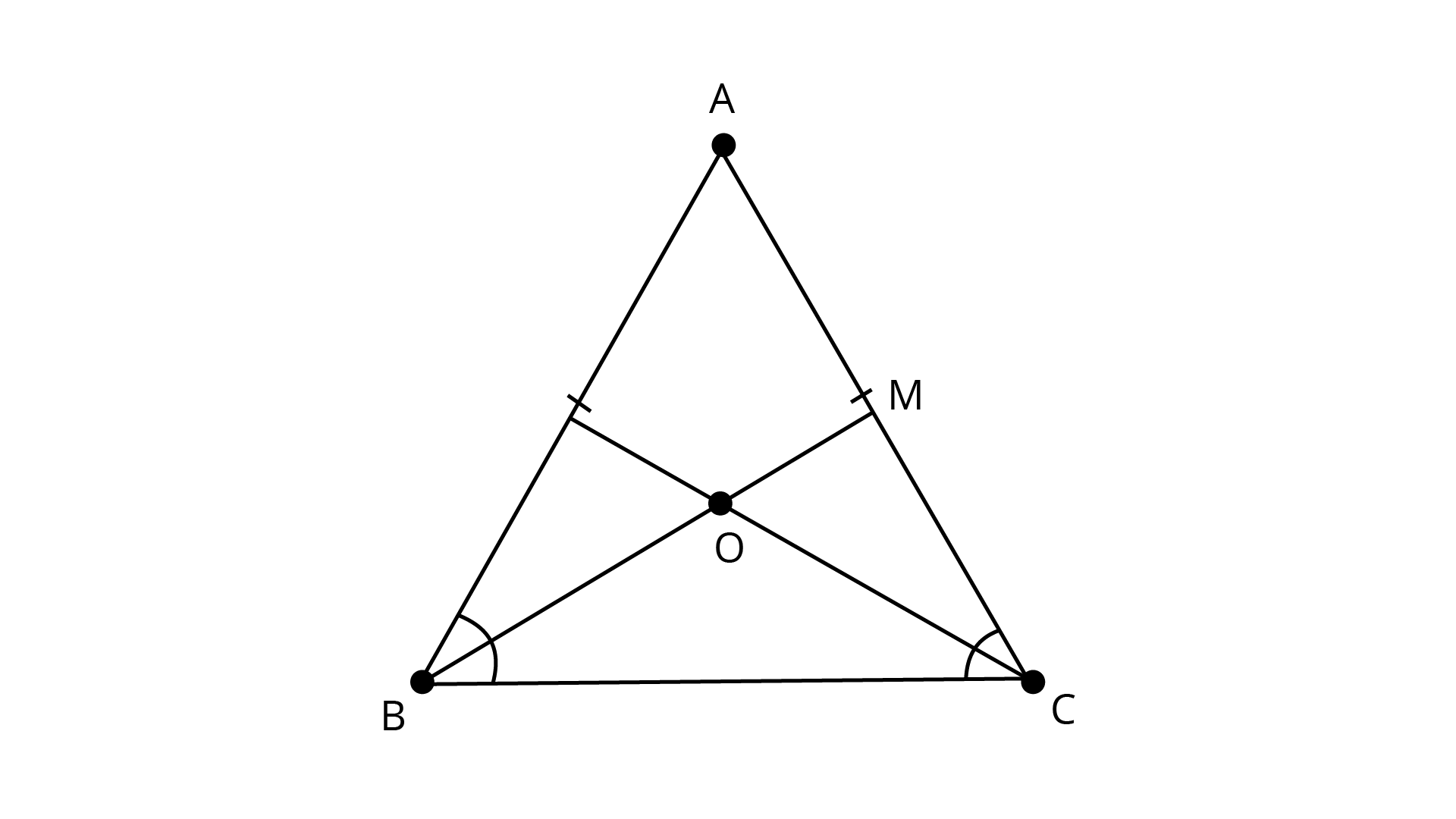
Ans: Given,

Lines \[{\text{OB}}\] and \[{\text{OC}}\] are the bisectors of \[\angle B{\text{ and }}\angle C\] of an isosceles \[{{\Delta ABC}}\] such that \[{\text{AB  =  AC}}\] which intersect each other at \[{\text{O}}\]and ${\text{BO}}$ is produced to ${\text{M}}$.

In \[{{\Delta ABC}}\],

\[{\text{AB  =  AC}}\](given)

\[\angle ACB = \angle ABC\]……. The Opposite angles to equal sides are equal.

\[\dfrac{1}{2}\angle ACB = \dfrac{1}{2}\angle ABC\]           (Dividing both sides by 2)

Now, OB and OC are the bisector of \[\angle B\] and \[\angle C\]

We know that:

The bisector divides a given angle into two angles with equal measures.

\[\angle OCB = \angle OBC \ldots  \ldots {\text{ }}\left( 1 \right)\]

Now, from equation (1), we have

\[\Rightarrow \angle MOC = \angle OBC + \angle OBC\]

\[\Rightarrow \angle MOC = \angle OBC\]

\[\Rightarrow \angle MOC = 2\angle ABC\]

(Since, \[{\text{OB}}\] is the bisector of \[\angle B\])

10. Bisectors of the angles \[B\] and \[C\] of an isosceles triangle\[{\text{}}ABC\] with \[AB  =  AC\] intersect each other at $O$. Show that the external angle adjacent to \[\angle ABC\] is equal to \[\angle BOC\].

Ans: Bisectors of the angles \[{\text{B}}\] and \[{\text{C}}\] of an isosceles triangle\[{\text{ABC}}\] with \[{\text{AB  =  AC}}\] intersect each other at ${\text{O}}$

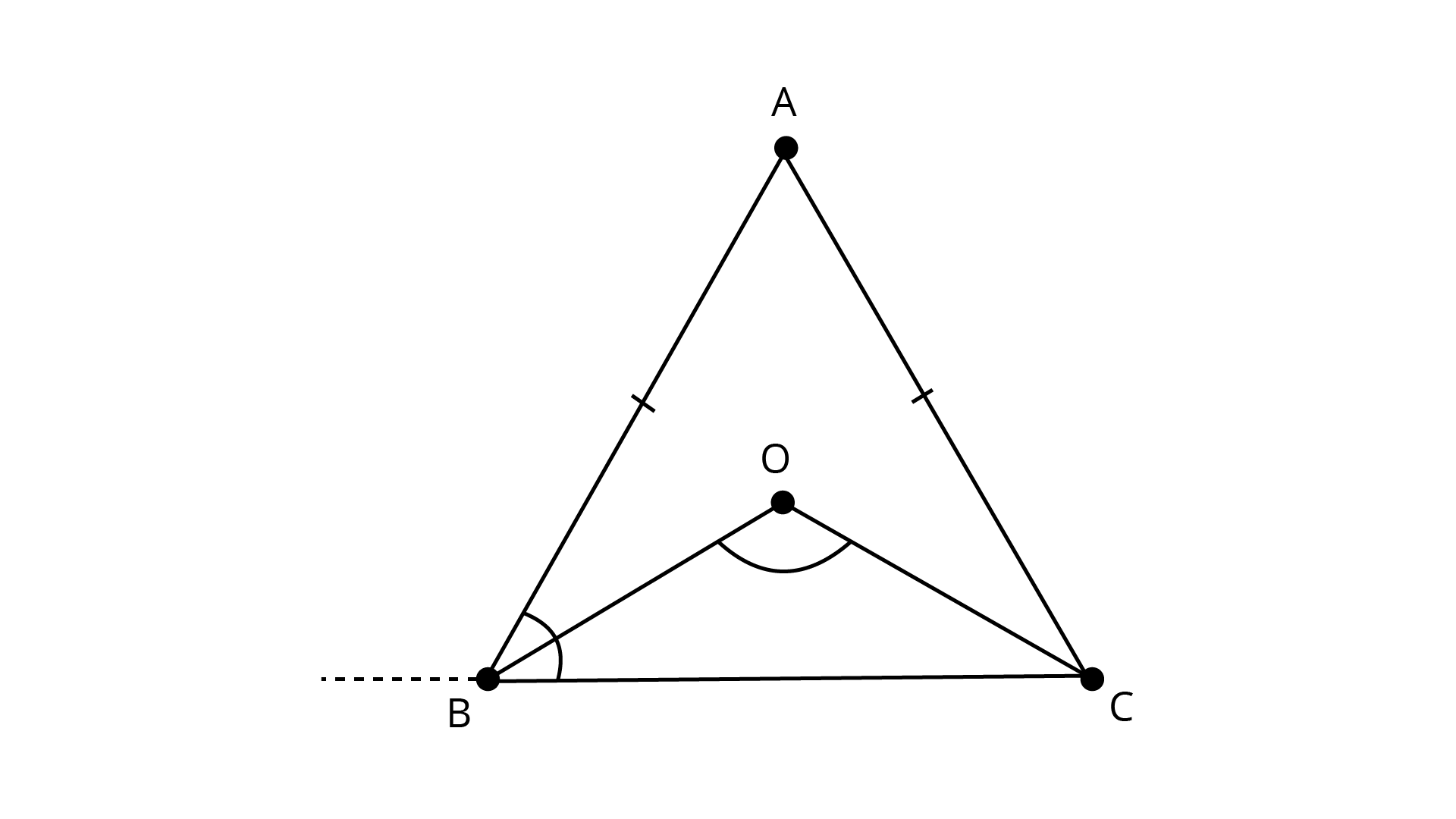
In \[{{\Delta ABC}}\]

\[{\text{AB  =  AC}}\]

\[\angle ACB = \angle ABC\]

\[\dfrac{1}{2}\angle ACB = \dfrac{1}{2}\angle ABC\]

\[\angle OCB = \angle OBC\]               …. (1)

Since, BO and CO are the bisectors of $\angle ABC{\text{ and }}\angle {\text{ACB}}$.

In \[{{\Delta BOC}}\],

\[\angle OBC + \angle OCB + \angle BDC = 180^\circ \]    (Sum of angles in a triangle is ${180^\circ }$)

\[2\angle OBC + \angle BOC = 180^\circ \]               from equation (1)

\[\angle ABC + \angle BOC = 180^\circ \]                 ($\because BO$ is the bisectors of $\angle ABC$)

\[{180^\circ } - \angle DBA + \angle BOC = 180^\circ \]       ($\because DBC$ is a straight line)

   $- \angle DBA + \angle BOC = 0$

  $\angle BOC = \angle DBA$ 

11. In Fig, AD is the bisector of \[\angle BAC\]. Prove that \[AB > BD\]

Ans: In  \[{{\Delta ABC}}\]

Let \[\angle 1 = \angle BAD,\angle 2 = \angle DAC,\angle 3 = BDA\]

AD is the bisector of \[\angle BAC\]

\[\angle 1 = \angle 2\]…(i)

Also in \[{{\Delta ADC}}\]

\[\angle 3 = \angle 2 + \angle C\]            (ext. angle is equal to sum of opposite interior angles)

\[\angle 3 > \angle 2\]            (ext. angle is greater than one of the interior angles)

But \[\angle 1 = \angle 2\]

\[\angle 3 > \angle 1\]             (Sides opposite greater angle is greater)

\[AB > BD\]

Hence proved.

Sample Question 1: In Fig. 7.9, ABC is a right triangle and right angled at B such that \[\angle BCA = 2\angle BAC\]. Show that hypotenuse \[AC  =  2 BC\].

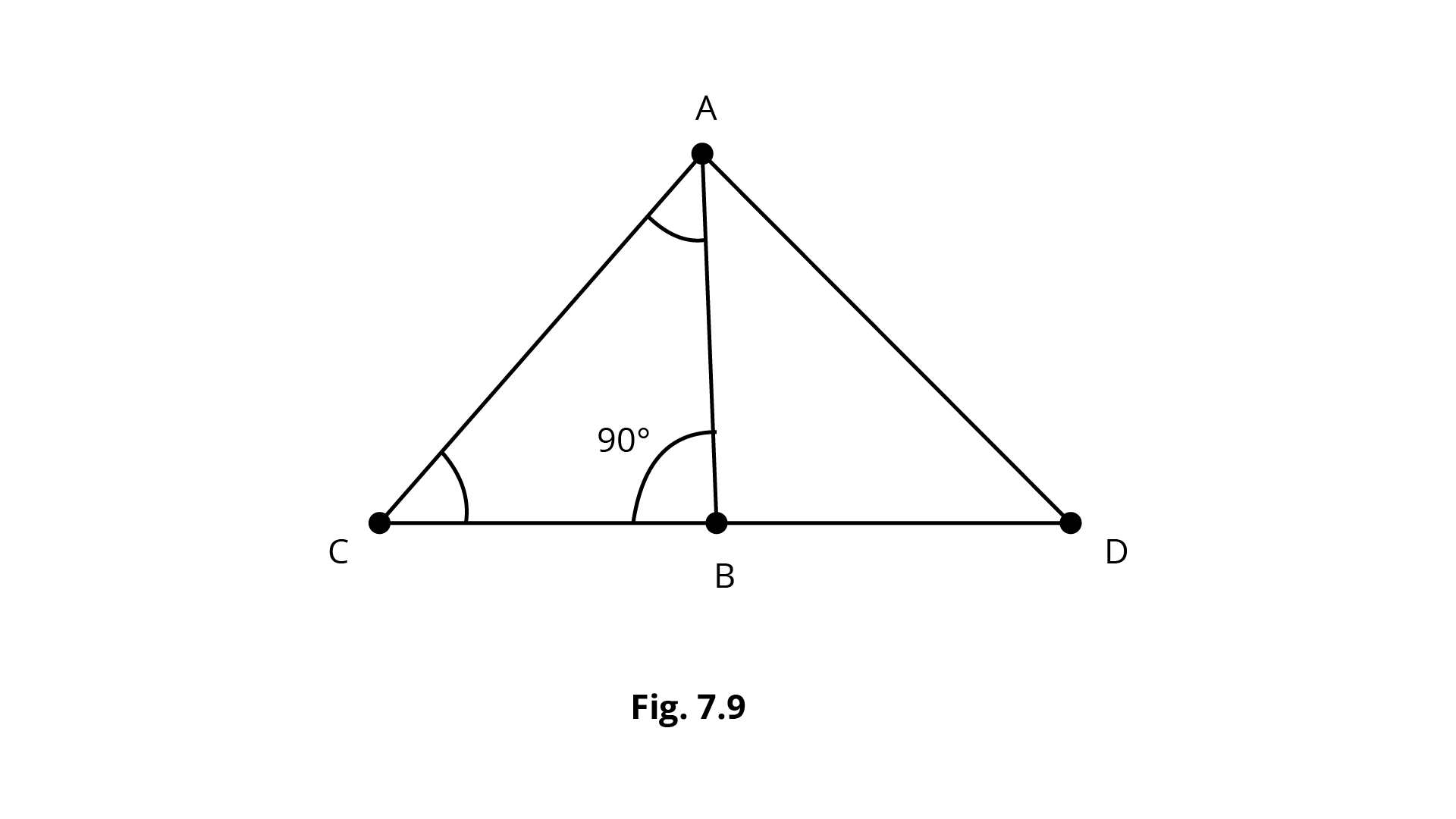
Ans:  Produce \[{\text{CB}}\] to a point \[{\text{D}}\] such that \[{\text{BC  =  BD}}\]  and join \[{\text{AD}}\].

 In \[{{\Delta ABC}}\] and \[{{\Delta ABD}}\], we have \[{\text{BC  =  BD}}\]  (By construction)

 \[{\text{AB}}\] is common in both triangles

\[\angle ABC = \angle ABD\] (Each of 90°)

 Therefore\[,\Delta {\text{ }}ABC \cong \Delta ABD\] (SAS)

 So, \[\angle CAB = \angle DAB\]                                     ..….(1) 

Let \[x = \angle CAB = \angle DAB\]

and  \[{\text{AC  =  AD}}\]                                             ……(2)

 Thus, 

  $\angle CAD = \angle CAB + \angle BAD$

  $\Rightarrow x + x = 2x$                  {From (1)}    …..(3)

 and \[\angle ACD = \angle ADB = x\]         {From (2), \[{\text{AC  =  AD}}\]}    …..(4)

 That is, \[{{\Delta ACD}}\] is an equilateral triangle.             {From (3) and (4)} 

or   \[{\text{AC  =  CD}}\], i.e., \[{\text{AC  =  2BC}}\]      {Since \[{\text{BC  =  BD}}\]}

Sample Question 2: Prove that if in two triangles two angles and the included side of

one triangle is equal to two angles and the included side of the other triangle, then the two triangles are congruent.

Ans: In two triangles two angles and the included side of one triangle is equal to two angles and the included side of the other triangle.

Draw the triangles.

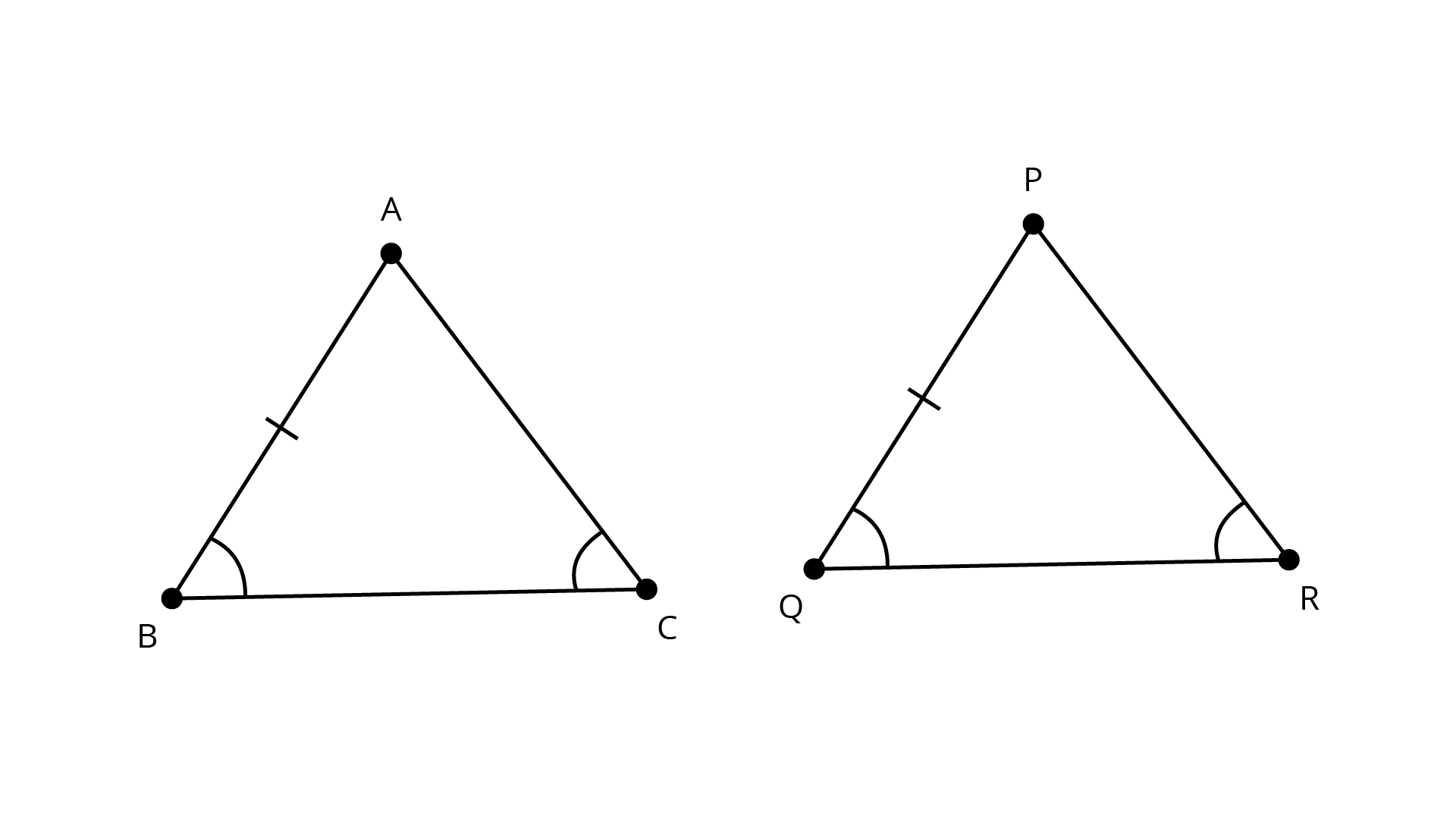
Let say,

\[\angle B = \angle Q\]

\[\angle C = \angle R\]

\[AB = PQ\]

\[\therefore \Delta ABC \cong \Delta PQR\](BY AAS)

Sample Question 3: If the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.

Ans: The bisector of an angle of a triangle also bisects the opposite side.

${{\Delta ABC}}$, \[{{AD}}\] bisects \[\angle A\] and ${\text{AD}}$ bisects ${\text{BC}}$. 

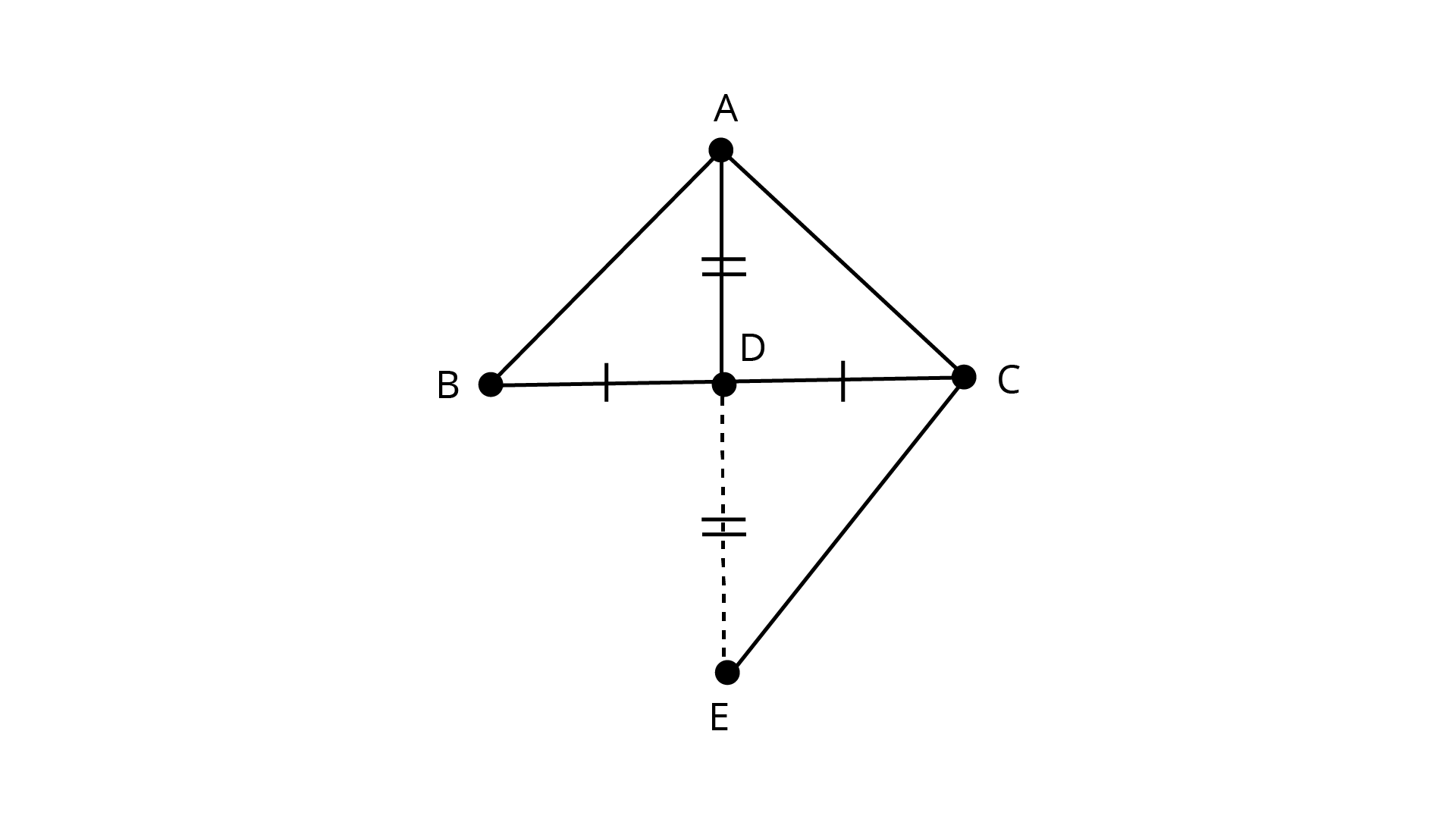
In ${{\Delta ABD}}$ and ${{\Delta ACD}}$,

$\angle DAB = \angle DAC$            (\[{\text{AD}}\] bisects $\angle {\text{A}}$)

$AD = AD({\text{Common}})$

${\text{BD}} = {\text{CD}}$    (${\text{AD}}$ bisects ${\text{BC}})$

$\Delta ABD \cong \Delta ACD$ (SAS rule)

Thus, ${\text{AB  =  AC}}$ (By cpct) 

We know that:

A triangle that has two sides of equal length is known as Isosceles triangle.

Hence, $\Delta ABD$ is an Isosceles triangle.

Sample Question 4: \[{\text{S}}\] is any point in the interior of \[{\Delta }PQR\]. Show that \[SQ  +  SR  <  PQ  +  PR.\]

Ans: \[{\text{S}}\] is any point in the interior of \[{{\Delta PQR}}\].

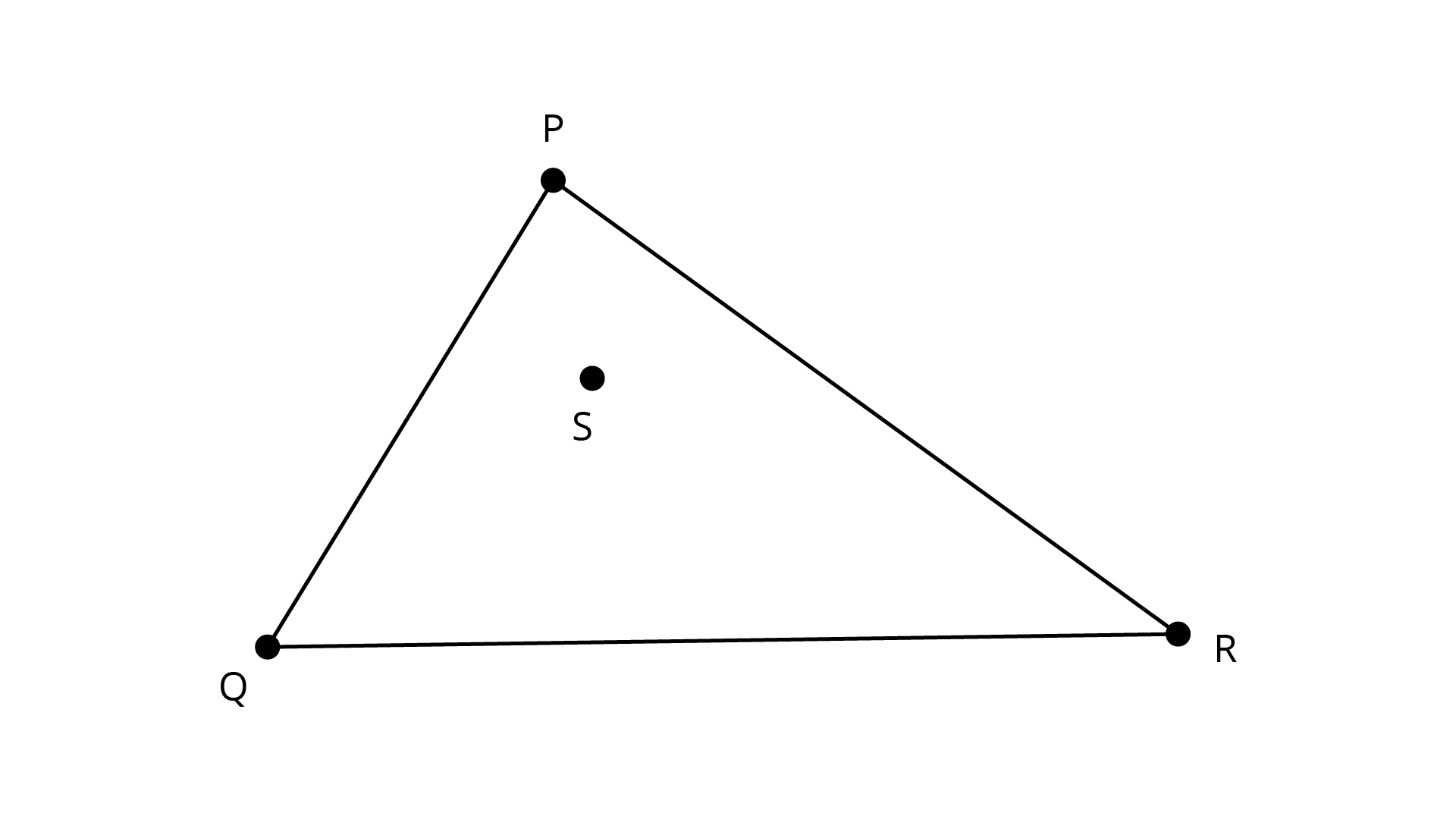
Let us project ${\text{QS}}$ to intersect ${\text{PR}}$ at ${\text{T}}$.

 From ${{\Delta PQT}}$, we have $PQ + PT > QT$

$PQ + PT > SQ + ST$ …(i)

$ST + TR > SR$ …(ii)

Adding equation (1) and (2), 

$PQ + PT + ST + TR > SQ + ST + SR$

$PQ + PT + TR > SQ + SR$

$PQ + PR > SQ + SR$

\[\Rightarrow SQ + SR < PQ + PR.\]

EXERCISE 7.4

1. Find all the angles of an equilateral triangle.

Ans: Given,

\[{{\Delta ABC}}\] is an equilateral triangle. 

In an equilateral triangle all the angles are equal.

\[\angle A = \angle B = \angle C = x\]

Sum of angles in a triangle \[ = 180^\circ \]

\[\angle A + \angle B + \angle C = 180^\circ \]

\[x + x + x = 180^\circ \]

\[x = 60^\circ \]

Thus, \[\angle A = \angle B = \angle C = 60^\circ \]

2. The image of an object placed at a point \[A\] before a plane mirror \[LM\] is seen at the point $B$ by an observer at \[D\] as shown in Fig. Prove that the image is as far behind the mirror as the object is in front of the mirror. 

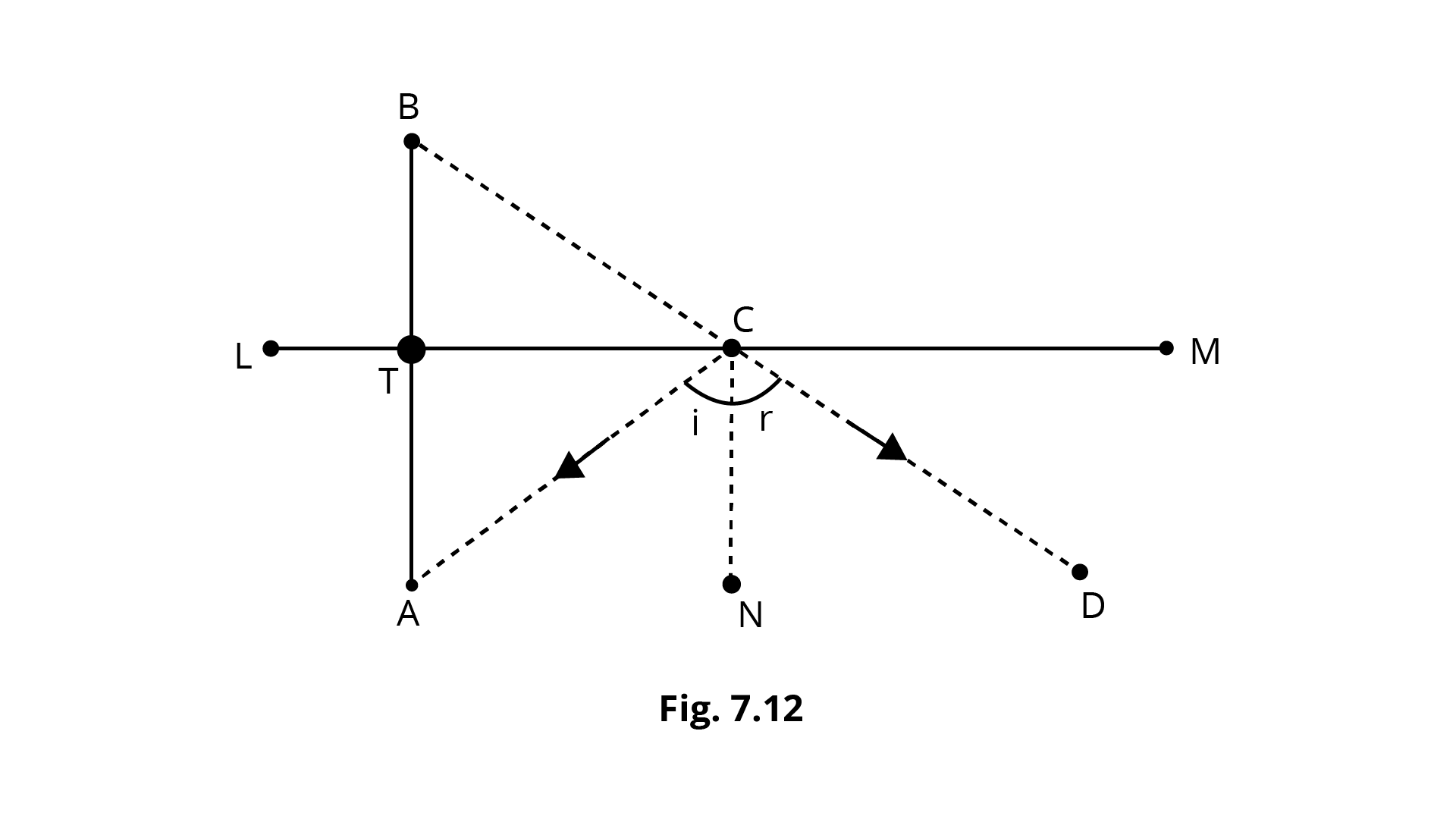
Ans: The image of an object placed at a point \[{\text{A}}\] before a plane mirror \[{\text{LM}}\] is seen at the point ${\text{B}}$ by an observer at \[{\text{D}}\] as shown in Fig.

From figure we need to prove that AT=BT

We have,

Angle of incidence = Angle of reflection

Therefore,

\[\angle ACN = \angle DCN.....\left( 1 \right)\]

Since, \[{\text{AB}}\parallel {\text{CN}}\] and \[{\text{AC}}\] is the transversal.

From the figure we know that \[\angle TAC{\text{ and }}\angle ACN\] are alternate angles.

\[\angle TAC = \angle CAN.....\left( 2 \right)\]

We know that \[{\text{AB}}\parallel {\text{CN and BD}}\] is the transversal.

From the figure we know that \[\angle TBC{\text{ and }}\angle DCN\] are corresponding angles.

\[\angle TBC = \angle DCN.....\left( 3 \right)\]

By considering the equation \[\left( 1 \right),\left( 2 \right){\text{ and }}\left( 3 \right)\]

We get,

\[\angle TAC = \angle TBC.....(4)\]

Now in \[{{\Delta ACT}}\] and \[{{\Delta BCT}}\]

\[\angle ATC = \angle BTC = 90^\circ \]

${\text{CT}}$ is common i.e., \[{\text{CT  =  CT}}\]

By AAS congruence criterion

\[\Delta ACT \cong \Delta BCT\]

\[{\text{AT  =  BT}}{\text{}}\left( {{\text{c}}{\text{.p}}{\text{.c}}{\text{.t}}} \right)\]

Therefore, it is proved that the image is as far behind the mirror as the object is in front of the mirror.

3. \[ABC\] is an isosceles triangle with \[AB  =  AC\] and \[D\] is a point on \[BC\] such that \[AD \bot BC\] (Fig. 7.13). To prove that \[\angle BAD = \angle CAD\], a student proceeded as follows:

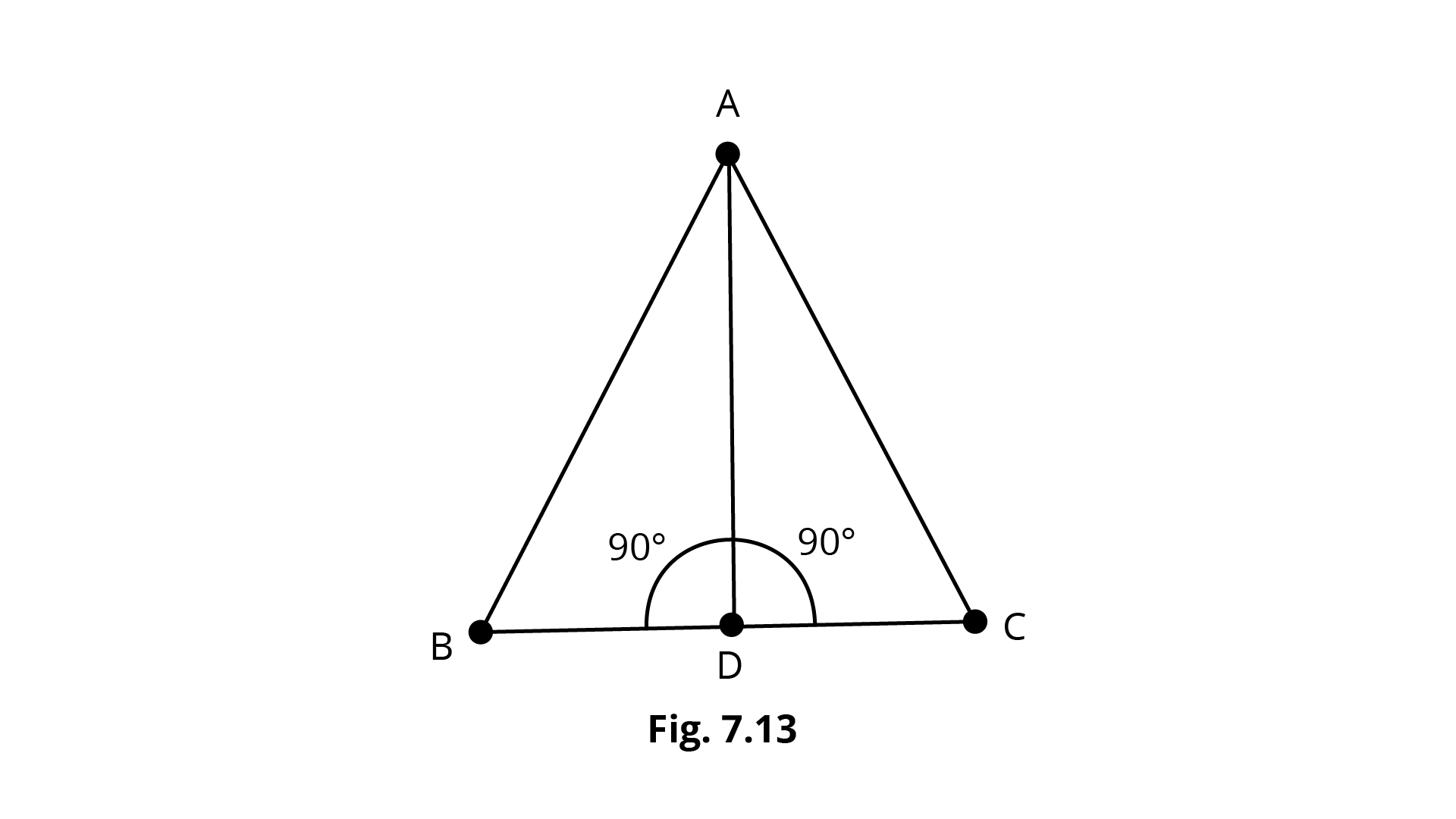
In \[\Delta  ABD\] and \[\Delta  ACD\],

\[{\text{}}AB  =  AC\] (Given) 

\[\angle B = \angle C\] (because\[AB  =  AC\])

 and \[\angle ADB = \angle ADC\]

Therefore, \[\Delta ABD \cong \Delta ACD\] (AAS)

 So, \[\angle BAD  = \angle CAD\] (cpct) 

What is the defect in the above arguments? 

{Hint: Recall how \[\angle B  = \angle C\] is proved when \[AB  =  AC\]}.

Ans: ${\text{In }}\Delta ABC,$

  $AB = AC$

  $\Rightarrow \angle ACB = \angle ABC$

  ${\text{In }}\Delta ABD{\text{ and }}\Delta ACD,$ 

   $AB = AC\quad $     (given)

   $\angle ABD = \angle ACD\quad $      (Proved above)

   $\angle ADB = \angle ADC$      (each ${90^\circ }$)

$\therefore \Delta ABD \cong \Delta ACD\quad $       (by AAS)

So, $\angle BAD = \angle CAD\quad $        (by CPCT)

So, the defect in the given argument is that firstly prove $\angle ABD = \angle ACD$ Hence, $\angle ABD = \angle ACD$ is a defect.

4. P is a point on the bisector of \[\angle ABC\]. If the line through\[{\text{}}P\], parallel to \[BA\] meet \[BC\]at \[Q\], prove that \[BPQ\] is an isosceles triangle.

Ans: Let BP is bisector of $\angle ABC$

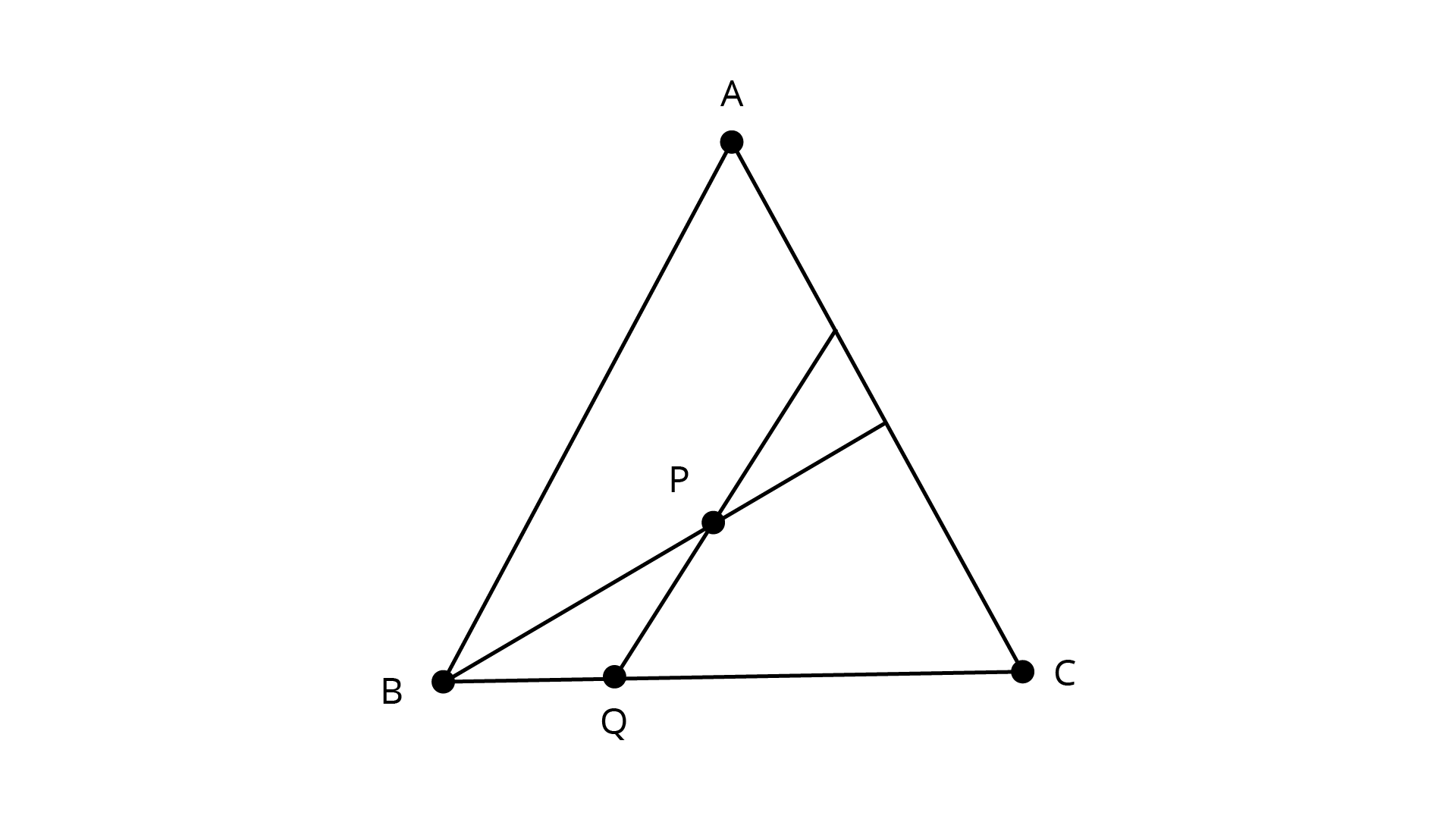
$\Rightarrow \angle ABP = \angle PBC$ …….(1)

Now,  (given) 

$\Rightarrow \angle BPQ = \angle ABP\quad  \ldots .(2)$  {Alternative angles}

From (1) and (2), we get

$\angle BPQ = \angle PBC$ Or $\angle BPQ = \angle PBQ$

Now, In ${{\Delta BPQ}}$

$\angle BPQ = \angle PBQ$

\[\Rightarrow \Delta {\text{BPQ}}\] is an isosceles triangle.

Hence proved.

5. ABCD is a quadrilateral in which AB  =  BC and AD  =  CD. Show that \[BD\] bisects both the angles ABC and ADC.

Ans: ABCD is a quadrilateral in which \[{\text{AB  =  BC and AD  =  CD}}{\text{.}}\]

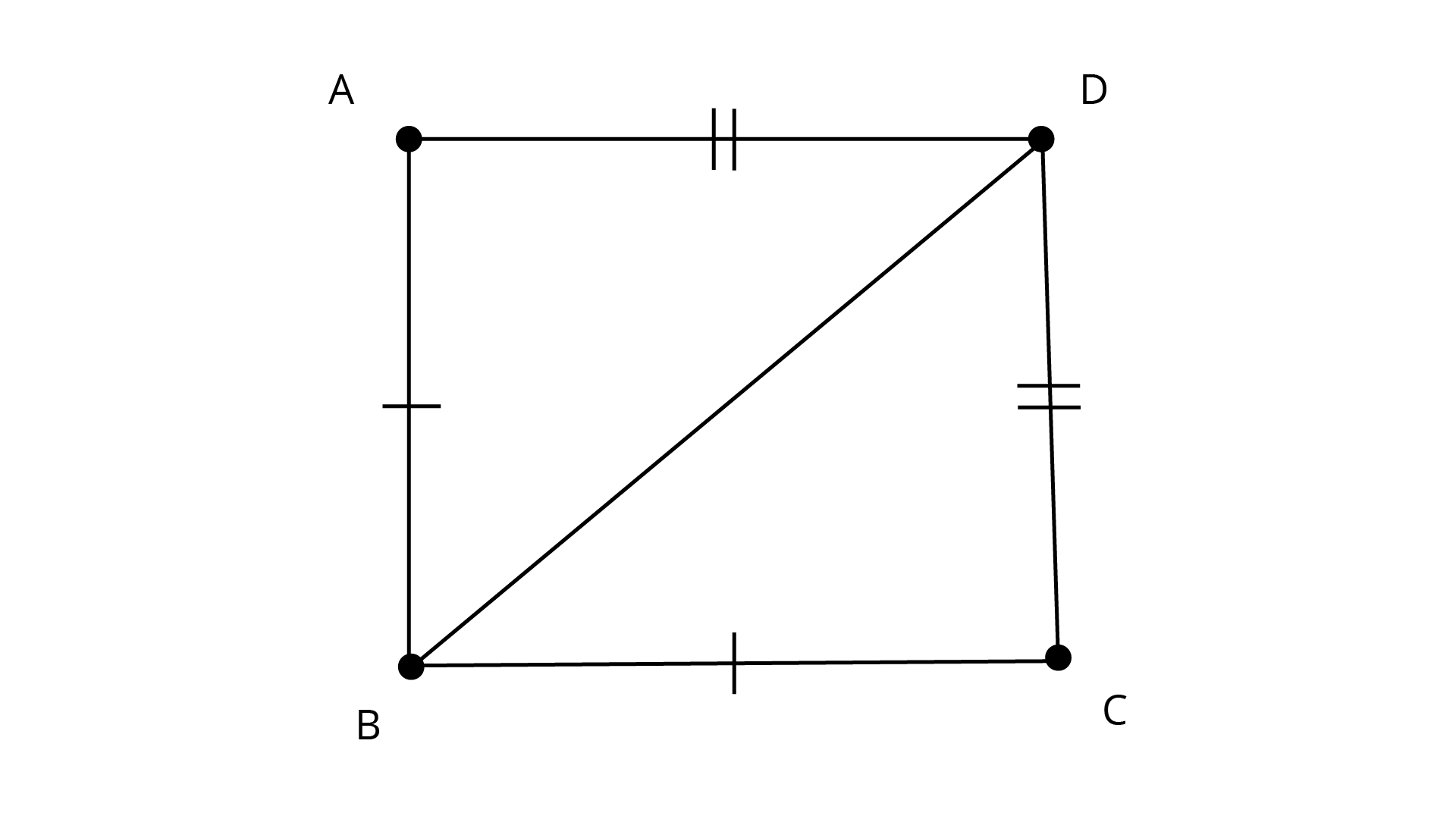
In\[{{\Delta ABD}}\] and \[{{\Delta CBD}}\],

\[{\text{AD  =  CD}}\]       (given )

\[{\text{BD  =  BD}}\]          ( Common )

\[{\text{AB  =  BC}}\]  ( given )

By SSS criterion of congruence, \[\Delta ABD \cong \Delta CBD\] 

By CPCT, we have 

\[\angle ABD = \angle CBD\]

\[\angle ADB = \angle CDB\]

We know that:

The bisectors divides a given angle into two angles with equal measures.

Hence, \[{\text{BD}}\] bisects both \[\angle ABC{\text{ and }}\angle ADE\].

6. ABC is a right triangle with \[AB  =  AC\]. Bisector of \[\angle A\] meets \[BC\] at \[D\]. Prove that \[BC = 2 AD\].

Ans: ABC is a right triangle with \[{\text{AB  =  AC}}\]. Bisector of \[\angle A\] meets \[{\text{BC}}\] at \[{\text{D}}\].

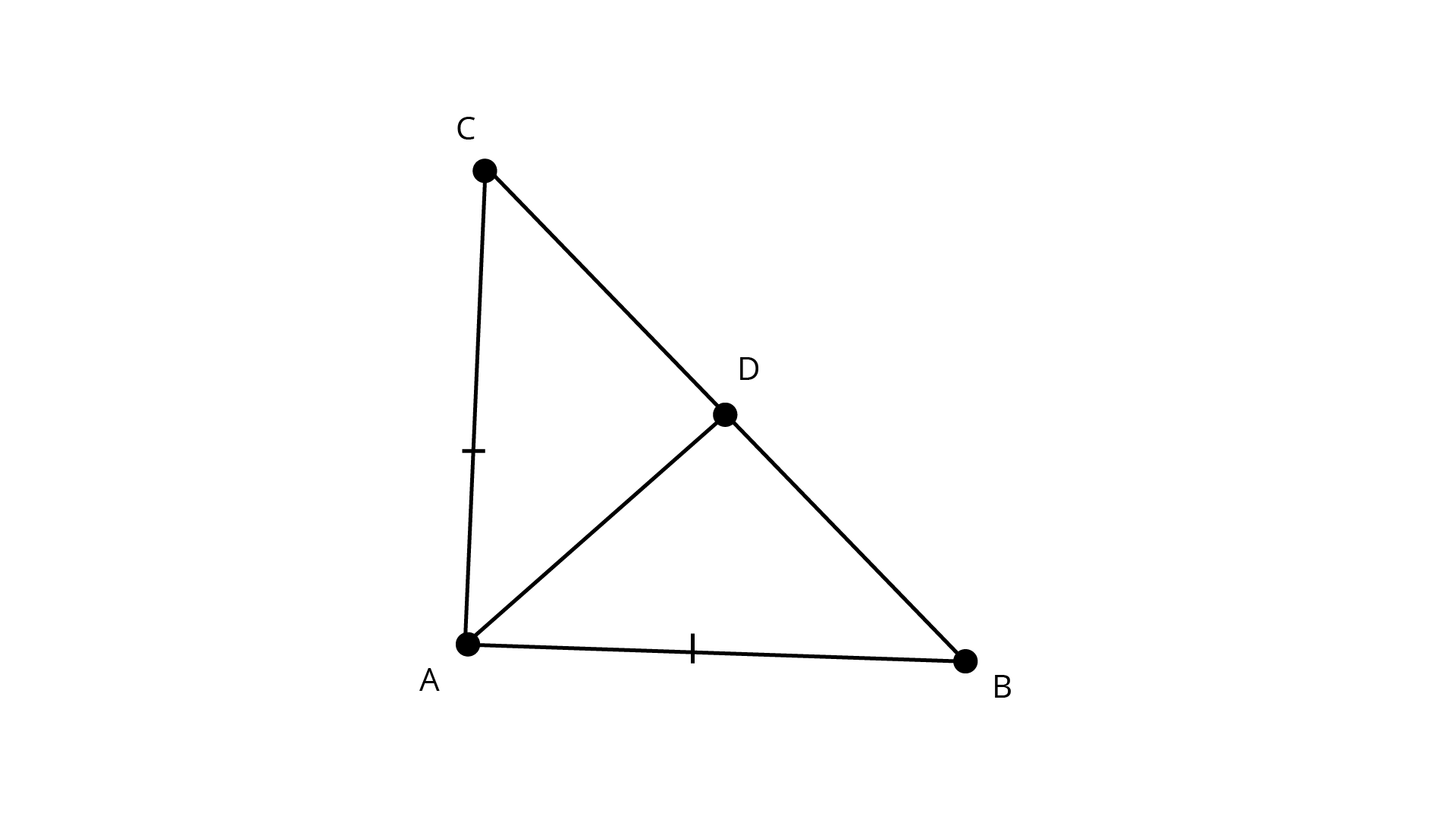
In \[{{\Delta ABD}}\] and \[{{\Delta ACD}}\],
\[{\text{AB  =  AC}}\] (given)

\[\angle BAD = \angle CAD\]

As ${\text{AD}}$ is bisector of $\angle {\text{A}}$ and ${\text{AD}} = {\text{AD}}$

$\Delta DAB \cong \Delta DAC$ (by SAS congruence rule)

$\angle ADB = \angle ADC$ ( by CPCT)

$\angle ADB = \angle ADC = 90^\circ$ (AD is also a perpendicular bisector)

and ${\text{BD  =  DC}}$

In ${{\Delta ABD}}$, by Pythagorean Theorem, we have

$A{D^2} + B{D^2} = A{B^2} \ldots $ (i)

In \[{{\Delta ACD}}\], by Pythagorean Theorem, we have

\[A{D^2} + D{C^2} = A{C^2} \ldots \] (ii)

Adding (i) and (ii), we get 

$2A{D^2} + B{D^2} + D{C^2} = A{B^2} + A{C^2}$

$2A{D^2} + B{D^2} + D{C^2} = B{C^2}$……… (Pythagorean Theorem)

$2A{D^2} + 2B{D^2} = B{C^2}$ ………………(BD = DC)

$2\left( {A{D^2} + B{D^2}} \right) = B{C^2}$………(AD = BC)

$4 A D^{2}=B C^{2}$

\[2AD = BC\]

Hence Proved.

7. \[O\] is a point in the interior of a square ABCD such that OAB is an equilateral
triangle. Show that \[\Delta OCD\] is an isosceles triangle.

Ans: \[{\text{O}}\] is a point in the interior of a square ABCD such that OAB is an equilateral triangle.

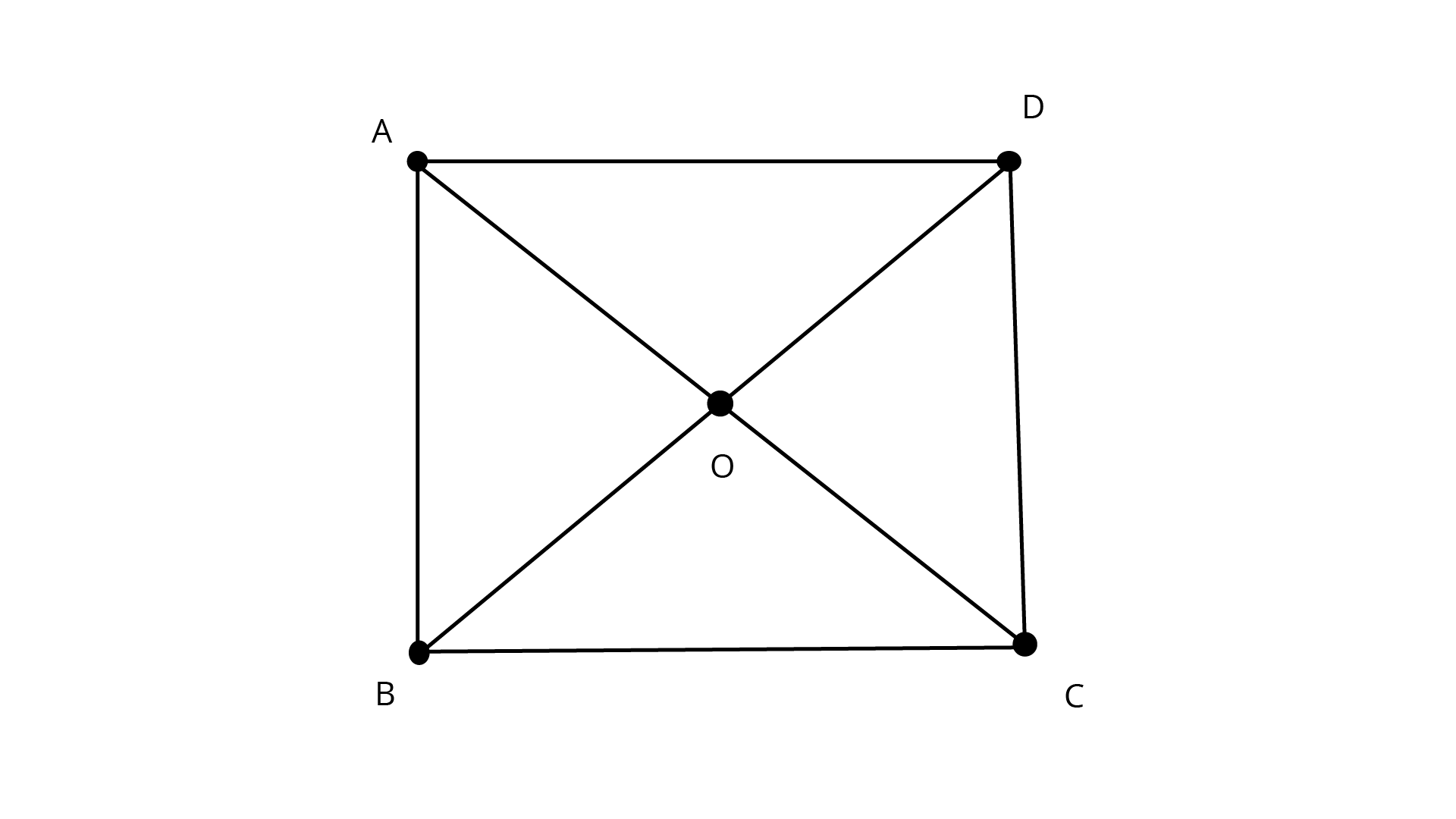
ln \[{{\Delta AOD}}\] and \[{{\Delta BOC}}\]

\[{\text{AD  =  BC}}\] (sides of the square)

\[\angle DAO = \angle CBD = 30^\circ \]  (\[90^\circ \] − angle of equilateral \[\Delta \] \[60^\circ \])

\[{\text{AO  =  OB}}\] (sides of equilateral of triangle are same)

\[\Delta AOD \cong \Delta BOC\] (SAS criterion)

then  \[{\text{OD  =  OC}}\]…..(CPCT)

So \[{{\Delta COD}}\] is an isosceles triangle.

8. ABC and DBC are two triangles on the same base \[BC\] such that \[A\] and \[D\] lie on the opposite sides of BC, AB  =  AC and DB  =  DC. Show that \[{\text{AD}}\] is the perpendicular bisector of BC.

Ans: \[{\text{ABC and DBC}}\] are two triangles on the same base \[{\text{BC}}\] such that \[{\text{A}}\] and \[{\text{D}}\] lie on the opposite sides of \[{\text{BC, AB  =  AC and DB  =  DC}}\].

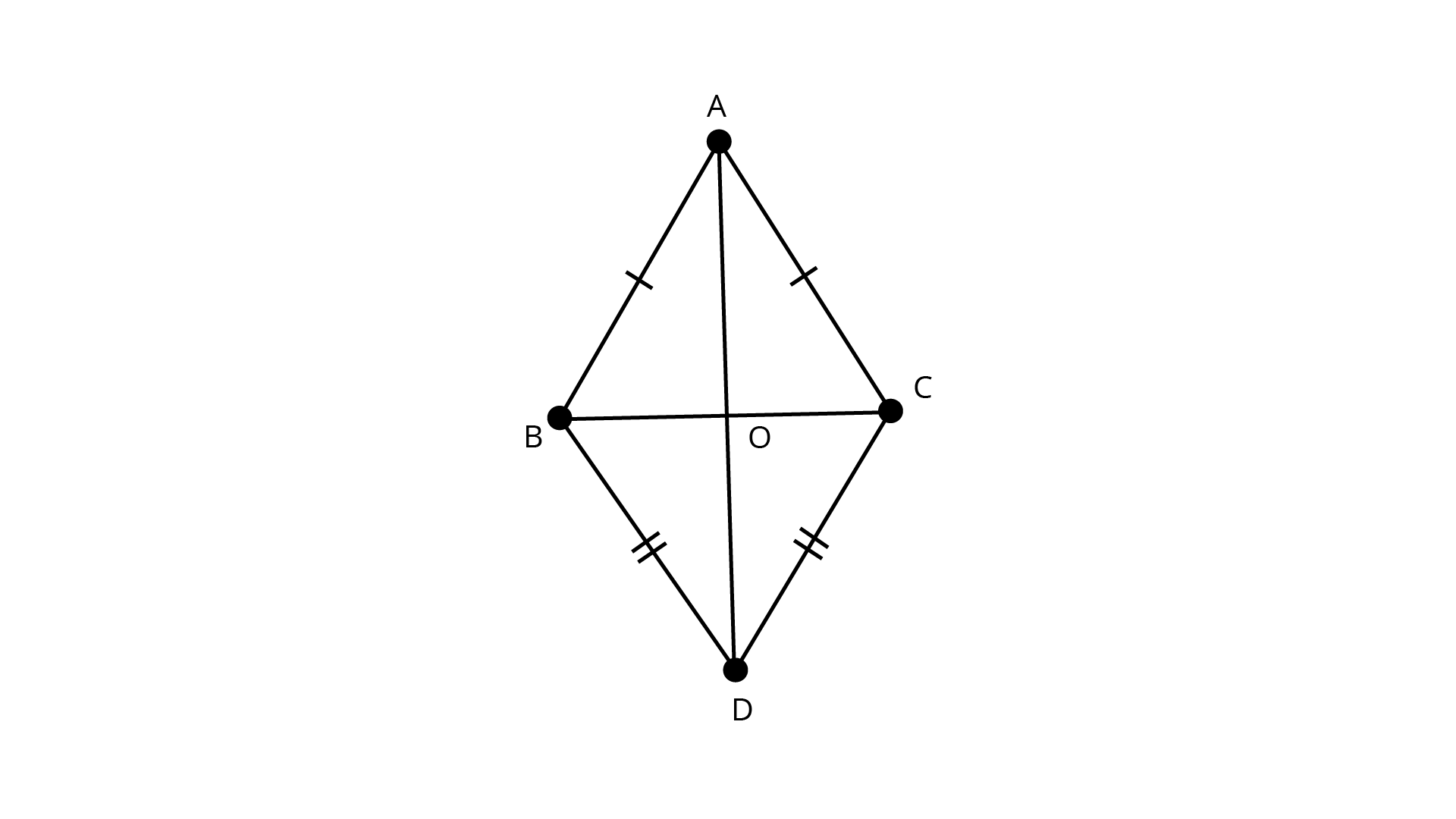
In \[{{\Delta ABD}}\] and \[{{\Delta ACD}}\] we have

AB = AC                       {given}

AD = DA                       {common} 

BD = DC                       {given}

\[\therefore \Delta ABD \cong \Delta ACD\] (By SSS)

\[\Rightarrow \angle BAD = \angle CAD\]  (by CPCT)

In \[{{\Delta ABC}}\]

\[\angle AOB = \angle AOC\] (The angle opposite to equal side are equal)

But  \[\angle AOB + \angle AOC = 180^\circ \] (linear pair)

\[\Rightarrow \angle AOB + \angle AOB = 180^\circ \]

\[\Rightarrow 2\angle AOB = 180^\circ \]

\[\therefore \angle AOB = 90^\circ \]

  Hence ${\text{AD}}$ is perpendicular to ${\text{BC}}$ and ${\text{AD}}$ bisects ${\text{BC}}$

\[\therefore \] ${\text{AD}}$ is the perpendicular bisector of ${\text{BC}}$.

9. ABC is an isosceles triangle in which\[AC  =  BC\]. \[AD\] and \[BE\] are respectively two altitudes to sides \[BC\] and \[AC\]. Prove that \[AE  =  BD\].

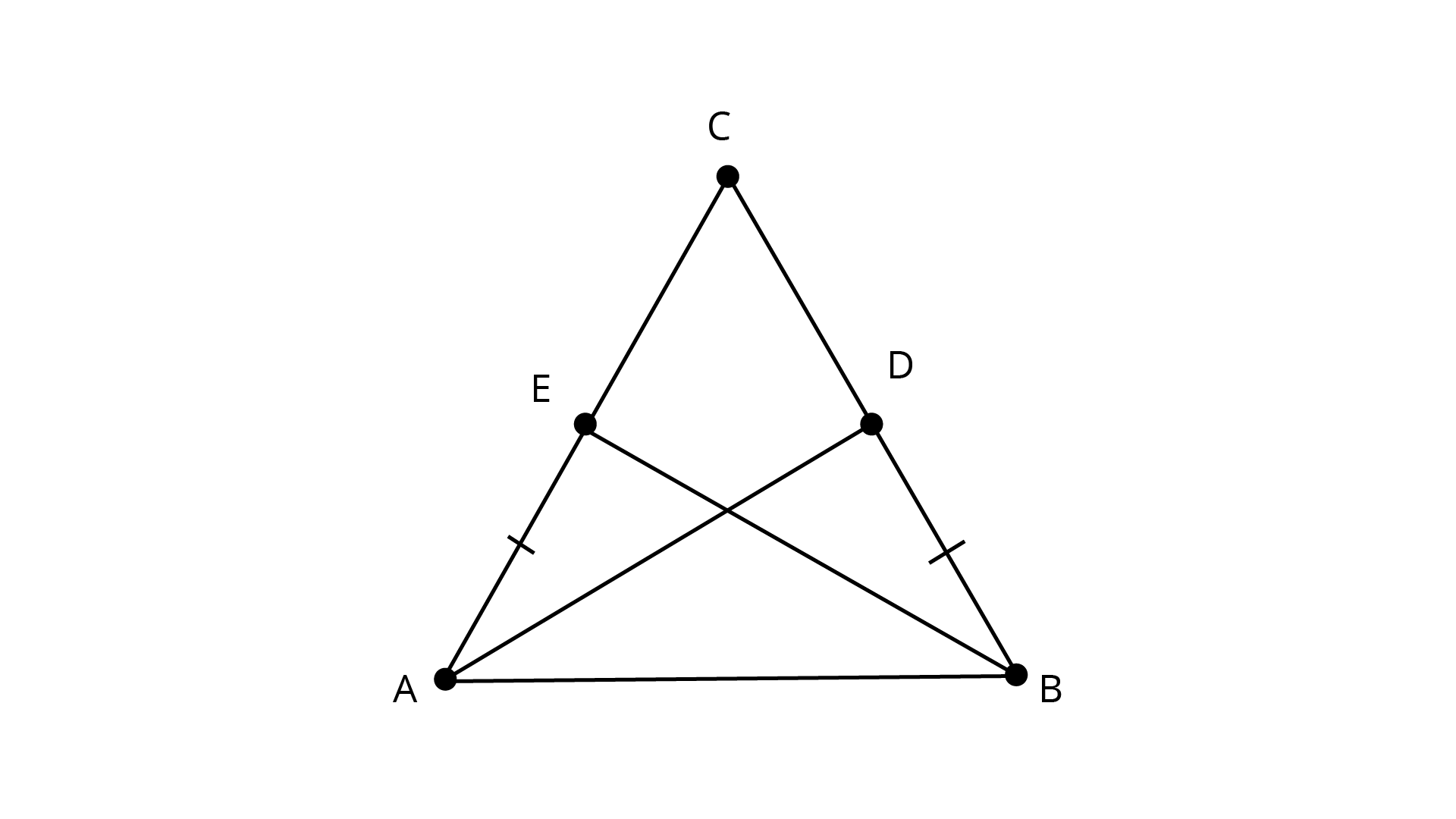
Ans: In \[{{\Delta ABC}}\],

\[{\text{AC  =  BC}}\] (given)

\[\angle EAB = \angle DBA \ldots \] (The angles opposite to equal sides are equal)

Now in \[{\Delta EAB}\] and \[{{\Delta DAB}}\]

\[\angle AEB = \angle ADB = 90^\circ \] (given)

\[\Delta DAB \cong \Delta EAB\] (by SAS)

and \[{\text{AB  =  AB}}\] (common)

\[\Delta DAB \cong \Delta EAB\] (by AAS congruence rule)

\[{\text{AE  =  BD}}\] (by c.p.c.t)

10. Prove that sum of any two sides of a triangle is greater than twice the median with respect to the third side.

Ans: Consider, ${{\Delta ABC}}$

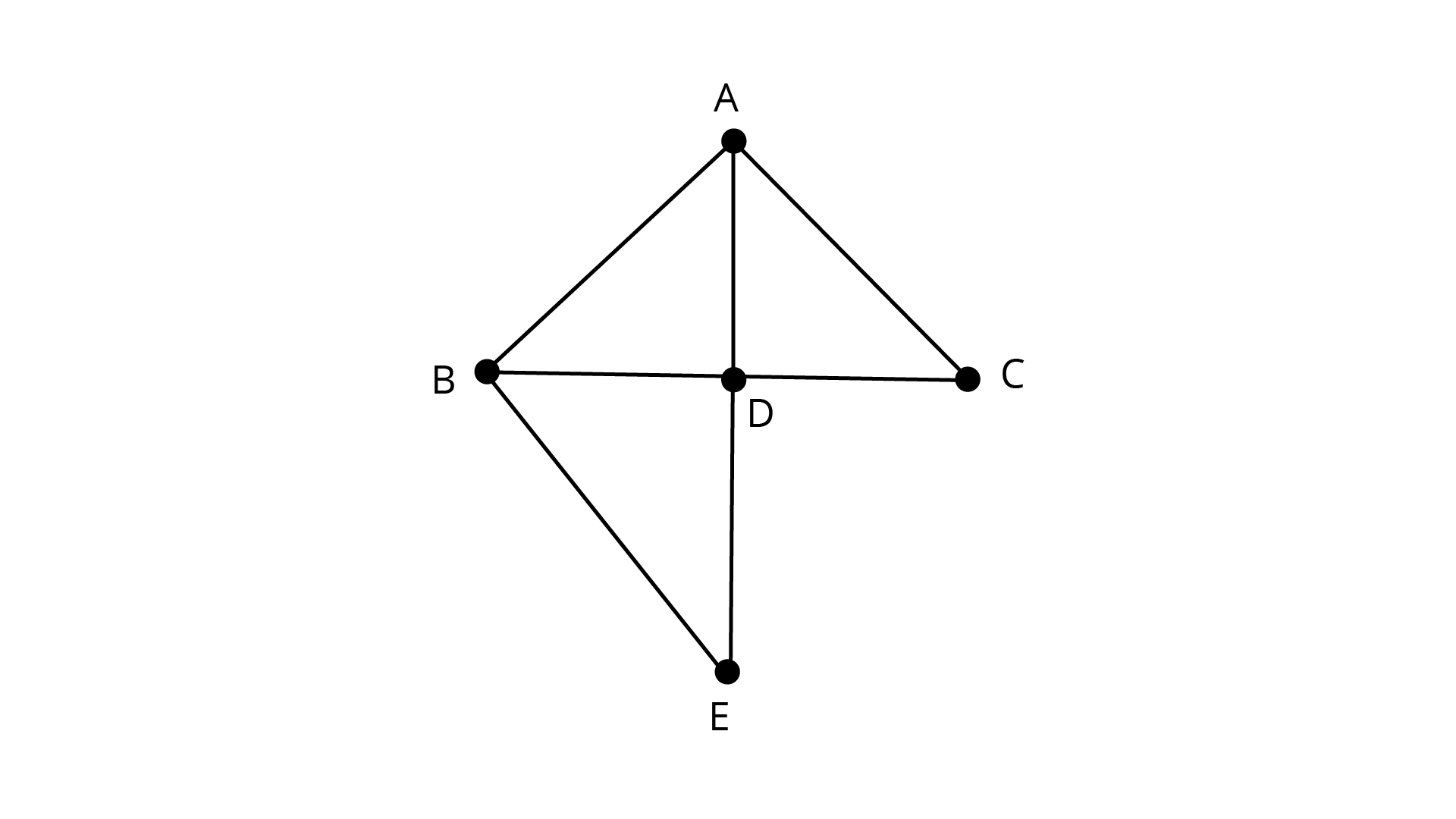
Produce \[{\text{AD}}\] to a point E that \[{\text{AD  =  DE}}\] and join \[{\text{BE}}\]

In ${{\Delta ADC}}$ and ${{\Delta EDB}}$ we have 

${\text{AD  =  DE}}$ (By construction)

${\text{DC  =  BD}}$ as ${\text{D}}$ is the midpoint 

\[\angle ADC = \angle EDB\](vertically opposite angles)

By SAS criterion of congruence, we have:

$\therefore \Delta ADC \cong \Delta EDB$ 

${\text{BE  =  AC}}$ (By CPCT)

Now in \[{{\Delta ABE}}\],

$AB + BE > AE$            (Sum of two side of a triangle is greater than third side)

$AB + AC > 2AD$

Hence the sum of any two sides of a triangle is greater than twice the median with respect to the third side.

11. Show that in a quadrilateral \[ABCD, AB + BC + CD + DA < 2\left( {BD + AC} \right)\].

Ans: A quadrilateral ABCD.

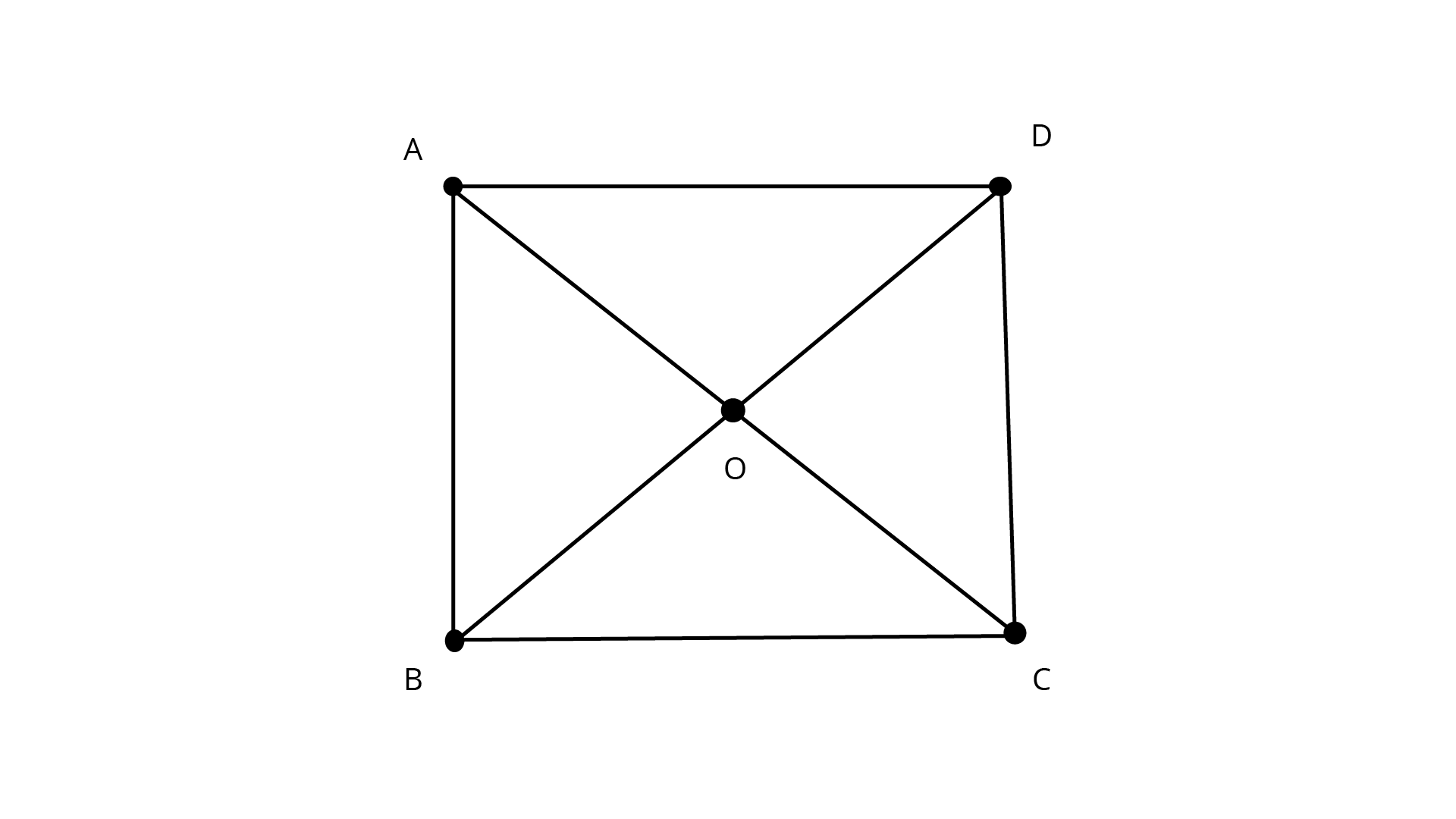
Since, the sum of lengths of any two sides in a triangle should be greater than the length of their side.

In $\Delta AOB,AB < OA + OB \ldots  \ldots  \ldots \left( i \right)$

In $\Delta BOC,BC < OB + OC \ldots  \ldots  \ldots \left( {ii} \right)$

In $\Delta COD,CD < OC + OD \ldots  \ldots  \ldots \left( {iii} \right)$

In  $\Delta AOD,DA < OD + OA \ldots  \ldots  \ldots \left( {iv} \right)$

On adding Equations. $(i),(ii),(iii){\text{and }}(iv)$, we get

$\Rightarrow AB + BC + CD + DA < 2OA + 2OB + 2OC + 2OD$

$\Rightarrow AB + BC + CD + DA < 2[(AO + OC) + (DO + OB)]$

$\Rightarrow AB + BC + CD + DA < 2(AC + BD)$

Hence, it is proved.

12. Show that in a quadrilateral \[ABCD, AB + BC + CD + DA > AC + BD.\]

Ans: A quadrilateral \[ABCD.\]

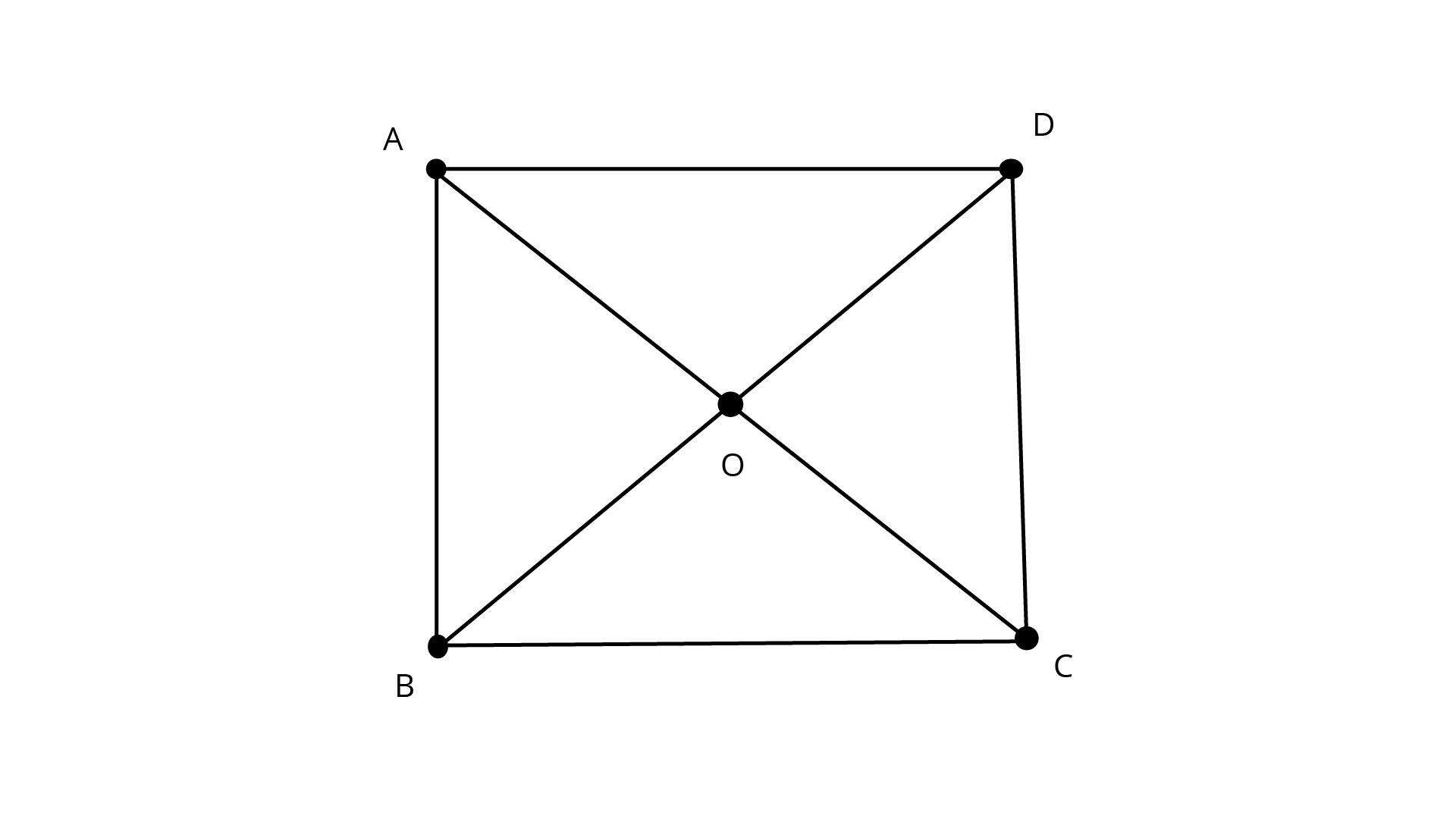
${\text{ABCD}}$ is a quadrilateral and ${\text{AC}}$, and ${\text{BD}}$ are the diagonals. 

Sum of the two sides of a triangle is greater than the third side. 

So, considering the triangles ${\text{ABC,}}{\text{BCD,}}{\text{CAD}}{\text{ and }}{\text{BAD}}$, we get 

$AB + BC > AC.....(i)$

$CD + AD > AC.....(ii)$

$AB + AD > BD.....(iii)$

$BC + CD > BD.....(iv)$

On adding Equations. ${\text{(i),(ii),(iii)}}{\text{and (iv)}}$, we get

$2(AB + BC + CA + AD) > 2(AC + BD)$

$\Rightarrow 2(AB + BC + CA + AD) > 2(AC + BD)$

$\Rightarrow (AB + BC + CA + AD) > (AC + BD)$

Hence Proved.

13. In a triangle \[ABC\], $D$ is the midpoint of side AC such that \[BD = \dfrac{1}{2}AC\]. Show that \[\angle ABC\] is a right angle.

Ans: In a triangle \[{\text{ABC}}\], ${\text{D}}$ is the midpoint of side AC such that \[BD =\dfrac{1}{2}AC\]

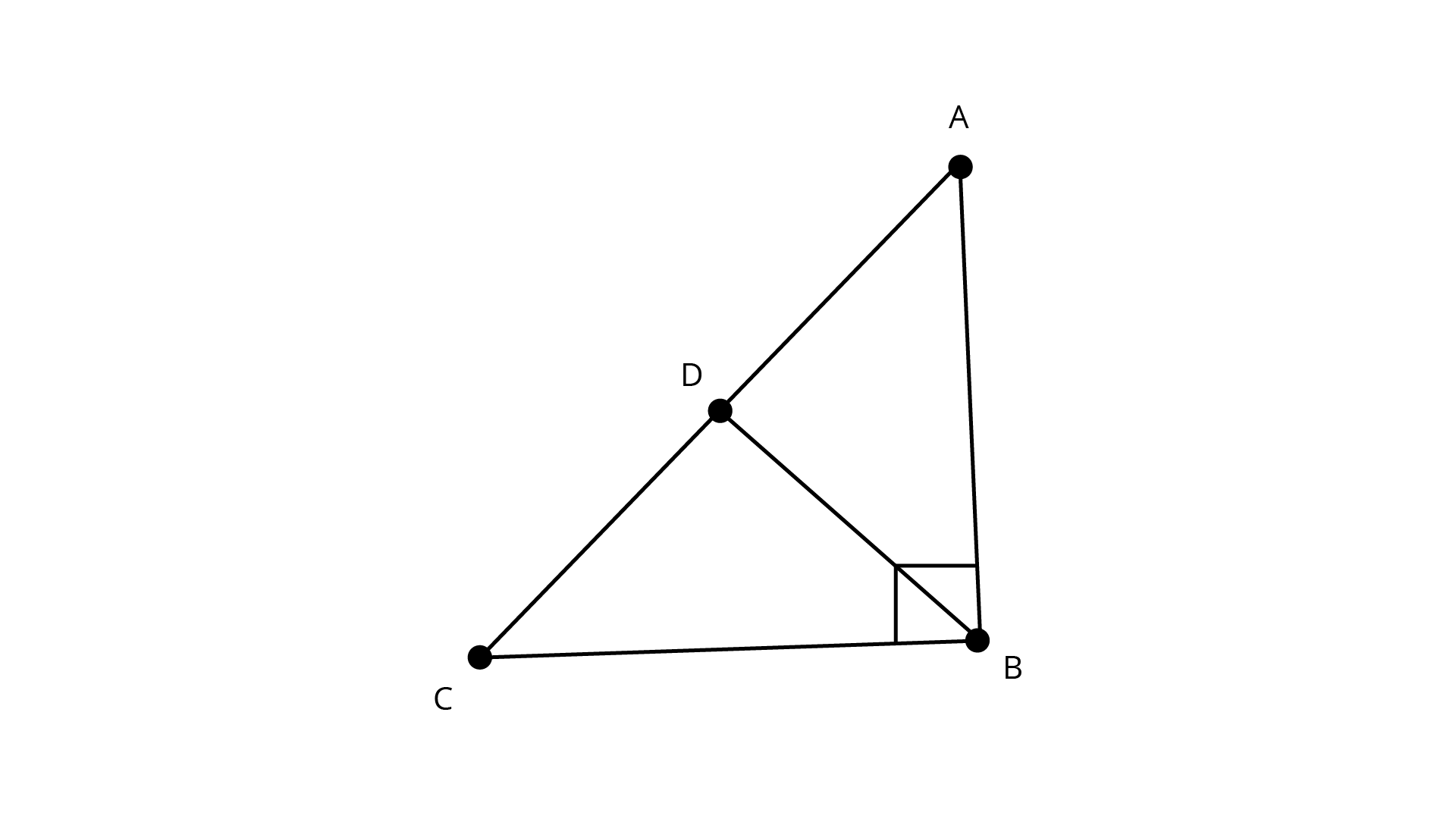
${\text{D}}$ is the midpoint of the line ${\text{AC}}$ .

\[AD = CD = {\text{ }}\dfrac{1}{2}{\text{ }}AC\]

It is given that \[BD = \dfrac{1}{2}AC\]

Therefore,

\[AD = BD = CD\]

Consider \[{\text{AD  =  BD}}\]

The angles opposite to equal sides are equal 

Therefore,

\[\angle BAD = \angle ABD{\text{ }} \ldots ..\left( 1 \right)\]

Now, consider \[{\text{CD  =  BD}}\]

The angles opposite to equal sides are equal 

Therefore,

\[\angle BCD{\text{ }} = \angle CBD{\text{ }} \ldots ..{\text{ }}\left( 2 \right)\]

By considering the angle sum property in \[{{\Delta ABC}}\]

\[\angle ABC + \angle BAC + \angle BCA = 180^\circ \]

it can be written as 

\[\angle ABC + \angle BAD + \angle BCD = 180^\circ \]

By using equation (1) and (2) we get

\[\angle ABC + \angle ABD + \angle CBD = 180^\circ \]

Therefore, 

\[\angle ABC + \angle ABC = 180^\circ \] (\[\angle ABD + \angle CBD = \angle ABC\] )

 By addition 

\[2\angle ABC = 180^\circ \]

By division \[\angle ABC = 90^\circ \]

Therefore, \[\angle ABC\] is a right angle.

14. In a right triangle, prove that the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse.

Ans: Let ${\text{ABC}}$ is a right triangle right angled at ${\text{B}}$. Let ${\text{B}}$ be the mid-point of the hypotenuse

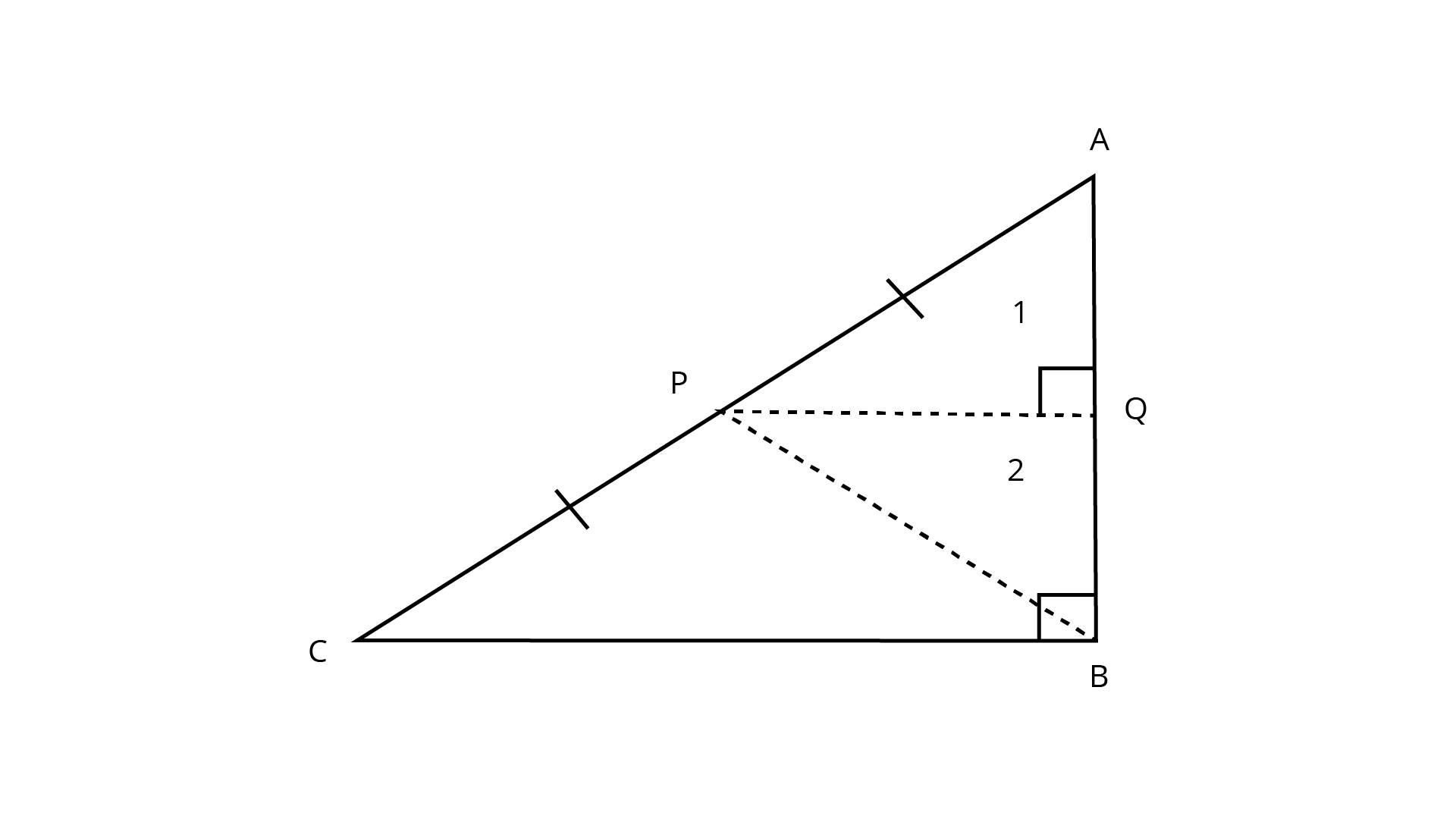
Draw through the point P.

\[\angle 1 = \angle B\] (corresponding angle) 

$\angle 2 = \angle 1 = {90^0}$

In $\Delta ABC,P$ is the midpoint of $AC$ and 

Q must be midpoint of AB (converse of mid-point theorem) $AQ = QB \ldots (i)$

Now in ${{\Delta AQP}}$ and ${{\Delta BPQ}}$

$AQ = QB$

$\angle 2 = \angle 1 = {90^0}$

$PQ = PQ$

By SAS criterion of congruence.

$\Delta AQP = \Delta BPQ$ 

${\text{AP  =  PB}}$    (CPCT) 

Thus, ${\text{AP  =  PB  =  PC}}$

Hence the line-segment joining the mid-point of the hypotenuse to the opposite vertex is half the hypotenuse.

15. Two lines $l$ and $m$ intersect at the point $O$ and $P$ is a point on a line $n$ passing through the point $O$ such that $P$ is equidistant from $l$ and $m$. Prove that $N$ is the bisector of the angle formed by $l$ and $m$.

Ans: Two lines $l$ and $m$ intersect at the point ${\text{O}}$ and ${\text{P}}$ is a point on a line $n$ passing through the point ${\text{O}}$ such that ${\text{P}}$ is equidistant from $l$ and $m$.

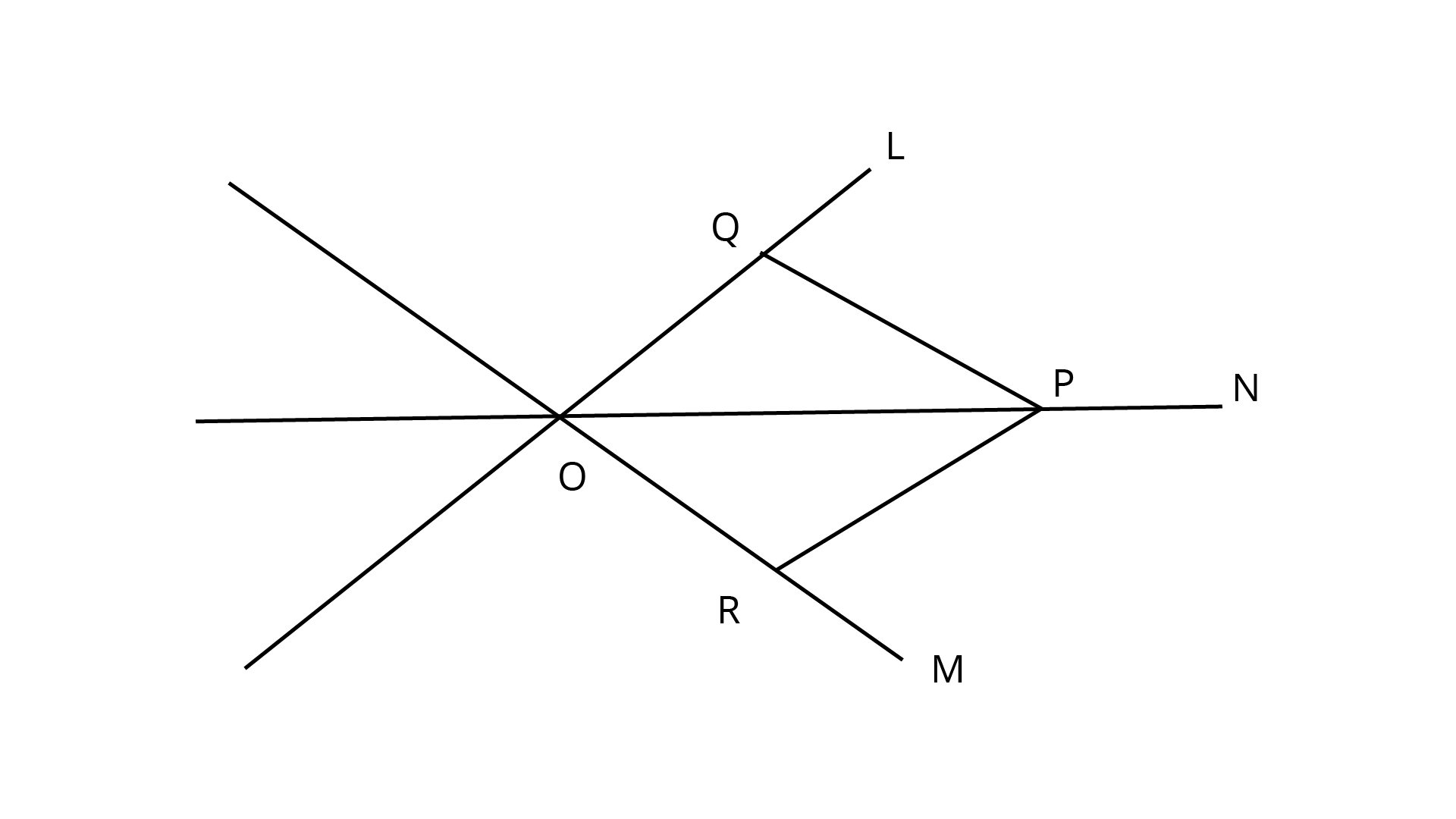
$\ln \Delta {\text{OQP}}$ and$\Delta {\text{ORP}}$, we have

$\angle PQO = \angle PRO$          {Each angle equal to $90^\circ$ }

${\text{OP  =  OP}}$                     {Common side}

${\text{PQ  =  QR}}$                     {Given}

So, by SAS criterion of congruence, we have

$\Delta OQP \cong \Delta ORP$

$\therefore \angle POQ = \angle POR[{\text{CPCT}}]$

We know that:

The bisector divides a given angle into two angles with equal measures.

So, ${\text{N}}$ is a bisector of $\angle QOR$.

Hence, proved.

16. Line segment joining the mid-points $M$ and $N$ of parallel sides $AB$ and $DC$, respectively of a trapezium \[ABCD\] is perpendicular to both the sides \[AB\]and \[DC\]. Prove that \[AD  =  BC\].

Ans: Line segment joining the mid-points ${\text{M}}$ and ${\text{N}}$ of parallel sides ${\text{AB}}$ and ${\text{DC}}$, respectively of a trapezium \[{\text{ABCD}}\] is perpendicular to both the sides \[{\text{AB}}\]and \[{\text{DC}}\].

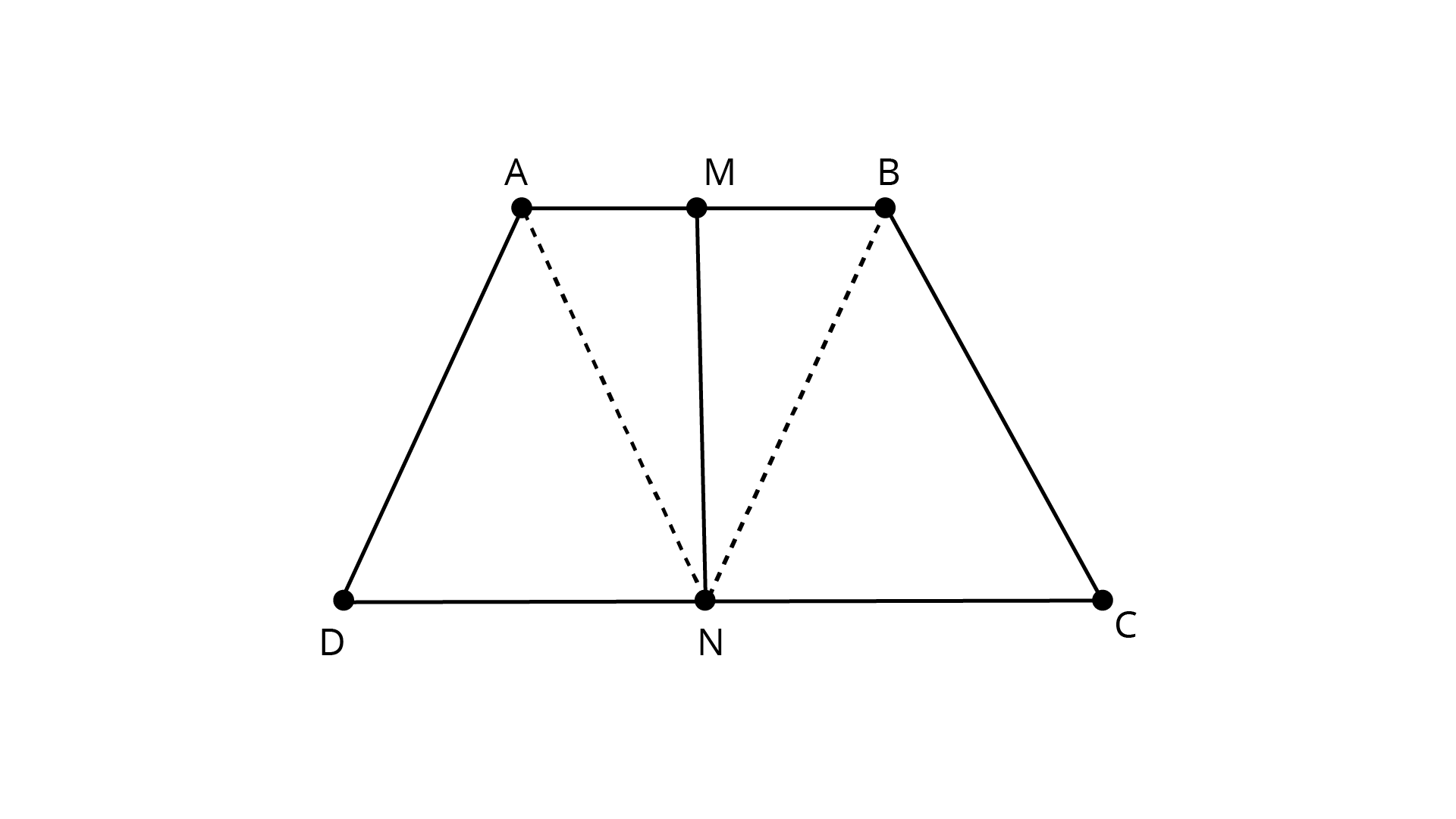
Draw \[{\text{AN}}\] and \[{\text{BN}}\] at the point \[{\text{N}}\]

Consider \[{{\Delta ANM}}\] and \[{{\Delta BNM}}\]

We know that M is the midpoint of the line ${\text{AB}}$

Therefore, 

${\text{AM}} = {\text{BM}}$

From the figure it is given that

$\angle AMN = \angle BMN = 90^\circ$

MN is common i.e. \[{\text{MN  =  MN}}\]

By SAS criterion of congruence

$\Delta ANM \cong \Delta BNM$

${\text{AN}} = {\text{BN           }}({\text{CPCT}}) \ldots ({\text{1}})$

$\angle ANM = \angle BNM{\text{       (CPCT)}}$

Subtracting LHS and RHS by ${90^\circ }$

$90^\circ  - \angle ANM = 90^\circ  - \angle BNM$

So we get

$\angle AND = \angle BNC \ldots (2)$

Now, consider ${{\Delta AND}}$ and ${{\Delta BNC}}$

${\text{AN  =  BN}}$

$\angle AND = \angle BNC$    (from (i))

We know that ${\text{N}}$ is the midpoint of the line ${\text{DC}}$

$DN = CN$

By SAS criterion of congruence

$\Delta AND \cong \Delta BNC$

\[AD = BC{\text{              (CPCT)}}\]

Therefore, it is proved that \[{\text{AD  =  BC}}\]

17. \[ABCD\] is a quadrilateral such that diagonal \[AC\] bisects the angles $A$ and $C$. Prove that AB  =  AD and CB  =  CD.

Ans: \[{\text{ABCD}}\] is a quadrilateral such that diagonal \[{\text{AC}}\] bisects the angles ${\text{A}}$ and ${\text{C}}$.

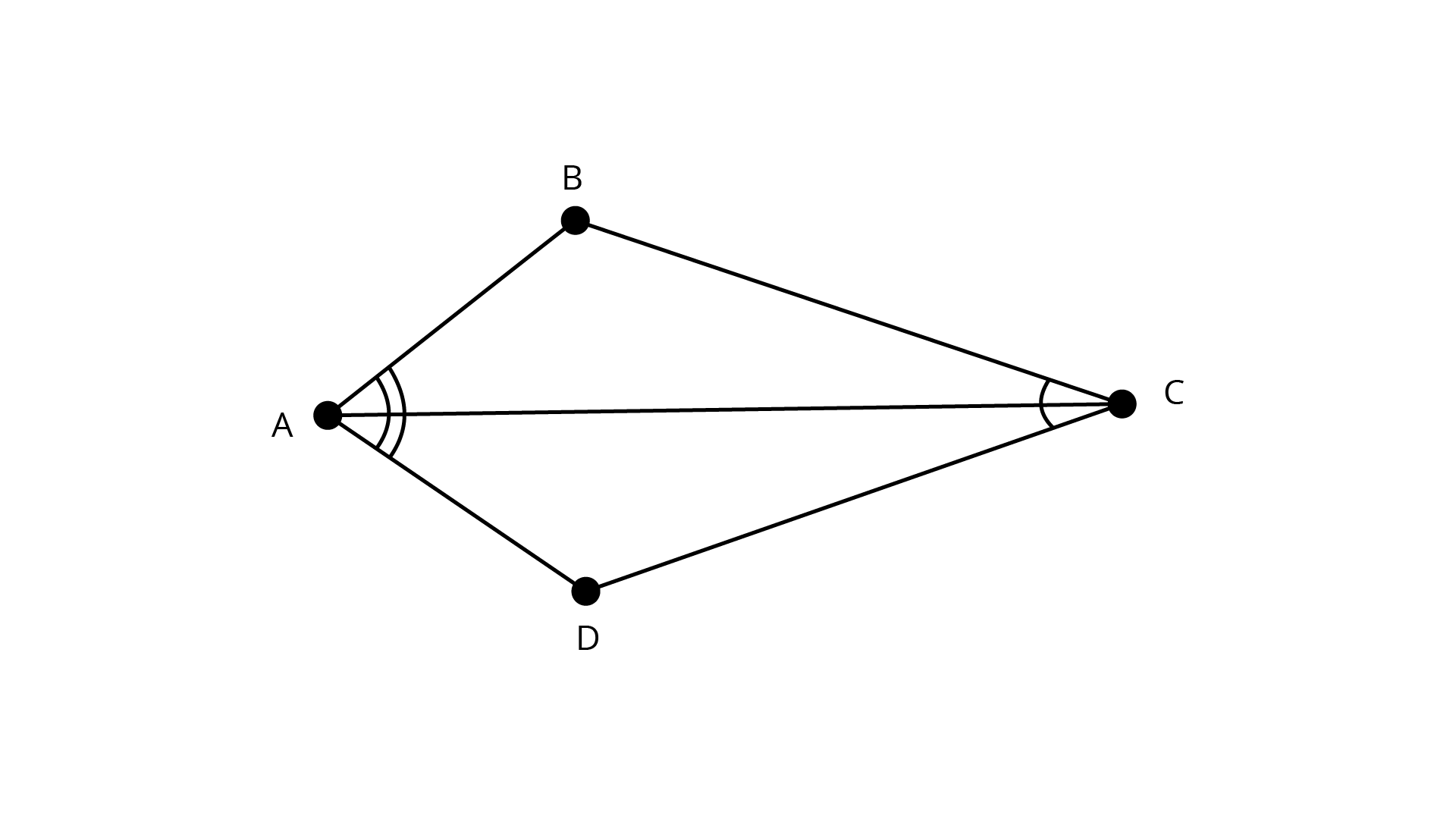
Ans: In $\Delta {\text{ABC}}$ and $\Delta {\text{ADC}}$

$\angle {\text{BAC}} = \angle {\text{DAC}}$               (given)

$\angle ACB = \angle ACD$                 (given)

${\text{AC  =  AC}}$                           (common)

$\therefore \Delta ABC \cong \Delta ADC$               (by ASA)

\[\therefore {\text{AB  =  AD}}\] And ${\text{CB  =  CD}}$ by ${\text{CPCT}}$

18. \[ABC\] is a right triangle such that \[AB  =  AC\] and bisector of angle \[C\] intersects the side\[AB at D\]. Prove that\[AC + AD = BC\].

Ans: \[{\text{ABC}}\] is a right triangle such that \[{\text{AB  =  AC}}\] and bisector of angle \[{\text{C}}\] intersects the side AB at D.

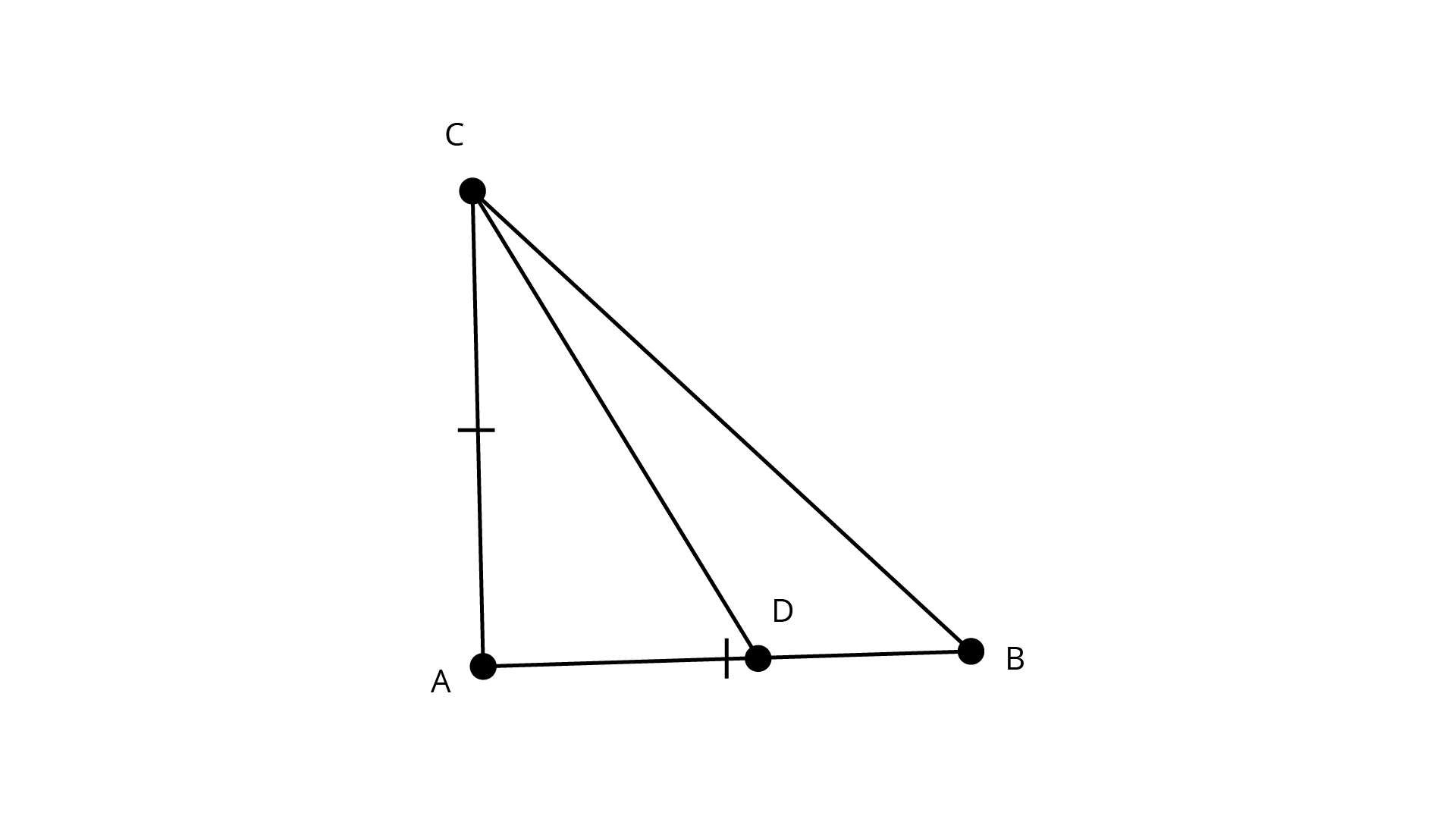
Let ${\text{AB  =  AC  =  a}}$ and ${\text{AD  =  b}}$.

${{\Delta ABC}}$ is right angled at  \[{\text{B}}\]

$\Rightarrow A{B^2} + A{C^2} = B{C^2}$ $\Rightarrow BC = a\sqrt 2 $

$BD = AB - AD = a - b$.

We know that:

Angle bisector theorem: An angle bisector of a triangle divides the opposite side into two segments that are proportional to the other two sides.

$\dfrac{{AD}}{{BD}} = \dfrac{{AC}}{{BC}}$

$\Rightarrow \dfrac{b}{{a - b}} = \dfrac{a}{{a\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }}$

$\Rightarrow b = \dfrac{a}{{1 + \sqrt 2 }} = a(\sqrt 2  - 1)$

$\Rightarrow a + b = a\sqrt 2 $

But, we know $AC = a,AD = b,BC = a\sqrt 2 $

$\Rightarrow AC + AD = BC$. 

Hence proved.

19. AB and CD are the smallest and largest sides of a quadrilateral \[ABCD\]. Out of \[\angle B\] and \[\angle D\] decide which is greater.

Ans: \[{\text{AB and CD}}\] are the smallest and largest sides of a quadrilateral \[{\text{ABCD}}\].

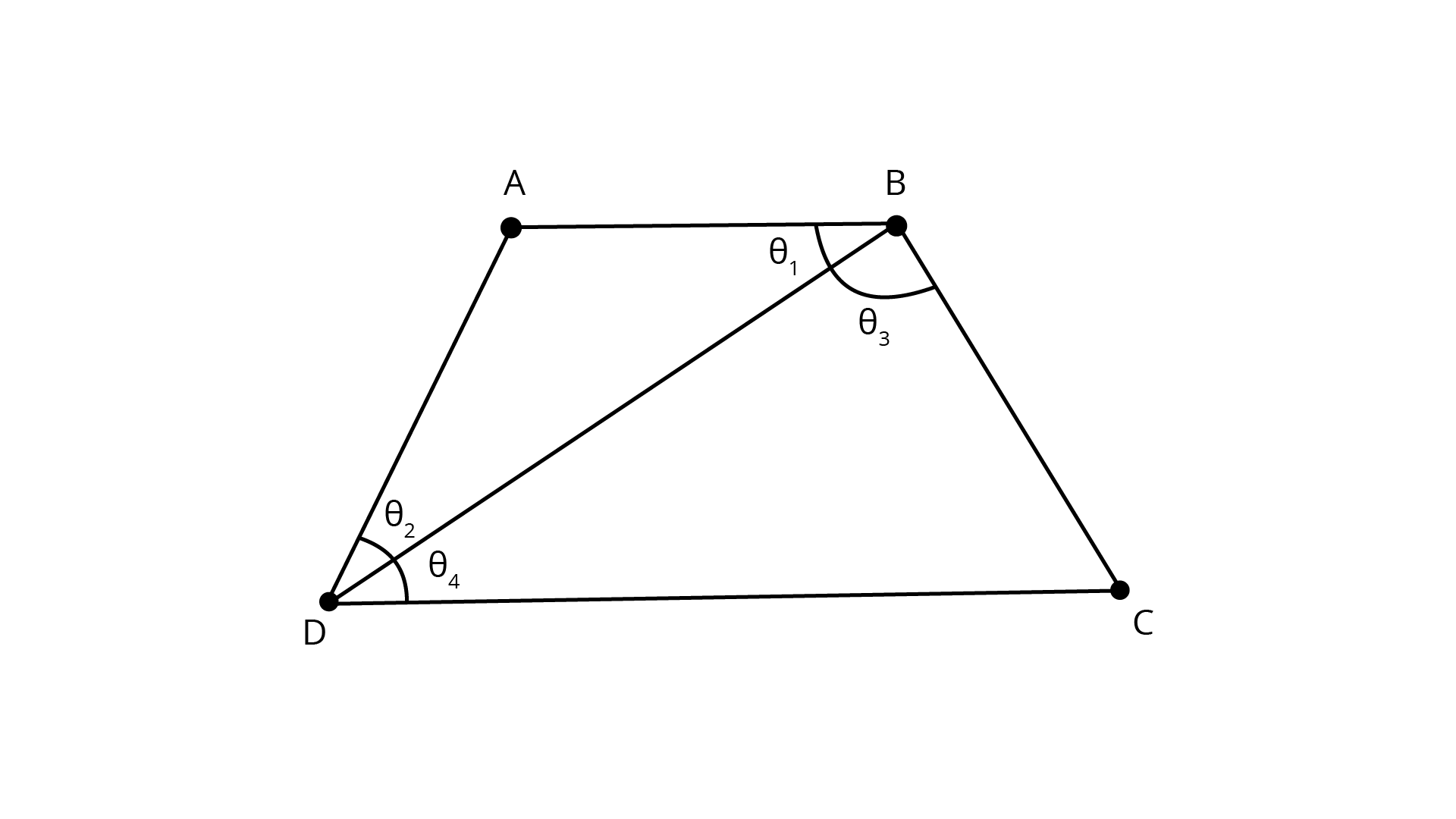
Here, \[{\text{AB}}\] as the smallest side and \[{\text{CD}}\] as the largest side. 

Join the diagonal${\text{BD}}$.

 Label the angles as \[{\theta _1},{\theta _2},{\theta _3},{\theta _4}\] as shown in figure. 

Now in ${{\Delta ABD}}$,

$AB < AD$ (Since \[{\text{AB}}\] is the smallest side in \[{\text{ABCD}}\])

$\Rightarrow {\theta _2} < {\theta _1}.....(1)$

Similarly in ${{\Delta BCD}}$, 

$BC < CD$ (Since \[{\text{CD}}\] is the largest side in \[{\text{ABCD}}\])

$\Rightarrow {\theta _4} < {\theta _3}.....(2)$

Adding equations (1) and (2), we get:

${\theta _2} + {\theta _4} < {\theta _1} + {\theta _3}$

$\angle D < \angle B$

Hence, $\angle B$ will be greater.

20. Prove that in a triangle, other than an equilateral triangle, angle opposite the longest side is greater than \[\dfrac{2}{3}\] of a right angle.

Ans: \[{{\Delta PQR}}\] is a triangle, other than an equilateral triangle.

${\text{PR}}$ is the longest side.

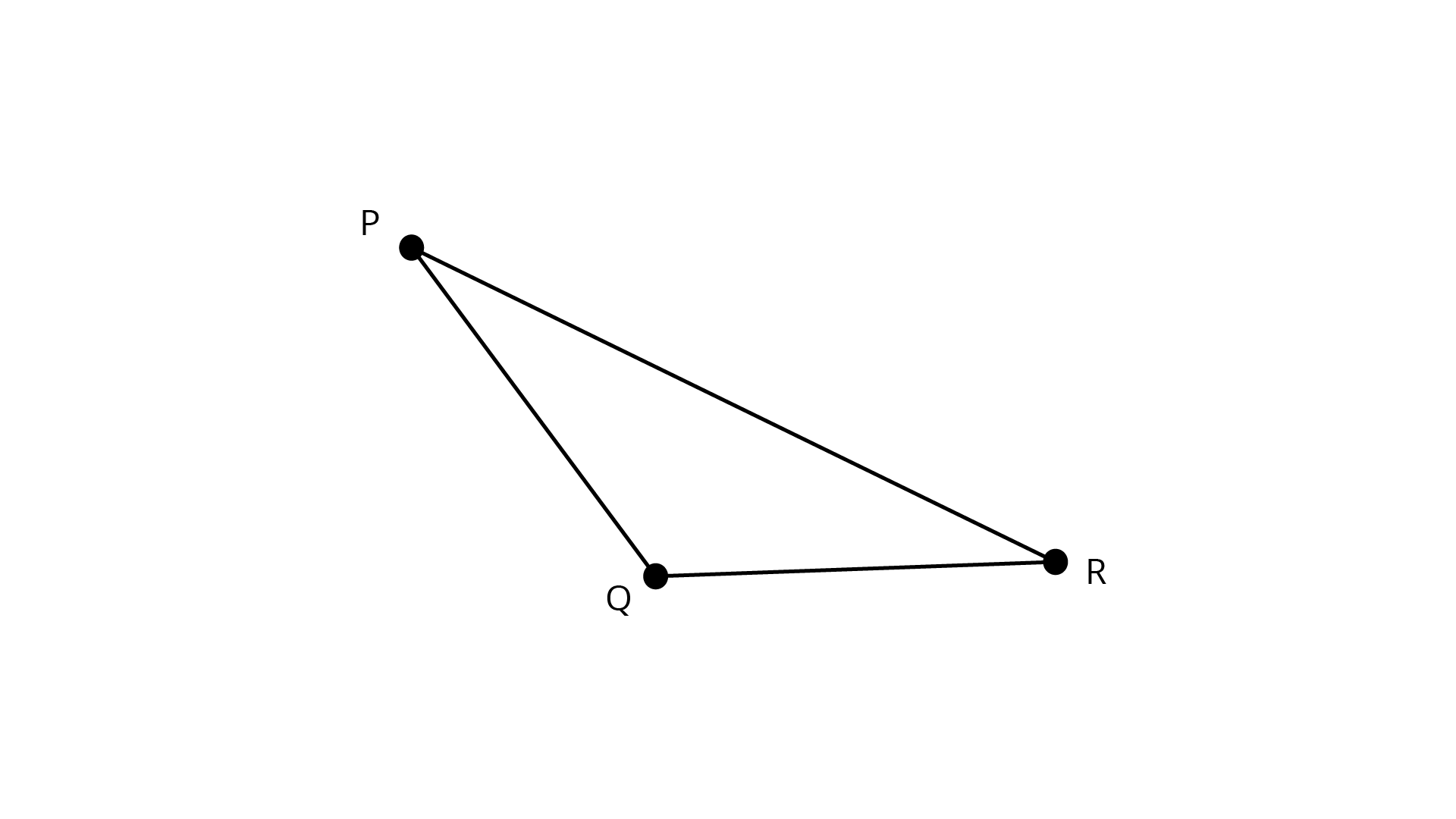
We know that:

The angle opposite greater side is greater.

${\text{PR}} > {\text{PQ}}$.

$\angle Q > \angle R..............(1)$

Also, $PR > QR$

$\angle Q > \angle P.............(2)$

By adding both the equations

$\angle Q + \angle Q > \angle R + \angle P$

Therefore, 

$2\angle Q > \angle R + \angle P$

Adding $\angle Q$ on both LHS and RHS, we get:

$2\angle Q + \angle Q > \angle R + \angle P + \angle Q$

\[\because \] $\angle R + \angle P + \angle Q = 180^\circ .....................({\text{The sum of all angles of triangle is }}180^\circ {\text{)}}$

So we get

$3\angle Q > {180^\circ }$

$\angle Q > {60^\circ }$

Rewrite the terms, we get:

$\angle Q > \dfrac{2}{3}\left( {{{90}^\circ }} \right)$

$\angle Q > \dfrac{2}{3}$ of a right angle

Hence, in a triangle, other than an equilateral triangle, the angle opposite the longest side is greater $\dfrac{2}{3}$ of a right angle.

21. ABCD is quadrilateral such that AB  =  AD and CB  =  CD. Prove that \[AC\] is the perpendicular bisector of \[BD\].

Ans: ABCD is quadrilateral such that \[{\text{AB  =  AD and CB  =  CD}}\].

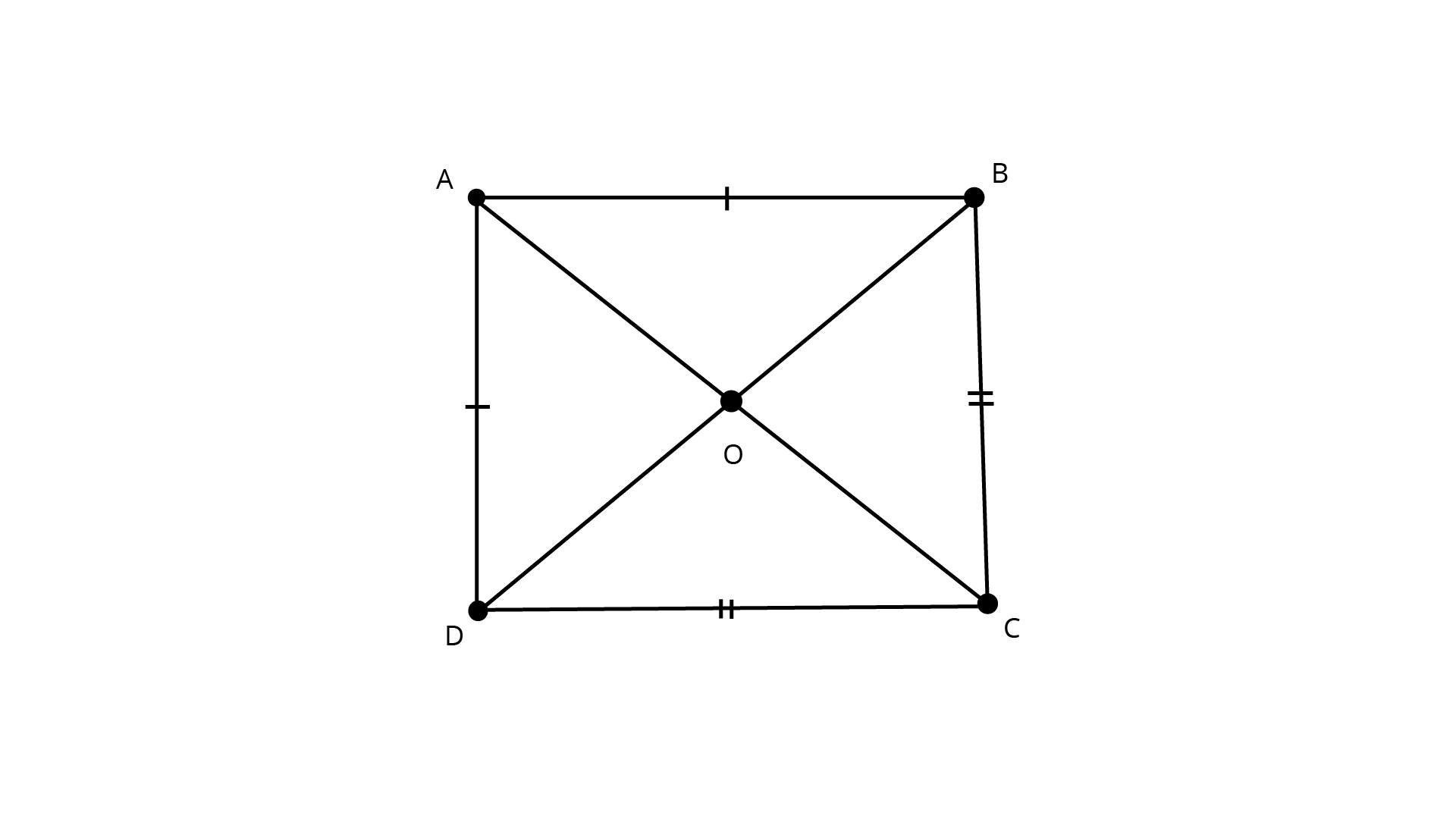
In \[{{\Delta ABC}}\] and \[{{\Delta ADC}}\]

\[{\text{AB  =  AD}}\] (given)

\[{\text{BC  =  CD}}\] (given)

\[{\text{AC  =  AC}}\] (common side)

\[\Delta ABC \cong \Delta ADC\] (By SSS)

\[{\text{AB  =  AD}}\] (given)

\[\therefore {\text{AO  =  AO}}\] (common)

\[\angle BAO = \angle DAO\] (By CPCT) 

\[\Rightarrow \Delta AOB \cong \Delta AOD\] (SAS)

\[{\text{DO  =  BO}}.....\left( i \right)\] (CPCT)

\[\angle AOD = \angle AOB\] (CPCT)

\[\angle AOD + \angle AOB = 180^\circ \]

\[\Rightarrow \angle AOD = \angle AOB = 90^\circ \]

\[{\text{AC}}\] is a perpendicular bisector of \[{\text{BD}}\].

NCERT Exemplar Class 9 Maths Solutions for Chapter 7 Talks About:

• The part starts with the depiction of the triangles, which includes the properties of triangles. 

• Congruence triangles form when three sides of two triangles are identical to fit into one another. 

• The SAS Congruence rule states that two triangles are congruent, provided that the point in every triangle is equivalent, and the sides holding these points are likewise equivalent. 

• Yet, the ASA congruence rule is not the same as that of SAS Congruence. 

• The ASA Congruence rule states that two triangles are consistent in case two points of every triangle are equivalent and the normal side holding them is additionally equivalent. 

• No two rules of congruence triangles are similar, so various conditions are utilized to solve the problem. 

• The chapter finishes with different theorems used to take care of various triangle problems.

Conclusion

The study material can be extra valuable to students stalling out at a specific sum since we esteem time to the most and believe that students should limit the wastage of time. Download maths NCERT solutions class 9 prepared by a master teacher at Vedantu.