Find Complete Class 9 Maths Chapter 3 Coordinate Geometry Questions and Answers With Easy Solutions | FREE PDF Download
FAQs on NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry
1. What is the stepwise method for solving NCERT Class 9 Maths Chapter 3 Exercise 3.1 as per the latest CBSE-approved guidelines?
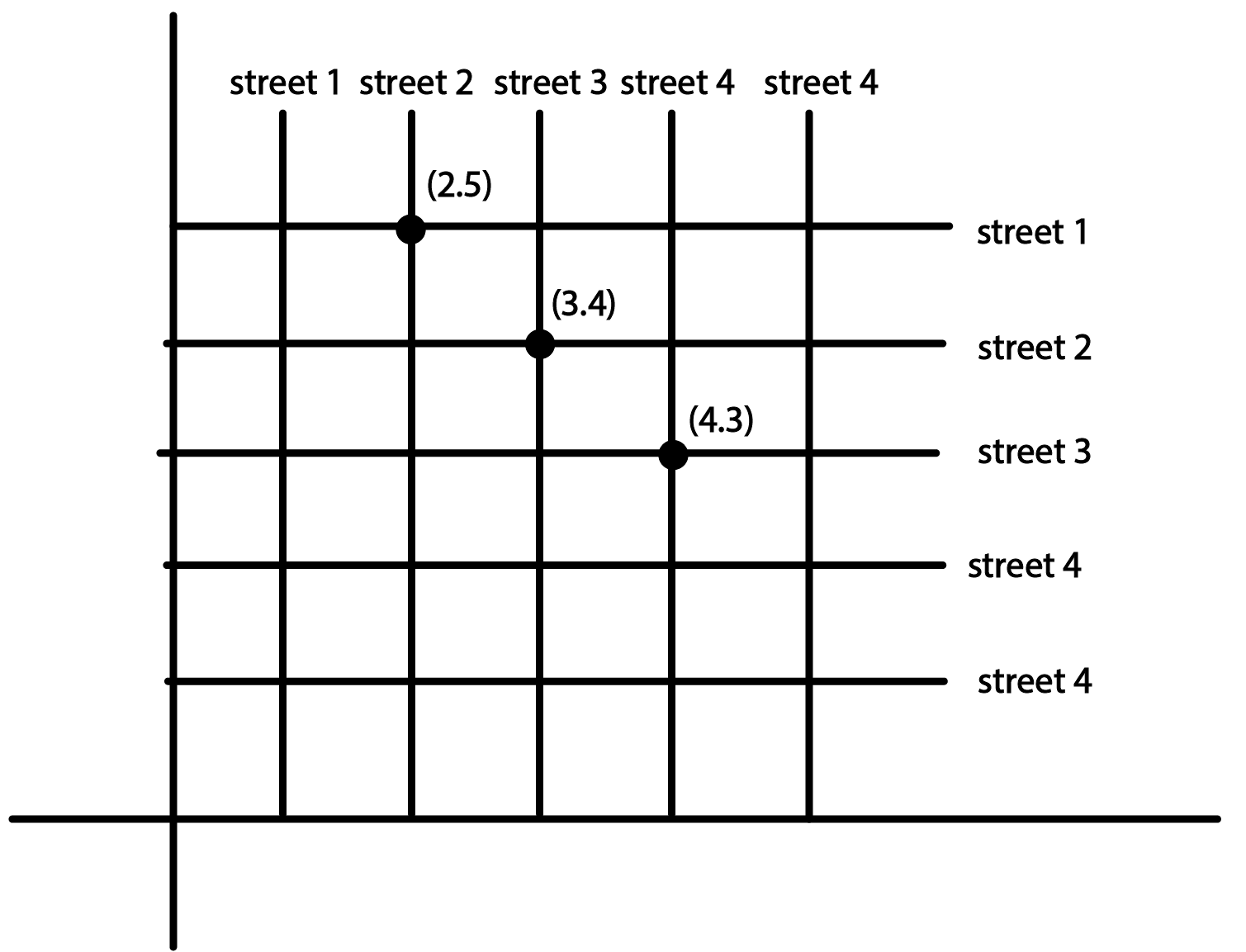
To solve Exercise 3.1 of NCERT Class 9 Maths Chapter 3 (Coordinate Geometry) as per the updated CBSE 2025–26 syllabus, always begin by identifying the x-axis and y-axis on the Cartesian plane. For each question, plot or read the given coordinates, specify the quadrant, and follow the order: move parallel to the x-axis first (abscissa), then parallel to the y-axis (ordinate). Give justification for the location or sign of coordinates as instructed in the NCERT answer key format. Ensure that your answer strictly follows the official NCERT solution presentation style.
2. Where can I download the NCERT Solutions for Class 9 Maths Chapter 3 PDF in both English and Hindi medium?
You can download the complete NCERT Solutions for Class 9 Maths Chapter 3 'Coordinate Geometry' in PDF format, including both English and Hindi medium answers, directly from the Vedantu NCERT Solutions portal. The solutions are provided in a CBSE-approved, stepwise, textbook-compatible format and are regularly updated as per the latest 2025–26 syllabus. Look for the official 'Download PDF' button on the chapter solutions page for instant access.
3. How do I solve Exercise 3.2 of Class 9 Maths Chapter 3 using the NCERT pattern?
To solve Exercise 3.2 of Class 9 Maths Chapter 3 (Coordinate Geometry), use the NCERT stepwise method: read each problem carefully, identify the coordinates, and refer to how the Cartesian plane is divided into four quadrants. Plot the required points, specify in which quadrant each point lies, and justify your answer according to the sign conventions of abscissa and ordinate. Complete your solution using the NCERT-approved answer format for exercises.
4. Are these solutions to Class 9 Maths Chapter 3 exercises verified and correct as per CBSE NCERT standards?
Yes, all solutions provided for Class 9 Maths Chapter 3 are fully verified, accurate, and match the latest CBSE-approved NCERT textbook answer key. Each step follows the official NCERT structure and is designed to help students score full marks by aligning answers to the updated marking scheme for the academic year 2025–26.
5. Can I get stepwise explanations for all exercises in NCERT Class 9 Maths Chapter 3, including Exercise 3.3 and Exercise 3.4?
Absolutely, you can get detailed, stepwise explanations for every question in all exercises—including Exercise 3.3 and 3.4—of NCERT Class 9 Maths Chapter 3 on Vedantu. Each answer is provided in a clear, CBSE-format manner with each logical reasoning and calculation broken down for easy understanding as per the 2025–26 syllabus.
6. How can I access the NCERT solutions for Class 9 Maths Chapter 3 Exercise 3.1 in Hindi medium?
Hindi medium NCERT solutions for Class 9 Maths Chapter 3 Exercise 3.1 are available in PDF and online view formats on the Vedantu NCERT Solutions platform. The format and steps strictly follow the NCERT answer writing style and CBSE's correct Hindi terminology, ensuring that students from Hindi medium backgrounds receive CBSE-aligned answers to all questions.
7. Does the NCERT answer key for Class 9 Maths Chapter 3 cover all intext and back-exercises in the official textbook?
Yes, the NCERT Solutions for Class 9 Maths Chapter 3 provide complete, stepwise answers to all intext questions, back exercises, and every question listed in the official CBSE NCERT textbook for the chapter 'Coordinate Geometry.' This includes explanations for all exercises: 3.1, 3.2, 3.3, and 3.4, ensuring full syllabus coverage.
8. Why is the stepwise presentation of solutions important in Class 9 Maths Chapter 3 as per CBSE requirements?
Stepwise presentation is important in NCERT Class 9 Maths Chapter 3 because it ensures all method marks are awarded, as per the latest CBSE evaluation criteria. The answers must show logical steps such as identification of axes, plotting of points, quadrant selection, and sign justification, which are all required in CBSE-approved solutions to score maximum marks.
9. What should I do if I get different answers from my textbook and the NCERT solutions for a question in Chapter 3?
If you get different answers, double-check your steps with the official NCERT Solutions for Class 9 Maths Chapter 3. All answers on Vedantu are meticulously checked according to the NCERT answer key and latest CBSE 2025–26 marking scheme. If discrepancies remain, follow the logic and steps outlined in the NCERT solution, as this is the CBSE-approved method your examiner will use for evaluation.
10. Are the NCERT Solutions for Class 9 Maths Chapter 3 suitable for school assignments and board preparation?
Yes, the provided NCERT Solutions for Class 9 Maths Chapter 3 are perfect for school assignments, homework, and even for CBSE board exam preparation. All solutions are presented as per NCERT textbook guidelines, so you can confidently use them to complete your school work or revise for exams according to the latest CBSE 2025–26 format.
11. What is the structure of a correct answer for plotting points in Exercise 3.1, and how does it follow the NCERT pattern?
A correct answer for a plotting question in Exercise 3.1 (Coordinate Geometry) should begin by stating the coordinates, identifying the x-axis and y-axis, describing the required movement from the origin, and plotting the point accordingly. You must also specify in which quadrant the point lies, as per the signs of the abscissa and ordinate. The format must mirror the NCERT pattern: clear labeling, logical order of steps, and justification for each coordinate placement.
12. What are some common mistakes students make in solving Chapter 3 (Coordinate Geometry) questions, and how can NCERT solutions help avoid them?
Common mistakes include confusing the abscissa and ordinate (reversing x and y values), placing points in the wrong quadrant, and not following the stepwise explanation required in the NCERT answer format. Using the official NCERT Solutions for Class 9 Maths Chapter 3 helps you understand the proper sequence, correct terminology, and ensures step-by-step accuracy based on CBSE requirements.
13. Is every step in the NCERT Solutions for Exercise 3.2 necessary to write in school exams?
Yes, every step provided in the NCERT Solutions for Exercise 3.2 is necessary to write as per the CBSE and NCERT marking scheme. Each step explains the logic, calculation, and justification of quadrant or sign, which are all required for full marks. Make sure to show your working and don’t skip any intermediate explanation, as per the NCERT-approved format.
14. Can I use these NCERT solutions for competitive exams that require Class 9 maths knowledge?
Yes, these NCERT Solutions for Class 9 Maths Chapter 3 follow the textbook pattern and provide a clear stepwise explanation, making them ideal for competitive exams that are based on CBSE/NCERT curriculum. They provide the foundational logic and method expected in entrance exams and Olympiads.
15. How does the NCERT answer key address the sign conventions for coordinates in different quadrants for Chapter 3?
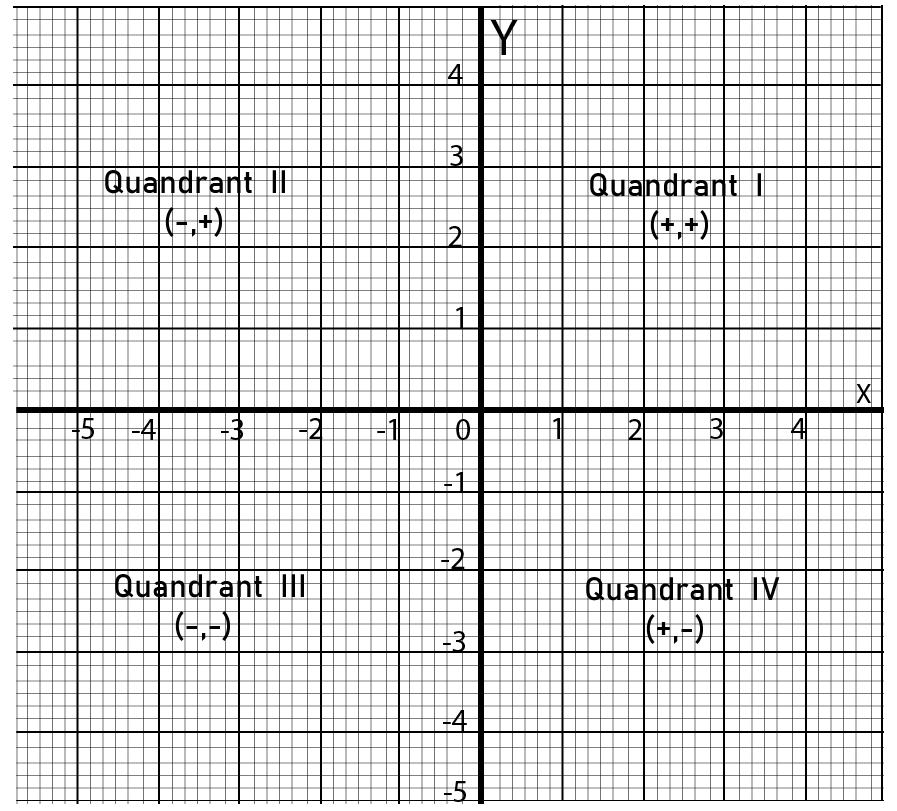
The NCERT answer key for Chapter 3 clearly specifies the sign conventions: in Quadrant I, both x and y are positive; in Quadrant II, x is negative and y is positive; in Quadrant III, both x and y are negative; in Quadrant IV, x is positive and y is negative. The stepwise solutions provided always clarify this convention for each plotted point as per the NCERT pattern, thus aligning with CBSE’s official evaluation scheme.