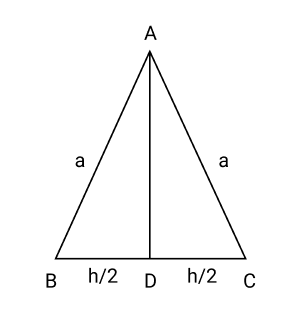
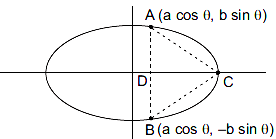
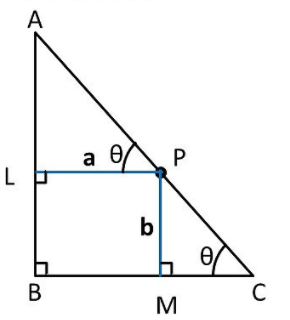
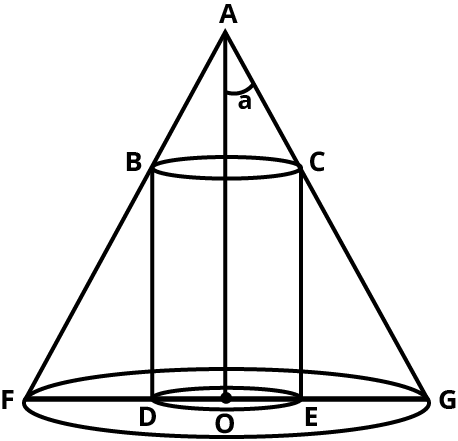
Maths Miscellaneous Exercise Class 12 Chapter 6 Questions and Answers - Free PDF Download
FAQs on NCERT Solutions For Class 12 Maths Miscellaneous Exercise Chapter 6 Application Of Derivatives - 2025-26
1. How do NCERT Solutions for Class 12 Maths Chapter 6 help students understand the Application of Derivatives more effectively?
NCERT Solutions for Class 12 Maths Chapter 6 provide step-by-step explanations for each problem, making complex derivative applications easier to grasp. By following each method, students develop a clear understanding of concepts like maxima and minima, rate of change, increasing and decreasing functions, and tangents and normals, as required by the CBSE syllabus.
2. What types of problems are typically solved using the Application of Derivatives in the Miscellaneous Exercise?
The Miscellaneous Exercise features a variety of problems, including:
- Optimization tasks (finding maximum or minimum values)
- Rate of change related word problems
- Questions on increasing and decreasing intervals
- Application-based scenarios involving tangents, normals, and geometric shapes
These problems reinforce the practical use of derivatives in different contexts.
3. Why is it crucial to practice stepwise solutions for the Application of Derivatives as shown in NCERT Solutions?
Practicing stepwise solutions ensures that students learn the correct procedure for solving derivative applications, avoid common calculation errors, and can clearly present logical reasoning in exams, which is vital for scoring well in CBSE board assessments.
4. What key strategies should be followed when solving challenging questions in the Miscellaneous Exercise of Chapter 6?
Key strategies include:
- Breaking down each question into smaller steps
- Identifying which formula or theorem applies, such as maxima/minima tests
- Checking the sign of derivatives for increasing or decreasing nature
- Reviewing solved examples for similar question patterns
- Interpreting word problems carefully before solving equations
5. Are there any common mistakes students should be aware of in the Application of Derivatives Miscellaneous Exercise?
Yes, common mistakes include:
- Incorrect differentiation, especially with composite or implicit functions
- Not properly checking critical points for maxima/minima
- Misinterpreting the intervals of increase or decrease
- Ignoring units or context in word problems
Reviewing NCERT Solutions helps students avoid these errors through clear examples.
6. How does understanding the methods in NCERT Solutions prepare students for higher-level exams and real-world applications?
Learning the systematic approach in NCERT Solutions gives students a foundation for tackling advanced questions in competitive exams and helps them apply calculus concepts in practical fields like physics, engineering, and economics.
7. In the context of CBSE board exams, how often do miscellaneous exercise questions from Application of Derivatives appear?
Questions similar to those in the Miscellaneous Exercise frequently appear in board exams, typically comprising 1 to 2 comprehensive questions that require applying multiple concepts. Mastering these solutions is important for full-length or higher-order thinking questions.
8. What should a student do if they face difficulty understanding a particular application of derivatives problem in the solutions?
If a problem seems difficult:
- Revisit the relevant theory or concept introduced earlier in the chapter
- Practice similar examples in the NCERT textbook
- Refer back to the stepwise breakdown in the solution for clarity
- Discuss with teachers or peers to resolve doubts
9. How do NCERT Solutions ensure alignment with the latest CBSE 2025–26 syllabus for Class 12 Maths?
All solutions are updated as per the latest CBSE 2025–26 guidelines, ensuring coverage of every topic, updated problem patterns, and the inclusion of skill-based and application-oriented questions according to the official syllabus requirements.
10. Can solving only NCERT Solutions guarantee full marks in the Application of Derivatives section for board exams?
While practicing NCERT Solutions thoroughly is often sufficient to solve most board exam questions, students should also focus on understanding underlying principles, practicing additional sample questions, and regularly revising core concepts for maximum marks.
11. What should students focus on when dealing with optimization problems in the Miscellaneous Exercise?
When solving optimization problems, students must:
- Identify the quantity to optimize (maximize or minimize)
- Formulate the objective function and apply necessary constraints
- Use differentiation to find critical points and apply the second derivative test for confirmation
12. How does one verify if a function is increasing or decreasing using derivatives in these exercises?
To check if a function is increasing or decreasing, compute its first derivative. If the derivative is positive on an interval, the function is increasing there; if the derivative is negative, it is decreasing on that interval. This approach directly follows CBSE and NCERT methods.
13. Why is it important to interpret the context of word problems before applying derivative techniques?
Interpreting the context ensures the correct formulation of mathematical models, prevents misunderstanding of quantities involved, and helps select the appropriate derivative and optimization technique for accurate, real-world answers.
14. How can using NCERT Solutions boost confidence for tackling unseen questions in board exams?
By practicing a variety of well-explained solutions, students become familiar with problem-solving techniques, learn to avoid common mistakes, and can approach new and unseen questions methodically during the board exams.
15. What are the benefits of cross-verifying answers with stepwise NCERT Solutions during self-study?
Cross-verification:
- Reveals calculation errors early
- Helps understand where mistakes occur in logic or method
- Builds a habit of stepwise verification, critical for CBSE answer scripts
- Provides confidence that solutions are accurate and aligned with the official answer key