NCERT Solutions for Class 12 Maths Chapter 6 Application Of Derivatives Ex 6.3

1. Find the maximum and minimum values, if any, of the following given by

1. $f\left( x \right)={{\left( 2x-1 \right)}^{2}}+3$ 

2. $f\left( x \right)=9{{x}^{2}}+12x+2$ 

3. $f\left( x \right)=-{{\left( x-1 \right)}^{2}}+10$ 

4. $g\left( x \right)={{x}^{3}}+1$ 

Ans: 

i) The given function is $f\left( x \right)={{\left( 2x-1 \right)}^{2}}+3$.

It can be observed that ${{\left( 2x-1 \right)}^{2}}\ge 0$ for every $x\in R$.

Therefore, $f\left( x \right)={{\left( 2x-1 \right)}^{2}}+3\ge 3$ for every $x\in R$.

The minimum value of $f$ is attained when $2x-1=0$ 

$2x-1=0,x=\frac{1}{2}$ 

Minimum value of $f\left( \frac{1}{2} \right)={{\left( 2.\frac{1}{2}-1 \right)}^{2}}+3=3.$ 

Hence, function $f$ does not have a maximum value.

ii) The given function is $f\left( x \right)=9{{x}^{2}}+12x+2={{\left( 3{{x}^{2}}+2 \right)}^{2}}-2$.

It can be observed that ${{\left( 3{{x}^{2}}+2 \right)}^{2}}\ge 0$ for every $x\in R$.

Therefore, $f\left( x \right)={{\left( 3{{x}^{2}}+2 \right)}^{2}}-2\ge -2$ for every $x\in R$.

The minimum value of $f$ is attained when $3x+2=0$ 

$3x+2=0,x=-\frac{2}{3}$ 

Minimum value of $f\left( -\frac{2}{3} \right)={{\left( 3\left( \frac{-2}{3} \right)+2 \right)}^{2}}-2=-2.$ 

Hence, function $f$ does not have a maximum value.

iii) The given function is $f\left( x \right)=-{{\left( x-1 \right)}^{2}}+10.$.

It can be observed that ${{\left( x-1 \right)}^{2}}\ge 0$ for every $x\in R$.

Therefore, $f\left( x \right)=-{{\left( x-1 \right)}^{2}}+10\le 10$ for every $x\in R$.

The minimum value of $f$ is attained when $\left( x-1 \right)=0$ 

$x-1=0,x=0$ 

Minimum value of $f=f\left( 1 \right)=-{{\left( 1-1 \right)}^{2}}+10=10$ 

Hence, function $f$ does not have a maximum value.

vi) The given function is $g\left( x \right)={{x}^{3}}+1$.

Hence, function $g$ neither has a maximum value nor a minimum value.

2. Find the maximum and minimum values, if any, of the following functions given by

i) $f\left( x \right)=\left| x+2 \right|-1$ 

Ans: We know that $\left| x+2 \right|\ge 0$ for every $x\in R$ 

Therefore, $f\left( x \right)=\left| x+2 \right|-1\ge -1$ for every $x\in R$

The minimum value of $f$ is attained when $\left| x+2 \right|=0$ 

 $\Rightarrow x=-2$ 

Minimum value of $f=f\left( -2 \right)=\left| -2+2 \right|-1=-1$ 

Hence, function $f$ does not have a maximum value.

ii) $g\left( x \right)=-\left| x+1 \right|+3$ 

Ans: We know that $-\left| x+1 \right|\le 0$ for every $x\in R$ 

Therefore, $g\left( x \right)=-\left| x+1 \right|+3\le 3$ for every $x\in R$

The minimum value of $g$ is attained when $\left| x+1 \right|=0$ 

 $\Rightarrow x=-1$ 

Minimum value of $g=g\left( -1 \right)=-\left| -1+1 \right|+3=3$ 

Hence, function $g$ does not have a maximum value.

iii) $h\left( x \right)=\sin 2x+5$ 

Ans: We know that $-1\le \sin 2x\le 1$ 

$  -1+5\le \sin 2x+5\le 1+5 $  

$  4\le \sin 2x+5\le 6 $  

Hence, the maximum and minimum values of $h$ are $6\And 4$ respectively.

vi) $f\left( x \right)=\left| \sin 4x+3 \right|$ 

Ans: We know that $-1\le \sin 4x\le 1$ 

$  2\le \sin 4x+3\le 4 $  

$  2\le \left| \sin 4x+3 \right|\le 4 $  

Hence, the maximum and minimum values of $f$ are $4\And 2$ respectively.

v) $h\left( x \right)=x+4,x\in \left( -1,1 \right)$ 

Ans: Here, if a point ${{x}_{0}}$ is closest to $-1$ , then we find $\frac{{{x}_{0}}}{2}+1<{{x}_{0}}+1$ for all ${{x}_{0}}\in \left( -1,1 \right)$.

Also, if ${{x}_{1}}$ is closet to $-1$ , then we find${{x}_{1}}+1<\frac{{{x}_{1}}+1}{2}+1$ for all ${{x}_{0}}\in \left( -1,1 \right)$.

Hence, function $h\left( x \right)$ has neither maximum nor minimum value at $\left( -1,1 \right).$

3. Find the local maxima and local minima, if any, of the following functions. Find also the local maximum and the local minimum values, as the case may be:

i) $f\left( x \right)={{x}^{2}}$

Ans: $f\left( x \right)={{x}^{2}}$ 

$\therefore f'\left( x \right)=2x$ 

Now, $f'\left( x \right)=0\Rightarrow x=0$ 

Thus, $x=0$ is the only critical point that could be the point of local maxima or local minima of $f.$ 

We have ${f}''\left( 0 \right)=2$, which is positive.

Therefore, by second derivative test,$x=0$ is a point of local minima and local minimum value of $f$ at $x=0$ is $f\left( 0 \right)=0.$ 

ii) $g\left( x \right)={{x}^{3}}-3x$

Ans: $g\left( x \right)={{x}^{3}}-3x$ 

$\therefore {g}'\left( x \right)=3{{x}^{2}}-3$ 

Now,

$  {g}'\left( x \right)=0\Rightarrow 3{{x}^{2}}=3\Rightarrow x=\pm 1 $  

$  {g}''\left( x \right)=6x $  

$  {g}''\left( 1 \right)=6>0 $  

$  {g}''\left( -1 \right)=-6<0 $  

By second derivative test, $x=1$ is a point of local minima and local minimum value of $g$ at $x=1$ is $g\left( 1 \right)={{1}^{3}}-3=-2.$

iii) $h\left( x \right)=\sin x+\cos .0<x<\frac{\pi }{2}$

Ans: $h\left( x \right)=\sin x+\cos .0<x<\frac{\pi }{2}$ 

$  \therefore {h}'\left( x \right)=\cos x+\sin x $  

$  {h}'\left( x \right)=0\Rightarrow \sin x=\cos x\Rightarrow \tan x=1 $  

$  \Rightarrow x=\frac{\pi }{4}\in \left( 0,\frac{\pi }{2} \right) $  

$  {h}''\left( x \right)=-\sin x-\cos x $  

$  {h}''\left( \frac{\pi }{4} \right)=-\left( \frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}} \right) $  

$  =-\frac{1}{\sqrt{2}}=-\sqrt{2}<0 $  

Therefore, by second derivative test, $x=\frac{\pi }{4}$ is a point of local maxima and the local maximum value of $h$ at $x=\frac{\pi }{4}$   

$  h\left( \frac{\pi }{4} \right)=\sin \frac{\pi }{4}+\cos \frac{\pi }{4} $  

$  =\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}. $

iv) $f\left( x \right)=\sin x-\cos x,0<x<2\pi $

Ans: $f\left( x \right)=\sin x-\cos x,0<x<2\pi $ 

$  \therefore {f}'\left( x \right)=\cos x+\sin x $  

$  {f}'\left( x \right)=0\Rightarrow \cos x=-\sin x $  

$  \tan x=-1\Rightarrow x=\frac{3\pi }{4},\frac{7\pi }{4}\in \left( 0,2\pi  \right) $  

$  {f}''\left( x \right)=-\sin x+\cos x $  

$  {f}''\left( \frac{3\pi }{4} \right)=-\sin \frac{3\pi }{4}+\cos \frac{3\pi }{4}=-\sqrt{2}<0 $  

$  {f}''\left( \frac{7\pi }{4} \right)=-\sin \frac{7\pi }{4}+\cos \frac{7\pi }{4}=\sqrt{2}>0 $  

Therefore, by second derivative test, $x=\frac{3\pi }{4}$ is appoint of local maxima and the local maximum value of $f$ at $x=\frac{3\pi }{4}$ is 

$f\left( \frac{3\pi }{4} \right)=\sin \frac{3\pi }{4}\cos \frac{3\pi }{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2}.$ However, $x=\frac{7\pi }{4}$ is a point of local minima and the local minimum value of $f$ at $x=\frac{7\pi }{4}$

is $f\left( \frac{7\pi }{4} \right)=\sin \frac{7\pi }{4}-\cos \frac{7\pi }{4}=-\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{2}}=-\sqrt{2.}$

v) $f\left( x \right)={{x}^{3}}-6{{x}^{2}}+9x+15$

Ans: $f\left( x \right)={{x}^{3}}-6x+9x+15$ 

$  \therefore {f}'\left( x \right)=3{{x}^{2}}-12x+9 $  

$  f\left( x \right)=0\Rightarrow 3\left( {{x}^{2}}-4x+3 \right)=0 $  

$  \Rightarrow 3\left( x-1 \right)\left( x-3 \right)=0 $  

$  \Rightarrow x=1,3 $  

Now,

$  {f}''\left( x \right)=6x-12=6\left( x-2 \right) $  

$  {f}''\left( 1 \right)=6\left( 1-2 \right)=-6<0 $  

$  {f}''\left( 3 \right)=6\left( 3-2 \right)=-6>0 $  

Therefore, by second derivative test, $x=1$ is a point of local maxima and the local maximum value of $f$ at $x=1$ is $f\left( 1 \right)=1-6+9+15=19$. However, $x=3$ is a point of local minima and the local minimum value of $f$ at $x=3$ is $f\left( 3 \right)=27-54+27+15=15.$

vi) $g\left( x \right)=\frac{x}{2}+\frac{2}{x},x>0$

Ans: $g\left( x \right)=\frac{x}{2}+\frac{2}{x},x>0$ 

$  \therefore {g}'\left( x \right)=\frac{1}{2}-\frac{2}{{{x}^{2}}} $  

$  Now, $  

$  {g}'\left( x \right)=0gives\frac{2}{{{x}^{2}}}=\frac{1}{2} $  

$  \Rightarrow {{x}^{2}}=4\Rightarrow x=\pm 2 $  

Since $x>0$ we take $x=2$.

Now, 

$  {g}''\left( x \right)=\frac{4}{{{x}^{3}}} $  

$  {g}''\left( 2 \right)=\frac{4}{{{2}^{3}}}=\frac{1}{2}>0 $  

Therefore, by second derivative test,  $x=2$ is a point of local minima and the local minimum value of $g$ at $x=2$ is $g\left( 2 \right)=\frac{2}{2}+\frac{2}{2}=1+1=2.$

vii) $g\left( x \right)=\frac{1}{{{x}^{2}}+2}$

Ans: $g\left( x \right)=\frac{1}{{{x}^{2}}+2}$ 

$  \therefore {g}'\left( x \right)=\frac{-\left( 2x \right)}{{{\left( {{x}^{3}}+2 \right)}^{2}}} $  

$  {g}'\left( x \right)=0\Rightarrow \frac{-\left( 2x \right)}{{{\left( {{x}^{3}}+2 \right)}^{2}}}=0\Rightarrow x=0 $  

Now, for values close to $x=0$ and to the left of $0,{g}'\left( x \right)>0$. Also, for values close to $x=0$ and to the right of ${g}'\left( x \right)<0.$ 

Therefore, by first derivative test $x=0$ is a point of local maxima and the local maximum value of $g\left( 0 \right)is\frac{1}{0+2}=\frac{1}{2}.$

viii) $f\left( x \right)=x\sqrt{1-x},x>0$

Ans: $f\left( x \right)=x\sqrt{1-x},x>0$ 

  $  \therefore {f}'\left( x \right)=x\sqrt{1-x}+x.\frac{1}{2\sqrt{1-x}}\left( -1 \right)=\sqrt{1-x}-\frac{x}{2\sqrt{1-x}} $  

 $  =\frac{2\left( 1-x \right)-x}{2\sqrt{1-x}}=\frac{2-3x}{2\sqrt{1-x}} $  

 $  {f}'\left( x \right)=0\Rightarrow \frac{2-3x}{2\sqrt{1-x}}=0 $  

 $  \Rightarrow 2-3x=0\Rightarrow x=\frac{2}{3} $  

 $  {f}''\left( x \right)=\frac{1}{2}\left[ \frac{\sqrt{1-x}\left( -3 \right)-\left( 2-3x \right)\left( \frac{-1}{2\sqrt{1-x}} \right)}{1-x} \right] $  

 $  =\frac{\sqrt{1-x}\left( -3 \right)+2\left( 2-3x \right)\left( \frac{1}{2\sqrt{1-x}} \right)}{2\left( 1-x \right)} $  

 $  =\frac{3x-4}{4{{\left( 1-x \right)}^{\frac{3}{2}}}} $  

 $  {f}'\left( \frac{2}{3} \right)=\frac{2-4}{4{{\left( \frac{1}{3} \right)}^{\frac{3}{2}}}}=\frac{-1}{2{{\left( \frac{1}{3} \right)}^{\frac{3}{2}}}}<0 $   

Therefore, by second derivative test, $x=\frac{2}{3}$ is a point of local 

maxima and the local maximum value of $f$ at $x=\frac{2}{3}$ is $f\left( \frac{2}{3} \right)=\frac{2-4}{4{{\left( \frac{1}{3} \right)}^{\frac{3}{2}}}}=\frac{-1}{2{{\left( \frac{1}{3} \right)}^{\frac{3}{2}}}}<0$.

4. Prove that the following functions do not have maxima or minima:

i) $f\left( x \right)={{e}^{x}}$

Ans: $f\left( x \right)={{e}^{x}}$ 

$\therefore {f}'\left( x \right)={{e}^{x}}$ 

Now, if  ${f}'\left( x \right)=0$ then ${{e}^{x}}=0$. But the exponential function can never assume $0$ for any value of $x$.

Therefore, there does not exist $c\in R$ such that ${f}'\left( c \right)=0$.

Hence, function $f$ does not have maxima or minima.

ii) $g\left( x \right)=\log x$

Ans: We have,

$  g\left( x \right)=\log x $  

$  \therefore {g}'\left( x \right)=\frac{1}{x} $  

Since $\log x$ is defined for a positive number $x,{g}'\left( x \right)>0$ for any $x$

Therefore, there does not exist  $c\in R$ such that ${g}'\left( c \right)=0$.

Hence, function $g$ does not have maxima or minima.

iii) $h\left( x \right)={{x}^{3}}+{{x}^{2}}+x+1$

Ans: We have,

$  h\left( x \right)={{x}^{3}}+{{x}^{2}}+x+1 $  

$  \therefore {h}'\left( x \right)=3{{x}^{2}}+2x+1 $  

Now,

Therefore, there does not exist $c\in R$ such that ${h}'\left( c \right)=0$.

Hence, function $h$ does not have maxima or minima.

5. Find the absolute maximum value and the absolute minimum value of the following functions in the given intervals:

i) $f\left( x \right)={{x}^{3}},x\in \left[ -2,2 \right]$ 

Ans: The given function is $f\left( x \right)={{x}^{3}}$.

$\therefore {f}'\left( x \right)=3{{x}^{2}}$ 

Now,

${f}'\left( x \right)=0\Rightarrow x=0$ 

Then, we evaluate the value of $f$ at critical point $x=0$ and at endpoints of the interval $\left[ -2,2 \right]$.

$  f\left( 0 \right)=0 $  

 $  f\left( -2 \right)={{\left( -2 \right)}^{3}}=-8 $  

 $  f\left( 2 \right)={{\left( 2 \right)}^{3}}=8 $  

Hence, we can conclude that the absolute maximum value of $f$ on $\left[ -2,2 \right]$ is $8$ occurring at $x=-2$. Also, the absolute minimum value of $f$  on $\left[ -2,2 \right]$ is $-8$ occurring at $x=-2$.

ii) $f\left( x \right)=\sin x+\cos x,x\in \left[ 0,\pi  \right]$ 

Ans: The given function is $f\left( x \right)=\sin x+\cos x$ 

$\therefore {f}'\left( x \right)=\cos x-\sin x$ 

Now,

$  {f}'\left( x \right)=0\Rightarrow \sin x=\cos x $  

$  \Rightarrow \tan x=1\Rightarrow x=\frac{\pi }{4} $  

Then, we evaluate the value of $f$ at critical point $x=\frac{\pi }{4}$ and at the endpoints of the interval $\left[ 0,\pi  \right]$.

  $  f\left( \frac{\pi }{4} \right)=\sin \frac{\pi }{4}+\cos \frac{\pi }{4}=\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}=\sqrt{2} $  

 $  f\left( 0 \right)=\sin 0+\cos 0=1 $  

 $  f\left( \pi  \right)=\sin \pi +\cos \pi =1 $  

Hence, we can conclude that the absolute maximum value of $f$ on $\left[ 0,\pi  \right]$ is $\sqrt{2}$ occurring at $x=\frac{\pi }{4}$. Also, the absolute minimum value of $f$ on $\left[ 0,\pi  \right]$ is $-1$ occurring at $x=\pi $.

iii) $f\left( x \right)=4x-\frac{1}{2}{{x}^{2}},x\in \left[ -2,\frac{9}{2} \right]$ 

Ans: The given function is $f\left( x \right)=4x-\frac{1}{2}{{x}^{2}}$ 

$\therefore {f}'\left( x \right)=4x-\frac{1}{2}{{x}^{2}}$

Now,

${f}'\left( x \right)=0\Rightarrow x=4$ 

Then, we evaluate the value of $f$ at critical point $x=4$ and at the endpoints of the interval $\left[ -2,\frac{9}{2} \right]$.

  $  f\left( 4 \right)=16-\frac{1}{2}\left( 16 \right)=8 $  

 $  f\left( -2 \right)=-8-\frac{1}{2}\left( 4 \right)=-10 $  

 $  f\left( \frac{9}{2} \right)=4\left( \frac{9}{2} \right)-\frac{1}{2}{{\left( \frac{9}{2} \right)}^{2}}=18-\frac{81}{8}=7.875 $  

Hence, we can conclude that the absolute maximum value of $f$ on $\left[ -2,\frac{9}{2} \right]$ is $8$ occurring at $x=4$. Also, the absolute minimum value of $f$ on $\left[ -2,\frac{9}{2} \right]$ is $-10$ occurring at $x=-2$.

iv) $f\left( x \right)={{\left( x-1 \right)}^{2}}+3,x\in \left[ -3,1 \right]$

Ans: The given function is $f\left( x \right)={{\left( x-1 \right)}^{2}}+3$ 

$\therefore {f}'\left( x \right)=2\left( x-1 \right)$

Now,

${f}'\left( x \right)=0\Rightarrow 2\left( x-1 \right)=0,x=1$ 

Then, we evaluate the value of x at critical point $x=1$ and at the endpoints of the interval $\left[ -3,1 \right]$.

  $  f\left( 1 \right)={{\left( 1-1 \right)}^{2}}+3=3 $  

 $  f\left( -3 \right)={{\left( -3-1 \right)}^{2}}+3=19 $  

Hence, we can conclude that the absolute maximum value of f on $\left[ -3,1 \right]$ is $19$ taking place at $x=-3$. Also, the absolute minimum value of f on $\left[ -3,1 \right]$ is $3$ taking place at $x=1$.

6. Find the maximum profit that a company can make if the profit function is given by $p\left( x \right)=41-24x-18{{x}^{2}}$.

Ans: The profit function is given as $p\left( x \right)=41-24x-18{{x}^{2}}$.

$  \therefore {p}'\left( x \right)=-24-36x $  

$  {p}''\left( x \right)=-36 $  

$  Now, $  

$  {p}'\left( x \right)=0 $  

$  \Rightarrow x=\frac{-24}{36}=-\frac{2}{3} $  

$  Also, $  

$  {p}''\left( \frac{-2}{3} \right)=-36<0 $  

By second derivatives test, $x=-\frac{2}{3}$ is the point of local maximum of $p$

Therefore, Maximum profit = $p\left( -\frac{2}{3} \right)$ 

$  =41-24\left( -\frac{2}{3} \right)-18{{\left( -\frac{2}{3} \right)}^{2}} $  

$  =41+16-8 $  

$  =49 $  

Hence, the maximum profit that the company can make is $49$ units.

7. Find both the maximum value and the minimum value of $3x^{4}-8x^{3}+ 12x^{2}-48x+25$ on the interval [0,3].

Ans:  Let’s take f(x) = $3x^{4}-8x^{3}+ 12x^{2}-48x+25$ on [0,3]

${f}'\left ( x \right ) = 12x^{3}-24x^{2}+24x-48$

Now ${f}'\left ( x \right ) = 0$

$12x^{3}-24x^{2}+24x-48 = 0$

$x^{3}-2x^{2}+2x-4=0$

$\left ( x-2 \right )\left ( x^{2}+2 \right )=0$

$x=2 or x=\pm \sqrt{2}$

As $ x=\pm \sqrt{2}$ is imaginary, therefore this value is not considered.

At x=2, f(2) = 3(16)-8(8)+12(4)-48(2)+25 = -39

At x=0, f(0) = 3(0)-8(0)+12(0)-48(0)+25 = 25

At x=3, f(3) = 3(81)-8(27)+12(9)-48(3)+25 = 16

Therefore, the minimum value of the given function is -39 and maximum value is 25.

8. At what points in the interval $\left[ 0,2\pi  \right]$ does the function $\sin 2x$ attain, its maximum value?

Ans: Let 

$  f\left( x \right)=\sin 2x $  

$  \therefore {f}'\left( x \right)=2\cos 2x $  

$  Now, $  

$  {f}'\left( x \right)=0\Rightarrow \cos 2x=0 $  

$  \Rightarrow 2x=\frac{\pi }{2},\frac{3\pi }{2},\frac{5\pi }{2},\frac{7\pi }{2} $  

$  \Rightarrow x=\frac{\pi }{4},\frac{3\pi }{4},\frac{5\pi }{4},\frac{7\pi }{4} $  

Then, we evaluate the values of $f$ at critical points 

$x=\frac{\pi }{4},\frac{3\pi }{4},\frac{5\pi }{4},\frac{7\pi }{4}$ and at the endpoints of

the interval $\left[ 0,2\pi  \right]$.

$  f\left( \frac{\pi }{4} \right)=\sin \frac{\pi }{2}=1, $  

$  f\left( \frac{3\pi }{4} \right)=\sin \frac{3\pi }{2}=-1, $  

$  f\left( \frac{5\pi }{4} \right)=\sin \frac{5\pi }{2}=1, $  

$  f\left( \frac{7\pi }{4} \right)=\sin \frac{7\pi }{2}=-1, $  

$  f\left( 0 \right)=\sin 0=0, $  

$  f\left( 2\pi  \right)=\sin 2\pi =0 $  

Hence, we can conclude that the absolute maximum value of 

$f\left[ 0,2\pi  \right]$ is occurring at $x=\frac{\pi }{4}$ and $x=\frac{5\pi }{4}.$

9. What is the maximum value of the function $\sin x+\cos x$?

Ans: Let $f\left( x \right)=\sin x+\cos x$ 

$  \therefore {f}'\left( x \right)=\cos x-\sin x $  

$  {f}'\left( x \right)=0\Rightarrow \sin x=\cos x $  

$  \Rightarrow \tan x=1\Rightarrow x=\frac{\pi }{4},\frac{5\pi }{4},... $  

$  {f}'\left( x \right)=-\sin x-\cos x=-\left( \sin x+\cos x \right) $  

Now, when $\left( \sin x+\cos x \right)$ is positive, i.e., 

when sin x and cos x are both positive, f” (x) will be negative.

We also know that in the first quadrant, both sin x and cos x are positive. Then, ${f}''\left( x \right)$ will be 

negative when $x\in \left( 0,\frac{\pi }{2} \right)$.

As a result, we consider $x=\frac{\pi }{4}$ 

${f}''\left( \frac{\pi }{4} \right)=-\left( \sin \frac{\pi }{4}+\cos \frac{\pi }{4} \right)=-\left( \frac{2}{\sqrt{2}} \right)=-\sqrt{2}<0$ 

By second derivative test, $f$ will be the maximum at $x=\frac{\pi }{4}$ and the 

maximum value of $f$ is  $f\left( \frac{\pi }{4} \right)=\sin \frac{\pi }{4}+\cos \frac{\pi }{4}=\frac{1}{\sqrt{2}}\times \frac{1}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}.$

10. Find the maximum value of $2{{x}^{3}}-24x+107$ in the interval $\left[ 1,3 \right]$ 

Find the maximum value of the same function in $\left[ -3,-1 \right]$.

Ans: Let $f\left( x \right)=2{{x}^{3}}-24x-107$    

$  \therefore {f}'\left( x \right)=6{{x}^{2}}-24=6\left( {{x}^{2}}-4 \right) $  

$  Now, $  

$  {f}'\left( x \right)=0\Rightarrow 6\left( {{x}^{2}}-4 \right)=0 $  

$  \Rightarrow {{x}^{2}}=4\Rightarrow x=\pm 2 $  

We first consider the interval $\left[ 1,3 \right]$.

Then, we evaluate the value of $f$ at the critical point $x\in \left[ 1,3 \right]$ and at the endpoints of the interval $\left[ 1,3 \right]$.

$  f\left( 2 \right)=2\left( 8 \right)-24\left( 2 \right)+107=75 $  

$  f\left( 1 \right)=2\left( 1 \right)-24\left( 1 \right)+107=85 $  

$  f\left( 3 \right)=2\left( 27 \right)-24\left( 3 \right)+107=89 $  

Hence, the absolute maximum value of $f\left( x \right)$ in the interval $\left[ 1,3 \right]$ is

$89$ occurring at $x=3$.

Next, we consider the interval $\left[ -3,-1 \right]$.

Evaluate the value of $f$ at the critical point $x\in \left[ 1,3 \right]$ and at 

the endpoints of the interval $\left[ -3,-1 \right]$.

$  f\left( -3 \right)=2\left( -27 \right)-24\left( -3 \right)+107=125 $  

$  f\left( -1 \right)=2\left( -1 \right)-24\left( -1 \right)+107=129 $  

$  f\left( -2 \right)=2\left( -8 \right)-24\left( -2 \right)+107=139 $  

Hence, the absolute maximum value of $f\left( x \right)$ in the interval $\left[ -3,-1 \right]$ is

$139$ occurring at $x=-2$.

11. It is given that at $x=1$ the function ${{x}^{4}}-62{{x}^{2}}+ax+9$ attains its maximum value, on the interval $\left[ 0,2 \right]$. Find the value of a.

Ans: Let $f\left( x \right)={{x}^{4}}-62{{x}^{2}}+ax+9$ 

$\therefore {f}'\left( x \right)=4{{x}^{2}}-124x+a$ 

It is given that function $f$ attains its maximum value on the interval 

$\left[ 0,2 \right]$ at $x=1$.

$  \therefore {f}'\left( 1 \right)=0 $  

$  \Rightarrow 4-124+a=0 $  

$  \Rightarrow a=120 $  

Hence, the value of $a$ is $120.$

12. Find the maximum and minimum values of $x+\sin 2x$ on $\left[ 0,2\pi  \right].$ 

Ans: Let $f\left( x \right)=x+\sin 2x$ 

$  \therefore {f}'\left( x \right)=1+2\cos 2x $  

$  Now,{f}'\left( x \right)=0\Rightarrow \cos 2x=-\frac{1}{2}=\cos \frac{2\pi }{3} $  

$  2x=2\pi \pm \frac{2\pi }{3},n\in Z $  

$  \Rightarrow x=\pi \pm \frac{\pi }{3},n\in Z $  

$  \Rightarrow x=\frac{\pi }{3},\frac{2\pi }{3},\frac{4\pi }{3},\frac{5\pi }{3}\in \left[ 0,2\pi  \right] $  

Then, we evaluate the value of at $f$critical points $\Rightarrow x=\frac{\pi }{3},\frac{2\pi }{3},\frac{4\pi }{3},\frac{5\pi }{3}$ and the end points of the interval $\left[ 0,2\pi  \right]$.

$  f\left( \frac{\pi }{3} \right)=\frac{\pi }{3}+\sin \frac{2\pi }{3}=\frac{\pi }{3}+\frac{\sqrt{3}}{2} $  

$  f\left( \frac{2\pi }{3} \right)=\frac{2\pi }{3}+\sin \frac{4\pi }{3}=\frac{2\pi }{3}-\frac{\sqrt{3}}{2} $  

$  f\left( \frac{4\pi }{3} \right)=\frac{4\pi }{3}+\sin \frac{8\pi }{3}=\frac{4\pi }{3}+\frac{\sqrt{3}}{2} $  

$  f\left( \frac{5\pi }{3} \right)=\frac{5\pi }{3}+\sin \frac{10\pi }{3}=\frac{5\pi }{3}-\frac{\sqrt{3}}{2} $  

$  f\left( 0 \right)=0+\sin 0=0 $  

$  f\left( 2\pi  \right)=2\pi +\sin 4\pi =2\pi  $  

Hence, we can conclude that the absolute maximum value of $f\left( x \right)$ in 

the interval $\left[ 0,2\pi  \right]$ is $2\pi $ occurring at $x=2\pi $ and the absolute maximum value of $f\left( x \right)$ in the interval $\left[ 0,2\pi  \right]$ is $0$ occurring at $x=0.$

13. Find two numbers whose sum is $24$  and whose product is as large as possible.

Ans: Let one number be $x$. Then, the other number is $\left( 24-x \right)$.

Let $p\left( x \right)$ denote the product of the two numbers. Thus, we have:

$  P\left( x \right)=x\left( 24-x \right)=24x-{{x}^{2}} $  

$  \therefore {P}'\left( x \right)=24-2x $  

$  {P}''\left( x \right)=-2 $  

$  Now, $  

$  {P}'\left( x \right)=0\Rightarrow x=12 $  

$  Also, $  

$  {P}''\left( 12 \right)=-2<0 $  

By second derivative test, $x=12$ is the point of local maxima of P.

Hence, the product of the numbers is the maximum when the numbers are  $12$ and $24-12=12.$ 

14. Find two positive numbers $x$ and $y$such that $x+y=60$ and $x{{y}^{3}}$ is maximum.

Ans: It is assumed that the two numbers are $x$ and $y$ such that $x+y=60$.

$y=60-x$ 

Let $f\left( x \right)=x{{y}^{3}}$ 

$  \Rightarrow f\left( x \right)=x{{\left( 60-x \right)}^{3}} $  

$  \therefore {f}'\left( x \right)={{\left( 60+x \right)}^{3}}-3x{{\left( 60-x \right)}^{2}} $  

$  ={{\left( 60+x \right)}^{3}}\left[ 60-4x \right] $  

$  And, $  

$  {f}''\left( x \right)=-2\left( 60-x \right)\left( 60-4x \right)-4{{\left( 60-x \right)}^{2}} $  

$  =-2\left( 60-x \right)\left( 180-6x \right) $  

$  =-12\left( 60-x \right)\left( 30-x \right) $  

$  Now,{f}'\left( x \right)=0 $  

$  \Rightarrow x=60,15 $  

When $x=60,{f}''\left( x \right)=0$ 

When $x=15,{f}''\left( x \right)=-12\left( 60-15 \right)\left( 30-15 \right)<0.$ 

By second derivative test, $x=15$ is a point of local maxima of f.

Thus, function $x{{y}^{3}}$ maximum when $x=15$ and $y=60-15=45$.

Hence, the required numbers are 15 and 45.

15. Find two positive numbers x and y such that their sum is 35 and the product ${{x}^{2}}{{y}^{5}}$  is a maximum.

Ans: Let one number be x. Then, the other number is $y=\left( 35-x \right)$ 

Let $p\left( x \right)={{x}^{2}}{{y}^{5}}$. Then, we have:

$  P\left( x \right)={{x}^{2}}{{\left( 35-x \right)}^{5}} $  

$  \therefore {P}'\left( x \right)=2x{{\left( 35-x \right)}^{5}}-5{{x}^{2}}{{\left( 35-x \right)}^{4}} $  

$  =x{{\left( 35-x \right)}^{4}}\left[ 2\left( 35-x \right)-5x \right] $  

$  =7x{{\left( 35-x \right)}^{4}}\left( 10-x \right) $  

$  And, $  

$  {P}''\left( x \right)=7{{\left( 35-x \right)}^{4}}\left( 10-x \right)+7x\left[ -{{\left( 35-5 \right)}^{4}}-4{{\left( 35-x \right)}^{3}}\left( 10-x \right) \right] $  

$  =7{{\left( 35-x \right)}^{4}}\left( 10-x \right)-7x{{\left( 35-x \right)}^{4}}-28x{{\left( 35-x \right)}^{3}}\left( 10-x \right) $  

$  =7{{\left( 35-x \right)}^{3}}\left[ 350-45x+{{x}^{2}}-35x+{{x}^{2}}-40x+4{{x}^{2}} \right] $  

$  =7{{\left( 35-x \right)}^{3}}\left( 6{{x}^{2}}-120x+350 \right) $  

$  Now,{P}'\left( x \right)=0\Rightarrow x=0,x=35,x=10 $  

$  When,x=35,{f}'\left( x \right)=f\left( x \right)=0 $  

$  y=35-35=0. $  

This makes the product equal to 0.

When $x=0,y=35-0=35$ and the product ${{x}^{2}}{{y}^{5}}$ will be 0.

$x=0$ and $x=35$ cannot be the possible values of x.

When $x=10$ we have:

${P}''\left( x \right)=7{{\left( 35-10 \right)}^{3}}\left( -250 \right)<0$ 

By second derivative test, P(x) will be the maximum when $x=10$ and 

$y=35-10=25$.

Hence, the required numbers are 10 and 25.

16. Find two positive numbers whose sum is 16 and the sum of whose cubes is minimum.

Ans: Let one number be x. Then, the other number is $\left( 16-x \right)$.

Let the sum of the cubes of these numbers be denoted by S(x). Then, 

$  S\left( x \right)={{x}^{3}}+{{\left( 16-x \right)}^{3}} $  

$  \therefore {S}'\left( x \right)=3{{x}^{2}}-3{{\left( 16-x \right)}^{2}}, $  

$  {S}''\left( x \right)=6x+6\left( 16-x \right) $  

$  Now,{S}'\left( x \right)=0\Rightarrow 3{{x}^{2}}-3{{\left( 16-x \right)}^{2}}=0 $  

$  \Rightarrow {{x}^{2}}-{{\left( 16-x \right)}^{2}}=0 $  

$  \Rightarrow x=\frac{256}{32}=8 $  

$  Now, $  

$  {S}''\left( 8 \right)=6\left( 8 \right)+6\left( 16-8 \right)=96>0 $  

By second derivative test, x = 8 is the point of local minima of S.

Hence, the sum of the cubes of the numbers is the minimum when the numbers are 8 and 16 –8= 8.

17. A square piece of tin od side 18 cm is to be made into a box without a top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?

Ans: Let the side of the square be cut off by x cm. 

Then, the length and the breath of the box will be (18 – 2x) cm each.

The box has a height of x cm. As a result, the box's volume V(x) is given by,

$  V\left( x \right)=x{{\left( 18-2x \right)}^{2}} $  

$  \therefore {V}'\left( x \right)={{\left( 18-2x \right)}^{2}}-4x\left( 18-2x \right) $  

$  =\left( 18-2x \right)\left[ 18-2x-4x \right] $  

$  =12\left( 9-x \right)\left( 3-x \right) $  

$  And, $  

$  {V}'\left( x \right)=12\left[ -\left( 9-x \right)-\left( 3-x \right) \right] $  

$  =-24\left( 6-x \right) $  

$  Now,{v}'\left( x \right)=0\Rightarrow x=9,3 $  

If x = 9, then the length and the breadth will become 0.

$  \therefore x=9 $  

$  \Rightarrow x=3 $  

$  Now,{V}''\left( 3 \right)=-24\left( 6-3 \right)=-72<0 $  

Therefore, by second derivative test, x = 3 is the point of maxima of V.

As a result, the volume of the box obtained is the biggest achievable by removing a square of side 3 cm from each corner of the square tin and building a box from the remaining sheet.

18. A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without a top, by cutting off squares from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is the maximum possible?

Ans: Let the side of the square be cut by x cm.

Then, the height of the box is x, the length is $45-2x$ , and the breadth is $24-2x$.

$  V\left( x \right)=x\left( 45-2x \right)\left( 24-2x \right) $  

$  =4{{x}^{3}}-138{{x}^{2}}+1080x $  

$  {V}'\left( x \right)=12{{x}^{2}}-276+1080 $  

$  =12\left( {{x}^{2}}-23x+90 \right) $  

$  =12\left( x-18 \right)\left( x-5 \right) $  

$  {V}''\left( x \right)=24x-276=12\left( 2x-23 \right) $  

$  Now,{V}'\left( x \right)=0\Rightarrow x=18,5 $  

It is not possible to cut off a square of side 18 cm from each corner of the rectangular sheet,

Thus, x cannot be equal to 18.

$  x=5 $  

$  Now,{V}''\left( 5 \right)=12\left( 10-23 \right)=-156<0 $  

Therefore, by second derivative test x = 5 is the point of maxima.

Hence, the side of the square to be cut off to make the volume of the box maximum possible is 5cm.

19. Show that of all the rectangles inscribed in a given fixed circle, the square has the maximum area.

Ans: Let a rectangle of length l and breadth b be inscribed in the given circle of radius a.

Then, the diagonal of length 2a cm passes through the center.

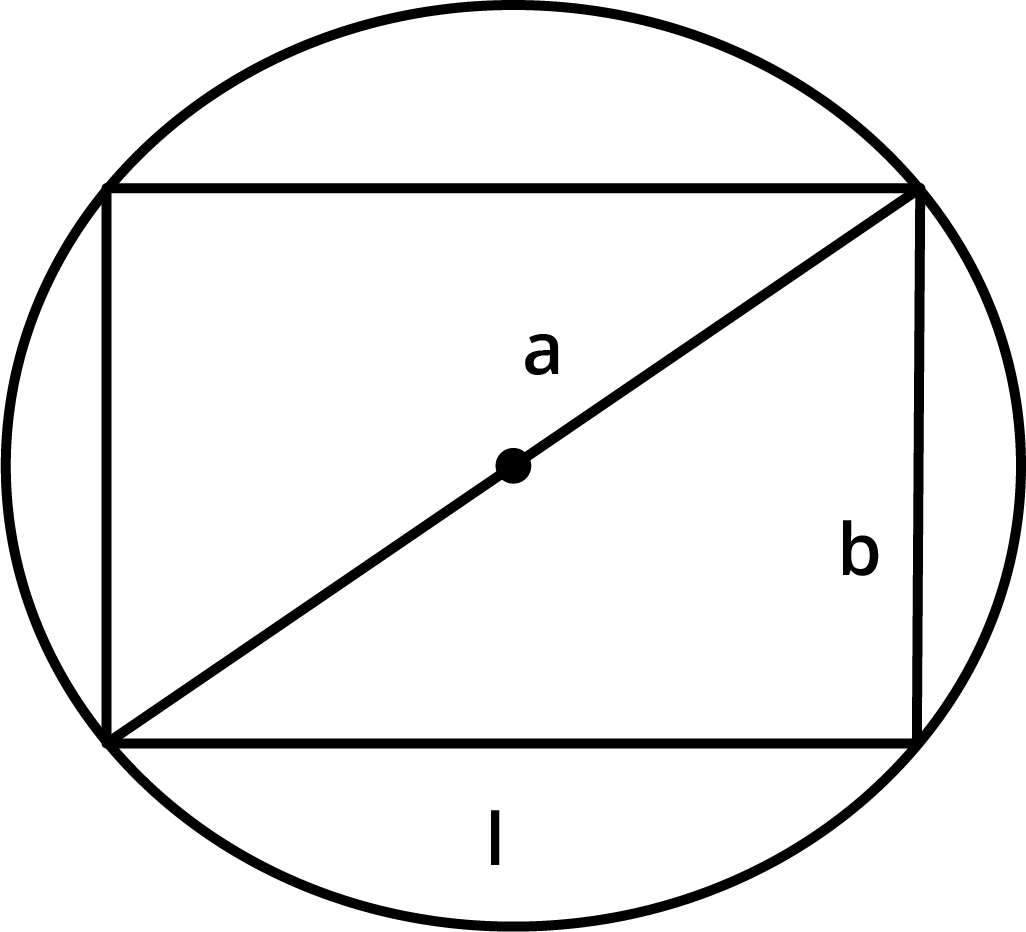
By Pythagoras theorem, we have:

$  {{\left( 2a \right)}^{2}}={{l}^{2}}+{{b}^{2}} $  

$  \Rightarrow {{b}^{2}}=4{{a}^{2}}-{{l}^{2}} $  

$  \Rightarrow b=\sqrt{4{{a}^{2}}-{{l}^{2}}} $  

Area of the rectangle,$A=l\sqrt{4{{a}^{2}}-{{l}^{2}}}$ 

$  \therefore \frac{dA}{dl}=\sqrt{4{{a}^{2}}-{{l}^{2}}}+l\frac{1}{2\sqrt{4{{a}^{2}}-{{l}^{2}}}}\left( -2l \right)=\sqrt{4{{a}^{2}}-{{l}^{2}}}+\frac{{{l}^{2}}}{\sqrt{4{{a}^{2}}-{{l}^{2}}}}=\frac{4{{a}^{2}}-2{{l}^{2}}}{\sqrt{4{{a}^{2}}-{{l}^{2}}}} $  

$  \frac{{{d}^{2}}A}{d{{l}^{2}}}=\frac{\sqrt{4{{a}^{2}}-{{l}^{2}}}\left( -4l \right)-\left( 4{{a}^{2}}-2{{l}^{2}} \right)\frac{\left( -2l \right)}{2\sqrt{4{{a}^{2}}-{{l}^{2}}}}}{\left( 4{{a}^{2}}-{{l}^{2}} \right)} $  

$  =\frac{\left( 4{{a}^{2}}-{{l}^{2}} \right)\left( -4l \right)+1\left( 4{{a}^{2}}-2{{l}^{2}} \right)}{{{\left( 4{{a}^{2}}-{{l}^{2}} \right)}^{\frac{3}{2}}}} $  

$  =\frac{-2l\left( 6{{a}^{2}}-{{l}^{2}} \right)}{{{\left( 4{{a}^{2}}-{{l}^{2}} \right)}^{\frac{3}{2}}}} $  

$Now,\frac{dA}{dl}=0$ gives $4{{a}^{2}}=2{{l}^{2}}\Rightarrow l=\sqrt{2a}$ 

$\Rightarrow b=\sqrt{4{{a}^{2}}-2{{a}^{2}}}=\sqrt{2{{a}^{2}}}=\sqrt{2a}$ 

Now, when $l=\sqrt{2a}$ 

$\frac{{{d}^{2}}A}{d{{l}^{2}}}=\frac{-2\left( \sqrt{2a} \right)\left( -6{{a}^{2}}-2{{a}^{2}} \right)}{2\sqrt{2{{a}^{3}}}}=\frac{-8\sqrt{2{{a}^{3}}}}{2\sqrt{2{{a}^{3}}}}=-4<0$ 

By second derivative test, when $l=\sqrt{2a}$ then the area of the rectangle is the maximum.

Since $l=b=\sqrt{2a}$the rectangle is a square.

Hence, it has been proved that the square has the maximum area of all the rectangles inscribed in the given fixed circle. 

20. Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.

Ans: Let r and h denote the cylinder’s radius and height respectively.

Then, the cylinder has the following Surface Area (S):

$  S=2\pi {{r}^{2}}+2\pi rh $  

$  \Rightarrow h=\frac{S-2\pi {{r}^{2}}}{2\pi r} $  

$  =\frac{S}{2\pi }\left( \frac{1}{r} \right)-r $  

Let V be the volume of the cylinder. Then,

$  V=\pi {{r}^{2}}h=\pi {{r}^{2}}\left[ \frac{S}{2\pi }\left( \frac{1}{r} \right)-r \right]=\frac{Sr}{2} $  

$  =-\pi {{r}^{3}}=\frac{S}{2\pi }\left( \frac{1}{r} \right)-r $  

$  Then,\frac{dV}{dr}=\frac{S}{2}-3\pi {{r}^{2}},\frac{{{d}^{2}}V}{d{{r}^{2}}}=-6\pi r $  

$  Now,\frac{dV}{dr}=0\Rightarrow \frac{S}{2}=3\pi {{r}^{2}}\Rightarrow {{r}^{2}}=\frac{S}{6\pi } $  

When ${{r}^{2}}=\frac{S}{6\pi }$ then $h=\frac{6\pi {{r}^{2}}}{2\pi }\left( \frac{1}{r} \right)-r=3r-r=2r$ 

Hence, the volume is the maximum when the height is twice the radius i.e. when the height is equal to the diameter.

21. Of all the closed cylindrical cans (right circular), of a given volume of 100 cubic centimeters, find the dimensions of the can which has the minimum surface area?

Ans: Let r and h denote the cylinder’s radius and height respectively.

Then, the cylinder has the following volume (V),

$  V=\pi {{r}^{2}}h=100 $  

$  \therefore h=\frac{100}{\pi {{r}^{2}}} $  

The cylinder has the following surface area (S),

$  S=2\pi {{r}^{2}}+2\pi rh=2\pi {{r}^{2}}+\frac{200}{r} $  

$  \frac{dS}{dr}=0\Rightarrow 4\pi r=\frac{200}{{{r}^{2}}} $  

$  \Rightarrow {{r}^{3}}=\frac{200}{4\pi }=\frac{50}{\pi } $  

$  \Rightarrow r={{\left( \frac{50}{\pi } \right)}^{\frac{1}{3}}} $  

Now, it is observed that when $r={{\left( \frac{50}{\pi } \right)}^{\frac{1}{3}}},\frac{{{d}^{2}}S}{d{{r}^{2}}}>0.$ 

By second derivative test, when the radius of the cylinder is ${{\left( \frac{50}{\pi } \right)}^{\frac{1}{3}}}$ cm, the surface area is the minimum.

When $r={{\left( \frac{50}{\pi } \right)}^{\frac{1}{3}}},h=2{{\left( \frac{50}{\pi } \right)}^{\frac{1}{3}}}cm.$ 

Hence the required dimensions of the can which has the minimum surface area are given as $radius={{\left( \frac{50}{\pi } \right)}^{\frac{1}{3}}}cm$ and $height=2{{\left( \frac{50}{\pi } \right)}^{\frac{1}{3}}}cm.$ 

22. A Wire of length 28 m is to be cut into two pieces. One of the pieces is to be made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the circle is minimum?

Ans: Let a piece of length l be cut from the given wire to make a square.

Then, the other piece of wire to be made into a circle is of length $\left( 28-l \right)m.$ 

Let r be the circle's radius. Then $2\pi r=28-l\Rightarrow r=\frac{1}{2\pi }\left( 28-l \right).$ 

The combined areas of the square and the circle (A) is given by,

$A={{\pi }^{2}}+{{r}^{2}}$ (side of the square)

$  =\frac{{{l}^{2}}}{16}+\pi {{\left[ \frac{1}{2\pi }\left( 28-l \right) \right]}^{2}} $  

$  =\frac{{{l}^{2}}}{16}+\frac{1}{4\pi }{{\left( 28-l \right)}^{2}} $  

$  \therefore \frac{dA}{dl}=\frac{2l}{16}+\frac{2}{4\pi }\left( 28-l \right)\left( -1 \right)=\frac{l}{8}-\frac{1}{2\pi }\left( 28-l \right) $  

$  \frac{{{d}^{2}}A}{d{{l}^{2}}}=\frac{l}{8}+\frac{1}{2\pi }>0 $  

$  Now,\frac{dA}{dl}=0\Rightarrow \frac{l}{8}-\frac{1}{2\pi }\left( 28-l \right)=0 $  

$  \Rightarrow \left( \pi +4 \right)l-112=0 $  

$  \Rightarrow l=\frac{112}{\pi +4} $  

Thus, when $l=\frac{112}{\pi +4},\frac{{{d}^{2}}A}{d{{l}^{2}}}>0$ 

By second derivative test, area (A) is the minimum when $l=\frac{112}{\pi +4}$ . Hence, when the length of the wire is$\frac{112}{\pi +4}$ cm in making the square the combined area is the minimum while the length of the wire in making the  circle is $28-\frac{112}{\pi +4}=\frac{28\pi }{\pi +4}cm.$

23. Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is $\frac{8}{27}$ of the volume of the sphere.

Ans: Let r and h be the radius and height of the cone respectively inscribed in a sphere of radius R.

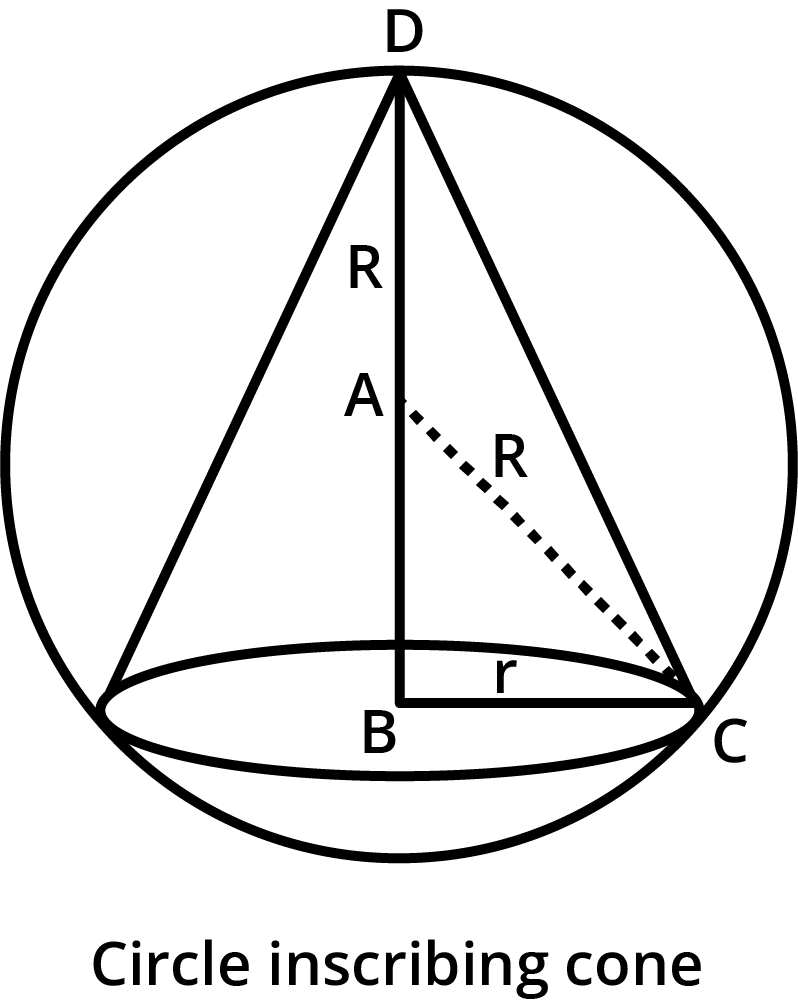
Let V be the volume of the cone.

Then, $V=\frac{1}{3}\pi {{r}^{2}}h$ 

Height of the cone is given by,

$h=R+AB=R+\sqrt{{{R}^{2}}-{{r}^{2}}}$                                                  (ABC is a right triangle)

$  V=\frac{1}{3}\pi {{r}^{2}}\left( R+\sqrt{{{R}^{2}}-{{r}^{2}}} \right) $  

$  =\frac{1}{3}\pi {{r}^{2}}R+\frac{1}{3}\pi {{r}^{2}}\sqrt{{{R}^{2}}-{{r}^{2}}} $  

$  \frac{dV}{dr}=\frac{2}{3}\pi rR+\frac{2}{3}\pi r\sqrt{{{R}^{2}}-{{r}^{2}}}+\frac{1}{3}\pi {{r}^{2}}.\frac{\left( -2r \right)}{2\sqrt{{{R}^{2}}-{{r}^{2}}}} $  

$  =\frac{2}{3}\pi rR+\frac{2}{3}\pi r\sqrt{{{R}^{2}}-{{r}^{2}}}-\frac{1}{3}\pi .\frac{{{r}^{3}}}{\sqrt{{{R}^{2}}-{{r}^{2}}}} $  

$  =\frac{2}{3}\pi rR+\frac{2\pi {{R}^{2}}-3\pi {{r}^{3}}}{3\sqrt{{{R}^{2}}-{{r}^{2}}}} $  

$  \frac{{{d}^{2}}V}{d{{r}^{2}}}=\frac{2}{3}\pi rR+\frac{9\left( {{R}^{2}}-{{r}^{2}} \right)\left( 2\pi {{R}^{2}}-9\pi {{r}^{2}} \right)+2\pi r{{R}^{2}}-3\pi {{r}^{4}}}{27{{\left( {{R}^{2}}-{{r}^{2}} \right)}^{\frac{3}{2}}}} $  

$  Now,\frac{dV}{dr}=0\Rightarrow \pi \frac{2}{3}rR=\frac{3\pi {{r}^{3}}-2\pi {{R}^{2}}}{3\sqrt{{{R}^{2}}-{{r}^{2}}}} $  

$  \Rightarrow 2R=2R\sqrt{{{R}^{2}}-{{r}^{2}}}=3{{r}^{2}}-2{{R}^{2}} $  

$  \Rightarrow 4{{R}^{4}}-4{{R}^{2}}{{r}^{2}}=9{{r}^{4}}+4R $  

$  \Rightarrow 9{{r}^{4}}=8{{R}^{2}}{{r}^{2}} $  

$  \Rightarrow {{r}^{2}}=\frac{8}{9}{{R}^{2}} $  

When ${{r}^{2}}=\frac{8}{9}{{R}^{2}}$ then $\frac{{{d}^{2}}V}{d{{r}^{2}}}<0$ 

By second derivative test, the volume of the cone is the maximum when   

${{r}^{2}}=\frac{8}{9}{{R}^{2}}$.

When ${{r}^{2}}=\frac{8}{9}{{R}^{2}},h=R+\sqrt{{{R}^{2}}-\frac{8}{9}{{R}^{2}}}=R+\frac{R}{3}=\frac{4}{3}R$ 

Therefore, 

$  =\frac{1}{3}\pi \left( \frac{8}{9}{{R}^{2}} \right)\left( \frac{4}{3}R \right) $  

$  =\frac{8}{27}\left( \frac{4}{3}\pi {{R}^{3}} \right) $  

$  =\frac{8}{27}\times \left( Volume \right) $  

Hence, the volume of the largest cone that can be inscribed in the sphere is $\frac{8}{27}$ the volume of the sphere.

24. Show that the right circular cone of the least curved surface and given volume has an altitude equal to $\sqrt{2}$ times the radius of the base.

Ans: Let r and h be the radius and the altitude of the cone respectively.

Then, the cone has the following volume (V):

$V=\frac{1}{3\pi }\pi {{r}^{2}}h\Rightarrow h=\frac{3V}{{{r}^{2}}}$ 

The cone has the following surface area (S),

$S=\pi rl$  (l = slant height)

$  =\pi r\sqrt{{{r}^{2}}+{{h}^{2}}} $  

$  =\pi r\sqrt{{{r}^{2}}+\sqrt{\frac{9{{V}^{2}}}{{{\pi }^{2}}{{r}^{4}}}}}=\pi \frac{r\sqrt{{{9}^{2}}{{r}^{2}}+{{V}^{2}}}}{\pi {{r}^{2}}} $  

$  =\frac{1}{r}\sqrt{{{\pi }^{2}}{{r}^{6}}+9{{V}^{2}}} $  

$  \frac{dS}{dr}=\frac{r.\frac{6{{\pi }^{2}}{{r}^{5}}}{2\sqrt{{{\pi }^{2}}{{r}^{6}}+9{{V}^{2}}}}-\sqrt{{{\pi }^{2}}{{r}^{6}}+9{{V}^{2}}}}{{{r}^{2}}} $  

$  =\frac{2{{\pi }^{2}}{{r}^{6}}-9{{V}^{2}}}{{{r}^{2}}\sqrt{{{\pi }^{2}}{{r}^{6}}+9{{V}^{2}}}} $  

$Now,\frac{dS}{dr}=0\Rightarrow 2{{\pi }^{2}}{{r}^{6}}=9{{V}^{2}}\Rightarrow {{r}^{6}}=\frac{9{{V}^{2}}}{2{{\pi }^{2}}}$ 

Thus, it can be easily verified that when ${{r}^{6}}=\frac{9{{V}^{2}}}{2{{\pi }^{2}}},\frac{{{d}^{2}}S}{d{{r}^{2}}}<0$ 

By second derivative test, the surface area of the cone is the least when ${{r}^{6}}=\frac{9{{V}^{2}}}{2{{\pi }^{2}}}$

When, ${{r}^{6}}=\frac{9{{V}^{2}}}{2{{\pi }^{2}}},h=\frac{3V}{\pi {{r}^{2}}}{{\left( \frac{2{{\pi }^{2}}{{r}^{6}}}{9} \right)}^{\frac{1}{2}}}=\frac{3}{\pi {{r}^{2}}}\frac{\sqrt{2\pi {{r}^{3}}}}{3}=\sqrt{2}r$

Hence, for a given volume, the right circular cone of the least curved surface has an altitude equal to $\sqrt{2}$ times the radius of the base.

25. Show that the semi-vertical angle of the cone of the maximum volume and of the given slant height is tan-1$\sqrt{2}$.

Ans: Let $\theta $ be the semi-vertical angle of the cone.

It is clear that $\theta \in \left[ 0,\frac{\pi }{2} \right]$ 

Let r, h, and l be the radius, height, and the slant height of the cone respectively.

The slant height of the cone is given as constant.

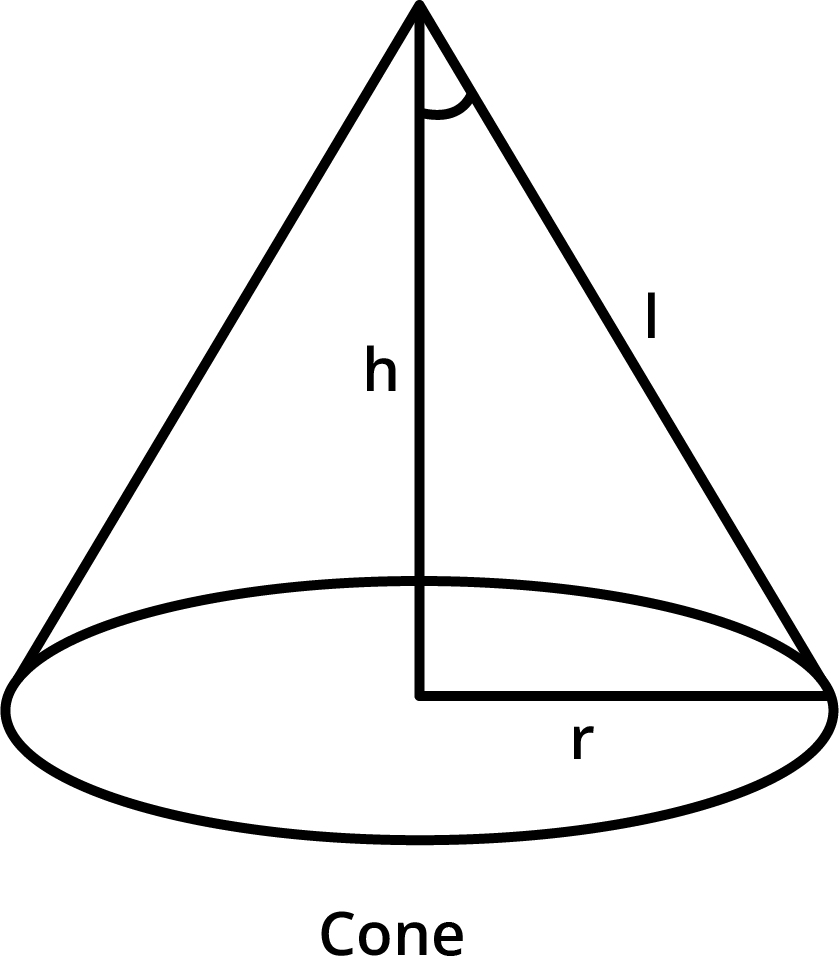
Now r = l $\sin \theta $ and h = l $\cos \theta $ 

The volume (V) of the cone is given by,

$  V=\frac{1}{3}\pi {{r}^{2}}h $  

$  =\frac{1}{3}\pi \left( {{l}^{2}}{{\sin }^{2}}\theta  \right)\left( l\cos \theta  \right) $  

$  =\frac{1}{3}\pi {{l}^{3}}{{\sin }^{2}}\theta \cos \theta  $  

$  \therefore \frac{dV}{d\theta }=\frac{{{l}^{3}}\pi }{3}\left[ {{\sin }^{2}}\theta \left( -\sin \theta  \right)+\cos \theta \left( 2\sin \theta \cos \theta  \right) \right] $  

$  =\frac{{{l}^{3}}\pi }{3}\left[ -{{\sin }^{3}}\theta +2\sin \theta {{\cos }^{2}}\theta  \right] $  

$  \frac{{{d}^{2}}V}{d{{\theta }^{2}}}=\frac{{{l}^{3}}\pi }{3}\left[ -3{{\sin }^{2}}\theta \cos \theta +2{{\cos }^{3}}\theta -4{{\sin }^{2}}\theta \cos \theta  \right] $  

$  =\frac{{{l}^{3}}\pi }{3}\left[ 2{{\cos }^{2}}\theta -7{{\sin }^{2}}\theta \cos \theta  \right] $  

$  Now,\frac{dV}{d\theta }=0 $  

$  \Rightarrow {{\sin }^{3}}\theta =2\sin \theta {{\cos }^{2}}\theta  $  

$  \Rightarrow \tan \theta =2 $  

$  \Rightarrow \theta ={{\tan }^{-1}}\sqrt{2} $  

Now, when $\theta ={{\tan }^{-1}}\sqrt{2},$then ${{\tan }^{2}}\theta =2$ or ${{\sin }^{2}}\theta =2{{\cos }^{2}}\theta $ 

Then,

$\frac{{{d}^{2}}V}{d{{\theta }^{2}}}=\frac{{{l}^{3}}\pi }{3}\left[ 2{{\cos }^{3}}\theta -14{{\cos }^{3}}\theta  \right]=-4\pi {{l}^{3}}{{\cos }^{3}}\theta <0$     (For $\theta \in \left[ 0,\frac{\pi }{2} \right]$)

By second derivative test, the volume (V) is the maximum when $\theta ={{\tan }^{-1}}\sqrt{2}$. Hence, the semi-vertical angle of the cone of the maximum volume is  ${{\tan }^{-1}}\sqrt{2}$ for a given slant height.

26. Show that semi-vertical angle of right circular cone of given surface area and maximum volume is $sin^{-1}\left ( \frac{1}{3} \right )$

Ans: Let’s assume x be the radius and y be the height of the cone and semi-vertical angle be $\Theta$. 

And, Total Surface area of cone (S) = $\pi x \sqrt{x^{2}+y^{2}}+\pi x^{2}$

$x\sqrt{x^{2}+y^{2}} +x^{2}=\frac{S}{\pi}$

Let’s say $\frac{S}{\pi}=k$

$x\sqrt{x^{2}+y^{2}} = k-x^{2}$

Squaring on both sides

$x^{2}\left ( x^{2}+y^{2} \right )=\left ( k-x^{2} \right )^{2}$

$x^{2}y^{2} = k^{2}-2kx^{2}$

$x^{2}=\frac{k^{2}}{y^{2}+2k}$   ……(1)

Volume of cone (V) = $\frac{1}{3}\pi x^{2}y$

= $\frac{1}{3}\pi \left ( \frac{k^{2}}{y^{2}+2k} \right )y$

= $\frac{1}{3}\pi k^{2}\left ( \frac{y}{y^{2}+2k} \right )$

Derive on both sides

$\frac{dV}{dy}= \frac{1}{3}\pi k^{2}\frac{d}{dy}\frac{y}{y^{2}+2k}$

= $\frac{1}{3}\pi k^{2}\left [ \frac{\left ( y^{2}+2k \right ).1-y.2y}{\left ( y^{2}+2k \right )^{2}} \right ]$    [Using quotient rule]

$\frac{dV}{dy}=\frac{1}{3}\pi k^{2}\frac{\left ( 2k-y^{2} \right )}{\left ( y^{2}+2k \right )^{2}}$   …….(2)

Now $\frac{dV}{dy}=0$

$\frac{1}{3}\pi k^{2}\frac{\left ( 2k-y^{2} \right )}{\left ( y^{2}+2k \right )^{2}}=0$

$2k-y^{2}=0$

$y^{2}=2k$

$y=\pm \sqrt{2k}$

Height can’t be negative so we neglect $y=- \sqrt{2k}$

So, $y=\sqrt{2k}$

As, $\frac{dV}{dy}> 0$, therefore, Volume is maximum at $y = \sqrt{2k}$

From equation (1),  We get,

$x^{2}=\frac{k^{2}}{2k+2k}=\frac{k^{2}}{4k}=\frac{k}{4}$

$x=\frac{\sqrt{k}}{2}$

Now, Semi-vertical angle of the cone  $sin\theta = \frac{x}{\sqrt{x^{2}+y^{2}}}$

= $\frac{\frac{\sqrt{k}}{2}}{\sqrt{\frac{k}{4}+2k}}=\frac{\sqrt{k}}{2}\times \sqrt{\frac{4}{9k}} = \frac{1}{3}$

Which implies

$\theta  = sin^{-1}\frac{1}{3}$

27. The point on the curve ${{x}^{2}}=2y$ which is nearest to the point (0, 5) is

(A) ($2\sqrt{2}$,4)           

(B) ($2\sqrt{2}$,0) 

(C) (0, 0)

(D) (2, 2)

Ans: The given curve is ${{x}^{2}}=2y$ 

For each value of x, y will be $\frac{{{x}^{2}}}{2}$ the position of the point will be $\left( x,\frac{{{x}^{2}}}{2} \right)$

The distance d(x) between the points $\left( x,\frac{{{x}^{2}}}{2} \right)$ and $\left( 0,5 \right)$ is given by

$  d\left( x \right)=\sqrt{{{\left( x-0 \right)}^{2}}+{{\left( \frac{{{x}^{2}}}{2}-5 \right)}^{2}}}=\sqrt{\frac{{{x}^{4}}}{4}-4{{x}^{2}}+25} $  

$  \therefore {d}'\left( x \right)=\frac{\left( {{x}^{3}}-8x \right)}{\sqrt{{{x}^{4}}-16{{x}^{2}}+100}} $  

$  Now,{d}'\left( x \right)=0\Rightarrow {{x}^{3}}-8x=0 $  

$  \Rightarrow x=0,\pm 2\sqrt{2} $  

And ${d}''\left( x \right)=\frac{\left( {{x}^{4}}-16{{x}^{2}}+100 \right)\left( 3{{x}^{2}}-8 \right)-2{{\left( {{x}^{3}}-8x \right)}^{2}}}{{{\left( {{x}^{4}}-16{{x}^{2}}+100 \right)}^{\frac{3}{2}}}}$ 

When $x=0$ then ${d}''\left( x \right)=\frac{36\left( -8 \right)}{{{6}^{3}}}<0$ 

When $x=\pm 2\sqrt{2}$ then $d\left( x \right)>0$ 

By second derivative test, d(x) is the minimum at $x=\pm 2\sqrt{2}$.

When $x=\pm 2\sqrt{2},y=4.$

Hence, the point on the curve ${{x}^{2}}=2y$ which is nearest to the point $\left( 0,5 \right)$ 

is $\left( \pm 2\sqrt{2},4 \right).$ 

Therefore, the correct option is A.

28. For all real values of x, the minimum value of $\frac{1-x+{{x}^{2}}}{1+x+{{x}^{2}}}$ is

(A) 0   

(B) 1  

(C) 3   

(D) $\frac{1}{3}$ .

Ans: Let $f\left( x \right)=\frac{1-x+{{x}^{2}}}{1+x+{{x}^{2}}}$ 

$  {f}'\left( x \right)=\frac{\left( 1+x+{{x}^{2}} \right)\left( -1-2x \right)-\left( 1-x+{{x}^{2}} \right)\left( 1+2x \right)}{{{\left( 1+x+{{x}^{2}} \right)}^{2}}} $  

$  =\frac{2\left( {{x}^{2}}-1 \right)}{{{\left( 1+x+{{x}^{2}} \right)}^{2}}} $  

$  \therefore {f}'\left( x \right)=0\Rightarrow {{x}^{2}}=1\Rightarrow x=\pm 1 $  

$  Now,{f}''\left( x \right)=4\frac{\left( 1+3x-{{x}^{3}} \right)}{{{\left( 1+x+{{x}^{2}} \right)}^{3}}} $  

$  And,{f}''\left( 1 \right)=\frac{4\left( 1+3-1 \right)}{{{\left( 1+1+1 \right)}^{3}}}=\frac{4}{9}>0 $  

$  And,{f}''\left( -1 \right)=\frac{4\left( 1-3+1 \right)}{{{\left( 1+1+1 \right)}^{3}}}=\frac{-4}{27}<0 $  

By second derivative test, f is the minimum at $x=1$ and the minimum 

value is given by $f\left( 1 \right)=\frac{1}{3}$ 

The correct option is D.

29. The maximum value of ${{\left[ x\left( x+1 \right)+1 \right]}^{\frac{1}{3}}},0\le x\le 1$ is

(A) ${{\left( \frac{1}{3} \right)}^{\frac{1}{3}}}$ 

(B) $\frac{1}{2}$ 

(C) 1 

(D) 0

Ans: Let $f\left( x \right)={{\left[ x\left( x+1 \right)+1 \right]}^{\frac{1}{3}}}.$ 

$  \therefore {f}'\left( x \right)=\frac{2x+1}{3{{\left[ x\left( x+1 \right)+1 \right]}^{\frac{2}{3}}}} $  

$  Now,f\left( x \right)=0\Rightarrow x=-\frac{1}{2} $  

But, x = -1/2 is not part of the interval [0,1]

Now, evaluate the value of f at the endpoints of the interval [0, 1] {i.e., 

at x = 0 and x =1}.

$  f\left( 0 \right)={{\left[ 0\left( 0-1 \right)+1 \right]}^{\frac{1}{3}}}=1 $  

$  f\left( 0 \right)={{\left[ 1\left( 1-1 \right)+1 \right]}^{\frac{1}{3}}}=1 $  

Hence, we can conclude that the maximum value of  f is 1 in the 

interval [0, 1].

The correct option is 13.

Conclusion

NCERT of Class 12 Maths Ch 6 ex 6.3 has provided a deep understanding of the application of derivatives in various mathematical contexts. This exercise covered critical topics such as the rate of change, equations of tangents and normals, increasing and decreasing functions, finding maxima and minima, and using derivatives for approximation. Mastery of these concepts is vital for students aiming to excel in calculus and related fields in higher mathematics.

Class 12 Maths Chapter 6: Exercises Breakdown

CBSE Class 12 Maths Chapter 6 Other Study Materials

NCERT Solutions for Class 12 Maths | Chapter-wise List

Given below are the chapter-wise NCERT 12 Maths solutions PDF. Using these chapter-wise class 12th maths ncert solutions, you can get clear understanding of the concepts from all chapters.

Related Links for NCERT Class 12 Maths in Hindi

Explore these essential links for NCERT Class 12 Maths in Hindi, providing detailed solutions, explanations, and study resources to help students excel in their mathematics exams.

Important Related Links for NCERT Class 12 Maths