Important Questions for CBSE Class 12 Physics Chapter 3 - Current Electricity 2024-25

Very Short Answer Questions: (1 Marks)

1. If the temperature of a good conductor decreases, how does the relaxation time of electrons in the conductor change? 

Ans: It is known that, 

$\rho =\frac{m}{n{{e}^{2}}\tau }$ 

Therefore, if the temperature of a good conductor decreases, collision decreases and thus the relaxation time of electrons increases which in turn decreases the resistivity. 

2. If potential difference $V$ applied across a conductor is increased to $2V$, how will the drift velocity of the electron change?

Ans: It is known that,

${{V}_{d}}=\frac{eE\tau }{m}=\frac{eV\tau }{lm}$

When the potential difference across a conductor is doubled, the drift velocity of the electron gets doubled.

3. What is the value of current $I$ at $O$ in the adjoining circuit?

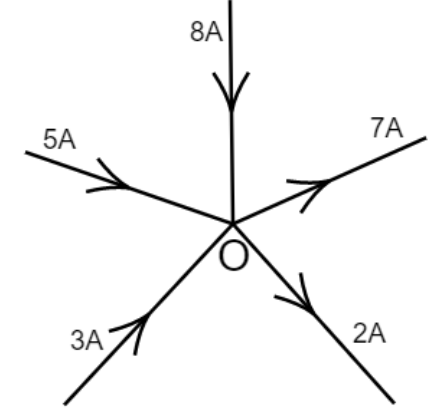
Ans: Total current at O is given by,

$i=5+3-2-7+8$ 

$\Rightarrow i=16-9$

$\Rightarrow i=7A$

Therefore, the current $I$ at $O$is $i=7A$.

4. State one condition for maximum current to be drawn from the cell?

Ans: It is known that,

$I=\frac{E}{R+r}$

To find maximum current, internal resistance must be zero.

5. Resistivities of copper, silver and manganin are $1.7\times {{10}^{-8}}m$, $1.0\times {{10}^{-8}}m$ and $44\times {{10}^{-8}}m$ respectively which of these is the best conductor?

Ans: The resistance is directly proportional to specific resistance (resistivity), when length and area of cross-section is made constant.$R=\frac{\rho l}{A}$

Hence, silver is the best conductor as its specific resistance is less.

6. Draw the graph showing the variation of conductivity with temperature for a metallic conductor? 

Ans: The conductivity for a metallic conductor decreases with the increase in temperature.   

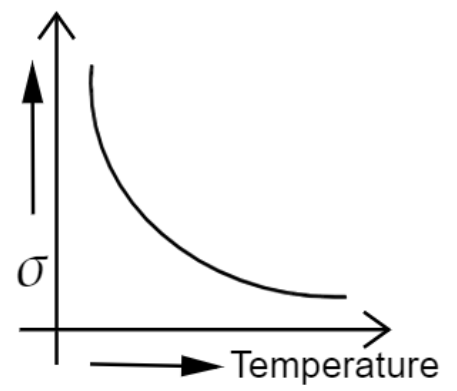
7. If a wire is stretched to double its length, what will be its new resistivity? 

Ans: There will be no change in resistivity because resistivity depends only on the nature of the material. 

8. Name any one material having a small value of temperature coefficient of resistance. Write one use of this material?

Ans: Material having a small value of temperature coefficient of resistance is Nichrome. It is an alloy used for making standard resistance coil. 

9. Two wires $A$ and $B$ are of the same metal and of same length have their areas of cross section in the ratio $2:1$ if the same potential difference is applied across each wire in turn, what will be the ratio of current flowing in $A$ & $B$ ?

Ans: It is known that,

$I=\frac{V}{R}$ and $R<\frac{1}{A}$

When area of cross section is $2:1$ then the ratio of current flowing in $A$ & $B$ will be $1:2$.

Very Short Answer Questions: (2 Marks)

1. Two electric bulbs A and B are marked \[\mathbf{220V}\],$40W$ and $220V$$60W$ respectively. Which one has a higher resistance?

Ans: It is known that,

$R=\frac{{{V}^{2}}}{p}$ 

For Bulb $A$, ${{R}_{1}}=\frac{{{(220)}^{2}}}{40}=1210\Omega $ 

For Bulb $B$, ${{R}_{2}}=\frac{{{(220)}^{2}}}{60}=806.67\Omega $ 

Therefore, bulb $A$ has higher resistance.

2. A Carbon resistor has three strips of red colour and a gold strip. What is the value of the resistor? What is its tolerance? 

Ans: It is given that,

\[R\text{ }R\text{ }R\text{ }Gold=(22\times {{10}^{2}})\pm 5%\]

Therefore, value of the resistor$=2200\Omega $ and tolerance$=\pm 5%$

3. Determine the voltage drop across the resistor ${{R}_{1}}$ in the circuit given below with \[\mathbf{E}=\text{ }\mathbf{60V}\], ${{R}_{1}}=18\Omega $, ${{R}_{2}}=10\Omega $, ${{R}_{3}}=5\Omega $ and ${{R}_{4}}=10\Omega $.

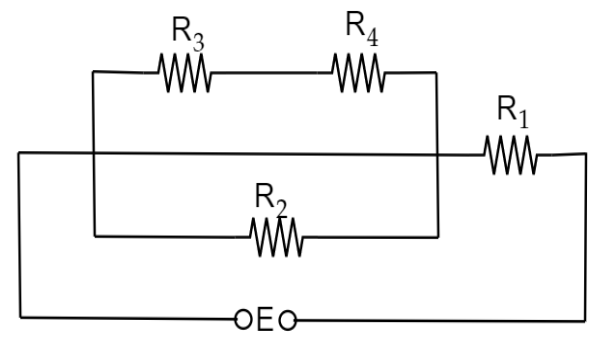
Ans: In the given circuit,

${{R}_{3}}\And {{R}_{4}}$ are in series

$R'={{R}_{3}}+{{R}_{4}}$

\[\Rightarrow R'=5+10=15\Omega \]

Then, $R'\And {{R}_{2}}$ are in parallel

$\frac{1}{R''}=\frac{1}{{{R}^{1}}}+\frac{1}{{{R}_{2}}}$ 

$\Rightarrow \frac{1}{R''}=\frac{1}{15}+\frac{1}{10}$

$\Rightarrow \frac{1}{R''}=\frac{4+6}{60}=\frac{10}{60}$

$\Rightarrow R''=\frac{60}{10}=6\Omega $

Then ${{R}_{1}},R''$ are series

${{R}_{net}}=R''+{{R}_{1}}$ 

$\Rightarrow {{R}_{net}}=6+18=24\Omega $ 

Current: $I=\frac{V}{R}=\frac{60}{24}\text{ampere}$ 

Voltage drop across ${{R}_{1}}=I{{R}_{1}}=\frac{60}{24}\times 18$ 

$\Rightarrow {{V}_{1}}=45v\text{olts}$

Therefore, voltage drop across the resistor ${{R}_{1}}$ is $45volts$.

4. Two heated wires of the same dimensions are first connected in series and then it’s parallel to a source of supply. What will be the ratio of heat produced in the two cases? 

Ans: It is known that,

$\text{ }H={{I}^{2}}\operatorname{R}t$    $\left( I=\frac{V}{R} \right)$

$\Rightarrow H=\frac{{{V}^{2}}}{{{R}^{2}}}\times R\times t$ 

$\Rightarrow H=\frac{{{V}^{2}}}{R}t$

$\Rightarrow H\propto \frac{1}{R}$

\[\frac{\text{ }{{\text{H}}_{\text{series}}}\text{ }}{\text{ }{{\text{H}}_{\text{parallel}}}\text{ }}=\frac{\text{ }{{\text{R}}_{\text{parallel}}}\text{ }}{\text{ }{{\text{R}}_{\text{series}}}\text{ }}\]

\[\Rightarrow \frac{\frac{1}{\left( \frac{1}{R}+\frac{1}{R} \right)}}{R+R}=\frac{R/2}{2R}=\frac{R}{2R\times 2}=\frac{1}{4}\]

Therefore, the ratio of heat produced is$1:4$.

5. V.i graph for a metallic wire at two different temperatures is shown in the figure. Which of these two temperatures is higher and why? 

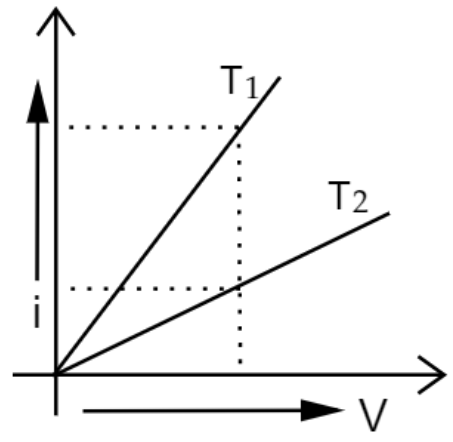
Ans: From the graph: 

$Slope=\frac{i}{V}$

It is known that, $\frac{i}{V}=\frac{1}{R}$

It means that the smaller the slope, the larger the resistance.

As the resistance increases, temperature also increases.

Temperature of ${{T}_{2}}$ is higher because ${{T}_{2}}$ has a small slope.

6. A set of n-identical resistors, each of resistance $R$ ohm when connected in series have an effective resistance of $X$ ohm and when the resistors are connected in parallel the effective resistance is $Y$ ohm. Find the relation between $R$,$X$ and $Y$? 

Ans: It is given that,

n-resistors connected in series 

$\Rightarrow X=nR$    ……$(1)$

n-resistors connected in parallel

$\Rightarrow Y=\frac{R}{n}$     ……$(2)$

Multiply equations $(1)$ and $(2)$

$\Rightarrow XY=nR\times \frac{R}{n}$ 

$\Rightarrow XY={{R}^{2}}$

$\Rightarrow R=\sqrt{XY}$

7. Show that the resistance of a conductor is given by $R=\frac{ml}{n{{e}^{2}}\tau A}$.

Ans: Consider a conductor of length $l$  and area $A$.

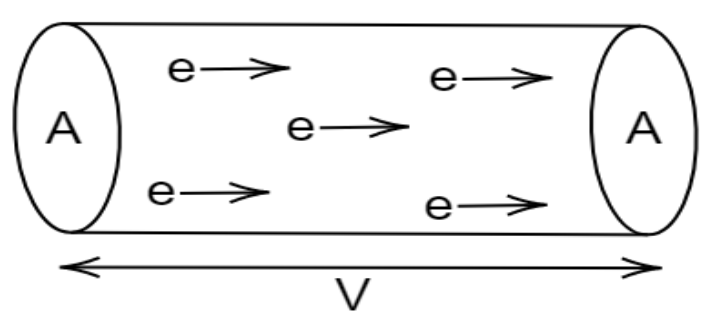
If electric field $E$ is applied across the conductor, 

The drift velocity of electrons ${{v}_{d}}$ is given by:

${{v}_{d}}=\frac{eE}{m}\tau $

It is known that, $I=neA{{v}_{d}}$

$\Rightarrow \text{I}=\operatorname{neA}\left( \frac{eE}{m}\tau  \right)$; $E=\frac{V}{l}$

$\Rightarrow \text{I}=\operatorname{neA}\left( \frac{eV}{ml}\tau  \right)$

$\Rightarrow \frac{V}{I}=\frac{ml}{n{{e}^{2}}A\tau }$;$\frac{V}{I}=R$

$\Rightarrow R=\frac{m}{n{{e}^{2}}\tau }\left( \frac{l}{A} \right)$

$\Rightarrow \text{R}=\frac{ml}{n{{e}^{2}}\tau A}$

Therefore, the resistance of the conductor, $\text{R}=\frac{ml}{n{{e}^{2}}\tau A}$

8. Figure shows a piece of pure semiconductor $S$ in series with a variable resistor $R$ and a source of constant voltage $V$. Would you increase and decrease the value of $R$ to keep the reading of ammeter $(A)$ constant, when semiconductor $S$ is heated? Give reasons.

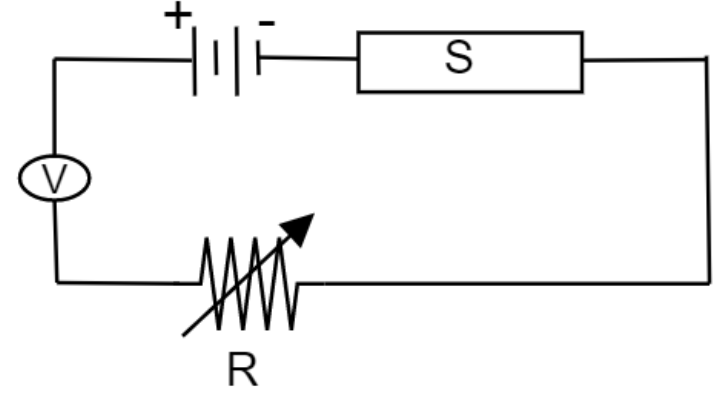
Ans: On increasing the temperature, resistance of the semiconductor decreases. So, to increase the temperature, the semiconductor $S$ is heated.

To maintain constant current in ammeter, total resistance of the circuit should remain unchanged.

Therefore, the value of $R$ has to be increased.

9. Why is constantan or manganin used for making standard resistors?

Ans: Constantan or manganin are alloys of high resistivity and low temperature coefficient of resistance. So, these are used for making standard resistors.

10. What are ohmic and non-ohmic resistors? Give one example of each?

Ans: Ohmic resistors are resistors which obey ohm’s law. Eg: Metals 

Non-ohmic resistors are resistors which do not obey ohm’s law. Eg: semiconductor diode, transistor etc.

11. The storage battery of a car has an emf of $12V$. If the internal resistance of the battery is $0.4\Omega $, what is the maximum current that can be drawn from the battery?

Ans: It is given that,

Emf of the battery, \[E=\text{ }12\text{ }V~\] 

Internal resistance of the battery\[,r=\text{ }0.4\text{ }\Omega ~\] 

It is known that,

$V=E-iR$

To get maximum current from that battery:

$\Rightarrow E-iR=0$

$\Rightarrow E=iR$

$\Rightarrow i=\frac{E}{R}=\frac{12}{0.4}$

$\Rightarrow i=30A$

Therefore, the maximum current drawn from the given battery,$i=30A$.

12. In a potentiometer arrangement, a cell of emf $1.25V$ gives a balance point at $35.0cm$ length of the wire. If the cell is replaced by another cell and the balance point shifts to $63.0cm$, what is the emf of the second cell?

Ans: It is given that,

Emf of the cell, ${{E}_{1}}=1.25V$  

Balance point of the potentiometer, ${{l}_{1}}=35cm$ 

The cell is replaced by another cell of emf  ${{E}_{2}}$ 

New balance point of the potentiometer,  ${{l}_{2}}=63cm$ 

Balance condition of potentiometer: $\frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{l}_{1}}}{{{l}_{2}}}$ 

$\Rightarrow {{E}_{2}}={{E}_{1}}\times \frac{{{l}_{2}}}{{{l}_{1}}}$

$\Rightarrow {{E}_{2}}=1.25\times \frac{63}{35}=2.25~\text{V}$

Hence, the emf of the second cell $2.25V$.

13. What conclusion can you draw from the following observations on a resistor made of alloy manganin?

Ans: It can be concluded that the ratio of voltage with current is constant and is equal to $19.7$ i.e., it obeys Ohm’s law. Therefore, manganin is an ohmic conductor.

From Ohm’s law, $\frac{V}{I}=R$ i.e., the ratio of voltage with current is the resistance of the conductor. Thus, the resistance of manganin is $19.7\Omega $.

Short Answer Questions: (3 Marks)

1. What happens to the resistance of the wire when its length is increased to twice its original length?

Ans: It is known that,

$R=\rho \frac{l}{A}=\rho (\frac{l}{\pi {{r}^{2}}})$ 

It is given that, 

New length of the wire, $l'=2l$ 

Let, the new radius be $r'$.

As volume of the wire remains the same: $\pi {{\text{r}}^{2}}\ell =\pi {{(r')}^{2}}\ell '$ 

$\Rightarrow \pi {{r}^{2}}l=\pi {{(r')}^{2}}2\ell $

\[\Rightarrow {{(r')}^{2}}=\frac{{{r}^{2}}}{2}\]

New resistance, $R'=\rho \left( \frac{l'}{\pi r{{'}^{2}}} \right)$

$\Rightarrow R'=\rho \frac{2l}{\pi \left( \frac{{{r}^{2}}}{2} \right)}$

$\Rightarrow R'=\rho \left( \frac{4l}{\pi {{r}^{2}}} \right)$

$\Rightarrow R'=4\rho \left( \frac{l}{\pi {{r}^{2}}} \right)$

$\Rightarrow R'=4R$

Hence, new resistance becomes four times the original resistance.

2. Mark the direction of current in the circuit as per Kirchhoff’s first rule. What is the value of the main current in the shown network? 

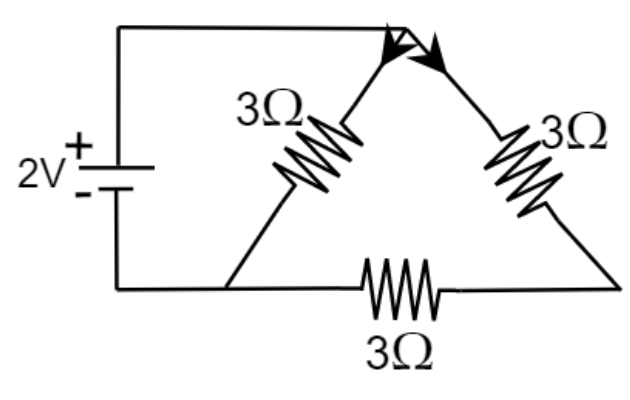
Ans: In the given figure,

${{R}_{2}}$ and ${{R}_{3}}$ are in series

$\Rightarrow R=3+3=6\Omega $ 

$R$ and ${{R}_{1}}$ are in parallel

$\frac{1}{{{R}_{net}}}=\frac{1}{R}+\frac{1}{{{R}_{1}}}$ 

$\Rightarrow \frac{1}{{{R}_{net}}}=\frac{1}{6}+\frac{1}{3}=\frac{3+6}{18}$

$\Rightarrow {{R}_{net}}=\frac{18}{9}=2\Omega $

Net current: $I=\frac{V}{R}$

$I=\frac{2}{2}=1A$ 

Therefore, net current is $1A$.

3. 

(a) Why do we prefer a potentiometer to measure the emf of a cell rather than a voltmeter?

Ans: Potentiometer is based on a null method i.e.; it draws no current from the cell. Emf of a cell is equal to the terminal potential difference when no current flows from the cell. Therefore, a potentiometer is preferred to measure the emf of a cell rather than a voltmeter.

(b) With suitable circuit diagram, show how emfs of 2 cells can be compared using a potentiometer?

Ans: Potentiometer works on the principle that when a constant current flows through the wire of uniform area of cross-section then

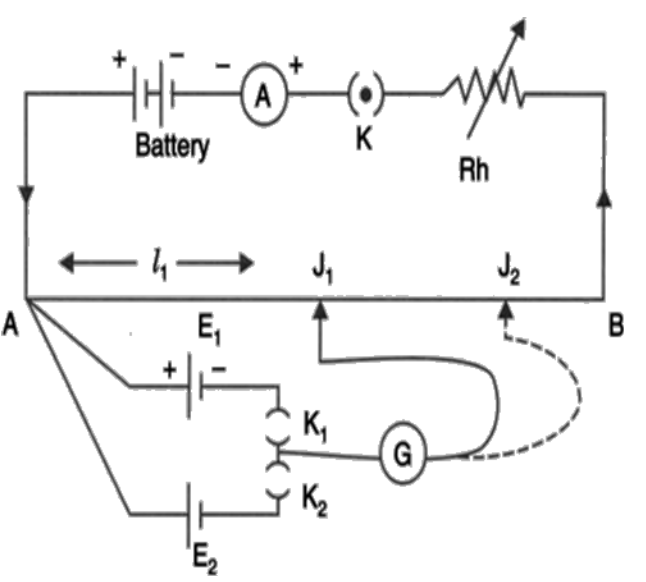
Condition: 

Close the switch 1 and 3 such that ${{E}_{1}}$comes in the circuit.

Potential Difference across AJ is ${{V}_{AJ}}<{{I}_{1}}$ 

It is known that, no current flows between ${{E}_{1}}$  and  ${{V}_{AJ}}$ 

$\Rightarrow {{V}_{AJ}}={{E}_{1}}$

${{E}_{1}}<{{l}_{1}}$

$\Rightarrow {{E}_{1}}=k{{l}_{1}}$    ……$(1)$

Condition: 

Close the switch 2 and 3 such that ${{E}_{2}}$ comes in the circuit and balance point is obtained of ${{J}_{1}}$ .

Since no current flows between $A{{J}_{1}}$ and ${{E}_{2}}$

$\Rightarrow {{V}_{A{{J}_{1}}}}={{E}_{2}}$

${{E}_{2}}<{{l}_{2}}$

$\Rightarrow {{E}_{2}}=k{{l}_{2}}$  ……$(2)$

$\Rightarrow {{V}_{AJ}}={{E}_{2}}=k{{l}_{2}}$  

Dividing equations $(1)$ and $(2)$

$\Rightarrow \frac{{{E}_{1}}}{{{E}_{2}}}=\frac{k{{l}_{1}}}{k{{l}_{2}}}$ 

$\Rightarrow \frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{l}_{1}}}{{{l}_{2}}}$

Therefore, $\frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{l}_{1}}}{{{l}_{2}}}$.

4. Potential difference $V$ is applied across the ends of copper wire of length $l$ and diameter $D$. What is the effect on drift velocity of electrons if

(a) \[V\] is doubled 

Ans: It is known that,

${{V}_{d}}=\frac{I}{neA}=\frac{V}{R(neA)}$

$\Rightarrow {{V}_{d}}=\frac{V}{\left( \rho \frac{\ell }{A} \right)(neA)}=\frac{V}{ne\rho \ell }$

Therefore, when $V$ is doubled, drift velocity gets doubled.

(b) $\ell $ is doubled

Ans:  It is known that,

${{V}_{d}}=\frac{I}{neA}=\frac{V}{R(neA)}$

$\Rightarrow {{V}_{d}}=\frac{V}{\left( \rho \frac{\ell }{A} \right)(neA)}=\frac{V}{ne\rho \ell }$

Therefore, when $l$ is doubled, drift velocity gets halved.

(c) D is doubled 

Ans: It is known that,

${{V}_{d}}=\frac{I}{neA}=\frac{V}{R(neA)}$

$\Rightarrow {{V}_{d}}=\frac{V}{\left( \rho \frac{\ell }{A} \right)(neA)}=\frac{V}{ne\rho \ell }$

Therefore, as $V$ is independent of $D$, drift velocity remains unchanged.

5. What is drift velocity? Derive expression for drift velocity of electrons in a good conductor in terms of relaxation time of electrons? 

Ans: Drift velocity is defined as the average velocity with which free electrons get drifted in a direction opposite to that of an electric field.

Let, $m$ be the mass of the electron and $e$ be the charge of electrons.

When electric field $E$ is applied, acceleration acquired by the electron is $a=\frac{eE}{m}$.

From, first equation of motion: $v=u+at$ 

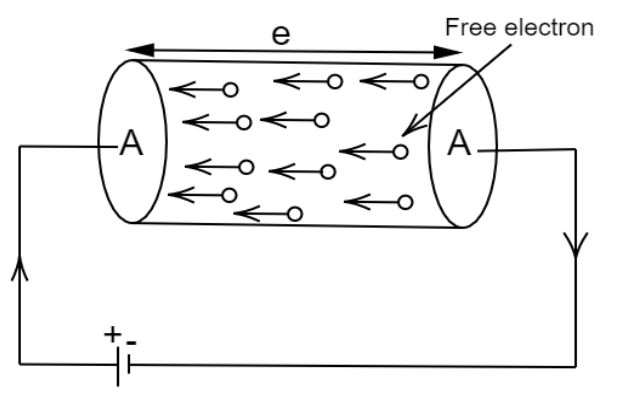
Average initial velocity, $u=OV={{v}_{d}}$

Relaxation time, $t=\tau $

$\Rightarrow {{v}_{d}}=a\tau $ 

$\Rightarrow {{v}_{d}}=\frac{eE\tau }{m}$

Where,

$e$ is the change on electron 

$E$ is the electric field intensity 

$\tau $  is the relaxation time 

$m$ is the mass of electron

Therefore, the expression for drift velocity of electrons in a good conductor in terms of relaxation time of electrons is ${{v}_{d}}=\frac{eE\tau }{m}$.

6. The potentiometer circuit shown, the balance (null) point is at $X$. State with reason, where the balance point will be shifted when 

(Image will be uploaded soon)

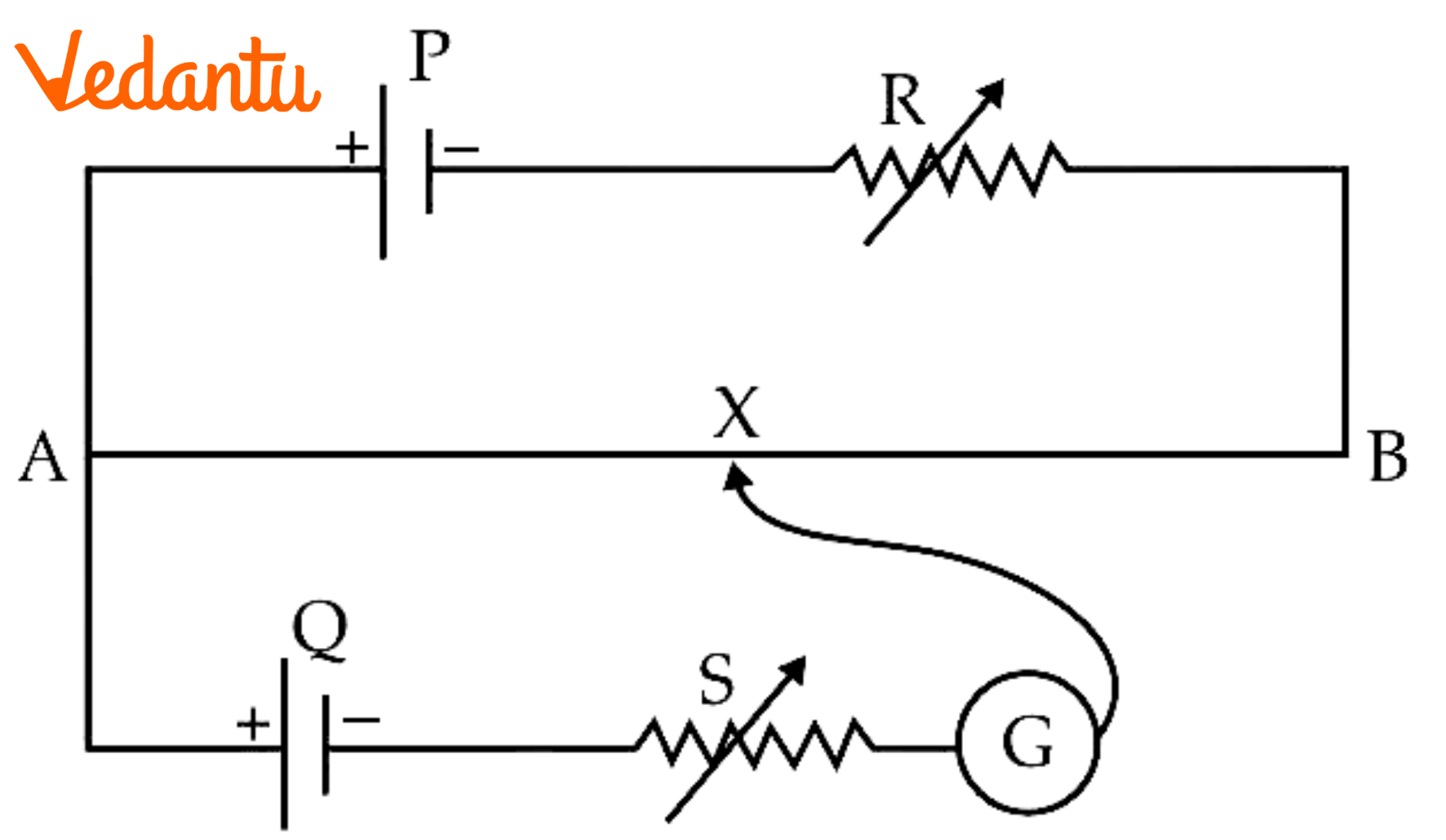
(a) Resistance R is increased, keeping all parameters unchanged. 

Ans: If resistance $R$ is increased, then the current through potentiometer wire $AB$ will decrease. Therefore, the potential difference across $A$ will decrease and balance point shifts towards $B$. 

(b) Resistance S is increased, keeping R constant.

Ans: If resistance $S$ is increased, then the terminal potential difference of the battery will decrease. Therefore, the balance point will be obtained at a smaller length and thus shifts towards $A$. 

(c) Cell P is replaced by another cell whose emf is lower than that of cell Q.

Ans: If cell $P$ is replaced by another cell whose emf is lower than that of cell Q, then the potential difference across $AB$ will be less than that of emf Q. Therefore, the balance point will not be obtained.

7.

(a) Using the principle of Wheatstone bridge describes the method to determine the specific resistance of a wire in the laboratory. Draw the circuit diagram and write the formula used? 

Ans: Firstly, close the Key $(k)$ and move the jockey along the wire till a certain point $B$ is reached where the galvanometer shows no deflection. Therefore, the bridge is said to be balanced. 

If $Rcm$is the resistance per cm length of the wire then.

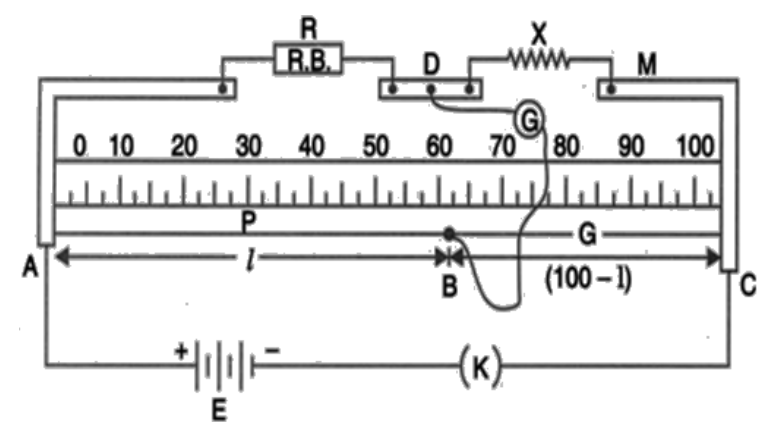
$\frac{R}{X}=\frac{lRcm}{(100-l)Rcm}$ 

$X=\frac{R(100-l)}{l}$

It is known that,

$P=\frac{XA}{l'}$, $l'$is the length if the wire

$P=\frac{R(100-l)A}{l(l')}$ 

Therefore, the point is located at, $P=\frac{R(100-l)A}{l(l')}$.

(b) In a Wheatstone bridge experiment, a student by mistake connects key $(k)$ in place of galvanometer and galvanometer $(G)$ in place of Key $(K)$. What will be the change in the deflection of the bridge? 

Ans: If the bridge is balanced, then there will be no current in the key. Therefore, constant current flows through the galvanometer and thus there will be no change in deflection of the bridge.

8. Two primary cells of emf ${{E}_{1}}$ and ${{E}_{2}}$  are connected to the potentiometer wire $AB$ as shown in the figure if the balancing length for the two combinations of the cells are $250cm$ and $400cm$. Find the ratio of ${{E}_{1}}$ and ${{E}_{2}}$ .

 (Image will be uploaded soon)

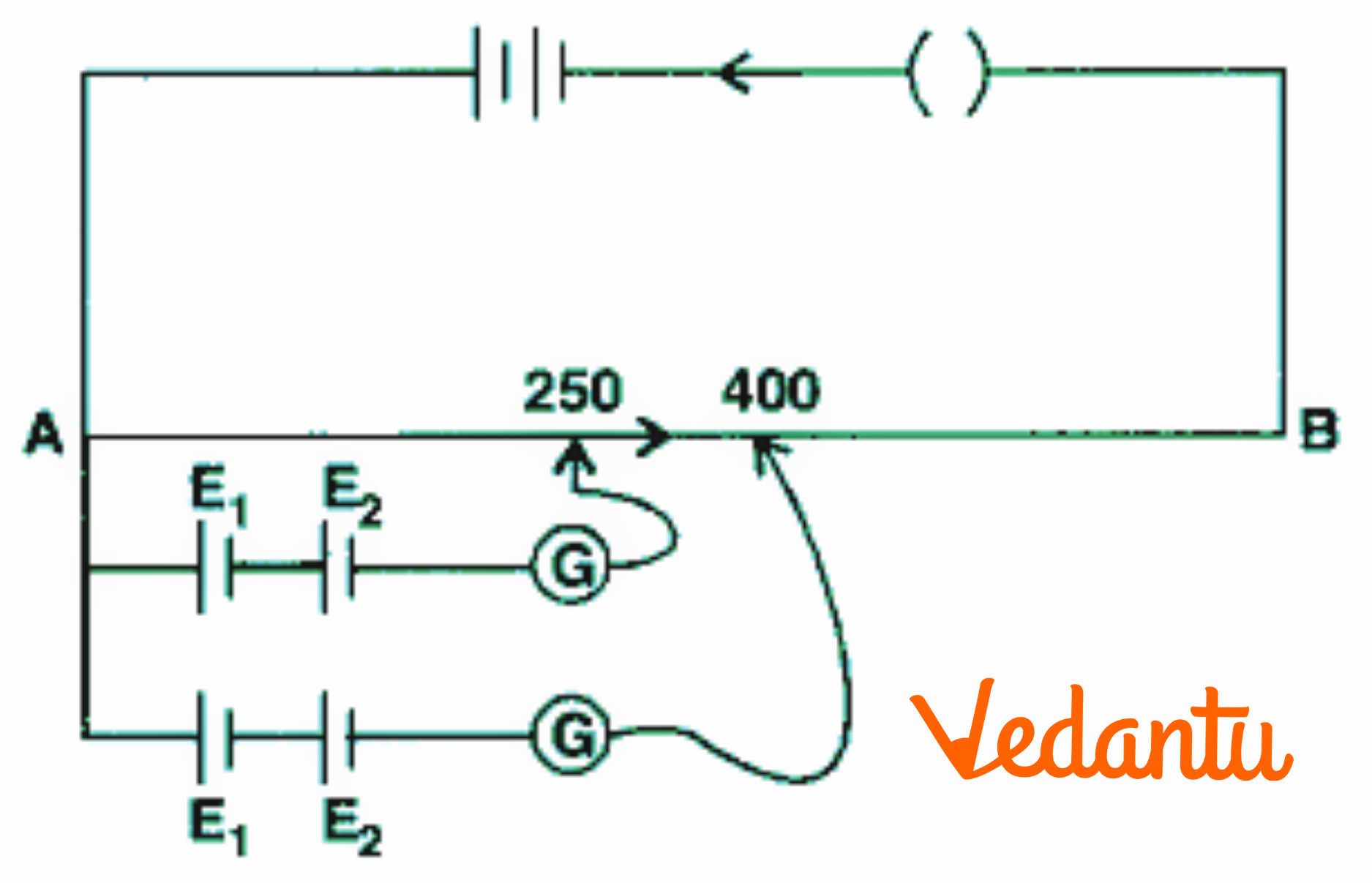
Ans: It is known that,$E=kl$

$\text{ }{{E}_{1}}-{{E}_{2}}=K\times 250$   ……$(1)$

${{E}_{1}}+{{E}_{2}}=K\times 400$   ……$(2)$

Adding equations $(1)$ and $(2)$

$2{{E}_{1}}=250~K+400K$

\[2{{E}_{1}}=250~K+400\] 

$2{{E}_{1}}=650K$ 

${{E}_{1}}=\frac{650}{2}K$

${{E}_{1}}=325K$

Substituting ${{E}_{1}}=325K$ in equation$(1)$

$\text{ 325K}-{{E}_{2}}=K\times 250$

${{E}_{2}}=325K-250K$

${{E}_{2}}=75K$

Divide ${{E}_{1}}$ and ${{E}_{2}}$

\[\Rightarrow \frac{{{E}_{1}}}{{{E}_{2}}}=\frac{325K}{75K}\]

\[\Rightarrow \frac{{{E}_{1}}}{{{E}_{2}}}=4.33\]

The ratio of ${{E}_{1}}$ and ${{E}_{2}}$ is $4.33$.

9. Explain with the help of a circuit diagram, how the value of an unknown resistance can be determined using a Wheatstone bridge? 

Ans: In this case \[P,\text{ }Q,\text{ }R\] are known resistance and $X$ is an unknown resistance.

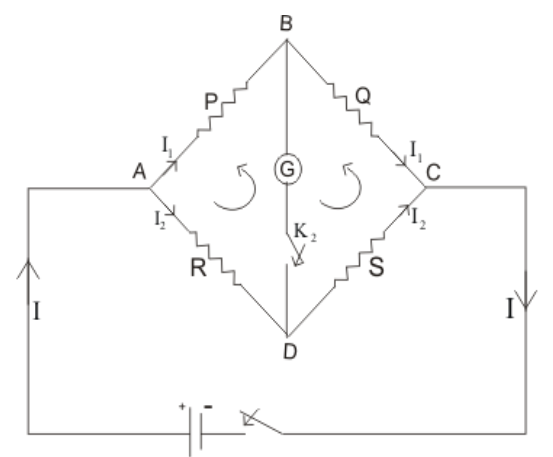
Applying Kirchhoff’s law for closed path \[ABDA\]. 

${{I}_{1}}P+{{I}_{3}}G-{{I}_{2}}R=0$    ……$(1)$

For closed path \[~BCDB\]

$({{I}_{1}}-{{I}_{3}})Q-({{I}_{2}}+{{I}_{3}})X-{{I}_{3}}G=0$   …… $(2)$

The bridge is said to be balanced when no current flows through the galvanometer. 

$\Rightarrow Ig=0$ $({{I}_{g}}={{I}_{3}})$

Equation $(1)\Rightarrow {{I}_{1}}P={{I}_{2}}R$

\[\Rightarrow \frac{{{I}_{1}}}{{{I}_{2}}}=\frac{R}{P}\]      ……$(3)$

Equation $(2)\Rightarrow {{I}_{1}}Q={{I}_{2}}X$

\[\Rightarrow \frac{{{I}_{1}}}{{{I}_{2}}}=\frac{X}{Q}\]      ……$(4)$

Equating equations $(3)$and $(4)$

$\frac{R}{P}=\frac{X}{Q}\Rightarrow X=\frac{RQ}{P}$ 

10. Find the current drawn from a cell of emf  $1V$ and internal resistance \[\frac{2}{3}\Omega \] connected to the network shown in the figure. $E=1V$ , $r=\frac{2}{3}\Omega $.

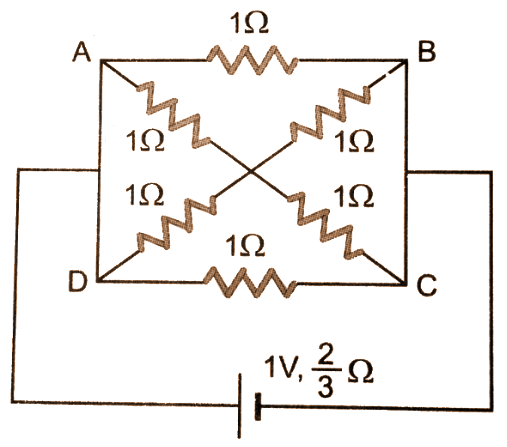
Ans: The circuit can be redrawn as follows:

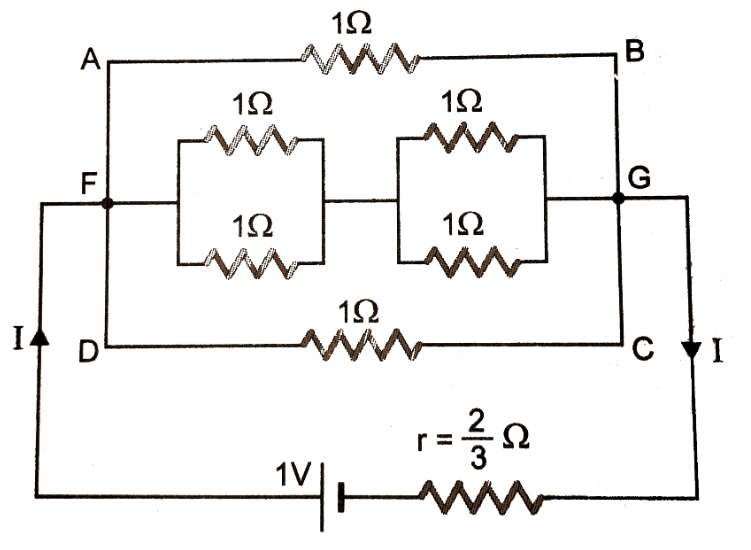
$\Rightarrow \text{ }\frac{I}{{{R}_{1}}}=\frac{1}{1}+\frac{1}{1}$ 

$\Rightarrow \frac{1}{{{R}_{1}}}=2$

$\Rightarrow {{R}_{1}}=\frac{1}{2}$

Similarly,

$\Rightarrow {{R}_{2}}=\frac{1}{2}$

$R={{R}_{1}}+{{R}_{2}}$

$\Rightarrow R=\frac{1}{2}+\frac{1}{2}$

$\Rightarrow R=1\Omega $

(Image will be uploaded soon)

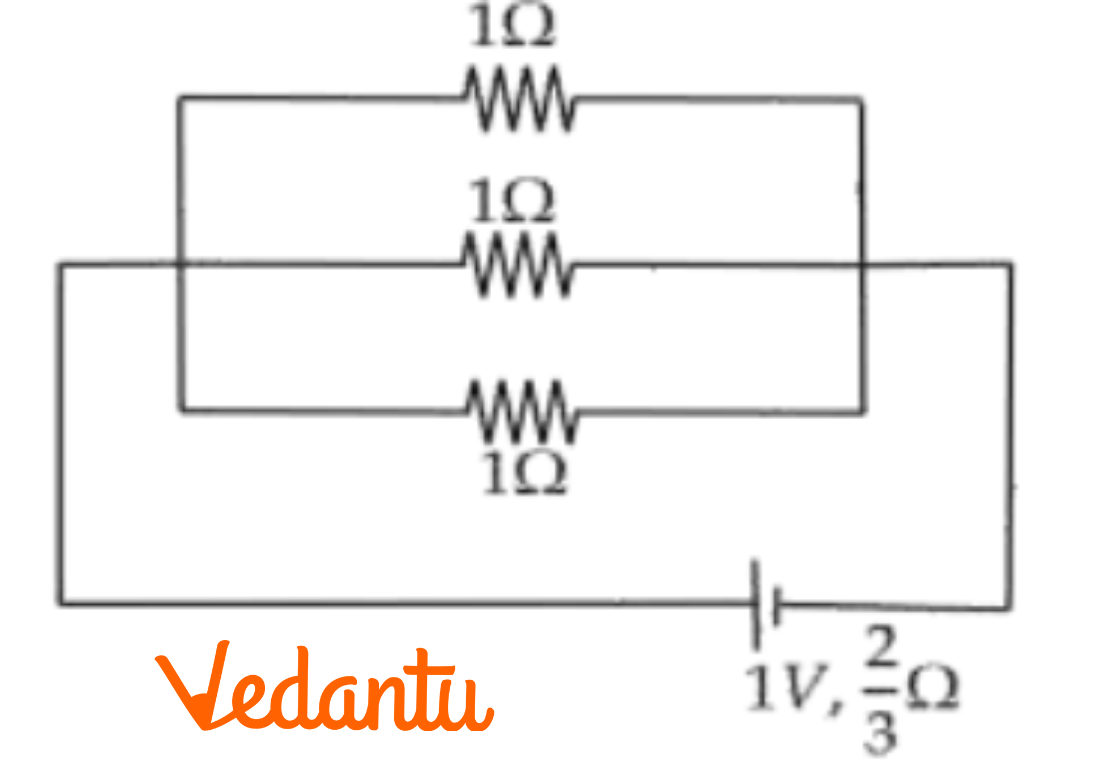
Here, \[1\Omega ,1\Omega \] and \[1\Omega \] are in parallel.

$\Rightarrow \frac{1}{{{R}_{net}}}=\frac{1}{1}+\frac{1}{1}+\frac{1}{1}$

$\Rightarrow \frac{1}{Rnet}=\frac{3}{1}$

$\Rightarrow \text{ Rnet }=\frac{3}{1}\Omega ~$

$\text{I}=\frac{E}{R+r}=\frac{1}{\frac{3}{1}+\frac{3}{3}}=\frac{3}{3}=1A$

$\Rightarrow I=1A$

Current drawn from a cell of emf  $1V$ is $I=1A$.

11.

(a) State and explain Kirchhoff’s law? 

Ans: Kirchhoff’s first law: It states that the algebraic sum of currents at a junction in an electrical circuit is always zero. 

(Image will be uploaded soon)

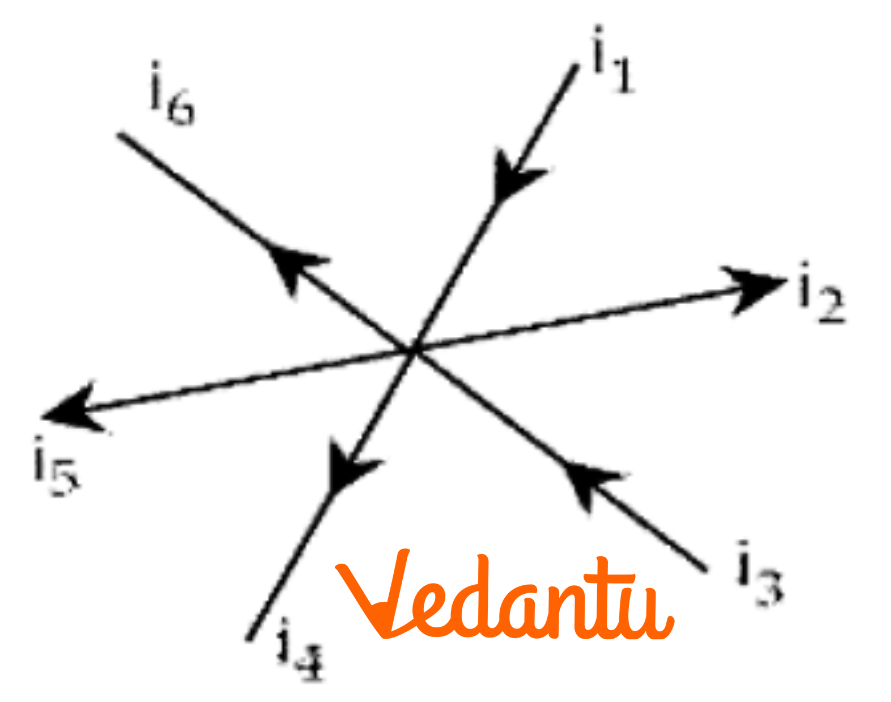
$\Rightarrow {{i}_{1}}-{{i}_{2}}+{{i}_{3}}-{{i}_{4}}-{{i}_{5}}-{{i}_{6}}=0$ 

Kirchhoff’s second law: It states that in any closed part of an electrical circuit, the algebraic sum of emf is equal to the algebraic sum of the products of resistances and current flowing through them. Eg: For closed path \[ABCA~\]

(Image will be uploaded soon)

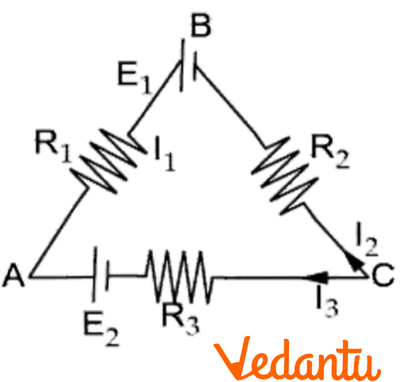
${{R}_{1}}{{I}_{1}}-{{R}_{3}}{{I}_{3}}+{{R}_{2}}{{I}_{2}}-{{E}_{1}}+{{E}_{2}}=0$ 

${{E}_{1}}-{{E}_{2}}={{R}_{1}}{{I}_{1}}-{{R}_{3}}{{I}_{3}}+{{R}_{2}}{{I}_{2}}$

(b) In the network shown, find the values of current ${{I}_{1}},{{I}_{2}},{{I}_{3}}$.

(Image will be uploaded soon)

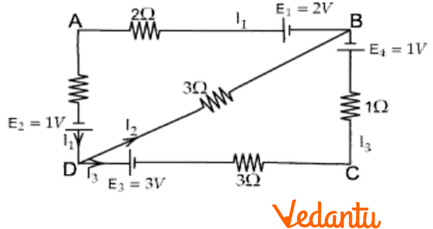
Ans: Applying Kirchhoff’s law at point D

${{I}_{1}}={{I}_{2}}+{{I}_{3}}$      ……$(1)$

For closed path \[ABDA\]

$2{{I}_{1}}+1-2+{{I}_{1}}+3{{I}_{2}}=0$ 

$3{{I}_{1}}+3{{I}_{2}}-1=0$

$3{{I}_{1}}+3{{I}_{2}}=1$       ……$(2)$

For closed path \[DBCD\]

$3{{I}_{2}}-1-{{I}_{3}}-3{{I}_{3}}+3=0$

$3{{I}_{2}}-4{{I}_{3}}+2=0$

$4{{I}_{3}}-3{{I}_{2}}-2=0$

$4{{I}_{3}}-3{{I}_{2}}=2$     ……$(3)$

Substituting $(1)$ in $(2)$

$(2)\Rightarrow 3({{I}_{2}}+{{I}_{3}})+3{{I}_{2}}=1$

$(2)\Rightarrow 6{{I}_{2}}+3{{I}_{3}}=1$

$(3)\Rightarrow 4{{I}_{3}}-3{{I}_{2}}=2$

$2\times (3)\Rightarrow 8{{I}_{3}}-6{{I}_{2}}=4$       ……$(4)$

$(3)+(4)=11{{I}_{3}}=5$

$\Rightarrow {{I}_{3}}=\frac{5}{11}A$

Substituting ${{I}_{3}}$ in equation $(3)$

$\Rightarrow 4(\frac{5}{11})-3{{I}_{2}}=2$

$\Rightarrow \frac{20}{11}-3{{I}_{2}}=2$

$\Rightarrow \frac{20}{11}-2=3{{I}_{2}}$

$\Rightarrow \frac{-2}{11}=3{{I}_{2}}$

$\Rightarrow {{I}_{2}}=\frac{-2}{33}A$

Substituting ${{I}_{2}}$,${{I}_{3}}$ in equation $(1)$

${{I}_{1}}=\frac{-2}{33}+\frac{5}{11}$

$\Rightarrow {{I}_{1}}=\frac{13}{33}A$

Currents are ${{I}_{1}}=\frac{13}{33}A$, ${{I}_{2}}=\frac{-2}{33}A$ and ${{I}_{3}}=\frac{5}{11}A$.

12. The variation of resistance of a metallic conductor with temperature is given in figure.

(Image will be uploaded soon)

(Image will be uploaded soon)

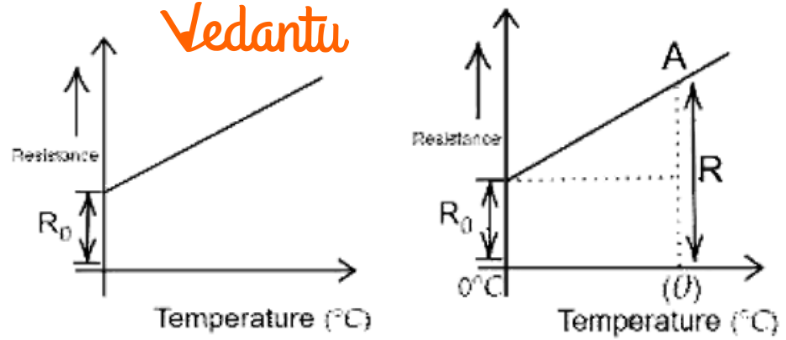
(a) Calculate the temperature coefficient of resistance from the graph.

Ans: It is known that,

Temperature coefficient of Resistance:$\alpha =\frac{R-{{R}_{0}}}{{{R}_{0}}\theta }$ 

where $R$ is the resistance of the conductor and $\theta $ is the temperature corresponding to point A. 

(b) State why the resistance of the conductor increases with the rise in temperature. 

Ans: It is known that, 

$R=\rho \frac{l}{A}=\frac{m}{n{{e}^{2}}\tau }(\frac{t}{A})$

where $\rho $is the resistivity.

When temperature increases, the number of collisions increases, average relaxation time decreases, therefore resistance increases. 

13. A circle ring having negligible resistance is used to connect four resistors of resistances \[\mathbf{6R},\mathbf{6R},\mathbf{6R}\] and $R$ as shown in the figure. Find the equivalent resistance between points A & B.

(Image will be uploaded soon)

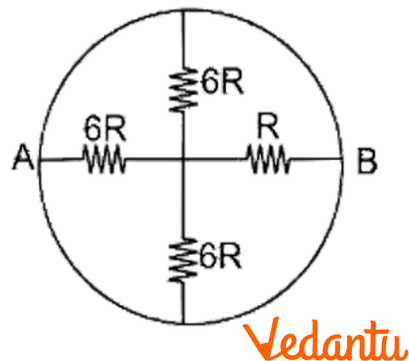
Ans: The given circuit can be redrawn as follows:

(Image will be uploaded soon)

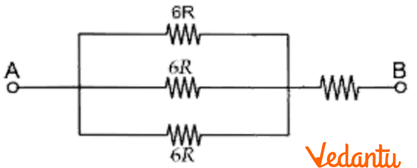
\[6R,6R\] and $6R$ are in parallel.

$\Rightarrow \frac{1}{{{R}_{s}}}=\frac{1}{6R}+\frac{1}{6R}+\frac{1}{6R}$ 

$\Rightarrow \frac{1}{{{R}_{s}}}=\frac{3}{6R}$

$\Rightarrow {{R}_{S}}=\frac{6R}{3}=2R$ 

(Image will be uploaded soon)

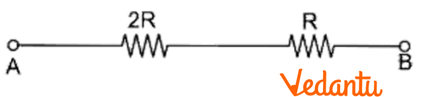
${{R}_{S}}=2R$ and $R$ are in series.

${{R}_{net}}=2R+R$ 

${{R}_{net}}=3R$

14. A battery of emf $E$ and internal resistance $r$ sends a current, ${{I}_{1}},{{I}_{2}}$ when connected to an external resistance of ${{R}_{1}},{{R}_{2}}$  respectively. Find the emf. and internal resistance of the battery.

Ans: It is given that,

$E$ is the emf of a battery

$r$ is the internal resistance which sends currents ${{I}_{1}},{{I}_{2}}$

${{R}_{1}},{{R}_{2}}$ are external resistances

Current ${{I}_{1}}$ can be written as: ${{I}_{1}}=\frac{E}{{{R}_{1}}+r}$

$E={{I}_{1}}({{R}_{1}}+r)$  ……$(1)$

Similarly, $E={{I}_{2}}({{R}_{2}}+r)$ ……$(2)$

From equations $(1)$ and $(2)$

$\Rightarrow {{I}_{1}}({{R}_{1}}+r)={{I}_{2}}({{R}_{2}}+r)$

$\Rightarrow {{I}_{2}}r-{{I}_{1}}r={{I}_{1}}{{R}_{1}}-{{I}_{2}}{{R}_{2}}$

$\Rightarrow r\left( {{I}_{2}}-{{I}_{1}} \right)={{I}_{1}}{{R}_{1}}-{{I}_{2}}{{R}_{2}}$

${*{35}{l}} \Rightarrow r=\frac{{{I}_{1}}{{R}_{1}}-{{I}_{2}}{{R}_{2}}}{{{I}_{2}}-{{I}_{1}}}$

Emf of the battery,$E$

$\Rightarrow E={{I}_{1}}\left( {{R}_{1}}+r \right)$

$\Rightarrow E={{I}_{1}}\left[ {{R}_{1}}+\frac{{{\text{I}}_{1}}{{\text{R}}_{1}}-{{\text{I}}_{2}}{{\text{R}}_{2}}}{{{\text{I}}_{2}}-{{\text{I}}_{1}}} \right]$

$\Rightarrow E={{I}_{1}}\left[ \frac{{{\text{I}}_{2}}{{\text{R}}_{1}}-{{\text{I}}_{1}}{{R}_{1}}+{{I}_{1}}{{\text{R}}_{1}}-{{\text{I}}_{2}}{{\text{R}}_{2}}}{{{\text{I}}_{2}}-{{\text{I}}_{1}}} \right]$

$\Rightarrow E=\frac{{{I}_{1}}{{I}_{2}}\left( {{\text{R}}_{1}}-{{\text{R}}_{2}} \right)}{{{\text{I}}_{2}}-{{\text{I}}_{1}}}$

Therefore, emf and internal resistance of the battery are $E=\frac{{{I}_{1}}{{I}_{2}}\left( {{\text{R}}_{1}}-{{\text{R}}_{2}} \right)}{{{\text{I}}_{2}}-{{\text{I}}_{1}}}$ 

and 

${*{35}{l}} r=\frac{{{I}_{1}}{{R}_{1}}-{{I}_{2}}{{R}_{2}}}{{{I}_{2}}-{{I}_{1}}}$

15. Find the value of unknown resistance $X$ in the circuit shown in the figure if no current flows through the section AO. Also calculate the current drawn by the circuit from the battery of emf. $6V$ and negligible internal resistance. 

(Image will be uploaded soon)

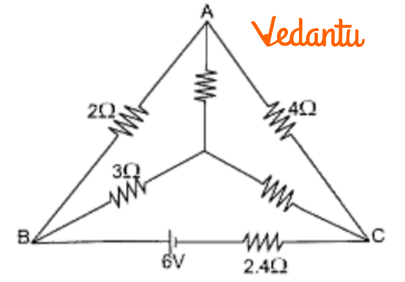
Ans: It is given that no current flows through AO then the circuit is said to be a balanced Wheatstone bridge. 

$\Rightarrow \frac{2}{4}=\frac{3}{X}$ 

$\Rightarrow X=\frac{12}{2}=6$

$\Rightarrow X=6\Omega $

In branch AO, \[I=0\]

Resistance of $10\Omega $ between A and O is ineffective and the circuit is reduced to:

(Image will be uploaded soon)

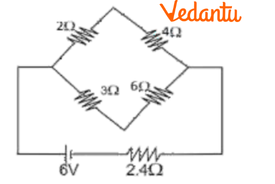
\[2\Omega \] and \[4\Omega \] are in series; \[3\Omega \] and \[6\Omega \] are in series

(Image will be uploaded soon)

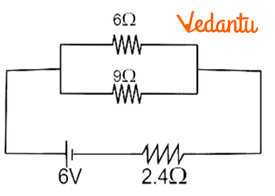
6Ω and 9Ω are in parallel.

$\Rightarrow \frac{1}{{{R}_{P}}}=\frac{1}{6}+\frac{1}{9}=\frac{9+6}{54}=\frac{15}{54}$ 

$\Rightarrow {{R}_{P}}=\frac{54}{15}\Omega $

${{R}_{P}}$ and \[2.4\Omega \] are in series

$\Rightarrow {{R}_{eff}}=2.4+\frac{54}{15}$ 

$\Rightarrow {{R}_{eff}}=\frac{24}{10}+\frac{54}{15}=\frac{360+540}{150}=\frac{900}{150}$

$\Rightarrow {{R}_{eff}}=6\Omega $

Current: $I=\frac{V}{R}=\frac{6}{6}=1$

$\Rightarrow I=1A$

Therefore, the unknown resistance $X=6\Omega $ and current drawn by the circuit from the battery is $I=1A$.

16. 

(a) Obtain ohm’s law from the expression for electrical conductivity.

Ans: It is known that,

$I=neA{{v}_{d}}$

$J=\frac{I}{A}=ne{{v}_{d}}$

${{V}_{d}}=\frac{eE\tau }{m}$

$\Rightarrow J=\frac{n{{e}^{2}}E\tau }{m}$ ; $J=\sigma E$

$\sigma =\frac{J}{E}=\frac{n{{e}^{2}}\tau }{m}$

Let $l$ and $A$ be the length and area of the wire.

$I=JA$

$\Rightarrow I=\frac{n{{e}^{2}}E\tau }{m}\times A$ ; $(E=\frac{V}{l})$

$\Rightarrow I=\frac{n{{e}^{2}}V\tau }{ml}A$ 

$\Rightarrow V=\left( \frac{m}{n{{e}^{2}}\tau } \right)\left( \frac{l}{A} \right)I$ 

$\therefore V=RI$

$\Rightarrow R=\rho \frac{l}{A}$ where, $\rho =\frac{m}{n{{e}^{2}}\tau }$(Specific resistance of a wire)

(b) A cylindrical wire is stretched to increase its length by $10%$ calculate the percentage increase in resistance?

Ans: It is given that; the length of cylindrical wire is stretched to increase its length by $10%$.

Let, the original length be $l$ and the new length be $l'$.

$\Rightarrow l'=l+\frac{10}{100}l$ 

$\Rightarrow l'=1.1l$

$\Rightarrow \frac{l'}{l}=1.1$

As the volume of the wire remains the same

$Al=A'l'$

$\frac{A'}{A}=\frac{l}{l'}$

It is known that, $\text{R=}\rho \frac{l}{A}$

$R'=\rho \frac{l'}{A'}$

$\Rightarrow \frac{R'}{R}=\frac{l'}{A'}\times \frac{A}{l}$

\[\Rightarrow \frac{R'}{R}=\frac{l'}{l}\times \frac{l'}{l}={{\left( \frac{l'}{l} \right)}^{2}}\]

$\Rightarrow \frac{R'}{R}={{(1.1)}^{2}}=1.21$

Thus, the percentage increase in Resistance is $\frac{R'-R}{R}\times 100=21%$.

17. The current $I$ flows through a wire of radius $r$ and the free electron drift with a velocity ${{\upsilon }_{d}}$ what is the drift velocity of electrons through a wire of same material but having double the radius, when a current of $2I$ flows through it?

Ans: It is known that,

$I=neA{{v}_{d}}$

$\Rightarrow {{v}_{d}}=\frac{I}{neA}=\frac{I}{ne\pi {{r}^{2}}}$  ……$(1)$

If ${{v}_{d}}'$ is the drift velocity of electrons in the second wire

$vd'=\frac{I'}{nA'e}$ 

$\Rightarrow vd'=\frac{2I}{n4\pi {{r}^{2}}e}$

$\Rightarrow vd'=\frac{1}{2}(\frac{I}{n\pi {{r}^{2}}e})$   ……$(2)$

From equations $(1)$ and $(2)$

$\Rightarrow vd'=\frac{vd}{2}$ 

Therefore, the drift velocity gets reduced to half.

18. Three identical cells, each of emf. $2V$ and unknown internal resistance are connected in parallel. This combination is connected to a $5$ ohm resistor. If the terminal voltage across the cell is \[\mathbf{1}.\mathbf{5}\] volt. What is the internal resistance of each cell? Hence define the internal resistance of a cell? 

Ans: It is given that,

\[E=2V,\text{ }V=1.5V,\text{ }R=5\text{ }\Omega \]

Total internal resistance =  $\frac{r}{3}$ 

Internal resistance $r$ is equal to: $r=\left( \frac{E}{V}-1 \right)R$ 

$\Rightarrow \frac{r}{3}=\left( \frac{2}{1.5}-1 \right)5$

$\Rightarrow \frac{r}{3}=\left( \frac{2-1.5}{1.5} \right)5$

$\Rightarrow r=\left( \frac{0.5}{1.5} \right)15$

$\Rightarrow r=50ohm$

The resistance offered by the electrolyte of the cell, when the electric current flows through it, is called the internal resistance of a cell. In this case, internal resistance is equal to $r=50ohm$.

19. Using Kirchhoff’s law, determine the current ${{I}_{1}},{{I}_{2}},{{I}_{3}}$  for the network shown.

(Image will be uploaded soon)

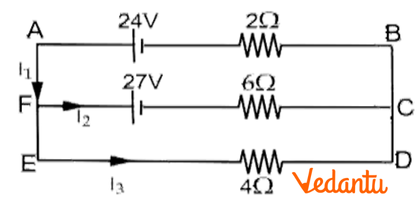
Ans: In the given figure, applying junction rule at point F

$\Rightarrow {{I}_{1}}={{I}_{2}}+{{I}_{3}}$    ……$(1)$

Loop rule for \[BAFCB\]

$\Rightarrow 2{{I}_{1}}+6{{I}_{2}}-24+27=0$ 

$\Rightarrow 2{{I}_{1}}+6{{I}_{2}}+3=0~$    …… $(2)$

Loop rule for FCDEF

$\Rightarrow 27+6{{I}_{2}}-4{{I}_{3}}=0$  …….$(3)$

Substituting ${{I}_{1}}$ in equation$(2)$

$(2)\Rightarrow 2({{I}_{2}}+{{I}_{3}})+6{{I}_{2}}+3=0~$

$(2)\Rightarrow 2{{I}_{3}}+8{{I}_{2}}+3=0$

$2\times (2)\Rightarrow 2(2{{I}_{3}}+8{{I}_{2}}+3)=0$

$2\times (2)\Rightarrow 4{{I}_{3}}+16{{I}_{2}}+6=0$   …….$(4)$

$(4)+(3)\Rightarrow 27+6+22{{I}_{2}}=0$

$\Rightarrow {{I}_{2}}=\frac{-33}{22}=\frac{-3}{2}$

$\Rightarrow {{I}_{2}}=-1.5A$

Substitute ${{I}_{2}}$ in equation $(2)$

$\Rightarrow 2{{I}_{1}}+6(-1.5)+3=0~$ 

$\Rightarrow 2{{I}_{1}}=6$

$\Rightarrow {{I}_{1}}=3A$

Substitute ${{I}_{1}},{{I}_{2}}$ in equation $(1)$

$\Rightarrow 3=-1.5+{{I}_{3}}$

$\Rightarrow {{I}_{3}}=4.5A$

Therefore, the currents are ${{I}_{1}}=3A$,${{I}_{2}}=-1.5A$and ${{I}_{3}}=4.5A$.

20. Show that when a current is divided between two resistances in accordance with Kirchhoff’s laws, the heat provided is minimum.

Ans: Consider two resistances ${{R}_{1}},{{R}_{2}}$  in parallel with ${{i}_{1}},{{i}_{2}}$ currents flowing in it. Using Kirchhoff’s first law,

$i={{i}_{1}}+{{i}_{2}}$    ……$(1)$

(Image will be uploaded soon)

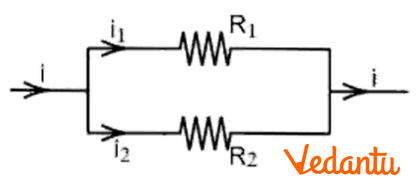
${{i}_{1}}{{R}_{1}}-{{i}_{2}}{{R}_{2}}=0$ 

$\frac{{{i}_{1}}}{{{i}_{2}}}=\frac{{{R}_{2}}}{{{R}_{1}}}.$

Heat produced in the circuit in $t$ seconds is $H=i_{1}^{2}{{R}_{1}}t+{{i}_{2}}^{2}{{R}_{2}}t$$\Rightarrow H={{i}_{1}}^{2}{{R}_{1}}t+{{\left( i-{{i}_{1}} \right)}^{2}}{{R}_{2}}t$ 

If the heat produced is minimum then $\frac{dH}{d{{i}_{1}}}=0$ 

$\Rightarrow 2{{\text{i}}_{1}}{{\text{R}}_{1}}\text{t}+2\left( \text{i}-{{\text{i}}_{1}} \right)(-1){{\text{R}}_{2}}\text{t=0}$ 

\[\Rightarrow 2\left( \text{i}-{{\text{i}}_{1}} \right){{\text{R}}_{2}}\text{t}=2{{\text{i}}_{1}}{{\text{R}}_{1}}\text{t}\]

\[\Rightarrow \left( i-{{i}_{1}} \right){{R}_{2}}={{i}_{1}}{{R}_{1}}\]

\[\Rightarrow \frac{{{i}_{1}}}{{{i}_{2}}}=\frac{{{R}_{2}}}{{{R}_{1}}}\]

Therefore, it is proved in accordance with Kirchhoff’s law.

21. 

(a) Define emf. of a cell? On what factors does it depend? 

Ans: Emf of a cell is defined as the potential difference between the two electrodes of the cell in open Circuit (when no current is drawn).

It depends on the following factors:

(a) Nature of Electrodes 

(b) Nature and concentration of the Electrolytes 

(c) Temperature of the cell. 

(b) Figure below shows a $2.0V$ potentiometer used for the determination of internal resistance of a $1.5V$ cell. The balance point of the cell in the open circuit is $76.3cm$. When a resistance of $9.5\Omega $ is used in the external circuit of the cell the balance point shifts to $64.8cm$ length of the potentiometer. Determine the internal resistance of the cell.

(Image will be uploaded soon)

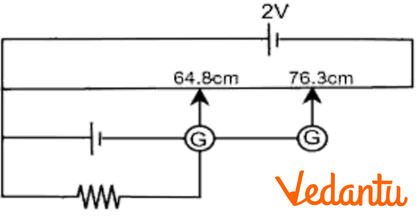
Ans: It is known that,

Internal resistance of the cell, $\text{r}=\text{R}\left( \frac{{{\ell }_{1}}-{{\ell }_{2}}}{{{\ell }_{2}}} \right)$

It is given that,

${{\ell }_{1}}=76.3~\text{cm, }{{\ell }_{2}}=64.8~\text{cm, R}=9.5\Omega $

$\Rightarrow \text{r}=9.5\left( \frac{76.3-64.8}{64.8} \right)$

$\Rightarrow r=1.68\Omega $

Therefore, the internal resistance of the cell, $r=1.68\Omega $.

22. A battery of emf 10 V and internal resistance $3\Omega $ is connected to a resistor. If the current in the circuit is 0.5 A, what is the resistance of the resistor? What is the terminal voltage of the battery when the circuit is closed?

Ans: In the above question it is given that:

Emf of the battery, E = 10 V

Internal resistance of the battery, $r=3\Omega $

Current in the circuit, $I=0.5A$ 

Consider the resistance of the resistor to be $R$.

Therefore, using Ohm’s law,

$I=\frac{E}{R+r}$

$R+r=\frac{E}{I}$

$\Rightarrow R+r=\frac{10}{0.5}$

$\Rightarrow R+r=20$

$\therefore R=20-3=17\Omega $

Let the terminal voltage of the resistor be $V$.

Using Ohm's law,

$V=IR$

$\Rightarrow V=0.5\times 17=8.5V$

Thus, the resistance of the resistor is $17\Omega $ and the terminal voltage is $8.5V$ .

23.

(a) Three resistors $1\Omega $ , $2\Omega $ and $3\Omega $ are combined in series. What is the total resistance of the combination?

Ans: In the above question it is given that three resistors of resistances  $1\Omega $ , $2\Omega $ and $3\Omega $  are combined in series. 

The total resistance of the combination is the algebraic sum of individual resistances.

Hence the total resistance is given by:

Total Resistance $=1+2+3=6\Omega $

(b) If the combination is connected to a battery of emf $12V$ and negligible internal resistance, obtain the potential drop across each resistor.

Ans: Consider the current flowing through the circuit to be $I$.

Emf of the battery, $E=12V$

Total resistance of the circuit, $R=6\Omega $

The relation for current using Ohm’s law is given by:

$I=\frac{E}{R}$

$\Rightarrow I=\frac{12}{6}=2A$

Consider the potential drop across $1\Omega $ resistor to be ${{V}_{1}}$ .

Using Ohm’s law, the value of ${{V}_{1}}$ can be obtained as:

${{V}_{1}}=2\times 1=2V$ …… (1)

Consider the potential drop across $2\Omega $ resistor to be ${{V}_{2}}$ .

Again, using Ohm’s law, the value of ${{V}_{2}}$ can be obtained as:

${{V}_{2}}=2\times 2=4V$ …… (2)

Consider potential drop across $3\Omega $ resistor to be ${{V}_{3}}$ .

$\therefore {{V}_{3}}=2\times 3=6V$ ...... (3)

Hence, the potential drop across $1\Omega $ , $2\Omega $ and $3\Omega $  resistors are $2V$ , $4V$ and $6V$ respectively.

24. At room temperature ${{27.0}^{\circ }}C$, the resistance of a heating element is $100\Omega $. What is the temperature of the element if the resistance is found to be $117\Omega $, given that the temperature coefficient of the material of the resistor is $1.70\times {{10}^{-4}}^{\circ }{{C}^{-1}}$ ?

Ans: In the above question it is given that:

Room temperature, $T={{27.0}^{\circ }}C$

Resistance of the heating element at $T$ , $R=100\Omega $

Consider ${{T}_{1}}$ as the increased temperature of the filament.

Therefore, resistance of the heating element at ${{T}_{1}}$, ${{R}_{1}}=117\Omega $

Temperature coefficient of the material of the filament, $\alpha =1.70\times {{10}^{-4}}^{\circ }{{C}^{-1}}$

We know that,

$\alpha =\frac{{{R}_{1}}-R}{R\left( {{T}_{1}}-T \right)}$

$\therefore \left( {{T}_{1}}-T \right)=\frac{{{R}_{1}}-R}{R\alpha }$

$\Rightarrow \left( {{T}_{1}}-27 \right)=\frac{117-100}{100\times 1.70\times {{10}^{-4}}}$

$\Rightarrow \left( {{T}_{1}}-27 \right)=1000$

$\therefore {{T}_{1}}={{1027}^{\circ }}C$

Therefore, at ${{1027}^{\circ }}C$ , the resistance of the element is $117\Omega $ .

25. A negligibly small current is passed through a wire of length 15 m and uniform cross-section $6.0\times {{10}^{-7}}{{m}^{2}}$ , and its resistance is measured to be $5.0\Omega $ . What is the resistivity of the material at the temperature of the experiment?

Ans: In the above question it is given that:

Length of the wire, $l=15m$

Area of cross-section of the wire, $a=6.0\times {{10}^{-7}}{{m}^{2}}$

Resistance of the material of the wire, $R=5.0\Omega $

Let resistivity of the material of the wire be $\rho $

We know that resistance is related to resistivity as:

$R=\rho \frac{l}{A}$

$\Rightarrow \rho =\frac{RA}{l}$

$\Rightarrow \rho =\frac{5\times 6.0\times {{10}^{-7}}}{15}$

$\therefore \rho =2\times {{10}^{-7}}{{m}^{2}}$

Therefore, the resistivity of the material is $2\times {{10}^{-7}}{{m}^{2}}$ .

26. A silver wire has a resistance of \[2.1\Omega \] at ${{27.5}^{\circ }}C$ , and a resistance of $2.7\Omega $ at ${{100}^{\circ }}C$. Determine the temperature coefficient of resistivity of silver.

Ans: In the above question it is given that:

Temperature, ${{T}_{1}}={{27.5}^{\circ }}C$.

Resistance of the silver wire at ${{T}_{1}}$ is ${{R}_{1}}=2.1\Omega $ .

Temperature, ${{T}_{2}}={{100}^{\circ }}C$ .

Resistance of the silver wire at ${{T}_{2}}$ is ${{R}_{2}}=2.7\Omega $ .

Let the temperature coefficient of silver be $\alpha $ .

It is related to temperature and resistance by the formula:

$\alpha =\frac{{{R}_{2}}-{{R}_{1}}}{{{R}_{1}}\left( {{T}_{2}}-{{T}_{1}} \right)}$

$\Rightarrow \alpha =\frac{2.7-2.1}{2.1\left( 100-27.5 \right)}={{0.0039}^{\circ }}{{C}^{-1}}$

Hence the temperature coefficient of silver is ${{0.0039}^{\circ }}{{C}^{-1}}$.

27. A heating element using nichrome connected to a 230 V supply draws an initial current of 3.2A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is ${{27}^{\circ }}C$ ? Temperature coefficient of resistance of nichrome averaged over the temperature range involved is $1.70\times {{10}^{-4}}^{\circ }{{C}^{-1}}$ .

Ans: In the above question it is given that:

Supply voltage is $V=230V$

Initial current drawn is ${{I}_{1}}=3.2A$.

Let the initial resistance be ${{R}_{1}}$ .

Therefore, using Ohm’s law,

${{R}_{1}}=\frac{V}{{{I}_{1}}}$

$\Rightarrow {{R}_{1}}=\frac{230}{3.2}=71.87\Omega $

Steady state value of the current is ${{I}_{2}}=2.8A$.

Let the resistance of the steady state be ${{R}_{2}}$ .

Therefore, using Ohm’s law.

${{R}_{2}}=\frac{V}{{{I}_{2}}}$

$\Rightarrow {{R}_{2}}=\frac{230}{2.8}=82.14\Omega $

Temperature coefficient of nichrome is $\alpha =1.70\times {{10}^{-4}}^{\circ }{{C}^{-1}}$ .

Initial temperature of nichrome is ${{T}_{1}}={{27}^{\circ }}C$.

Let the steady state temperature reached by nichrome be ${{T}_{2}}$ .

Now using the formula of $\alpha $,

$\alpha =\frac{{{R}_{2}}-{{R}_{1}}}{{{R}_{1}}\left( {{T}_{2}}-{{T}_{1}} \right)}$

$\Rightarrow \left( {{T}_{2}}-{{T}_{1}} \right)=\frac{{{R}_{2}}-{{R}_{1}}}{{{R}_{1}}\alpha }$

$\Rightarrow \left( {{T}_{2}}-27 \right)=\frac{82.14-71.87}{71.87\times 1.70\times {{10}^{-4}}}$

$\Rightarrow {{T}_{2}}-27=840.5$

$\therefore {{T}_{2}}={{867.5}^{\circ }}C$

Hence the steady temperature of the heating element is ${{867.5}^{\circ }}C$ .

28. A storage battery of emf 8.0 V and internal resistance $0.5\Omega $ is being charged by a 120 V DC supply using a series resistor of $15.5\Omega $. What is the terminal voltage of the battery during charging? What is the purpose of having a series resistor in the charging circuit?

Ans: In the above question it is given that:

Emf of the storage battery is $E=0.8V$.

Internal resistance of the battery is $r=0.5\Omega $ .

DC supply voltage is $V=120V$

Resistance of the resistor is $R=15.5\Omega $.

Consider effective voltage in the circuit to be $V'$.

$V'=V-E$

$V'=120-8=112V$

Now, the current flowing in the circuit is $I$ and the resistance $R$ is connected in series to the storage battery. 

Therefore, using Ohm’s law,

$I=\frac{V'}{R+r}$

$\therefore I=\frac{112}{15.5+0.5}=7A$

Hence voltage across resistor $R$will be:

$IR=7\times 15.5=108.5V$

DC supply voltage = Terminal voltage of battery + Voltage drop across $R$

Terminal voltage of battery $=120-108.5=11.5V$

A series resistor in a charging circuit is responsible for limiting the current drawn from the external source. The current will be extremely high in its absence which is very dangerous.

29. The number density of free electrons in a copper conductor estimated in Example is $8.5\times {{10}^{28}}{{m}^{-3}}$ . How long does an electron take to drift from one end of a wire 3.0 m long to its other end? The area of cross-section of the wire is $2.0\times {{10}^{-6}}{{m}^{2}}$ and it is carrying a current of 3.0 A.

Ans: In the above question it is given that:

Number density of free electrons in a copper conductor is $n=8.5\times {{10}^{28}}{{m}^{-3}}$.

Length of the copper wire is $l=3.0m$.

Area of cross-section of the wire is $A=2.0\times {{10}^{-6}}{{m}^{2}}$.

Current carried by the wire is $I=3.0A$.

Now we know that:

$I=nAe{{V}_{d}}$

Where,

$e$ is the electric charge of magnitude $1.6\times {{10}^{-19}}C$.

${{V}_{d}}$ is the drift velocity and

\[Drift\text{ }velocity=\frac{\text{Length of the wire }\left( \text{l} \right)}{\text{Time taken to cover }\left( \text{t} \right)}\]

$I=nAe\frac{l}{t}$

$\Rightarrow t=\frac{nAel}{I}$

$\Rightarrow t=\frac{3\times 8.5\times {{10}^{28}}\times 2\times {{10}^{-6}}\times 1.6\times {{10}^{-19}}}{3.0}$

$\therefore t=2.7\times {{10}^{4}}s$ .

Hence the time taken by an electron to drift from one end of the wire to the other is $2.7\times {{10}^{4}}s$.

30. The earth’s surface has a negative surface charge density of ${{10}^{-9}}C{{m}^{-2}}$ . The potential difference of $400kV$ between the top of the atmosphere and the surface results (due to the low conductivity of the lower atmosphere) in a current of only $1800A$ over the entire globe. If there were no mechanism of sustaining atmospheric electric fields, how much time (roughly) would be required to neutralize the earth’s surface? (This never happens in practice because there is a mechanism to replenish electric charges, namely the continual thunderstorms and lightning in different parts of the globe). (Radius of earth = $6.37\times {{10}^{6}}m$.)

Ans: In the above question it is given that:

Surface charge density of the earth is $\sigma ={{10}^{-9}}C{{m}^{-2}}$.

Current over the entire globe is $I=1800A$.

Radius of the earth is $r=6.37\times {{10}^{6}}m$.

Surface area of the earth is given by:

$A=4\pi {{r}^{2}}$

$\Rightarrow A=4\pi \times {{\left( 6.37\times {{10}^{6}} \right)}^{2}}$

$\therefore A=5.09\times {{10}^{14}}{{m}^{2}}$

Charge on the earth surface is given by:

$q=\sigma A$

$\Rightarrow q={{10}^{-9}}\times 5.09\times {{10}^{14}}$

$\therefore q=5.09\times {{10}^{5}}C$

Now if time taken to neutralize the earth’s surface is $t$, then

Current, $I=\frac{q}{t}$

$\Rightarrow t=\frac{q}{I}$

$\Rightarrow t=\frac{5.09\times {{10}^{5}}}{1800}=282.77s$

Therefore, the time taken to neutralize the earth’s surface is $282.77s$.

31. Choose the Correct Alternative:

(a) Alloys of metals usually have (greater/less) resistivity than that of their constituent metals.

Ans: Alloys of metals usually have greater resistivity than that of their constituent metals.

(b) Alloys usually have much (lower/higher) temperature coefficients of resistance than pure metals.

Ans: Alloys usually have lower temperature coefficients of resistance than pure metals.

(c) The resistivity of the alloy manganin is nearly independent of/increases rapidly with increase of temperature.

Ans: The resistivity of the alloy, manganin, is nearly independent of increase of temperature.

(d) The resistivity of a typical insulator (e.g., amber) is greater than that of a metal by a factor of the order of $\left( {{10}^{22}}/{{10}^{3}} \right)$.

Ans: The resistivity of a typical insulator is greater than that of a metal by a factor of the order of ${{10}^{22}}$ .

32. Determine the current drawn from a $12V$ supply with internal resistance $0.5\Omega $ by the infinite network shown in Figure. Each resistor has $1\Omega $ resistance.

(Image will be uploaded soon)

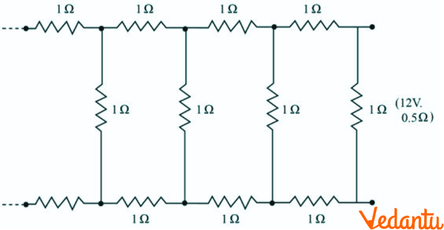
Ans: In the above question it is given that the resistance of each resistor connected in the given circuit is $R=1\Omega $.

Let the equivalent resistance of the given circuit be $R'$.

As the network is infinite the equivalent resistance is given by the relation,

$R'=2+\frac{R'}{\left( R'+1 \right)}$

$\Rightarrow {{\left( R' \right)}^{2}}-2R'-2=0$

$\Rightarrow R'=\frac{2\pm \sqrt{12}}{2}=1\pm \sqrt{3}$

As only positive value is acceptable,

$\therefore R'=1+\sqrt{3}$

Internal resistance of the circuit is $r=0.5\Omega $.

Therefore, total resistance $=2.73+0.5=3.23\Omega $.

Using Ohm’s law,

$I=\frac{V}{R}=\frac{12}{3.23}=3.72A$.

Therefore, the current drawn is $3.72A$.

33. Figure 3.34 shows a potentiometer circuit for comparison of two resistances. The balance point with a standard resistor $R=10.0\Omega $ is found to be \[\mathbf{58}.\mathbf{3cm}\] while that with the unknown resistance $X$ is \[\mathbf{68}.\mathbf{5}\text{ }\mathbf{cm}\]. Determine the value of $X$. What might you do if you failed to find a balance point with the given cell of emf $\varepsilon $ ?

(Image will be uploaded soon)

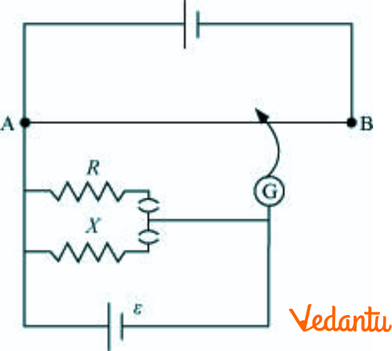
Ans: In the above question it is given that:

Resistance of the standard resistor is $R=10.0\Omega $ .

Balance point for this resistance is at a distance ${{l}_{1}}=58.3cm$.

Current in the potentiometer wire is $i$.

Hence, potential drop across $R$ is ${{E}_{1}}=iR$.

Resistance of the unknown resistor is $X$.

Balance point for this resistance is at a distance ${{l}_{2}}=68.5cm$.

Hence, potential drop across $X$ is ${{E}_{2}}=iX$.

The relation connecting emf and balance point is,

$\frac{{{E}_{1}}}{{{E}_{2}}}=\frac{{{l}_{1}}}{{{l}_{2}}}$

$\Rightarrow \frac{iR}{iX}=\frac{{{l}_{1}}}{{{l}_{2}}}$

$\Rightarrow X=\frac{{{l}_{1}}}{{{l}_{2}}}\times R=\frac{68.5}{58.3}\times 10=11.749\Omega $ .

Therefore, the value of the unknown resistance $X$ is $11.749\Omega $.

If we fail to find a balance point with the given cell of emf $\varepsilon $, then the potential drop across $R$and $X$ is reduced by putting a resistance in series with it. 

A balance point is obtained only if the potential drop across $R$ or $X$ is smaller than the potential drop across the potentiometer wire AB. 

34. Figure shows a $2.0V$ potentiometer used for the determination of internal resistance of $1.5V$ cell. The balance point of the cell in the open circuit is $76.3cm$. When a resistor of $9.5\Omega $ is used in the external circuit of the cell, the balance point shifts to $64.8cm$ length of the potentiometer wire. Determine the internal resistance of the cell.

(Image will be uploaded soon)

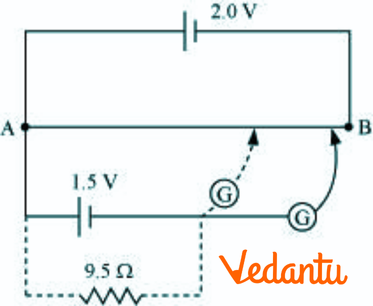
Ans: In the above question it is given that:

Balance point of the cell in the open circuit is ${{l}_{1}}=76.3cm$.

An external resistance $R$ of resistance $9.5\Omega $ is connected to the circuit.

New balance point of the circuit is at a distance ${{l}_{2}}=64.8cm$ .

Current flowing through the circuit  $=I$ .

The relation connecting resistance and emf is:

$r=\left( \frac{{{l}_{1}}-{{l}_{2}}}{{{l}_{2}}} \right)R$

$\Rightarrow r=\left( \frac{76.3-64.8}{64.8} \right)9.5=1.68\Omega $

Hence the internal resistance of the cell is $1.68\Omega $ . 

Long Answer Questions: (5 Marks)

1.

(a) Three resistors $2\Omega $ , $4\Omega $ and $5\Omega $  are combined in parallel. What is the total resistance of the combination?

Ans: In the above question it is given that there are three resistors of resistances $2\Omega $ , $4\Omega $ and $5\Omega $. 

They are connected in parallel. 

Hence, total resistance $R$ of the combination will be:

$\frac{1}{R}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}$

$\Rightarrow \frac{1}{R}=\frac{1}{2}+\frac{1}{4}+\frac{1}{5}=\frac{19}{20}$

$\therefore R=\frac{20}{19}\Omega $

Therefore, total resistance of the combination is $\frac{20}{19}\Omega $ .

(b) If the combination is connected to a battery of emf $20V$ and negligible internal resistance, determine the current through each resistor, and the total current drawn from the battery.

Ans: In the above question it is given that:

Emf of the battery, $V=20V$

Current ${{I}_{1}}$ flowing through resistor ${{R}_{1}}$ is given by:

${{I}_{1}}=\frac{V}{{{R}_{1}}}$

$\Rightarrow {{I}_{1}}=\frac{20}{2}=10A$

Current ${{I}_{2}}$ flowing through resistor ${{R}_{2}}$ is given by:

${{I}_{2}}=\frac{V}{{{R}_{2}}}$

$\Rightarrow {{I}_{2}}=\frac{20}{4}=5A$

Current ${{I}_{3}}$ flowing through resistor ${{R}_{3}}$ is given by:

${{I}_{3}}=\frac{V}{{{R}_{3}}}$

$\Rightarrow {{I}_{3}}=\frac{20}{5}=4A$

Hence the total current will be:

$I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}$

$\therefore I=10+5+4=19A$

Therefore, the current through resistors $2\Omega $ , $4\Omega $ and $5\Omega $ is $10A$ , $5A$ and $4A$ respectively and the total current is $19A$.

2. Determine the current in each branch of the network shown in figure:

(Image will be uploaded soon)

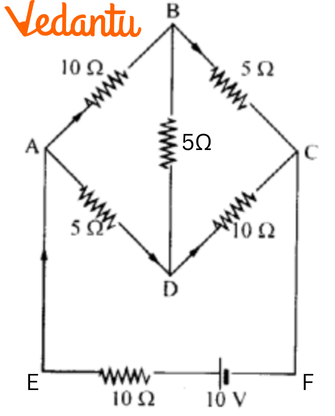
Ans: Current flowing through various branches of the circuit is represented in the given figure.

(Image will be uploaded soon)

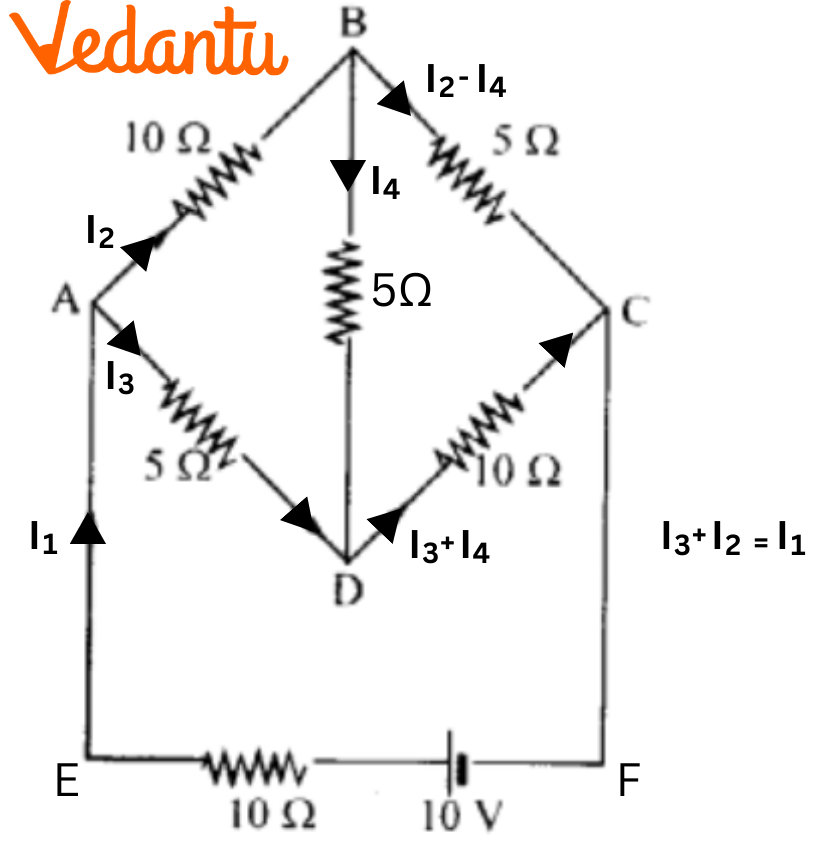
Consider

${{I}_{1}}=$Current flowing through the outer circuit

${{I}_{2}}=$Current flowing through branch AB

${{I}_{3}}=$Current flowing through branch AD

${{I}_{2}}-{{I}_{4}}=$Current flowing through branch BC

${{I}_{3}}+{{I}_{4}}=$Current flowing through branch CD

${{I}_{4}}=$Current flowing through branch BD

For the closed circuit ABDA, potential is zero i.e.,

$10{{I}_{2}}+5{{I}_{4}}-5{{I}_{3}}=0$

$2{{I}_{2}}+{{I}_{4}}-{{I}_{3}}=0$

${{I}_{3}}=2{{I}_{2}}+{{I}_{4}}$ …… (1)

For the closed circuit BCDB, potential is zero i.e.,

$5\left( {{I}_{2}}-{{I}_{4}} \right)-10\left( {{I}_{3}}+{{I}_{4}} \right)-5{{I}_{4}}=0$

$5{{I}_{2}}+5{{I}_{4}}-10{{I}_{3}}-10{{I}_{4}}-5{{I}_{4}}=0$

$5{{I}_{2}}-10{{I}_{3}}-20{{I}_{4}}=0$

${{I}_{2}}=2{{I}_{3}}+4{{I}_{4}}$ …… (2)

For the closed circuit ABCFEA, potential is zero i.e.,

$-10+10\left( {{I}_{1}} \right)+10\left( {{I}_{2}} \right)+5\left( {{I}_{2}}-{{I}_{4}} \right)=0$

$10=15{{I}_{2}}+10{{I}_{1}}-5{{I}_{4}}$

$3{{I}_{3}}+2{{I}_{1}}-{{I}_{4}}=2$ …… (3)

From equations (1) and (2), we obtain

${{I}_{3}}=2\left( 2{{I}_{3}}+4{{I}_{4}} \right)+{{I}_{4}}$

${{I}_{3}}=4{{I}_{3}}+8{{I}_{4}}+{{I}_{4}}$

$-3{{I}_{3}}=9{{I}_{4}}$

$-3{{I}_{4}}=+{{I}_{3}}$ …… (4)

Putting equation (4) in equation (1), we obtain

${{I}_{3}}=2{{I}_{2}}+{{I}_{4}}$

$-4{{I}_{4}}=2{{I}_{2}}$ …… (5)

It is evident from the given figure that,

${{I}_{1}}={{I}_{3}}+{{I}_{2}}$ ……. (6)

Putting equation (6) in equation (1), we obtain

$3{{I}_{2}}+2\left( {{I}_{3}}+{{I}_{2}} \right)-{{I}_{4}}=2$

$5{{I}_{2}}+2{{I}_{3}}-{{I}_{4}}=2$ …… (7)

Putting equations (4) and (5) in equation (7), we obtain

$5\left( -2{{I}_{4}} \right)+2\left( -3{{I}_{4}} \right)-{{I}_{4}}=2$

$-10{{I}_{4}}-6{{I}_{4}}-{{I}_{4}}=2$

$17{{I}_{4}}=-2$

${{I}_{4}}=-\frac{2}{17}A$

Equation (4) reduces to

${{I}_{3}}=-3\left( {{I}_{4}} \right)$

${{I}_{3}}=-3\left( -\frac{2}{17} \right)=\frac{6}{17}A$

${{I}_{2}}=-2\left( {{I}_{4}} \right)$

${{I}_{2}}=-2\left( -\frac{2}{17} \right)=\frac{4}{17}A$

${{I}_{2}}-{{I}_{4}}=\frac{4}{17}-\left( -\frac{2}{17} \right)=\frac{6}{17}$

${{I}_{3}}+{{I}_{4}}=\frac{6}{17}+\left( \frac{-2}{17} \right)=\frac{4}{17}A$

${{I}_{1}}={{I}_{3}}+{{I}_{2}}$

$\therefore {{I}_{1}}=\frac{6}{17}+\frac{4}{17}=\frac{10}{17}A$

Therefore, current in branch AB $=\frac{4}{17}A$

Current in branch BC $=\frac{6}{17}A$

Current in branch CD $=\frac{-4}{17}A$

Current in branch AD $=\frac{6}{17}A$

Current in branch BD $=\left( \frac{-2}{17} \right)A$

Total current $=\frac{4}{17}+\frac{6}{17}+\frac{-4}{17}+\frac{6}{17}+\frac{-2}{17}=\frac{10}{17}A$ .

3.

(a) In a metre bridge [Fig. 3.27], the balance point is found to be at $39.5cm$ from the end A, when the resistor Y is of $12.5\Omega $ . Determine the resistance of $X$. Why are the connections between resistors in a Wheatstone or meter bridge made of thick copper strips?

Ans: A metre bridge with resistors $X$ and $Y$ is represented in the given figure.

(Image will be uploaded soon)

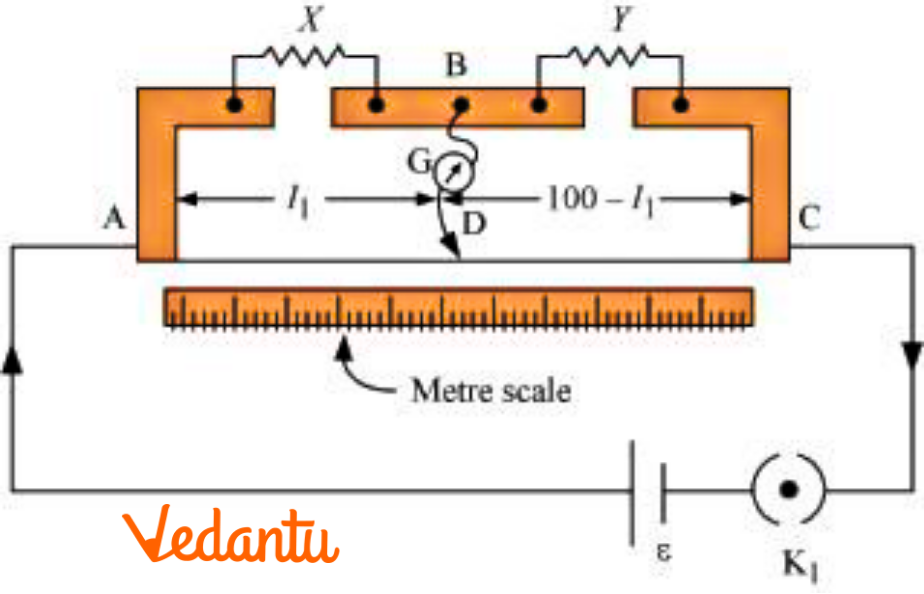
In the above question it is given that:

Balance point from end A is at distance, ${{l}_{1}}=39.5cm$

Resistance of the resistor \[Y=12.5\Omega \] .

Condition for the balance is,

$\frac{X}{Y}=\frac{100-{{l}_{1}}}{{l}_{1}}$

$\therefore X=\frac{100-39.5}{39.5}\times 12.5=8.2\Omega $

Hence, the resistance of resistor $X$ is $8.2\Omega $.

The connection between resistors in a Wheatstone or metre bridge is made of thick copper strips which helps to minimize the resistance. Hence it is not taken into consideration in the bridge formula.

(b) Determine the balance point of the bridge above if $X$ and $Y$are interchanged.

Ans: Now, if $X$ and $Y$are interchanged, then ${{l}_{1}}$ and $100-{{l}_{1}}$ also gets interchanged.

Hence the balance point of the bridge will be $100-{{l}_{1}}$ from $A$.

$\therefore 100-{{l}_{1}}=100-39.5=60.5cm$

Hence, the balance point is $60.5cm$ from $A$.

(c) What happens if the galvanometer and cell are interchanged at the balance point of the bridge? Would the galvanometer show any current?

Ans: When the galvanometer and cell are interchanged at the balance point of the bridge, the galvanometer will show no deflection. As there is zero deflection, no current would flow through the galvanometer.

4.

(a) Six lead-acid types of secondary cells each of emf 2.0 V and internal resistance $0.015\Omega $ are joined in series to provide a supply to a resistance of $8.5\Omega$ . What is the current drawn from the supply and its terminal voltage?

Ans: In the above question it is given that:

Number of secondary cells is $n=6$.

Emf of each secondary cell is $E=2.0V$.

Internal resistance of each cell is $r=0.015\Omega $ .

Series resistor is connected to the combination of cells.

The resistance of the resistor $R$ is $8.5\Omega $.

If the current drawn from the supply is $I$, then 

$I=\frac{nE}{R+nr}$

$\Rightarrow I=\frac{6\times 2}{8.5+6\times 0.015}$

$\therefore I=1.39A$

Now the Terminal voltage will be

$V=IR=1.39\times 8.5=11.87V$

Therefore, the current drawn from the supply is $1.39A$ and the terminal voltage is $11.87V$.

(b) A secondary cell after long use has an emf of $1.9V$ and a large internal resistance of $380\Omega $. What maximum current can be drawn from the cell? Could the cell drive the starting motor of a car?

Ans: After long use, 

Emf of the secondary cell will be $E=1.9V$.

Internal resistance of the cell is $r=380\Omega $ .

Therefore, maximum current $=\frac{E}{r}$

$\Rightarrow \frac{E}{r}=\frac{1.9}{380}=0.005A$.

Hence the maximum current drawn from the cell is $0.005A$. Since a large current is required to start the motor of a car, the cell cannot be used to start a motor.

5. Two wires of equal length, one of aluminium and the other of copper have the same resistance. Which of the two wires is lighter? Hence explain why aluminium wires are preferred for overhead power cables.

${{\rho }_{Al}}=2.63\times {{10}^{8}}\Omega m$, ${{\rho }_{Cu}}=1.72\times {{10}^{-8}}\Omega m$, $\text{Relative density of Al}=2.7$, $\text{Relative density of Cu}=8.9$

Ans: In the above question it is given that:

Resistivity of aluminium is ${{\rho }_{Al}}=2.63\times {{10}^{8}}\Omega m$.

Relative density of aluminium is ${{d}_{1}}=2.7$.

Consider ${{l}_{1}}$ to be the length of aluminium wire, ${{m}_{1}}$ as its mass, resistance of the copper wire as ${{R}_{2}}$, and area of cross-section of the copper wire as ${{A}_{2}}$.

Therefore, 

${{R}_{1}}={{\rho }_{1}}\frac{{{l}_{1}}}{{{A}_{1}}}$ …… (1)

And 

${{R}_{2}}={{\rho }_{2}}\frac{{{l}_{2}}}{{{A}_{2}}}$ …… (2)

But we have ${{R}_{1}}={{R}_{2}}$

$\therefore {{\rho }_{1}}\frac{{{l}_{1}}}{{{A}_{1}}}={{\rho }_{2}}\frac{{{l}_{2}}}{{{A}_{2}}}$

Also, we have ${{l}_{1}}={{l}_{2}}$.

\[\therefore \frac{{{\rho }_{1}}}{{{A}_{1}}}=\frac{{{\rho }_{2}}}{{{A}_{2}}}\]

i.e., $\frac{{{A}_{1}}}{{{A}_{2}}}=\frac{{{\rho }_{1}}}{{{\rho }_{2}}}$

$\therefore \frac{{{A}_{1}}}{{{A}_{2}}}=\frac{2.63\times {{10}^{8}}}{1.72\times {{10}^{-8}}}=\frac{2.63}{1.72}$

Now the mass of the aluminium wire is given by:

${{m}_{1}}=Volume\times Density$

$\therefore {{m}_{1}}={{A}_{1}}{{l}_{1}}\times {{d}_{1}}={{A}_{1}}{{l}_{1}}{{d}_{1}}$ …… (3)

Similarly, mass of the copper wire is given by:

${{m}_{2}}=Volume\times Density$

$\therefore {{m}_{2}}={{A}_{2}}{{l}_{2}}\times {{d}_{2}}={{A}_{2}}{{l}_{2}}{{d}_{2}}$ …… (4)

Dividing equation (3) by equation (4), we get:

$\frac{{{m}_{1}}}{{{m}_{2}}}=\frac{{{A}_{1}}{{l}_{1}}{{d}_{1}}}{{{A}_{2}}{{l}_{2}}{{d}_{2}}}$

As ${{l}_{1}}={{l}_{2}}$,

$\frac{{{m}_{1}}}{{{m}_{2}}}=\frac{{{A}_{1}}{{d}_{1}}}{{{A}_{2}}{{d}_{2}}}$

As \[\frac{{{A}_{1}}}{{{A}_{2}}}=\frac{2.63}{1.72}\]

$\frac{{{m}_{1}}}{{{m}_{2}}}=\frac{2.63}{1.72}\times \frac{2.7}{8.9}=0.46$

It indicated that ${{m}_{1}} < {{m}_{2}}$.

Therefore, aluminium is lighter than copper.

Since aluminium is lighter, it is preferred for overhead power cables over copper.

6. Answer the Following Questions:

a. A steady current flow in a metallic conductor of the non-uniform cross section. Which of these quantities is constant along with the conductor: current, current density, electric field, drift speed?

Ans: In the above question it is given that a steady current flows in a metallic conductor of the non-uniform cross-section. Therefore, the current flowing through the conductor is constant.

Current density, electric field, and drift speed are inversely proportional to the area of cross-section. Hence, they are not constant.

b. Is ohm’s law universally applicable for all conducting elements? If not, give examples of elements which do not obey Ohm’s law.

Ans: Ohm’s law is not universally applicable for all conducting elements.

Vacuum diode semiconductor is a non-ohmic conductor. Therefore, Ohm’s law is not valid for it.

c. A low voltage supply from which one needs high currents must have very low internal resistance. Why?

Ans: According to Ohm’s law, $V=IR$ .

It states that Voltage $\left( V \right)$  is directly proportional to current $\left( I \right)$ .

Therefore, 

$I=\frac{V}{R}$

where, $R$ is the internal resistance of the source. 

If V is low, then R must be very low, for high current drawn from the source.

d. A high tension (HT) supply of, say, 6 kV must have a very large internal resistance. Why?

Ans: A high tension supply of a very large internal resistance is required in order to prohibit the current from exceeding the safety limit. 

If the internal resistance is very low, then the current drawn exceeds the safety limits in case of a short circuit.

7.

(a) Given n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?

Ans: In the above question it is given that the total number of resistors are $n$ where resistance of each resistor is $R$.

i. When $n$ resistors are connected in series the effective resistance will be maximum when it is a product of $nR$ . Hence, maximum resistance of the combination is given by ${{R}_{1}}=nR$ .

ii. The effective resistance is the minimum when resistors are connected in parallel. Therefore, the effective resistance ${{R}_{2}}$ is given by ${{R}_{2}}=\frac{R}{n}$ .

The ratio of the maximum to the minimum resistance will be

$\Rightarrow \frac{{{R}_{1}}}{{{R}_{2}}}=\frac{nR}{R/n}={{n}^{2}}$

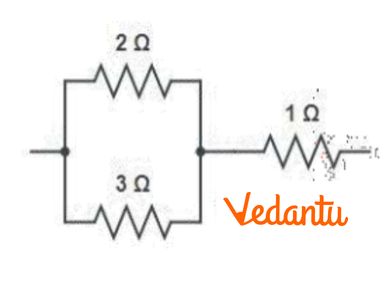
(b) Given the resistances of $1\Omega ,2\Omega ,3\Omega $ , how will you combine them to get an equivalent resistance of (i) $\left( 11/3 \right)\Omega $ (ii) $\left( 11/5 \right)\Omega $ (iii) $6\Omega $ (iv) $\left( 6/11 \right)\Omega $ ?

Ans: In the above question it is given that: 

${{R}_{1}}=1\Omega ,{{R}_{2}}=2\Omega ,{{R}_{3}}=3\Omega $

(i) For equivalent resistance of $\left( 11/5 \right)\Omega $:

Consider the circuit diagram given below.

(Image will be uploaded soon)

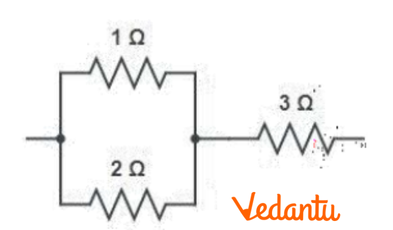
Equivalent resistance for the circuit will be:

$R'=\frac{2\times 1}{2+1}+3=\frac{2}{3}+3=\frac{11}{3}\Omega $

(ii) For equivalent resistance of $\left( 11/3 \right)\Omega $:

Consider the circuit diagram given below.

(Image will be uploaded soon)

Equivalent resistance for the circuit will be:

$R'=\frac{2\times 3}{2+3}+1=\frac{6}{5}+1=\frac{11}{5}\Omega $

(iii) For equivalent resistance of $6\Omega $:

Consider the circuit diagram given below.

(Image will be uploaded soon)

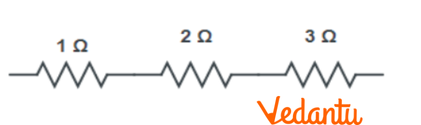
Equivalent resistance for the circuit will be:

$R'=1+2+3=6\Omega $

(iv) For equivalent resistance of $\left( 6/11 \right)\Omega $:

Consider the circuit diagram given below.

(Image will be uploaded soon)

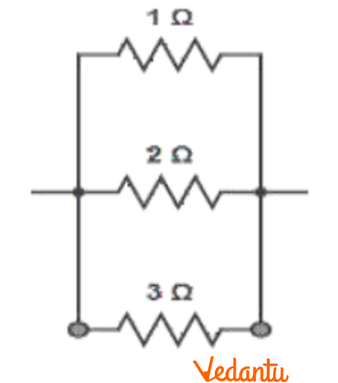
Equivalent resistance for the circuit will be:

$R'=\frac{1\times 2\times 3}{1\times 2+2\times 3+3\times 1}=\frac{6}{11}\Omega $

(b)

(Image will be uploaded soon)

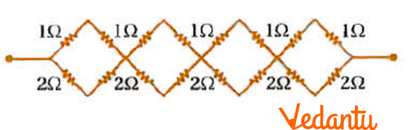
Ans:  Consider first small loop, two resistors of resistance $1\Omega $ each are connected in series.

Therefore, their equivalent resistance $=1+1=2\Omega $ .

Now two resistors of resistance $2\Omega $ each are connected in series.

Therefore, their equivalent resistance $=2+2=4\Omega $ .

Hence the circuit is resolved to:(Image will be uploaded soon)

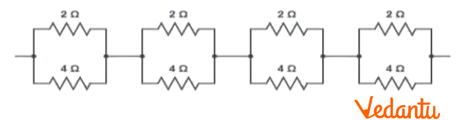
Here  $2\Omega $ and $4\Omega $ resistors are connected in parallel in all the four loops.

Therefore, equivalent resistance $R'$ is given by,

$R'=\frac{2\times 4}{2+4}=\frac{8}{6}=\frac{4}{3}\Omega $

The circuit further results into:

(Image will be uploaded soon)

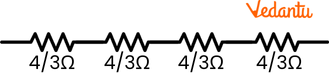
Four resistors are connected in series.

Therefore, equivalent resistance of the given circuit will be $\frac{4}{3}\times 4=\frac{16}{3}\Omega $ .

(c) 

(Image will be uploaded soon)

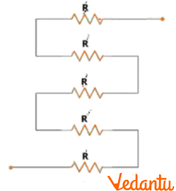
Ans: In the circuit it is given that five resistors of resistance $R$ are connected in series. 

Therefore, equivalent resistance of the circuit $=R+R+R+R+R=5R$ .

8. Figure shows a potentiometer with a cell of $2.0V$ and internal resistance $0.40\Omega $ maintaining a potential drop across the resistor wire AB. A standard cell which maintains a constant emf of $1.02V$ (for very moderate currents up to a few mA) gives a balance point at $67.3cm$ length of the wire. To ensure very low currents drawn from the standard cell, a very high resistance of $600k\Omega $ is put in series with it, which is shorted close to the balance point. The standard cell is then replaced by a cell of unknown emf $\varepsilon $ and the balance point found similarly, turns out to be at $82.3cm$length of the wire.

(Image will be uploaded soon)

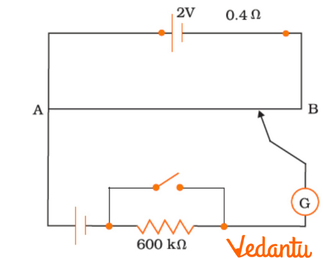
(a) What is the value of $\varepsilon $ ?

Ans: In the above question it is given that constant emf of the given standard cell is ${{E}_{1}}=1.02V$.

The balance point on the wire is at a distance ${{l}_{1}}=67.3cm$.

When the cell of unknown emf $\varepsilon $ is replaced, the standard cell new balance point shifts to $l=82.3cm$.

The relation connecting emf and balance point is,

$\frac{{{E}_{1}}}{{{l}_{1}}}=\frac{\varepsilon }{l}$

$\Rightarrow \varepsilon =\frac{l}{{{l}_{1}}}\times {{E}_{1}}=\frac{82.3}{67.3}\times 1.02=1.247V$

Therefore, the value of unknown emf is $1.247V$.

(b) What purpose does the high resistance of $600k\Omega $ have?

Ans: The purpose of using the high resistance of $600k\Omega $ is to reduce the current through the galvanometer when the movable contact is far from the balance point.

(c) Is the balance point affected by this high resistance?

Ans: The balance point is not affected by the presence of high resistance.

(d) Is the balance point affected by the internal resistance of the driver cell?

Ans: The balance point is not affected by the internal resistance of the driver cell.

(e) Would the method work in the above situation if the driver cell of the potentiometer had an emf of $1.0V$ instead of $2.0V$?

Ans: The method would not work if the driver cell of the potentiometer had an emf of $1.0V$ instead of $2.0V$ because if the emf of the driver cell of the potentiometer is less than the emf of the other cell, then the balance point would not exist on the wire.

(f) Would the circuit work well for determining an extremely small emf, say of the order of a few mV (such as the typical emf of a thermos-couple)? If not, how will you modify the circuit?

Ans: The circuit would not work well for determining an extremely small emf. Due to the instability in the circuit, the balance point would be close to the end A. Hence, there is a large percentage error.
The given circuit can be modified by connecting a series resistance with the wire AB. 

The potential drop across AB is slightly greater than the measured emf. The percentage error would be small.

CBSE Class 12 Physics Chapter-3 Important Questions - Free PDF Download

Class 12 Physics Chapter 3 Important Questions- What is Ohm’s Law?

Among the set of class 12 physics ch 3 important questions, Ohm’s Law is a very crucial topic. This law determines the relationship between electric current and potential difference. The current that flows through the conductor is directly proportional to the applied voltage. Further, it provided that all the physical conditions and temperature needs to remain constant. This is important because in certain components when electricity is passed it elevates the temperature. A classic example of this Ohm’s Law violation is the light bulb’s filament. This law was verified by German physicist Georg Simon Ohm and hence the law is named after him. 

Ohm’s Law Equation = V= IR 

Where, 

V= voltage across the conductor.

I= current passing through the conductor.

R= resistance offered by the conductor in the flow of current. 

There are also class 12 physics chapter 3 extra questions provided at the end of the chapter. 

State the Factors Affecting Resistivity in Chapter 3 Physics Class 12 Important Questions?

There are certain materials in which electric charge easily passes through the object. The electric resistance evaluates how much restriction is provided in this flow of electric charge within the circuit. These are some of the factors which affect electric resistance. The following factors determine the electrical resistance of a conductor. 

• The length of the conducting device.

• The cross-sectional area of the conducting device.

• The material of the conducting device.

• The temperature of the conducting material. 

Here, the electrical resistance is directly proportional to the length of the conducting device and inversely proportional to the cross-sectional area of the conductor. The following relation is denoted by this given equation below:

R = pL/A

Where, 

p= resistivity of the material (measured in ohm meter, Ωm)

This is an important question of chapter 3 physics class 12 for students appearing in their 12th boards. 

Explain Kirchhoff's Law in Context to Physics Class 12 Chapter 3 Important Questions?

Kirchoff's law is a key idea in class 12 significant issues about current electricity. German physicist Gustav Kirchoff created a few principles in 1845 that govern the exchange of energy and current within an electrical circuit. Kirchoff's Current and Voltage Laws are the names given to both of these laws. Let's examine each of these two laws in greater detail.

Kirchhoff’s 1st Law (Current Law)

According to the 1st Law of Kirchhoff, the total current entering the node or junction is equal to the charge leaving the node or junction, as no charge is lost. This states the algebraic sum of every current entering and leaving the node is equal to zero. 

Kirchoff’s 2nd Law (Voltage Law)

According to the 2nd Law of Kirchhoff, the sum of every voltage drop is equal to the voltage around the loop in the same loop for any closed network and also equals zero. The algebraic sum of every voltage in the loop has to be zero and it is known as the conservation of energy.  

CBSE Class 12 Physics Chapter 3 Important Questions- What are the Two Types of Resistance?

There are basically two main types of resistors. This incorporates the resistors in parallel and resistors in series. In case of resistors in parallel, the difference among every resistor remains the same. Moreover, this difference is equal to the applied difference. While resistors in series the same amount of current flows through each resistor whenever there is any change.

Conclusion 

The conclusion on important questions for CBSE Class 12 Physics Chapter 3 - Current Electricity is that practicing relevant and well-curated questions is crucial for a comprehensive understanding of the chapter and for exam preparation. By solving important questions, students can enhance their problem-solving skills, reinforce the concepts learned, and become familiar with the application of theoretical knowledge in various scenarios related to current electricity. 

Important questions for CBSE Class 12 Physics Chapter 3 may cover a range of topics including electric current, Ohm's law, resistance, electrical circuits, Kirchhoff's laws, and the combination of resistors. These questions can be designed to assess students' understanding of theoretical concepts, ability to apply formulas and laws, and aptitude for solving circuit-related problems.

It is important to note that while solving important questions is helpful, it should be complemented with a thorough understanding of the underlying principles and concepts. Therefore, students are advised to focus on conceptual clarity and regular practice to excel in CBSE Class 12 Physics Chapter 3 - Current Electricity.

Important Related Links for CBSE Class 12 Physics