Important Questions for CBSE Class 12 Physics Chapter 9 - Ray Optics and Optical Instruments

What is Ray?

In optics, a ray is referred to as an idealized model of light which is obtained by using a line perpendicular to the wavefronts of the actual light ray. The ray has to point to the direction of the energy flow. 

Topics Under Ray Optics

• Rectilinear Propagation of Light 

• Reflection of Light

• Spherical Mirrors

• Refraction of Light 

• Thin Lens

• Prism 

• Chromatic and Monochromatic Aberrations in Lens

• Optical Instruments 

Let Us Discuss the Above Briefly. 

• Rectilinear Propagation of Light - This refers to the propensity of light that travels along a straight line without any interference. 

• Reflection of Light - Reflection of light refers to the change in direction of wavelength between two different mediums such that the light way returns to its source of origin. 

• Spherical Mirrors - A spherical mirror refers to a mirror that has the shape of a piece cut out of a spherical shape. In this chapter, we are going to learn about the centre of curvature, normal, radius of curvature, pole of a mirror, principal axis, and also paraxial rays.

• Refraction of Light - Refraction refers to the bending of light while it passes through one transparent medium to another. In this chapter, we are going to learn about - reflective index, the law of refraction or Snell’s Law, refraction through a curved surface, total internal reflection, double refraction from a plain surface, single refraction from a plain surface, the relation between object distance and image distance refraction, and linear magnification of spherical refracting surfaces.

• Lens - There are mainly two types of lenses - convex and concave lenses. In this chapter, we are going to learn about certain features of lenses like - centre of curvature, the radius of curvature, principal axis, optical centre, principal foci, first principal focus F1, second principal focus F2, and focal length.

• Prism - Prism refers to the optical transparent element which refracts light. At least one side of the prism has to be angled, it cannot have two parallel surfaces. In this chapter, we have to concentrate on the features, importance, and various formulas of a prism. 

• Chromatic and Monochromatic Aberrations - Chromatic Aberrations refer to the effect which is produced due to the dispersion of different wavelengths of light through different angles. This leads to the failure of focusing the lens. 

On the other hand, Monochromatic Aberrations refer to the distortion created by quasi-monochromatic lights. 

• Optical Instruments - We use several optical instruments in our daily lives. These instruments are made after applying the properties of reflection, refraction, and dispersion, and other properties and laws of optics. 

An optical instrument refers to a device that helps to enhance images for viewing or for finding out their properties. 

• Eye - Our eyes are a very important yet unique example of optical instruments. Our eyes are filled with many interconnected nerve fibres and cells which sense the intensity of light and colour. The retina of our eye contains nerve cells that are rod-like or cone-like and that senses light, converts it into electrical signals, and sends it to the brain through optic nerves. 

• Simple Microscope - A simple microscope is a magnifying glass that is made out of a converging lens with a small focal length. When a microscope is held close to the eye, we can see a magnified erect but virtual image of the actual object. However, a compound microscope is a little more complex with two converging lenses, an eyepiece with moderate focal length, and a large aperture. It also has an objective lens of small focal length and short aperture.  Also, the ciliary muscles present in our eyes help to modify the shape and focal length of the lens inside the eyes.  

• Telescope - Telescope is a device that allows people to look at objects which are very far away. Telescopes are usually used for observing planets, stars, etc, in the solar system. Telescopes have objective lenses with large aperture and considerable focal length along with an eye lens that has a small focal length and aperture. This helps people to see things which are far away from us. 

Important Questions Class 12 Physics Chapter 9

1 Mark Questions

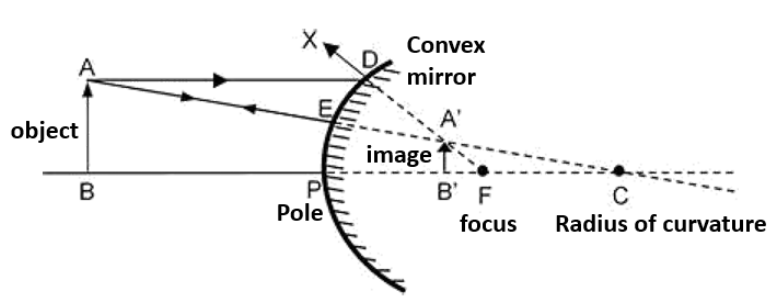
1.  A person standing before a concave mirror cannot see his image unless he is beyond the centre of curvature. Why?

Ans: Let a man stand beyond focus i.e., between focus and centre of curvature, then the image formed will be real and inverted and is formed beyond C (beyond him). Thus, he cannot see the image. 

But if he stands beyond C, the image will be formed between focus and centre of curvature which is in front of him and thus he will be able to see his reflected image.

2. For what angle of incidence, the lateral shift produced by a parallel-sided glass plate is maximum?

Ans: We know that lateral shift $d$ is given as,

\[d=\dfrac{t}{\cos r}\sin \ (i-r)\]

For lateral shift $d$ to be maximum, $sin\ (i-r)$ must be maximum i.e., $i-r$ must be minimum. This happens when $i={{90}^{{}^\circ }}$.

\[\Rightarrow d=\dfrac{t}{\cos r}\sin ({{90}^{\circ }}-r)\] 

$\Rightarrow D=t$

Then, we can say that lateral shift is maximum.

3. You read a newspaper, because of the light it reflects. Then why do you not see even a faint image of yourself in the newspaper?

Ans: We know that image is formed due to the regular reflection of light. 

However, when we read a newspaper, there is diffused (irregular) reflection of light, thus we are not able to see even a faint image of ourselves on the newspaper.

4. A substance has a critical angle of \[\mathbf{4}{{\mathbf{5}}^{{}^\circ }}\] for a yellow light, then what is its refractive index?

Ans: We know that the refractive index is given as below:

\[\mu =\dfrac{1}{\sin C}\]
Substituting the values, we have

$\mu =\dfrac{1}{\sin {{45}^{{}^\circ }}}=\dfrac{1}{\left( 1/\sqrt{2} \right)}$

$\Rightarrow \mu =\sqrt{2}$ 

5. An object is placed between the pole and the focus of a concave mirror produces a virtual and enlarged image. Justify using mirror formula.

Ans: We know that the mirror formula is as given below,

\[\dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f}\]

\[\Rightarrow v=\dfrac{uf}{u-f}\]

Now magnification, $m=\dfrac{v}{u}$.

$\Rightarrow m=\dfrac{\dfrac{uf}{u-f}}{u}$

$\Rightarrow m=\dfrac{f}{u-f}$

For a concave mirror, 

\[f=-ve\]

\[u=-ve\] 

Given \[u<\text{ }f\]; 

\[\therefore m=+ve\], hence enlarged image is produced.

6. A converging and diverging lens of equal focal lengths are placed coaxially in contact. Find the focal length and power of the combination.

Ans: We know that the lens formula is as given below,

\[\dfrac{1}{F}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}\]

For converging lens \[{{f}_{1}}=+f\]

For diverging lens \[{{f}_{2}}=-f\]

$\Rightarrow \dfrac{1}{F}=\dfrac{1}{f}-\dfrac{1}{f}$

$\Rightarrow F=\dfrac{1}{0}\Rightarrow F=\infty $

Since  \[P=\dfrac{1}{F}=\dfrac{1}{\infty }=0\]

Hence, the power of the combination of the lens is \[P=0\].

7. The refractive index of a material of a convex lens is \[{{n}_{1}}\]. It is immersed in a medium of refractive index \[{{n}_{2}}\]. A parallel beam of light is incident on the lens. Trace the path of the emergent rays when \[{{n}_{2}}>{{n}_{1}}\].

Ans: We know that for  \[{{n}_{2}}>{{n}_{1}}\] then the convex lens behaves as a concave lens as shown below.

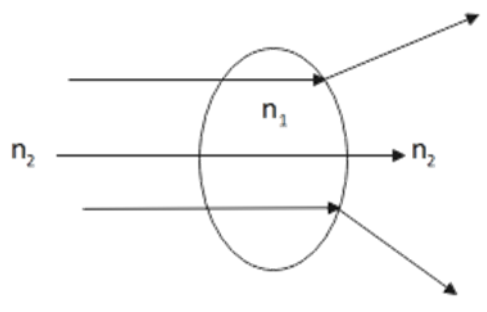
8. In a telescope the focal length of the objective and the eye piece are $\mathbf{60}\ \mathbf{cm}$ and $\mathbf{5}\ \mathbf{cm}$ respectively. What is (1) its magnification power? (2) the tube length?   

Ans: 

1. We know that magnification \[M=-\dfrac{{{f}_{o}}}{{{f}_{e}}}=\dfrac{-60}{5}=-12\]

2. The tube length is \[L={{f}_{o}}+{{f}_{e}}=60+5=65cm\].

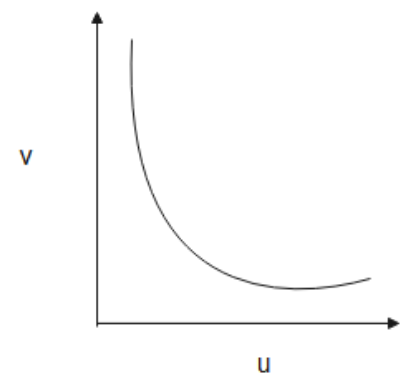
9. Show the variation of $u$ and $v$ in the case of a convex mirror.

Ans: The variation of $u$ and $v$ in a convex mirror is as shown below.

10. Two lenses having focal length \[{{f}_{1}}\] and \[{{f}_{2}}\] are placed coaxially at a distance \[x\] from each other. What is the focal length of the combination?

Ans: The formula for the focal length of the combination of two lenses when placed coaxially at a distance $x$ from each other is as given below:

\[\dfrac{1}{F}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}-\dfrac{x}{{{f}_{1}}{{f}_{2}}}\]

11. Does short-sightedness (myopia) or long-sightedness (hypermetropia) imply necessarily that the eye has partially lost its ability of accommodation? If not, what might cause these defects of vision?

Ans: Myopia and hypermetropia are common eye defects.

A myopic or hypermetropic person need not necessarily suffer a partial loss in their eyes’ ability of accommodation.

Myopia occurs when the eye-balls engage in elongation from the front to the back whereas hypermetropia occurs when the eye-balls shorten themselves. 

On the other hand, when the eye-lens completely loses its ability of adjusting itself, then the defect is called presbyopia.

2 Mark Questions

1. What are optical fibres? Give their one use.

Ans: Optical fibres are thin and long strands of fine quality glass or quartz coated with a thin layer of material with refractive index less than that of the strands. 

They work on the principle of total internal reflection and thus, they avoid any loss in transfer of information.  

Uses 

Optical fibres are often used in medical investigations i.e., one can examine the inside view of stomach and intestine by a method called endoscopy.

2. How do the focal lengths of a lens change with increase in the wavelength of the light?

Ans: We know that \[\dfrac{1}{f}=(\mu -1)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\].

Also, \[\mu \propto \dfrac{1}{\lambda }\].

Clearly, when wavelength $(\lambda )$ increases, refractive index \[(\mu )\]  decreases. 

Similarly, $\mu \propto f$.

Clearly, as refractive index \[(\mu )\] decreases, focal length $(f)$ increases.

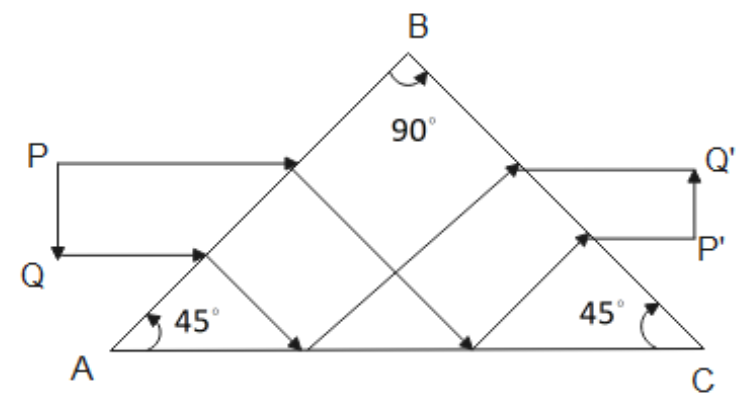
3. Show with a ray diagram, how an image is produced in a total reflecting prism?

Ans: Consider the two rays from the object PQ, as shown below.

They undergo total internal reflection firstly at the face AB and then at BC forming the final image \[{P}'{Q}'\] (real and inverted image).

4. The radii of the curvature of the two spherical surfaces which is a lens of required focal length are not the same. It forms an image of an object. The surfaces of the lens facing the object and the image are interchanged. Will the position of the image change? Ans: As we know that, 

\[\dfrac{1}{f}=(\mu -1)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]

When the radii of curvature \[{{R}_{1}}\] and \[{{R}_{2}}\] are interchanged, the focal length of the lens also changes. Hence, the position of the image will reduce gradually.

5. A thin converging lens has focal length (f) when illuminated by violet light. State with reason how the focal length of the lens will change if violet light is replaced by red light.

Ans: We know that, 

\[\dfrac{1}{f}=(n-1)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]

Since, $n$ for violet is more that $n$ for red colour, and since $m\propto f$, we can say that the focal length of the lens will decrease when violet light is replaced by red light.

6. Thin prism of angle \[{{60}^{\circ }}\] gives a deviation of \[{{30}^{\circ }}\]. What is the refractive index of the material of the prism? Ans: We know that the refractive index of a thin prism is as follows

\[n=\dfrac{\sin \left( \dfrac{A+{{\delta }_{m}}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}\]

Substituting the given values, we have

$n=\dfrac{\sin \left( \dfrac{60+30}{2} \right)}{\sin \dfrac{60}{2}}=\dfrac{\sin {{45}^{{}^\circ }}}{\sin {{30}^{{}^\circ }}}$

$\Rightarrow n=1.41$, which is the refractive index of the given thin prism.

7. Although the surfaces of a goggle lens are curved it does not have any power. Why? Ans: Since the two surfaces of a goggle lens are parallel i.e., one surface convex and the other concave, the resultant power of the two surfaces is zero as powers on both surfaces are equal but opposite in sign. 

\[p={{p}_{1}}+{{p}_{2}}=p+(-p)=0\]

8. A ray of light is incident normally on one face of the prism of apex angle \[{{30}^{\circ }}\] and refractive index \[\sqrt{2}\]. Find the angle of deviation for the ray of light.

Ans: Let us assume that the ray PQ falls normally on AB. 

Then, it goes straight to AC without any refraction (QR) as shown in the figure.

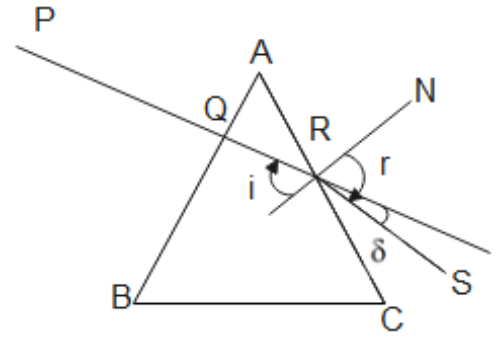
Also given that

$n=\sqrt{2}$;

$A={{30}^{{}^\circ }}$;

$i={{30}^{{}^\circ }}$

Applying Snell’s law for face AC,

$n=\dfrac{\sin r}{\sin {{30}^{{}^\circ }}}$

$\Rightarrow \sin r=\dfrac{1}{\sqrt{2}}$

$\Rightarrow r={{45}^{{}^\circ }}$

Now angle of deviation,

$\delta =r-i$

$\Rightarrow \delta ={{45}^{{}^\circ }}-{{30}^{{}^\circ }}$

$\Rightarrow \delta ={{15}^{{}^\circ }}$, is the angle of deviation.

9. Following data was recorded for values of object distance and corresponding values of image distance in the experiment on study of real image formation by a convex lens of power \[+5\text{ }D\]. One of the three observations is incorrect. Identify and give reason:

Ans: Given that $P=5D$

 We know that $P=\dfrac{1}{f}$

$\Rightarrow f=\dfrac{1}{5}=20cm$

Then,

$2f=40cm$

To find, which of the following observations are incorrect, consider the ray diagram as shown below, where it can be seen that when the object is placed between focus and twice the focus, the image is obtained after the measure if twice the focus.

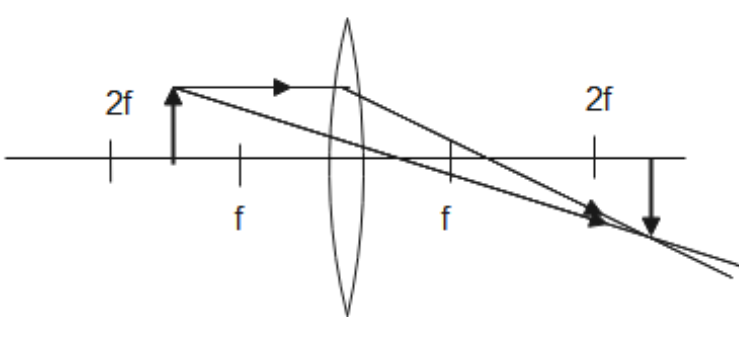
1. $u=25$ and $v=97$ is correct.

When the object is placed between $f=20cm$ and $2f=40cm$, the image is obtained after $2f=40cm$.

2. $u=30$ and $v=60$ is also correct.

When the object is placed between $f=20cm$ and $2f=40cm$, the image is obtained after $2f=40cm$.

3. $u=30$ and $v=37$ is incorrect. 

Here, when the object is placed between $f=20cm$ and $2f=40cm$, the image is obtained before $2f=40cm$.

Clearly, we can conclude that observation (3) is incorrect because both object and the image here lie between $f$ and $2\ f$.

10. Birds flying high in the air appear to be higher than in reality. Explain why?

Ans: Birds fly in air, which is a rarer medium when compared to the ground, which is denser.

The light from the birds when viewed will undergo refraction towards the normal. Thus, the birds appear to fly at a higher point. i.e., 

Apparent height > Real height

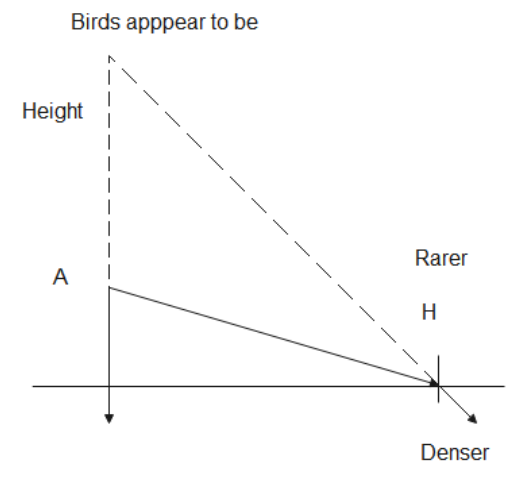
11. What is the focal length of a convex lens of focal length $30cm$ in contact with a concave lens of focal length $20cm$? Is the system a converging or a diverging lens? Ignore thickness of the lenses.

Ans: Given that,

Focal length of the convex lens, \[{{f}_{1}}=\text{ }30\text{ }cm\]

Focal length of the concave lens, \[{{f}_{2}}=-\text{ }20\text{ }cm\]

Focal length of the system of lenses \[=\text{ }f\]

Then the equivalent focal length of a system of two lenses in contact is given as:

\[\dfrac{1}{f}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}\]

\[\Rightarrow \dfrac{1}{f}=\dfrac{1}{30}-\dfrac{1}{20}=\dfrac{2-3}{60}=-\dfrac{1}{60}\]

\[\therefore f=-60cm\]

Hence, the focal length of the combination of lenses is $60\ cm$. The negative sign indicates that the system of lenses acts as a diverging lens.

12. The image of a small electric bulb fixed on the wall of a room is to be obtained on the opposite wall 3m away by means of a large convex lens. What is the maximum possible focal length of the lens required for the purpose?    

Ans: Given that,

Distance between the object and the image, \[d=\text{ }3\text{ }m\]

Maximum focal length of the convex lens \[~={{f}_{\max }}\]

For real images, the maximum focal length is given as:

\[{{f}_{\max }}=\dfrac{d}{4}=\dfrac{3}{4}=0.75m\]

Hence, for the required purpose, the maximum possible focal length of the convex lens is 0.75 m.

13. A screen is placed $90cm$ from an object. The image of the object on the screen is formed by a convex lens at two different locations separated by $20cm$. Determine the focal length of the lens.

Ans: Given that,  

Distance between the image (screen) and the object, \[D=\text{ }90\text{ }cm\]

Distance between two locations of the convex lens, \[d\text{ }=\text{ }20\text{ }cm\]

Focal length of the lens \[=\text{ }f\]

Focal length is related to \[d\] and D as:

\[f=\dfrac{{{D}^{2}}-{{d}^{2}}}{4D}=\dfrac{{{\left( 90 \right)}^{2}}-{{\left( 20 \right)}^{2}}}{4\times 90}=\dfrac{770}{36}=21.39cm\]

Therefore, the focal length of the convex lens is $21.39cm$.

14. You are given prisms made of crown glass and flint glass with a wide variety of angles. Suggest a combination of prisms which will 

1. Deviate a pencil of white light without much dispersion,

Ans: Place the two given prisms next to each other. 

Make sure that their bases are on the opposite sides of the incident white light, with   their faces touching each other.

When the white light is incident on the first prism, it will get dispersed. This acts as the incident light for the second prism and the dispersed light this time will recombine to give white light as a result of the combination of the two prisms.

2. Disperse (and displace) a pencil of white light without much deviation.

Ans: Take the system of the two prisms as suggested in answer (a).

Adjust (increase) the angle of the flint-glass-prism so that the deviations due to the combination of the prisms become equal. 

This combination will now disperse the pencil of white light without much deviation.

15. A myopic person has been using spectacles of power $-1.0$ dioptre for distant vision. During old age he also needs to use separate reading glass of power $+2.0$ dioptres. Explain what may have happened.

Ans: Given that the power of the spectacles used by the myopic person is \[P=\text{ }-\text{ }1.0\text{ }D\].

Focal length of the spectacles,

\[f=\dfrac{1}{P}=\dfrac{1}{-1\times {{10}^{-2}}}=-100cm\]

Hence, the far point of the person is $100cm$. He might have a normal near point of $25\ cm$. 

When he uses the spectacles, the objects placed at infinity produce virtual images at $100\ cm$.

He uses the ability of accommodation of the eye-lens to see the objects placed between $100\ cm$ and $25\ cm$.

During old age, the person uses reading glasses of power, \[{p}'=+2D\].

The ability of accommodation is lost in old age. This defect is called presbyopia. As a result, he is unable to see clearly the objects placed at $25\ cm$.

16. A person looking at a person wearing a shirt with a pattern comprising vertical and horizontal lines is able to see the vertical lines more distinctly than the horizontal ones. What is this defect due to? How is such a defect of vision corrected?

Ans: In the given case, the person is able to see vertical lines more distinctly than horizontal lines. 

This means that the refracting system (cornea and eye-lens) of the eye is not working effectively in different planes. This defect is called astigmatism. 

The person's eye has enough curvature in the vertical plane. However, the curvature in the horizontal plane is insufficient. 

Hence, sharp images of the vertical lines are formed on the retina, but horizontal lines appear blurred. This defect can be corrected by using cylindrical lenses.

17. A small telescope has an objective lens of focal length $140cm$ and an eyepiece of focal length $5.0cm$ . What is the magnifying power of the telescope for viewing distant objects when

1. The telescope is in normal adjustment (i.e., when the final image is at infinity)?

Ans: Given that, 

Focal length of the objective lens, \[{{f}_{o}}=\text{ }140\text{ }cm\]

Focal length of the eyepiece, \[{{f}_{e}}=\text{ }5\text{ }cm\]

Least distance of distinct vision, \[d\text{ }=\text{ }25\text{ }cm\]

When the telescope is in normal adjustment, its magnifying power is given as:

$m=\dfrac{{{f}_{o}}}{{{f}_{e}}}$

$\Rightarrow m=\dfrac{140}{5}=28$

Thus, the magnifying power is $28$. 

2. The final image is formed at the least distance of distinct vision 25cm?

Ans: When the final image is formed at \[d\], the magnifying power of the telescope is

given as:

$m=\dfrac{{{f}_{o}}}{{{f}_{e}}}\left[ 1+\dfrac{{{f}_{e}}}{d} \right]$

$\Rightarrow m=\dfrac{140}{5}\left[ 1+\dfrac{5}{25} \right]$

$\Rightarrow m=28\left[ 1+0.2 \right]$

$\Rightarrow m=28\times 1.2=33.6$

Thus, the magnifying power is $33.6$.

18. Light incident normally on a plane mirror attached to a galvanometer coil retraces backwards as shown in figure below. A current in the coil produces a deflection of \[{{3.5}^{\circ }}\] in the mirror. What is the displacement of the reflected spot of light on a screen placed $\mathbf{1}.\mathbf{5}\ \mathbf{m}$ away?

Ans: Given that, 

Angle of deflection, \[\theta ={{3.5}^{\circ }}\]

Distance of the screen from the mirror, \[D=1.5\text{ }m\]

The reflected rays get deflected by an amount twice the angle of deflection i.e., \[2\theta ={{7.0}^{\circ }}\]

The displacement (\[d\]) of the reflected spot of light on the screen is given as:

\[\tan 2\theta =\dfrac{d}{1.5}\]

\[\therefore d=1.5\times \tan {{7}^{\circ }}=0.184m=18.4cm\]

Hence, the displacement of the reflected spot of light is $18.4\ cm$.

3 Marks Questions

1. Find the radius of curvature of the convex surface of a plane convex lens, whose focal length is $\mathbf{0}.\mathbf{3}\ \mathbf{m}$ and the refractive index of the material of the lens is $\mathbf{1}.\mathbf{5}$.

Ans: Given that,

\[\mu =1.5\] 

\[f=0.3m\]

For plane convex lens,

${{R}_{2}}=-\infty $ and let \[{{R}_{1}}=R\].

Substituting these values in the formula for focal length,

$\dfrac{1}{f}=\left( \mu -1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$

$\Rightarrow \dfrac{1}{0.3}=\left( 1.5-1 \right)\left( \dfrac{1}{R}+\dfrac{1}{\infty } \right)$

$\Rightarrow \left( \dfrac{1}{R} \right)0.5=\dfrac{1}{0.3}$

$\Rightarrow R=0.15m$

Thus, the radius of curvature is $R=0.15m$.

2. Show that the limiting value of the angle of prism is twice its critical angle. Hence define critical angle.

Ans: We know that, 

Angle of the prism is given by \[A={{r}_{1}}+{{r}_{2}}\].

In a case of a triangular prism where ${{i}_{1}}={{i}_{2}}={{90}^{{}^\circ }}$, angle of refraction is given by ${{r}_{1}}={{r}_{2}}=C$.
where, $C$ is the critical angle.
Clearly, 

\[A={{r}_{1}}+{{r}_{2}}\]

$\Rightarrow A=C+C$

$\Rightarrow A=2C$

Therefore, the angle of incidence for which angle of refraction is \[{{90}^{\circ }}\], is called the critical angle.

3. Draw a labelled diagram of telescope when the image is formed at the least distance of distinct vision? Hence derive the expression for its magnifying power.

Ans:  We know that,

magnifying power \[=\dfrac{angle\,\text{ }subtended\text{ }\,by\,\text{ }the\text{ }\,image\,\text{ }at\,\text{ }the\text{ }\,eye}{angle\,\text{ }subtended\text{ }\,by\,\text{ }the\text{ }\,object\,\text{ }at\,\text{ }the\text{ }\,eye}\]

\[MP=\dfrac{\tan \beta }{\tan \alpha }=\dfrac{\beta }{\alpha }\] (Since angles are very small)

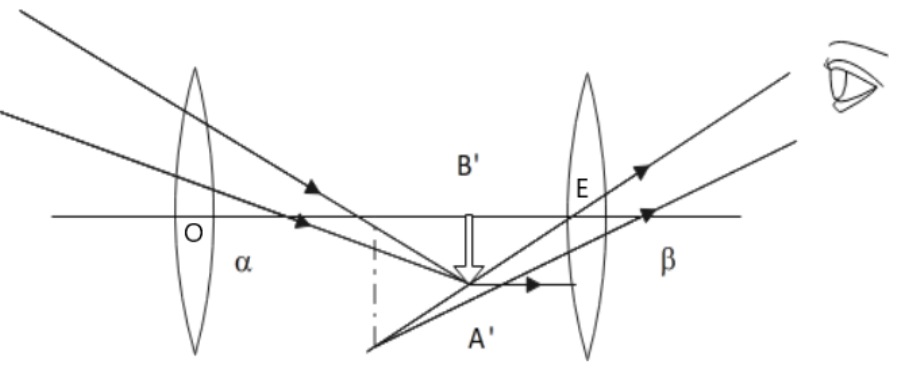
\[\tan \beta =\dfrac{{A}'{B}'}{{B}'E}\] and \[\tan \alpha =\dfrac{{A}'{B}'}{{B}'O}\]

$MP=\dfrac{{A}'{B}'}{{B}'E}\times \dfrac{{A}'{B}'}{{B}'O}$

$MP=\dfrac{{B}'O}{{B}'E}=\dfrac{{{f}_{o}}}{-{{v}_{e}}}$

\[MP=\dfrac{-{{f}_{o}}}{-{{v}_{e}}}\]......(i)

For eye piece,

$\dfrac{1}{v}-\dfrac{1}{v}=\dfrac{1}{{{f}_{e}}}$

$-\dfrac{1}{D}-\dfrac{1}{-{{v}_{e}}}=\dfrac{1}{{{f}_{e}}}$

Multiply by D,

\[-1+\dfrac{D}{{{v}_{e}}}=\dfrac{D}{{{f}_{e}}}\]

\[\dfrac{D}{{{v}_{e}}}=\dfrac{D}{{{f}_{e}}}+1\]

\[\dfrac{1}{{{v}_{e}}}=\dfrac{1}{{{f}_{e}}}+\dfrac{1}{D}=\dfrac{1}{{{f}_{e}}}\left( 1+\dfrac{{{f}_{e}}}{D} \right)\]

Substituting in (i),

\[MP=\dfrac{-{{f}_{o}}}{{{f}_{e}}}\left( 1+\dfrac{{{f}_{e}}}{D} \right)\]

4. Drive the expression for the angle of deviation for a ray of light passing through an equilateral prism of refracting angle A.

Ans: Consider the given diagram:

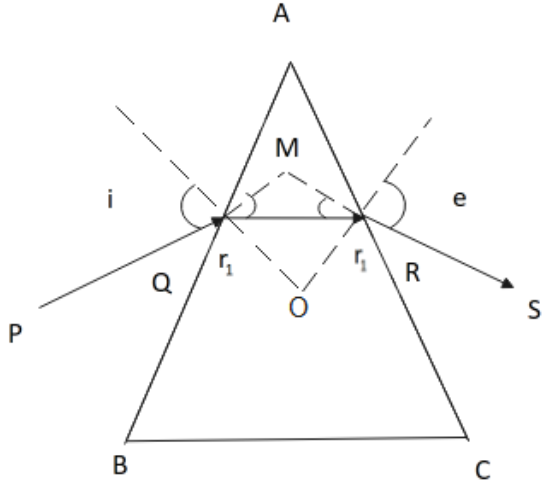
At the surface AB, 

\[{{\delta }_{1}}=i-{{r}_{1}}\]

At the surface AC,

\[{{\delta }_{2}}=e-{{r}_{2}}\]

Thus,

\[\delta ={{\delta }_{1}}+{{\delta }_{2}}\]

\[\delta =i+e-\left( {{r}_{1}}+{{r}_{2}} \right)\] ......(1) 

Now, in quadrilateral AQOR,

\[\angle A+\angle Q+\angle O+\angle R={{360}^{\circ }}\]

\[\Rightarrow \angle A+\angle O={{180}^{\circ }}\] ......(2)

Also, in \[\Delta QOR\],

\[\angle Q+\angle O+\angle R={{180}^{\circ }}\]

Or

\[{{r}_{1}}+{{r}_{2}}+\angle O={{180}^{\circ }}\] ......(3)

From (2) and (3),

\[{{r}_{1}}+{{r}_{2}}=A\] ......(4)

Substituting equation (4) in equation (1)

\[\delta =i+e-A\]

Or

\[A+\delta =i+e\]

5. Draw a ray diagram to illustrate image formation by a Newtonian type reflecting telescope. Hence state two advantages of it over refracting type telescopes.

Ans: The ray diagram of the Newtonian type reflecting telescope is as shown below.

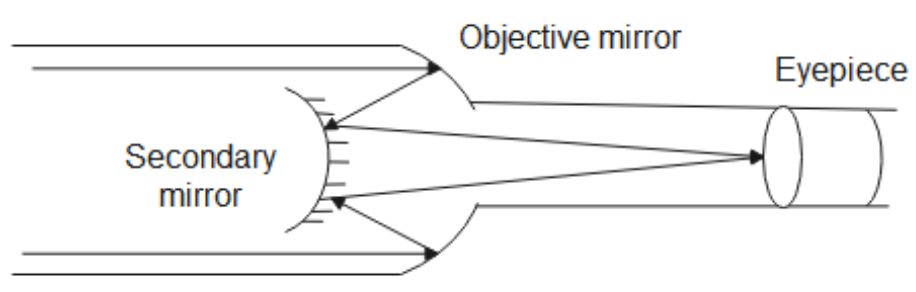
Advantages 

The image formed in a reflecting type telescope is free from chromatic aberrations. 

The image formed is very bright due to its large light-gathering power. 

6. The magnifying power of an astronomical telescope in the normal adjustment position is $100\ $. The distance between the objective and the eye piece is  $101\ cm$. Calculate the focal length of the objective and the eye piece.

Ans: Given that, 

\[{{f}_{o}}+{{f}_{e}}=101cm\] ......(1)

\[M=\left| \dfrac{{{f}_{o}}}{{{f}_{e}}} \right|=100\]

\[{{f}_{o}}=100{{f}_{e}}\]  ......(2)

Substituting equation (2) in equation (1),

${{f}_{e}}+100{{f}_{e}}=101$

$\Rightarrow 101{{f}_{e}}=101$ 

$\Rightarrow {{f}_{e}}=1cm$ 

Substituting \[{{f}_{e}}\] in equation (2),

${{f}_{o}}=100\times 1$ 

${{f}_{o}}=100cm$ 

Thus, the focal length of the eye-piece is 1cm whereas the focal length of the objective is 100cm.

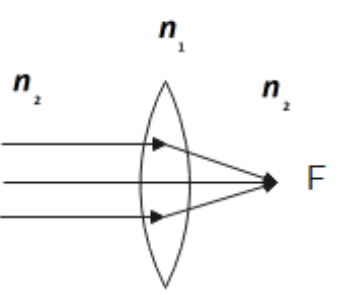
7. A convex lens made up of refractive index \[{{\mathbf{n}}_{\mathbf{1}}}\] is kept in a medium of refractive index \[{{\mathbf{n}}_{\mathbf{2}}}\]. Parallel rays of light are incident on the lens. Complete the path of rays of light emerging from the convex lens if 

1. \[{{n}_{1}}>{{n}_{2}}\]

Ans: When \[{{n}_{1}}>{{n}_{2}}\], the lens behaves as a convex lens.

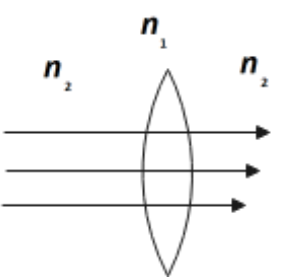
2. \[{{n}_{1}}={{n}_{2}}\]

Ans: When \[{{n}_{1}}={{n}_{2}}\], the lens behaves as a plane plate and thus, no refraction takes place.

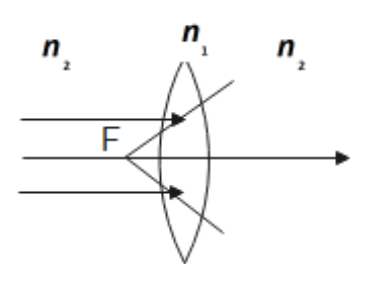
3. \[{{n}_{1}}<{{n}_{2}}\]

Ans: When \[{{n}_{1}}<{{n}_{2}}\], the lens behaves as a convex lens.

8. Derive the relation  \[\dfrac{\mathbf{1}}{\mathbf{f}}=\dfrac{\mathbf{1}}{{{\mathbf{f}}_{\mathbf{1}}}}+\dfrac{\mathbf{1}}{{{\mathbf{f}}_{\mathbf{2}}}}\], where ${{\mathbf{f}}_{\mathbf{1}}}$ and \[{{\mathbf{f}}_{\mathbf{2}}}\] are focal lengths of two thin lenses and $\mathbf{F}$ is the focal length of the combination in contact. 

Ans: Consider two thin lenses in contact having focal length \[{{f}_{1}}\] and \[{{f}_{2}}\].

For the first lens, 

\[\dfrac{1}{{{v}_{1}}}-\dfrac{1}{u}=\dfrac{1}{{{f}_{1}}}\] ......(1)

For the second lens, \[{{I}_{1}}\] acts as an object which forms the final image \[I\].

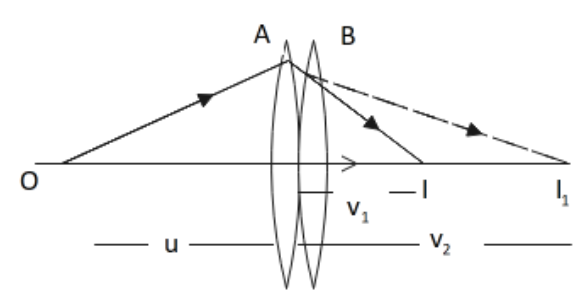
Clearly, \[\dfrac{1}{v}-\dfrac{1}{{{v}_{1}}}=\dfrac{1}{{{f}_{2}}}\] ......(2)

Adding equations (1) & (2) 

\[\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}=\dfrac{1}{v}-\dfrac{1}{u}+\dfrac{1}{{{v}_{1}}}-\dfrac{1}{{{v}_{1}}}\]

\[\Rightarrow \dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}=\dfrac{1}{v}-\dfrac{1}{u}\]

Using lens formula \[\left( \dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{F} \right)\], 

\[\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}=\dfrac{1}{F}\]

For $n$ number of thin lenses in contact,  

\[\dfrac{1}{F}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}+\dfrac{1}{{{f}_{3}}}+......+\dfrac{1}{{{f}_{n}}}\]

Hence the derivation.

9. A convex lens has a focal length $\mathbf{0}.\mathbf{2}\ \mathbf{m}$ and made of glass \[\left( \mathbf{\mu }=\mathbf{1}.50 \right)\]is immersed in water \[\left( \mathbf{\mu }=\mathbf{1}.\mathbf{33} \right)\]. Find the change in focal length of the lens.

Ans: Given,

${{f}_{a}}=\text{ }0.2m$; \[^{a}{{\mu }_{g}}=1.50\]

It is known that

\[\dfrac{1}{{{f}_{a}}}=\left( {{\ }^{a}}{{\mu }_{g}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]

$\Rightarrow \dfrac{1}{0.2}=\left( 1.50-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$

\[\Rightarrow \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}}=10\] ......(1)

Now, 

\[^{w}{{\mu }_{g}}=\dfrac{{}^{a}{{\mu }_{g}}}{{}^{a}{{\mu }_{w}}}=\dfrac{1.50}{1.33}=1.128\]

Also, the focal length of the lens when immersed in water would be

\[\dfrac{1}{{{f}_{w}}}=\left( {}^{w}{{\mu }_{g}}-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]

$\Rightarrow \dfrac{1}{{{f}_{w}}}=\left( 1.128-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)$

$\Rightarrow \dfrac{1}{{{f}_{w}}}=\left( 0.128 \right) \times 10=1.28$

$\Rightarrow {{f}_{w}}=\dfrac{1}{1.28}$

$\Rightarrow {{f}_{w}}=0.78m$

Thus, the change in focal length is given by

${{f}_{w}}-{{f}_{a}}=0.78-0.20=0.58m$

10. A reflecting type telescope has a concave reflector of radius of curvature $\mathbf{120}\ \mathbf{cm}$. Calculate the focal length of eye piece to achieve a magnification of $\mathbf{20}$.

Ans: Given that 

\[M=20\]

\[R=120cm\] (Concave reflector)

\[{{f}_{o}}=\dfrac{R}{2}=\dfrac{-120}{2}=-60cm\]

\[M=\dfrac{{{f}_{o}}}{{{f}_{e}}}\Rightarrow \dfrac{-60}{{{f}_{e}}}=-20\]

\[\Rightarrow {{f}_{e}}=3cm\]

Thus, the focal length of the eye-piece is 3cm.

11. Show that a convex lens produces an N time magnified image, when the object distances from the lens have magnitude \[\left( \mathbf{f}\pm \dfrac{\mathbf{f}}{\mathbf{N}} \right)\]. Here f is the magnitude of the focal length of the lens. Hence find two values of object distance u, for which convex lens of power $\mathbf{2}.\mathbf{5}\ \mathbf{D}$ will produce an image that is four times as large as the object? 

Ans: We know that the magnifying power is given by

\[M=\dfrac{f}{v+f}\]

For real image \[m=-N\];

\[\Rightarrow -N=\dfrac{f}{u+f}\Rightarrow u+f=\dfrac{-f}{N}\] 

\[\Rightarrow u=-\left( f+\dfrac{f}{N} \right)\] ......(1)

For virtual image \[m=N\];

\[\Rightarrow N=\dfrac{f}{u+f}\]

\[\Rightarrow u+f=-f+\dfrac{f}{N}\]

\[\Rightarrow u=-\left( f-\dfrac{f}{N} \right)\] ......(2)

From equation (1) & (2) we can say that magnification produced by a lens can be N if 

\[u=-\left( f\pm \dfrac{f}{N} \right)\].

Now, power of the lens \[P=2.5\text{ }D\].

\[f=\dfrac{1}{P}=\dfrac{1}{2.5}m\]

\[\Rightarrow f=\dfrac{1}{2.5}\times 100=40cm\]

It is given that

\[M=\pm 4\]

\[\Rightarrow \pm 4=\dfrac{40}{u+40}\]

\[\Rightarrow u+40=\pm 10\]

\[\Rightarrow u=-40\pm 10\]

\[\Rightarrow u=30cm\] or \[-50cm\]

These are the two values of object distances.

12. Define total internal reflection of light. Hence write two advantages of total reflecting prisms over a plane mirror. 

Ans: The phenomenon of reflection of light when a ray of light traveling from a denser medium getting reflected back into the same denser medium provided the angle of incidence is greater than the angle called critical angle is called total internal reflection.

Advantages 

1. It does require silvering.

2. Multiple reflections do not take place in a reflecting prism. Due to this, only one image is formed, which is very bright.

13. An equiconvex lens of radius of curvature R is cut into two equal parts by a vertical plane, so it becomes a plano-convex lens. If f is the focal length of equiconvex lens, then what will be focal length of the planoconvex lens?

Ans: We know that

\[\dfrac{1}{f}=\left( n-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]

For equiconvex lens \[{{R}_{1}}={{R}_{2}}=R\]

\[\dfrac{1}{f}=\left( n-1 \right)\left( \dfrac{1}{R}-\dfrac{1}{-R} \right)\]

\[\Rightarrow \dfrac{1}{f}=\left( n-1 \right)\left( \dfrac{1}{R}+\dfrac{1}{R} \right)\]

\[\Rightarrow \dfrac{1}{f}=\dfrac{2\left( n-1 \right)}{R}\]   ......(1)

For plano-convex lens,

\[{{R}_{1}}=R\] and \[{{R}_{2}}=\infty \]

Clearly,

\[\dfrac{1}{{{f}'}}=\left( n-1 \right)\left( \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right)\]

\[\Rightarrow \dfrac{1}{{{f}'}}=\left( n-1 \right)\left( \dfrac{1}{R}-\dfrac{1}{\infty } \right)\]

\[\Rightarrow \dfrac{1}{{{f}'}}=\dfrac{\left( n-1 \right)}{R}\] ......(2)

From (1) & (2)

\[\dfrac{{{f}'}}{f}=2\Rightarrow {f}'=2f\]

14. A converging lens of focal length $\mathbf{6}.\mathbf{25}\ \mathbf{cm}$ is used as a magnifying glass if near point of the observer is $\mathbf{25}\ \mathbf{cm}$ from the eye and the lens is held close to the eye. Calculate

1. Distance of Object From the Lens.

Ans: It is known that,

\[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\]

Given,

\[f=6.25cm\]

\[v=-25cm\]

Substituting these values in the first expression,

\[\dfrac{1}{u}=\dfrac{-1}{25}-\dfrac{1}{6.25}=\dfrac{-1}{5}\]

\[\Rightarrow u=-5cm\]

2. Angular Magnification

Ans: Angular magnification is given by

\[m=1+\dfrac{D}{F}=1+\dfrac{25}{6.25}\]

$\Rightarrow m=1+4=5$

3. Angular Magnification When Final Image is Formed at Infinity.

Ans: When the image is formed at infinity,

\[m=\dfrac{D}{F}=\dfrac{25}{6.25}=4\]

15. Draw a graph to show that variation of angle of deviation ${{\mathbf{\delta }}_{\mathbf{m}}}$with that of angle of incidence i for a monochromatic ray of light passing through a glass prism of refracting angle A. Hence deduce the relation.

\[\mathbf{\mu }=\dfrac{\sin \left( \dfrac{\mathbf{A}+{{\mathbf{\delta }}_{m}}}{\mathbf{2}} \right)\ }{\sin \left( \dfrac{\mathbf{A}}{\mathbf{2}} \right)}\]

Ans: For the minimum deviation position, \[i=\dfrac{{{\delta }_{m}}+A}{2}\].

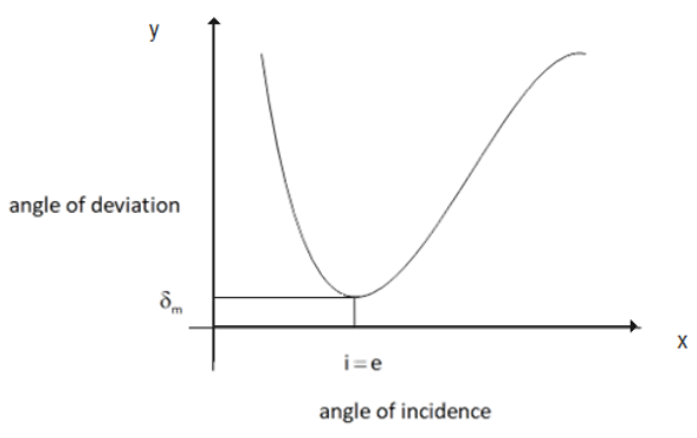
Also, \[\angle i=\angle e\].

Now, \[{{r}_{1}}={{r}_{2}}=r\] (say).

We know that: 

\[\angle i=\angle e={{\delta }_{m}}+A\]  ......(1)

Also,

\[{{r}_{1}}+{{r}_{2}}=A\]

\[\Rightarrow 2r=A\]

\[\Rightarrow r=\dfrac{A}{2}\]

Applying minimum deviation condition is equation (1);

\[2i={{\delta }_{m}}+A\]

\[\Rightarrow i=\dfrac{{{\delta }_{m}}+A}{2}\]

Applying Snell’s law,

\[\mu =\dfrac{\sin i}{\sin r}\]

\[\Rightarrow \mu =\dfrac{\sin \left( \dfrac{A+\delta {}_{m}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}\]

16. An object of size $\mathbf{3}.\mathbf{0}\ \mathbf{cm}$ is placed $\mathbf{14}\ \mathbf{cm}$ in front of a concave lens of focal length $\mathbf{21}\ \mathbf{cm}$. Describe the image produced by the lens. What happens if the object is moved further away from the lens? 

Ans: Given that,

Size of the object, \[{{h}_{1}}=3\text{ }cm\]

Object distance, \[u=-\text{ }14\text{ }cm\]

Focal length of the concave lens, \[f=-\text{ }21\text{ }cm\]

Let image distance \[=v\]

According to the lens formula, we have the relation:

\[\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}\]

Substituting the given values,

\[\Rightarrow \dfrac{1}{v}=-\dfrac{1}{21}-\dfrac{1}{14}=\dfrac{-2-3}{42}=\dfrac{-5}{42}\]

\[\therefore v=-\dfrac{42}{5}=-8.4cm\]

Hence, the image is formed on the other side of the lens, 8.4 cm away from it. The negative sign shows that the image is erect and virtual. 

The magnification of the image is given as: 

\[m=\dfrac{\operatorname{Im}age\text{ }\,height\,\left( {{h}_{2}} \right)}{Object\text{ }\,height\,\left( {{h}_{1}} \right)}=\dfrac{v}{u}\]

\[\Rightarrow {{h}_{2}}=\dfrac{-8.4}{-14}\times 3=0.6\times 3=1.8cm\]

Hence, the height of the image is $1.8cm$.

If the object is moved further away from the lens, then the virtual image will move toward the focus of the lens, but not beyond it. Also, the size of the image will decrease with the increase in the object distance.

17. A beam of light converges at a point P. Now a lens is placed in the path of the convergent beam $\mathbf{12}\ \mathbf{cm}$ from P. At what point does the beam converge if the lens is

1. A convex lens of focal length $\mathbf{20}\ \mathbf{cm}$

Ans: In the given situation, the object is virtual and the image formed is real.

Object distance, \[u=+12\text{ }cm\]

Focal length of the convex lens, \[f=20\text{ }cm\]

Image distance \[=v\]

According to the lens formula, we have the relation:

\[\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}\]

\[\Rightarrow \dfrac{1}{v}-\dfrac{1}{12}=\dfrac{1}{20}\]

\[\Rightarrow \dfrac{1}{v}=\dfrac{1}{20}+\dfrac{1}{12}=\dfrac{3+5}{60}=\dfrac{8}{60}\]

\[\therefore v=\dfrac{60}{8}=7.5cm\]

Hence, the image is formed $7.5cm$ away from the lens, toward its right. 

2. A concave lens of focal length $\mathbf{16}\ \mathbf{cm}$. 

Ans: Focal length of the concave lens, \[f=16\text{ }cm\]

Image distance \[=v\]

Object distance, \[u=+12\text{ }cm\]

According to the lens formula, we have the relation: 

\[\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}\]

\[\Rightarrow \dfrac{1}{v}=-\dfrac{1}{16}+\dfrac{1}{12}=\dfrac{-3+4}{48}=\dfrac{1}{48}\]

\[\therefore v=48cm\]

Hence, the image is formed $48cm$ away from the lens, toward its right.

18. Double-convex lenses are to be manufactured from a glass of refractive index 1.55, with both faces of the same radius of curvature. What is the radius of curvature required if the focal length is to be $20cm$? 

Ans: Given that,

Refractive index of glass, \[\mu =1.55\]

Focal length of the double-convex lens, \[f=20\text{ }cm\]

Radius of curvature of one face of the lens \[={{R}_{1}}=R\] 

Radius of curvature of the other face of the lens \[={{R}_{2}}=-R\] 

Let radius of curvature of the double-convex lens \[=R\]

The value of R can be calculated as:

\[\dfrac{1}{f}=\left( \mu -1 \right)\left[ \dfrac{1}{{{R}_{1}}}-\dfrac{1}{{{R}_{2}}} \right]\]

\[\Rightarrow \dfrac{1}{20}=\left( 1.55-1 \right)\left[ \dfrac{1}{R}+\dfrac{1}{R} \right]\]

\[\Rightarrow \dfrac{1}{20}=0.55\times \dfrac{2}{R}\]

\[\Rightarrow R=0.55\times 2\times 20=22cm\]

Hence, the radius of curvature of the double-convex lens is $22cm$.

19. A small telescope has an objective lens of focal length $\mathbf{144}\ \mathbf{cm}$ and an eyepiece of focal length $\mathbf{6}.\mathbf{0}\ \mathbf{cm}$. What is the magnifying power of the telescope? What is the separation between the objective and the eyepiece?

Ans: Given,

Focal length of the objective lens, \[{{f}_{o}}=144\text{ }cm\]

Focal length of the eyepiece, \[{{f}_{e}}=6.0\text{ }cm\]

The magnifying power of the telescope is given as: 

\[m=\dfrac{{{f}_{o}}}{{{f}_{e}}}=\dfrac{144}{6}=24\]

The separation between the objective lens and the eyepiece is calculated as:

\[D={{f}_{o}}+{{f}_{e}}=144+6=150cm\]

Hence, the magnifying power of the telescope is $24\ $and the separation between the objective lens and the eyepiece is $150\ cm$.

20. 

1. A giant refracting telescope at an observatory has an objective lens of focal length 15 m. If an eyepiece of focal length 1.0 cm is used, what is the angular magnification of the telescope?

Ans: Given that,

Focal length of the objective lens, 

\[{{f}_{o}}=15m=15\times {{10}^{2}}cm\]

Focal length of the eyepiece,

\[{{f}_{e}}=1.0cm\]

The angular magnification of a telescope is given as: 

\[\alpha =\dfrac{{{f}_{o}}}{{{f}_{e}}}=\dfrac{15\times {{10}^{2}}}{1.0}=1500\]

Hence, the angular magnification of the given refracting telescope is 1500. 

2. If this telescope is used to view the moon, what is the diameter of the image of the moon formed by the objective lens? The diameter of the moon is \[\mathbf{3}.\mathbf{48}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{6}}}\mathbf{m}\], and the radius of lunar orbit is \[\mathbf{3}.\mathbf{8}\times \mathbf{1}{{\mathbf{0}}^{\mathbf{8}}}\mathbf{m}\].

Ans: Given that,

Diameter of the moon, \[d=3.48\times {{10}^{6}}m\]

Radius of the lunar orbit, \[{{r}_{o}}=3.8\times {{10}^{8}}m\]

Let \[d'\] be the diameter of the image of the moon formed by the objective lens. 

The angle subtended by the diameter of the moon is equal to the angle subtended by the image. 

\[\Rightarrow \dfrac{d}{{{r}_{0}}}=\dfrac{d'}{{{d}_{0}}}\]

\[\Rightarrow \dfrac{3.48\times {{10}^{6}}}{3.8\times {{10}^{8}}}=\dfrac{d'}{15}\]

\[\Rightarrow d'=\dfrac{3.48}{3.8}\times {{10}^{-2}}\times 15\]

\[\Rightarrow d'=13.74\times {{10}^{-2}}m=13.74cm\]

Hence, the diameter of the moon's image formed by the objective lens is $13.74cm$.

21. A small pin fixed on a table top is viewed from above from a distance of 50 cm. By what distance would the pin appear to be raised if it is viewed from the same point through a 15 cm thick glass slab held parallel to the table? Refractive index of glass \[\mathbf{\mu }=\mathbf{1}.\mathbf{5}\]. Does the answer depend on the location of the slab? 

Ans: Given that, actual depth of the pin, \[d=15\text{ }cm\].

Refractive index of glass, \[\mu =1.5\]

Let the apparent depth of the pin \[=d'\].

Ratio of actual depth to the apparent depth is equal to the refractive index of glass, i.e.,

\[\mu =\dfrac{d}{d'}\]

\[\Rightarrow d'=\dfrac{d}{\mu }\]

\[\Rightarrow d'=\dfrac{15}{1.5}=10cm\]

Now, the distance by which the pin appears to be raised \[=d-d'=15-10=5cm\].

For a small angle of incidence, this distance does not depend upon the location of the slab.

22. A man with normal near point (25 cm) reads a book with small print using a magnifying glass: a thin convex lens of focal length 5 cm. 

1. What is the closest and the farthest distance at which he should keep the lens from the page so that he can read the book when viewing through the magnifying glass?

Ans: Given that,

Focal length of the magnifying glass, \[f=5\text{ }cm\]

Least distance of distance vision, \[d=25\text{ }cm\]

Let the object distance $=u$ 

Image distance, \[v=-d=-25\text{ }cm\]

According to the lens formula, we have:

\[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\]

\[\Rightarrow \dfrac{1}{u}=\dfrac{1}{v}-\dfrac{1}{f}\]

\[\Rightarrow \dfrac{1}{u}=\dfrac{1}{-25}-\dfrac{1}{5}=\dfrac{-5-1}{25}=\dfrac{-6}{25}\]

\[\Rightarrow u=-\dfrac{25}{6}=-4.167cm\]

Hence, the closest distance at which the person can read the book is $4.167cm$. 

For the object at the farthest possible distance, the image distance \[(v')=\infty \]. 

According to the lens formula, we have: 

\[\dfrac{1}{f}=\dfrac{1}{v'}-\dfrac{1}{u'}\]

\[\Rightarrow \dfrac{1}{u'}=\dfrac{1}{\infty }-\dfrac{1}{5}=-\dfrac{1}{5}\]

\[\therefore u'=-5cm\]

Hence, the farthest distance at which the person can read the book is $5cm$.

2. What is the maximum and the minimum angular magnification (magnifying power) possible using the above simple microscope?

Ans: Maximum angular magnification is given by the relation: 

\[{{\alpha }_{\max }}=\dfrac{d}{\left| u \right|}=\dfrac{25}{\left| \dfrac{25}{6} \right|}=6\]

Minimum angular magnification is given by the relation:

\[{{\alpha }_{\min }}=\dfrac{d}{\left| u' \right|}=\dfrac{25}{5}=5\]

23. A card sheet divided into squares each of size $1m{{m}^{2}}$ is being viewed at a distance of 9 cm through a magnifying glass (a converging lens of focal length 9 cm) held close to the eye.

1. What is the magnification produced by the lens? How much is the area of each square in the virtual image?

Ans: Given that, 

Size of each square, \[a=1\text{ }m{{m}^{2}}\]

Object distance, \[u=-\text{ }9\text{ }cm\]

Focal length of a converging lens, \[f=10\text{ }cm\]

For image distance \[v\], the lens formula can be written as: 

\[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\]

\[\Rightarrow \dfrac{1}{10}=\dfrac{1}{v}+\dfrac{1}{9}\]

\[\Rightarrow \dfrac{1}{v}=-\dfrac{1}{90}\]

\[\therefore v=-90cm\]

Magnification, \[m=\dfrac{v}{u}\]

\[\Rightarrow m=\dfrac{-90}{-9}=10\]

\[\therefore \] Area of each square in the virtual image \[={{10}^{2}}\times a\]

\[\Rightarrow A={{10}^{2}}\times 1=100m{{m}^{2}}\]

\[\Rightarrow A=1c{{m}^{2}}\]

2. What is the angular magnification (magnifying power) of the lens?

Ans: Magnifying power of the lens \[=\dfrac{d}{\left| u \right|}=\dfrac{25}{9}=2.8\]

3. Is the magnification in (a) equal to the magnifying power in (b)? Explain.

Ans: The magnification in (a) is not the same as the magnifying power in (b).

The magnification magnitude is \[\left( \left| \dfrac{v}{u} \right| \right)\] and the magnifying power is \[\left( \dfrac{d}{\left| u \right|} \right)\]. 

The two quantities will be equal only when the image is formed at the near point.

24.

1. At what distance should the lens be held from the figure in Exercise 9.29 in order to view the squares distinctly with the maximum possible magnifying power? 

Ans: The maximum possible magnification is obtained when the image is formed at the near point \[(d=25\text{ }cm)\].

Here,

Image distance, \[v=-\text{ }d=-25\text{ }cm\]

Focal length, \[f=10cm\]

Object distance \[=u\]

According to the lens formula, we have:

\[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\]

\[\Rightarrow \dfrac{1}{u}=\dfrac{1}{v}-\dfrac{1}{f}\]

\[\Rightarrow \dfrac{1}{u}=\dfrac{1}{-25}-\dfrac{1}{10}=\dfrac{-2-5}{50}=-\dfrac{7}{50}\]

\[\therefore u=-\dfrac{50}{7}=-7.14cm\]

Hence, to view the squares distinctly, the lens should be kept $7.14cm$ away from them.

2. What is the magnification in this case? 

Ans: Magnification \[=\]\[\left| \dfrac{v}{u} \right|=\dfrac{25}{7.14}=3.5\]

3. Is the magnification equal to the magnifying power in this case? Explain.

Ans: Here, 

Magnifying power \[=\dfrac{d}{\left| u \right|}=\dfrac{25}{7.14}=3.5\]

Thus, it can be concluded that since the image is formed at the near point (25 cm), the magnifying power is equal to the magnitude of magnification.

25. What should be the distance between the object in Exercise 9.30 and the magnifying glass if the virtual image of each square in the figure is to have an area of \[\mathbf{6}.\mathbf{25m}{{\mathbf{m}}^{\mathbf{2}}}\]? Would you be able to see the squares distinctly with your eyes very close to the magnifier? (Note: Exercises 9.29 to 9.31 will help you clearly understand the difference between magnification in absolute size and the angular magnification (or magnifying power) of an instrument.)

Ans: Given,

Area of the virtual image of each square, \[A=6.25m{{m}^{2}}\]

Area of each square, \[{{A}_{0}}=6.25m{{m}^{2}}\]

The linear magnification of the object can be calculated as:

\[m=\sqrt{\dfrac{A}{{{A}_{0}}}}=\sqrt{\dfrac{6.25}{1}}=2.5\]

However,

\[m=\dfrac{v}{u}\]

\[\Rightarrow v=mu=2.5u\]......(1)

Now,

Focal length of the magnifying glass, \[f=10\text{ }cm\].

According to the lens formula, we have the relation:

\[\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}\]

\[\Rightarrow \dfrac{1}{10}=\dfrac{1}{2.5u}-\dfrac{1}{u}=\dfrac{1}{u}\left( \dfrac{1}{2.5}-\dfrac{1}{1} \right)=\dfrac{1}{u}\left( \dfrac{1-2.5}{2.5} \right)\]

\[\therefore u=-\dfrac{1.5\times 10}{2.5}=-6cm\]

and 

\[v=2.5u=2.5\times 6=-15cm\]

The virtual image is formed at a distance of $15cm$, which is less than the near point (i.e., 25 cm) of a normal eye. Thus, it cannot be seen distinctly with the help of eyes.

26. 

1. For the telescope described in Exercise 9.34 (a), what is the separation between the objective lens and the eyepiece? 

Ans: Given,

Focal length of the objective lens, \[{{f}_{o}}=140\text{ }cm\].

Focal length of the eyepiece, \[{{f}_{e}}=5\text{ }cm\].

In normal adjustment, the separation between the objective lens and the eyepiece is the sum of focal length of the objective lens and that of the eye piece. 

\[\Rightarrow D={{f}_{o}}+{{f}_{e}}=140+5=145\text{ }cm\]

2. If this telescope is used to vie a 100m tall tower 3km away, what is the height of the image of the tower by the objective lens?

Ans: Given,

Height of the tower, \[{{h}_{1}}=100\text{ }m\]

Distance of the tower (object) from the telescope, \[u=3\text{ }km=3000m\]

The angle subtended by the tower at the telescope is given as: 

\[\theta =\dfrac{{{h}_{1}}}{u}=\dfrac{100}{3000}=\dfrac{1}{30}rad\]

The angle subtended by the image produced by the objective lens is given as: 

\[\theta =\dfrac{{{h}_{2}}}{{{f}_{o}}}=\dfrac{{{h}_{2}}}{140}rad\]

Where, 

\[{{h}_{2}}=\] Height of the image of the tower formed by the objective lens. 

\[\Rightarrow \dfrac{1}{30}=\dfrac{{{h}_{2}}}{140}\]

\[\Rightarrow {{h}_{2}}=\dfrac{140}{30}=4.7cm\]

Therefore, the objective lens forms a $4.7cm$ tall image of the tower.

3. What is the height of the final image of the tower if it is formed at 25cm?

Ans: Given, the image is formed at a distance, \[d=25\text{ }cm\]. 

The magnification of the eyepiece is given by the relation:

\[m=1+\dfrac{d}{{{f}_{e}}}\]

\[\Rightarrow m=1+\dfrac{25}{5}=1+5=6\]

Height of the final image \[=m{{h}_{2}}=6\times 4.7=28.2cm\]

Therefore, the height of the final image of the tower is $28.2cm$.

5 Mark Questions

1. Prove that

$\dfrac{{{n}_{2}}}{v}-\dfrac{{{n}_{1}}}{u}=\dfrac{{{n}_{2}}-{{n}_{1}}}{R}$

When refraction occurs of a convex spherical refracting surface and the ray travels from rarer to denser medium.

Ans: The ray is travelling from a rarer medium to a denser medium as shown in the figure.

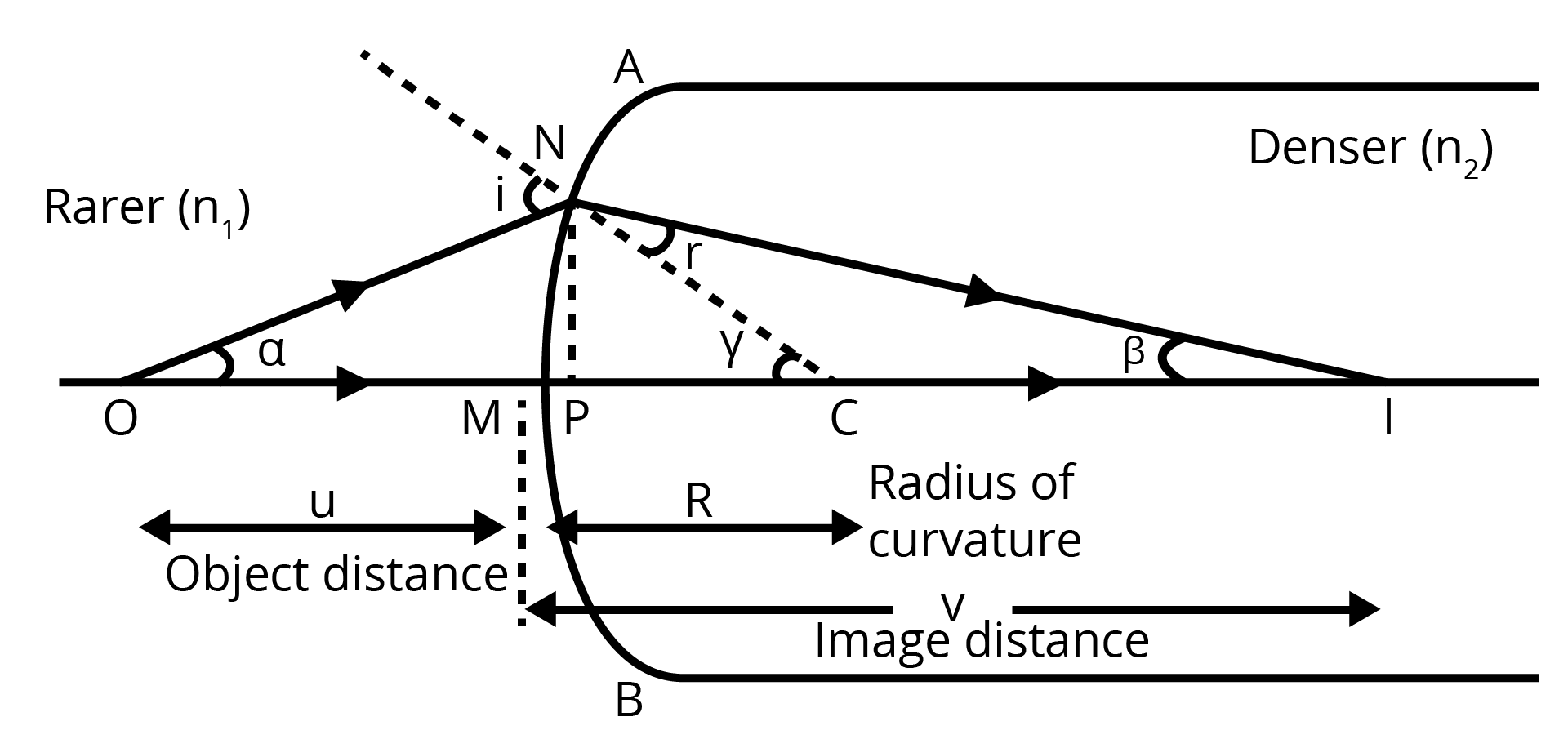
Now, we have $\Delta NOC$,

We get,

$i=\alpha +\gamma $……(1)

From figure,

$\tan \alpha =\dfrac{MN}{OM}$

$\tan \beta =\dfrac{MN}{MI}$

$\tan \gamma =\dfrac{MN}{MC}$

For small angle, $\alpha =\dfrac{MN}{OM}$, $\beta =\dfrac{MN}{MI}$, $\gamma =\dfrac{MN}{MC}$

Now equation (1) becomes,

$\Rightarrow i=\dfrac{MN}{OM}+\dfrac{MN}{MC}$

Similarly, $r=\gamma -\beta $

$\Rightarrow r=\dfrac{MN}{MC}-\dfrac{MN}{MI}$

Using Snell’s Law,

${{n}_{1}}\sin i={{n}_{2}}\sin r$

For small angle, 

${{n}_{1}}i={{n}_{2}}r$

Now, we put the value of i and r in the above equation,

\[{{n}_{1}}\left[ \dfrac{MN}{OM}+\dfrac{MN}{MC} \right]={{n}_{2}}\left[ \dfrac{MN}{MC}-\dfrac{MN}{MI} \right]\]……(2)

Put $OM=-u,MI=v,MC=R$ in equation (2),

\[\Rightarrow {{n}_{1}}\left[ \dfrac{1}{OM}+\dfrac{1}{MC} \right]={{n}_{2}}\left[ \dfrac{1}{MC}-\dfrac{1}{MI} \right]\]

\[\Rightarrow \dfrac{{{n}_{2}}}{MI}+\dfrac{{{n}_{1}}}{OM}=\dfrac{{{n}_{2}}-{{n}_{1}}}{MC}\]

\[\Rightarrow \dfrac{{{n}_{2}}}{v}+\dfrac{{{n}_{1}}}{-u}=\dfrac{{{n}_{2}}-{{n}_{1}}}{R}\]

\[\Rightarrow \dfrac{{{n}_{2}}}{v}-\dfrac{{{n}_{1}}}{u}=\dfrac{{{n}_{2}}-{{n}_{1}}}{R}\]

Hence, Proved.

2. A lens forms a real image of an object. The distance of the object. From the lens is u cm and the distance of the image from the lens is v cm. The given graph shows the variation of v and u

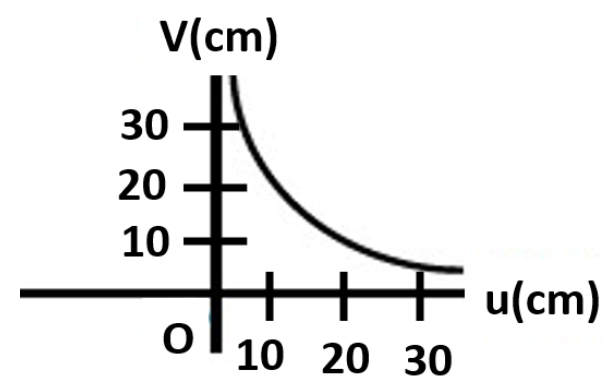
1. What is the nature of the lens?

Ans: The lens is a convex lens.

2. Using the graph find the focal length of the lens?

Ans: We use lens formula,

$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$

When $u\to \infty ,v=10cm$

$\Rightarrow \dfrac{1}{f}=\dfrac{1}{10}-\dfrac{1}{\infty }$

$\Rightarrow \dfrac{1}{f}=\dfrac{1}{10}$

$\Rightarrow f=10cm$

3. Draw a ray diagram to show the formation of image of same size as that of object in case of converging lens hence derive lens equation?

Ans: The below figure shows the formation of same size of image as that of object. 

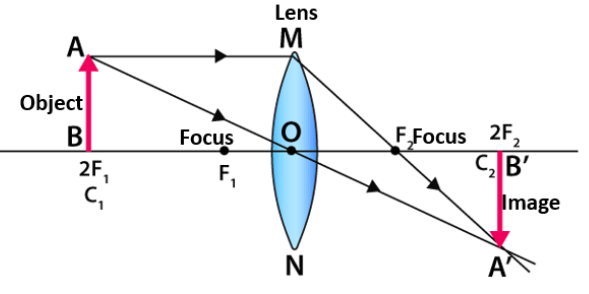
From above figure, $\Delta ABO\And \Delta A'B'O$ are similar.

$\dfrac{B'O}{BO}=\dfrac{A'B'}{AB}$ ……(1)

$\Delta MO{{F}_{2}}\And \Delta A'B'{{F}_{2}}$ are similar.

$\dfrac{MO}{O{{F}_{2}}}=\dfrac{A'B'}{B'{{F}_{2}}}$

And, we know,

$MO=AB$

 $\Rightarrow \dfrac{AB}{O{{F}_{2}}}=\dfrac{A'B'}{B'{{F}_{2}}}$

$\Rightarrow \dfrac{B'{{F}_{2}}}{O{{F}_{2}}}=\dfrac{A'B'}{AB}$ ……(2)

From (1) & (2),

$\dfrac{B'{{F}_{2}}}{O{{F}_{2}}}=\dfrac{B'O}{BO}$

Put $BO=-u,B'O=v,O{{F}_{2}}=f,B'{{F}_{2}}=v-f$ in above equation,

$\Rightarrow \dfrac{v-f}{f}=\dfrac{v}{-u}$

$\Rightarrow -uv+fu=vf$

Divide by $uvf$

$\Rightarrow -\dfrac{1}{f}+\dfrac{1}{v}=\dfrac{1}{u}$

$\Rightarrow \dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$

This is derived.

3. By stating sign conventions and assumptions used derive the relation between $u,v\And f$ in case of a concave mirror?

Ans: Sign Conventions:

1. All distances are estimated from the mirror's pole. 

2. Distance measured in the incident light direction is positive, and those measured in the direction opposite to the incident light are negative. 

3. Height estimated upwards is positive and height estimated downwards is negative.

Assumptions: 

1. Spherical mirror's aperture is supposed to be very small.

2. The incident and refracted rays form small angles with the principal axis.

This figure shows an image produced by the concave mirror.

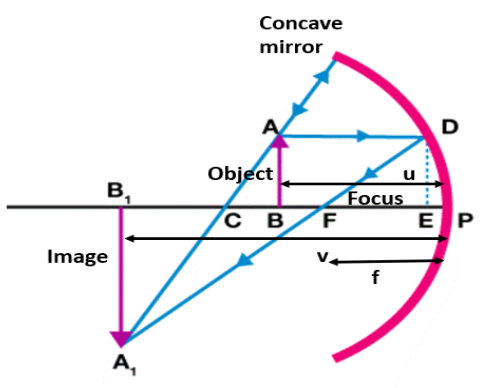
$\angle ACB=\angle {{A}_{1}}C{{B}_{1}}$ [opposite angles]

$\angle ABC=\angle {{A}_{1}}{{B}_{1}}C$ [right angles]

This gives, $\angle BAC=\angle C{{A}_{1}}{{B}_{1}}$

$\dfrac{AB}{{{A}_{1}}{{B}_{1}}}=\dfrac{BC}{{{B}_{1}}C}$   ……(1)

$\Delta FED\sim \Delta F{{A}_{1}}{{B}_{1}}$

$\dfrac{ED}{{{A}_{1}}{{B}_{1}}}=\dfrac{EF}{F{{B}_{1}}}$

Also, $ED=AB$

$\dfrac{AB}{{{A}_{1}}{{B}_{1}}}=\dfrac{EF}{F{{B}_{1}}}$

Combining (1) and (2),

$\dfrac{BC}{{{B}_{1}}C}=\dfrac{EF}{F{{B}_{1}}}$

We are considering that E is close to P, so, $EF=PF$

$\dfrac{BC}{{{B}_{1}}C}=\dfrac{PF}{F{{B}_{1}}}$

From figure, 

$BC=-R-(-u),{{B}_{1}}C=-v-(-R),PF=-f,F{{B}_{1}}=-v-(-f)$

Now,

$\Rightarrow \dfrac{-R+u}{-v+R}=\dfrac{-f}{-v+f}$

$\Rightarrow uv-uf-Rv+Rf=Rf-vf$

$\Rightarrow uv-uf-Rv=-vf$

Put $R=2f$

$\Rightarrow uv-uf-2fv=-vf$

$\Rightarrow uv-uf-fv=0$

Dividing by $uvf$

$\dfrac{1}{f}=\dfrac{1}{u}+\dfrac{1}{v}$

Hence, derived.

4. 

1. A person looking at a mesh of crossed wires is able to see the vertical lines more distinctly than the horizontal wires. What is the effect due to? How is such a defect of vision corrected?

Ans: In the given case, the person can see vertical lines more precisely than horizontal lines. 

This means that the eye's refracting system (cornea and eye-lens) is not working similarly in different planes. This defect is named astigmatism. 

The person's eye has sufficient curvature in the vertical plane. However, the horizontal plane's curvature is insufficient. Hence, sharp vertical lines are made on the retina, but horizontal lines seem blurred. 

This defect can be fixed by using cylindrical lenses.

2. A man with normal near point (\[\mathbf{25cm}\]) reads a book with small print using a magnifying glass: a thin convex lens of focal length 5cm. 

1. What is the closest and the farthest distance at which he can read the book when viewing through the magnifying glass?

Ans: Given that,

Focal length of the magnifying glass, \[f=5\text{ }cm\]

Least distance of distance vision, \[d=25\text{ }cm\]

Closest Object distance \[=u\]

Image distance, $v=-d=-25cm$

Using lens formula,

$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$

$\Rightarrow \dfrac{1}{5}=\dfrac{1}{-25}-\dfrac{1}{u}$

$\Rightarrow u=\dfrac{-25}{6}cm=-4.167cm$

Hence, the nearest distance at which the person can read the book is \[4.167\text{ }cm.\]

For the object at the farthest distance $(u')$, the image distance $(v')=\infty $

Using lens formula,

$\dfrac{1}{f}=\dfrac{1}{v'}-\dfrac{1}{u'}$

$\Rightarrow \dfrac{1}{5}=\dfrac{1}{\infty }-\dfrac{1}{u'}$

$\Rightarrow u'=-5cm$

Hence, the farthest distance at which the person can read the book is \[5cm.\]

2. What is the maximum and minimum angular magnificent (magnifying power) possible using the above simple microscope?

Ans: The formula for maximum angular magnification is given by:

${{a}_{\max }}=\dfrac{d}{|u|}$

$\Rightarrow {{a}_{\max }}=\dfrac{25}{\dfrac{25}{6}}=6$

The formula for minimum angular magnification is given by:

${{a}_{\min }}=\dfrac{d}{|u'|}$

$\Rightarrow {{a}_{\min }}=\dfrac{25}{5}=5$

Thus, the maximum and the minimum angular magnification (magnifying power) possible using the given simple microscope are $6$ and $5$ respectively.

5. Four double convex lens with following specifications are available?

1. Which of the given four lenses should be selected as objective and eyepiece to construct an astronomical telescope and why? What will be the magnifying power and length of the tube of this telescope?

Ans: The telescope’s objective should be of large aperture so that it can receive maximum light and should be of large focal length so that it can produce maximum magnification.

From table, we choose lens A as objective and lens D as eyepiece due to small aperture and small focal length.

${{f}_{o}}=100cm,{{f}_{e}}=5cm$

Magnification, 

$m=\dfrac{{{f}_{o}}}{{{f}_{e}}}$

$m=\dfrac{100}{5}=20$

Normal length, $L={{f}_{0}}+{{f}_{e}}=100+5=105cm$

The magnification is $20$ and the length of telescope’s tube is $105cm$.

2. An object is seen with the help of a simple microscope, firstly in red light and then is blue light. Will the magnification be same in both the cases? Why?

Ans: The focal length of lens is small for violet light than red light and magnifying power is inversely dependent on the focal length. So, magnification for violet light will be larger.

6. A small candle, \[2.5\text{ }cm\] in size is placed at \[27\text{ }cm\] in front of a concave mirror of radius of curvature \[36cm\]. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved?

Ans: We have,

Size of the candle, $h=2.5cm$

Let image size $=h'$

Object distance, $u=-27cm$

concave mirror’s curvature radius, $R=-36cm$

Focal length of the concave mirror, $f=\dfrac{R}{2}=-18cm$

Using mirror formula,

$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$

$\Rightarrow \dfrac{1}{v}=\dfrac{1}{f}-\dfrac{1}{u}$

Where, u is the object distance, 

v is the image distance and 

f is the focal length.

Now, we put given values,

$\Rightarrow \dfrac{1}{v}=\dfrac{1}{-18}-\dfrac{1}{-27}$

$\Rightarrow \dfrac{1}{v}=\dfrac{-3+2}{54}$

$\Rightarrow \dfrac{1}{v}=\dfrac{-1}{54}$

$\Rightarrow v=-54cm$

Therefore, the screen should be 54 cm away from the mirror to get a sharp image.

The formula for magnification of image is given by:

$m=\dfrac{h'}{h}=-\dfrac{v}{u}$

$\therefore h'=-\dfrac{v}{u}\times h$

$\Rightarrow h'=-\dfrac{-54}{-27}\times 2.5$

$\Rightarrow h'=-5cm$

The height of the image of the candle is \[5\text{ }cm\]. The negative sign shows that the image is inverted and real.

If the candle is moved nearer to the mirror, then the screen will have to be moved far from the mirror in order to get the image.

7. A \[\mathbf{4}.\mathbf{5}\text{ }\mathbf{cm}\] needle is placed \[\mathbf{12cm}\] away from a convex mirror of focal length \[\mathbf{15cm}\]. Give the location of the image and the magnification. Describe what happens as the needle is moved farther from the mirror.

Ans: Given that,

Height of the needle, \[{{h}_{1}}\text{ }=\text{ }4.5cm\]

Object distance, \[u\text{ }=\text{ }-12cm\]

Focal length of the convex mirror, \[f\text{ }=\text{ }15cm\]

Image distance \[=\text{ }v\]

Using mirror formula,

$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$

$\Rightarrow \dfrac{1}{v}=\dfrac{1}{f}-\dfrac{1}{u}$

Now, we put given values,

$\Rightarrow \dfrac{1}{v}=\dfrac{1}{15}-\dfrac{1}{-12}$

$\Rightarrow \dfrac{1}{v}=\dfrac{4+5}{60}$

$\Rightarrow \dfrac{1}{v}=\dfrac{9}{60}$

$\Rightarrow v=6.7cm$

Hence, the needle’s image is \[6.7\text{ }cm\] away from the mirror and it is on the mirror’s other side.

The formula for magnification of image is given by:

$m=\dfrac{{{h}_{2}}}{{{h}_{1}}}=-\dfrac{v}{u}$

$\therefore {{h}_{2}}=-\dfrac{v}{u}\times {{h}_{1}}$

$\Rightarrow {{h}_{2}}=-\dfrac{6.7}{-12}\times 4.5$ 

$\Rightarrow {{h}_{2}}=2.5cm$

Hence, magnification, 

$m=\dfrac{2.5}{4.5}=0.56$

The image’s height is 2.5cm. The positive sign shows that the image is virtual, erect, and diminished.

If the needle is moved away from the mirror, the image will also move farther from the mirror, and the size of the image will decrease gradually.

8. A tank is filled with water to a height of \[\mathbf{12}.\mathbf{5}\text{ }\mathbf{cm}\]. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be \[\mathbf{9}.\mathbf{4cm}\]. What is the refractive index of water? If water is replaced by a liquid of refractive index \[\mathbf{1}.\mathbf{63}\] up to the same height, by what distance would the microscope have to be moved to focus on the needle again?

Ans: Given that,

Actual depth of the needle in water, \[{{h}_{1}}=12.5cm\]

Apparent depth of the needle in water, \[{{h}_{2}}=9.4cm\]

Refractive index of water $=\mu $

The formula for refractive index is given by:

$\mu =\dfrac{{{h}_{1}}}{{{h}_{2}}}$

Put the given values,

$\mu =\dfrac{12.5}{9.4}$

$\mu \approx 1.33$

Hence, the water’s refractive index is about \[1.33\].

When water is replaced by a liquid of refractive index, $\mu '=1.63$.

The actual depth of the needle will be the same, but it's apparent depth will vary.

Let \[y\] be the new apparent depth of the needle. 

We will use the relation given below:

$\mu '=\dfrac{{{h}_{1}}}{y}$

$\therefore y=\dfrac{{{h}_{1}}}{\mu '}$

$\Rightarrow y=\dfrac{12.5}{1.63}$

$\Rightarrow y=7.67cm$

We get the new apparent depth of the needle to be \[7.67cm\]. It is less than ${{h}_{2}}$. Therefore, the microscope should be moved up to focus the needle again.

The distance by which the microscope would be moved up\[=\text{ }9.4\text{ }\text{ }7.67\text{ }=\text{ }1.73cm\].

9. Figures (a) and (b) show refraction of a ray in air incident at \[\mathbf{60}{}^\circ \] with the normal to a glass-air and water air interface, respectively. Predict the angle of refraction in glass when the angle of incidence in water is \[\mathbf{45}{}^\circ \] with the normal to a water-glass interface [figure (c)].

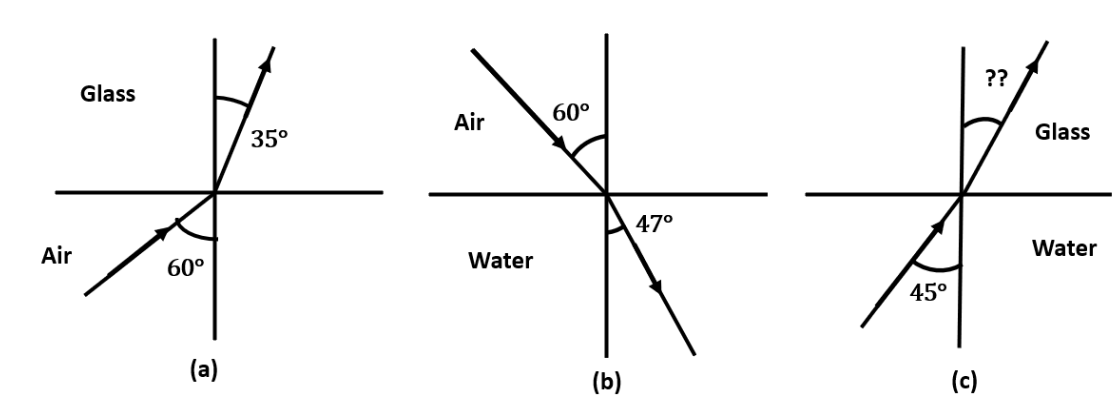
Ans: Given that,

For the glass -air interface,

Angle of incidence, \[i=\text{ }60{}^\circ \]

Angle of refraction, $r=35{}^\circ $

We can use Snell’s law,

$\mu _{g}^{a}=\dfrac{\sin i}{\sin r}$

$\Rightarrow \mu _{g}^{a}=\dfrac{\sin 60{}^\circ }{\sin 35{}^\circ }$

$\Rightarrow \mu _{g}^{a}=1.51$……(i)

For the air-water interface,

Angle of incidence, \[i=\text{ }60{}^\circ \]

Angle of refraction, $r=47{}^\circ $

We can use Snell’s law,

$\mu _{w}^{a}=\dfrac{\sin i}{\sin r}$

$\Rightarrow \mu _{w}^{a}=\dfrac{\sin 60{}^\circ }{\sin 47{}^\circ }$

$\Rightarrow \mu _{w}^{a}=1.184$……(ii)

Using (i) and (ii), the relative refractive index of glass with respect to water can be derived as:

$\mu _{g}^{w}=\dfrac{\mu _{g}^{a}}{\mu _{w}^{a}}$

$\Rightarrow \mu _{g}^{w}=\dfrac{1.51}{1.184}$

$\Rightarrow \mu _{g}^{w}=1.275$

For the glass - water interface,

Angle of incidence, \[i=\text{ 45}{}^\circ \]

Angle of refraction, $=r$

We can use Snell’s law,

$\mu _{g}^{w}=\dfrac{\sin i}{\sin r}$

$\Rightarrow 1.275=\dfrac{\sin 45{}^\circ }{\sin r}$

$\Rightarrow \sin r=0.5546$

$\Rightarrow r={{\sin }^{-1}}(0.5546)$

\[\Rightarrow r=38.68{}^\circ \]

Hence, the angle of refraction at the water – glass interface is $38.68{}^\circ $.

10. A small bulb is placed at the bottom of a tank containing water to a depth of \[\mathbf{80}\text{ }\mathbf{cm}\]. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is \[\mathbf{1}.\mathbf{33}.\](Consider the bulb to be a point source.)

Ans: Provided that,

Bulb’s actual depth in water, ${{d}_{1}}=80cm=0.8m$

Water’s refractive index, \[\mu =1.33\]

The following diagram represents the given setup:

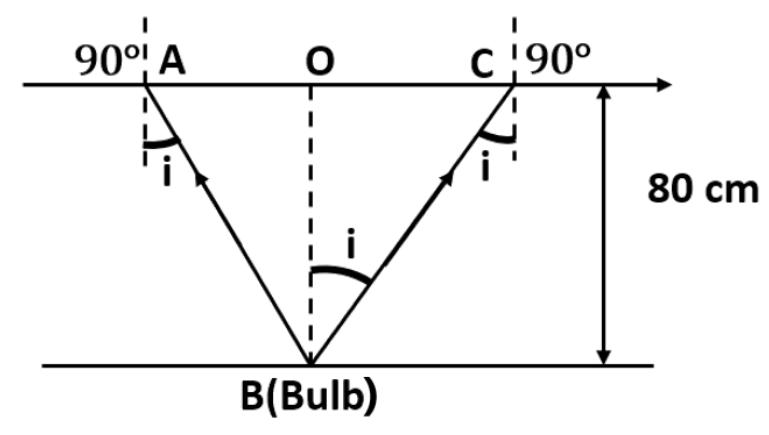
Where, i is the Angle of incidence 

r is the Angle of refraction, $r=90{}^\circ $

As the bulb acts as a point source, the emergent light would be considered as a circle of radius, $R=\dfrac{AC}{2}=AO=OB$

Snell’s law may be used as follows:

$\mu =\dfrac{\sin r}{\sin i}$

$\Rightarrow 1.33=\dfrac{\sin 90{}^\circ }{\sin i}$

$\Rightarrow \sin i=\dfrac{1}{1.33}$

$\Rightarrow i=48.75{}^\circ $

Considering the given diagram, we have the relation:

$\tan i=\dfrac{OC}{OB}=\dfrac{R}{{{d}_{1}}}$

$\Rightarrow R=\tan 48.75{}^\circ \times 0.8$

$\Rightarrow R=0.91m$

Area of the surface of water $=\pi {{R}^{2}}=\pi {{(0.91)}^{2}}=2.61{{m}^{2}}$

Clearly, the area of the water surface through which the light from the bulb could project is about $2.61{{m}^{2}}$.

11. A prism is made of glass of unknown refractive index. A parallel beam of light is incident on a face of the prism. The angle of minimum deviation is measured to be \[\mathbf{40}{}^\circ \]. What is the refractive index of the material of the prism? The refracting angle of the prism is \[\mathbf{60}{}^\circ \]. If the prism is placed in water (refractive index \[\mathbf{1}.\mathbf{33}\]), predict the new angle of minimum deviation of a parallel beam of light.

Ans:  The minimum deviation angle and the angle of prism is as shown in figure given below: 

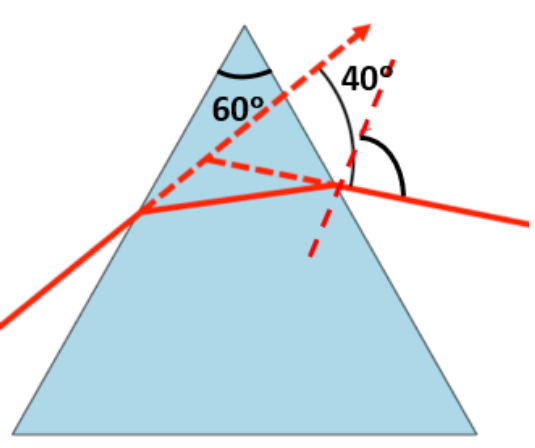
Angle of minimum deviation, ${{\delta }_{m}}=40{}^\circ $ 

Angle of the prism, $A=60{}^\circ $

Refractive index of water, $\mu =1.33$

Refractive index of the material of the prism $=\mu '$

The relation between angle of deviation with refractive index is given by:

$\mu '=\dfrac{\sin \left( \dfrac{A+{{\delta }_{m}}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}$

$\Rightarrow \mu '=\dfrac{\sin \left( \dfrac{60{}^\circ +40{}^\circ }{2} \right)}{\sin \left( \dfrac{60{}^\circ }{2} \right)}=\dfrac{\sin 50{}^\circ }{\sin 30{}^\circ }$

$\Rightarrow \mu '=1.532$

Hence, the refractive index of the prism is \[1.532\].

Since the prism is placed in water, let $\delta {{'}_{m}}$ be the new angle of minimum deviation for the same prism. 

The below figure shows the angle of prism and the unknown minimum deviation angle.

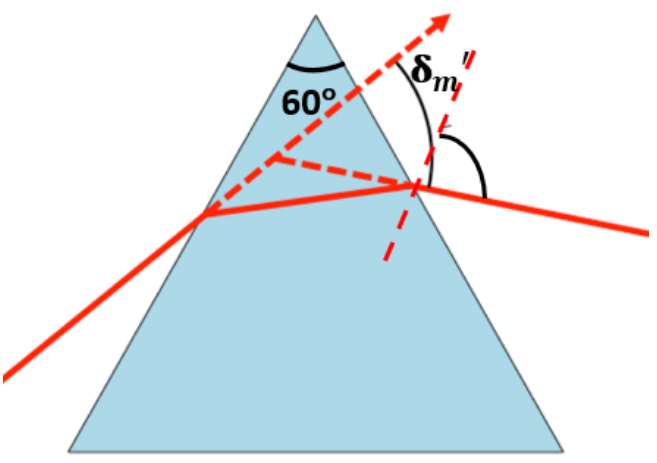
The refractive index of glass with respect to water is given by the relation:

$\mu _{g}^{w}=\dfrac{\mu '}{\mu }=\dfrac{\sin \left( \dfrac{A+\delta {{'}_{m}}}{2} \right)}{\sin \left( \dfrac{A}{2} \right)}$

$\Rightarrow \dfrac{\mu '}{\mu }\sin \left( \dfrac{A}{2} \right)=\sin \left( \dfrac{A+\delta {{'}_{m}}}{2} \right)$

$\Rightarrow \sin \left( \dfrac{A+\delta {{'}_{m}}}{2} \right)=\dfrac{1.532}{1.33}\sin \left( \dfrac{60{}^\circ }{2} \right)=0.5759$

$\Rightarrow \dfrac{A+\delta {{'}_{m}}}{2}={{\sin }^{-1}}\left( 0.5759 \right)=35.16{}^\circ $

$\Rightarrow 60{}^\circ +\delta {{'}_{m}}=70.32{}^\circ $

$\Rightarrow \delta {{'}_{m}}=10.32{}^\circ $

Hence, the new minimum angle of deviation is $10.32{}^\circ $.

12. A compound microscope consists of an objective lens of focal length \[\mathbf{2}.\mathbf{0}\text{ }\mathbf{cm}\] and an eyepiece of focal length \[\mathbf{6}.\mathbf{25}\text{ }\mathbf{cm}\] separated by a distance of \[\mathbf{15}\text{ }\mathbf{cm}\]. How far from the objective should an object be placed in order to obtain the final image at: 

1. The least distance of distinct vision (\[\mathbf{25}\text{ }\mathbf{cm}\])? What is the magnifying power of the microscope?

Ans: Given that,

Focal length of the objective lens, \[{{f}_{1}}=2.0\text{ }cm\]

Focal length of the eyepiece, \[{{f}_{2}}=\text{ }6.25\text{ }cm\]

Distance between the objective lens and the eyepiece, \[d\text{ }=\text{ }15\text{ }cm\]

Least distance of distinct vision, \[d'\text{ }=\text{ }25\text{ }cm\]

lmage distance for the eyepiece, \[{{v}_{2}}=-25\text{ }cm\]

Object distance for the eyepiece \[=\text{ }{{u}_{2}}\]

Using lens formula,

$\dfrac{1}{{{v}_{2}}}-\dfrac{1}{{{u}_{2}}}=\dfrac{1}{{{f}_{2}}}$

$\Rightarrow \dfrac{1}{{{u}_{2}}}=\dfrac{1}{{{v}_{2}}}-\dfrac{1}{{{f}_{2}}}$

$\Rightarrow \dfrac{1}{{{u}_{2}}}=\dfrac{1}{-25}-\dfrac{1}{6.25}$

$\Rightarrow \dfrac{1}{{{u}_{2}}}=\dfrac{-5}{25}$

$\Rightarrow {{u}_{2}}=-5cm$

The distance of image for the objective lens, ${{v}_{1}}=d+{{u}_{2}}=15-5=10cm$.

The distance of object for the objective lens $={{u}_{1}}$

Using lens formula,

$\dfrac{1}{{{v}_{1}}}-\dfrac{1}{{{u}_{1}}}=\dfrac{1}{{{f}_{1}}}$

$\Rightarrow \dfrac{1}{{{u}_{1}}}=\dfrac{1}{{{v}_{1}}}-\dfrac{1}{{{f}_{1}}}$

$\Rightarrow \dfrac{1}{{{u}_{1}}}=\dfrac{1}{10}-\dfrac{1}{2}$

$\Rightarrow \dfrac{1}{{{u}_{1}}}=\dfrac{-4}{10}$

$\Rightarrow {{u}_{1}}=-2.5cm$

Magnitude of the object distance, $|{{u}_{1}}|=2.5cm$.

The compound microscope’s magnifying power is given by the relation:

$m=\dfrac{{{v}_{1}}}{|{{u}_{1}}|}\left( 1+\dfrac{d'}{{{f}_{2}}} \right)$

$\Rightarrow m=\dfrac{10}{2.5}\left( 1+\dfrac{25}{6.25} \right)$

$\Rightarrow m=4(1+4)=20$

Hence, the magnifying power of the microscope is $20$.

2. At infinity? What is the magnifying power of the microscope?

Ans: Given that, the final image is formed at infinity.

The distance of image of the eyepiece, ${{v}_{2}}=\infty $ 

The distance of object of the eyepiece $={{u}_{2}}$

Using lens formula,

$\dfrac{1}{{{v}_{2}}}-\dfrac{1}{{{u}_{2}}}=\dfrac{1}{{{f}_{2}}}$

$\Rightarrow \dfrac{1}{{{u}_{2}}}=\dfrac{1}{{{v}_{2}}}-\dfrac{1}{{{f}_{2}}}$

$\Rightarrow \dfrac{1}{{{u}_{2}}}=\dfrac{1}{\infty }-\dfrac{1}{6.25}$

$\Rightarrow {{u}_{2}}=-6.25cm$

The distance of image for the objective lens, ${{v}_{1}}=d+{{u}_{2}}=15-6.25=8.75cm$.

The distance of object for the objective lens $={{u}_{1}}$

Using lens formula,

$\dfrac{1}{{{v}_{1}}}-\dfrac{1}{{{u}_{1}}}=\dfrac{1}{{{f}_{1}}}$

$\Rightarrow \dfrac{1}{{{u}_{1}}}=\dfrac{1}{{{v}_{1}}}-\dfrac{1}{{{f}_{1}}}$

$\Rightarrow \dfrac{1}{{{u}_{1}}}=\dfrac{1}{8.75}-\dfrac{1}{2}$

$\Rightarrow {{u}_{1}}=-2.59cm$

Magnitude of the object distance, $|{{u}_{1}}|=2.59cm$.

The compound microscope’s magnifying power is given by the relation:

$m=\dfrac{{{v}_{1}}}{|{{u}_{1}}|}\left( \dfrac{d'}{|{{u}_{2}}|} \right)$

$\Rightarrow m=\dfrac{8.75}{2.59}\left( \dfrac{25}{6.25} \right)$

$\Rightarrow m=13.51$

Hence, the magnifying power of the microscope is $13.51$.

13. A person with a normal near point (\[\mathbf{25}\text{ }\mathbf{cm}\]) using a compound microscope with objective of focal length \[\mathbf{8}.\mathbf{0}\text{ }\mathbf{mm}\] and an eyepiece of focal length \[\mathbf{2}.\mathbf{5}\text{ }\mathbf{cm}\] can bring an object placed at \[\mathbf{9}.\mathbf{0}\text{ }\mathbf{mm}\] from the objective in sharp focus. What is the separation between the two lenses? Calculate the magnifying power of the microscope.

Ans: Given that,

Focal length of the objective lens, \[{{f}_{o}}=8\text{ }mm=0.8\text{ }cm\]

Focal length of the eyepiece, \[{{f}_{e}}=2.5\text{ }cm\]

The distance of the object for the Objective lens, \[{{u}_{o}}=-9.0\text{ }mm=-0.9\text{ }cm\]

Least distance of distant vision, \[d=25\text{ }cm\]

Image distance for the eyepiece, \[{{v}_{e}}=-d=-25\text{ }cm\]

Object distance for the eyepiece, ${{u}_{e}}$

Using lens formula,

$\dfrac{1}{{{v}_{e}}}-\dfrac{1}{{{u}_{e}}}=\dfrac{1}{{{f}_{e}}}$

$\Rightarrow \dfrac{1}{{{u}_{e}}}=\dfrac{1}{{{v}_{e}}}-\dfrac{1}{{{f}_{e}}}$

$\Rightarrow \dfrac{1}{{{u}_{e}}}=\dfrac{1}{-25}-\dfrac{1}{2.5}$

$\Rightarrow \dfrac{1}{{{u}_{e}}}=\dfrac{-11}{25}$

$\Rightarrow {{u}_{e}}=-2.27cm$

Using lens formula, we can obtain image distance for the objective lens,${{v}_{o}}$, is given by:

$\dfrac{1}{{{v}_{o}}}-\dfrac{1}{{{u}_{o}}}=\dfrac{1}{{{f}_{o}}}$

$\Rightarrow \dfrac{1}{{{v}_{o}}}=\dfrac{1}{{{u}_{o}}}+\dfrac{1}{{{f}_{o}}}$

$\Rightarrow \dfrac{1}{{{v}_{o}}}=\dfrac{1}{0.8}-\dfrac{1}{0.9}$

$\Rightarrow \dfrac{1}{{{v}_{o}}}=\dfrac{0.1}{0.72}$

$\Rightarrow {{v}_{o}}=7.2cm$

The distance between the objective lens and the eyepiece,  $|{{u}_{e}}|+{{v}_{o}}=2.27+7.2=9.47cm$

The microscope’s magnifying power is given by the relation:

$m=\dfrac{{{v}_{o}}}{|{{u}_{o}}|}\left( 1+\dfrac{d}{{{f}_{e}}} \right)$

$\Rightarrow m=\dfrac{7.2}{0.9}\left( 1+\dfrac{25}{2.5} \right)$

$\Rightarrow m=8(1+10)=88$

Hence, the magnifying power of the microscope is $88$.

14. Use the mirror equation to deduce that: 

1. an object placed between \[\mathbf{f}\] and \[~\mathbf{2f}\] of a concave mirror produces a real image beyond \[\mathbf{2f}\].

Ans: For a concave mirror, $f<0$.

When the object is placed on the left side of the mirror, then $u<0$.

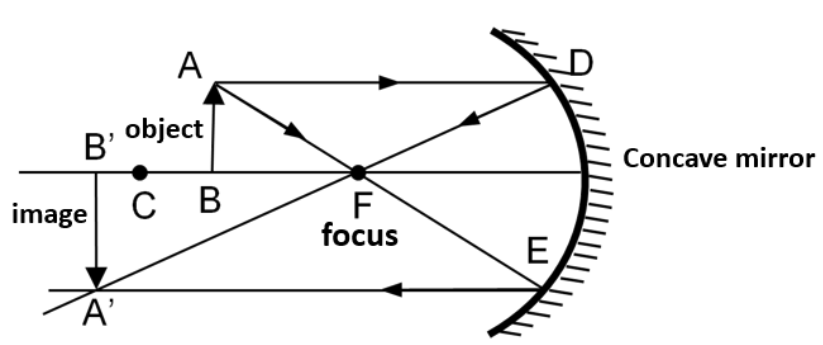
Using mirror formula,

$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$

$\Rightarrow \dfrac{1}{v}=\dfrac{1}{f}-\dfrac{1}{u}$……(1)

If the object placed between $f$ and $2f$ $i.e.,2f<u<f$:

$\Rightarrow \dfrac{1}{2f}>\dfrac{1}{u}>\dfrac{1}{f}$

$\Rightarrow -\dfrac{1}{2f}<-\dfrac{1}{u}<-\dfrac{1}{f}$

$\Rightarrow \dfrac{1}{f}-\dfrac{1}{2f}<\dfrac{1}{f}-\dfrac{1}{u}<0$……(2)

Using equation (1), we get

$\Rightarrow \dfrac{1}{2f}<\dfrac{1}{v}<0$

Since $\dfrac{1}{v}$ is negative, $v$ is negative.

$\Rightarrow \dfrac{1}{2f}<\dfrac{1}{v}$

$\Rightarrow 2f>v$

$\Rightarrow -v>-2f$

Therefore, image will lie beyond $2f$.

2. a convex mirror always produces a virtual image independent of the location of the object.

Ans: For a convex mirror, $f>0$.

When the object is placed on the left side of the mirror, then $u<0$.

Using mirror formula,

$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$

$\Rightarrow \dfrac{1}{v}=\dfrac{1}{f}-\dfrac{1}{u}$

Using equation (2), we get:

$\dfrac{1}{v}<0$

$\Rightarrow v>0$

Thus, the image is formed on the mirror’s back side. 

Hence, a convex mirror always gives a virtual image, regardless of the object distance.

3. The virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.

Ans: For a convex mirror, $f>0$.

Using mirror formula,

$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{f}$

$\Rightarrow \dfrac{1}{v}=\dfrac{1}{f}-\dfrac{1}{u}$

But we have, $u<0$

$\therefore \dfrac{1}{v}>\dfrac{1}{f}$

$\Rightarrow v<f$

Hence, the image formed is diminished and is located between the focus and the pole.

4. An object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.

Ans: For a concave mirror, $f<0$.

When the object is placed on the left side of the mirror, then $u<0$.

The object is placed between the focus and the pole.

$\therefore f>u>0$

$\Rightarrow \dfrac{1}{f}<\dfrac{1}{u}<0$

$\Rightarrow \dfrac{1}{f}-\dfrac{1}{u}<0$

$\therefore \dfrac{1}{v}<0$

$\Rightarrow v>0$

The image is formed on the mirror’s right side. Hence, it is a virtual image.

For $u<0,v>0$ 

$\Rightarrow \dfrac{1}{u}>\dfrac{1}{v}$

$\Rightarrow v>u$

Magnification, $m=\dfrac{v}{u}>1$

Hence, the formed image is enlarged.

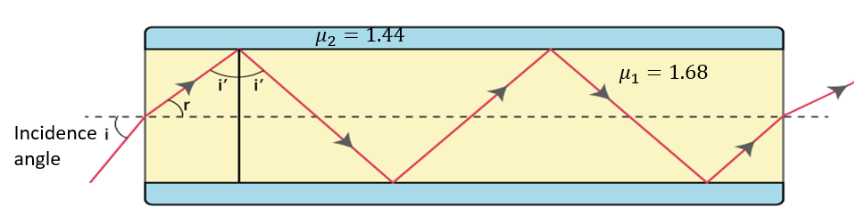
15. 

1. Figure shows a cross-section of a 'light pipe' made of a glass fibre of refractive index \[\mathbf{1}.\mathbf{68}\]. The outer covering of the pipe is made of a material of refractive index \[\mathbf{1}.\mathbf{44}\]. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure?

Ans: Given that,

Refractive index of the glass fibre, ${{\mu }_{1}}=1.68$

Refractive index of the outer covering of the pipe, ${{\mu }_{2}}=1.44$

Angle of incidence \[=\text{ }i\]

Angle Of refraction \[=\text{ }r\]

Angle of incidence at the interface \[=\text{ }i'\]

The refractive index ($\mu $) of the inner core - outer core interface is given as:

$\mu =\dfrac{{{\mu }_{2}}}{{{\mu }_{1}}}=\dfrac{1}{\sin i'}$

\[\Rightarrow \sin i'=\dfrac{{{\mu }_{1}}}{{{\mu }_{2}}}\]

\[\Rightarrow \sin i'=\dfrac{1.44}{1.68}=0.8571\]

For the critical angle, total internal reflection (TIR) takes place only when $i>i'$.

That is, when $i>59{}^\circ $.

Maximum angle of reflection, ${{r}_{\max }}=90{}^\circ -i'=90{}^\circ -59{}^\circ =31{}^\circ $.

Let ${{i}_{\max }}$ be the maximum incidence angle.

The refractive index at the air – glass interface, ${{\mu }_{1}}=1.68$.

We can use the relation for the maximum angles of incidence and reflection as:

${{\mu }_{1}}=\dfrac{\sin {{i}_{\max }}}{\sin {{r}_{\max }}}$

\[\Rightarrow \sin {{i}_{\max }}={{\mu }_{1}}\times \sin {{r}_{\max }}\]

\[\Rightarrow \sin {{i}_{\max }}=1.68\times \sin 31{}^\circ \]

\[\Rightarrow \sin {{i}_{\max }}=0.8652\]

\[\Rightarrow {{i}_{\max }}\approx 60{}^\circ \]

Thus, all the ray’s incident at angles lying in the range $0<i<60{}^\circ $  will suffer total internal reflection.

2. What is the answer if there is no outer covering of the pipe?

Ans: If the outer covering of the pipe is not present, then:

Refractive index of the outer pipe $={{\mu }_{1}}$

Refractive index of air \[=\text{ }1\]

For the angle of incidence  \[i\text{ =}90{}^\circ \], we can use Snell’s law at the air – pipe interface as

${{\mu }_{2}}=\dfrac{\sin i}{\sin r}$

$\Rightarrow 1.68=\dfrac{\sin 90{}^\circ }{\sin r}$

$\Rightarrow \sin r=\dfrac{1}{1.68}$

$\Rightarrow r=36.5{}^\circ $

$\therefore i'=90{}^\circ -36.5{}^\circ =53.5{}^\circ $

Since, $i'>r$, all incident rays will suffer total internal reflection.

16. Answer the following questions: 

1. You have learnt that plane and convex mirrors produce virtual images of objects. Can they produce real images under some circumstances? Explain.

Ans: Yes. Plane and convex mirrors can provide real images as well. 

If the light rays converging at a point behind a plane mirror (or a convex mirror) are reflected on a screen placed in front of the mirror, then an actual image will be formed.

2. A Virtual image, we always say, cannot be caught on a screen. Yet when we ‘see' a virtual image, we are obviously bringing it on to the ‘screen' (i.e., the retina) of our eye. Is there a contradiction?

Ans: No. A virtual image is made when light rays diverge. 

The convex lens of the eye makes these divergent rays converge at the retina. The virtual image works as an object for the lens to provide an actual image in this situation.

3. A diver underwater, looks obliquely at a fisherman standing on the bank of a lake. Would the fisherman look taller or shorter to the diver than what he actually is?

Ans: The diver is in the water, and the fisherman is on the land. Water is a denser medium than air. 

It is provided that the diver is viewing the fisherman. This shows that the light rays are traveling from a denser medium to a rarer medium. 

Hence, the refracted rays will go away from the normal. As a result, the fisherman will seem to be taller.

4. Does the apparent depth of a tank of water change if viewed obliquely? If so, does the apparent depth increase or decrease?

Ans: Yes, the apparent depth decreases. The tank's apparent depth of water varies when viewed obliquely. 

This is because the light deviates on traveling from one medium to another. The tank's apparent depth, when viewed obliquely, is less than the near-normal viewing.

5. The refractive index of diamond is much greater than that of ordinary glass. Is this fact of some use to a diamond cutter?

Ans: The diamond's refractive index is more than that of ordinary glass. 

The critical angle for diamond is smaller than that for glass. 

A diamond cutter utilizes a large angle of incidence to guarantee that the light entering the diamond is totally reflected from its face. This is the cause for the sparkling effect of a diamond.

17. 

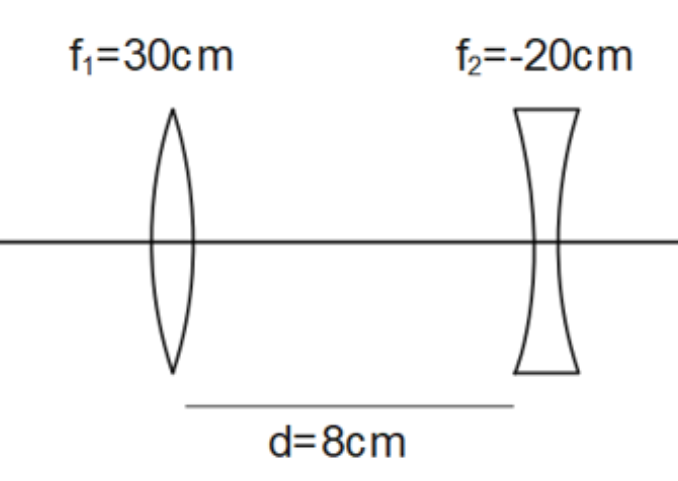
1. Determine the 'effective focal length' of the combination of the two lenses in Exercise 9.10, if they are placed \[\mathbf{8}.\mathbf{0}\text{ }\mathbf{cm}\] apart with their principal axes coincident. Does the answer depend on which side of the combination a beam of parallel light is incident? Is the notion of effective focal length of this system useful at all?

Ans: Consider the diagram below which represents the combination of two lenses.

Here,

Focal length of the convex lens, \[{{f}_{1}}=30\text{ }cm\]

Focal length of the concave lens, \[{{f}_{2}}=-20\text{ }cm\]

Distance between the two lenses, \[d=8.0\text{ }cm\]

First, consider the case when the parallel beam of light falls on the convex lens.

Using lens formula, 

$\dfrac{1}{{{v}_{1}}}-\dfrac{1}{{{u}_{1}}}=\dfrac{1}{{{f}_{1}}}$

Where, object distance, ${{u}_{1}}=\infty $

Image distance $={{v}_{1}}$

$\Rightarrow \dfrac{1}{{{v}_{1}}}=\dfrac{1}{30}-\dfrac{1}{\infty }=\dfrac{1}{30}$

$\Rightarrow {{v}_{1}}=30cm$

The image will serve as a virtual object for the concave lens.

Using lens formula, 

$\dfrac{1}{{{v}_{2}}}-\dfrac{1}{{{u}_{2}}}=\dfrac{1}{{{f}_{2}}}$

Where, object distance $={{u}_{2}}$.

${{u}_{2}}=30-8=22cm$

Image distance $={{v}_{2}}$.

$\Rightarrow \dfrac{1}{{{v}_{2}}}=\dfrac{1}{22}-\dfrac{1}{20}=\dfrac{-1}{220}$

$\Rightarrow {{v}_{2}}=-220cm$

The parallel incident beam seems to diverge from a point, that is, $220-\dfrac{d}{2}=220-4=216cm$ from the centre of the combination of the two lenses.

Secondly, when the parallel beam of light falls, from the left, on the concave lens;

Using lens formula, 

$\dfrac{1}{{{v}_{2}}}-\dfrac{1}{{{u}_{2}}}=\dfrac{1}{{{f}_{2}}}$

Where, object distance, ${{u}_{2}}=-\infty $.

Image distance $={{v}_{2}}$.

$\Rightarrow \dfrac{1}{{{v}_{2}}}=\dfrac{1}{-20}-\dfrac{1}{\infty }=\dfrac{1}{-20}$

$\Rightarrow {{v}_{2}}=-20cm$

The image will serve as a real object for the convex lens.

Using lens formula, 

$\dfrac{1}{{{v}_{1}}}-\dfrac{1}{{{u}_{1}}}=\dfrac{1}{{{f}_{1}}}$

Where, object distance, $={{u}_{1}}$.

${{u}_{1}}=-(20+8)=-28cm$.

Image distance $={{v}_{1}}$.

$\Rightarrow \dfrac{1}{{{v}_{1}}}=\dfrac{1}{30}+\dfrac{1}{-28}=\dfrac{-1}{420}$

$\Rightarrow {{v}_{1}}=-420cm$

Hence, the parallel incident beam seems to diverge from a point, that is $=420-4=416cm$ from the left of the centre of the combination of the two lenses. 

Thus, the answer does depend on the combination side at which the parallel beam of light is incident. The notion of effective focal length does not appear to be useful for this combination.

2. An object \[\mathbf{1}.\mathbf{5}\text{ }\mathbf{cm}\] in size is placed on the side of the convex lens in the arrangement (a) above. The distance between the object and the convex lens is \[\mathbf{40cm}\]. Determine the magnification produced by the two-lens system, and the size of the image.

Ans: Consider the given diagram of the previous arrangement as follows:

Here, it is said that,

Height of the image, \[{{h}_{1}}=1.5\text{ }cm\]

Object distance from the side of the convex lens, ${{u}_{1}}=-40cm$

$|{{u}_{1}}|=40cm$

Using lens formula, 

$\dfrac{1}{{{v}_{1}}}-\dfrac{1}{{{u}_{1}}}=\dfrac{1}{{{f}_{1}}}$

$\Rightarrow \dfrac{1}{{{v}_{1}}}=\dfrac{1}{30}+\dfrac{1}{-40}=\dfrac{1}{120}$

$\Rightarrow {{v}_{1}}=120cm$

Magnification, $m=\dfrac{{{v}_{1}}}{|{{u}_{1}}|}$

$\Rightarrow m=\dfrac{120}{40}=3$

Hence, the magnification due to the convex lens is \[3\].

The image made by the convex lens acts as an object for the concave lens.

Using lens formula, 

$\dfrac{1}{{{v}_{2}}}-\dfrac{1}{{{u}_{2}}}=\dfrac{1}{{{f}_{2}}}$

Where, object distance $={{u}_{2}}$.

${{u}_{2}}=120-8=112cm$.

Image distance $={{v}_{2}}$.

$\Rightarrow \dfrac{1}{{{v}_{2}}}=\dfrac{1}{-20}+\dfrac{1}{112}=\dfrac{-92}{2240}$

$\Rightarrow {{v}_{2}}=-\dfrac{2240}{92}cm$

Magnification, $m'=\dfrac{|{{v}_{1}}|}{|{{u}_{1}}|}$

$\Rightarrow m'=\dfrac{2240}{92}\times \dfrac{1}{112}=\dfrac{20}{92}$

Hence, the magnification due to the concave lens is $\dfrac{20}{92}$.

The magnification due to the combination of the two lenses is calculated as:

$m\times m'=3\times \dfrac{20}{92}=0.652$

Thus,

$\dfrac{{{h}_{2}}}{{{h}_{1}}}=0.652$

$\Rightarrow {{h}_{2}}=0.652\times 1.5=0.98cm$

Clearly, the height of the image is \[0.98cm\].

18. At what angle should a ray of light be incident on the face of a prism of refracting angle \[\mathbf{60}{}^\circ \] so that it just suffers total internal reflection at the other face? The refractive index of the material of the prism is \[\mathbf{1}.\mathbf{524}\].

Ans: Consider the given figure below:

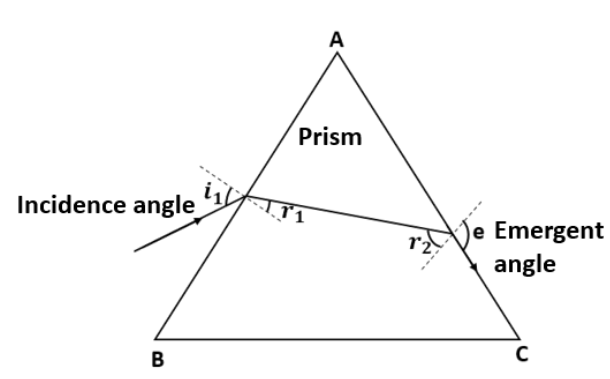
Angle of prism, $A=60{}^\circ $

\[{{i}_{1}}\] is the incidence angle.

${{r}_{2}}$${{r}_{1}}$ is the refracted angle.

 is the angle of incidence at the face AC.

$e$is the emergent angle, $e=90{}^\circ $.

Using Snell’s law,

$\mu =\dfrac{\sin e}{\sin {{r}_{2}}}$

$\Rightarrow 1.524=\dfrac{\sin 90{}^\circ }{\sin {{r}_{2}}}$

$\Rightarrow \sin {{r}_{2}}=0.6562$

$\Rightarrow {{r}_{2}}\approx 41{}^\circ $

For refraction through prism, angle $A={{r}_{1}}+{{r}_{2}}$.

We get,

${{r}_{1}}=A-{{r}_{2}}=60{}^\circ -41{}^\circ $

$\therefore {{r}_{1}}=19{}^\circ $

Using Snell’s law,

$\mu =\dfrac{\sin {{i}_{1}}}{\sin {{r}_{1}}}$

$\Rightarrow 1.524=\dfrac{\sin {{i}_{1}}}{\sin 19{}^\circ }$

$\Rightarrow \sin {{i}_{1}}=0.496$

$\Rightarrow {{i}_{1}}=29.75{}^\circ $

Hence, the incidence angle is $29.75{}^\circ $.

19. For a normal eye, the far point is at infinity and the near point of distinct vision is about \[\mathbf{25cm}\] in front of the eye. The cornea of the eye provides a converging power of about \[\mathbf{40}\] dioptres, and the least converging power of the eye-lens behind the cornea is about \[\mathbf{20}\] dioptres. From this rough data estimate the range of accommodation (i.e., the range of converging power of the eye-lens) of a normal eye.

Ans: Given that,

Least distance of distinct vision, \[d=25\text{ }cm\]

Far point of a normal eye, $d'=\infty $

Converging power of the cornea, ${{P}_{c}}=40D$

Least converging power of the eye-lens, ${{P}_{e}}=20D$

To see the objects at infinity, the eye uses its least converging power. 

Power of the eye-lens, $P={{P}_{c}}+{{P}_{e}}=40+20=60D$

Power of the eye-lens is given as:

$P=\dfrac{1}{f}$

$\Rightarrow f=\dfrac{1}{P}$

$\Rightarrow f=\dfrac{1}{60}m=\dfrac{5}{3}cm$

Object distance, $u=-d=-25cm$

Image distance, $v=f=\dfrac{5}{3}cm$

Using lens formula,

$\dfrac{1}{f'}=\dfrac{1}{v}-\dfrac{1}{u}$

$\Rightarrow \dfrac{1}{f'}=\dfrac{3}{5}-\dfrac{1}{-25}=\dfrac{16}{25}c{{m}^{-1}}$

Power, $P=\dfrac{1}{f'}\times 100$

$\Rightarrow P=\dfrac{16}{25}\times 100=64D$

Power of the eye lens $=64-40=24D$

Hence, the range of accommodation of the eye-lens is from \[20\text{ }D\] to \[24\text{ }D.\]

20. 

1. The angle subtended at the eye by an object is equal to the angle subtended at the eye by the virtual image produced by a magnifying glass. In what sense then does a magnifying glass provide angular magnification?

Ans: Though the image size is larger than the object, the angular size of the image is equivalent to the angular size of the object. 

A magnifying glass supports one seeing the objects closer than the least distance of distinct vision. A closer object produces a larger angular size. 

A magnifying glass gives angular magnification. Without magnification, the object cannot be located closer to the eye. With magnification, the object can be set much closer to the eye.

2. In viewing through a magnifying glass, one usually positions one's eyes very close to the lens. Does angular magnification change if the eye is moved back?

Ans: Yes, the angular magnification varies. 

When the length between the eye and a magnifying glass rises, the angular magnification reduces slightly because the subtended angle at the eye is imperceptibly less than the lenses. 

Image distance does not have any impact on angular magnification.

3. Magnifying power of a simple microscope is inversely proportional to the focal length of the lens. What then stops us from using a convex lens of smaller and smaller focal length and achieving greater and greater magnifying power?

Ans: The convex lens's focal length cannot be reduced by a more significant amount. 

This is because making lenses having tiny focal lengths is not easy. 

Spherical and chromatic aberrations are created by a convex lens having a petite focal length.

4. Why must both the objective and the eyepiece of a compound microscope have short focal lengths?

Ans: The angular magnification produced by the compound microscope’s eyepiece is:

$\left[ \left( \dfrac{25}{{{f}_{e}}} \right)+1 \right]$

Where, ${{f}_{e}}$ is the eyepiece's focal length.

It can be seen that if ${{f}_{e}}$ is small, then angular magnification of the eyepiece will be great.

The angular magnification of the compound microscope’s objective lens is given as $\dfrac{{{f}_{o}}}{{{u}_{o}}}$.

${{u}_{o}}$: Object distance for the objective lens

${{f}_{o}}$: Objective's focal length

The magnification is large when ${{u}_{o}}>{{f}_{o}}$. 

In the case of a microscope, the object is placed close to the objective lens. Hence, the object distance is tiny. 

Since ${{u}_{o}}$ is small, ${{f}_{o}}$ will be smaller. Therefore, ${{f}_{e}}$ and  ${{f}_{o}}$ are both small for the given condition.

5. When viewing through a compound microscope, our eyes should be positioned not on the eyepiece but a short distance away from it for best viewing. Why? How much should be that short distance between the eye and eyepiece?

Ans: We cannot collect much-refracted light when we put our eyes too close to the compound microscope's eyepiece. 

As a result, the field view reduces substantially. Hence, the image's clarity gets blurred. 

The best view of the eye for seeing through a compound microscope is at the eye-ring connected to the eyepiece. The exact location of the eye depends on the separation between the objective lens and the eyepiece.

21. An angular magnification (magnifying power) of \[\mathbf{30X}\] is desired using an objective of focal length \[\mathbf{1}.\mathbf{25}\text{ }\mathbf{cm}\] and an eyepiece of focal length \[\mathbf{5}\text{ }\mathbf{cm}.\] How will you set up the compound microscope?

Ans: Given that,

Focal length of the objective lens, ${{f}_{o}}=1.25cm$

Focal length of the eyepiece, \[{{f}_{e}}=5\text{ }cm\]

Least distance of distinct vision, \[d\text{ }=\text{ }25\text{ }cm\]

Angular magnification of the compound microscope \[=\text{ }30X\]

Total magnifying power of the compound microscope, \[m\text{ = }30\]

The eyepiece’s angular magnification is given by:

${{m}_{e}}=1+\dfrac{d}{{{f}_{e}}}$

\[\Rightarrow {{m}_{e}}=1+\dfrac{25}{5}\]

$\Rightarrow {{m}_{e}}=6$

The objective lens angular magnification is given by:

$m={{m}_{o}}{{m}_{e}}$

$\Rightarrow {{m}_{o}}=\dfrac{m}{{{m}_{e}}}$

\[\Rightarrow {{m}_{o}}=\dfrac{30}{6}=5\]

We have, 

${{m}_{o}}=\dfrac{{{v}_{o}}}{-{{u}_{o}}}$

\[\Rightarrow 5=\dfrac{{{v}_{o}}}{-{{u}_{o}}}\]

\[\Rightarrow {{v}_{o}}=-5{{u}_{o}}\]……(1)

Using lens formula,

$\dfrac{1}{{{f}_{o}}}=\dfrac{1}{{{v}_{o}}}-\dfrac{1}{{{u}_{o}}}$

$\Rightarrow \dfrac{1}{1.25}=\dfrac{1}{-5{{u}_{o}}}-\dfrac{1}{{{u}_{o}}}$

$\Rightarrow {{u}_{o}}=-1.5cm$

And, \[{{v}_{o}}=-5{{u}_{o}}=-5\times -1.5=7.5cm\]

The object should be placed \[1.5cm\] away from the objective lens to get the desired magnification.

Using lens formula,

$\dfrac{1}{{{f}_{e}}}=\dfrac{1}{{{v}_{e}}}-\dfrac{1}{{{u}_{e}}}$

Where, ${{v}_{e}}=-d=-25cm$

$\Rightarrow \dfrac{1}{5}=\dfrac{1}{-25}-\dfrac{1}{{{u}_{e}}}$

$\Rightarrow {{u}_{e}}=-4.17cm$

Separation between the eyepiece and the objective lens $=|{{u}_{e}}|+|{{v}_{o}}|$

$|{{u}_{e}}|+|{{v}_{o}}|=4.17+7.5=11.67cm$

Therefore, the separation between the eyepiece and the objective lens should be \[11.67cm.\]

22. A Cassegrain telescope uses two mirrors as shown in figure. Such a telescope is built with the mirrors \[\mathbf{20}\text{ }\mathbf{mm}\] apart. If the radius of curvature of the large mirror is \[\mathbf{220}\text{ }\mathbf{mm}\] and these all mirror is \[\mathbf{140mm}\], where will the final image of an object at infinity be?

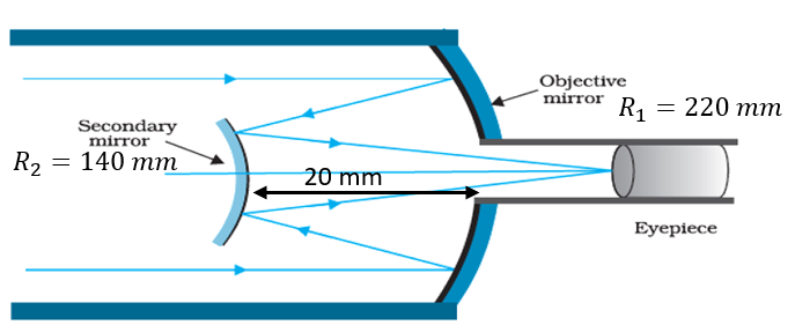
Ans: A Cassegrain telescope contains two mirrors, one is objective mirror and second one is secondary mirror. We need to find the distance of final image from secondary mirror. 

Given: distance between the objective mirror and the secondary mirror, \[d=20mm\]

Radius of curvature of the objective mirror, \[{{R}_{1}}=220\text{ }mm\]

Hence, objective mirror’s focal length, ${{f}_{1}}=\dfrac{{{R}_{1}}}{2}=110mm$

Secondary mirror’s radius of curvature, \[{{R}_{2}}=140\text{ }mm\]

Secondary mirror’s focal length, ${{f}_{2}}=\dfrac{{{R}_{2}}}{2}=70mm$

The image of an object set at infinity, made by the objective mirror, will serve as a virtual object for the secondary mirror.

Hence, the secondary mirror’s virtual object distance, $u={{f}_{1}}-d$

$\Rightarrow u=110-20=90mm$

Using mirror formula,

$\dfrac{1}{u}+\dfrac{1}{v}=\dfrac{1}{{{f}_{2}}}$

$\Rightarrow \dfrac{1}{v}=\dfrac{1}{{{f}_{2}}}-\dfrac{1}{u}$

Now, we put given values,

$\Rightarrow \dfrac{1}{v}=\dfrac{1}{70}-\dfrac{1}{90}$

$\Rightarrow \dfrac{1}{v}=\dfrac{9-7}{630}$

$\Rightarrow \dfrac{1}{v}=\dfrac{2}{630}$

$\Rightarrow v=315mm$

Clearly, the final image will be made \[315\text{ }mm\] away from the secondary mirror.

23. Figure shows an equiconvex lens (of refractive index \[\mathbf{1}.\mathbf{50}\]) in contact with a liquid layer on top of a plane mirror. A small needle with its tip on the principal axis is moved along the axis until its inverted image is found at the position of the needle. The distance of the needle from the lens is measured to be \[\mathbf{45}.\mathbf{0}\text{ }\mathbf{cm}\]. The liquid is removed and the experiment is repeated. The new distance is measured to be \[\mathbf{30}.\mathbf{0}\text{ }\mathbf{cm}\]. What is the refractive index of the liquid?

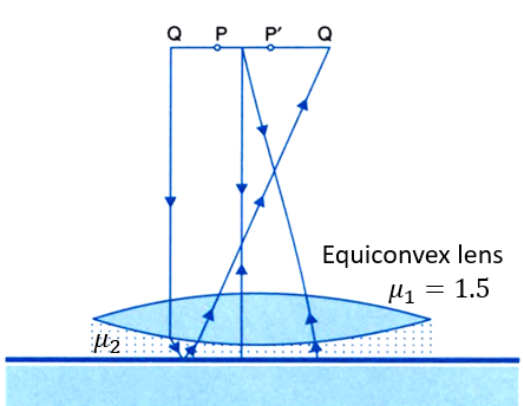
Ans: An equiconvex lens is in touch with a liquid layer on a plane mirror top. A small needle placed on the principal axis is moved along the axis until its inverted image will be at the position of the needle.

Convex lens’ focal length, \[{{f}_{1}}=30\text{ }cm\]

The liquid will behave as a mirror. 

Liquid’s focal length \[=\text{ }f{}_{2}\]

System’s focal length, \[f\text{ }=\text{ }45\text{ }cm\]

The equivalent focal length is given as:

$\dfrac{1}{f}=\dfrac{1}{{{f}_{1}}}+\dfrac{1}{{{f}_{2}}}$

$\Rightarrow \dfrac{1}{{{f}_{2}}}=\dfrac{1}{f}-\dfrac{1}{{{f}_{1}}}$

$\Rightarrow \dfrac{1}{{{f}_{2}}}=\dfrac{1}{45}-\dfrac{1}{30}=-\dfrac{1}{90}$

$\therefore {{f}_{2}}=-90cm$

Let the lens’s refractive index be ${{\mu }_{1}}$ and curvature radius of one surface be \[R.\]

Hence, the curvature radius of the other surface is \[\text{ }R\].

We use,

$\dfrac{1}{{{f}_{1}}}=\left( {{\mu }_{1}}-1 \right)\left[ \dfrac{1}{R}-\dfrac{1}{-R} \right]$

$\Rightarrow \dfrac{1}{30}=\left( 1.5-1 \right)\left[ \dfrac{2}{R} \right]$

$\therefore R=30cm$

Let ${{\mu }_{2}}$ be the liquid’s refractive index.

Liquid’s curvature radius on the side of the plane mirror $=\infty $.

Curvature radius of the liquid on the side of the lens, \[R=-\text{ }30\text{ }cm\].

We use,

$\dfrac{1}{{{f}_{2}}}=\left( {{\mu }_{2}}-1 \right)\left[ \dfrac{1}{R}-\dfrac{1}{\infty } \right]$

$\Rightarrow \dfrac{-1}{90}=\left( {{\mu }_{2}}-1 \right)\left[ \dfrac{1}{-30}-0 \right]$

$\Rightarrow \left( {{\mu }_{2}}-1 \right)=\dfrac{1}{3}$

$\Rightarrow {{\mu }_{2}}=1.33$

Clearly, the liquid’s refractive index is \[1.33.\]

Relevance of Ray Optics in Future

Ray optics is a crucial chapter in the class 12 syllabus. Not only will there be a substantial number of questions from this chapter in the school examination, but it is also vital for competitive exams later on. This chapter deals with how light reflects from objects or surfaces, the energy of electromagnetic waves, etc. the study of optics is a very important lesson as it is used heavily in several instruments and technologies all over the world. It is very important for students who wish to study physics later on as well as for students who wish to appear in competitive exams in the future. 

Why is it Important to Study Important Questions for Ray Optics Class 12?

Class 12 Ray Optics Important questions are very important for students because it will help them to prepare properly for the exams. The study notes, revision notes, and the important questions are all carefully researched and compiled to make sure that students can easily understand the chapter. It will help them to read the chapter carefully, make their own notes, and practice the questions so that they can save precious time during the exams, recognise the questions easily, solve them and fetch good marks. 

How Will Studying from Vedantu’s Important Questions for Ray Optics Class 12 CBSE Help Students?

Vedantu is an online platform which provides study materials for students. It is the one-stop destination for all students. The study notes and important questions are now also available in downloadable PDFs so that students can refer to the notes or questions anywhere and anytime they want. 

The study notes, revision notes, and important questions of ray optics class 12 are written by our experts, especially for our students. These notes and questions are written after careful research and evaluation of the syllabus topics as given by the board and also based on the previous years’ question papers. 

Our experts who write these notes have immense knowledge about the respective chapters given so that they can easily and properly explain all the given topics.  We also make sure that all possible questions are given so that students can be best prepared before examinations so that they can score good marks. 

How to Study for Ray Optics from Vedantu Notes? 

The following is the proforma we suggest our students follow while studying from Vedantu’s notes and important questions for CBSE class 12 physics ray optics -

• Study the chapter carefully from Vedantu’s class notes. They are now available in downloadable PDF format so that students can study anywhere anytime. 

• Draw and practice the given diagrams for a better understanding of the topics. 

• Take help from online classes being conducted on the Vedantu website.

• Solve the important questions of ray optics class 12 CBSE for self-evaluation.

• Keep practising to make sure that all the questions and concepts are familiar before examinations. 

Introduction to Ray Optics

What is Ray?

In optics, a ray is referred to as an idealized model of light which is obtained by using a line perpendicular to the wavefronts of the actual light ray. The ray has to point to the direction of the energy flow. 

Topics Under Ray Optics

• Rectilinear Propagation of Light 

• Reflection of Light

• Spherical Mirrors

• Refraction of Light 

• Thin Lens

• Prism 

• Chromatic and Monochromatic Aberrations in Lens

• Optical Instruments 

Let Us Discuss the Above Briefly. 

• Rectilinear Propagation of Light - This refers to the propensity of light that travels along a straight line without any interference. 

• Reflection of Light - Reflection of light refers to the change in direction of wavelength between two different mediums such that the light way returns to its source of origin. 

• Spherical Mirrors - A spherical mirror refers to a mirror that has the shape of a piece cut out of a spherical shape. In this chapter, we are going to learn about the centre of curvature, normal, radius of curvature, pole of a mirror, principal axis, and also paraxial rays.

• Refraction of Light - Refraction refers to the bending of light while it passes through one transparent medium to another. In this chapter, we are going to learn about - reflective index, the law of refraction or Snell’s Law, refraction through a curved surface, total internal reflection, double refraction from a plain surface, single refraction from a plain surface, the relation between object distance and image distance refraction, and linear magnification of spherical refracting surfaces.

• Lens - There are mainly two types of lenses - convex and concave lenses. In this chapter, we are going to learn about certain features of lenses like - centre of curvature, the radius of curvature, principal axis, optical centre, principal foci, first principal focus F1, second principal focus F2, and focal length.

• Prism - Prism refers to the optical transparent element which refracts light. At least one side of the prism has to be angled, it cannot have two parallel surfaces. In this chapter, we have to concentrate on the features, importance, and various formulas of a prism. 

• Chromatic and Monochromatic Aberrations - Chromatic Aberrations refer to the effect which is produced due to the dispersion of different wavelengths of light through different angles. This leads to the failure of focusing the lens. 

On the other hand, Monochromatic Aberrations refer to the distortion created by quasi-monochromatic lights. 

• Optical Instruments - We use several optical instruments in our daily lives. These instruments are made after applying the properties of reflection, refraction, and dispersion, and other properties and laws of optics. 

An optical instrument refers to a device that helps to enhance images for viewing or for finding out their properties. 

• Eye - Our eyes are a very important yet unique example of optical instruments. Our eyes are filled with many interconnected nerve fibres and cells which sense the intensity of light and colour. The retina of our eye contains nerve cells that are rod-like or cone-like and that senses light, converts it into electrical signals, and sends it to the brain through optic nerves. 

• Simple Microscope - A simple microscope is a magnifying glass that is made out of a converging lens with a small focal length. When a microscope is held close to the eye, we can see a magnified erect but virtual image of the actual object. However, a compound microscope is a little more complex with two converging lenses, an eyepiece with moderate focal length, and a large aperture. It also has an objective lens of small focal length and short aperture.  Also, the ciliary muscles present in our eyes help to modify the shape and focal length of the lens inside the eyes.  

• Telescope - Telescope is a device that allows people to look at objects which are very far away. Telescopes are usually used for observing planets, stars, etc, in the solar system. Telescopes have objective lenses with large aperture and considerable focal length along with an eye lens that has a small focal length and aperture. This helps people to see things which are far away from us. 

Conclusion 

To conclude, we can say that ray optics is a very important chapter on which students should pay a lot of attention and effort. They can take help from Vedantu’s study notes, revision notes, and the physics class 12 ray optics important questions. This will help students to study better, prepare themselves for every type of question that might appear in the examinations, and fetch good marks in the finals. Also, it is a very important chapter for various competitive exams so students will be able to refer to these notes later on from our website. 

Important Related Links for CBSE Class 12 Physics