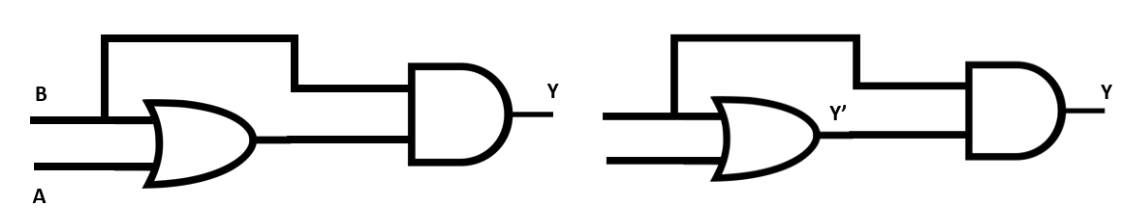Semiconductor Electronic Material Devices And Simple Circuits Class 12 important questions with answers PDF download



FAQs on CBSE Important Questions for Class 12 Physics Semiconductor Electronic Material Devices And Simple Circuits - 2025-26
1. What are the most important topics in Chapter 14, Semiconductor Electronics, for the CBSE Class 12 board exam 2025-26?
For the CBSE Class 12 board exam, the most important topics from this chapter include:
- Energy Bands: Differentiating between conductors, insulators, and semiconductors.
- Semiconductor Types: Intrinsic vs. Extrinsic, p-type vs. n-type, and the concept of doping.
- p-n Junction Diode: Formation, biasing (forward and reverse), and V-I characteristics.
- Diode Applications: Working principles of Half-wave and Full-wave rectifiers.
- Special Purpose Diodes: Zener diode as a voltage regulator, Photodiode, and LED.
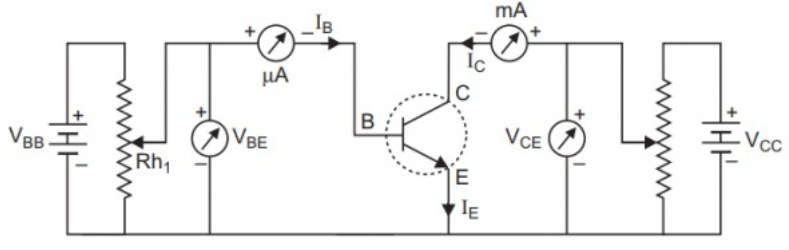
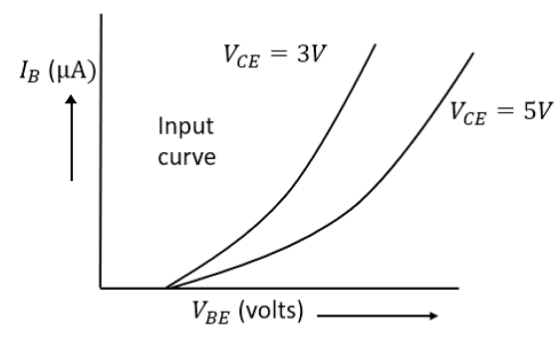
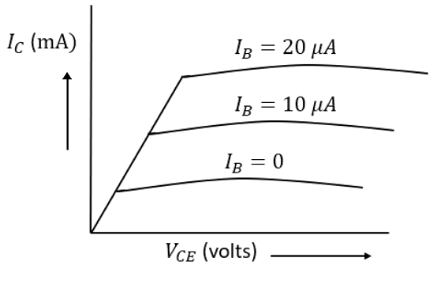
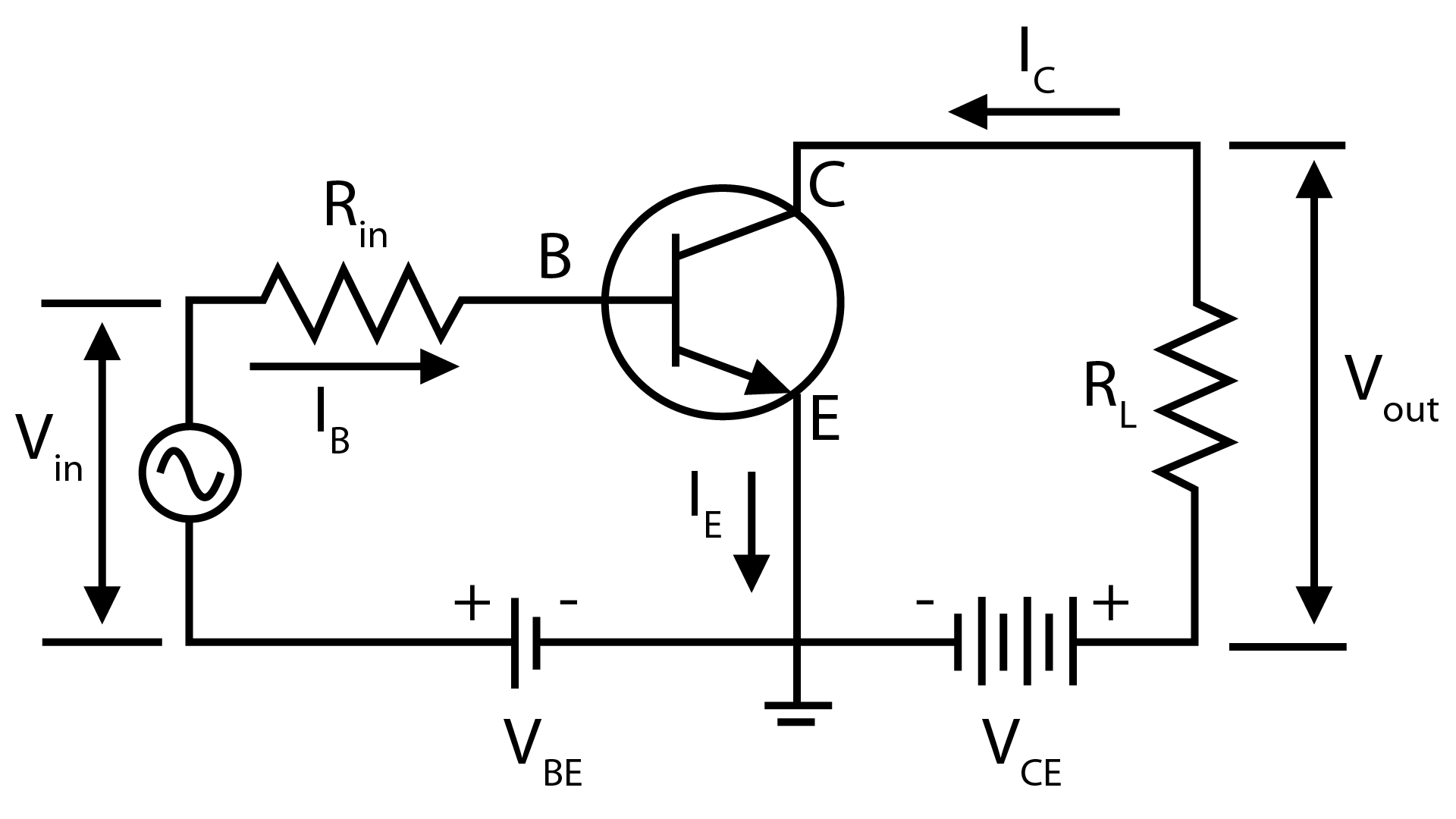
- Transistors: Basic action, characteristics of a CE amplifier, and its use as a switch.
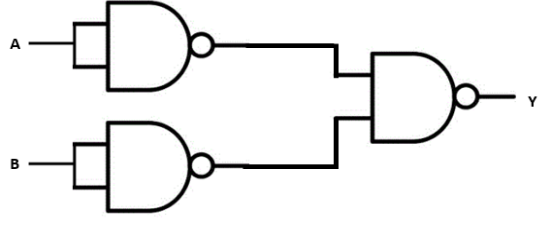
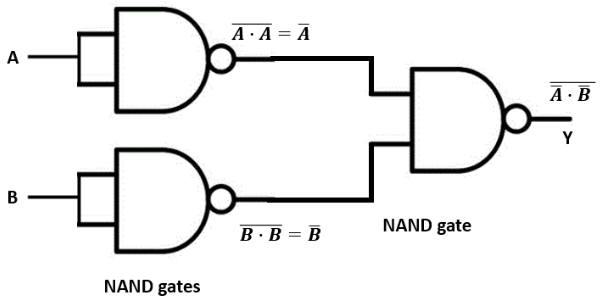
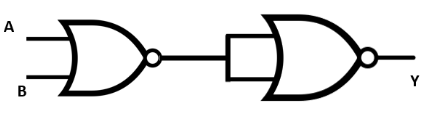
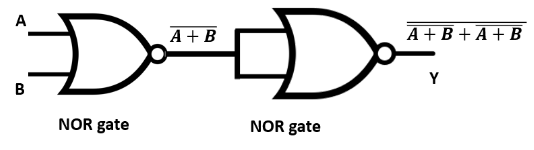
- Logic Gates: Understanding the operation and truth tables for AND, OR, NOT, NAND, and NOR gates.
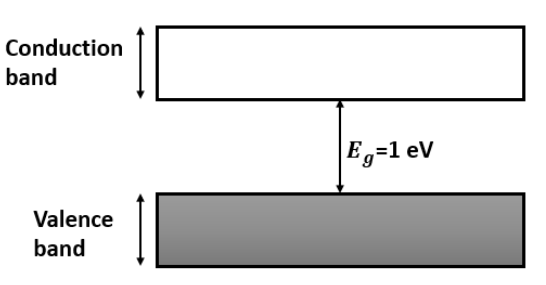
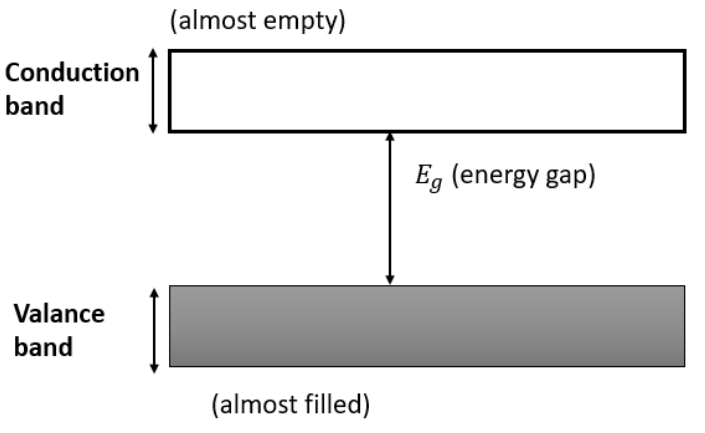
2. How can we distinguish between conductors, insulators, and semiconductors using the energy band theory?
Based on the energy band theory, these materials are distinguished by the energy gap (Eg) between their valence and conduction bands:
- In conductors, the valence band and conduction band overlap, so there is no energy gap. This allows electrons to move freely, resulting in high conductivity.
- In insulators, there is a very large energy gap (Eg > 3 eV) between the valence and conduction bands. Electrons cannot easily jump to the conduction band, making them poor conductors of electricity.
- In semiconductors, the energy gap is small (Eg < 3 eV). At room temperature, some electrons gain enough thermal energy to jump to the conduction band, allowing for moderate conductivity which can be controlled by doping.
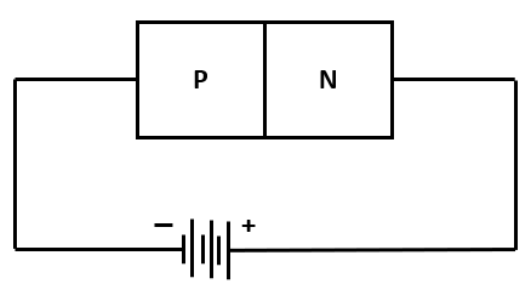
3. What is a p-n junction? Explain the formation of the depletion region and potential barrier.
A p-n junction is formed when a p-type semiconductor is brought into close contact with an n-type semiconductor. During its formation, electrons from the n-region diffuse to the p-region, and holes from the p-region diffuse to the n-region due to the concentration gradient. This diffusion creates an area near the junction that is depleted of free charge carriers, known as the depletion region. The accumulation of immobile positive ions in the n-region and negative ions in the p-region sets up an electric field and a potential difference across the junction. This potential difference, which opposes further diffusion of charge carriers, is called the potential barrier.
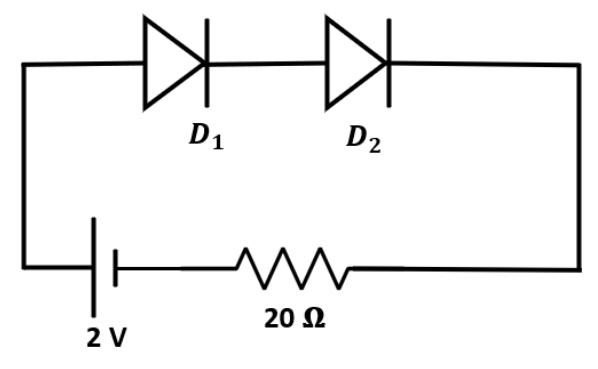
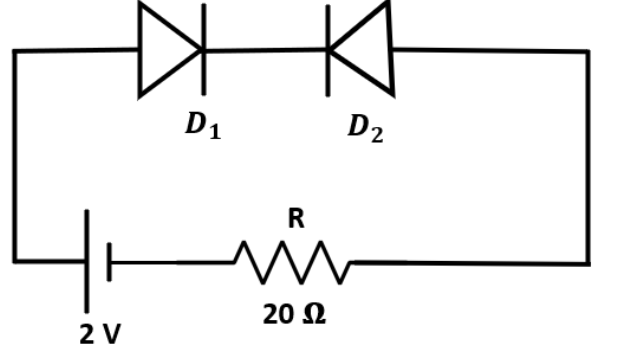
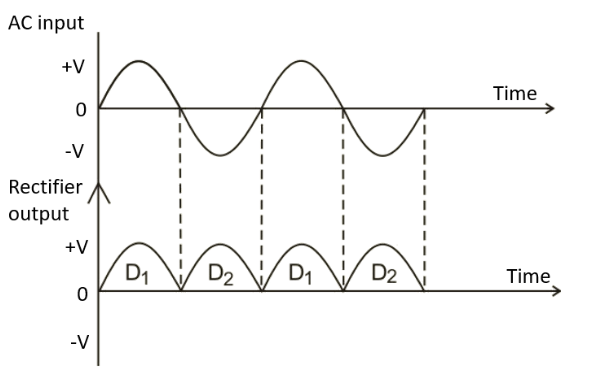
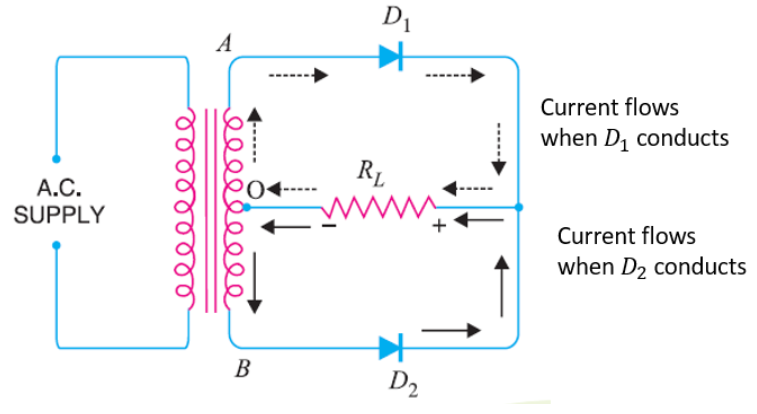
4. Explain the working of a full-wave rectifier and state its output frequency for a 50 Hz input AC signal.
A full-wave rectifier converts both halves of an AC input signal into a pulsating DC output. It typically uses two diodes and a center-tapped transformer.
- During the positive half-cycle of the AC input, diode D1 is forward-biased and conducts, while D2 is reverse-biased and does not. Current flows through the load resistor.
- During the negative half-cycle, diode D2 becomes forward-biased and conducts, while D1 is reverse-biased. Current again flows through the load resistor in the same direction.
Since both halves of the input cycle are utilised, the output frequency is twice the input frequency. For an input of 50 Hz, the output frequency of a full-wave rectifier will be 100 Hz.
5. What is the fundamental difference between forward biasing and reverse biasing of a p-n junction diode?
The fundamental difference lies in the connection to the voltage source and its effect on the depletion region:
- Forward Biasing: The p-type region is connected to the positive terminal and the n-type region to the negative terminal of the battery. This applied voltage opposes the potential barrier, reducing the width of the depletion region and allowing a large current to flow due to majority charge carriers. The diode offers very low resistance.
- Reverse Biasing: The p-type region is connected to the negative terminal and the n-type region to the positive terminal. This applied voltage supports the potential barrier, increasing the width of the depletion region and blocking the flow of majority carriers. Only a very small current (due to minority carriers) flows, and the diode offers very high resistance.
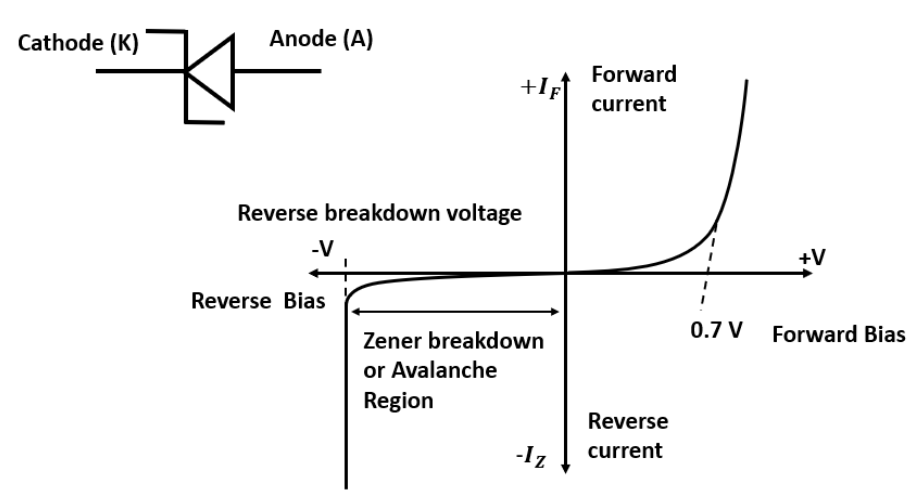
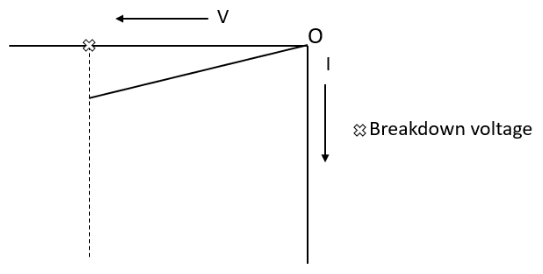
6. Describe the V-I characteristics of a Zener diode and explain its role as a voltage regulator.
The V-I characteristics of a Zener diode are similar to a normal p-n junction diode in forward bias. However, in reverse bias, it exhibits a controlled breakdown at a specific voltage called the Zener voltage (Vz). After this breakdown, the voltage across the diode remains nearly constant even as the current changes significantly. This property allows it to be used as a voltage regulator. When connected in reverse bias across a fluctuating voltage source, it maintains a constant output voltage equal to Vz across the load, absorbing any excess voltage.
7. A transistor has a current amplification factor (β) of 100 and a base current (IB) of 20µA. For a common-emitter configuration, calculate the collector current (IC) and emitter current (IE).
The calculations are as follows:
1. To find Collector Current (IC):
The current amplification factor (β) is given by the formula β = IC / IB.
Therefore, IC = β × IB = 100 × 20 µA = 2000 µA or 2 mA.
2. To find Emitter Current (IE):
The emitter current is the sum of the base current and the collector current: IE = IB + IC.
IE = 20 µA + 2000 µA = 2020 µA or 2.02 mA.
8. What are the most important types of numerical problems from the Semiconductors chapter for the Class 12 Physics exam?
For the Class 12 exam, you should focus on numericals based on:
- Doping and Carrier Concentration: Calculating electron and hole concentrations in doped semiconductors using the law of mass action (nenh = ni2).
- Transistor Parameters: Problems involving current gain (α and β), emitter, base, and collector currents (IE = IB + IC), and voltage/power gain in amplifiers.
- Diode Equation: Calculating forward current or dynamic resistance using the diode current equation.
- Photodiode and Band Gap Energy: Determining if a photodiode can detect a specific wavelength of light based on its band gap energy (E = hc/λ).
9. Explain why the base region of a transistor must be very thin and lightly doped for effective amplification.
The base region of a transistor is made thin and lightly doped to ensure most of the charge carriers from the emitter pass through to the collector.
- Thin Base: A thin base region reduces the transit time for charge carriers, minimising the chance for them to recombine with the majority carriers in the base. This ensures a high collector current.
- Light Doping: A low concentration of majority carriers in the base means there are fewer carriers available for recombination with the injected emitter carriers. This results in a very small base current (IB) and a large collector current (IC), which is essential for achieving a high current amplification factor (β = IC/IB).
10. A photodiode is fabricated from a semiconductor with a band gap of 2.0 eV. Can it detect light of wavelength 6000 Å? Justify your answer with calculations.
Yes, the photodiode can detect this light. Here's the justification:
1. First, calculate the energy (E) of the incident light using the formula E = hc/λ.
- Wavelength, λ = 6000 Å = 6000 × 10-10 m
- Planck's constant, h ≈ 6.63 × 10-34 J·s
- Speed of light, c = 3 × 108 m/s
2. Substitute the values: E = (6.63 × 10-34 × 3 × 108) / (6000 × 10-10) J ≈ 3.315 × 10-19 J.
3. Convert this energy to electron volts (eV) by dividing by 1.6 × 10-19 J/eV: E ≈ 3.315 × 10-19 / 1.6 × 10-19 ≈ 2.07 eV.
4. Conclusion: For a photodiode to detect light, the energy of the incident photons (E) must be greater than or equal to the semiconductor's band gap (Eg). Since the incident light's energy (2.07 eV) is greater than the band gap (2.0 eV), the photodiode can absorb the photon and generate an electron-hole pair, thus detecting the signal.
11. In a common-emitter (CE) amplifier, why is the output voltage 180° out of phase with the input voltage?
This 180° phase reversal in a CE amplifier occurs due to the way the circuit operates. The output voltage is measured at the collector (VCE), which is given by the equation VCE = VCC - ICRC, where VCC is the supply voltage and RC is the collector resistor. When a positive half-cycle of the input AC signal is applied to the base, the forward bias of the emitter-base junction increases. This causes a large increase in the collector current (IC). As IC increases, the voltage drop across RC (ICRC) also increases. Consequently, the output voltage VCE decreases. This means a positive input signal results in a negative-going output signal, creating the 180° phase shift.
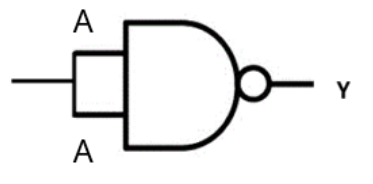
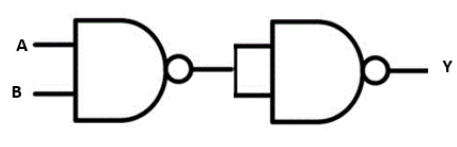
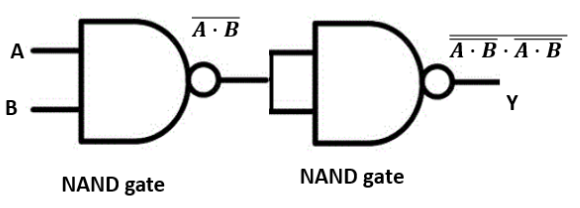
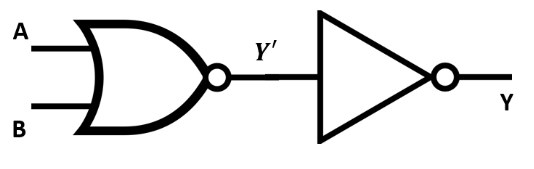
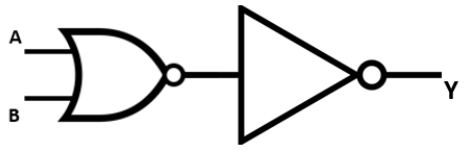
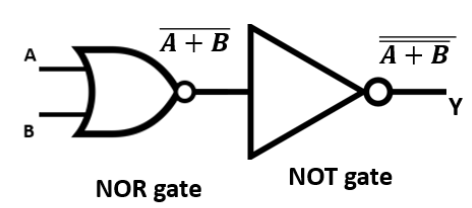
12. How do you identify the logic operation performed by a combination of basic logic gates, for example, the output of a NAND gate fed into a NOT gate?
To identify the logic operation, you should trace the Boolean expression step-by-step.
For the given example (NAND followed by NOT):
- Let the inputs be A and B.
- The output of the NAND gate is Y1 = (A.B)'.
- This output Y1 is then fed into a NOT gate.
- The final output Y will be the negation of Y1, so Y = (Y1)' = ((A.B)')'.
Using De Morgan's theorems or the property of double negation ((X)')' = X, we find that Y = A.B. This Boolean expression corresponds to the AND gate. Therefore, the combination performs the function of an AND gate.
13. If a pure silicon crystal is doped simultaneously with an equal concentration of Arsenic (pentavalent) and Indium (trivalent) atoms, what type of semiconductor will it become?
The resulting semiconductor will behave almost like an intrinsic (pure) semiconductor. This is because the pentavalent Arsenic atoms are donors, providing extra electrons, while the trivalent Indium atoms are acceptors, creating holes. When their concentrations are equal, each free electron donated by an Arsenic atom will be captured by a hole created by an Indium atom. This process, known as compensation, effectively neutralizes the effect of both dopants, leaving the charge carrier concentration nearly equal to that of a pure semiconductor.